Five-phase space vector carrier-based PWM for third harmonic injection

Abstract

Five-phase AC drives allow a third harmonic voltage to be fed into the stator winding – in addition to the fundamental voltage – to generate a third harmonic magnetic air gap field. This allows the generation of an additional small constant torque. Furthermore, the undesirable saturation harmonics that occur with saturated iron can be compensated. The desired third harmonic voltage is commonly generated via time-consuming space vector PWM algorithms, which are not well-suited for real-time application, or via look-up tables, which require an increased storage capacity. In our case, the desired third harmonic voltage is generated in the five-phase voltages by adding a non-sinusoidal zero-sequence voltage with five times the fundamental frequency to the fundamental voltage reference signals in carrier-based pulse width modulation (PWM) with a constant switching frequency. This is equivalent to a space vector PWM method (SVPWM) and avoids a significantly high calculation effort. The PWM algorithm programmed in MATLAB in real time allows the fast generation of a third harmonic voltage per phase with freely definable amplitude and phase shift without requiring a lot of storage capacity.

Zusammenfassung

Fünfphasige Drehstromantriebe erlauben es, neben der Spannungsgrundschwingung eine dritte harmonische Oberschwingungsspannung in die Statorwicklung zur Erzeugung einer dritten magnetischen Luftspalt-Feldoberwelle einzuspeisen. Damit kann ein zusätzliches kleines konstantes Drehmoment erzeugt werden. Weiterhin kann damit die bei gesättigtem Eisen auftretende, unerwünschte Sättigungsoberschwingung kompensiert werden. Die gewünschte dritte harmonische Spannung wird üblicherweise über zeitaufwändige Raumzeigermodulations-Algorithmen erzeugt, die für Echtzeitanwendungen nicht gut geeignet sind, oder über Nachschlagetabellen, die eine erhöhte Speicherkapazität erfordern. In unserem Fall wird die gewünschte dritte Spannungsoberschwingung in den fünf Phasenspannungen durch das Hinzufügen einer nichtsinusförmigen Nullspannung mit fünffacher Grundfrequenz zur grundfrequenter Spannungsvorgabe bei der trägerbasierten Pulsweitenmodulation (PWM) mit konstanter Schaltfrequenz erzeugt. Dies entspricht einer PWM mit dem Raumzeigerverfahren (Space Vector–PWM: SVPWM) und vermeidet einen deutlich erhöhten Rechnungsaufwand. Der in MATLAB programmierte PWM-Algorithmus in Echtzeit gestattet die schnelle Erzeugung einer dritten Spannungsoberschwingung je Phase mit frei einstellbarer Amplitude und Phasenlage ohne großen Speicherplatzbedarf.

1 Introduction

Although three-phase drives remain the standard in most applications, research on multiphase drives has gained momentum due to their higher efficiency and higher torque-per-volume ratio, compared to their three-phase counterparts [1, 2]. A further factor favouring the use of a phase count bigger than three is the fact that variable speed drives operate with power electronics without restriction of the three phases from the public grid. The additional degree of freedom regarding the voltage generation demands appropriate control and modulation strategies suited for real-time application when operating multiphase drives. This paper focuses on the injection of an arbitrary $3^{\text{rd}}$ harmonic voltage, which allows, for example, to maximise the output torque for induction machines and PM synchronous machines or to compensate saturation harmonics.

The most common strategy for the voltage generation is the Pulse Width Modulation (PWM) of the DC-link voltage. Widely used switching strategies for the power electronics are the continuous carrier-based modulation strategies with (1) a sinusoidal modulation signal [3, 4], (2) Fifth Harmonic Injection (FHI) [3, 4] and (3) Space Vector Modulation (SVM) with its continuous (SVPWM) and discontinuous (DPWM) variants [5,6,7,8,9,10,11,12,13,14,15,16]. The carrier-based PWM with a reference modulation signal is similar to the three-phase system, where the reference signal (mostly a sine wave function) is compared to a high frequency carrier signal of fixed frequency to determine the switching instants of the ten power electronic switches. To increase the output voltage amplitude and thus improve the DC-link voltage utilisation, [4] expands for multiphase systems the concept of injecting a harmonic signal to the sinusoidal reference signal to achieve a peak reduction of the modulation signals. For three-phase systems, the $3^{\text{rd}}$ harmonic is injected, as it cancels out in the line-to-line voltages and does not lead to additional stator currents in Y‑connected windings. For a five-phase system, it is the $5^{\text{th}}$ harmonic that yields the same behaviour. In [3], the method for optimal amplitude and phase of the $5^{\text{th}}$ harmonic component which achieve the largest peak reduction for improved DC voltage utilisation is described.

The SVPWM algorithm in [17] for three-phase systems selects the neighbouring space vectors of a needed reference voltage space vector, which have $2^{3}=8$ discrete values, to approximate, by selected conducting time intervals of the power switches, the reference voltage space vector. In [5,6,7,8,9,10,11,12,13,14,15,16] strategies implementing neighbouring space vector values of a five-phase system by using different combinations of $2^{5}=32$ discrete space vector values are discussed. The preferred method selects four neighbouring discrete space vector values to nullify an unwanted $3^{\text{rd}}$ harmonic voltage component [5, 7, 11, 12, 18]. Further development on PWM strategies focused on methods to allow a $3^{\text{rd}}$ harmonic voltage in order to generate an additional and constant torque component, as it was mentioned above. Although different in detail, all these described methods [8, 13, 18,19,20,21,22,23] show rather complex algorithms for the selection of suitable discrete space vector values, the calculation of conduction time intervals of the power switches and lastly the definition of the switching order for minimal switching losses. These steps are computationally time-consuming and thus not well-suited for real-time application. Methods which are in favour for online application follow different approaches, such as the definition of modulation functions based on the calculation of duty cycles [11, 15] or the use of look-up tables by running the algorithm offline and storing the resulting data [18, 20]. However, though faster, the latter solution requires more storage capacity.

Only a few publications, [9, 16] for a five-phase or [24] for a nine-phase system, mention the method of adding the triangle zero-sequence signal as an equivalent of SVPWM, as it is done for three-phase systems. This strategy is faster and simpler to be implemented online and does not require much storage capacity. In [9, 16] the focus is on the peak reduction of the fundamental reference signal for sinusoidal feeding of the drive to improve the utilisation of the DC-link voltage. By injecting an arbitrary $3^{\text{rd}}$ harmonic component in addition to the fundamental component, our contribution expands the idea by adding a non-sinusoidal zero-sequence signal for an additional injection of an arbitrary $3^{\text{rd}}$ harmonic component.

Sect. 2 briefly describes the concept of three-phase space vector modulation and its equivalence to the addition of a $3^{\text{rd}}$ harmonic triangle zero-sequence signal. Sect. 3 defines the five-phase voltage reference signals, used as input for the considered algorithm. Sect. 4 describes the differences and challenges of five-phase space vector PWM compared to a three-phase system, and introduces the SVPWM algorithm in [18]. Sect. 5 explains how the modulation signals are generated for the carrier-based PWM, based on the addition of a non-sinusoidal zero-sequence signal, and for the SVPWM algorithm of [18] with MATLAB. Sect. 6 compares the resulting modulation signals of both modulation schemes for three different examples and performs a Fast Fourier Transform (FFT) analysis on the zero-sequence signals.

2 Three-phase space vector modulation

The concept of SVM [17] is based on the fact that the switching combinations of a three-phase inverter can be considered to be discrete space vectors in the $\alpha\beta$ plane gained by applying Clarke’s transformation matrix. With $2^{3}=8$ possible combinations, the $\alpha\beta$ plane is divided into six sectors by six active discrete space vectors, which are separated by $\frac{{360}^{\circ}}{2\cdot 3}={60}^{\circ}$, respectively. The remaining two switching combinations are associated with zero space vectors (either all three upper or lower power switches are conducting) giving eight different discrete space vector values.

The needed reference voltage space vector is used as input. First, the sector in which the reference space vector is located, is identified. From that, the two active discrete space vectors neighbouring that sector are determined. The conduction time intervals $t_{1}$ and $t_{2}$ of the power switches for both space vectors are calculated to approximate the reference space vector. If the sum $t_{1}+t_{2}$ is smaller than the predefined sampling period $T_{\text{s}}$, the remaining time $t_{0}=T_{\text{s}}-(t_{1}+t_{2})$ is used for operating the zero space vectors. The allocation of $t_{0}$ to each of the two zero space vectors is the “degree of freedom”, resulting from SVM, from which different modulation schemes arise. These schemes divided into groups are a) the continuous symmetrical SVPWM and b) the discontinuous DPWM. In both cases, the algorithm is computationally time-consuming and not well-suited for real-time applications. Hence, [25] introduced the idea of an equivalent modulation scheme, based on carrier-based PWM, where a triangle zero-sequence signal

$$u_{0}=-\frac{1}{2}\cdot(u_{\text{ref,max}}+u_{\text{ref,min}})$$

(1)

is added to the reference phase voltage signals $u_{\text{ref,U}}$, $u_{\text{ref,V}}$ and $u_{\text{ref,W}}$, where $u_{\text{ref,max}}=\text{max}(u_{\text{ref,U}},u_{\text{ref,V}},$ $u_{\text{ref,W}}{)}$ and $u_{\text{ref,min}}=\text{min}(u_{\text{ref,U}},u_{\text{ref,V}},u_{\text{ref,W}})$ holds, in order to determine the modulation signals

$$u_{\text{mod},x}=u_{\text{ref},x}+u_{0}\quad\text{for}\quad x=\text{U},\text{V}\quad\text{and}\quad\text{W}.$$

(2)

The zero-sequence $u_{0}$ signal has a frequency three times higher than the fundamental frequency $f_{1}$ and does not have any impact on the line-to-line voltages as it cancels out according to u_mod,U − u_mod,V = u_ref,U − u_ref,V + u₀ − u₀. This solution is a good alternative due to its simplicity and fast implementation and is used in the following for five-phase drives.

3 Reference signals

For a five-phase drive ($m=5$), according to (2), five reference signals $u_{\text{ref},x}$ are introduced per phase:

$$\begin{aligned}u_{\text{ref},x} = {}& m_{\text{a,1}}\cdot\text{cos}\left(\omega_{1}t-n_{x}\cdot\frac{2\pi}{5}\right)\\& +m_{\text{a,3}}\cdot\text{cos}\left(3\cdot\omega_{1}t-3\cdot n_{x}\cdot\frac{2\pi}{5}-\varphi_{3}\right).\end{aligned}$$

(3a)

$$\begin{aligned} & x=\text{a, b, c, d, e (five phases)}\end{aligned}$$

(3b)

$$\begin{aligned} & n_{x}:n_{\text{a}}=0,n_{\text{b}}=1,n_{\text{c}}=2,n_{\text{d}}=3,n_{\text{e}}=4.\end{aligned}$$

(3c)

In (3), the electric fundamental angular frequency is $\omega_{1}=2\pi\cdot f_{1}$, and $3\omega_{1}$ constitutes the $3^{\text{rd}}$ harmonic. Both $\omega_{1}$- and $3\omega_{1}$-voltage components form a symmetrical five-phase system in (3), where the phases are phase-shifted to each other either by $\frac{2\pi}{5}$ or $3\cdot\frac{2\pi}{5}$ respectively to generate either the fundamental or the $3^{\text{rd}}$ harmonic voltage component. The $3^{\text{rd}}$ harmonic component is phase-shifted with respect to the fundamental component by $\varphi_{3}$. The amplitudes of both reference components are described by the amplitude modulation ratios $m_{\text{a,1}}$ and $m_{\text{a,3}}$, which refer the sinusoidal reference phase voltage amplitudes $\hat{U}_{\text{ref,1}}$ and $\hat{U}_{\text{ref,3}}$ to half the DC-link voltage $\frac{U_{\text{DC}}}{2}$ (4). Therefore, the reference and modulation signals are given in p.u..

$$m_{\text{a},i}=\frac{\hat{U}_{\text{ref},i}}{U_{\text{DC}}/2}\quad\text{with}\quad i=1\quad\text{and}\quad 3.$$

(4)

4 Five-phase space vector modulation

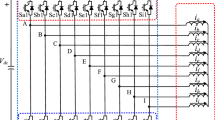
Fig. 1 shows the circuit for a five-phase two-level Voltage Source Inverter (VSI) where the upper power switches in each phase leg are represented by ideal switches and given boolean variables $S_{\text{a}},\ldots,S_{\text{e}}$. These adopt only “1” (switch ON) or “0” (switch OFF) as values. We assume ideal switching, thus the lower power switches in each phase leg represent the negative logic of the respective upper power switches $\overline{S}_{\text{a}},\ldots,\overline{S}_{\text{e}}$. Therefore only the five upper switches are considered. In [12, 14], the phase voltages $u_{x\text{n}}$, where $x=\text{a}$, b, c, d, e (five phases), are defined as in (5).

$$\displaystyle u_{\text{an}}=U_{\text{DC}}\cdot\left(\frac{4}{5}\cdot S_{\text{a}}-\frac{1}{5}\cdot\left(S_{\text{b}}+S_{\text{c}}+S_{\text{d}}+S_{\text{e}}\right)\right)$$

(5a)

$$\displaystyle u_{\text{bn}}=U_{\text{DC}}\cdot\left(\frac{4}{5}\cdot S_{\text{b}}-\frac{1}{5}\cdot\left(S_{\text{a}}+S_{\text{c}}+S_{\text{d}}+S_{\text{e}}\right)\right)$$

(5b)

$$\displaystyle u_{\text{cn}}=U_{\text{DC}}\cdot\left(\frac{4}{5}\cdot S_{\text{c}}-\frac{1}{5}\cdot\left(S_{\text{a}}+S_{\text{b}}+S_{\text{d}}+S_{\text{e}}\right)\right)$$

(5c)

$$\displaystyle u_{\text{dn}}=U_{\text{DC}}\cdot\left(\frac{4}{5}\cdot S_{\text{d}}-\frac{1}{5}\cdot\left(S_{\text{a}}+S_{\text{b}}+S_{\text{c}}+S_{\text{e}}\right)\right)$$

(5d)

$$\displaystyle u_{\text{en}}=U_{\text{DC}}\cdot\left(\frac{4}{5}\cdot S_{\text{e}}-\frac{1}{5}\cdot\left(S_{\text{a}}+S_{\text{b}}+S_{\text{c}}+S_{\text{d}}\right)\right)$$

(5e)

[12, 14] transform the phase voltages in (5) into the $\alpha\beta_{1}$- and $\alpha\beta_{3}$-planes with a matrix similar to Clarke’s transformation matrix adapted to five-phase systems (6).

$$\small\begin{bmatrix}u_{\alpha 1}\\ u_{\beta 1}\\ u_{\alpha 3}\\ u_{\beta 3}\\ u_{0}\end{bmatrix} = \frac{2}{5}\begin{bmatrix}1&\text{cos}\left(\frac{2\pi}{5}\right)&\text{cos}\left(\frac{4\pi}{5}\right)&\text{cos}\left(\frac{6\pi}{5}\right)&\text{cos}\left(\frac{8\pi}{5}\right)\\[2pt] 0&\text{sin}\left(\frac{2\pi}{5}\right)&\text{sin}\left(\frac{4\pi}{5}\right)&\text{sin}\left(\frac{6\pi}{5}\right)&\text{sin}\left(\frac{8\pi}{5}\right)\\[2pt] 1&\text{cos}\left(\frac{6\pi}{5}\right)&\text{cos}\left(\frac{12\pi}{5}\right)&\text{cos}\left(\frac{18\pi}{5}\right)&\text{cos}\left(\frac{24\pi}{5}\right)\\[2pt] 0&\text{sin}\left(\frac{6\pi}{5}\right)&\text{sin}\left(\frac{12\pi}{5}\right)&\text{sin}\left(\frac{18\pi}{5}\right)&\text{sin}\left(\frac{24\pi}{5}\right)\\[2pt] \frac{1}{2}&\frac{1}{2}&\frac{1}{2}&\frac{1}{2}&\frac{1}{2}\end{bmatrix}\begin{bmatrix}u_{\text{an}}\\ u_{\text{bn}}\\ u_{\text{cn}}\\ u_{\text{dn}}\\ u_{\text{en}}\end{bmatrix}$$

(6)

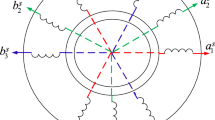
The five upper power switches in the VSI (Fig. 1) have $2^{5}=32$ different possible switching combinations. Each of the 32 switching combinations is inserted in (5) and mapped onto the $\alpha\beta_{1}$- and $\alpha\beta_{3}$-planes with (6). This results in 30 different active discrete space vectors and two zero space vectors. The active space vectors divide the $\alpha\beta_{1}$-plane for the $\omega_{1}$-voltage in ten sectors, with each sector covering an angle of $\frac{{360}^{\circ}}{2\cdot 5}={36}^{\circ}$. Consequently, each sector has three neighbouring discrete space vectors on each side (Fig. 2a). These three active discrete space vectors per side are classified into three different categories $S,M,L$ based on their magnitudes: Small, Medium and Large ($S$ / $M$ / $L$)($0.25\cdot U_{\text{DC}}$ / $0.40\cdot U_{\text{DC}}$ / $0.65\cdot U_{\text{DC}}$). It is needed to consider a second $\alpha\beta_{3}$-plane (Fig. 2b) where the space vectors for the $3^{\text{rd}}$ harmonic reference components are located. This second plane also contains all 30 active discrete space vectors, but they are located in different sectors with respect to their counterparts in the $\alpha\beta_{1}$-plane. The large vectors ($L$) in the $\alpha\beta_{1}$-plane become small ($S$) in the $\alpha\beta_{3}$-plane and the small vectors ($S$) in the $\alpha\beta_{1}$-plane become large ($L$) in the $\alpha\beta_{3}$-plane (Fig. 2b). For example, the discrete voltage space vector $25_{10}=11001_{2}$ results from the switching combination $S_{\text{a}}=1$, $S_{\text{b}}=1$, $S_{\text{c}}=0$, $S_{\text{d}}=0$ and $S_{\text{e}}=1$. The phase voltages thus result in $u_{\text{an}}=0.4\cdot U_{\text{DC}}$, $u_{\text{bn}}=0.4\cdot U_{\text{DC}}$, $u_{\text{cn}}=-0.6\cdot U_{\text{DC}}$, $u_{\text{dn}}=-0.6\cdot U_{\text{DC}}$ and $u_{\text{en}}=0.4\cdot U_{\text{DC}}$, and mapped onto the $\alpha\beta_{1}$- and $\alpha\beta_{3}$-planes: $u_{\alpha 1}=0.65\cdot U_{\text{DC}}$, $u_{\beta 1}=0$, $u_{\alpha 3}=-0.25\cdot U_{\text{DC}}$, $u_{\beta 3}=0$ and $u_{0}=0$ (Fig. 2).

Fig. 1

Five-phase two-level voltage source inverter (VSI) with ideal switches

Fig. 2

Resulting 32 discrete space vectors for each five-phase inverter switching combination projecting a the fundamental components onto the $\alpha\beta_{1}$ plane and b the $3^{\text{rd}}$ harmonic components onto the $\alpha\beta_{3}$ plane. The dashed black arrows show the switching sequence for a sector within a sampling period $T_{\text{s}}$ for the SVPWM algorithm based on neighbouring space vectors (similar to [12])

4.1 Five-phase space vector PWM algorithm with neighbouring vectors

First, it must be decided how many and which of the neighbouring space vectors are required for approximating the reference space vector. As the discrete space vectors are present in both $\alpha\beta_{1}$- and $\alpha\beta_{3}$-planes simultaneously, the generation of a $\omega_{1}$-voltage reference space vector leads to the inevitable creation of a $3^{\text{rd}}$ harmonic [5, 7, 11, 12, 18]. If for example the two largest vectors ($L$) per sector in the $\alpha\beta_{1}$-plane are selected to generate a fundamental voltage space vector, a small $3^{\text{rd}}$ harmonic voltage space vector is created in the $\alpha\beta_{3}$-plane. Therefore [5, 7, 11, 12, 18] concluded that choosing only four neighbouring space vectors in the $\alpha\beta_{1}$-plane is a good solution, especially large ($L$) and medium ($M$), in order to nullify the $3^{\text{rd}}$ harmonic voltage space vector. The SVPWM scheme implementing neighbouring large ($L$) and medium ($M$) space vectors in the $\alpha\beta_{1}$-plane is therefore the most commonly used strategy. Not using the small space vectors in the $\alpha\beta_{1}$-plane is justified by realising that these would produce very large $3^{\text{rd}}$ harmonic voltage components, which are unwanted if the purely feeding of a fundamental voltage component is the objective. Therefore, the algorithm runs as follows: detection of the sector, selection of neighbouring discrete space vectors and calculation of conduction time intervals $t_{1}$, $t_{2}$, $t_{3}$ and $t_{4}$. In our case, the injection of a $3^{\text{rd}}$ harmonic component is also of interest. Therefore, Fig. 3 displays the regions of possible combinations of $m_{\text{a,1}}$ and $m_{\text{a,3}}$ which are possible with the SVPWM, based on neighbouring large ($L$) and medium ($M$) discrete space vectors. The regions in Fig. 3 were generated by running the previously described algorithm in MATLAB for each point in the grid defined by $\varphi_{3}=0:\frac{\pi}{20}:\pi$, $m_{\text{a,1}} = 0:0.001:1.25$ and $m_{\text{a,3}} = 0:0.001:1.25$. If the resulting conduction time intervals $t_{1}$, $t_{2}$, $t_{3}$ and $t_{4}$ satisfied the conditions $t_{1} \geq 0$, $t_{2} \geq 0$, $t_{3} \geq 0$, $t_{4} \geq 0$ and $t_{1} + t_{2} + t_{3} + t_{4} \leq T_{\text{s}}$, the respective ($\varphi_{3}$, $m_{\text{a,1}}$, $m_{\text{a,3}}$)-values were stored. When the $3^{\text{rd}}$ harmonic is nullified ($m_{\text{a,3}}=0$), the maximum amplitude for the fundamental results in $m_{\text{a,1,max}}=1.05$. In Fig. 3 it can also be seen that a $3^{\text{rd}}$ harmonic component can only be injected in addition to the fundamental component if it is either in phase ($\varphi_{3}={0}^{\circ}$) or phase opposition ($\varphi_{3}={180}^{\circ}$). This is due to the fact that if $\varphi_{3}\neq{0}^{\circ}\quad\text{or}\quad{180}^{\circ}$, the $3^{\text{rd}}$ harmonic space vector component would not lie in the same sector determined by the fundamental component.

Fig. 3

Simulation of the regions of possible combinations of $m_{\text{a,1}}$ and $m_{\text{a,3}}$ for the SVPWM algorithm implementing two medium ($M$) and two large ($L$) neighbouring space vectors with MATLAB

4.2 Five-phase space vector PWM algorithms

To overcome the limits for the $3\omega_{1}$-component of Fig. 3, new algorithms which are not limited to choosing only neighbouring space vectors have been developed such as in [18]. This leads to the results in Fig. 4. The implementation of the algorithm of [18] demands more computational effort and is therefore not well-suited for real-time applications. It searches a combination of four suitable discrete space vectors, based on their linear independence, and then calculates the conduction time intervals, which have to fulfill the following conditions: $t_{1}\geq 0$, $t_{2}\geq 0$, $t_{3}\geq 0$, $t_{4}\geq 0$ and $t_{1}+t_{2}+t_{3}+t_{4}\leq T_{\text{s}}$. In addition to that, the algorithm selects the order of the applied active space vectors in order to minimise the number of switching events. To speed up the implementation of the algorithm, it is solved offline and the results are stored into look-up tables. The gain in speed comes at a cost of increased storage space requirement.

Fig. 4

Simulation of the regions of possible combinations of $m_{\text{a,1}}$ and $m_{\text{a,3}}$ with MATLAB for the carrier-based PWM method which is equivalent to the general SVPWM algorithm from Sect. 5.2 (Ex.: example, see Sect. 6)

5 Generating the modulation signals

Contrary to Sect. 4.2, the addition of a non-sinusoidal zero-sequence signal, with five times the fundamental frequency, is fast and easy to implement and does not require large amounts of storage capacity. In order to compare the carrier-based PWM, based on the addition of a zero-sequence signal, with the SVPWM algorithm of Sect. 4.2, the modulation signals similar to Sect. 2 are generated for each scheme .

5.1 Carrier-based PWM with zero-sequence signal

The modulation signals for the carrier-based PWM are generated similarly to (2) by adding the zero-sequence signal

$$u_{0}=-\frac{1}{2}\cdot(u_{\text{ref,max}}+u_{\text{ref,min}}),$$

(7)

with $u_{\text{ref,max}}=\text{max}(u_{\text{ref,a}},u_{\text{ref,b}},u_{\text{ref,c}},u_{\text{ref,d}},u_{\text{ref,e}})$ and $u_{\text{ref,min}}=\text{min}(u_{\text{ref,a}},u_{\text{ref,b}},u_{\text{ref,c}},u_{\text{ref,d}},u_{\text{ref,e}})$, to all five reference signals in (3).

5.2 Generalised SVPWM algorithm

To generate the modulation signals for the generalised SVPWM algorithm from [18], the algorithm was coded with MATLAB. The algorithm first needs a reference vector with four components, which are the components of the reference voltage vectors in the $\alpha\beta_{1}$- and $\alpha\beta_{3}$-planes, projected onto the four axis $\alpha_{1}$, $\beta_{1}$, $\alpha_{3}$ and $\beta_{3}$:

$$\overset{\rightarrow}{U}_{\text{ref}}=[u_{\text{ref},\alpha 1}\quad u_{\text{ref},\beta 1}\quad u_{\text{ref},\alpha 3}\quad u_{\text{ref},\beta 3}]^{\text{T}}.$$

(8)

5.2.1 Selection criteria

The selection parameter

$$P_{i}=\frac{\overset{\rightarrow}{U}_{\text{ref}}\cdot\overset{\rightarrow}{U}_{\text{fix},i}}{|\overset{\rightarrow}{U}_{\text{fix},i}|^{q}}\quad\text{with}\quad i=1,2,\ldots,30;\quad q=2$$

(9)

is calculated for each of the 30 discrete active space vectors

$$\overset{\rightarrow}{U}_{\text{fix},i}=[u_{\text{fix},i,\alpha 1}\quad u_{\text{fix},i,\beta 1}\quad u_{\text{fix},i,\alpha 3}\quad u_{\text{fix},i,\beta 3}]^{\text{T}}$$

(10)

and arranged in descending order. The magnitude of the discrete active space vectors $\overset{\rightarrow}{U}_{\text{fix},i}$ in the denominator of (9) is increased by the exponent $q=2$ in order to prioritise the smaller vectors. Once the list of 30 $P_{i}$-values is sorted accordingly, it is used to find the four best suited discrete space vectors $\overset{\rightarrow}{U}_{\text{fix},j}$, $\overset{\rightarrow}{U}_{\text{fix},k}$, $\overset{\rightarrow}{U}_{\text{fix},l}$ and $\overset{\rightarrow}{U}_{\text{fix},m}$ where $j$, $k$, $l$ and $m$ are the numbers of the selected active discrete space vectors, $1\leq j,\ k,l,m\leq 30$. The four selected discrete space vectors must be linear independent from each other. The algorithm iterates through all the elements $P_{i}(x)$ of the sorted list $P_{i}$, starting with the first four elements ($P_{j}(1)$, $P_{k}(2)$, $P_{l}(3)$, $P_{m}(4)$), where $x=1,\ldots,30$ is a variable element in the $P_{i}$-list. The algorithm takes the discrete space vectors related to the individual elements $P_{i}(x)$ and tests their linear dependence. First, the linear dependence of the discrete space vectors of $P_{j}(1)$ and $P_{k}(2)$ is tested. If linear dependence exists, $P_{k}(2)$ is ignored and $P_{k}(3)$ is tested together with $P_{j}(1)$. If $P_{k}(x)$ iterates through all the values of the list, the whole process starts again with $P_{j}(2)$ and $P_{k}(3)$. This process is repeated, until a linear independent pair of $\overset{\rightarrow}{U}_{\text{fix},j}$ and $\overset{\rightarrow}{U}_{\text{fix},k}$ is found. Next, a third discrete space vector $\overset{\rightarrow}{U}_{\text{fix},l}$ ($P_{l}(x)$) is selected to test the linear dependence of all three discrete space vectors. The first candidate of $P_{l}(x)$ belongs to the $P_{i}$-value, following the selected $P_{k}(x)$ value. If linear dependence exists, then the next $P_{l}(x)$ element is tested. If again all remaining $P_{l}(x)$ values have been tested without proving linear independence, the next suitable ($P_{j}(x)$, $P_{k}(x)$) pair is selected and the search for $P_{l}(x)$ starts again. The same process is followed to find the fourth discrete space vector $\overset{\rightarrow}{U}_{\text{fix},m}$ ($P_{m}(x)$). If the input reference vector $\overset{\rightarrow}{U}_{\text{ref}}$ can be realised, the algorithm delivers four linearly independent discrete space vectors $\overset{\rightarrow}{U}_{\text{fix},j}$, $\overset{\rightarrow}{U}_{\text{fix},k}$, $\overset{\rightarrow}{U}_{\text{fix},l}$ and $\overset{\rightarrow}{U}_{\text{fix},m}$.

5.2.2 Calculation of the conducting time intervals

The four selected discrete space vectors are arranged as a matrix which is used to calculate the conducting time intervals $t_{1}$, $t_{2}$, $t_{3}$ and $t_{4}$ of the power switches in (11).

$$\displaystyle\begin{bmatrix}t_{1}\\ t_{2}\\ t_{3}\\ t_{4}\end{bmatrix}=T_{\text{s}}\cdot\begin{bmatrix}\overset{\rightarrow}{U}_{\text{fix},j}&\overset{\rightarrow}{U}_{\text{fix},k}&\overset{\rightarrow}{U}_{\text{fix},l}&\overset{\rightarrow}{U}_{\text{fix},m}\end{bmatrix}^{-1}\cdot\overset{\rightarrow}{U}_{\text{ref}}.$$

(11)

If the result of (11) satisfies $t_{1}\geq 0$, $t_{2}\geq 0$, $t_{3}\geq 0$, $t_{4}\geq 0$ and $t_{1}+t_{2}+t_{3}+t_{4}\leq T_{\text{s}}$, the search is stopped, but if one of the conditions is not held, the iterative search in Sect. 5.2.1 continues with a new set of discrete space vectors.

5.2.3 Switching frequency

When four suitable space vectors have been selected, the next step is to determine their switching order, together with both zero space vectors $\overset{\rightarrow}{U}_{\text{fix},0}$ and $\overset{\rightarrow}{U}_{\text{fix},31}$. The sequence of these space vectors is determined by the order with the least amount of switching events. The algorithm of [18] no longer ensures that each inverter phase leg switches only once per switching cycle $T_{\text{s}}$. Therefore the switching frequency $f_{\text{sw}}$ is not constant and the switching pattern is not equal for all five phase legs. Thus, [18] calculates a mean switching frequency $\overline{f}_{\text{sw}}$ for every possible permutation of switching sequences. The permutation with the lowest average switching frequency is selected. For this calculation a whole period of the fundamental output voltage $T_{1}=\frac{1}{f_{1}}$ is considered, thus increasing the calculation effort. Therefore, we focus on the number of switching events within one switching period $T_{\text{s}}$.

5.2.4 Determination of the switching sequence

At this point, the selected active discrete space vectors $\overset{\rightarrow}{U}_{\text{fix},j}$, $\overset{\rightarrow}{U}_{\text{fix},k}$, $\overset{\rightarrow}{U}_{\text{fix},l}$, $\overset{\rightarrow}{U}_{\text{fix},m}$ and $\overset{\rightarrow}{U}_{\text{fix},0}$ and $\overset{\rightarrow}{U}_{\text{fix},31}$ are represented by their number ($j,k,l,m,0,31$) via a 5 bit binary number. Each bit of the number is assigned to one of the five phase legs. A digit “1” represents the upper switch of a phase leg being “on”, and “0” represents that same switch being “off”. For example, for $25_{10}=11001_{2}$, going from left to right, phases a, b, c, d and e are “on”, “on”, “off”, “off” and “on”, respectively. With this information, all $6!=720$ permutations of the six available discrete space vectors are tested. The test consists of counting for each combination the amount of switching state changes “1$\rightarrow{}$0” and “0$\rightarrow{}$1”, in each of the five phase legs ($z_{\text{sw,a}}$, $z_{\text{sw,b}}$, $z_{\text{sw,c}}$, $z_{\text{sw,d}}$, $z_{\text{sw,e}}$). For this, “switching vectors” $\overset{\rightarrow}{S}_{\text{a}},{\ldots},\overset{\rightarrow}{S}_{\text{e}}$ for each phase leg are defined. For example, for the switching sequence shown in Fig. 2, which is described by $0_{10}=00000_{2}\rightarrow{}16_{10}=10000_{2}\rightarrow{}24_{10}=11000_{2}\rightarrow{}25_{10}=11001_{2}\rightarrow{}29_{10}=11101_{2}\rightarrow{}31_{10}=11111_{2}$, the switching vectors for each phase leg a,…, e result in

$$\displaystyle\overset{\rightarrow}{S}_{\text{a}}=[0\quad 1\quad 1\quad 1\quad 1\quad 1]^{\text{T}}\rightarrow{}z_{\text{sw,a}}=1$$

(12)

$$\displaystyle\overset{\rightarrow}{S}_{\text{b}}=[0\quad 0\quad 1\quad 1\quad 1\quad 1]^{\text{T}}\rightarrow{}z_{\text{sw,b}}=1$$

(13)

$$\displaystyle\overset{\rightarrow}{S}_{\text{c}}=[0\quad 0\quad 0\quad 0\quad 1\quad 1]^{\text{T}}\rightarrow{}z_{\text{sw,c}}=1$$

(14)

$$\displaystyle\overset{\rightarrow}{S}_{\text{d}}=[0\quad 0\quad 0\quad 0\quad 0\quad 1]^{\text{T}}\rightarrow{}z_{\text{sw,d}}=1$$

(15)

$$\displaystyle\overset{\rightarrow}{S}_{\text{e}}=[0\quad 0\quad 0\quad 1\quad 1\quad 1]^{\text{T}}\rightarrow{}z_{\text{sw,e}}=1.$$

(16)

The mean value of switching instances $\overline{z}$ for all five phase legs is computed with

$$\overline{z}=\frac{z_{\text{sw,a}}+z_{\text{sw,b}}+z_{\text{sw,c}}+z_{\text{sw,d}}+z_{\text{sw,e}}}{5}$$

(17)

and the permutation with the lowest value is selected. For the switching sequence ($0\rightarrow{}16\rightarrow{}24\rightarrow{}25\rightarrow{}29\rightarrow{}31$) acc. to (12–16), each phase leg has one single switching state change “$0\rightarrow{}1$”. The mean value of switching instances results therefore in $\overline{z}=\frac{5\cdot 1}{5}=1$.

5.2.5 Generation of the modulation signals

As described in Sect. 4.2, the SVPWM algorithm does not utilise modulation signals. However, for the comparison to the proposed carrier-based PWM, these modulation signals have to be computed from the SVPWM algorithm. These modulation signals are generated via the duty cycles similar to [11]. The algorithm always puts the zero space vectors at the beginning and end of the switching cycles, which leads to an active time vector for the conducting states

$$\overset{\rightarrow}{t}=\left[\frac{t_{0}}{2}\quad t_{1}\quad t_{2}\quad t_{3}\quad t_{4}\quad\frac{t_{0}}{2}\right]^{\text{T}},$$

(18)

which contains the active time for the zero space vectors (19).

$$t_{0}=T_{\text{s}}-\sum_{i=1}^{4}t_{i}$$

(19)

In (18) this time $t_{0}$ is the first and last elements of $\overset{\rightarrow}{t}$; hence the sorted “active times” for the active voltage space vectors lie in between. To compute the duty cycles for each phase leg $D_{\text{a}},{\ldots},D_{\text{e}}$, the switching vectors $\overset{\rightarrow}{S}_{\text{a}},{\ldots},\overset{\rightarrow}{S}_{\text{e}}$ are multiplied with the time vector $\overset{\rightarrow}{t}$ via scalar vector product (20).

$$\displaystyle D_{x}=\overset{\rightarrow}{t}\cdot\overset{\rightarrow}{S}_{x}$$

(20a)

$$\displaystyle x= \text{a, b, c, d, e (five phases)}.$$

(20b)

5.3 Possible combinations of $m_{\text{a,1}}$ and $m_{\text{a,3}}$

The range of possible combinations of $m_{\text{a,1}}$ and $m_{\text{a,3}}$ is shown in Fig. 4. The regions in Fig. 4 were generated similarly to Fig. 3 with MATLAB. First, the same grid defined in Sect. 4.1 was defined: $\varphi_{3}=0:\frac{\pi}{20}:\pi$, $m_{\text{a,1}}=0:0.001:1.25$ and $m_{\text{a,3}}=0:0.001:1.25$. The modulation signals defined in Sect. 5.1 were generated for each point in the grid and only when these were $\geq-1$ and $\leq 1$ for a whole fundamental electric period $T_{1}$, the ($\varphi_{3}$, $m_{\text{a,1}}$, $m_{\text{a,3}}$)-values were stored. The process was also conducted with the algorithm from Sect. 5.2, where the ($\varphi_{3}$, $m_{\text{a,1}}$, $m_{\text{a,3}}$)-values were stored whenever the resulting conduction time intervals $t_{1}$, $t_{2}$, $t_{3}$ and $t_{4}$ satisfied the conditions $t_{1}\geq 0$, $t_{2}\geq 0$, $t_{3}\geq 0$, $t_{4}\geq 0$ and $t_{1}+t_{2}+t_{3}+t_{4}\leq T_{\text{s}}$. The resulting regions for both algorithms, described in Sects. 5.1 and 5.2, were identical. For comparative reasons, the range of possible combinations of $m_{\text{a,1}}$ and $m_{\text{a,3}}$ for carrier-based PWM without zero-sequence signal addition is shown in Fig. 5. The regions in Fig. 5 were generated in the same manner as the regions in Fig. 4. When no zero-sequence is added, the reference signals in (3) directly become the modulation signals. Obviously the region of possible combinations of $m_{\text{a,1}}$ and $m_{\text{a,3}}$ for the SVPWM algorithm in [18] is larger than for the algorithm with neighbouring space vectors (Fig. 3). It allows also more combinations of $m_{\text{a,1}}$ and $m_{\text{a,3}}$ than the method where no zero-sequence is added to the reference signals. This proves that the zero-sequence signal addition allows a peak reduction for a broader range of modulation. The regions of possible combinations of $m_{\text{a,1}}$ and $m_{\text{a,3}}$ in Figs. 4 and 5 shift their limits in dependence of the chosen phase-shift $\varphi_{3}$. The region shared by all possible ${0}^{\circ}\leq|\varphi_{3}|\leq{180}^{\circ}$ in Fig. 4 coincides with the ones shown in [22, 23]. The addition of a $3^{\text{rd}}$ harmonic component becomes interesting for the operation of five-phase electric AC motors. Since five-phase motors can generate a $3^{\text{rd}}$ harmonic magnetic air gap field in addition to the fundamental field, the $3^{\text{rd}}$ harmonic voltage can be used to generate this field component. Due to its small magnetizing inductance the torque generation through the $3^{\text{rd}}$ harmonic field yields higher losses and is not recommended at small loads. At high loads and saturation the $3^{\text{rd}}$ harmonic field component increases the efficiency and the output torque. The $3^{\text{rd}}$ harmonic voltage that is required for such operation typically requires the combinations of $m_{\text{a,1}}$ and $m_{\text{a,3}}$ in Fig. 4 fulfilling the condition $m_{\text{a,3}}\lesssim 0.25\cdot m_{\text{a,1}}$ with $m_{\text{a,1}}\in[0,1.05]$ to be possible for any value of $\varphi_{3}$. Furthermore, in the field weakening range, it is possible, depending on the choice of $m_{\text{a,3}}> 0$ and $\varphi_{3}$, to increase the range of the applicable fundamental voltage $u_{\text{s,1}}$ past $m_{\text{a,1}}=1.05$ up to $m_{\text{a,1}}\approx 1.21$.

Fig. 5

Simulation of the regions of possible combinations of $m_{\text{a,1}}$ and $m_{\text{a,3}}$ with MATLAB for the carrier-based PWM method without zero-sequence signal addition

6 Comparing the carrier-based PWM and SVPWM algorithms

In order to show the identical results in the signal shape for the modulation signals of the carrier-based PWM with non-sinusoidal zero-sequence signal addition (method A) and the SVPWM algorithm of [18] (method B) for an arbitrary $3^{\text{rd}}$ harmonic voltage injection, three possible combinations of $m_{\text{a,1}}$ and $m_{\text{a,3}}$ from Fig. 4 are compared in the examples 1, 2, 3.

$$\begin{aligned}\displaystyle\begin{array}[]{llll}\text{example 1: }&m_{\text{a,1}}=1,&\quad m_{\text{a,3}}=0.&\quad\varphi_{3}={0}^{\circ}.\\ \text{example 2: }&m_{\text{a,1}}=0.4,&\quad m_{\text{a,3}}=0.6.&\quad\varphi_{3}={30}^{\circ}.\\ \text{example 3: }&m_{\text{a,1}}=1.1,&\quad m_{\text{a,3}}=0.3,&\quad\varphi_{3}={153}^{\circ}.\end{array}\end{aligned}$$

Example 1 represents the pure sinusoidal feeding with $\omega_{1}$. Only the fundamental is injected, and the zero-sequence signal has the well-known shape of a triangle signal. The comparison of both – identical in shape – modulation signals for methods A and B is given in Fig. 6. Example 2 shows a case which acc. to Fig. 4 is possible for all values of $\varphi_{3}$ (${0}^{\circ}\leq|\varphi_{3}|\leq{180}^{\circ}$), where the $3^{\text{rd}}$ harmonic voltage has a bigger amplitude than the fundamental voltage (Fig. 7). Example 3 is only possible for phase-shift values ${144}^{\circ}<|\varphi_{3}|<180$${}^{\circ}$. The resulting identical modulation signals are compared in Fig. 8.

Fig. 6

Comparison of the resulting modulation signals of example 1, with $m_{\text{a,1}}=1$, $m_{\text{a,3}}=0$ and $\varphi_{3}={0}^{\circ}$, based on a carrier-based PWM with addition of a zero-sequence signal and b on the SVPWM algorithm [18] from Sect. 5.2

Fig. 7

As Fig. 6 but for $m_{\text{a,1}}=0.4$, $m_{\text{a,3}}=0.6$ and $\varphi_{3}={30}^{\circ}$ (example 2)

Fig. 8

As Fig. 6 but for $m_{\text{a,1}}=1.1$, $m_{\text{a,3}}=0.3$ and $\varphi_{3}={153}^{\circ}$ (example 3)

6.1 Comparison of the modulation signals

From Fig. 6–8 it becomes apparent that the wave forms of the modulation signals for methods A and B are the same. The only difference is the scaling on the ordinate and an offset of 0.5. The modulation signals resulting directly from SVPWM [18] have values between 0 to 1 because they are defined by the duty cycles in (20), which are the sum of the computed “active times”. Since the values for $t_{0},\ldots,t_{4}$ cannot be negative, the resulting duty cycles and modulation signals are also positive. If the offset of 0.5 is subtracted from the modulation signals, resulting from method B, and afterwards multiplied by 2, the identical modulation signals, gained from the addition of the non-sinusoidal zero-sequence signal, are obtained. Given that the modulation signals for methods A and B are equal, it also becomes apparent why method A is preferred due to it being better suited for real-time application and not requiring large amounts of storage. Contrary to the proposition in [18], method A does not require the storage of large look-up tables. With respect to the reduced calculation time, method A only requires simple addition, multiplication and logical comparison operations compared to the many tasks present in method B: calculation of 30 $P_{i}$ values, sorting these, repeatedly iterating through these, calculating the conducting time intervals and determining the switching sequence.

6.2 Analysis of the zero-sequence signals

As stated before, the addition of the zero-sequence signal (7) does not have an effect on the line-to-line voltages and does not produce additional stator currents in the five-phase Y‑connected windings. In a five-phase system, the harmonic voltage components $n=5,10,15,\ldots$ fulfill these conditions. To demonstrate this, an FFT analysis is performed on the resulting zero-sequence signals for examples 1, 2 and 3, to confirm that these only contain harmonics that are a multiple of five. As mentioned in [16] and shown by FFT analysis in Fig. 9a, the zero-sequence signal for pure sinusoidal feeding, shown in Fig. 6a, consists of the $5^{\text{th}}$, $15^{\text{th}}$, etc. harmonics. For the other two examples in Figs. 7a and 8a, the signal wave form deviates from the triangle. However, the FFT analysis, shown in Fig. 9b and c respectively, shows similar FFT spectra with mainly the $5^{\text{th}}$ and $15^{\text{th}}$ harmonics appearing. The main difference are the amplitudes $|u_{0}(n)|$ and phase-shifts of the harmonic components. Thus, the zero-sequence signals from all three examples 1, 2 and 3 satisfy the condition of only containing harmonics which are a multiple of five. It is confirmed that the application of the signal (7) is also valid for an arbitrary injection of a $3^{\text{rd}}$ harmonic component and equivalent to the SVPWM algorithm of [18].

Fig. 9

FFT analysis of the resulting zero-sequence signals $u_{0}$ for a example 1: $m_{\text{a,1}}=1$, $m_{\text{a,3}}=0$, $\varphi_{3}={0}^{\circ}$ b example 2: $m_{\text{a,1}}=0.4$, $m_{\text{a,3}}=0.6$, $\varphi_{3}={30}^{\circ}$ and (3) example 3: $m_{\text{a,1}}=1.1$, $m_{\text{a,3}}=0.3$, $\varphi_{3}={153}^{\circ}$

7 Conclusion

The carrier-based PWM method for three-phase systems based on the addition of a triangle zero-sequence signal with three times the fundamental frequency to the reference signal, is successfully adapted to a five-phase system. It is known from [9, 16] that this adaptation works for the injection of a pure sinusoidal fundamental component. This work expands this concept showing that the addition of the non-sinusoidal zero-sequence signal with five times the fundamental frequency works for five-phase systems to inject arbitrary fundamental and $3^{\text{rd}}$ harmonic components at the same time. To do this, a five-phase SVPWM algorithm from [18] was studied. This algorithm allows a broader spectrum of permissible combinations of fundamental and $3^{\text{rd}}$ harmonic components than the well-established SVPWM algorithm, based on selecting neighbouring space vectors [12]. Instead of the time-consuming SVPWM algorithm [18], the addition of a non-sinusoidal zero-sequence signal is considered, which is more suitable for real-time applications. It is also favoured in order to avoid an increased data storage via look-up tables. The SVPWM algorithm of [18] was coded in MATLAB in order to generate the modulation signals for comparison with the method implementing the non-sinusoidal zero-sequence signal, proving the identical results of both methods, with three examples from the region of possible combinations of fundamental and $3^{\text{rd}}$ harmonic components. Finally, an FFT analysis was performed on the resulting zero-sequence signals to prove that these still fulfill the conditions of containing only harmonics which are multiples of five.