1 Introduction

Sintering occurring in tunnel drainage is a significant problem. In order to drain the mountain water from the tunnel, it is necessary to install drainage pipes. Saturated mountain water, portlandite from the shotcrete of the tunnel wall and the pressure difference at the transition to the earth’s atmosphere lead to the formation of calcite, and therefore to the formation of deposits in the pipes [1, 2]. For the maintenance of the tunnel it is necessary to remove the deposits in order to ensure the successful drainage of the mountain water. While it is possible to remove deposits with pressure brushes for thin layer thicknesses, it is necessary to use more time-consuming and expensive removal methods for thicker layers or to completely replace the pipe. For this reason it is important to recognize a deposit in good time. Therefore should be used a measuring system, which simply can be retrofitted to the already existing drainage pipes. Because of the electrical properties of the materials (calcite, water, U‑PVC), the design of a measuring system based on impedance measurements was investigated. Two different methods are offered: impedance spectroscopy and impedance tomography [3,4,5]. In impedance spectroscopy, the impedance between two electrodes is measured over a frequency range. By correctly modeling an equivalent circuit of the device under test and calculating the parameters by fitting the model to the measurements obtained, it may be possible to establish a correlation between the desired state and model parameters. The relationship obtained can then be used to estimate the state. Impedance spectroscopy is applied nowadays, for example, to analyze the composition of material mixtures and to the study batteries [6]. Impedance tomography, on the other hand, makes it possible to draw conclusions about the distribution of permittivity and conductivity by means of pairwise measurements over several electrodes attached around the circumference of the pipe. From these the distribution of the materials inside the pipe can be estimated and the calcite thickness measured. Mainly the use of impedance tomography for medical application is studied, but EIT can also be used for geophysical and industrial application for nondestructive testing [7, 8].

The paper is organized as follows. In Sect. 2 a measuring system is presented which is based on impedance spectroscopy, followed by Sect. 3 that discusses the impedance tomography and its properties. In addition, Sect. 3 shows a simple impedance tomography hardware and the results obtained with it. The paper is concluded in Sect. 4 with a discussion and comparison of the two methods and an outlook.

Notation: lower case bold characters denote vectors, upper case bold characters matrices and \(\vec{(\ldots)}\) vectors. \(f(\mathbf{x})\) is a function that depends on \(\mathbf{x}\). \(\nabla\) is the Nabla operator. \(O(\left\|{\ldots}\right\|^{n})\) stands for the terms of order higher \(n-1\) in the Taylor polynomial. \((\ldots)^{\prime}\) is the first derivative. × is the cross product and ⋅ the dot product symbol. ı is the imaginary unit, f frequency and \(\underline{\ldots}\) denotes a complex number.

2 A measuring method based on impedance spectroscopy

Since the measuring system has to be added on drainage pipes in tunnels, it has to be designed to be installed potentially a thousand times for long tunnel segments, therefore a method was sought with a lowest possible installation, data acquisition, and computing effort. The authors in [9] devise a method that allows to even estimate the shape of interfaces between different media, but for the price of a high computational load which ist clearly unsuitable for the current task, since we aim for keeping the necessary measurement setup as simple and cost effective as possible in order to reduce the associated costs for a later and widespread application. To meet these requirements the model of the drainage pipe was simplified as much as possible using suitable assumptions.

In the following subsections the used model of the drainage pipe is presented and the developed measuring method is described. Finally, the advantages and disadvantages of the presented measuring system are discussed.

2.1 Experimental setup

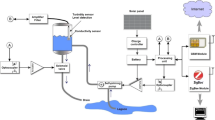
A replica of the tunnel’s drainage pipe with a diameter of 150 mm was created in the laboratory for later measurements (Fig. 1). The following assumptions were made for this purpose:

  • Since the formation of calcite via chemical reactions in the laboratory is time consuming, the calcite has been replaced by quartz sand of appropriate grain size, mimicking most characteristics of calcite.

  • The calcite-water interface as well as the water-air interface was assumed to be horizontal. This resulted in a model that was symmetrical around the vertical axis, which eases somewhat the mathematical problem.

  • The drainage pipe used for the test setup was not set in concrete but was surrounded by air. So the electric field and the associated parallel connected conductance on the pipe’s outside is modeled too low, but this is not relevant.

In order to have an overview of the model, it was necessary to characterize the involved materials. A measuring probe consisting of a cylindrical container with two copper electrodes inside, one on the top and one on the bottom [10], was used. The values obtained for permittivity and electrical conductivity at a frequency of \(6\times 10^{6}\,\text{Hz}\) are given in Table 1. The comparison with the numerical values from [10] shows that the electrical conductivities of sand and calcite do not deviate significantly. The value of the permittivity, however, differs by a factor 3 (\(\varepsilon_{\text{calcit}}\approx 3\cdot\varepsilon_{\text{sand}}\)), but this can safely be neglected since a larger value of \(\varepsilon\) renders the associated equations more easy to solve.

Fig. 1
figure 1

Experimental setup. In the background the impedance analyzer

Full size image
Table 1 Permittivity and electrical conductivity values at \(f=6\times 10^{6}\,\text{Hz}\)
Full size table

2.2 Considerations that led to the measurement method

The idea of the method was to measure the calcite thickness through the resulting displacement of the water. Due to the different permittivities and electrical conductivities this would result in a change of the spatial impedance distribution of the contents of the pipe. In order to not expose the electrodes to chemical attack by the mountain water, the electrodes were attached to the outside of the drainage pipe. The resulting impedance measurement can be modeled by connecting two capacitors \(C_{1}\) and \(C_{2}\) and an impedance \(\underline{Z}_{\text{DUT}}(\text{thickness CaCO}_{3},\text{thickness H}_{2}\text{O})\) in series (see Fig. 2) [11]. The insulating pipe wall which separates the electrodes from the inside of the pipe (marked with DUT) is described by the capacitances \(C_{1}\) and \(C_{2}\) [12]. Since the thickness of the pipe wall can be considered constant as well as the electrode’s area is the same, \(C_{1}=C_{2}=C\) applies. The impedance \(\underline{Z}_{\text{DUT}}\) describes the impedance resulting from a layered dielectricum of different permittivities. So, the total impedance which results from a measurement between two electrodes is

$$\underline{Z}_{\text{ges}}=\underline{Z}_{\text{DUT}}+\frac{2}{\imath\omega C}$$
(1)

where \(\omega\) is the angular frequency at which the measurement is done.

Fig. 2
figure 2

Circuit model of the pipe

Full size image

The search for a simple measuring system leads to the consideration of whether it would be possible to place the electrodes in such a way that only two electrodes are required for measurement: the current is applied to one electrode and the resulting potential difference between that electrode and the other is measured. Through the assumption of symmetry between the left and right side of the content and the a priori knowledge over the shape of the deposits/water it is only necessary to determine the thickness of calcite and water in the pipe. There are two possible combinations which would be possible for a setup with two electrodes, these are shown in Fig. 3. If the electrodes are positioned as shown in Fig. 3 A [4], it is possible to compensate the large distance between the electrodes with a larger area by increasing the angular width of both electrodes. For arrangement B an attempt would be made to collocate the electrodes in such a way that, on the one hand, they are close enough to each other to detect even low sand heights, and on the other hand, they should not be so close that the field lines only run through the pipe wall. Arrangement B was studied in order to achieve the goal of a low cost measurement setup, as smaller electrodes would be needed. In addition, arrangement A would not be applicable as there are slots on the upper side of the pipes (not shown here) through which the water enters the pipes.

Fig. 3
figure 3

Possible positions of the electrodes (in red). Sand in khaki, water in blue and the pipe in orange

Full size image

An impedance analyzer 4194A from HP was used for the measurement. It allows to record 401 measuring points over a maximum measuring range of 1 kHz to 40 MHz. The measurement was controlled from a computer via Auto Sequence Programming and GPIB. The measured values obtained were read directly into Matlab and processed. With a lumped parameter model, an inherent distributed parameter model is approximated to a more or less good extent, but since electrochemical relaxation processes are involved, there is also a continuum of time constants that cannot be modeled with simple equivalent circuit diagrams. As a consequence, due to the complexity of the measuring object, which consists of several layered materials with different frequency dependent permittivities and electrical conductivities, the search for a model valid over an extended frequency range was difficult. Based on the assumption that impedance spectroscopy is primarily not about finding a model that describes the measurement object physically correctly, but one that allows to estimate the desired states [13], such a sufficiently well approximating model was sought. Furthermore, if one consider that the difficulty is to model a circuit that is generally valid or at least valid for the frequencies under consideration, then a suggestion would be to no longer focus on the frequency range, but to find a single frequency that allows to differentiate between water and calcite. It is therefore desirable to find a model and an associated frequency for which a parameter value of the model is directly related to the water or sand level and another or the same frequency, at which another parameter value clearly depends on the thickness of the other or on both materials.

2.3 Results

The search for a suitable equivalent circuit and the significant frequency was carried out empirically. The measurement setup described above was created in the laboratory. 80 cm long and 6.5 mm wide electrodes were placed lengthways at 5 mm distance on the underside of the pipe. Measurements were carried out over different water and sand heights. Since the measurement is capacitively coupled, the frequency must be selected large enough to reduce the impedance component resulting from the pipe wall. However, if the frequency is too high, the penetration depth turned out to be significantly less. From these considerations a favorable frequency range between 2 MHz and 7 MHz was determined.

A resistance-capacitance parallel connection was chosen as an equivalent circuit. The resulting values for resistance (\(R_{p}\)) and capacitance (\(C_{p}\)) were calculated for each measurement and its dependence on water and sand height was analyzed at each frequency. It was found that at a frequency of 6.33 MHz the value of the capacitance is almost independent of the sand layer height. The value of R, on the other hand, clearly depends on both sand and water layer heights. This leads to the assumption of a possible measurement method. Combining the obtained values in a 3D plot a surface can be obtained, that has the calculated \(R_{p}\) and \(C_{p}\) values as well as the sand height as coordinates. To measure the sand height, it would be necessary to measure the impedance at 6.33 MHz, compute the \(R_{p}\) and \(C_{p}\) values and use these and the surface from Fig. 4 to deduce the sand height.

Fig. 4
figure 4

Resulting surface approximated to the measuring points (in red) \(x\)-axis: Sand level, \(y\)-axis: \(C_{p}\), \(z\)-axis: \(R_{p}\)

Full size image

2.4 Evaluation of the method

The new method is characterized by its simple hardware. In order to use the system, it is necessary to add two electrodes to the drainage pipes. The required computing power of the system has also been reduced to a minimum: there is no need to solve inverse problems or minimize error functions. This procedure simplifies the effort involved to: a measurement of a complex valued \(\underline{Z}\), a conversion of phase and amplitude values into resistance \(R_{p}\) and capacitance \(C_{p}\) and finally to the estimation of the sand height by the surface of Fig. 4 with the obtained \(R_{p}\) and \(C_{p}\) values.

On the other hand, the disadvantage of this measuring process, as for every measuring system whose calibration or calculation of the parameters is based on measurements, is that it is only possible to estimate sand heights, which were simulated or tested. It is also important to clarify how the density of the sand and the electrical conductivity of the water affect the measuring process.

3 Electrical Impedance Tomography

Electrical Impedance Tomography (EIT) is based on the measurement of the potential distribution over the boundary of an analyzed object and is aimed at obtaining an estimate of the distribution of electric conductivity and/or permittivity inside the analyzed object. For this purpose, electrodes are placed around the circumference and used for excitation and measurement. Different curvature of the field lines generated by excitation are due to different spatial electrical conductivity and permittivity distributions. By measuring the potential differences over pairs of electrodes, conclusions can be drawn about the distribution of permittivity and electrical conductivity within the object. In this subsection the used, designed and realized, inexpensive EIT system is presented and its application for the measurement of calcite layer thicknesses submerged under a layer of unknown thickness of water is examined. The realized EIT system consists of a power source, various multiplexers, used to select the current driven electrodes and the electrodes used for the measurement, and two true – RMS detectors. Using Fig. 5 the measuring process can be summarized as follows: with each measurement sinusoidal current of chosen frequency is delivered to one electrode (\(k\)), one of the adjacent electrodes is switched to ground (\(k+1\)) and the resulting potential difference between the remaining electrodes are measured, whereby the measurements are only taken between adjacent electrodes (e.g. \(\ell\) and \(\ell+1\)). This is repeated until every possible combination has been run through.

Fig. 5
figure 5

Measuring principle of EIT

Full size image

3.1 Forward problem

The problem described above: to deduce the distribution of permittivity and electrical conductivity from the measurements of the potentials at the boundary of the vessel, is an inverse problem. In order to solve the inverse problem it is necessary to formulate the forward problem correctly. Assuming low excitation frequencies and assuming that the threedimentional problem can be simplified to a 2D problem, the area inside the drainage pipe, \(\Omega\subset\mathbb{R}^{2}\), can be in general described by Maxwell’s equations [11].

$$\begin{aligned}\nabla\times\vec{H} & =\vec{J}+\frac{\partial\vec{D}}{\partial t}\end{aligned}$$
(2)
$$\begin{aligned}\nabla\times\vec{E} & =-\frac{\partial\vec{B}}{\partial t}\end{aligned}$$
(3)
$$\begin{aligned}\nabla\cdot\vec{B} & =0\end{aligned}$$
(4)
$$\begin{aligned}\nabla\cdot\vec{D} & =\rho\end{aligned}$$
(5)

If a harmonic excitation is assumed, Eq. (3) is set to zero and a complex notation is used, the derivative can be converted into a multiplication with the factor \(\imath\omega\). Furthermore, by using the relationships between field strengths and material properties

$$\vec{D}=\varepsilon\vec{E}\quad\mathrm{and}\quad\vec{J}=\sigma\vec{E}\;.$$
(6)

Eq. (2) can be rewritten as follows:

$$\nabla\times\vec{H}=(\sigma+\imath\omega\varepsilon)\vec{E}\;.$$
(7)

Assuming a curl-free field (\(\nabla\times\vec{E}=\vec{0}\)), the differential equation for the potential results

$$\vec{E}=-\nabla\varphi\;.$$
(8)

Taking the divergence of Eq. (7) and using Eq. (8) for \(\vec{E}\), the forward problem in \(\Omega\) can be summarized as follows [11, 14, 15]

$$\nabla\cdot(\gamma(x,y,\omega)\nabla\varphi(x,y,\omega))=\vec{0}\quad(x,y)\in\Omega$$
(9)

with

$$\gamma(x,y,\omega)=\sigma(x,y,\omega)+\imath\omega\varepsilon(x,y,\omega)\;.$$
(10)

Through both Dirichlet and Neumann conditions the boundary conditions can be set [16]. The boundary potentials are restricted to potentials on electrodes. For this applies the condition

$$\int_{\partial\Omega}\gamma\frac{\partial\varphi}{\partial\vec{n}}=\begin{cases}+i\quad\text{for exitation electrode}\\ -i\quad\text{for ground electrode}\\ 0\quad\text{else}\end{cases}$$
(11)

where \(\vec{n}\) is the normal unit vector out of the electrode and \(i=\hat{I}\sin\omega t\) is the excitation current.

The high conductivity of the electrodes is modeled through a constant potential, however it is necessary to consider a contact impedance (\(z_{l}\)) between each electrode and the DUT to receive good results, this results in the following constraint [14]

$$\varphi+z_{l}\gamma\frac{\partial\varphi}{\partial\vec{n}}=V_{l}\quad\text{on electrode }\ell.$$
(12)

3.2 Hardware

The circuit consists of four parts: the current source, the current measuring circuit, the multiplexers and a differential amplifier and will be discussed next. Fig. 6 shows the block diagram of the used EIT system.

Fig. 6
figure 6

Block diagram of the used EIT system

Full size image

3.2.1 Current source

A voltage-controlled current source (VCCS) based on an advanced Howland circuit was used [17]. The VCCS was controlled by a function generator from Agilent (33210A). In Fig. 7 the structure of the VCCS can be seen. The frequency was set by the function generator. From the Kirchhoff’s loop and node laws, follows:

$$i_{L}=\frac{\frac{R_{4}}{R_{3}+R_{4}}\cdot U_{\text{in}}}{(\frac{R_{1}}{R_{2}+R_{1}}-\frac{R_{3}}{R_{4}+R_{3}})\cdot R_{L}+\frac{R_{1}\cdot R_{5}}{R_{1}+R_{2}}}$$
(13)

where \(i_{L}\) is the current which flows through \(R_{L}\) and \(U_{\text{in}}\) the voltage coming from the function generator. Choosing the resistor so that

$$R_{1}\cdot R_{4}=R_{2}\cdot R_{3}$$
(14)

will simplify Eq. (13) to

$$i_{L}=\frac{R_{4}}{R_{3}\cdot R_{5}}U_{\text{in}}\;.$$
(15)

Thus the current can be adjusted by trimming the resistor \(R_{5}\) or by changing the input signal amplitude. A current with an amplitude in the mA range and a frequency between 1 kHz–200 kHz is usually set, the exact value depends on the application.

Fig. 7
figure 7

Structure of the VCCS based on the advanced Howland circuit

Full size image

3.2.2 Current measuring

To measure the injected current a shunt-resistor was added between the ground electrode (see Fig. 5 electrode \(k\)) and ground. The voltage at the resistor is amplified through a non-inverting amplifier. Through a True RMS – to – DC converter the output signal of the OPV is then converted to a DC voltage. The value obtained was transferred to Matlab via the ADC of the microcontroller.

3.2.3 Multiplexer

The measuring system for selecting the current injecting, ground and measuring electrodes, consists of two 4‑channel Analog Multiplexer/Demultiplexer (IC 4052) and four 8‑channel Analog Multiplexer/Demultiplexer (IC 4051) [17]. The signal \(i_{L}\) (see Fig. 6), coming from the current source, and ground are alternately switched by the first IC 4052 between two IC 4051. The electrodes, numbered 1 to 16, are divided into even and odd between the IC4051s. This means that alternately an odd electrode is fed with current and an even electrode is switched to ground and then vice versa. The circuit is controlled by an Arduino microprocessor in such a way that the 1st and 2nd electrodes are used first, then the 2nd and 3rd etc. The other half of the multiplexers were used for the selection of the electrodes used for the voltage difference measurement, they connect the electrodes to the instrumentation amplifier. The principle is the same as the one described before and the multiplexer are again controlled via the microcontroller.

3.2.4 Differential Amplifier

The instrumentation amplifier INA163 was used to measure the voltage difference [18]. It amplifies the difference between two input signal voltages. The gain can be adjusted by an external resistor. In order to avoid DC voltage errors caused by bias currents, a resistor to ground is added to block any spurious DC component at each input. The voltage signal obtained was then transformed to a DC voltage through a True RMS – to – DC converter and sent via a USB connection to the computer from the microcontroller.

3.2.5 Experimental setup for EIT

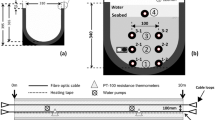
For first experiments instead of a pipe a 3D printed cylinder-shaped tank was used for the tomography application. Rectangular notches were left out while printing inside around the circumference for the electrodes, in order to render the geometry an almost perfect cylinder. In the center of each notch a hole through the wall was made to connect the cables to the electrodes. The electrodes were punched from a copper sheet. A perspex panel was added to the tank for later measurements (see Fig. 12). This allows the tank and its content to be brought into an upright position just like a horizontally oriented pipe.

Fig. 8
figure 8

Tank used for the measurements

Full size image

3.3 Image reconstruction algorithm

The aim of EIT is to determine the distribution of electrical conductivity and permittivity. For this, the previously described forward problem must be solved inversely. Because the measuring system is limited to the detection of the amplitude of the supply current and measured voltage, only the determination of the distribution of the absolute value of the impedance in the analyzed cross section is targeted. To solve the inverse problem stated in Eq. (9) it has to be discretized, which results in

$$\boldsymbol{v}=f(\boldsymbol{\kappa})$$
(16)

where \(\boldsymbol{v}\) is the vector containing all the voltages measured and \(\boldsymbol{\kappa}\) is the vector whose elements correspond to the impdance of one pixel. Performing the Taylor polynomial [19] \(f(\boldsymbol{\kappa})\) can be linearized

$$f(\boldsymbol{\kappa})=f(\boldsymbol{\kappa}_{0})+f^{\prime}(\boldsymbol{\kappa}_{0})(\boldsymbol{\kappa}-\boldsymbol{\kappa}_{0})+O(\left\|\boldsymbol{\kappa}-\boldsymbol{\kappa}_{0}\right\|^{2})$$
(17)

Summarizing the term \(f(\boldsymbol{\kappa})-f(\boldsymbol{\kappa}_{0})\) to \(\delta\boldsymbol{v}\), \(\boldsymbol{\kappa}-\boldsymbol{\kappa}_{0}\) to \(\delta\boldsymbol{\kappa}\) and defining \(f^{\prime}(\boldsymbol{\kappa}_{0})\) as \(\boldsymbol{J}\) the inverse problem can be rewritten as

$$\delta\boldsymbol{v}=\boldsymbol{J}\delta\boldsymbol{\kappa}$$
(18)

Because the inverse problem is ill-posed, various algorithms and regularization schemes have been proposed [14, 20, 21]. The main disadvantage of these methods is that the obtained result highly depends of the choice of hyperparameters as well as the regularization has to be chosen based on a priori knowledge. For this reason the Structure-Aware Sparse Bayesian Learning (SA-SBL) [22, 23] algorithm has been implemented and used in this work. The SA-SBL algorithm does not depend on a priori knowledge, has improved robustness to Gaussian measurement noise and thus removes irrelevant components. The implementation of the algorithm is based on the one proposed by Liu et al. in [22]. Through the Bayesian approach the minimization of the error between the measured data and the model \(d(\delta\boldsymbol{v},\boldsymbol{J}\delta\boldsymbol{\kappa})\) results in a Type II Maximum Likelihood estimation. The main step for the application of the SA-SBL algorithm is the factorization of \(\delta\boldsymbol{\kappa}\). Through this the linear model (18) can be rewritten as

$$\delta\boldsymbol{v}=\boldsymbol{J}\delta\boldsymbol{\kappa}=\boldsymbol{J}\boldsymbol{\Psi}\boldsymbol{x}=\boldsymbol{\Phi}\boldsymbol{x}\;.$$
(19)

Consequently a block sparse model is obtained and the SA-SBL algorithm can be applied. Since this article does not aim in particular at the derivation of the algorithm used, but rather at the presentation of the reconstructions obtained with it, we will not go into this in more detail but refer to the corresponding literature [22, 23].

3.4 Measurements and reconstructions

The measuring system and the algorithm were used for tree different measurements. A frequency of 20 kHz was used for each measurement. Since SA-SBL is used for difference imaging, as mentioned before, the values in the following reconstruction images are relative values to the impedance distribution used for linearization. Accordingly, they do not indicate the exact numerical value of the impedance, but the change in amount. In contrast to an absolute reconstruction algorithms, the focus with difference imaging is not on determining the correct impedance values, but on detecting the contrast between the inclusion and the background [24]. For this reason, no color bar will be added to the images in the following. It is generally accepted that blue stands for a negative change in impedance and red for a positive one, the darker the color, the greater the change.

In the first attempt, the tank was filled with water. One measurement with an insulating (\(\sigma\rightarrow 0\)) plastic cylindrical inclusion (height: 6,5 cm, diameter: 2,7 cm) was taken, then another cylindrical inclusion (height: 6,5 cm, diameter: 3,1 cm) made of brass (\(\sigma\rightarrow\infty\)) was added and a second measurement was taken. The measurement was intended to examine whether and how well different materials/objects can be distinguished. The results obtained are shown in Fig. 9. As it can be seen in the figure, the two cylinders and their various impedances can be detected by the measuring system. The SA-SBL algorithm suppresses interferences well, only small noise effects can be observed at the edge. For comparison, Fig. 10 shows the results obtained with other solution algorithms for the measurements with two cylinders. It is easy to observe that without a Bayesian approach, more significant noise artifacts occur. However, no components of the objects are lost, while with the SA-SBL algorithm the two cylinders have a smaller cross-sectional area. The rightmost image in Fig. 10 shows how a clearer transition between the areas is obtained using a regularization approach based on \(l_{1}\) minimization [25], in contrast with the smooth transitions in the other images.

Fig. 9
figure 9

Reconstructed images by using the proposed measuring system and the SA-SBL algorithm. In the first image only one plastic cylinder in the second the plastic cylinder and one of brass

Full size image
Fig. 10
figure 10

Reconstructed images (from left to right) with: one step Gauss-Newton reconstruction (Tikhonov prior), one step Gauss-Newton reconstruction (Noser prior), one step Gauss-Newton reconstruction (Laplace filter prior), one step Gauss-Newton reconstruction (automatic hyperparameter selection), Total Variation reconstruction

Full size image

The second attempt aimed to examine the measuring system with regard to the detection of calcite. Calcite samples 6 and 7 from our paper [10] were used as specimen. The properties of the samples are summarized in Table 2. The images obtained after the reconstruction can be seen in Fig. 11. One can see how the calcite samples can be recognized well in both cases. The values in the graphs on the right are, as previously introduced in Eq. (18), relative changes in the impedance and were normalized using the absolute value of the maximal value obtained. It can be seen that the measurements and the algorithm recognize the different impedances of the two samples: for the first sample the minimum value of the reconstruction is \(-0.89\) and for the second sample \(-1\) (as it is the maximal absolute value), which means that the second sample has a lower impedance, this agrees with the values of Table 2.

Table 2 Porosity and conductivity values of the calcite probes at a frequency of 20 kHz [10]
Full size table
Fig. 11
figure 11

Reconstructed images of the calcite probes using the proposed measuring system. Probe 7 above, 6 below. In the left column one sees the photos of the samples, the middle column shows the obtained reconstructions and the right shows the obtained values of the reconstruction for the comparison

Full size image

In the last experiment, the tank was raised up and filled with water up to a certain height (see Fig. 12). The disadvantage in this case is that a measurement is only possible between those electrodes that are in contact with water. These active electrodes were determined by observing the measured current values. Those electrodes for which a current value below a certain threshold was measured were not taken into account. The reduced number of electrodes is a clear disadvantage for the reconstruction in this case. The uneven distribution of the electrodes, which results from the fact that there is no electrode lying on the water surface, results in poorer resolution for objects that are not strictly bound to the lower area of the tank.

Fig. 12
figure 12

Reconstructed images using the proposed measuring system and the SA-SBL algorithm. Plastic cylinder at two different positions and tank half filled with water

Full size image

In this case, two measurements were carried out with a plastic cylinder. For the first measurement the cylinder was positioned on the bottom of the tank (a), for the second at half of the water height (b). The experimental set-up and the reconstructions that have been obtained are shown in Fig. 12. As it can be seen in the figure, the insulating cylinder is detected in both cases. In case (a), however, only the cylinder is detected, while in case (b) errors occur. As I said before, this is due to the fact that the cylinder is closer to the water surface and therefore has less influence on the electrodes.

4 Summary and outlook

In this article two different methods are presented which are suitable for the detection of calcite deposits in drainage pipes. Both build on the fact that sand and water have different physical properties that allow them to be discerned by the proposed methods.

The first is a very simple system that consists exclusively of two electrodes and which requires very little computing effort. The disadvantage, however, is that its evaluation is based on calibration impedance measurements. It is therefore necessary to measure all possible combinations in advance in order to make statements about them. However, if this was done, a computational and cost-effective measuring system can be obtained. Furthermore, the influence of different conductivities of water or of different sand densities was not determined neither was is investigated if the system behaves the same with calcite instead of sand. This should still be investigated.

The second method is based on electrical impedance tomography. The measuring system consists of 16 electrodes, the current is measured by an RMS-to-DC converter, whereby the water level is deduced and the active electrodes are defined. In this article a possible measurement circuit is presented as well as the results obtained with it and with the SA-SBL algorithm. Three different measurements were carried out. The first showed the basic results that the measuring system delivers and how different materials can be detected. With the second measurement it was shown that calcite can be detected with the measuring system. Finally, the last measurement showed that the measuring system also works in an upright position. The measurement, however, was carried out with a plastic cylinder instead of calcite and only for one water level. It should be further investigated whether thin deposits of calcite on the electrodes can be detected. Also it has to be defined how much water must be contained in the tank in order to get reasonable results. A possible suggestion for further work would be to try out different electrode positions. It could as well be the case that better images are obtained by also detecting the phase and thus the real and imaginary part of the impedance. The big disadvantage of the method is that a comparative measurement is necessary. A continuous measurement over time and an algorithm based on [19] could be appropriate in this context.