1 Introduction

The constantly increasing amount of renewable energy sources in combination with a liberalized energy market poses major challenges for the European synchronous grid. On the other hand, the urgently needed grid expansion is progressing only slowly, which in turn leads to higher utilization and a lower stability reserve in the power grid.

The steady displacement of conventional power plants in favor of climate protection and the associated reduction of rotating mass is an enormous challenge for power system stability. The result of this is, that less mechanical energy storage is available. Consequences of this are the larger frequency deviations as well as the higher frequency gradients, when disturbances occur. Hydropower plants not only fulfill essential tasks by providing green energy, but also play a major role in maintaining a stable power system.

The larger and the more extensive an interconnected power system is, the more likely is the occurrence of inter-area oscillations [18]. Thereby one generator group oscillates against the other over long transmission lines. In [5], the global oscillation modes of the synchronous grid of continental Europe are elaborated. The typical frequency range of inter-area oscillations in this interconnected system is 0.1 Hz to 0.5 Hz ([11], [5]).

Switching operations or changes in the generator or demand structure, as well as faults of operating resources such as long transmission lines with large power transfer can be the cause of inter-area oscillations. An example of this is the occurrence of inter-area oscillations in the European power system due to the failure of a 400 kV transmission line between France and Spain on December 1, 2016 [3].

Inter-area oscillations reduce the maximum transferable power in the electrical grid, stress mechanical components and can lead to unwanted shutdowns in the power system and the worst case would be a blackout. The reasons mentioned above make it necessary to provide additional damping capability in the grid. In hydropower plants this can be achieved by an additional power system stabilizer (PSS) in the generator voltage control.

About the use of a power system stabilizer in the excitation path of the generator (PSS-E) as a damping element, a lot of research and literature such as ([10], [13] and [16]) and standards, such as [8], have been published. [2] can be mentioned as one of the first publications in which the speed signal from the generator has been fed back for oscillation damping via generator excitation. The PSS must introduce a signal with opposite phase to the electric air gap torque via the generator excitation [10] for an effective damping behavior. Due to the strong dependence of voltage regulation with network conditions and the mutual influence of neighboring voltage controllers, the local design of a PSS-E is not necessarily the optimal solution for use in larger power systems [4]. For extended grids, the use of the PSS-E therefore represents a significantly higher design effort.

In [19] as well as in [21] the significant improvement of the damping behavior by an additional power system stabilizer in the turbine governor path (PSS-G) with a high dynamic governor system is presented. For hydropower plants, in [20] the advantageous application of the PSS-G as a damping device is discussed. According to [19] and [20], the governor is only weakly coupled to the power system, which means that changes in grid impedance or node voltages have no big influence to the governor system. This robust behavior of the governor-turbine system allows the locally designed PSS-G to be used directly for a multi-machine model, which greatly simplifies its design.

The successful use of an optimal state space controller for a linear single machine infinite bus system (SMIBS) is presented in [22]. The high damping potential due to optimal controller through a state feedback as well as through an output feedback is discussed in [14]. Robust control algorithms as well as robust placement of eigenvalues against parameter variations are presented in [15].

The aim of this work is to improve the damping capability of hydropower control systems by using combined control strategies in the case of inter-area oscillations. Therefore the possible damping potential with a power system stabilizer through the generator excitation (PSS-E) as well as over the governor control path (PSS-G) and their combined use (PSS-EG), is investigated. In addition, the damping possibilities that can be obtained by using an optimal state space controller with an observer (PSS-LQR) are analyzed. In this work, the control strategies are first evaluated regarding to their damping capability in a nonlinear SMIBS and subsequently in a nonlinear three-machine power system.

2 Constraints with hydro governors

The hydraulic pressure surge or water hammer effect occurs for example, when the flow of a fluid in a pipeline is changed via a valve. Very fast valve movements result in a large pressure surge. Because of this, the gradient of the valve velocity must be limited according to the hydraulic system in order to avoid mechanical damage [7]. However, this is of course a strong limitation with regard to the dynamics to be introduced by the hydro governor. The opening as well as closing speed of the turbine valve is in this work set to 0.05 pu/s, which is typically achieved in fast hydro storage power plants. It should be mentioned here that the following methods in this work can be used for Pelton, Francis and also for Kaplan turbines. The criterion is therefore not the turbine type, but the maximum achievable speed gradient of the valve as an actuator.

The behavior of an ideal lossless hydraulic turbine can be described according to [10] by the transfer function

$$ \Delta P_{m}(s) = \frac{1 - T_{w} s}{1 + \frac{1}{2} T_{w} s} \Delta G(s) \quad \text{with} \quad T_{w} = \frac{Q\,L}{g\,H\,A} $$
(1)

The water starting time \(T_{w}\) is the time that passes until the water in the pressure pipe with the cross-section \(A\), the length \(L\) and the head \(H\) has reached the flow \(Q\). The transfer function from (1) describes the initial increase of the turbine power when the valve closes, respectively there is a brief reduction of power when the valve opens. Due to this behavior of the hydraulic turbine, the oscillation tendency of the speed-controlled generator is significantly increased. The typical bandwidth of a hydro governor according to [7] ranges from 0.03 Hz to 1 Hz and the step response exhibits rise times from 1 s to 25 s. This illustrates the low dynamics of speed control via a water turbine and due to the hydraulic and mechanical boundary conditions. Despite the low control dynamics, the hydraulic turbine controller for low-frequency oscillations can positively contribute to oscillation damping.

3 Single machine infinite bus system

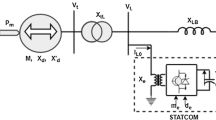
In order to be able to evaluate the individual control strategies, they are first examined in the so called single machine infinite bus system (SMIBS). Figure 1 represents such a model, in which a synchronous generator is connected via a transmission line to an infinite bus with \(V_{b} \angle \theta _{b}\). The generator is coupled to a hydraulic turbine which is speed controlled by the hydro governor. By changing the excitation \(E_{fd}\) through the voltage regulator (AVR), the voltage of the generator \(V_{t}\) can be adjusted. In addition, in Fig. 1, the principal way of implementing a PSS-E in the voltage regulator path and a PSS-G in the hydro governor control path is shown.

Fig. 1.
figure 1

SMIBS with hydro governor and PSS-E as well as PSS-G

Full size image

The synchronous generator with stiff grid connection from Fig. 1, is modeled as IEEE Model 1.1, with a generator excitation in the d-axis and an equivalent damper winding in the q-axis. According to [13], the time behavior of the generator can be described with differential equations (2) to (7) and algebraic equations (8) to (10).

$$ \frac{d \delta }{dt} = \omega - \omega _{s} $$
(2)
$$ \frac{d \omega }{dt} = \frac{\omega _{s}}{2H} ( T_{M} - T_{E} -D ( \omega - \omega _{s}) ) $$
(3)
$$ \frac{d E^{\prime }_{q}}{dt} = \frac{1}{T^{\prime }_{d0} } ( -E^{\prime }_{q} - ( X_{d} - X^{\prime }_{d} ) I_{d} + E_{fd} ) $$
(4)
$$ \frac{d E^{\prime }_{d}}{dt} = \frac{1}{T^{\prime }_{q0} } ( -E^{\prime }_{d} + ( X_{q} - X^{\prime }_{q} ) I_{q} ) $$
(5)

Where the electrical air gap torque of the generator is given by

$$ T_{E} = E^{\prime }_{d} I_{d} + E^{\prime }_{q} I_{q} + ( X^{\prime }_{q} - X^{\prime }_{d} ) I_{d} I_{q} $$
(6)

The dynamics of the generator excitation \(E_{fd}\) is defined by

$$ \frac{d E_{fd}}{dt} = \frac{1}{T_{A}} ( -E_{fd} + K_{A} ( V_{ref} - V_{t} )) $$
(7)

From the algebraic equations according to [13], the generator currents can be expressed in polar form

$$ \left [{\textstyle\begin{array}{c} I_{d} \\ I_{q} \\ \end{array}\displaystyle }\right ] = \left [{\textstyle\begin{array}{c@{\quad }c} -(R_{s} + R_{e}) & ~~(X^{\prime }_{q} + X_{e}) \\ -(X^{\prime }_{d} + X_{e}) & -(R_{s} + R_{e}) \\ \end{array}\displaystyle }\right ]^{-1} \left [{\textstyle\begin{array}{c} V_{b} \sin (\delta - \theta _{b}) - E^{\prime }_{d} \\ V_{b} \cos (\delta - \theta _{b}) - E^{\prime }_{q} \\ \end{array}\displaystyle }\right ] $$
(8)

as well as the generator stator voltage in dq-representation

$$\begin{gathered} V_{d} = R_{e} I_{d} - X_{e} I_{q} + V_{b} \sin (\delta - \theta _{b}) \end{gathered}$$
(9)
$$\begin{gathered} V_{q} = R_{e} I_{q} + X_{e} I_{d} + V_{b} \cos (\delta - \theta _{b}) \end{gathered}$$
(10)

as well as the generator terminal voltage with \(V_{t} = \sqrt{V_{d}^{2} + V_{q}^{2}} \) can be calculated.

3.1 Design of a power system stabilizer

For the design of the power system stabilizer as well as the state space controller as damping element (PSS-LQR), the nonlinear simulation model from (2) to (10) is linearized around a specified operating point. This leads to the well-known Heffron-Phillips model given by [6]. In Fig. 2 this classical model, extended by the hydro governor, the servo dynamics and a linear hydraulic turbine behavior, is shown.

Fig. 2.
figure 2

Heffron-Phillips model with hydro governor

Full size image

The voltage regulator has an amplitude limitation and the hydro governor, due to the hydraulic system, has a limitation of the gradient of the valve speed in addition to the amplitude limitation. In the model shown in Fig. 2, it can be seen that electromechanical oscillations can be influenced either via the electric air gap torque \(\Delta T_{e}\) or via the mechanical torque of the turbine \(\Delta T_{m}\). The electric air gap torque \(\Delta T_{e2}\) influenced via the PSS-E is given by

$$\begin{aligned} \Delta T_{e2}(s) = G_{ex}(s) G_{psse}(s) \Delta \omega (s) \end{aligned}$$
(11)

The behavior of the voltage regulator with excitation according to [2] can be described by the transfer function \(G_{ex}(s)\) with \(\Delta V_{ref}(s) \rightarrow \Delta T_{e2}(s)\) from Fig. 2, neglecting the angle \(\Delta \delta \) over \(K_{4}\) and \(K_{5}\), with

$$\begin{aligned} G_{ex}(s) = \frac{K_{2} K_{3} K_{A}}{K_{3} K_{6} K_{A} + (1 + s K_{3} T^{\prime }_{d0})(1 + s T_{A})} \end{aligned}$$
(12)

The transfer function of the PSS-E is given by [10] through

$$\begin{aligned} G_{psse}(s) = \frac{\Delta \nu _{psse}(s)}{\Delta \omega (s)} = K \underbrace{\left ( \frac{s T_{p}}{1 + sT_{p}} \right )}_{ \substack{High~pass}} \underbrace{ \left ( \frac{1 + sT_{1}}{1 + sT_{2}} \right )^{n} }_{ \substack{Phase~shift}} \end{aligned}$$
(13)

In order to achieve a positive damping effect with the PSS-E, the lead element must have the phase shift of the generator excitation \(G_{ex}(s)\). The high-pass filter allows the PSS-E to act on the voltage regulator only during speed changes, and this prevents voltage offset during steady-state operation. With the factor \(K\) the damping influence of the PSS-E can be defined.

The design of the PSS-G is to be carried out in the same way as for the PSS-E and the transfer function for the PSS-G is used from (13). The mechanical torque \(\Delta T_{m}\) provided by the PSS-G is given by

$$\begin{aligned} \Delta T_{m}(s) = \underbrace{\left ( \frac{1}{1 + sT_{g}} \right )}_{ \substack{Servo}} \underbrace{ \left ( \frac{1 - T_{w} s}{1 + \frac{1}{2} T_{w} s} \right ) }_{ \substack{Turbine}} G_{pssg}(s) \Delta \omega (s) \end{aligned}$$
(14)

In order for the damping capability to be improved by the PSS-G via the path of governor control path, it must compensate the phase shift of the hydraulic turbine and the servo dynamics [19].

For the design of the PSS-LQR, which in principle corresponds to a combination of a PSS-E and a PSS-G, the linear and time-invariant Heffron-Phillips model from Fig. 2 is integrated to the state space representation with system order \(n = 8\).

$$\begin{aligned} \mathbf{\Delta \dot{x}} &= \mathbf{A}\boldsymbol{\Delta} \mathbf{x} + \mathbf{B} \boldsymbol{\Delta} \mathbf{u} \end{aligned}$$
(15)
$$\begin{aligned} \mathbf{\Delta y} &= \mathbf{C}\boldsymbol{\Delta} \mathbf{x} + \mathbf{D} \boldsymbol{\Delta} \mathbf{u} \end{aligned}$$
(16)

The state vector \(\boldsymbol{\Delta} \mathbf{x} \) is determined by

$$\begin{aligned} \boldsymbol{\Delta} \mathbf{x} = \begin{pmatrix} \Delta \delta & \Delta \omega & \Delta E^{\prime }_{q} & \Delta E_{fd} & \Delta G & \Delta x_{i} & \Delta x_{w} & \Delta x_{t} \end{pmatrix}^{T} \in \mathbb{R}^{n} \end{aligned}$$
(17)

The multiple input multiple output (MIMO) system from (15) has two inputs, the power reference \(\Delta P_{0}\) and the voltage reference \(\Delta V_{ref}\), which are combined in the vector \(\boldsymbol{\Delta} \mathbf{u}\) from (18). The speed deviation \(\Delta \omega \) as well as the output signal of the hydro governor \(\Delta P_{g}\) are measurable and thus represent suitable output variables of the dynamic system (15).

$$\begin{aligned} \boldsymbol{\Delta} \mathbf{u} = \begin{pmatrix} \Delta P_{0} & \Delta V_{ref} \end{pmatrix} \in \mathbb{R}^{m} \qquad \boldsymbol{\Delta} \mathbf{y} = \begin{pmatrix} \Delta \omega & \Delta P_{g} \end{pmatrix}^{T} \in \mathbb{R}^{p} \end{aligned}$$
(18)

The dynamics matrix \(\mathbf{A} \in \mathbb{R}^{n\times n}\) of the MIMO system, assuming that the gain factor of the hydro governor is set as \(K_{p} = 0\), is constructed as follows.

$$\begin{aligned} \mathbf{A} = \begin{pmatrix} 0 & \omega _{0} & 0 & 0 & 0 & 0 & 0 & 0 \\ \frac{-K_{1}}{T_{j}} & \frac{-K_{D}}{T_{j}} & \frac{-K_{2}}{T_{j}} & 0 & \frac{-2}{T_{j}} & 0 & \frac{6}{T_{j} T_{w}} & 0 \\ \frac{-K_{4}}{T^{\prime }_{d0} } & 0 & \frac{-1}{T^{\prime }_{d0} K_{3}} & \frac{1}{T^{\prime }_{d0} } & 0 & 0 & 0 & 0 \\ \frac{-K_{A} K_{5}}{T_{A}} & 0 & \frac{-K_{A} K_{6}}{T_{A}} & \frac{-1}{T_{A}} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & \frac{-1}{T_{g}} & \frac{1}{T_{g}} & 0 & 0 \\ 0 & -K_{i} & 0 & 0 & 0 & -K_{i} (\sigma + \sigma _{t}) & 0 & \frac{K_{i} \sigma _{t}}{T_{t}} \\ 0 & 0 & 0 & 0 & 1 & 0 & \frac{-2}{T_{w}} & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & \frac{-1}{T_{t}} \\ \end{pmatrix} \end{aligned}$$
(19)

The input matrix \(\mathbf{B} \in \mathbb{R}^{n\times m}\) and the output matrix \(\mathbf{C} \in \mathbb{R}^{p\times n}\) are given by

$$\begin{aligned} \mathbf{B} = \begin{pmatrix} 0 & 0 & 0 & 0 & \frac{1}{T_{g}} & 0 & 0 & 0 \\ 0 & 0 & 0 & \frac{K_{A}}{T_{A}} & 0 & 0 & 0 & 0 \\ \end{pmatrix}^{T} \qquad \mathbf{C} = \begin{pmatrix} 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ \end{pmatrix} \end{aligned}$$
(20)

The direct feedthrough matrix \(\mathbf{D} \in \mathbb{R}^{p\times m}\) is set as a zero matrix. The necessary condition of controllability \((\mathbf{A}, \mathbf{B}) \) for the state space controller design as well as the observability of \((\mathbf{A}, \mathbf{C}) \) are satisfied. The closed-loop control system, consisting of the system of (15) with speed-controlled generator and the state feedback \(\boldsymbol{\Delta} \mathbf{u} = - \mathbf{K}^{T} \boldsymbol{\Delta} \mathbf{x}\) as damping element, is characterized by

$$\begin{aligned} \mathbf{\Delta \dot{x}} &= \left (\mathbf{A} - \mathbf{B \mathbf{K}^{T} } \right )\boldsymbol{\Delta} \mathbf{x} \end{aligned}$$
(21)

In order to place the eigenvalues of the autonomous system \(\left (\mathbf{A} - \mathbf{B} \mathbf{K}^{T} \right )\) optimally with respect to the fastest possible decay of oscillations that occur, the method of the linear quadratic regulator (LQR) according to [9] is used. This is an optimal controller design procedure in which the state feedback matrix \(\mathbf{K}^{T}\) is designed in such a way that the quadratic objective function

$$ J = \frac{1}{2} \int _{0}^{\infty } \mathbf{x}^{T} \mathbf{Q} \mathbf{x} + \mathbf{u}^{T} \mathbf{R} \mathbf{u}~dt \quad \rightarrow \quad \mathrm{min,} $$
(22)

considering the weighting matrices \(\mathbf{Q}\) and \(\mathbf{R}\), becomes minimal. In order to be able to damp the dominant electromechanical mode as best as possible, the modal weighting, as shown in [17], is used. This allows the regulator to direct influence the dominant oscillatory mode via the diagonal matrix \(\mathbf{M}\). The matrix \(\boldsymbol{\Phi }\) from (23) corresponds to the right eigenvector matrix of \(\mathbf{A}\) from (19).

$$ \mathbf{Q} = \mathbf{\hat{Q}}^{T} \mathbf{\hat{Q}} \quad \text{mit} \quad \mathbf{\hat{Q}} = \boldsymbol{\Phi } \mathbf{M} \boldsymbol{\Phi } ^{-1} $$
(23)

For the estimation of non-measured state variables, a Luenberger observer according to [12] with

$$\begin{aligned} \mathbf{\Delta \dot{\hat{x}}} &= \left (\mathbf{A} - \mathbf{L} \mathbf{C} \right )\mathbf{\Delta \hat{x}} + \mathbf{B} \boldsymbol{\Delta} \mathbf{u} + \mathbf{L} \mathbf{\Delta y} \end{aligned}$$
(24)

is applied.

The observer contains a model of the controlled system and a correction matrix \(\mathbf{L}\). The estimation error is defined by \(\boldsymbol{\Delta} \mathbf{e} = \boldsymbol{\Delta} \mathbf{x} -\boldsymbol{\Delta} \mathbf{\hat{x}} \). It should be mentioned that the placement of the eigenvalues of the matrix from the estimation error dynamics \(\left (\mathbf{A} - \mathbf{L} \mathbf{C} \right ) \) is again carried out using the LQR method.

3.2 Simulation results

The SMIBS from the beginning of Chap. 3 with the differential equations (2) to (7) and the algebraic equations (8) to (10) is applied as simulation model. The used hydro governor with the hydraulic turbine is presented in Fig. 2. The parameters of the first machine of the WECC three-machine model from [1] and [16] are applied as parameters for single-machine simulation model. For calculating the eigenvalues of the SMIBS, the dynamics matrix \(\mathbf{A}\) from (19) of the linearized system from (15) is used.

Due to the weak connection of the synchronous generator from Fig. 1 to the stiff grid, the electromechanical mode with \(s = \sigma + j \omega _{d} = -0.02 + \jmath \, 3. 26 \) has a damping ratio \(\zeta = -\sigma / \sqrt{\sigma ^{2} + \omega _{d}^{2}} \) of 0.75% and a natural frequency of 0.52 Hz. In Fig. 3, the time response of the grid frequency and the generator voltage \(V_{t}\), triggered by a voltage dip at \(V_{b}\) with a remaining voltage of 70% at \(t = 0.5\) s with a duration of 1 s, is shown. It can be seen in the frequency signal in Fig. 3 that the generator with speed control via the hydro governor (Gen+Hyd.-Gov.) has a higher tendency to oscillate than the one which is only operated with constant power (Gen only). The reason is the reduction of the damping ratio of the electromechanical mode due to the negative influence of the hydraulic pressure surge.

Fig. 3.
figure 3

Voltage dip at \(V_{b}\), starting at \(t = 0.5\) s and lasting 1 s, triggering an oscillation with 0.52 Hz. Top: grid frequency \(f\), bottom: generator voltage \(V_{t}\)

Full size image

By adding a power system stabilizer in the excitation path of the generator (PSS-E), the damping ratio of the dominant mode with \(s = -0.17 + \jmath \, 3.3 \) can be increased to \(5,07\)%. In Fig. 3, the improved damping behavior with the PSS-E can be seen in the frequency signal. At the same time, due to the PSS-E, the generator is excited with higher dynamics, which results in an increased oscillation behavior in the voltage characteristic \(V_{t}\) from Fig. 3 as a result.

When a power system stabilizer in the hydro governor control path (PSS-G) is added, the damping ratio of the dominant mode with \(s = -0.35 + \jmath \, 3.2 \) can be significantly increased to 10.72%. In the frequency response from Fig. 3, the clearly faster decaying oscillation due to the PSS-G can be seen. Since the generator excitation is not influenced by the PSS-G, this does not affect the generator voltage \(V_{t}\), compared to the basic version (Gen+Hyd.-Gov.). The occurring 0.52 Hz oscillation has the consequence of the PSS-G that the maximum actuating valve speed of 0.05 pu/s has already been reached. In Fig. 4, the limitation of the control gradient at the hydro governor output \(\Delta P_{g}\) from 1.5 s to 3 s can be clearly seen. When using the PSS-G, it must be ensured that it is only used in the case of correspondingly low-frequency oscillations where the turbine valve is not operated permanently at the maximum velocity gradient.

Fig. 4.
figure 4

Voltage dip at \(V_{b}\), starting at \(t = 0.5\) s and lasting 1 s, triggering an oscillation with 0.52 Hz. Top: hydro governor output \(\Delta P_{g}\) with PSS-G, bottom: PSS-E signal \(\Delta \nu _{PSSE}\)

Full size image

When using a PSS-E and PSS-G (PSS-EG) in combination, a damping ratio of 16.41% can be achieved for the dominant eigenvalue with \(s = -0.53 + \jmath \, 3.2 \). At the same time, the PSS-EG again increases the oscillation behavior at the generator voltage, because of the negative influence of the PSS-E.

With an optimal model-based controller (PSS-LQR) as a damping device, again additional signals are applied via the generator excitation and via the turbine controller in order to be able to damp the dominant oscillation mode in the best possible way. In Fig. 3, it can be seen that with the PSS-LQR the frequency oscillation decays fastest and for the dominant mode with \(s = -0.46 + \jmath \, 3.27 \), a damping ratio of 13.85% is achieved. The PSS-EG has a higher damping ratio than the PSS-LQR, but the PSS-LQR can respond more dynamically to changes due to the state feedback. When the PSS-EG is used as a damping device, an additional oscillation mode occurs at the turbine mechanics as well as with the PSS-G, which has negative effect on the damping behavior of the system. The higher dynamic response of the PSS-LQR compared with the PSS variants is shown in Fig. 4 by the immediate response in the \(\Delta \nu _{psse}\) and \(\Delta P_{g}\) signals, from 0.5 s to 1.5 s. The PSS-E output signals \(\Delta \nu _{psse}\) are not limited in their gradient, but they are limited to \(\pm 5\)% so that neighboring generators are not negatively affected in a multi machine system.

3.3 Investigation of the robustness

In order to investigate the robustness of the control strategies, the external connection impedance \(Z_{e}\) of the single-machine model is varied. As shown in Fig. 5, this results in a shift of the conjugate complex eigenvalue of the electromechanical mode from point 1 of 0.80 Hz to point 2 with 0.09 Hz, which corresponds to the typical frequency range of inter-area oscillations. The control strategies for oscillation damping (PSS-E, PSS-G, PSS-EG and PSS-LQR) have been designed for a natural frequency of the dominant mode with \(0,52\) Hz. From the top plot in Fig. 5 it can be seen that with decreasing natural frequency, the real part is shifted a bit further to the left for the generator with a hydro governor (Gen+Gov.-Hyd.). This means that the damping capability of the turbine controller increases a bit with decreasing natural frequency. The mechanical mode can be damped better by the generator with the hydro governor from frequencies lower than 0.15 Hz than the generator without speed control (Gen only). In comparison, the variation of the natural frequency by the external impedance has no significant influence on the generator without turbine governor (Gen only).

Fig. 5.
figure 5

Shift of the electromechanical eigenvalues by variation of \(Z_{e}\). Top: eigenvalue of the generator with hydro governor and no PSS. Middle: eigenvalue with PSS-E, PSS-G and PSS-EG. Bottom: eigenvalues with PSS-LQR

Full size image

The middle plot from Fig. 5, shows the influence of the PSS variants on the electromechanical eigenvalue very clearly. Here, the damping capability decreases continuously with decreasing frequency for all PSS variants. Compared to the PSS-E, the PSS-G can provide a significantly higher damping capability for the entire frequency range under consideration. Having a look at the PSS-EG, the damping behavior can be significantly improved again, especially at higher frequencies because of the influence of the PSS-E. The improved degree of damping by means of the PSS-G and PSS-EG can only be achieved if the actuating speed of the valve is sufficiently high for the frequencies to be damped. The other eigenvalues, are not significantly shifted by the PSS variants, which ensures the asymptotic stability for the considered frequency range.

In the lower picture from Fig. 5 the influence of the frequency variation with the PSS-LQR is shown. With decreasing frequency, the degree of damping of the electromechanical eigenvalue by the PSS-LQR increases very strongly and is significantly higher than with the PSS-EG. The eigenvalue of the generator excitation in the complex plane is shifted piecewise to the right by the PSS-LQR with decreasing frequency. From frequencies lower than 0.16 Hz, the eigenvalue is shifted to the right plane with real parts greater then zero due to the influence of the observer, which results in a generator instability.

After quadrupling the external impedance \(Z_{e}\), an 0.21 Hz oscillation, starting at \(t = 2\) s, is shown in Fig. 6. As mentioned before and illustrated in Fig. 5 also evident, the PSS-LQR exhibits a very robust behavior for this low-frequency oscillation and achieves the highest damping capability. With the PSS-E only a small improvement is achieved and with the PSS-G as well as the PSS-EG the damping of the oscillation, compared to the standard case (Gen+Hyd.-Gov.), can still be improved somewhat. The PSS variants prove to be significantly less robust to parameter uncertainties than the PSS-LQR, for frequencies greater than 0.16 Hz. To increase the robustness of the PSS and thus achieve improved damping capability over a wider frequency range, this requires parallel operation of multiple PSS, which significantly increases the design effort. The stable frequency range of the PSS-LQR can be increased by robust placement of eigenvalues, such as \(H_{\infty }\) control according to [15].

Fig. 6.
figure 6

Frequency oscillation after increased external impedance \(Z_{e}\) with resulting signal frequency of 0.21 Hz after voltage dip at \(V_{b}\) by 30%, starting at \(t = 2\) s and lasting 1 s.

Full size image

4 Three-machine model

In the three-machine model shown in Fig. 7, the damping capability of the PSSEG and that of the optimal state space controller (PSS-LQR) are investigated. All three machines are speed controlled by a hydro governor. The transient response of each generator is modeled using nonlinear differential equations in dq-coordinates according to [16] and neglecting saturation effects on the generators. Algebraic equations form the relationships of the generator currents, as well as the voltages and angles at the stator and in the network according to [16]. The electrical network is characterized by a node admittance matrix \(\mathbf{Y}_{n}\) and load flow calculations are used to calculate the initial states. Static load models with constant power are modeled at nodes 5, 6 and 8. Generator 1 is connected to generators 2 and 3 via a long transmission line with high impedance. There is a low impedance connection between generators 2 and 3. The inertia constant \(H\) is significantly larger for generator 1 with 23.64 than for generator 2 with 6.4 as well as 3.01 for the third machine according to the WECC three-machine model from [1]. The water starting time \(T_{w}\) is set to 1 s for all three hydraulic systems. The limitations for the PSS-E and PSS-G are set to the same values as the single-machine model for all three generators, with \(\Delta \nu _{psse,max} = \pm 5\)% and \(\Delta P_{g,rate} = \pm 0.05\) pu/s.

Fig. 7.
figure 7

Basic structure of three-machine model with base power = 100 MVA, output power G1 = 94 MW, output power G2 = 163 MW and output power G3 = 85 MW

Full size image

4.1 Modal analysis

In order to be able to evaluate the occurring oscillations by means of the modal analysis, the nonlinear three-machine model from Fig. 7 is linearized around a specific operating point. Due to the weak connection of generator 1, the damped natural frequency of the dominant eigenvalue \(s_{1} = \sigma _{1} + j \omega _{d,1} \) is 0.53 Hz and has a low damping ratio \(\zeta _{1} = -\sigma _{1} / \sqrt{\sigma _{1}^{2} + \omega _{d,1}^{2}} \) of 3.2%. From Fig. 8, it can be seen that at the 1st mode, generator 1 oscillates by 180 degrees phase shift against the remaining two generators. Generator 1 has the highest value of the normalized inertia constant \(H\), which is why it has the smallest amplitude in Fig. 8. The second oscillation mode, which is not as pronounced, characterizes the oscillation behavior from generator 2 to generator 3. The remaining modes have a significantly larger damping ratio of 15% and thus do not have a relevant effect on the oscillation behavior.

Fig. 8.
figure 8

Modal analysis: on the left the dominant oscillation mode, on the right the mode between generator 2 and 3

Full size image

The k-th participation factor \(p_{ik}\) to the i-th eigenvalue, is the product of the k-th component of the right eigenvector \(v_{R,ik}\) and the left eigenvector \(w_{L,ik}\), with \(p_{ik} = w_{L,ik} v_{R,ik}\) [16]. The participation factor can be used to identify those states with the greatest influence when oscillations occur. The analysis of the normalized participation vector of the dominant oscillation mode from Fig. 9 clearly shows that generator 2 with the electromechanical states, generator angle \(\delta _{2}\) and speed \(\omega _{2} \), has the greatest influence on the oscillation behavior. Compared to generator 2, generators 1 and 3 have a significantly lower influence with the states of the angle and speed with approximately 30%.

Fig. 9.
figure 9

Participation factors of the first 10 states of the dominant 1st mode

Full size image

The consideration of the participation vector makes it clear, that an improved damping capability at generator 2 leads to a significantly higher degree of damping at the dominant oscillation mode. However, the use of the optimal model-based controller is only useful for generator 1, because the connection to the rest of the system corresponds most closely to a single machine infinite bus system with a stiff grid connection.

In Fig. 10 the mode shapes of the PSS-LQR at generator 1 and the PSS-EG at generator 2 are shown. Due to the use of the PSS-EG at generator 2, the damping ratio can be increased to \(10,07\)%. With the PSS-LQR, this is more than doubled to \(6{,}86\)% compared to the basic variant, but the damping via generator 1 is not as effective as via generator 2. If generator 2 is only equipped with a PSS-E, a damping ratio of 4.84% can be achieved. In case a PSS-G is used without a PSS-E at generator 2, a value of 7.87% can be reached, which illustrates the high damping potential via the hydro governor control path.

Fig. 10.
figure 10

Modal analysis: left mode shapes with PSS-LQR at generator 1, right mode shapes with PSS-EG at generator 2

Full size image

4.2 Simulation results

In top picture of Fig. 11 the time response of the three-machine simulation model without additional damping devices is shown after a short circuit at node 5 with a duration of 100 ms. Due to the highest normalized inertia of generator 1, the short-circuit has much less effect in the frequency response than is the case compared to the other two generators. The plot 11 again illustrates the results using the modal analysis. With the PSS-EG on generator 2, the oscillation that occurs decays the fastest. The damping capability of the PSS-LQR at generator 1 is lower than with the PSS-EG, but compared to the basic variant (Gen+Hyd.-Gov.), the oscillation can be damped more efficiently. The significant voltage drop at node 2 after the short circuit is shown in Fig. 12. The oscillation occurring at generator node 2 decreases again more quickly with the PSS-EG than with the PSS-LQR or than with the basic variant the case is.

Fig. 11.
figure 11

Comparison of frequencies after short circuit with 100 ms at node 5. Top: standard behavior, middle: PSS-LQR at generator 1, bottom: PSS-EG at generator 2

Full size image
Fig. 12.
figure 12

Comparison of voltage at generator 2, after short circuit with 100 ms at node 5

Full size image

5 Summary and conclusion

In this work it could be shown that the combined use of a PSS-E and PSS-G in a hydropower plant control system can significantly improve the damping behavior with regard to inter-area oscillations. The PSS-G can provide significantly greater damping capability for low-frequency oscillations via the hydro governor than the PSS-E via the generator excitation. The combined use of PSS-E and PSS-G has not resulted in any negative mutual interference. The reasonable use of a PSS-G as well as a PSS-EG requires a high dynamic hydro governor and correspondingly large velocity gradients of the turbine valve. The combined control strategies require additional consideration of the increased mechanical load on the generator shaft and the actuator. With an optimal state space controller as damping element (PSS-LQR), the highest damping capability could be achieved in the single-machine model. The application of this method in the three-machine model used is not quite as effective as compared to the PSS-EG. This is because the PSS-LQR is only useful where the generator connection is similar to that of the SMIBS-model.

This represents a massive limitation of this method, in addition to the high design effort. Conversely, this does not mean that a generator with such a connection is automatically the optimal choice in terms of the best possible damping capability. This highlights the importance of the overall consideration of the power system with respect to the best possible use of damping methods. The PSS-LQR has been shown to be an extremely robust method in the single-machine model for a defined wide frequency band. Generator instability can occur with such a PSS-LQR for very large parameter deviations. This requires accurate knowledge of all necessary parameters during design and makes robust eigenvalues placement in practical application mandatory. The PSS-EG is simpler in design and can be applied more precisely to the generator with the greatest influence on the oscillation behavior in the grid. However, the mutual influence of the voltage regulators of neighboring generators by the PSS-E must be taken into account. To increase robustness with the PSS, several of them must be connected in parallel. The promising results with the PSS-EG make it clear that hydropower plants with appropriate control strategies can increase the damping capability with respect to inter-area oscillations in the power system and thus make an important contribution to increasing power system stability.