Abstract
In this paper, we take a look at Austria’s renewable energy targets established in the Renewable Energy Expansion Act (EAG), aiming to annually generate an additional 10 TWh of wind power by 2030. We conduct a GIS (geographic information system)-based analysis to determine average wind power density in Austria on a cellular level while considering prohibited regions, such as national parks, where building wind turbines might not be allowed. The calculated expansion potential for all remaining regions of Austria is allocated to the closest corresponding transmission nodes. Furthermore, we suggest an optimization algorithm to geographically distribute the expansion of wind power capacity to applicable transmission nodes. Finally, we conduct a case study to validate the algorithm using historical data on expansion and utilize it to predict an annual scenario for wind power expansion from 2021 to 2030 on a regional level. The total expansion required to achieve the goal of 10 TWh is assessed to be 4 GW based on predefined full load hours while assuming an exponential increase in annually added capacity (from 250 MW in 2021 to 590 MW in 2030).
Zusammenfassung
Diese Arbeit befasst sich mit dem im österreichischen Erneuerbaren-Ausbau-Gesetz (EAG) festgelegten Ziel, bis 2030 jährlich zusätzlich 10 TWh aus Windkraft zu erzeugen. Wir führen eine GIS (Geographic Information System)-basierte Analyse durch, um die durchschnittliche Windenergiedichte auf zellulärer Ebene unter Berücksichtigung von Ausschlusszonen wie Nationalparks, in denen der Bau von Windkraftanlagen nicht erlaubt sein kann, zu bestimmen. Das berechnete Expansionspotential für alle übrigen Gebiete Österreichs wird den räumlich nächstgelegenen Übertragungsknoten zugeordnet. Darüber hinaus schlagen wir einen Optimierungsalgorithmus vor, um die Erweiterung der Windkraftkapazität geografisch auf die entsprechenden Übertragungsknoten zu verteilen. Schließlich führen wir eine Fallstudie durch, um den Algorithmus anhand historischer Expansionsdaten zu validieren und daraus ein jährliches Szenario für den Ausbau der Windenergie von 2021 bis 2030 auf regionaler Ebene vorherzusagen. Die insgesamt erforderliche Kapazitätserweiterung zur Erreichung des Ziels von 10 TWh wird anhand der vordefinierten Volllaststunden mit 4 GW berechnet, wobei von einer exponentiellen Erhöhung der jährlich zugebauten Windkraftkapazität ausgegangen wird (von 250 MW im Jahr 2021 auf 590 MW im Jahr 2030).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The European electricity sector is facing radical changes as the European Union (EU) aims to achieve climate neutrality by 2050 (net zero greenhouse gas emissions). By then, projections estimate electricity to represent 53% of final energy demand [1]. In order to tackle those sophisticated challenges, EU Member States are adopting their national energy and climate strategies. Austria set the objective of 100% renewable electricity by 2030 (national balance) [2]. Wind power plays a key role in achieving this target, as the technology is expected to provide 10 TWh of additional annual generation.
To determine resulting effects on the electricity system, it is essential to integrate wind energy into electricity economic models. In general, renewable penetration/generation targets are defined as top-down scenarios for given years, which presents a challenge since none or only few specific expansion projects including corresponding locations are determined yet. However, locational information (e.g. feed-in transmission system node) is a necessary condition for electricity economic models to determine significant load flows and identify congestions on a transmission system level. One such model is ATLANTIS, which is developed at the Institute of Electricity Economics and Energy Innovation at Graz University of Technology [3]. ATLANTIS is an optimization model determining the optimal power flow in a transmission network. Model results include detailed information on electricity generation per power plant, power flow, etc.
Wind power generation is limited to cut-in (between 2.5 and 4.5 m/s) and cut-out (between 20 and 34 m/s) wind speeds. Lower wind speeds are not sufficient to initialize turbine rotation while at higher wind speeds turbines are shut down to prevent mechanical damage [4]. Given those limits, average wind speeds represented in wind maps (for a given height above ground) do not reflect wind power potential properly, as they may result from a sequence of (very) high and (very) low wind speeds. Therefore, our analysis of wind power density is based on a Weibull distribution which reflects the probability of different wind speeds at a given location.
This paper is organized as follows: in Sect. 2, candidate areas and their wind power potentials are associated to corresponding transmission nodes; Sect. 3 describes our novel algorithm for optimizing wind power expansion planning; in Sect. 4, the algorithm is evaluated by actual wind power expansion from 1995 to 2020; in Sect. 5, the algorithm is applied to transform Austria’s 10 TWh top-down wind power target into specific annual expansion plans per transmission node. Sect. 6 discusses the results and ultimately, Sect. 7 presents the final conclusion.
2 Determining wind power potential
Utilizing a GIS (geographic information system)-based analysis, we determine the average wind power density of candidate areas per transmission node on a cellular level. The developed six-step method is depicted in Fig. 1.
-
Step 1:
Calculation of wind power density for each cell.
-
Step 2:
Determination of prohibited areas.
-
Step 3:
Exclusion of prohibited areas.
-
Step 4:
Assigning candidate areas to transmission nodes (closest spatial distance).
-
Step 5:
Computation of available wind power potential per transmission node.
-
Step 6:
Computation of average wind power density per transmission node.
We calculate the Austrian wind power density \(\mathit{Wpd}\) (1) for a grid of square cells (resolution 250 m) based on data from Global Wind Atlas (Technical University of Denmark [5]). The database provides the shape parameter \(k\) and scale parameter \(a\) of the applied Weibull distribution as well as air density \(\rho \) per cell. Those parameters are available for specific heights above ground (10, 50, 100, 150 and 200 m). In Austria, current average hub-height is approximately 90 m (calculated based on [6]), thus the dataset for 100 m is applied.Footnote 1 With respect to cut-in and cut-out wind speeds, only the velocity spectrum \(v\) from 5 to 25 m/s is considered. The rate at which wind power plants can transform kinetic wind energy into electricity is limited by the power coefficient \(c_{P}\). According to Betz’s law, the theoretical limit of \(c_{P}\) is 0.593 but practically the factor is 0.500 which is applied in this work.
Exclusion of prohibited areas due to legal or technical circumstances is crucial for deriving relevant results. Prohibitions include:
-
(a)
Areas with slopes exceeding 15° [7].
-
(b)
Areas 2000 m above sea level.Footnote 2
- (c)
-
(d)
Settlement areas [10].Footnote 3
Applying aforementioned restrictions, a theoretically available area of 41602 km2 is derived. Table 1 summarizes the results per federal state. Vienna, which is the smallest, most urbanized federal state features 15 km2, while Lower Austria features 10667 km2 of applicable area. The authors in [11] find that in general 0.5 W/m2 of wind power capacity can be installed without turbines interfering with each other (0.3 W/m2 for areas lager 10000 km2). Since there is no single continuous area larger than 10000 km2, 0.5 W/m2 is used to determine the maximum technical potential.
Available areas are assigned to their closest transmission nodes using a spatial analysis. From the aggregated area per node, we calculate the maximum technical potential per node \(P_{n}\) limiting wind power expansion in the model. Since areas with higher wind power potentials should be utilized first, we aggregate the wind power density per node and normalize it by the nodes corresponding area to determine its average wind power density \(\mathit{AWp} d_{n}\) (Fig. 1, bottom right side).
3 Utilizing optimization for annual wind power expansion
Since the national target of 10 TWh annual wind power generation by 2030 represents a top-down formulation, annual expansion plans have to be derived and implemented to the model. Since a private investor’s objective is to maximize profits (generally by maximizing their electricity generation), it is very likely that areas with higher wind power potential will be utilized first. Moreover, from a social welfare maximization point of view, it is more efficient to use the areas with the highest potential first. We apply an optimization algorithm maximizing the overall utilized wind power potential (2), while distributing the required wind power capacity across all nodes until 2030.

Constraint (3) represents the residual potential (difference of potential \(P_{n}\) as determined in Sect. 2 and already installed wind power capacity per node) limiting total expansion capacity at node \(n\). Constraint (4) specifies the annual expansion target to be met. Constraint (5) represent the limitation, that expansion at node \(n\) is only possible every \(x\) years to achieve a better distribution across the nodes. Finally, constraint (6) represents maximum expansion per node while considering the cooldown phase between new installations.
4 Validation
To validate our approach, we model wind power expansion from 1995-2020 for Austria. For \(C_{t}^{\mathit{year}}\) we use annual expansion data from [12]. For 1995, \(P_{n}^{\mathit{res}}\) is equal to the potential \(P_{n}\) determined in Sect. 2 since up to this point zero applicable area has been utilized. \(\overline{C}_{n, t}^{\mathit{year}}\) is limited to 15 MW/year. Expansion is set to be possible every \(x=2\) years per node. We compare the results to actual expansion within set timeframe on a NUTS-3 level.
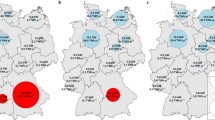
Figure 2 depicts actual installed capacity as well as modelling results for 2020. Reality and modelling results diverge due to various federal states’ legislations, prohibiting or promoting certain areas which are not considered in the optimization. Key findings are:
-
(a)
In Northern Burgenland (AT112) and the south of Vienna (AT127) realized expansion is higher than optimization results.
-
(b)
There are five areas where optimization results in expansion levels exceed 100 MW. However, actual expansion levels are less than 100 MW.
-
(c)
Carinthia (AT212) has high expansion potential. However, little has been utilized yet due to regulations based on visibility issues.
-
(d)
Lower Austria and Styria: Variance in expansion density due to ‘suitability and priority zones’ specified by the federal states [13], [14].
-
(e)
Region (AT122) is prohibited due to ‘near-natural tourism zones’ and ‘alpine regions worthy of protection’ [15].
-
(f)
In Styria, regions (AT223) and (AT224) hold the highest expansion potential. Region (AT224) includes several suitability zones (Fürstkogel, Herrenstein, Pongratzer Kogel) as well as priority zones (Steinriegel, Pretul). Some smaller wind park projects have already been realized (Herrenstein, Pongratzer Kogel, Plankogel). However, since total capacity is less than 100 MW, region (AT224) is not highlighted in Fig. 2 (top).
Optimization results for 1995-2020 reveal a spatial distribution pattern close to actual expansion, despite the lack of integration of legal restrictions. However, achieving the ambitious expansion target implicates adaptation of legal restrictions. Therefore, we consider our optimization applicable for simulating future wind power expansion.
5 Case study: 10 TWh top-down scenario
We conduct a case study, modelling wind power expansion from 2021-2030. As initial starting point, we refer to georeferenced data on existing wind power plants for 2020 found in [6] and depicted in Fig. 3. Utilizing a spatial analysis, we reference those wind power plants to their closest transmission nodes. For 2020, \(P_{n}^{\mathit{res}}\) is equal to \(P_{n}\) reduced by existing capacity. Again, \(\overline{C}_{n, t}^{\mathit{year}}\) is limited to 15 MW/year and expansion per node is limited to every other year (\(x=2\)).
Existing wind power plants as of 2020 [6]
According to (7), total wind power \(C_{2030}\) corresponding to the energy target \(E_{2030}\) of 10 TWh is determined. \(\mathit{FLH}\) represents full load hours applicable for wind power plants (in Austria: 2500 h/year [2]). This results in a 4 GW expansion target by 2030.
To reach this target, we assume an exponential increase in annual expansion, depicted in Fig. 4.
Modelling results per transmission node are depicted in Fig. 5. As expected, in already highly utilized regions expansion levels are relatively low (compare to (AT112), (AT127) and (AT126) in Fig. 2 and Fig. 3). Aggregated annual expansion is summarized in Table 2 in descending order.
6 Discussion and prospects
The presented findings illustrate the ambitiousness of Austria’s 2030 wind energy target. However, due to ongoing electrification, especially in industry and the transport sector, national electricity generation is estimated to be 81 TWh in 2040 compared to 70 TWh in 2020 and 71 TWh in 2030 [16]. This presents yet another challenge for wind power expansion and the power system in general. Repowering of existing wind parks and further exploitation of candidate areas alongside enhancements in hub-height will be the setscrews of the future. In the context of spatially distributed intermittent renewables the role of transmission system expansion cannot be overlooked. Generally, there are two categories of wind turbines. Turbines with nominal power of up to 2.5 MW are commonly connected to separate medium voltage substations (generally 20 kV or 30 kV in Austria), while turbines with nominal power above 2.5 MW tend to come with a transformer and medium voltage gas-insulated switchgear integrated to the nacelle. However, the nominal power of wind power plants commonly exceeds local electricity demand, which facilitates connecting those plants to 110 kV substations where the power flow enters the 110 kV power grid. During off-peak demand and peaking wind power generation the 220 kV, respectively 380 kV transmission system can facilitate storing excess energy in pumped storage hydro power plants. However, in our opinion the most urgent factor towards successful expansion and system integration of wind power in years to come is expansion of the 110 kV network.
7 Conclusion
In this paper, we apply a GIS-based analysis to determine average wind power density on a cellular level. We allocate the technical wind power potential \(C_{n}\) to corresponding transmission nodes. We re-formulate the Austrian national top-down scenario of 10 TWh additional wind power generation by 2030 as an annual expansion target. We derive a novel algorithm to optimize wind power expansion, validate it by modelling historic expansion and utilize it to model wind power expansion for 2021–2030.
The technical potential of 20.8 GW (see Table 1) is similar to the study in [17], determining 23.7 GW. However, the study does not exclude all prohibited areas like nature protection zones and maximum altitude is set to 2100 m. As expected, our conservative approach results in a lower technical potential. Despite the integration of legal restrictions, the algorithm provides proper results when validated. Since it is likely that legal restrictions will be relaxed in order to achieve expansion targets they will be even less of a factor.
In future research, additional prohibited areas like airports and power lines could be excluded. Furthermore, the process of allocating wind power plants to the spatially closest transmission node could be refined, for example by introducing a weight factor and different building costs per NUTS-3 region reflecting investor’s total costs. As our approach demonstrates, Austria’s sophisticated renewable electricity target can be achieved. However, governmental monitoring is obligatory and interventions necessary if annual expansion levels fall short.
Notes
Average hub-height is expected to increase. Therefore, future analysis based on dataset for 150 and 200 m is considered.
In Austria, approval of wind power projects is regulated on federal state level. Since legislation varies in federal states, we take a conservative approach and therefore excluded areas 2000 m above sea level.
The Global Human Settlement Model Grid (GHS-SMOD) is based on a square cellular approach (resolution 1000 m) and classifies cells as one of eight categories (from ‘urban centre’ to ‘very low-density rural area’). In our analysis, only ‘low-density rural areas’ and ‘very low-density rural areas’ have been considered.
References
European Commission (2018): A Clean Planet for all. A European long-term strategic vision for a prosperous, modern, competitive and climate neutral economy. Com(2018), 773, 114.
BMK (2021): Erneuerbaren-Ausbau-Gesetz.
Stigler, H., Bachhiesl, U., Nischler, G., Feichtinger, G. (2016): ATLANTIS: techno-economic model of the European electricity sector. Central European Journal of Operations Research, 24(4), 965–988. https://doi.org/10.1007/s10100-015-0413-8.
Quaschning, V. (2019): Regenerative Energiesysteme.
Technical University of Denmark Global Wind Atlas 3.0. https://globalwindatlas.info. (Accessed Dec. 06, 2019).
IG Windkraft (2021): Windrad-Landkarte. https://www.igwindkraft.at/?xmlval_ID_KEY[0]=1055. (Accessed Apr. 08, 2021).
Prinz, T., Biberacher, M., Gadoche, S., Mittlböck, M., Schardinger, I., Zocher, D. (2009): Energie und Raumentwicklung – Räumliche Potenziale erneuerbarer Energieträger. Wien.
European Environment Agency (2020): Natura 2000 data – the European network of protected sites https://www.eea.europa.eu/data-and-maps/data/natura-11#tab-gis-data. (Accessed Apr. 09, 2021).
European Environment Agency (2019): Nationally designated areas (CDDA). https://www.eea.europa.eu/data-and-maps/data/nationally-designated-areas-national-cdda-14. (Accessed Apr. 09, 2020).
European Commission (2019): GHS-SMOD 2019. https://ghsl.jrc.ec.europa.eu/ghs_smod2019.php (Accessed Apr. 08, 2021).
Miller, L. M., Kleidon, A. (2016): Wind speed reductions by large-scale wind turbine deployments lower turbine efficiencies and set low generation limits. Proceedings of the National Academy of Sciences of the United States of America, 113(48), 13570–13575. https://doi.org/10.1073/pnas.1602253113.
IG Windkraft (2021): Windkraftleistung in Österreich Ende 2020 und Prognose 2021. https://www.igwindkraft.at/fakten/?xmlval_ID_KEY%5B0%5D=1234. (Accessed Apr. 14, 2021).
Amt der NÖ Landesregierung (2021): Verordnung über ein Sektorales Raumordnungsprogramm über die Windkraftnutzung in NÖ. Available: www.ris.bka.gv.at [Online].
Amt der Steiermärkischen Landesregierung Abteilung 17 Landes- und Regionalentwicklung (2019): Entwicklungsprogramm für den Sachbereich Windenergie. Available: https://www.landesentwicklung.steiermark.at/cms/dokumente/12755541_154267170/b6afc021/SAPRO_Wind_2019_SUP_Umweltbericht_2019-09-25a.pdf. (Accessed Apr. 15, 2021) [Online].
Umweltplanung ZT GmbH, K. (2021): Umweltbericht zum NÖ SekROP Windkraftnutzung ergänzte Fassung basierend auf der Verordnung über ein Sektorales Raumordnungsprogramm über die Windkraftnutzung in NÖ, LGBl. 8001/1-0, 2014. Available: https://www.raumordnung-noe.at/fileadmin/root_raumordnung/land/landesentwicklungsplanung/ROP_Windkraft/SekROP-Windkraft_Umweltbericht_Endergebnis_LGBl-8001-1-0.pdf. (Accessed: Apr. 15, 2021) [Online].
BMK (2019): Integrierter nationaler Energie- und Klimaplan für Österreich. Available: https://www.bmk.gv.at/dam/jcr:032d507a-b7fe-4cef-865e-a408c2f0e356/Oe_nat_Energie_Klimaplan.pdf. (Accessed: Aug. 11, 2021) [Online].
Winkelmeier, H., Krenn, A., Zimmer, F. (2014): Das realisierbare Windpotential Österreichs für 2020 und 2030.
Funding
Open access funding provided by Graz University of Technology.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access Dieser Artikel wird unter der Creative Commons Namensnennung 4.0 International Lizenz veröffentlicht, welche die Nutzung, Vervielfältigung, Bearbeitung, Verbreitung und Wiedergabe in jeglichem Medium und Format erlaubt, sofern Sie den/die ursprünglichen Autor(en) und die Quelle ordnungsgemäß nennen, einen Link zur Creative Commons Lizenz beifügen und angeben, ob Änderungen vorgenommen wurden. Die in diesem Artikel enthaltenen Bilder und sonstiges Drittmaterial unterliegen ebenfalls der genannten Creative Commons Lizenz, sofern sich aus der Abbildungslegende nichts anderes ergibt. Sofern das betreffende Material nicht unter der genannten Creative Commons Lizenz steht und die betreffende Handlung nicht nach gesetzlichen Vorschriften erlaubt ist, ist für die oben aufgeführten Weiterverwendungen des Materials die Einwilligung des jeweiligen Rechteinhabers einzuholen. Weitere Details zur Lizenz entnehmen Sie bitte der Lizenzinformation auf http://creativecommons.org/licenses/by/4.0/deed.de.
About this article
Cite this article
Gaugl, R., Klatzer, T., Bachhiesl, U. et al. GIS-based optimization – achieving Austria’s 2030 wind energy target. Elektrotech. Inftech. 138, 590–596 (2021). https://doi.org/10.1007/s00502-021-00932-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00502-021-00932-y