Evaluation and loss estimation of a high-speed permanent magnet synchronous machine with hairpin windings for high-volume fuel cell applications

Abstract

High-speed machines offer several advantages, such as small sizes, avoidance of mechanical gears, and low maintenance, which has led to considerable research dedicated to them in the past decade. In recent times, rectangular wire windings with a hairpin structure have gained prominence in traction motors in the electromobility sector due to their high slot fill factor, simple production, and good thermal properties. Taking these advantages into consideration, this paper analyzes the possibility of using a high-speed permanent magnet synchronous machine (PMSM) with hairpin windings as an electric turbo compressor in fuel cell applications and outlines the critical design aspects.

Zusammenfassung

Die Vorteile von Hochdrehzahlmaschinen, wie geringe Abmessungen, Vermeidung mechanischer Getriebe und geringer Wartungsaufwand, haben in den letzten Jahren vermehrt zur Forschungsarbeiten auf diesem Gebiet geführt. Im Elektromobilitätsbereich wurde der Einsatz rechteckiger Hairpin-Wicklungen in Traktionsmaschinen vorangetrieben, da diese einen sehr hohen Kupferfüllfaktor bieten, leicht zu fertigen sind und gute thermische Eigenschaften aufweisen. Unter Berücksichtigung dieser Vorteile werden in dieser Arbeit die Möglichkeit untersucht, eine permanentmagneterregte Hochdrehzahlmaschine mit Hairpin-Wicklungen als elektrischen Luftverdichter in Brennstoffzellenanwendungen einzusetzen, und die kritischen Auslegungsaspekte behandelt.

1 Introduction

Mobile fuel cells in automotive applications demand highly pressurized particle-free air (oxygen) supply for optimal power generation with high efficiency and power density. In recent years, the trend is tending towards higher mass flow and pressure ratios, and this is achieved by means of high-speed turbo compressors. These units are directly driven by electric motors with contact-free bearings and power electronic converters, and as in the case of every electrical component in automotive environment, they must have an optimized lifetime in order to be resource-friendly, occupy small space and should weigh as less as possible. Furthermore, they also must be designed cost-optimized and easy to be manufactured to cater to the high-volume manufacturing.

A technical survey reveals the state of the art in high-speed motor development that is linked with sustainable mobility. One example is a two-pole, iron-core, liquid-cooled PMSM operating up to a speed of 110 000 min⁻¹ developed in [1]. Another is [2] that operates at 120 000 min⁻¹ delivering 12 kW. Innovative concepts such as the use of amorphous metals in rotor [3] appear promising and they still have to further mature for market acceptance. It is noticeably clear that PMSM with no rotor saliency dominate the high-speed motor sector and for speeds above 100 000 min⁻¹ they are the preferred choice. A recent report [4] clearly states that along with the well-known design challenges such as mechanical rotor design, machine loss minimization, efficient heat transfer, more and more serial production related issues are appearing in the foreground.

The manufacturing-related challenges and the selection of a specific material/process have a causal connection with the design constraints that forced them in the first place. The focus is on the question of how the stator of the high-speed electric motor is wound and how the individual coils are arranged inside the slots. Round bundled wires manufactured with pull-in technology is the status quo but they are associated with longer and complicated production process. In recent times, rectangular wire winding, in the form of hairpin structure, has gained prominence in traction applications due to their high slot-fill factor, good thermal characteristics and relatively easy manufacturability. However, for high-speed applications they suffer from high AC copper losses and are usually not preferred without any special corrective measures such as using litz-wires which increase the cost.

Another design issue which directly influences material selection is the rotor losses and the associated temperature rise of the magnets. To prevent irreversible demagnetization of the magnets, rare-earth magnets such as Neodymium-iron-boron (NdFeB) with high coercivity are employed. Dysprosium is used to raise the coercivity for such demanding applications and a projection made by [5] indicates the vulnerability in its supply chain. An alternative to NdFeB is Samarium-cobalt (SmCo) which has a superior temperature stability. They work well for prototypes [6] when the temperature distribution of the magnets is not well known, and the functionality takes the primary importance. However, substituting NdFeB with SmCo for mass produced electric motors is potentially still a risky decision in terms of global material availability.

Due to the above-mentioned issues this article presents a performance evaluation of a high-speed PMSM equipped with hairpin windings to be used as a turbo compressor drive. Comparisons of detailed electromagnetic and thermal analysis with a similar motor with round bundled wires are made and critical features are highlighted.

2 Requirements and system description

To make a comparison, two machine topologies are defined (PMSM-RW – The original prototype stator with round bundled winding, PMSM-HW – The new stator with hairpin winding) and the characteristic data are presented in Table 1. The main components are shown in Fig. 1.

Fig. 1.

Axial cross section of the evaluated compressor motor

Table 1. Characteristic machine data

The relevant features of the topology PMSM-RW, against which PMSM-HW is compared, are addressed below. It is designed with a two-pole PM rotor and a distributed ($q_{\mathrm{s}}$ = 2), double-layer, short-pitched ($W$/$\tau _{\mathrm{p}}$ = 5/6) stator winding with a fundamental winding factor of 0.933. The total number of turns per slot per layer is 4 with 14 parallel stranded conductors per turn and an individual conductor diameter of 0.8 mm. PMSM-RW has a parallel tooth configuration whereas PMSM-HW, due to inherent manufacturing requirements associated with hairpin windings, have a parallel slot configuration. This feature has a massive influence on the performance and will be described in detail. The slots are filled with insulating epoxy-resin, theoretically increasing the thermal conductivity between the copper and stator iron by a factor of about 4. The rotor comprises of a cylindrical magnet without laminated back-iron. A 2 mm thick titanium-alloy ring (TiAl6V4) assures the safe magnet fixation up to 20% overspeed. The machine is cooled with a water jacket cooling with a water/glycol mixture and an average inlet temperature of 68 °C.

An optimized 15 kVA drive inverter with increased switching frequency (up to 120 kHz) using wide-band-gap power semiconductors has been developed specifically for this application and shown in Fig. 2. Among the various influencing factors and dependencies between electrical machine and drive inverter, the current ripple and additional losses in the machine rotor due to inverter time harmonics are of particular importance. Since these losses are a direct function of switching frequency and modulation index, by using higher switching frequency and employing a sine filter the losses are shifted from the machine’s rotor to the drive inverter, where they can be efficiently cooled.

Fig. 2.

Developed inverter power stage prototype for the SMD devices

3 PMSM with hairpin windings

The design criteria and choices for hairpin windings are elaborated in this section. The direction of insertion of the rectangular wire windings can either be radial or axial. For the radial insertion direction, the windings can be pre-twisted and pre-connected, but the process requires an open-slot configuration. However, open slots generate big torque and field pulsations, and this predominantly increases the rotor losses and hence avoided. The next consideration is the slot shape. In the case of rectangular wire windings, due to manufacturing and mechanical reasons, the slot shape is always parallel. This has two major effects – reduction of stator iron losses for an equivalent magnetic loading and increased thermal conductivity between the winding and stator iron.

The first effect of iron loss reduction can be demonstratively seen in Fig. 3. Since there is only a single pinching point in the magnetic flux path where the tooth tapers down near the air gap, the flux has more space to relax in the stator tooth region elsewhere. This causes a reduction in the amplitude of the flux density and thus a reduction in the iron losses. For a current loading of 400 A/cm, the absolute values of the iron losses are 232 W for PMSM-RW and 157 W for PMSM-HW.

Fig. 3.

Comparison of iron loss density ($p$_v,Fe,s) distribution in the stator between PMSM-RW and PMSM-HW with PM-Excitation and a current loading of 400 A/cm

The second effect is the increased thermal conductivity between slot copper and stator iron, and this leads to efficient heat transfer. This is because in parallel slot configuration the heat flux has a uniform path all around the heat source whereas it is not the case with parallel tooth. Also, the round bundled wires heat up non-homogeneously with hot spots developing at the center of the slots. Figure 4 shows the results of a sensitivity analysis where the temperature rise in the stator winding for both PMSM-RW and PMSM-HW are calculated for different values of copper and iron losses with a 2d FEM thermal model. With the same material parameters (thermal resistivity values for air, insulation, epoxy resin filling, copper and iron) and cooling (equivalent heat transfer coefficient at the stator outer surface, $\alpha$_Th= 2000 Wm⁻²K⁻¹), PMSM-HW has a better thermal utilization factor of up to 80%.

Fig. 4.

Thermal sensitivity analysis for the topologies PMSM-RW and PMSM-HW – The data points shown are the losses required to raise the stator winding temperature to 180 °C for the same cooling conditions

The next step is to calculate the optimal conductor height. At the rated fundamental frequency of 2 kHz and 20 °C, the penetration depth for the field in the copper winding is 1.48 mm. Both the skin- and the proximity effects are captured by 2d magnetoharmonic FEM calculations at the rated frequency of 2 kHz and a series of simulations show the dependency of the AC copper losses on the conductor height in Fig. 5. At one extreme, the installation space allows a maximum of 8 conductors per slot with an individual height of 2 mm. A decrease in conductor height causes a reduction in AC copper losses until 1 mm and the relation can be approximated by a quadratic polynomial. This means the rate of change of AC copper loss is maximum around 2 mm and linearly reduces to zero around 1 mm. The optimal conductor height would in this case be 1 mm. Due to manufacturing tolerances and process related issues the conductor height is instead chosen to be 1.5 mm which is still a good compromise. This frees up 2.5 mm of space in the yoke and the stator outer diameter is reduced from 86 mm to 81 mm. The DC stator phase resistance at 20 °C is calculated to be 16.72 m$\Omega$ for PMSM-HW.

Fig. 5.

Dependency of stator copper losses ($P$_v,Cu,s) on individual slot conductor height ($h$_Cu,s). The AC copper losses are calculated at a supply frequency of 2 kHz and a constant phase current amplitude of 28.0 A_Eff

Interesting to note is the fact that for a specific stator inner bore dimension, increasing the outer diameter does not increase the utilization because of the resulting high AC copper losses. Instead, the rotor diameter can be increased, but this leads to increased mechanical stress due to higher centrifugal force and opens other design issues.

3.1 Electromagnetic analysis

The cross-sectional view of PMSM-HW is shown in Fig. 6. The pole coverage ratio of the parallel magnetized rotor magnet is $\alpha _{\mathrm{p}}$ = 1. Parallel magnetization leads to considerable reduction in higher order harmonics and the air gap flux density distribution is sinusoidal apart from the tooth modulations.

Fig. 6.

2d cross section of PMSM-HW with stator bore diameter, $d$_si = 25.0 mm and stator outer diameter, $d$_so = 81.0 mm

In order to avoid excessive stator losses, the flux densities in the yoke and teeth are not chosen as high as that of a highly utilized PMSM. This implies that the machine is not driven into saturation at all. Numerical simulations are carried out and “Locked Rotor” simulations enable to determine the machine generated torque for various current densities and current angles. For a DC-bus voltage level of 340 V, there is no requirement of field weakening. The electromagnetic torque and power versus speed characteristics are determined solely by maximum-torque-per-ampere (MTPA) control. Accounting for all the losses, the mechanical torque and power are calculated. The considered machine topology can be classified as a “large air gap” machine since the rotor lacks a back iron and consists only of materials with relative permeability, $\mu _{\mathrm{r}}\ \sim$ 1. Consequently, the main inductance is very low, and it is of comparable magnitude with the leakage inductances. Computation and modelling the leakage inductances become a crucial part for such machines and will be discussed in detail. Leakage inductances can be classified in general as self and mutual inductance components of slot leakage flux, higher order Fourier harmonics and end winding overhang. The portion due to slot leakage flux and higher order spatial harmonics can be easily calculated with either approximate magnetic field distribution inside the slots or by simple 2d magnetostatic FEM simulations. The average $d$- and $q$-axis inductances ($L$_dd,s and $L$_qq,s respectively) can be calculated from the stator current dependent flux linkages ($\Psi _{\mathrm{d}}$($i_{\mathrm{d}}$,$i_{\mathrm{q}}$) and $\Psi _{\mathrm{q}}$($i_{\mathrm{d}}$,$i_{\mathrm{q}}$)) using (1) and (2). The inductances are calculated as mean values for $N$ different rotor positions to include the slotting harmonics. Since the topology exhibits a non-salient feature and no saturation, the calculated $d$- and $q$-axis inductances are equal and amount to 64.2 μH for all values of currents. However, this value does not include the end winding overhang inductance.

The average $d$- and $q$-axis inductances are,

$$\begin{aligned} L_{\mathrm{dd},\mathrm{s}} =& \frac{\sum _{i = 1}^{N} \frac{\left ( \psi _{\mathrm{d}}^{i}(i_{\mathrm{d}},i_{\mathrm{q}}) - \psi _{\mathrm{d}}^{i}(i_{\mathrm{q}}) \right )}{i_{\mathrm{d}}}}{N} \end{aligned}$$

(1)

$$\begin{aligned} L_{\mathrm{qq},\mathrm{s}} =& \frac{\sum _{i = 1}^{N} \frac{\left ( \psi _{\mathrm{q}}^{i}(i_{\mathrm{d}},i_{\mathrm{q}}) - \psi _{\mathrm{q}}^{i}(i_{\mathrm{d}}) \right )}{i_{\mathrm{q}}}}{N} \end{aligned}$$

(2)

A more complicated task is to predict the portion due to end winding overhang. [7] proposes a method in which the end windings are dissected into polygon trains and formulating a limited number of Neumann integrals to calculate the mutual and self-inductances. According to Kürzel mentioned in [8], empirical data collected from model coil arrangements were used to develop a closed-form expression given by (3) for the end winding self-inductance in terms of “permeance coefficient” for a double layer winding depending on the geometrical and winding parameters alone. The calculated end winding self-inductances with the above-mentioned methods are 32.2, 22.1 μH respectively showing that the leakage inductances are in the same order of magnitude as the main inductance.

The closed form expression for the end winding overhang inductance is,

$$ L_{\mathrm{ov}} = \mu _{0} \cdot N_{\mathrm{ph},\mathrm{s}}^{2} \cdot \frac{2}{p} \cdot l_{\mathrm{ov}} \cdot \lambda _{\mathrm{ov}} $$

(3)

For a double layer winding the dimensionless “permeance coefficient” [8] is defined by,

$$ \lambda _{\mathrm{ov}} = \frac{3}{40}\left [ 1 + \frac{2 \cdot p \cdot l_{\mathrm{ov}}}{\pi d_{\mathrm{si}}} \right ] $$

(4)

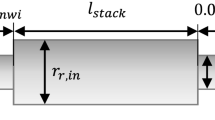
For a winding overhang length ($l$_ov) of 116 mm, substituting the relevant parameters in (3) yields an inductance of 22.1 μH.

In a strict sense the field distribution in the end winding region is 3-dimensional and a partial 3d FEM model (Fig. 7), without the rotor, taking advantage of the symmetry is constructed and a single magnetostatic simulation is performed to determine the self-inductance. This yields a result of 27 μH.

Fig. 7.

Partial 3d FEM Model used in numerical calculations for determining the winding overhang leakage inductance

4 Loss estimation

The power flow in a high-speed PMSM can be visualized by the Sankey diagram (Fig. 8). The individual losses and calculation methods along with the discussions are presented in the following sections.

Fig. 8.

Sankey diagram (drawn to scale) of the power flow in motor operation for PMSM-HW. The chosen operating point is $M_{\mathrm{N}}$ = 0.75 Nm @ $n_{\mathrm{N}}$ = 120 000 min⁻¹ with $U$_DC = 340 V_DC. The depicted losses are 1) stator AC copper losses ($P$_v,Cu,s,AC), 2) stator iron losses along with the additional losses due to inverter time harmonics ($P$_v,Fe,s + $P$_v,Zus), 3) eddy current losses in the magnet and titanium ring ($P$_v,Ft,M+B), 4) air friction losses ($P$_v,LR) with a calculated efficiency of 95.1%

4.1 Stator copper losses

The copper losses in the windings are influenced by,

• Increase in resistance due to frequency dependent skin- and proximity- effects.

• Increase in resistance due to transient increase in temperature.

The frequency dependent effects can be characterized by a “skin- and proximity-effect” factor $k_{\mathrm{R}}$. As simple analytical formula fails to provide a fully accurate prediction of these factors [9], numerical 2d magnetoharmonic FEM calculations at different frequencies and constant current amplitude are carried out for both the slot and overhang regions. A simplified simulation involving a 2d slice of the 3d overhang provides an approximate $k_{\mathrm{R}}$ factor for that region. Figure 9 shows the factor in dependence of frequency. The effective $k_{\mathrm{R}}$ value is used to calculate the increase in stator phase resistance at the corresponding supply frequency.

Fig. 9.

Numerically (2d FEM) calculated skin- and proximity-effect factors in dependence of the stator current frequency

The results show that the effective increase in stator phase resistance is 2.98 times the DC value for rectangular wire windings. The penalty paid here should be compensated by the higher fill factor and effective heat transfer as will be shown by the thermal analysis.

4.2 Air friction losses

Air friction losses are especially important in high-speed drive systems as they increase in a cubic rate with the rotational speed. Since they not only depend on the motor geometry and surface finish of the components, but also on the surrounding fluid temperature and pressure, they may vary depending on the environment where the drive is implemented. The calculations are based on [10], where empirical coefficient data were developed for small power electrical machines.

The rotor is axially subdivided into $N$ sections depending on the mechanical clearance between the rotating element and the stationary part surrounding it. The total air friction losses ($P$_v,LR) are given by (5) and are calculated for each $i$th section (radius $r_{\mathrm{i}}$ in m, axial length $l_{\mathrm{i}}$ in m, mechanical clearance $\delta _{\mathrm{i}}$ in m) and summed up.

$$ P_{\mathrm{v},\mathrm{LR}} = \sum _{i = 1}^{N} c_{\mathrm{Fr},\mathrm{air},\mathrm{i}} \cdot \pi \cdot \rho _{\mathrm{air}}(\vartheta ) \cdot \omega _{\mathrm{m}}^{3} \cdot r_{\mathrm{i}}^{4} \cdot L_{\mathrm{i}} $$

(5)

where

$L_{\mathrm{i}} = r_{\mathrm{i}} + l_{\mathrm{i}}$, in $\mathrm{m}$

$\omega _{\mathrm{m}}$, angular velocity of the rotor in rad/s

$\rho$_air($\theta$), air density at temperature $\theta$ K in kg m⁻³

$c$_Fr,air,i, air friction coefficient of the $i$th section

The air friction coefficients are calculated according to [10] depending on the flow regime. The air friction losses predominantly do not change for a given speed. As the temperature in the airgap increases, it may decrease slightly. The turbulent nature of the fluid in the airgap also contributes positively to that the thermal conductivity between the rotating rotor and stator increases.

4.3 Stator iron losses

Since the stator core losses form a significant portion of the losses, several techniques are adopted to reduce them.

• Lower airgap flux density compared to a highly utilized PMSM. The fundamental airgap flux density amplitude lies around 0.66 T.

• By employing high-frequency, low-loss electrical steel sheets where the loss data are available till the frequency of interest.

Under load, the excitations present are PM-field and the sinusoidal armature current loading. Magnetostatic FEM simulations at different rotor positions provide the flux densities in the discretized stator yoke and teeth elements for an electrical period. The temporal variation of the spatial flux densities is then calculated in the post processing stage. The specific loss curves for the stator steel sheet at different frequencies provided by the manufacturer are used to estimate the total iron loss by separating the hysteresis, eddy-current and additional loss coefficients through curve fitting techniques.

4.4 Rotor losses and losses due to inverter time harmonics

The eddy currents in the magnets and titanium shield flow due to two reasons:

• The resultant field is modulated by the stator teeth as the rotor rotates (called tooth pulsations) and causes a temporal and spatial change in the flux density, which results in the flow of eddy currents.

• The time harmonics of the stator current due to PWM inverter voltage cause a temporal variation in the flux density, which also induce eddy currents. These losses occur in both the stator and rotor and a distinction is not made in this study.

There are various methods to estimate the pulsation induced eddy current losses and the most accurate is time-stepping FEM analysis. For the relevant frequencies (Tooth pulsation frequency, $f$_Tooth = 24 kHz), the penetration depth for titanium-alloy bandage is larger compared to its thickness ($\delta$_E,b = 4.27 mm, $h_{\mathrm{B}}$ = 2 mm). Thus, the bandage with its electrical conductivity acts only partially as a shield and prevents the flux from penetrating deep inside the rotor magnets. In this case, the large airgap also plays a vital role. This is apparent from the loss distribution where the eddy current losses in the bandage and magnet are $P$_Ft,B = 18.2 W and $P$_Ft,M = 1.0 W at rated conditions, respectively.

A simplified estimation technique for the losses due to inverter time harmonics is introduced. The frequency dependent phase impedance matrix of the motor model is formed from 2d magnetoharmonic FEM simulations by performing a frequency sweep at a particular rotor position. Since the machine is non-salient, the impedance values can be assumed rotor position invariant. This frequency dependent stator phase impedance Z_ph($\mu$), where $\mu$ = $f$/$f$_s,1 contains the skin- and proximity- factors of the windings, induced eddy currents in the bandage and magnets. The stator core losses and the corresponding impedance contributions are neglected, which can prove to be a major error source. At high frequencies (in the order of 10⁶ Hz), capacitive effects also play a role. So, impedance measurements on the real machine provide the most accurate results. Figure 10 shows the calculated complex impedance values. Once the impedance matrix is deduced, the voltage spectrum of the inverter output voltage (Fig. 11 shows the no-load line-line voltage spectrum for a switching frequency of 30 kHz and 90 kHz), containing the rms phase voltage harmonics ($U_{\mu }$), at a particular switching frequency and modulation index is used to calculate the total losses due to higher order time harmonics, $P$_v,Zus using (6). Figure 12 shows the calculated losses and as expected, additional losses can be reduced by increasing the switching frequency.

$$ P_{\mathrm{v},\mathrm{Zus}} = 3 \cdot \sum _{\mu = 2}^{\infty } \frac{(U_{\mu } )^{2}}{|\underline{Z}_{\mathrm{ph}}(\mu )|} \cdot \cos \theta _{\mathrm{Z}}(\mu ) $$

(6)

Fig. 10.

Calculated complex harmonic phase impedance values for different supply frequencies from 2d magnetoharmonic simulations for PMSM-HW

Fig. 11.

Calculated no-load output voltage spectrum of a 2-level inverter with space vector modulation for a switching frequency of (a) 30 kHz and (b) 90 kHz and a fundamental frequency, $f$_s,1 of 2 kHz with a modulation factor, $m$ of 0.9 for PMSM-HW

Fig. 12.

Calculated losses due to inverter time harmonics depending on the switching frequency for a two-level inverter without output sine filter and a modulation factor of 0.9 for PMSM-HW

5 Thermal analysis

The data calculated from the analysis is given in Table 2 for the rated operating point.

Table 2. Comparison of characteristic data for the two topologies at rated operating point

Figure 13 compares the efficiency difference between PMSM-RW and PMSM-HW for the complete operating region. It is seen that for partial loads, PMSM-HW has a better efficiency since the iron losses are lower. As the torque increases, the copper loss term becomes more significant and the efficiency decreases.

Fig. 13.

(a) Contour lines depicting the efficiency difference between PMSM-RW and PMSM-HW (b) Efficiency difference between PMSM-HW and PMSM-RW for different torques at rated speed of $n_{\mathrm{N}}$ = 120 000 min⁻¹

With the calculated data, a 3d FEM thermal study is carried out at operating point. The airgap region is modelled as thermally conductive region with a conductivity of 0.89 Wm⁻¹ K⁻¹ calculated from analytical formulae involving Nusselt number and Taylor coefficients [11]. This high value is due to the fact that the air region is turbulent, and the thermal connection is improved. Once the boundary conditions are set and the losses assigned, the temperature rise in the stator winding overhang (Fig. 14) and the rotor magnets (Fig. 15) are extracted.

Fig. 14.

Temperature distribution in the winding overhang region for the operating point for PMSM-HW. The hot spot temperature is 154 °C

Fig. 15.

Temperature distribution in rotor magnet for the operating point for PMSM-HW. The hot spot temperature is 162 °C at the axial extremities

Due to the skin- and proximity-effects, and due to the poor heat transfer, the hottest part of the winding is near the airgap. The end winding overhang is filled with epoxy-resin with a thermal conductivity of 0.15 Wm⁻¹ K⁻¹ for mechanical stability and also to increase the natural mechanical frequency. Simulations show that the heat transfer is not improved considerably (only 2 K reduction) when compared to no epoxy-resin fill. This can be explained by the fact that the thermal resistance between end winding and cooling jacket through epoxy-resin fill is still large compared to that of the path offered by the stator iron. Noticeable improvement occurs when the thermal conductivity of the epoxy resin is in the order of around 10 Wm⁻¹ K⁻¹, which is unrealistic. The magnet temperature remains around 155 °C (Fig. 15) at the center and increases progressively around the axial extremities where the heat transfer is poorer. Most of the rotor losses occur at the titanium bandage.

6 Conclusion

The possibility of employing rectangular wire windings, in the form of hairpins, for high-speed machines with a fundamental frequency of 2 kHz has been investigated in this case study. Due to its ease of production, better thermal characteristics and high mechanical robustness, hairpin windings have advantages in automotive large-scale applications.

Basic design rules for a high-speed compressor motor with hairpin windings have been introduced and compared with a prototype machine with round bundled windings. The topology with rectangular wire windings suffers from increased high frequency losses and therefore poorer efficiency (0.8% reduction at operating point) which can increase the system cost to an extent. A comprehensive loss estimation for the proposed machine was made and it has been shown via simulations that the topology with hairpin windings with better heat transfer and its inherent better thermal design is comparable with a round wire topology in terms of performance. A hardware validation was not part of this study and will be reserved for the future.