Abstract
Space limitations in duct applications, new industrial and health safety regulations require new absorber configurations. Micro-perforated panels (MPP) as used in micro-perforated absorbers (MPA) allow new sound absorber concepts in the category of metamaterials. In this contribution we investigate MPA designs for the low and mid-to-high frequency range and apply finite element (FE) simulations to precisely design absorber configurations for applications in room acoustics and axial fans. The investigations show that the MPA’s cavity configuration must be customized for the desired frequency range and has significant influence on fan performance when applied in a duct flow setup.
Zusammenfassung
Kompakte Bauweisen in Klimakanälen und neue Industrie- und Gesundheitsstandards motivieren die Suche nach neuartigen Schallabsorbern. Mikroperforierte Platten (MPP), angewendet in Mikroperforierten Absorbern (MPA), ermöglichen neue Absorberkonzepte in der Kategorie der Metamaterialien. In diesem Beitrag werden MPA-Konzepte für die Verwendung im niedrigen und hohen Frequenzbereich untersucht. Die Anwendung der Finiten Elemente(FE)-Methode erlaubt es, diese Absorber präzise für die Raumakustik und Anwendung bei Axialventilatoren auszulegen. Die Untersuchungen haben gezeigt, wie notwendig es ist, den wirksamen Frequenzbereich klar zu definieren und die signifikanten Einflüsse auf die Ventilatorkennlinie zu berücksichtigen.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
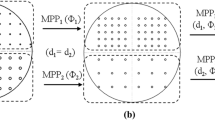
The simplest micro-perforated absorber (MPA) consists of one micro-perforated panel (MPP) as shown in Fig. 1 and a hermetically sealed air cavity of length \(L_{\textrm{c}}\) with a sound hard back plane (cf. Fig. 2 (b)) [14]. Within the slit-shaped micro-perforations (cf. Fig. 1 (a, b)) of the plate itself the kinetic wave energy of a plane standing traversing sound wave is reduced by particle velocity proportional friction losses. Particle velocity peaks at distances \(L_{\textrm{c}}=n\lambda /4\) \((n=1,3,5,\ldots)\) from the back end and thus at frequencies \(f_{\textrm{mid}}=c_{0}/\lambda \), with mid-frequency \(f_{\textrm{mid}}\) as the center frequency of an identified noise band, \(c_{0}\) as the speed of sound and \(\lambda \) as the wavelength, sound absorption reaches very high levels. For plane wave front acoustics, where the geometrical dimensions are smaller then the largest wavelengths, there exist analytical 1D transmission line models [18] based on the transfer matrix approach [4] for calculating the absorption behavior of an MPA. This is also the basis for the design of more complex geometrical absorber setups. More advanced setups [1, 19] are necessary, because the MPA requires a more thoroughly carried out design procedure than the conventional fibrous or foam based absorbers. In the latter case, the material is likely locally-reacting which results in a broadband absorption behavior and most often the cavity length \(L_{\textrm{c}}\) is the only required geometrical parameter. In contrast, the MPA is not per se locally reacting, depending on the dimensions and composition of the air cavity. The main advantages can be summarized as follows:
-
compact integrability within e.g. existing duct setups where space is limited
-
flow guidance (usage as guiding vanes, bends)
-
minimal maintenance requirements due to metal frame material
-
applicability in hazardous environments
-
suitability of efficient and accurate numerical simulation for absorption and space requirement optimization
The purpose of this contribution is to provide an overview of the design steps, the MPA’s applicability range, and also its limitations.
Parameters of the MPP specimen in impedance tube investigation according to [7]
1.1 Micro-perforated plates
The first design step is the selection of the micro-perforated plate. The materials to be presented here (cf. Fig. 1 (a, b)), are commercially available and cheap in production. Thin semi-finished metal plates with thickness \(t_{\textrm{MPP}}\) (cf. Fig. 2 (a)) are milled and thus only plastically deformed to achieve a perforated structure. Other possible ways to produce micro-perforations are laser/water-cutting or 3D printing. The acoustic pre-characterization requires two main parameters to be determined: the porosity \(\phi \) (open pore area to entire surface area) and the characteristic length \(d\) [3, 13]. For a more efficient modeling approach, one assumes circular holes that are uniformly distributed (cf. Fig. 1(a)). The hole diameter \(d=2r\) and separation \(w\) of the holes define the porosity \(\phi = \pi /4 (d/w)^{2}\). Both parameters are normally provided by the manufacturer. If they are not, one can use an equivalent fluid model approach to determine these parameters and the acoustic response of the material. In this contribution we use the model of Johnson-Champoux-Allard-Lafarge (JCAL) [2]. For thin metal frames, it’s application allows to reduce the characteristic length of the slotted material to circular pores [9].
1.2 Simulation framework
In the numerical simulation, the domain of the MPP is isotropic and homogeneous. It produces a comparable acoustic response as the real material, hence the term “equivalent”. Additionally, the usage of JCAL makes the assumption that the MPP frame material is perfectly rigid. Usually, this assumption can also be made in the final MPA application scenario, because a robust and firm mounting within an air duct is required.
The numerical simulation is based on solving the Helmholtz equation (1) in a spatially discretised domain with the Finite Element (FE) method for the acoustic pressure \(p_{\textrm{a}}\) [11]. Here, \(\omega \) is the circular frequency and \(\tilde{\rho }\) and \(\tilde{K}\) are the equivalent density and compression modulus. In the MPP domain these variables govern the absorption behavior and their values must be pre-determined for every frequency under consideration. However, the absorption dominating parameter is \(\tilde{\rho }\) (see (2)) and for the compression modulus choosing the standard ambient value \(K_{0}\) is sufficient.
In the air domain both \(\tilde{\rho }\) and \(\tilde{K}\) take on constant values under standard ambient conditions (\(\rho _{0}\), \(\: K_{0}\)).
The frequency depended equivalent density can be computed with porosity \(\phi \), dynamic viscosity \(\eta _{0}\), ambient air density \(\rho _{0}\) and tortuosity \(\alpha _{\infty }\) [2]. The latter is a length correction term that takes the fluid dynamic interaction of air streams of adjacent holes into account, as well as, correcting the thickness of plate for excess dynamic mass of the envisioned moving air plug volume in the pore.
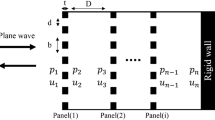
The MPP specimen (for typical values see Fig. 2 (a)) is placed in an impedance tube (cf. Fig. 2 (b)) with inner diameter \(D_{\textrm{tube}}={29}\) mm and microphone distance \(s={20}\) mm, which means that the plane wave front assumption holds up to \(f={6400}\) Hz [7]. Now, the measured reflection coefficient \(\tilde{r}_{\textrm{M}}\) and the simulated ones \(\tilde{r}_{\textrm{A}}\) obtained by 1D transmission line theory for each frequency \(f_{\textrm{i}}\) are compared. A genetic algorithm from the toolbox [15] performs the fitting between the two curves and returns values for \(d\) and \(\phi \) that minimize the error \(err\) according to
The comparison of such a fitting can be seen in Fig. 3. Both curves agree sufficiently well with each other. With the exception of the frequency range greater 5000 Hz. Here, it is suspected, that an additional viscous absorption effect occurs within the MPA arrangement in the impedance tube, which cannot be accounted for by using just one MPP in the 1D transmission line model. As it will turn out in chapter two, this effect does not have a significant influence on the robustness of the fitted model parameters and thus the transmission loss.
With the obtained parameters the more complex MPA setups can be simulated with the open source FE simulation tool openCFS [10, 17]. The key advantage of the described approach is that the real material parameters do not need to be known before, since they are also quite cumbersome to measure. Instead, the 1D analytical fitting is sufficient to determine the equivalent fluid’s acoustic behavior for the 3D application case. This is crucial for the design of a MPA, because it will be shown that such an absorber must be accurately designed for specific frequency ranges. The following design and application scenarios treat a room acoustics case without mean flow and a diffuse sound field as well as the application to an axial fan within a duct with a background flow field.
2 Mid to high frequency range – room acoustics
In a room acoustics application scenario the sound field will be diffuse and therefore sound wave fronts will impinge on the MPA from multiple directions which affects the effectiveness of the absorber in the mid-frequency range. In this frequency domain, the standard foam and fibrous based damping materials operate very efficiently due to their local reaction behavior. The MPA and especially its cavity must therefore be designed accordingly.
2.1 Measurement setup
To assess different MPA structures and compare them among each other and with standard damping materials, we compare the simulated and measured transmission loss (\(TL\)). The transmission loss of an absorber structure (brown section in Fig. 4 (a)) can be computed by
The measurement setup allows to measure the \(TL\) of an expansion chamber (cf. Fig. 4 (b)) with different MPA structures. By wave decomposition the incident sound power \(P_{\textrm{a},+}\) is separated from the reflected sound power \(P_{\textrm{a},-}\) [20, 21]. The same is done to obtain the transmitted sound power \(P_{\textrm{a},\textrm{$\tau $}}\) through bulk body of the expansion chamber. The transmission loss \(TL\) consists of a reflective and a dissipative part. However, by comparing the same expansion chamber in every scenario and only changing the absorber structure, the MPA dependent dissipative effect can be discerned in the diagrams. The measurements have to be performed twice with different end pieces (A, B in Fig. 4 (a)). The dimensions of the setup \(a={20}\) mm and \(s={18}\) mm allow measurements up to \(f={8500}\) Hz. The expansion chamber with quadratic cross section is made up of the MPP, cavity with dimension \(L_{\textrm{c}}={60}\) mm, \(l={300}\) mm and the bulk body with quadratic cross section of lateral length \(b={90}\) mm. Due to the cross section jumps at the beginning and end of the bulk body reflective damping at frequencies \(f_{\lambda /4,i}\) \((i=1,3,5,\ldots)\) will occur.
The expansion chamber with MPPs (cf. Fig. 5 and 6) has the following frequency dependent acoustic damping ranges:
-
\(f_{\textrm{c}}={1900}\) Hz is the first cut-on frequency of the bulk body chamber: below it, only plane waves propagate in the chamber. Above, higher order modes propagate and the sound field in the chamber becomes more diffuse. Here, a broadband and large sound reduction can be achieved.
-
\(f_{\textrm{1}}={3800}\) Hz is the second cut-on frequency of the expansion chamber: above, the sound field becomes even more diffuse and the typical \(TL\)-lobes (see black dashed lines in Fig. 5 (b)) due to \(\lambda /4\)-reflection damping blur to smaller very narrow \(TL\)-peaks. Here, sound reduction is less efficient.
-
\(f_{\textrm{2}}={6400}\) Hz marks the limit of the measured MPP specimen frequency behavior in the impedance tube, but also the diffusivity is very pronounced above that frequency region.
2.2 Results
The expansion chamber setup (cf. Fig. 4 (b)) allows to place MPP C within the main body chamber with quadratic cross section of dimension \(b\), or as a MPA attachment to the chamber which leaves the bulk chamber body unaltered. One can compare the MPA attachment to an absorber panel on the walls of a large room or a duct liner arrangement (cf. Sect. 3).
2.2.1 MPA compared to fibrous material
At first, the measured \(TL\) of a MPA with MPP C and cavity length \(L_{\textrm{c,60}}={60}\) mm is compared to the empty cavity and the cavity filled with inflammable fibrous absorber material used in climate ducts for trains (cf. Fig. 5 (a)). In the entire frequency range, the fibrous material performs better than the MPA, producing a larger and more broadband \(TL\). Compared to the empty cavity, the MPP however broadens the absorption lobes, beginning at \(f_{\textrm{c}}\), but reducing the maximum peaks in that region. Above \(f_{\textrm{1}}\) the MPP increases absorption constantly compared to the empty-cavity case. Below \(f_{\textrm{c}}\) in the plane wave frequency range, the MPP increases the \(TL\)-peaks compared to the expansion chamber without cavity by about 5-7 dB (see black dashed lobes in Fig. 5 (b)).
In climate ducts it is common practice to cover the absorber material from water and dust particles with a protective layer of tape or perforated sheet. As this is done (cf. Fig. 5 (b)), the absorption performance of the fibrous materials reduces strongly and the MPA’s \(TL\) is now comparable to the standard material. The MPA, however, does not require protective measures.
Depending on the desired frequency range, the MPA configuration has to be changed in order to obtain a broadband frequency and high absorption behavior. The following simulations will show the accuracy of the FE framework and provide information how to achieve these goals.
2.2.2 Simulated MPA configurations
The standard approach to broaden the absorption bandwith [19] of the MPA is to partition its cavity. In Fig. 6 (a) the simulated and measured \(TL\) of the double partitioned MPA is shown. Simulation and measurement showed good comparison, even greater \(f_{\textrm{2}}\), where the frequency dependent absorption behavior of the equivalent fluid is not verifiable by impedance tube data. This fact motivated the investigation of further completely different MPP configurations. The results are shown in Fig. 6 (b). The \(TL\) in the frequency range up to \(f_{\textrm{c}}\) can be enhanced by more partitions in the cavity, enhancing the local reaction behavior (configuration “1” in Fig. 6 (b)). Placing MPPs in direct line of sight to the source in a vertical tetra-layer arrangement in the bulk chamber is beneficial to the frequency range \(f_{\textrm{c}}\) to \(f_{\textrm{1}}\) and up to \(f_{\textrm{2}}\) (configuration “2” in Fig. 6 (b)). This scenario, as configuration 3, can be compared to the usage as a guiding vane in a duct baffle (waves impinging more inclined) or as noise source housing. A horizontal tetra-layer configuration in the bulk chamber increases the absorption in the frequency range greater \(f_{\textrm{2}}\), comparable to a splitter-silencer (configuration “3” in Fig. 6 (b)). The investigations show that different MPA configurations result in special absorption behavior depending on the frequency range. A general prediction of its sound reducing behavior, as in the case for fibrous or porous materials, is not possible.
3 Low frequency range – axial fan application
Assessing the effectiveness of a MPA for sound reduction in the frequency range up 1600 Hz (as low frequency limit) concerns its application near an axial fan operating at low Mach number conditions within a duct [6]. Beside the evaluation of sound emission spectra at three operating points of the fan characteristics, the influence of the MPA on the performance of the fan and vice versa is shown. The data allows to derive design recommendations for an MPA in a flow scenario.
3.1 Setup
The fan is operated within a micro-perforated duct section (\(D_{\textrm{MPA}}={506}\) mm) that has a cavity of length \(L_{\textrm{c}}={140}\) mm (cf. Fig. 8). The MPA has a length of \(L_{\textrm{MPA}}={440}\) mm and is connected to a standardized test rig [8, 22] via an inlet nozzle (cf. Fig. 7). The reference (R) case (\(D_{\textrm{duct}}={500}\) mm) with free inflow conditions and the fan in distance \(L_{\textrm{d}}={520}\) mm to the nozzle is compared to the setup with the MPA (M) (cf. Fig. 7 (a, b)). The MPA has three different configurations: empty cavity with MPP B (M) with no additional cavity partitioning, cavity segmentation in axial and azimuthal direction (MS1) and adding a MPP with larger flow resistivity (MS2) (cf. Fig. 7 and Fig. 8). The sound emission spectra are based on acoustic pressure signals recorded on five microphones placed in distance 1 m from the nozzle in upstream direction.
The mean flow stream lines are indicated in Fig. 8. The MPPs have a large flow resistance, but bias flow, however small, due to static pressure differences \(p_{\textrm{stat}}\) in the region upstream of the fan can not be ruled out. The tip gap flow patterns might be strongly altered by the presence of the MPP, changing recirculation and blade tip-vortex interaction intensity, since the tip gap clearance is changed compared to the reference case (\(D_{\textrm{duct}}\neq D_{\textrm{MPA}}\)). Thus, this configuration adds to unsteady blade forces induced aeroacoustic sound production. This source mechanism is especially important in the partial load range of the fan characteristic curve.
The MPA configuration MS1 has three cavities with the same length in axial direction (cf. Fig. 8). As in the room acoustics application, the goal is to obtain a more broadband sound reduction in comparison to the unpartitioned configuration. Adding the MPP with a larger flow resistivity (MS2) in the compartment near the fan aimed to reduce the flow through the MPP, thereby affecting recirculation from suction (upstream) to pressure (downstream) side of the fan and the tip gap noise source mechanism. In both latter cases the cavity was also partitioned in azimuthal direction (cf. Fig. 7 (b)).
3.2 Results
The investigated fan is forward-skewed and its aeroacoustic behavior has extensively been studied [5, 6, 12, 22]. The performance of the fan and MPA can be investigated in Fig. 10 (a–c). They show the total-to-static pressure rise of the four different setups and the total-to-static efficiency of the fan. The overall emitted sound pressure levels \(L_{\textrm{p}}\) at different operating points of the fan characteristic allow to see the performance of the MPA in partial load region (below 1.0 m3 s−1) and the steady region (above 1.6 m3 s−1). The fan design point was a volume flow rate of 1.4 m3 s−1 and rotational speed of 1486 rpm. In the measured sound emission spectra (sound pressure level (SPL), cf. Fig. 9 (a–c)) certain frequency regions can be discerned:
-
\(f_{\textrm{c,R}}={398}\) Hz: cut-off frequency of the reference setup; below this region all higher order modes are cut-off and only plane waves propagate, cf. Fig. 9 (a).
-
\(f_{\textrm{c,M}}={221}\) Hz: smaller cut-off frequency of the M setup without MPP sealing the cavity; below this region all higher order modes are cut-off and only plane waves propagate. The cut-off frequency changes, because cavity length \(L_{\textrm{c}}\) is added. The blade passing frequency is 223 Hz, almost identical to \(f_{\textrm{c,M}}\), and therefore not further highlighted, cf. Fig. 9 (a).
-
\(f_{\lambda /4,1}={190}\) Hz, \(f_{\lambda /4,2}={580}\) Hz and \(f_{\lambda /4,3}={970}\) Hz: resonance frequencies due to cavity length \(L_{\textrm{MPA}}\), same reflection damping mechanism as in the expansion chamber setup (see Sect. 2), cf. Fig. 9 (b).
-
\(f_{\lambda /2}={780}\) Hz: additional resonance frequency based on \(\lambda /2\)-reflection damping, cf. Fig. 9 (c).
The frequencies \(f_{\lambda /4,i}\) are derived from standard \(\lambda /4\)-reflection damping based on length \(L_{\textrm{MPA}}\) [16]. Comparing the spectra (cf. Fig. 9 (a–b)) shows that the M setup reduces sound emission substantially in the frequency regions of the MPA resonances at \(f_{\lambda /4,i=1,2,3}\) and \(f_{\lambda /2,1}\). However MPP B shifts the \(\lambda /4\)-peak absorption slightly to a lower frequency than calculated. The sound pressure spectra show that the reductions greater \(f={2}\) kHz are independent of the cavity configurations of the MPA. In the partial load range of the fan characteristic for frequencies above \(f={3}\) kHz, the MPP is responsible for a slight increase in sound pressure level, which is attributed to the flow over and bias flow through the MPP slits. Compared to the M case, the segmented cavity MS1 broadens sound reduction between \(f_{\textrm{c,R}}\) and \(f_{\lambda /4,1}\) and in a narrow frequency band above \(f={1}\) kHz. Adding the MPP with larger flow resistivity in the setup MS2 slightly reduces sound reduction induced by MPP B. When the overall sound pressure level decreases in the larger volume flow range, pronounced tonal components (cf. dashed red circles in Fig. 9 (b, c)) due to the blade passing frequency are visible. This phenomenon is attributed to the altered tip clearance compared to the reference setup and thus changed gap flow structures with bias flow (cf. Fig. 8). These flow structures interact with the blades and amplify this sound source mechanism.
Here, adding the MPP with larger flow resistivity seems to attenuate these tonal peaks (cf. yellow curve in Fig. 9 (b, c)) by either acoustically dampening them or decreasing the tip gap source strength mechanism. In all MPA configurations at low and high volume flow rates, the low frequency sound reduction in the subharmonic range below the blade passing frequency remains large.
The acoustic characteristics (cf. Fig. 10 (c)) reveal that at the lower volume flow rates up to \(\dot{V}={0.8}\) m3 s−1 the sound emission is significantly reduced in all MPA configurations. Above that range, the reduction is reduced to 2–3 dB. Above \(\dot{V}={1.5}\) m3 s−1 an influence of the cavity configuration is visible with MS1 producing larger reductions than the other cavity configurations.
The aerodynamic curves (cf. Fig. 10 (a, b)) show that due to the presence of the MPA the pressure difference of the fan decreases, even more pronounced in the MS1 setup. However, in the non-stationary range of \(\dot{V}\in [{0.6}~\mathrm{m}^{3}\, \mathrm{s}^{-1}; {0.9}~\mathrm{m}^{3} \mathrm{s}^{-1}]\) the pressure difference generated by the fan increases. The reduced pressure difference is for the most part caused by the difference in tip gap clearance (for additional data cf. [6]), but also added turbulence due to the larger surface roughness of the MPP and an increased back flow through the slits could add to the loss in efficiency (cf. Fig. 10 (b)) compared to the reference case. The investigated cavity configurations, with the exception of setup MS1 being more inefficient, have the same influence on the fan efficiency.
4 Conclusion
The investigations have demonstrated some advantages and limits of micro-perforated absorber (MPA) configurations. The proposed simulation framework applied to an aluminum plate based MPA has been demonstrated. The transmission loss of different MPAs attached and within an expansion chamber, intended for roomacoustics, show that is possible to substitute the conventional materials with specifically designed MPAs.
However, the experiments on an application scenario in the direct vicinity of an axial fan showed that care must be taken of the location of the MPA. Pressure build up and efficiency vary when the fan operates within the MPA duct section. Increased tonal components in the emission spectra lower the overall MPA performance. The results can be summarized as follows:
Mid to high frequency range
-
The JCAL based equivalent fluid modeling combined with FE allows to study complex MPA arrangements very accurately.
-
There is an optimal MPA configuration for a certain frequency range either by considering orientation to source or the frequency range as well as both.
-
For a combination of MPA variations, broad band frequency simulation have to be applied, because optimizing one frequency region might impair absorption in another bandwith.
Low frequency range
-
The effectiveness and overall performance of the MPA in a flow scenario depends on the flow field through the MPP or above and near it’s surface.
-
The fan’s efficiency is altered by a MPA in its vicinity negatively in most operational points.
-
The amount of sound reduction depends on the operating point of the fan characteristics. Thereby, in the steady range, the overall sound reduction is constant and depends on the cavity configuration.
-
The characteristic resonances of the MPA provide large sound reduction in finite bands below \(f={1600}\) Hz, which allows to customize the MPA.
References
Allam, S., Åbom, M. (2011): A new type of muffler based on micro-perforated panels. J. Vib. Acoust., 133(3), 031005. https://doi.org/10.1115/1.4002956.
Allard, J. F. (2015): Propagation of sound in porous media. London: Elsevier. https://doi.org/10.1002/9780470747339. Chap. 5
Atalla, N., Sgard, F. (2007): Modeling of perforated plates and screens using rigid frame porous media. J. Sound Vib., 303(5), 195–208. https://doi.org/10.1016/j.jsv.2007.01.012.
Chung, J. Y., Blaser, D. A. (1980): Transfer function method of measuring in-duct acoustic properties. II. Experiment. J. Acoust. Soc. Am., 68(3), 914–921. https://doi.org/10.1121/1.384779.
Czwielong, F., Krömer, F., Becker, S. (2019): Experimental investigations of the sound emission of axial fans under the influence of suction-side heat exchangers. In 25th AIAA/CEAS aeroacoustics conference, vol AIAA 2019-2618 session: acoustic/fluid dynamics interactions X. https://doi.org/10.2514/6.2019-2618.
Czwielong, F., Floss, S., Becker, S., Kaltenbacher, M. (2021): Influence of a micro-perforated duct absorber on sound emission and performance of axial fans. Appl. Acoust., 174, 107746. https://doi.org/10.1016/j.apacoust.2020.107746.
DIN EN ISO 10534 (2010): Acoustics – determination of sound absorption coefficient and impedance in impedance tubes – Part 2: transfer function method. Berlin Beuth Verlag.
DIN EN ISO 5801 (2017): Fan – performance testing using standardized airways. Berlin Beuth Verlag.
Jouen, L., Bécot, F. X. (2011): Acoustical characterization of perforated facings. J. Acoust. Soc. Am., 129(3), 1400–1406. https://doi.org/10.1121/1.3552887.
Kaltenbacher, M. (2015): Numerical simulation of mechatronic sensors and actuators – finite elements for computational multiphysics. 3rd ed. Berlin: Springer. https://doi.org/10.1007/978-3-642-40170-1.
Kaltenbacher, M., Floss, S. (2018): Nonconforming finite elements based on nitsche-type mortaring for inhomogenous wave equation. J. Theor. Comput. Acoust., 26(3), 1850028. https://doi.org/10.1142/S2591728518500287.
Krömer, F. J. (2018): Sound emission of low-pressure axial fans under distorted inflow conditions. Boca Raton: FAU University Press. https://doi.org/10.25593/978-3-96147-089-1. Doctoralthesis
Liu, L., Hua, X., Herrin, D. (2013): Estimation of effective parameters for microperforated panel absorbers and applications. Appl. Acoust., 75(75), 86–93. https://doi.org/10.3397/1/3761043.
Maa, D. Y. (1998): Potential of micro-perforated panel absorbers. J. Acoust. Soc. Am., 104(5), 2861–2866. https://doi.org/10.1121/1.423870.
MathWorks (2020): https://www.mathworks.com/discovery/genetic-algorithm.html. Online. Accessed 25 December 2020.
Möser, M., Müller, G. (2013): Handbook of engineering acoustics. Berlin Heidelberg: Springer. https://doi.org/10.1007/978-3-540-69460-1.
openCFS (2020): https://www.opencfs.org/index.html. Online. Accessed 25 December 2020.
Pierce, A. D. (1980): Acoustics – an introduction to its physical principles and applications. London: McGraw-Hil Inc. Chap. 7.
Sacks, S., Åbom, M. (2016): Modal filters for mitigation of in-duct sound. J. Acoust. Soc. Am., 29, 040004. https://doi.org/10.1121/2.0000473.
Song, B. H., Bolton, J. S. (2000): A transfer-matrix approach for estimating the characteristic impedance and wave numbers of limp and rigid porous materials. J. Acoust. Soc. Am., 107, 1131. https://doi.org/10.1121/1.428404.
Wu, T. W., Zhang, P., Cheng, C. Y. R. (1998): Boundary element method analysis of mufflers with an improved method for deriving the four-pole parameters. J. Sound Vib., 217(4), 767–779. https://doi.org/10.1006/jsvi.1998.1800.
Zenger, F. J., Renz, A., Becher, M., Becker, S. (2016): Experimental investigation of the noise emission of axial fans under distorted inflow conditions. J. Sound Vib., 383, 124–145. https://doi.org/10.1016/j.jsv.2016.07.035.
Funding
Open access funding provided by TU Wien (TUW).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access Dieser Artikel wird unter der Creative Commons Namensnennung 4.0 International Lizenz veröffentlicht, welche die Nutzung, Vervielfältigung, Bearbeitung, Verbreitung und Wiedergabe in jeglichem Medium und Format erlaubt, sofern Sie den/die ursprünglichen Autor(en) und die Quelle ordnungsgemäß nennen, einen Link zur Creative Commons Lizenz beifügen und angeben, ob Änderungen vorgenommen wurden. Die in diesem Artikel enthaltenen Bilder und sonstiges Drittmaterial unterliegen ebenfalls der genannten Creative Commons Lizenz, sofern sich aus der Abbildungslegende nichts anderes ergibt. Sofern das betreffende Material nicht unter der genannten Creative Commons Lizenz steht und die betreffende Handlung nicht nach gesetzlichen Vorschriften erlaubt ist, ist für die oben aufgeführten Weiterverwendungen des Materials die Einwilligung des jeweiligen Rechteinhabers einzuholen. Weitere Details zur Lizenz entnehmen Sie bitte der Lizenzinformation auf http://creativecommons.org/licenses/by/4.0/deed.de.
About this article
Cite this article
Floss, S., Czwielong, F., Becker, S. et al. Micro-perforated panels for noise reduction. Elektrotech. Inftech. 138, 171–178 (2021). https://doi.org/10.1007/s00502-021-00889-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00502-021-00889-y