Abstract
This article presents an overview of the major trends and challenges involved with the design of multi-band, multi-standard digitally-intensive radio frequency transceivers for next generation mobile communications. In addition, we discuss in detail one aspect of the implementation challenges, namely the occurrence and cancellation of self-interference especially in carrier aggregation modes. For that, we present a novel digital cancellation technique to jointly compensate the self-interference caused by transmit (Tx) modulated spurs and Tx second order intermodulation distortion products (IMD2) in the receiver. This architecture exploits the underlying relation between both types of interference and offers a low-complexity solution to mitigate the Tx-IMD2 interference. Simulation results show, that the proposed technique significantly suppresses both types of interference and restores the signal-to-noise ratio of the wanted signal within 0.3 dB from its value in the absence of interference, thereby achieving 30 dB of cancellation.
Zusammenfassung
Dieser Artikel gibt zunächst einen Überblick über aktuellen Trends und Herausforderungen bei der Entwicklung von Multi-Band, Multi-Standard HF-Transceivern für die nächste Mobilfunk-Generation, die einen hohen Anteil an digitaler Elektronik aufweisen. Im Anschluss wird im Detail auf ein spezielles Problem solcher Transceiver eingegangen, nämlich der Selbst-Interferenz, die durch den eigenen Sender verursacht wird und die vor allem im Carrier Aggregation-Modus auftritt. Die Problematik wird nicht nur detailliert erklärt, diese Arbeit präsentiert auch eine Methode zur Unterdrückung von Selbst-Interferenz mit den Mitteln der digitalen Signalverarbeitung. Der Algorithmus kann die durch den Sender verursachte so genannten “Modulated Spurs” und zusätzlich daraus entstehende Intermodulations-Produkte zweiter Ordnung kompensieren. Simulationsergebnisse zeigen, dass der vorgestellte Algorithmus beide Arten von Interferenz bei vertretbarem Rechenaufwand gut unterdrücken kann. Das Signal-Rausch-Verhältnis des gewünschten Empfangssignals erreicht bis auf eine Differenz von 0,3 dB den ursprünglichen Wert, was einer Unterdrückung der Interferenz um 30 dB entspricht.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Next generation radio frequency (RF) transceivers are intended to support future wireless standards featuring peak data rates up to several Gbps, low-latency, high spectral efficiency, more network reliability, and co-existence of heterogeneous radio access technologies (RATs). It is envisioned that a variety of technologies in the areas of networks, air interfaces, and devices together will be integrated in future. In addition, exploitation of new spectrum in the sub-6 GHz in combination with improved spectral efficiency given by higher-order multi-carrier based channel access and modulation schemes as well as massive multiple-input/multiple-output (MIMO) will enable to significantly increase the mobile link throughput. The maximum bandwidth aggregated by LTE will increase beyond several hundreds of MHz by 2020, which will have major impact on the 5G RATs in the sub-6 GHz region. The needs to enhance cell edge performance will also drive devices to increase the number of supported antenna ports, for both long term evolution (LTE) and any new 5G RAT. This imposes a huge number of challenges in order to build power efficient RF transceivers incorporating these diversified features. Industry and academia have already shifted their focus towards designing more flexible and reconfigurable transceivers and RF front-ends to reduce costs for external components while at the same time supporting multi-band, multi-standard features.
Cellular RF integrated circuits (ICs) in mobile handsets are usually implemented in ultra-deep submicron complementary metal-oxide-semiconductor (CMOS) technology. While RF transceivers were almost purely analog components around 15 years ago, a significant shift towards digitally assisted transceivers has occurred since then. With shrinking process technology digital circuits profit significantly in terms of clock speed, power consumption and chip area. The performance of the analog and RF circuits, however, decreases with shrinking transistor size, leading to an increasing gap between the digital and analog performance. Thus applying DSP in RF transceivers is a natural choice. Either digital signal processing (DSP) assists the RF circuits, e.g. by improving performance, or cancelling interference, or one can find a digital replacement of analog building blocks. Several digital-intensive transmitter and receiver architectures have been developed [1], replacing analog functionality by digital circuits. Compared to analog implementations, these architectures show a reduced process, voltage and temperature dependency, better scalability and simplified system re-configurability. Nowadays more and more sophisticated and adaptive DSP blocks are investigated and developed for RF transceivers since requirements are increasing dramatically. Many of the emerging problems can be solved with the aid of DSP solutions.
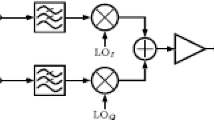
Figure 1 depicts a high level view of a state-of-the-art single band LTE RF transceiver. Here the transmit (Tx) signal is generated by a polar transmitter where the phase-modulated output of the phase locked loop (PLL) is combined with an amplitude-modulated signal and fed to the power amplifier (PA) [2]. The phase- and amplitude modulation information of the Tx signal are provided by the digital front-end (DFE). The off-chip components at the transmitter side are the PA used to amplify the transmitted signal and the duplexer, which is separating the Tx and receive (Rx) signals. On the Rx side the received RF signal is amplified by the low noise amplifier (LNA) which is connected to the duplexer by a matching network. Two Rx mixers driven by two \(90^{\circ }\) phase shifted local oscillator (LO) signals are recreating the complex valued in-phase quadrature-phase (IQ)-data from the received signal, which is then further processed by the DFE.
2 Trends and challenges
As highlighted in Fig. 1, the three central blocks in the RF transceiver are the PLL, Tx, and Rx subsystems. The following section provides an overview of the recent advances and challenges involved in those sub-systems.
2.1 RF digital-PLL
Major building blocks in RF transceivers are the PLLs necessary to stabilize the LOs which generate the RF carrier signals utilized for up- and down-conversion in Tx and Rx sub-systems. A PLL can be operated in different modes. One is the synthesizer mode where the PLL generates a constant but adjustable RF carrier frequency from a stable and low-noise reference clock. The main requirements for the generated RF carrier signal are low phase noise/timing jitter and low spurious emissions. The other mode is as a phase modulator which is a central block in polar transmitters. In this mode the PLL is used to generate the phase modulated signal which is then recombined with the amplitude modulation signal in the PA or the RF digital-to-analog converter (RF-DAC). Aside of low phase noise and spurious emissions, proper wide-band phase modulation and suppression of spectral images is of utmost importance here to achieve sufficiently low in-band and out-of-band signal distortion after recombining the phase modulated RF carrier with the amplitude modulation signal.
State-of-the-art RF synthesizers for mobile handset applications are usually realized as fractional-N RF Digital-PLLs (RF-DPLLs). Here the PLL control loop consists of at least a phase detector realized by means of a time-to-digital converter (TDC), a loop filter and a digitally-controlled oscillator (DCO). Most building blocks are realized by digital circuitry with the DCO and TDC being the only remaining mixed-signal building blocks [3]. The phase modulation is usually realized by means of two-point modulation where the signal is injected into the digital control loop at two points in order to achieve a flat and wide-band transfer characteristic of the phase modulator. RF-DPLL based phase modulators covering a multitude of cellular frequency bands, standards and modulation schemes are presented e.g. in [2, 4].
With the evolution in cellular mobile communication standards, the requirements on RF transceivers and thus also on RF-DPLLs increase. Due to the need of supporting several cellular RATs, carrier aggregation (CA) and MIMO antenna technology, a multitude of Tx and Rx chains with simultaneous operation have to be implemented in the transceiver. Therefore, several RF-DPLLs including multiple DCOs are required to cover all cellular frequency bands ranging from 700 MHz up to 6 GHz. The challenge here is to reduce the number of PLLs and DCOs to avoid problems arising from simultaneous operation like crosstalk due to magnetic coupling, but also to reduce area and power consumption. This can for example be achieved by utilizing digital-to-time converters (DTCs) [5] generating multiple, independently adjustable carrier signals from one common LO clock generated by a single PLL [6]. In addition, synthesizers with lower phase noise will be required since higher order modulation schemes like 256-QAM and 1024-QAM are included in the LTE and 5G standards to cope with the ever increasing requirements on data rates and spectral efficiency.
In order to utilize the RF-DPLL as phase modulator, several challenges arise. First, the limited tuning range of the DCOs and their inherent nonlinearity complicate the utilization with increasing signal bandwidths. Second, the two-point modulation requires precise path matching since an exponential increase in signal distortion is observed for increasing signal bandwidths and mismatches between the modulation paths [7]. Like for the synthesizer, DTCs could be utilized here too, avoiding two-point modulation of the RF-DPLL control loop with the effect of significantly reducing the required DCO frequency tuning range.
2.2 Transmitters
The transmitter generates a modulated RF carrier with adjustable power, sufficiently low in-band distortion and out-of-band spectral emissions from a band-limited digital input signal. Traditionally, the transmitter system has been strictly divided into digital and analog parts [1].
To benefit from shrinking process structures and to achieve a high degree of reconfigurability, digital-intensive approaches reducing the number of analog components have been developed.
Among the published architectures and CMOS implementations, which are evolving quickly, digital-polar-, digital-quadrature- and pulse-encoding-based switched-mode transmitter systems are most commonly found and have been proven feasible for wireless communications [8, 9]. Pulse encoding approaches generally require additional high-Q filtering after RF signal generation since a considerable amount of quantization noise arises out-of-band. Therefore, digital-quadrature and digital-polar architectures utilizing high dynamic range RF-DACs have become popular due to their superior out-of-band performance and output power tuning range. The RF-DAC introduced in [10], combining the functionality of the baseband DAC and the RF mixer, represents a key element of digitally intensive transmitter architectures [8] allowing for an efficient implementation on a single die and leveraging the benefits of CMOS technology scaling.
Whereas first RF-DAC implementations have been based on current steering DACs, latest designs for operation in the sub-6 GHz bands are usually based on switched capacitor circuits, called C-DACs [11]. One of the main reasons for that is given by the exploitation of precise capacitance ratios and better shrinking capabilities with process technology in comparison to designs based on current steering. Also, an essential benefit of C-DACs is their superior amplitude-to-amplitude and amplitude-to-phase linearity. The linearity represents an important requirement of circuits designed for spectral-efficient communication standards like LTE due to the non-constant envelope modulation originating from the specified channel access and modulation schemes in combination with in-band and out-of-band emission requirements.
Recently, a digitally-intensive multi-band, multi-standard cellular polar transmitter implemented in 28 nm CMOS utilizing RF C-DACs [12] with external PAs and two-point phase modulated RF-DPLL [4] has been shown to support 40 MHz contiguous intra-band carrier aggregation in LTE-A uplink while also covering 2G and 3G cellular standards. The current trend in RF-DAC design for digitally-intensive transmitter architectures is to increase their output power by embedding the PA functionality on chip (RF-DPA). However, no RF-DPA implementations covering LTE-A with sufficient dynamic range, output power and large bandwidth support have been shown yet.
2.3 Receivers
The Rx subsystem in the transceiver is responsible for the down-conversion and demodulation of the desired RF signal in the presence of unwanted noise and blockers. In the early years of communications the receivers used super-heterodyne architectures and large numbers of external analog filter components. However, with the tendency of chip integration and increased digital functionality, homodyne architectures, where the RF signal is directly downconverted to baseband, are used in state-of-the-art receivers.
In recent years, much attention has been paid towards the digitization of the receivers using wideband RF-ADCs [13, 14] and post-processing with sophisticated DSP concepts. This imposes a huge challenge in designing ADCs to meet the requirements such as linearity and dynamic range. In order to fulfill the strong and continuous demand for high data rates and to provide great flexibility to mobile operators, CA has been introduced in LTE-Advanced mobile communication systems [15]. Mobile transceivers which employ CA can simultaneously aggregate several carriers operating in different LTE bands to form a single larger aggregated bandwidth which may reach up to 100 MHz, thereby achieving high data rates up to 1 Gb/s and 500 Mb/s for the downlink and uplink, respectively [16]. With the continuous addition of new bands, the number of CA band combinations that an RF transceiver has to support has tremendously increased. To enable the CA feature, RF receivers should employ several Rx chains that have to be operated simultaneously. In addition, all the Rx chains have to be designed quite flexible and reconfigurable so that each chain can support multiple bands covering a wide frequency range. However, implementing CA in the mobile user equipments has given raise to several interference issues that desensitize the receiver.
Previous works investigate some of those problems which are tackled using DSP techniques [17–21]. Another critical issue that appears is the Tx modulated spur interference problem that occurs in LTE-CA frequency division duplex (FDD) transceivers [22, 23]. In addition, due to the non-linearities in the receiver Tx-induced second order intermodulation distortion (IMD2) interference can appear [24, 25]. In the remaining part of this article, we focus on a novel joint mitigation of Tx-modulated spur and IMD2 interference for LTE-CA direct-conversion receivers. The proposed low-complex digital cancellation technique can be applied in the presence of Tx modulated spurs, and exploits the underlying relation between the two types of interference.
3 Self-interference model
Figure 2 illustrates the generation of Tx modulated spur and Tx-IMD2 interferences in the Rx baseband in a CA transceiver employing a direct-conversion receiver. In FDD transceivers, the Tx and Rx paths are connected to the common antenna via the duplexer. If the Tx signal leaks through the duplexer to the receiver without any further attenuation, it will completely damage the sensitivity of the receiver. The duplexer needs to be a very high-Q band pass (BP) filter to select the Rx signal and suppress the Tx signal. A state-of-the-art duplexer provides Tx-Rx isolation of around 55 dB. In reference sensitivity scenario, where the Tx power level at the PA can reach as much as 27 dBm, the power of leaked Tx signal at the receiver input can reach up to \(-28~\mbox{dBm}\) due to limited Tx-Rx isolation. Furthermore, because of the presence of several clock sources and dividers to support the different bands for different CA scenarios, many harmonics are generated on the chip. Although an optimum routing of the clock lines in the layout helps in isolating the clocks, the crosstalk between the harmonics seems to be unavoidable because of the chip area constraints. This crosstalk generates so called continuous wave (CW) spurious signals (spurs). If a CW spur appears at the chip area where the Rx LO resides, and its frequency is close to the Tx frequency, it mixes down the Tx leakage signal to Rx baseband resulting in a so called Tx modulated spur self-interference. In addition, due to the non-linearities in the down conversion mixer unwanted IMD2 distortion components from the leaked Tx signal are produced around DC and at higher frequencies. Although, the Tx-IMD2 distortion components at higher frequencies are filtered away by the base band filtering stages while the distortion component around DC will directly interfere with the wanted signal and degrades its SNR. Figure 3 illustrates the block diagram of the transceiver that we consider to derive an equivalent baseband signal model of the addressed modulated spur and IMD2 self-interference.
3.1 Baseband modeling of the self-interference
Consider \(x_{\text{BB}}^{\text{Tx}}(t)\) as the digital complex baseband Tx signal. After upconverting this signal to the carrier frequency \(f_{\text{tx}}\) and amplification by the PA with gain \(A\), the Tx signal at the antenna output is expressed as
Due to the limited Tx-Rx isolation of the duplexer, some part of the Tx signal leaks through the duplexer stop band and appears at the Rx path input. The leaked Tx signal is given by
where \(h_{\text{RF}}^{\text{TxL}}(t)\) represents the impulse response of the duplexer Tx-Rx leakage channel. The symbol ‘∗’ denotes the convolution operation. Figure 4 depicts the measured Tx-Rx channel of a commercial LTE band3 duplexer when the antenna port is matched to \(50~\Omega\). The Tx and Rx frequency ranges of LTE band3 are given as 1710–1785 MHz and 1805–1880 MHz, respectively. The Tx-Rx attenuation is around 55 dB, however, the frequency response within the Tx stop band is highly frequency selective. Due to this behavior, the leaked Tx signal \(y_{\text{RF}}^{\text{TxL}}(t)\) is heavily distorted by the duplexer stop band frequency response. Using the equivalent baseband impulse response of the duplexer leakage channel \(h_{\text{BB}}^{\text{TxL}}(t)\), the leaked Tx signal from (2) can be rewritten as
and the corresponding equivalent baseband signal results in
By considering the wanted signal \(y_{\text{RF}}^{\text{Rx}}(t)\) at the carrier frequency \(f_{\text{rx}}\) and the thermal noise \(w_{\text{RF}}(t)\), the total received signal at the Rx LNA input can be written as
Due to the non-linear behavior of the LNA and the in-phase and quadrature-phase (IQ) down-conversion mixer stages, several second order signal components are generated. Therefore, at the mixer output, in addition to the down converted received signal the undesired IMD2 signal components are also present. The total signal at the mixer output can be expressed as
where \(G_{\text{lna}}\) denotes the gain of the LNA. The coefficients \(g_{1}\) and \(g_{2}\) represent the conversion gain of the mixer for the received signal and the 2nd order signal components, respectively [24]. Due to the mismatches in the baseband IQ branch, the generated IMD2 distortion is scaled different in both the paths. Therefore, the coefficient \(g_{2}\) is complex valued. The real and imaginary part of the \(g_{2}\) are determined by the receiver gain and the 2nd order input intercept point (IIP2) of the I and Q mixer and can be written as [24]
The term \(( y_{\text{RF}}^{\text{LNA,in}} )^{2}(t)\) can be expanded using (5) and is given by
In the reference sensitivity scenario, as the wanted signal is very weak, the IMD2 of it is very low and can be ignored and similarly, the IMD2 of the thermal noise can be neglected. As there is a baseband filtering stage before the ADC, the 4th, 5th and 6th terms in (8) are significantly suppressed by this filtering stage and thus can also be ignored. The only signal that drives the strong non-linearity is the Tx leaked signal. With these simplifications, (8) can be written as
In addition, at the mixer output an unwanted Tx modulated spur interference may be generated due to the cross talk between several clock sources as mentioned earlier. By considering the unwanted spur at the frequency \(f_{\text{sp}}\) and the gain of the spur as \(G_{\text{sp}}\), the Tx modulated spur at the mixer output is given by
By adding the Tx modulated spur to the mixer output signal and using (6), (9), and (10), the total signal before the Analog-to-Digital Conversion (ADC) can be expressed as
By inserting (3), (4), and (5) in (11) and performing some simplifications, the total received signal in discrete time domain is described as
where \(y_{\text{BB}}^{\text{Rx}} [n]\) and \(w_{\text{BB}} [n]\) represent the baseband equivalents of the wanted signal and the noise, respectively. The baseband spur offset is \(f_{\Delta} = f_{\text{tx}}-f_{\text{sp}}\), and the sampling frequency is denoted by \(f_{s}\). We can observe, that the third- and fourth-term in (12) represent the Tx modulated spur and Tx-IMD2 interference, respectively.
3.2 Proposed digital interference cancellation
Figure 5 illustrates the proposed digital interference cancellation architecture employed in the Rx baseband. The cancellation is carried out in two steps and is described in the following.
Stage 1: Tx modulated spur cancellation
In this stage, the Tx modulated spur is estimated by using the original baseband Tx as the reference signal. As the modulated spur has some frequency offset, the original Tx signal is frequency shifted before doing the estimation process. A least squares (LS) estimator is used to estimate the filter coefficients. The modulated spur replica is obtained by filtering the original Tx signal with the estimated filter. This replica is then subtracted from the received signal to suppress the modulated spur interference.
This procedure is now expressed analytically. Note, that during the estimation process in stage 1, except for the modulated spur term in (12), the rest of the signal components act as noise for the estimation and therefore can be combined into a single noise source. By doing some simplifications, (12) can be written in matrix/vector form as
where \(\textbf{X}_{\text{BB}}^{\text{TxS}}\) represents the convolution matrix that can be constructed from the frequency shifted Tx signal vector \(\textbf{x}_{\text{BB}}^{\text{TxS}}\). The overall channel coefficients vector is denoted by \(\textbf{{h}}_{\text{BB}}^{\text{Tot}} = [h_{0},h_{1},\ldots ,h_{M-1} ]^{\text{T}}\). The signals \(\textbf{y}_{\text{BB}}^{\text{Tot}}\) and \(\textbf{w}_{\text{BB}}^{\prime}\) represent the total received signal and the noise signal vectors, respectively. The above equation forms the standard linear model with the parameter vector \(\textbf{h}_{\text{BB}}^{\text{Tot}}\) to be estimated. An LS estimator can be formulated as
where \((\cdot)^{\text{H}}\) denotes the Hermitian transpose. By using this estimated channel coefficients, the estimated modulated spur signal in discrete time form can be derived as
This estimated signal is then subtracted from the total received signal in (12) to cancel the modulated spur interference in the received signal.
Stage 2: Tx - IMD2 cancellation
In this stage, we propose to use the squared envelope of the estimated modulated spur signal given in (15) as the reference signal to estimate the Tx-IMD2 interference. This is in contrast to the existing schemes [24, 25], where the original Tx signal is used to estimate the IMD2 interference. As will be shown below, the proposed Tx-IMD2 cancellation scheme has a very low complexity employing only a single tap filter to estimate the interference.
From (12) the IMD2 interference signal can be written as
By considering the modulated spur interference in Rx baseband as \(y_{\text{BB}}^{\text{Mod,sp}} [n]\) and using (12), the term \(x_{\text{BB}}^{\text{Tx}} \ast h_{\text{BB}}^{\text{TxL}} [n]\) can be expressed as
By substituting (17) in (16), the IMD2 interference can be re-written as
where \(g_{s}\) is the complex coefficient that describes the total scaling value. The real and imaginary parts of \(g_{s}\) represent the scaling of the IMD2 interference in I and Q branch, respectively. Note, that the envelope of the phase rotation term \(e^{\frac{-j 2 \pi f_{\Delta} n}{f_{s}}}\) is 1 and therefore, it is neglected in (18) (i.e., stage 2 processing). From (18), it is evident that the IMD2 interference can be estimated using the Tx modulated spur. As the modulated spur signal is estimated in stage 1 of the proposed cancellation scheme given in (15), its envelope of it is generated followed by a single tap filter. This filter coefficient can again be estimated by using an LS estimator as
where \(\widehat{\textbf{y}}_{\text{BB}}^{\text{sp}\_\text{env}}\) is the envelope of the estimated modulated spur signal and \(\textbf{y}_{\text{BB}}^{\text{Tot}\_\text{stg1}\_\text{op}}\) is the remaining signal in the Rx path after the stage 1 cancellation. By further simplifying (19), the final estimator can be written as
From (20), the IMD2 estimated signal can be derived as \(\widehat{y}_{\text{BB}}^{\text{imd2}} [n] = \widehat{y}_{\text{BB}}^{\text{sp}\_\text{env}} [n] \widehat{g}_{s}\), which is then subtracted from the remaining received signal.
4 Simulation results and discussion
For a proof of concept, the proposed digital cancellation architecture is evaluated with numerical simulations. The SNR improvement that is achieved at the output of each stage in the presented compensation architecture is discussed. For that, a MATLAB based LTE-FDD transceiver simulation chain is used where the behavior of each component in the chain is modeled to reflect realistic conditions. The synthesized impulse responses of the measured S-parameter data of a commercial LTE band 3 duplexer is used in the RF-front end. The Tx-Rx stop band response of the considered duplexer is as shown in Fig. 4.
To obtain a strong interference level in the Rx, the transceiver is operated in the reference sensitivity mode. The wanted signal and the Tx signal levels at the antenna are considered at \(-100~\mbox{dBm}\) and \(+23~\mbox{dBm}\), respectively. The receiver gain is set to 32 dB. In addition, the receiver 2nd order intercept point (IIP2) is set at \(+35~\mbox{dBm}\). An LTE 20 MHz full resource block (RB) allocated signal is used for both the wanted and the Tx signals. The RF blocks in the simulation chain are operated at a sampling frequency of 1.228 GHz. The Rx baseband is operating at an oversampling factor of 2 that represents a sampling frequency of 61.44 MHz. The center frequencies of the Tx and Rx carriers are at 1842.5 MHz and 1747.5 MHz, respectively. For simplicity, the noise figure (NF) of the receiver is set to 0 dB. Therefore, the only noise source in the receiver other than the considered interferences is the thermal noise with a power of \(-101.4~\mbox{dBm}\) within a 20 MHz LTE channel. Note, that the effective occupied bandwidth (BW) for a full RB allocated LTE20 wanted signal is 18 MHz. For that reason, all our SNR and SNIR evaluations are based on 18 MHz channel BW.
Figure 6 shows the spectrum of the baseband Rx signal when there is no interference (i.e., ideal case) and also when the interference is active. Without interference we only have the wanted signal and the thermal noise within the whole Rx signal. Therefore, in the ideal case, the SNR of the wanted signal is calculated as 1.4 dB. If the interference is active, the wanted signal is completely masked by the huge interference induced by the Tx-modulated spur and the Tx-IMD2 signal components. Note, that the Tx-modulated spur interference level is kept 20 dB above the wanted signal power level. In addition, the frequency offset of the spur in the baseband is considered to be at 2 MHz (i.e., \(f_{\Delta} = 2~\text{MHz}\)) as can be observed from the figure. The SNIR of the wanted signal in the presence of those two interferences is calculated as \(-19.50~\mbox{dB}\). The proposed cancellation technique is expected to recover the wanted signal SNR and is discussed in the following.
The spectrum of the Rx signal before and after the modulated spur interference cancellation is illustrated in Fig. 7. This cancellation is performed at stage 1 of the proposed architecture, where a 16 tap filter is used to estimate the channel. It can be observed, that the modulated spur is significantly suppressed from the Rx signal while the Tx-IMD2 interference is still visible in the spectrum. The Tx-IMD2 interference is treated in the next stage of the cancellation. The SNIR of the wanted signal after modulated spur cancellation is measured as \(-4.8~\mbox{dB}\) which shows a significant improvement compared to the case of no cancellation. It is worth to note, that in stage 1, all signals except the modulated spur act as a noise for the estimation. However, in stage 2, since the modulated spur is already suppressed significantly, ideally only the wanted signal and the thermal noise components act as a noise for the Tx-IMD2 filter estimation process.
In stage 2, a 1 tap filter is used to generate the IMD2 replica from the reference signal which is a major advantage of the proposed scheme in terms of computational complexity. Figure 8 depicts the spectral plot of the Rx signal before and after the IMD2 cancellation along with the ideal Rx signal. It can be observed, that the IMD2 interference is suppressed to the noise floor and the resulting Rx signal spectrum comes very close to the ideal Rx signal. To express the performance in numbers, the SNIR of the wanted signal after Tx-IMD2 cancellation is 1.1 dB which is within a 0.3 dB range of the wanted signal SNR without any interference. The proposed joint compensation scheme suppresses both types of interferences by 30.5 dB from the Rx signal. In order to evaluate the robustness of the proposed cancellation scheme, further simulations are performed with various antenna referred wanted signal levels ranging from \(-100~\mbox{dBm}\) to \(-50~\mbox{dBm}\) in the increasing steps of 10 dB. The evaluation results are summarized in Table 1.
5 Conclusion
In this article, we presented an overview of various key aspects and challenges involved in the design of a digital-intensive wireless transceiver with a special focus on the three major subsystems, namely, Tx, Rx, and PLL. Furthermore, we discussed in detail the origin of two types of self-interference, a critical issue that prominently appears in LTE-CA transceivers when operating in FDD mode. To mitigate such, we proposed a novel digital self-interference cancellation technique that exploits the underlying relation between the two types of interferences and offers a low-complex and flexible solution. The performance of the proposed technique was evaluated through simulations with measured duplexer characteristics and at various wanted signal levels. It was shown, that in the reference sensitivity scenario this architecture effectively cancels the self-interference and restores the SNR of the wanted signal within a 0.3 dB range from its value in the absence of the self-interference.
References
Staszewski, R. B. (2012): Digitally intensive wireless transceivers. IEEE Des. Test Comput., 29(6), 7–18.
Boos, Z., et al. (2011): A fully digital multimode polar transmitter employing 17b RF DAC in 3G mode. In IEEE international solid-state circuits conference (ISSCC) (pp. 376–378).
Staszewski, R. (2011): State-of-the-art and future directions of high-performance all-digital frequency synthesis in nanometer CMOS. IEEE Trans. Circuits Syst. I, Regul. Pap., 58(7), 1497–1510.
Buckel, T., et al. (2017): A highly reconfigurable RF-DPLL phase modulator for polar transmitters in multi-band/multi-standard cellular RFICs. In 2017 IEEE radio frequency integrated circuits symposium (RFIC), Honolulu, HI (pp. 104–107).
Sievert, S., et al. (2016): A 2 GHz 244 fs-resolution 1.2 ps-peak-INL edge interpolator-based digital-to-time converter in 28 nm CMOS. IEEE J. Solid-State Circuits, 51(12), 2992–3004.
Preyler, P., Preissl, C., Tertinek, S., Buckel, T., Springer, A. (2017): LO generation with a phase interpolator digital-to-time converter. IEEE Trans. Microw. Theory Tech.
Buckel, T., et al. (2014): Challenges in RF-DPLL design for wideband phase modulation supporting SC-FDMA in LTE uplink. In 44th European microwave conference (EuMC) (pp. 604–607).
Zimmermann, N., Thiel, B., Negra, R., Heinen, S. (2009): System architecture of an RF-DAC based multistandard transmitter. In 52nd IEEE international Midwest symposium on circuits and systems, 2009. MWSCAS ’09 (pp. 248–251).
Trampitsch, S., et al. (2017): A nonlinear switched state-space model for capacitive RF DACs. IEEE Trans. Circuits Syst. I, Regul. Pap., 64(6), 1342–1353.
Luschas, S., Schreier, R., Lee, H.-S. (2004): Radio frequency digital-to-analog converter. IEEE J. Solid-State Circuits, 39(9), 1462–1467.
Yoo, S.-M., Walling, J. S., Woo, E. C., Jann, B., Allstot, D. J. (2011): A switched-capacitor RF power amplifier. IEEE J. Solid-State Circuits, 46(12), 2977–2987.
Fulde, M., et al. (2017): A digital multimode polar transmitter supporting 40 MHz LTE Carrier Aggregation in 28 nm CMOS. In IEEE international solid-state circuits conference (ISSCC), San Francisco, CA (pp. 218–219).
Bagheri, R., et al. (2006): An 800 MHz to 5 GHz software-defined radio receiver in 90 nm CMOS. In 2006 IEEE international solid state circuits conference, San Francisco, CA (pp. 1932–1941).
Shibata, H., et al. (2012): A DC-to-1 GHz tunable RF \(\Delta\varSigma\) ADC achieving \(\mbox{DR}= 74~\mbox{dB}\) and \(\mbox{BW}=150~\mbox{MHz}\) at \(f_{0} = 450~\mbox{MHz}\) using 550 mW. IEEE J. Solid-State Circuits, 47(12), 2888–2897.
Pedersen, K. I., Frederiksen, F., Rosa, C., Nguyen, H., Garcia, L. G. U., Yuanye, W. (2011): Carrier aggregation for LTE-advanced: functionality and performance aspects. IEEE Commun. Mag., 49(6), 89–95.
Iwamura, M., Etemad, K., Fong, M., Nory, R., Love, R. (2010): Carrier aggregation framework in 3GPP LTE-advanced. IEEE Commun. Mag., 48(8), 60–67.
Gheidi, H., Dabag, H. T., Liu, Y., Asbeck, P. M., Gudem, P. (2015): Digital cancellation technique to mitigate receiver desensitization in cellular handsets operating in carrier aggregation mode with multiple uplinks and multiple downlinks. In Proc. of the IEEE radio and wireless symposium (RWS) (pp. 221–224).
Kiayani, A., Abdelaziz, M., Anttila, L., Lehtinen, V., Valkama, M. (2014): DSP-based suppression of spurious emissions at RX band in carrier aggregation FDD transceivers. In Proc. of the 22nd European signal processing conference (EUSIPCO) (pp. 591–595).
Dabag, H. T., Gheidi, H., Farsi, S., Gudem, P., Asbeck, P. M. (2013): All-digital cancellation technique to mitigate receiver desensitization in uplink carrier aggregation in cellular handsets. IEEE Trans. Microw. Theory Tech., 61(12), 4754–4765.
Dabag, H. T., Gheidi, H., Gudem, P., Asbeck, P. M. (2013): All-digital cancellation technique to mitigate self-jamming in uplink carrier aggregation in cellular handsets. In IEEE MTT-S international microwave symposium digest (IMS) (pp. 1–3).
Kiayani, A., Anttila, L., Valkama, M. (2014): Digital suppression of power amplifier spurious emissions at receiver band in FDD transceivers. IEEE Signal Process. Lett., 21(1), 69–73.
Kanumalli, R. S., Gebhard, A., Elmaghraby, A., Mayer, A., Schwartz, D., Huemer, M. (2016): Active digital cancellation of transmitter induced modulated spur interference in 4G LTE carrier aggregation transceivers. In IEEE 83rd vehicular technology conference (VTC spring), Nanjing (pp. 1–5).
Gebhard, A., Kanumalli, R. S., Neurauter, B., Huemer, M. (2016): Adaptive self-interference cancelation in LTE-A carrier aggregation FDD direct-conversion transceivers. In 2016 IEEE sensor array and multichannel signal processing workshop (SAM), Rio de Janerio (pp. 1–5).
Frotzscher, A., Fettweis, G. (2008): Baseband analysis of Tx leakage in WCDMA zero-IF-receivers. In 3rd international symposium on communications, control and signal processing (pp. 129–134).
Lederer, C., Huemer, M. (2011): Simplified complex LMS algorithm for the cancellation of second-order TX intermodulation distortions in homodyne receivers. In Proc. of the 45th Asilomar conference on signals, systems and computers (ASILOMAR) (pp. 533–537).
Acknowledgements
Open access funding provided by Johannes Kepler University Linz. The authors wish to acknowledge DMCE GmbH & Co KG as part of Intel for supporting this work carried out at the Christian Doppler Laboratory for Digitally Assisted RF Transceivers for Future Mobile Communications. The financial support by the Austrian Federal Ministry of Science, Research and Economy and the National Foundation for Research, Technology and Development is gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kanumalli, R.S., Buckel, T., Preissl, C. et al. Digitally-intensive transceivers for future mobile communications—emerging trends and challenges. Elektrotech. Inftech. 135, 30–39 (2018). https://doi.org/10.1007/s00502-017-0576-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00502-017-0576-1
Keywords
- RF
- mobile communications
- wireless communications
- signal processing
- interference cancellation
- carrier aggregation