Input nonlinearity compensation and chattering reduction in a mobile hydraulic forestry crane

Abstract

We present a sliding-mode-based control design for a telescopic link of a mobile-hydraulic forestry crane under bounded modeling uncertainties and external disturbances. Mobile hydraulic systems are typically subject to strong perturbation conditions and the design of resilient control solutions is an important challenge. Furthermore, nonlinear phenomena primarily, characterized by easily excited oscillations, an input nonlinearity, and friction, are dominating the dynamics. The proposed control scheme takes advantage of an input-nonlinearity compensation in order to overcome these problems and includes the formulation of a sliding-mode-control-based design. Two strategies for chattering attenuation are examined aimed at improving the controller performance. Experimental results performed over an industrial setup, including a comparison with a PID controller, confirm the efficacy of the proposed methodology.

Zusammenfassung

In dieser Arbeit wird eine Regelung für einen Teleskoparm eines mobilen hydraulischen Forstkrans mit Hilfe von Sliding Mode-Methoden entworfen. Da mobile Hydrauliksysteme üblicherweise starken Störungen unterworfen sind, ist die Entwicklung robuster Regelungen von entscheidender Bedeutung. Zusätzlich beeinflussen Reibung und eine Eingangsnichtlinearität das Systemverhalten. Das vorgestellte Regelungskonzept basiert auf der Kombination einer Kompensation der Eingangsnichtlinearität mit Methoden aus dem Bereich der strukturvariablen Systeme. Es werden zwei Möglichkeiten zur Reduktion des Chattering untersucht. Die Effizienz der vorgeschlagenen Methode wird durch Experimente gezeigt und mit einer PID-Regelung verglichen.

1 Introduction

Hydraulic actuators are the main components of mobile heavy-duty machinery, where high torques, speeds, and large ratios between the delivered force and the size of the actuator are required. Forestry, agriculture, and mining are traditional fields where such machines are typically used. Traditionally, they are controlled manually by a driver via a set of joysticks. However, in order to improve efficiency, to alleviate the stress, and to avoid accidents a design of automatic control strategies is required. In [6] and [7] a comparison of some of the most popular control strategies applied to a single-ended cylinder are presented, where adaptive, sliding mode, and PID controllers have claimed to be the most successful control strategies. In comparison with industrial hydraulics, where high precision sensors for pressures, positions, velocities, and accelerations of the cylinders are available, see e.g. [9, 10], and [1], on mobile hydraulics the instrumentation is limited and often includes only pressure transducers and low-accuracy position sensors. Additionally, there are other nonlinear phenomena, like the ones that can be modeled as a dead zone and a saturation, making the control design more difficult, see e.g. [2] and [3].

In this case, the sliding mode approach offers good robustness/insensitivity properties against external uncertainties or disturbances, see [6, 7] and [3]. The main disadvantage of the sliding mode controllers is the so-called chattering effect, which in part is originated by the required high frequency commutation of the control signal. Particularly, this is not suitable for electro-hydraulic or electro-mechanical actuators, where strict limitations over the frequency rate commutation are present. For this purpose, second order sliding modes have been proved to be effective in chattering attenuation by moving an implementation of discontinuity away from the plant input while at the same time preserving the sliding mode properties, see [4, 14] and [5].

In this paper, the position control of a mobile hydraulic system with an asymmetric cylinder is the subject of study. First, the dynamical model is presented. Then, a second order sliding mode design is performed taking into account bounded model uncertainties and external disturbances. There are crucial differences from previous works. In particular, we take into account the input nonlinearity of the actuator, which is typically present at industry-standard mobile hydraulic set-ups, and consider large displacements of the cylinder position in numerical models and experiments, as well as the need for chattering attenuation providing a continuous control signal. The proposed approach assumes that the cylinder position is available for measurement while the velocity is estimated by a second order sliding mode differentiator, see [18]. Furthermore, two techniques for chattering attenuation are explored in the paper: inclusion of estimated equivalent control and asymptotic second order sliding modes. For comparison purposes, a PID controller is implemented and tested in our laboratory hydraulic system.

The rest of the paper is organized as follows. The model description is presented in Sect. 2. In Sect. 3, the control methodology is introduced, including two approaches for chattering attenuation. The experimental results are presented in Sect. 5. After that, conclusions are drawn.

2 Telescopic link model

The experimental setup under study is a telescopic link of a prototype of a typical forestry crane. Such industrial equipment is widely used and is a subject of many researches aimed at automation of these systems, see [11, 12].

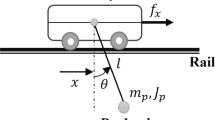
The telescopic link of the crane, see Fig. 1, consists of a double-acting single-side hydraulic cylinder and a solid load, which is attached to a piston of the cylinder. The position of the link, $x$, varies from 0 to 1.55 m; positive velocity $\dot{x}$ corresponds to extraction of the cylinder. A simplified model of this link’s dynamics can be taken as a restricted 1-DOF mechanical system actuated by a hydraulic force:

$$\begin{gathered} m\ddot{x}=f_{h}-f_{\mathrm{grav}}-f_{\mathrm{fric}}, \end{gathered}$$

(1)

$$\begin{gathered} f_{h}=\left \{ \textstyle\begin{array}{@{}l@{\quad }l} p_{a} A_{a}-p_{b} A_{b}, & \mbox{if variables are in } D, \\ f_{\mathrm{uncertain}}, & \mbox{otherwise}, \end{array}\displaystyle \right . \end{gathered}$$

(2)

where $m$ is the mass, $f_{\mathrm{grav}}$ is the gravity force, $f_{\mathrm{fric}}$ is the friction force, $f_{h}$ is the force generated by the hydraulics,

$$ D= \bigl\{ x\in (0,\bar{x}_{p}),\quad |\dot{x}|< \bar{x}_{v},\quad p _{a},p_{b}\in (p_{t},p_{s}) \bigr\} , $$

(3)

is defined by constant bounds, see Table 1, $p_{s}$ is the pump pressure, and $p_{t}$ is the return (exit) pressure, the piston areas $A_{a}$ and $A_{b}$ are known geometric parameters, $p_{a}$ and $p_{b}$ are the measured pressures in chambers $a$ and $b$ of the cylinder.

Fig. 1.

Industrial hydraulic forestry crane

Table 1. Physical parameters of the link

Remark 1

The position of the link, $x$, is limited by geometrical constrains, the velocity is limited by the maximum achievable flow from a pump, pressures are limited through a set of service anti-cavitation and pressure-relief valves, which, in particular, ensure $p_{t}\le p_{i} \le p_{s}$, $i=a,b$. These devices play a fault-preventing role and do not influence a normal operation. Moreover, the initial conditions are within the region $D$ and $f_{\mathrm{uncertain}}$ prevent from leaving the region.

Following [19], we posed the assumption that the valve is symmetric, i.e. $S_{a}=S_{b}$, where $S_{a}(u)$ and $S_{b}(u)$ denote non-negative areas of orifices for chambers $A$ and $B$; $S$ represent a signed area function: $\psi (u) = S_{a}(u)\mathrm{sign}(u) = S_{b}(u) \mathrm{sign}(u)$, where the absolute value of this function represents the opening area of the orifices and the sign indicates direction of the flow. The signed area can be defined as a function of the input signal, which can be approximated by a nonlinear static relation, see [2]. The shape of function $\psi$ strongly depends on the type of the valve. For industrial heavy duty systems, a common shape comprises a dead-zone, due to the leakage-prevention in closed-center spool, and saturation. On the other hand, pressures dynamics are

$$ \begin{aligned} \dot{p}_{a}&= \frac{\beta }{V_{a}(x)} ( - \dot{x} A_{a}+q_{a} ) ,\quad \text{if } p_{t}< p_{a}< p_{s}, \\ \dot{p}_{b} &= \frac{\beta }{V_{b}(x)} ( \dot{x} A_{b}-q_{b} ) ,\quad \text{if } p_{t}< p_{b}< p_{s}, \end{aligned} $$

(4)

for $i=a,b$, and initial conditions $p_{i}(0)$ $\in [p_{t},p_{s}]$; $V_{a}(x)=V_{a0}+x A_{a}$ and $V_{b}(x)=V_{b0}-x A_{b}$ are volumes of chambers $a$ and $b$ at the given piston position $x$, $V_{a0}$ and $V_{b0}$ are known geometric constants, $\beta$ is an unknown bulk modulus, $q_{a}$ and $q_{b}$ are flows to the chamber $a$ and from the chamber $b$; $p_{s}$ is the pump pressure, and $p_{t}$ is the return (exit or tank) pressure. The flow $q_{a}$ is positive when oil goes into chamber $a$, and the flow $q_{b}$ is positive when the oil goes out of chamber $b$. The flows distribution can be rewritten as:

$$ \textstyle\begin{array}{l} q_{a} = c_{a}\phi_{a}\psi (u), \qquad q_{b} = c_{b}\phi_{b}\psi (u), \end{array} $$

(5)

with $\phi_{a} =\sqrt{p_{s}-p_{a}} \frac{(\textrm{sign}(\psi (u)+1))}{2}-\sqrt{p_{a}-p_{t}}\frac{( \textrm{sign}(\psi (u)-1))}{2}$ and $\phi_{b} = \sqrt{p_{b}-p_{t}}\frac{( \textrm{sign}(\psi (u)+1))}{2}-\sqrt{p_{s}-p_{b}}\frac{( \textrm{sign}(\psi (u)-1))}{2}$. In industrial hydraulics systems, $\phi_{a} > 0$ and $\phi_{b} > 0$ are ensured by a set of safety valves that maintain a nonzero pressure difference. Besides, the time derivative of $f_{h}$ in the domain of interest is

$$ \dot{f}_{h}=-\varphi_{0} \dot{x}+ \varphi_{1} \psi (u) $$

(6)

where $\varphi_{0}=\beta ( \frac{A_{a}^{2}}{V_{a}(x)}+\frac{A_{b}^{2}}{V _{b}(x)})$ and $\varphi_{1}=\beta ( \frac{c_{a}A_{a}\varphi_{a}}{V _{a}(x)}+\frac{c_{b}A_{b} \varphi_{b}}{V_{b}(x)})$ with $0<\underline{ \varphi_{i}}\leq \varphi_{i}\leq \overline{\varphi_{i}}$ for $i=0,1$. Here $c_{a}$ and $c_{b}$ are constant coefficients, which depend on physical values (fluid density, discharge coefficient and other). For more details about the model see, e.g. [17] and [19].

3 Sliding-mode-control-based design

Given an appropriate feasible desired trajectory, $x_{\mathrm{ref}}(t)$, with a Lipschitz continuous first derivative, $\dot{x}_{\mathrm{ref}}(t)$, the objective is to design a control law, $u$, to make the cylinder position, $x$, track as close as possible $x_{\mathrm{ref}}(t)$. For this aim, the error variables are defined as

$$ e_{1}=x-x_{\mathrm{ref}}(t) \quad \hbox{and} \quad e_{2}= \dot{x}-\dot{x}_{\mathrm{ref}}(t) $$

(7)

Let us introduce the sliding variable $\sigma =e_{2}+\lambda e_{1}$, where $\lambda$ is a positive constant, $\lambda >0$. The velocity, $\dot{x}$, is not available for measurement, however, a good estimation can be obtained by a second order sliding mode differentiator, for which, in order to attenuate chattering and improve performance, the differentiator gain is designed as a time varying function, see [18] for a detailed description of the algorithm used within our study. The velocity estimation introduces an estimation error in $\sigma$, i.e. $\tilde{x}_{v_{2}}=\hat{x}_{v_{2}}-\dot{x}$, obtaining:

$$ \sigma =e_{2}+\lambda e_{1}+\tilde{x}_{v_{2}}. $$

(8)

Since $\ddot{x}_{\mathrm{ref}}(t)$ is assumed to be Lipschitz continuous, with the proposed sliding model differentiator, $\tilde{x}_{v_{2}}$, and $\dot{\tilde{x}}_{v_{2}}$ are bounded, see [18]. Besides, taking into account

$$ \dot{e}_{1}=e_{2}=\varphi_{0}^{-1} \varphi_{1}\psi (u)-\varphi_{0}^{-1} \dot{f}_{h}-\dot{x}_{\mathrm{ref}}(t), $$

and setting the variables $x_{1}=e_{1}$, $x_{2}=\sigma$, $z_{1}=p _{a}$ and $z_{2}=p_{b}$; with $\mathbf{x}=[x_{1},x_{2}]^{T}$ and $\mathbf{z}=[z_{1},z_{2}]^{T}$ the next state space representation is obtained:

$$\begin{gathered} \textstyle\begin{array}{l} \dot{\mathbf{z}}=\mathbf{Z}_{0}(t,\mathbf{x},\mathbf{z}), \qquad \dot{\mathbf{x}}=\mathbf{X}_{0}(t,\mathbf{x},\mathbf{z},u), \end{array}\displaystyle \\ \mathbf{Z}_{0}(\cdot )= \begin{bmatrix} \frac{\beta }{V_{a}}(-(x_{2}-\lambda x_{1}+\dot{x}_{\mathrm{ref}}-\tilde{x} _{v2}) A_{a}+q_{a}) \\ \frac{\beta }{V_{b}}((x_{2}-\lambda x_{1}+\dot{x}_{\mathrm{ref}}-\tilde{x} _{v2}) A_{b}-q_{b}) \end{bmatrix} \\ \mathbf{X}_{0}(\cdot )= \begin{bmatrix} -\lambda x_{1}+x_{2}-\tilde{x}_{v2} \\ \lambda \varphi_{0}^{-1}\varphi_{1}\psi (u)+g_{0} \end{bmatrix} , \end{gathered}$$

(9)

where the perturbation term, $g_{0}$ is given by $g_{0}=m^{-1}(f_{h}-f _{\mathrm{grav}}-f_{\mathrm{fric}}-\ddot{x}_{\mathrm{ref}})-\lambda \varphi^{-1}_{0}\dot{f}_{h}+ \dot{\tilde{x}}_{v2}-\lambda \dot{x}_{\mathrm{ref}}$. In order to ensure the convergence of variables $x_{1}=e_{1}$ and $x_{2}=\sigma$, the following standard first order sliding mode control law can be used

$$ u=-k_{p} x_{2}-k \operatorname{sign}(x_{2}) $$

(10)

The trajectories of system (9) under the control law (10) can be understood in the equivalent control sense, see [16]. The sliding mode enforcement occurs in the variable $x_{2}=\sigma$, i.e. $\sigma$ vanishes when $t$ reaches $t_{f}$. Once, the sliding mode is achieved, $\sigma \equiv 0$, the trajectories of system (9) are governed by the equivalent control, $u_{eq}$:

$$ u_{eq}=-\psi^{-1}\bigl(\varphi^{-1}_{1} \varphi_{0}\lambda^{-1}g_{0}\bigr) $$

(11)

substituting (11) in (9) the zero dynamics is obtained

$$\begin{gathered} \dot{\mathbf{z}} \leq \begin{bmatrix} \frac{\beta }{V_{a}} ( |\dot{x}_{\mathrm{ref}}(t)|A_{a}+c_{a}\phi_{a}| \psi (u_{eq})| ) \\ \frac{\beta }{V_{b}}(|\dot{x}_{\mathrm{ref}}(t)|A_{b}+c_{b}\phi_{b}|\psi (u _{eq})|) \end{bmatrix} , \end{gathered}$$

(12)

$$\begin{gathered} \textstyle\begin{array}{l} \dot{x}_{1}=-\lambda x_{1}-\tilde{x}_{v2}. \end{array}\displaystyle \end{gathered}$$

(13)

Note that $\lambda >0$, and the velocity estimation error, $\tilde{x}_{v2}$, is ultimately bounded (in absence of noise, $\tilde{x}_{v2}\rightarrow 0$ in finite time). Besides, the variables $\boldsymbol{z}$ and $x_{1}$, belong to the domain (3). By its nature, the vector variable $\boldsymbol{z}$ is of bounded variation, consequently the hydraulic force $f_{h}$ and its derivative $\dot{f}_{h}$ are bounded functions. Furthermore, $|\dot{x}_{\mathrm{ref}}(t)| \leq \bar{x}_{v}$ and $|\psi (u_{eq})|\leq \underline{\varphi^{-1} _{1}}\overline{\varphi_{0}}\lambda^{-1}\overline{g_{0}}$ which imply $\dot{f}_{h}$ remains bounded. Then, the partial solution $x_{1}$ of system (12)–(13) is uniformly ultimately bounded in the specified domain (3).

3.1 Chattering attenuation

In mobile hydraulic systems it is important to avoid chattering in the input to the valve by providing continuous or smooth control signals. Particularly, the telescopic link cannot move back and forth with high frequency. However, it is desirable at the same time to preserve the robustness of the closed-loop system to bounded model uncertainties and external disturbances. In this section two methods are proposed for this application: estimated equivalent control injection and asymptotic second order sliding mode (ASOSM).

3.1.1 Equivalent control estimation (via LPF)

The equivalent control action, $u_{eq}$, describes the average effect of the high frequency switching due to an implementation of the discontinuity present in the control law (10). Applying a low pass filter (LPF) to the term $k\operatorname{sign}(\sigma )$ this average value can be obtained, see [16] and [13]. The equivalent control can be estimated, on-line, as

$$ \textstyle\begin{array}{l} \tau \dot{\zeta }=-\zeta +\text{sign}(\sigma ), \qquad \hat{u}_{eq}=-k_{p}\sigma -k \zeta , \end{array} $$

(14)

where $\tau >0$ represents the time constant of the filter, which must be accurately tuned.

3.1.2 Asymptotic Second Order Sliding Modes (ASOSM)

Another strategy to attenuate the chattering effect is to increase the order of the sliding mode. In the case of the sliding variable, $\sigma$, with relative degree one, the order can be increasing if the term $k\operatorname{sign}(\sigma )$ is replaced by $\int_{0}^{t}k \operatorname{sign}(\sigma )\,d\tau$:

$$ u=-k_{p} \sigma -k \int_{0}^{t}\operatorname{sign}(\sigma )\,d\tau $$

(15)

With this strategy a continuous control signal is obtained; however, the convergence of the sliding variable $\sigma$ now is asymptotic, i.e. $t_{f}\rightarrow \infty$, see e.g. [8, page 65].

4 Static input-nonlinearity compensation

Two important steps in the control design are the compensation of the actuator dead zone and uncertainty reduction using a feedforward term. The inverse of a dead zone is a relay-type discontinuity that can be compensated if the inverse is known, [15]. This can be done at least locally, during most of the working ranges. In order to compensate the input-nonlinearity and reduce disturbances, the control input is re-defined as follows

$$ u=\hat{\psi }^{-1} \bigl(v_{i}+\dot{x}_{\mathrm{ref}}(t) \bigr), $$

(16)

where $v_{i}$ is taken either in the form of $\hat{u}_{eq}$ in (14) or in the form of $u$ in (15), $\dot{x}_{\mathrm{ref}}(t)$ is a feedforward term and $\hat{\psi }^{-1}(\cdot )$ is a static nonlinearity compensation function, which involves both the dead zone and the saturation, and a nonlinear shape between them, $\hat{\psi }(v)$ is presented in Fig. 2 and was identified by a set of open-loop experiments, see [2]. After applying the static nonlinear compensation (16), we obtain $\psi (u)=v_{i}+ \dot{x}_{\mathrm{ref}}(t)+\psi_{e}$, where $\psi_{e}$ represents the identification error, while $v_{i}$ can be defined as either $v_{i}=\hat{u}_{eq}$ or $v_{i}=-k_{p} \sigma -k \int_{0}^{t} \text{sign}(\sigma )\,d\tau$.

Fig. 2.

Identified input nonlinearity, normalized equivalent area $S$ vs normalized input signal $u$

5 Experiments

The experimental tests are carried out with a real-time platform dSpace 1401 at a sampling interval 1 ms using forward Euler integration method. The position of the telescopic link is measured with a wire-actuated encoder. The encoder provides 2381 counts for the range from 0 to 1.55 m; the quantization interval is $Q=0.651~\mbox{mm}$. The measured signal $x$ can be approximated as the position signal with an additive uniform noise with a variance $Q^{2}/12$. Due to the quantization interval, $Q$, the control law (16) can be modified in order to improve the initial transient and the steady-state error:

$$ u= \left \{ \textstyle\begin{array}{l@{\quad }l} 0, & \text{if } |e_{1}|< 0.004 \text{ and } |\dot{x}_{\mathrm{ref}}| = 0 \\ 0.95\operatorname{sign}(e_{1}), & \text{if }|e_{1}|>0.2 \\ \hat{\psi }^{-1} (v_{i}+\dot{x}_{\mathrm{ref}}(t) ), & \text{otherwise} \end{array}\displaystyle \right . $$

(17)

for $i=\text{PID},\text{LPF},\text{ASOSM}$. Such a modification is motivated as follows. First, if the reference signal is constant, i.e. $|\dot{x}_{\mathrm{ref}}| = 0$, then the controller is expected not to react on sufficiently small position tracking errors. Next, if the tracking error is large, which is typical for an initialization stage, then the simple control action given by the second row of (17) provides fast initial transients. Finally, the input-nonlinearity compensating controller is used in all other cases. It is worth noting that the second row of (17) is given rather for the sake of completeness of presentation, and it does not actually affect the experimental studies presented in the paper. The error bounds are heuristically tuned for the considered equipment.

The velocity is estimated with a second order sliding mode differentiator, see [18] for details. First, Fig. 3 shows the sliding mode controller (10) without an input-nonlinearity compensation, verifying big amplitude of chattering that degrade the overall performance. Second, the proposed static input-nonlinearity is considered.

Fig. 3.

EXP. $x$-cylinder position, $m$ vs $s$; control input, $\mathit{amp}$

An approximation for the input nonlinearity $\psi (u)$ of the industrial hydraulic system was identified by a set of open-loop experiments, see [2], and is presented in Fig. 2. For comparison purposes, a carefully tuned PID controller is implemented as well. In summary, (17) with the next control laws were considered as possible better alternatives to (10):

• (a) $v_{\text{PID}}= \displaystyle -k_{p} e_{1} -k_{d} \dot{e}_{1} - k_{i} \int_{0}^{t}e_{1}\, d \tau$, with $k_{p}=4$, $k_{d}=0.5$, $k_{i}= 1$.

• (b) $v_{\text{LPF}}=-k_{p}\sigma -k\zeta$, with $k_{p}=1$, $k=0.15$ and $\zeta$ as in (14) with $\tau =0.2$.

• (c) $v_{\text{ASOSM}}=-k_{p}\sigma -k\int_{0}^{t} \text{sign}(\sigma ) d\tau$, with $k_{p}=0.8$ and $k=0.2$.

A good performance and chattering attenuation is verified with the proposed approach, see Fig. 4 (compare to Fig. 3). Particularly, the ASOSM gives a slight increase in performance that is verified in the steady-state error, initial transient and chattering in the control signal. Tables 2 and 3, show the tracking errors for 3 different types of trajectories.

Fig. 4.

EXP. $x$-cylinder position and $e_{1}$-position error, $m$ vs $s$; control input, $\mathit{amp}$. (a) $v_{\mathrm{PID}}$, (b) $v_{\mathrm{LPF}}$, (c) $v_{\mathrm{ASOSM}}$

Table 2. $\|e_{1}\|_{\infty }=\max_{t_{0}\leq t\leq t_{1}}|e_{1}|$

Table 3. $\|e_{1}\|_{2}=\sqrt{\frac{1}{t_{1}-t_{0}}\int_{t_{0}}^{t_{1}}|e_{1}( \tau )|^{2}d\tau }$

6 Conclusions

The sliding mode technique provides insensitivity to certain uncertainties in an ideal case but suffers from chattering. Application of sliding mode control design to mobile hydraulic systems is discussed. The approach includes an approximate static inverse dead zone compensation together with a feedforward term. Besides, two strategies for chattering attenuation in the control signal are provided, improving the overall performance. Additionally, comparison with the PID controller is presented. We tested and validated the proposed scheme in an industrial platform, obtaining promising results. Extensions of second order sliding mode controllers applied to more general multi-link industrial hydraulic systems are considered for future work.