1 Introduction

Additive manufacturing using wire arc technology, especially Cold Metal Transfer (CMT), has become increasingly popular in the generation of large-scale and complex shaped 3D parts [1, 2]. Weaving deposition is a common method to improve the quality of the weld. It can uniform the structure, reduce pores, and improve mechanical properties [3]. However, heat input and solidification shrinkage during deposition causes distortions and residual stresses [4]. These can significantly affect the geometric accuracy and mechanical properties of the deposited material.

Process simulation offers the possibility to numerically predict the evolution of such stresses and distortions. Possible violations of geometric tolerances and high stress concentrations can be identified in advance. Expensive trial-and-error experiments can be reduced or eliminated.

However, to accurately simulate the additive manufacturing process, temperature-dependent material data, starting from room temperature till the melting point, is required [5]. Especially the temperature dependent yield stress has a significant effect on the residual stresses and distortions. Furthermore, experimental measurements play a crucial role in the calibration and validation of numerical models. For welding simulations, calibration involves determining key parameters, such as process efficiency, heat source geometry and boundary conditions, including emissivity and thermal convection. Typical calibration experiments involve the use of thermocouples to record the temperature field during deposition. Furthermore, cross-section micrographs of the welds and video footage of the molten pool can aid in refining the heat source model used in the simulation [6]. The validation of the process simulation’s mechanical response can be done by measuring distortions and residual stresses on the final geometry [7, 8]. Nonetheless, when relying on experimental results obtained post manufacturing, it can be challenging to identify the influence of certain numerical modeling parameters at a specific stage during the component’s build up phase. Therefore, different in situ monitoring methods have been used to investigate the evolving deformations occurring during additive manufacturing. Biegler et al. [6] used 3D-Digital Image Correlation (DIC) to measure the strains on the component during Laser Metal Deposition (LMD) additive manufacturing of 316L steel. Denlinger et al. [9] used a Laser Displacement Sensor (LDS) to measure the vertical displacement of a cantilevered substrate during manufacturing a Ti-6Al-4V wall structure using Selective Laser Melting (SLM). Li et al. [10] investigated the influence of deposition patterns during Wire Arc Additive manufacturing of H13 Steel by measuring distortions on a cantilevered substrate using a digital indicator. Lu et al. [11] used a combination of DIC and displacement sensors to validate the thermo-mechanical simulation of Laser Solid Forming (LSF).

Investigations on the simulation of weaving deposition in additive manufacturing or even welding are quite limited. One potential explanation for this is that the weaving motion is often not included in the g‑code or robot code. In this case, the weaving pattern must be incorporated into the simulation through either a coordinate transformation approach or path parametrization [12,13,14,15].

The goal of this research is to achieve a precise calibration of a finite element model for predicting the in-situ thermo-mechanical behavior of an ER 5183 workpiece fabricated using wire arc additive manufacturing with weaving deposition. Section 2 will outline the experimental setup along with the corresponding process parameters. The characterization of the temperature dependent mechanical material properties is shown in Sect. 3, followed by the detailed setup of the simulation model in Sect. 4. Sections 5 and 6 will finally provide a comparison and interpretation of the results obtained through numerical simulations and experiments.

2 Experiments

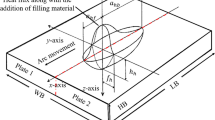
All deposition experiments are conducted at Fronius International, utilizing the Cold Metal Transfer (CMT) process. The objective of these experiments is to weld both a single-layer and a five-layer wall structure onto a one-sided clamped substrate plate, as illustrated in Fig. 1. The substrate plates have a length of 200 mm, a width of 100 mm, and a thickness of 15 mm. To minimize any unaccounted heat transfer into the welding table, the AA 5083 substrate plate is clamped to an insulation block made of glass-reinforced calcium silicate. To ensure that the substrate plates have minimal initial residual stresses, they are subjected to a 12-hour heat treatment at 300 °C prior to the experiments. An ER 5183 wire with a diameter of 1.2 mm serves as the filler material. The substrate plate is fixed in place using a clamping jaw made of steel. Figure 2 shows the contact line of the clamp on the substrate plate.

Fig. 1
figure 1

Experimental setup

Full size image
Fig. 2
figure 2

Schematic drawing showing locations of thermocouples (TC), the stress measurements, the displacement sensor and the clamping

Full size image

All weld seams are produced using weaving motion with 5.5 mm amplitude and 2.5 mm wavelength. The resulting weld seams are 100 mm long and approximately 14.5 mm wide The motion of the welding torch is facilitated by an ABB robot. All seams are welded using a wire feed speed of 8.5 m/min and a travel speed of 100 cm/min along the actual weaving trajectory. Average voltage and current are 15 V and 135 A for every seam. To maintain a consistent interlayer temperature of 100 °C, adjustments are made to the dwell times. The power source utilized is a Fronius iWave 500i AC/DC.

During the experiments, numerous measurements are conducted. The temperature fields within the components are recorded using 8 Type K thermocouples with diameter of 0.5 mm. Ceramic sleeves are employed to shield the thermocouples from the high temperature arc. The positions of the pre-drilled thermocouple-holes are illustrated in Fig. 2. Additional thermocouples are attached to the clamp and insulation. The temperature data is recorded with a sampling rate of 125 ms. Besides the temperature data, the deflection in the z‑direction of the unconstrained end of the substrate is monitored. For this purpose, a Mitutoyo 542-171 displacement sensor with a range of 10 mm, a resolution of 0.0005 mm, and a sampling rate of 1 ms is used. The location of the displacement measurement point is also shown in Fig. 2.

Post manufacturing, 3D scans of the final geometries are done by Fronius International utilizing a GOM ATOS 5 MV700. Residual stresses are measured at the Institute of Materials Science, Joining and Forming (IMAT, TU Graz) using the hole drilling method. The maximum drilling depth is 1 mm subdivided into 20 incremental drilling steps. For the single seam deposition sample, measurements are made on four locations. Three on the top of the surface, the measurement positions are shown in Fig. 2, and one at the center of the bottom surface. In case of the five-layer build, measurements are only taken at the center of the bottom surface.

3 Material Characterisation

The results of thermomechanical welding simulations significantly rely on accurate material properties [5]. Therefore, temperature-dependent Young’s modulus, flow curves, and the thermal expansion coefficient of the AA 5083 substrate material used in this study are characterized using in-house available test equipment.

In a first set of experiments, tensile tests are carried out using a DIL805A/D/T deformation dilatometer. To obtain temperature dependent material properties, tests were performed from 20 to 500 °C using a step size of approximately 50 °C. Heating and cooling rates are set to 10 K/s. The sample geometry used can be seen in Fig. 3. Young’s modulus and flow curves are calculated based on the derived force-displacement curves. Since manual fitting of the Young’s modulus resulted in significant fluctuations, values obtained in [16] are used as a reference. In most cases, the utilization of the reference values led to a good agreement with the experimental results. Only a few measurement points required slight adjustments of the reference values. As shown in Fig. 4, the value of the Young’s modulus decreases with an increase in temperature. At a temperature of 600 °C, it is artificially reduced to 1500 MPa. Artificially lowering the Young’s modulus has numerical reasons. It aims to prevent elements representing liquid material from introducing artificial stiffness. Flow curves are determined based on true stress-strain responses. At elevated temperatures flow curves are extrapolated using the Voce hardening law. This is necessary due to a lack of experimental points.

Fig. 3
figure 3

Specimen geometry

Full size image
Fig. 4
figure 4

Thermal expansion/Youngs modulus and flow curves for AA 5083

Full size image

The determination of the thermal expansion coefficient is carried out using the same dilatometer. Here, a cylindrical sample with a diameter of 4 mm and a length of 10 mm is used. Heating and cooling ramps are set to 5 K/min. The plot shown in Fig. 4 represents the instantaneous thermal expansion coefficient, calculated based on the change in length over time. Above liquidus temperature, the thermal expansion is set to zero, prohibiting “liquid” elements to thermally expand.

4 Numerical Model

The fully coupled thermo-mechanical FE analysis of the additive manufacturing process is performed using the commercial software Simufact Welding®.

The finite element model used for the simulation is shown in Fig. 5. Besides the substrate and the welds, it also includes the clamp and the insulation block. In order to reduce complexity, the weld seams are assumed to be rectangular, with a width of 14.5 mm and a height of 3 mm. The dimensions are averaged over the five-layer build and match the surface area \(A_{\mathrm{wall}}=220.5\,\mathrm{mm}^{2}\) measured from a cross-section micrograph (Fig. 7).

Fig. 5
figure 5

Finite element model

Full size image

4.1 Boundary Conditions

Contact formulations are used between substrate, insulation block, clamp and seam. No external clamping force is considered in this model. Instead, vertical movement of the nodes along the contact line of the clamp is prohibited using single point constraints. Hence, the clamp acts solely as a thermal heat sink. The heat transfer coefficient between substrate and insulation and between substrate and clamp are set to 300 and 1500 W/m2K, respectively. Convective and radiative boundary conditions are applied to all outer surfaces. The materials emissivity and the convection coefficient are assumed independent of the temperature and set to 0.2 and 6.4 W/m2K, respectively. The heat transfer coefficients and thermal boundary conditions were calibrated by trial and error, until the temperatures in the simulation are in good agreement with the temperatures measured in the experiments.

4.2 Material Modelling

To model the deposition of the melted filler material along the welding path, the quiet element method is used [17]. Elements which are not yet deposited are set to a quiet state with material properties that will not affect the rest of the model, like a low thermal conductivity or Young’s modulus. Based on the location of the heat source, elements are then continuously getting activated by the means of re-establishing their real thermo-physical properties.

Due to the lack of available data, the ER 5183 filler material is assumed to have the same material properties as the AA 5083 substrate material. Furthermore, the precise material of the clamp is unknown and assumed to be A283C grade steel. The thermo-physical properties of AA 5083 are taken from reference [16]. Mechanical properties are measured in-house as described in Sect. 3. Material properties of A283C are taken from Simufact’s own material database, material data for the glass-reinforced calcium silicate insulation block can be found in reference [18]. Due to a lack of information, the specific heat capacity and the Young’s modulus of the calcium silicate is assumed to be 400 J/kg K and 20 GPa, respectively.

4.3 Heat Source Modelling

The energy input during the AM process is modelled using Goldaks double ellipsoidal shaped heat source [19]. It prescribes a heat generation per unit volume in a moving reference frame and gives an approximation of the molten pool geometry moving along the welding path. A schematic representation of the heat source with its local coordinates x, y, z is given in Fig. 6.

Fig. 6
figure 6

Goldak Heat Source Model [19]

Full size image

The energy deposition is based on a Gaussian distribution and can be given by

$$\begin{aligned}q_{f}(x,y,z) & = \frac{6F_{f}\sqrt{3}Q}{\pi \sqrt{\pi}abc_{f}} \mathrm{exp} \left(\frac{-3x^{2}}{a^{2}}\right) \mathrm{exp} \left(\frac{-3y^{2}}{b^{2}}\right)\\&\quad\, \mathrm{exp} \left(\frac{-3z^{2}}{c_{f}^{2}}\right)\end{aligned}$$
(1)

for the positive z semi-axes and

$$\begin{aligned}q_{r}(x,y,z)&=\frac{6F_{r}\sqrt{3}Q}{\pi\sqrt{\pi} abc_{r}}\mathrm{exp} \left(\frac{-3x^{2}}{a^{2}}\right) \mathrm{exp} \left(\frac{-3y^{2}}{b^{2}}\right)\\ &\quad\, \mathrm{exp}\left(\frac{-3z^{2}}{c_{r}^{2}}\right)\end{aligned}$$
(2)

for the negative z semi-axes. The parameters a, b, cf and cr are semi-axes of the two ellipsoids as shown in Fig. 6. Ff and Fr are weighting factors to portion the weld power to the front and rear ellipsoid. They have to fulfil the relation \(F_{f}+F_{r}=2\). The term Q denotes the total amount of power penetrating the component and is calculated as a product of arc efficiency η, welding voltage U and welding current I, as \(Q=\eta UI\). To reduce the number of independent parameters, an additional constraint, which forces continuity of the function q across the z‑plane, is applied as;

$$F_{f}=2\frac{c_{f}}{c_{f}+c_{r}}=2-F_{r}$$
(3)

In this work two different approaches for modelling the heat source, HS1 and HS2, are investigated.

HS1 follows the real welding path including the weaving pattern. The heat source is assumed to be cylindrical and the parameters \(c_{f}=c_{r}=a=1.75\,\mathrm{mm}\) are set to match the outer boundary of the seam. The heat source’s depth is set to \(b=3.5\,\mathrm{mm}\) resulting in a penetration depth of 0.5 mm, which is in accordance with the fusion zone Az marked on the cross-section micrograph in Fig. 7. It should be noted that the fusion zone is relatively small. This is because, for the sake of simplifying the calibration process in the simulation, the same welding parameter set was applied to all layers. Typically, the first layer would be welded using a different parameter set, using more energy to establish better bonding to the substrate. Like the thermal boundary conditions, the process efficiency \(\eta =0.85\) is calibrated by comparing temperature curves with experimental results. Travel speed and power input are derived from measured values in the welding documentation.

Fig. 7
figure 7

Cross-section micrograph of the five-layer build and schematic representation of the used Heat Source Models HS1 an HS2

Full size image

Contrary to HS1, HS2 follows a straight trajectory along the centerline. To cover the complete weld bead, the heat source’s half-width is increased to \(a=7.25\,\mathrm{mm}\), while maintaining other heat source parameters equal. The travel speed of HS2 is adjusted to match the actual welding time. A schematic representation of the two heat sources is given in Fig. 7.

4.4 Mesh Study

Mesh size has a big influence on the results of the FE-Simulation. A finer mesh gives more accurate results, but also increases the computational effort. To find a good mix between accuracy and calculation time, a mesh sensitivity study is performed. The above-described model is used to simulate a single layer deposition with a subsequent 20-minute cooldown phase. Four refinement levels are investigated. The element size in the seam is varied from approx. 0.5 to 2 mm, in the substrate from 0.5 to 4 mm. The seam is discretised in such a way that the waypoints of the heat source’s trajectory align with nodes in the mesh. This allows for the trajectory to be coupled with the mesh, enabling the heat source to adapt its movement to the deformations of the component. In terms of the substrate, the refinement is only applied within a horizontal distance of approx. 8 mm to the weld seam. The remaining geometry is meshed using an element size of 4 mm.

This sensitivity study considers peak temperature, equivalent stress, maximum total displacement and calculation time. Temperatures and stresses are measured in a distance of 2.5 mm from the weld seam. This corresponds to the location of the experimental stress measurement point closest to the weld seam. All values are measured after the cooldown phase. The results of the sensitivity study are summarized in Table 1. Refinement level 1 shows big deviations in comparison to the other refinement levels. Beyond refinement level 2 no major changes can be observed. However, there is a substantial increase in calculation time from level 2 to level 3, and an even greater jump to level 4. Based on these results, its recommended to use level 2 for large scale simulations. For this study level 3 is chosen.

TABLE 1 Results of the mesh study
Full size table

5 Results

First, the verification of the numerical model, in terms of thermal history, distortions and residual stresses, is demonstrated with the use of HS1. Subsequently, a comparison of the simulations using HS1 and HS2 is given.

5.1 Thermal History

The thermal model is verified by comparing the temperature history results from the simulation and experimental data. All thermocouples are in good agreement with the simulation. This indicates that the heat input and the thermal boundary conditions have been set correctly. Figure 8 exemplarily shows the temperature development from selected thermocouples obtained by the simulation and the experimental trials. The waviness seen in the peaks of the temperature profiles results from the weaving during the welding process and is also well reflected by the simulation.

Fig. 8
figure 8

Comparison between the calculated and monitored thermal histories of selected thermocouples

Full size image

5.2 Distortions

The distortions of the numerical model are verified by comparing the measured z‑displacements with the results from the simulation. Figure 9 illustrates the z‑displacements in both the single-layer and the five-layer deposit. In the plot for the first layer, the weld time is additionally marked as “weld on”. At the beginning of the welding process, the substrate initially bends in the negative z‑direction due to the higher temperature and therefore higher thermal expansion on the top surface in contrast to the bottom surface. As welding continues, the substrate gradually bends in the positive z‑direction, primarily due to the solidification shrinkage of the weld seam. After welding has finished, a slight increase in the gradient of the displacement curve is observed before deformation completely ceases, indicating the complete solidification of the seam. During the cooldown phase, the displacement curve shows a slight decline. This pattern repeats for every layer, while most of the displacement already occurs after the deposition of the first layer.

Fig. 9
figure 9

Comparison between the calculated and measured distortions for the single-layer and the five-layer deposit

Full size image

The overall mechanical response of the simulation shows a good agreement with the measured data. The simulation slightly overestimates the deformation, while the decline of the displacement curve during the cooldown is less pronounced. It should be noted that the reason for the decline is not fully understood and will be subject to further investigations.

To validate the calculated global deformations of the substrates, 3D scans are conducted after manufacturing. These scans are imported into the Simufact Welding® software to compare the final surface deviations of the substrates post-declamping. Figure 10 shows the surface deviations of the substrates between the simulation and the 3D scan for the five-layer deposits. As shown in the histogram on the left, the deviations of most measured points remain within a range of 0.04 mm. It is important to note that, in case of the simulation, this comparison only considers the substrate, excluding the deposit. As a result, the plots exhibit higher deviations at the location of the deposit. Additionally, due to tolerances in the substrate dimensions of approximately 0.5 mm, the plot displays large deviations at the outer border, which do not reflect actual conditions.

Fig. 10
figure 10

Surface deviation of the five-layer build substrate between the simulation and scanned 3D data

Full size image

5.3 Residual Stress Measurements

To validate the calculated residual stresses, measurements using the “hole drilling method” were conducted in both the single-layer and the 5-layer deposits. All measurements show lower residual stresses close to the surface, followed by a steep gradient which levels out at greater depths. This behavior may be caused by measurement inaccuracies occurring near the surface. Therefore, the comparison with the simulation is based on measurements taken at a depth of 1 mm.

Figures 11 and 12 show comparisons between experimentally measured and calculated residual stresses. In the simulation, residual stresses are measured after removing all mechanical boundaries and a cooldown to room temperature. The calculated results are in good agreement with the experimental data, showing maximum deviations of approximately 20 MPa.

Fig. 11
figure 11

Calculated and measured residual stresses at the top surface of the substrate for the single-layer build

Full size image
Fig. 12
figure 12

Calculated and measured residual stresses at the bottom surface of the substrate for the single-layer and five-layer build

Full size image

Figure 11 shows transversal and longitudinal residual stress distributions at the substrate’s top center of the single-layer build. The stress distributions are plotted along the transverse axis, starting at the center of the weld seam. It should be noted that due to the lack of space, two out of the three experimental measurements were taken slightly off-center, as shown by the schematic drawings in the plots. It can be seen that the maximum longitudinal stress is nearly twice that of the transversal stress. The longitudinal tensile stresses near the weld line turn into compressive stresses at a distance of approximately 12.5 mm from the center along the transverse axis.

Figure 12 illustrates transversal and longitudinal residual stress distributions at the substrate’s bottom center, for both the single-layer and five-layer build. The transverse stress remains unchanged, while the maximum longitudinal stress has increased by approximately 40 MPa for the five-layer build.

5.4 Comparison Between HS1 and HS2

Figure 13 shows the temperature curves obtained using HS2 and HS1. Overall, the numerically calculated temperature curves are in a good agreement with the experimentally meassured ones using both heat source geometries. However, HS2 can not capture the temperature fluctuations within the peak temperature range caused by the weaving deposition.

Fig. 13
figure 13

Comparison of the monitored thermal history of TC2 and the calculation using HS1 and HS2

Full size image

The temperature distribution inaccuracies near the weld seam when using HS2 are also reflected in the molten pool geometry. A comparison of molten pool cross-sections in the simulation for HS1 and HS2, shown in Fig. 14, clearly demonstrates that unlike HS2, HS1 closely approximates the actual molten pool dimensions and, consequently, offers a more accurate representation of the temperature distribution near the seam.

Fig. 14
figure 14

Comparison of molten pool cross-sections of HS1 and HS2

Full size image

When looking at the displacments shown in Fig. 15, it can be seen that simulations using HS1 slightly overpredict the experimentally measured values, while the ones using HS2 underpredict them. The overall error between the experimentally and numerically determined deformation curve is much smaller using HS1.

Fig. 15
figure 15

Comparison of the monitored displacements and the calculation using HS1 and HS2

Full size image

6 Discussion/Conclusion

This work deals with the numerical simulation of the wire arc additive manufacturing process of ER 5183 utilizing weaving deposition. Two modeling approaches using different heat sources are investigated.

The first approach, Heat Source 1 (HS1), integrates the exact welding path, including the weaving pattern. In contrast, Heat Source 2 (HS2) follows a straight-line trajectory while accommodating weaving motion with an enlarged heat source geometry.

The findings indicate that the simulation model employing HS1 accurately reproduces the thermal history, even close to the molten pool. A a result, it provides an accurate representation of the mechanical response.

The simulation model using HS2 effectively captures the overall temperature evolution of the component. However, when compared to HS1, it shows greater deviations in the mechanical response. One potential reason for this discrepancy is that due to the simplified approach, HS2 does not accurately represent the temperature distribution close to the molten pool. This issue might be mitigated by introducing a more appropriate custom heat source, although this decision should be weighed against the incorporation of the weaving pattern.

In future studies the results from this calibration experiment will be validated with more complex geometries and more application-oriented clamping and cooling conditions. The effect of variable welding and movement parameters on the accuracy of the thermo-mechanical simulation will also be investigated. The goal is to establish a reliable simulation workflow to accurately predict the thermo-mechanical behavior of the wire arc additive manufacturing process for complex geometries.