1 Introduction

Additive manufacturing processes offer many possible applications, especially for industrial uses, due to their almost limitless design possibilities. Many processes [1], such as selective laser melting (SLM), selective laser sintering (SLS), electron beam melting (EBM), or 3D printing, have already found their way into industrial manufacturing. Nowadays, additive manufacturing is no longer limited to prototyping, metal additive manufacturing in particular enables the production of finished parts in small batches [2]. Additive processes offer several advantages over conventional processes, such as milling or turning. The production of lattice or lightweight structures is possible. Thus, topology-optimized components can be manufactured. Functional integration of assemblies can be realized. Holes, channels and cooling elements can be implemented directly in the printing process [3].

However, the manufacturing concept of the layer-by-layer structure of additive manufacturing also entails limitations. With most processes, the use of support structures [4] is required when building up geometries with an overhang angle of more than 45 degrees. The support structure also helps to prevent cracking, to compensate deformations due to high residual stresses, and to facilitate heat dissipation, since loose powder has very poor thermal conductivity [5]. These support elements have to be removed from the component during post-processing. In general, the rough surface finish of additively manufactured parts usually requires post-processing [6]. This applies in particular to functional surfaces. Fits but also holes and threads usually have to be reworked, since the components are connected to the build plate via the support structures and therefore form a rigid clamping of the parts on the build plate. These support structures can be used as clamping of the components for the machining post-processing. This machining concept has been established and researched at the IFT [7] and can be described by the term “Direct Machining”. This refers to the post-processing of SLM parts, which are connected to the building plate via the support structure. In this way, several parts can be reworked at the same time, which brings economic advantages because the parts do not have to be detached from the build plate beforehand and then reworked individually.

For DM [7], the prerequisite is that the support structures are designed in such a way that they can absorb the forces occurring during post-processing. The aim of the support structure is to give the component as much stability as possible while keeping the required volume of support elements to a minimum because the additional support structure increases the overall build time and the support material is waste and has to be disposed [8]. For the optimum design of the support geometry, it is important to know the loads that occur during post-processing. This requires knowledge of the component geometry and information on the post-processing activity (milling, drilling, etc.). Based on this, a newly developed calculation model determines the ideal parameters of the respective support structure for the following direct machining.

2 Theoretical Stress Model

The theoretical load model described here is initially limited to the investigation of normal stresses, such as those that occur during face milling.

2.1 Cutting Force during Face Milling

The process is used to create planar surfaces, so it is possible to compensate deviations in terms of dimensional and shape tolerance that occurred during the printing process [6]. In addition, this processing also serves to create surfaces with a significantly better surface quality than it is possible through layer-by-layer buildup in the SLM, SLS, or EBM processes.

The cutting force [9] results from the chip cross-section A and the specific cutting force, whereby the specific cutting force kc1.1 refers to a chip cross-section of 1 mm2.

$$A=a_{p}*f=b*h$$
(1)
$$F_{c}=k_{c1.1}*b*h=k_{c1.1}*a_{p}*f_{z}$$
(2)

Equation 2 gives the cutting force on a single cutting edge in maximum intervention. To calculate the average cutting force on a cutting edge, the average chip thickness hm is defined in the literature [8] by an approximation:

$$h_{m}=f_{z}\textit{*sinsin}\,\varphi \,\textit{*sinsin}\,\kappa$$
(3)

Figure 1 shows the meshing ratios for symmetrical face milling and on the right side the cutting force curve along the contact angle .

Fig. 1
figure 1

Cutting conditions for symmetric face milling [10]

Full size image

Assuming symmetrical machining, the following formulas for the average cutting force result, according to Degner [10]:

$$F_{cm}=\frac{180{^{\circ}}}{\varphi _{s}*\pi }*{\int }_{\varphi _{1}}^{\varphi _{2}}F_{c}*d_{\varphi }$$
(4)
$$F_{cm}=\frac{180{^{\circ}}}{\varphi _{s}*\pi }*k_{c}*b*f_{z}\textit{*sinsin}\,\kappa *\frac{2*a_{e}}{D}$$
(5)

Equation 5 includes the chip width b, the cutting arc angle φs, the specific cutting force kc, the feed per tooth fz, the setting angle κ, the operational reach ae and the tool diameter D.

2.2 Support Structures

Three different support variants [8] were used for the calculation model. Figure 2 shows the geometries of these support elements.

Fig. 2
figure 2

Support elements, Cross Support (left), Rod Support (center) & Block Support (right) [8]

Full size image

In all three cases, the geometry of a single support element is used to determine the cross-sectional properties. The most important properties, in relation to the strength calculation, are the geometrical moment of inertia Ix and the section modulus Wx. The calculation is limited to the determination of the axial section modulus, which is required later for the determination of the bending stress. Another important property is the cross-sectional area, because from this the volume and thus the material consumption of the support structure can be derived. The starting point for the calculation of the geometrical moment of inertia of the structure is the geometrical moment of inertia of a single support element. The following relationships result for the three variants:

$$I_{x{,}\text{block}}=\frac{a_{x}*{a_{y}}^{3}}{12}-\frac{(a_{x}-t)*{(a_{y}}-t)^{3}}{12}$$
(6)
$$I_{x{,}\mathrm{rod}}=\frac{\pi }{64}*\left({d_{\mathrm{rod}}}^{4}-\left(d_{\mathrm{rod}}-2*t\right)^{4}\right)$$
(7)
$$I_{x{,}\text{cross}}=\left({l_{\text{cross}}}^{3}+\left(l_{\text{cross}}-t\right)*t^{2}\right)*\frac{t}{12}$$
(8)

Steiner’s theorem then adds up the individual elements to the total cross section of the support structure. The formula for this is:

$$I_{x}={\sum }_{i=1}^{n_{sx}*n_{sy}}(I_{x{,}i}+A_{i}*{y_{ca}}^{2})$$
(9)

Equation 9 describes the geometrical moment of inertia of the entire support structure with Ix, the geometrical moment of inertia of a support element with Ix,i and its cross-sectional area with Ai. The distance between the centroid of an element and the overall centroid is defined as yca. The number of support elements in x‑ and y‑direction is given by nsx and nsy. From the previously determined geometrical moment of inertia, the section modulus can be calculated by knowing the edge fiber spacing ex,y, which is subsequently used to calculate the bending stress.

$$W_{x}=\frac{I_{x}}{e_{y}}\ or\ W_{y}=\frac{I_{y}}{e_{x}}$$
(10)

The cross-sectional area of the entire support structure can also be calculated based on the cross-section of a single support element. The individual areas are simply added up later to give the total cross-sectional area of the support structure. Another important value is the support volume, which is determined with the help of the cross-sectional area and the corresponding support height hs.

Table 1 shows the cross-sectional properties of the support structures [8] (“Block”, “Rod”, “Cross”) for three different configurations (“W”, “M”, “S”).

TABLE 1 Various support configurations [8]
Full size table

2.3 Notch Effect

The stress distribution depends not only on the external load and on the type of stress, but also very much on the cross-sectional changes (transitions, recesses, holes, grooves, etc.) [11]. Particularly at the transition between the building plate and the support structure as well as at the transition between the component and the support structure, discontinuous cross-sectional changes take place. Increased notch effects occur at these transitions, resulting in an increase in stress. This notch effect must be taken into account when optimizing or designing the support structures. FEM analyses are used to investigate different configurations of the support elements with regard to the notch effect that occurs. A very simple way to characterize the notch effect is by using the notch factor ασ, which is defined by the ratio of the stress peak σmax to the nominal stress σN [11]. The results of the analyses serve as the basis for defining approximation curves for the notch effect for the three support variants. These approximation curves are used to take the notch effect into account when designing the support parameters in the calculation model.

Fig. 3 shows the curves of the notch coefficients ασ as a function of the occurring normal stress. FEM analyses of different support configurations form the basis for these three approximation curves derived for block, rod and cross support. The analyses show that the influence of the notch effect is smallest for the block support and the largest notch coefficients occur for the cross support. The influence of the notch effect decreases with increasing normal stress for all structures.

Fig. 3
figure 3

Approximation curves for notch shape factor as a function of the occurring normal stress

Full size image

3 Optimization Process

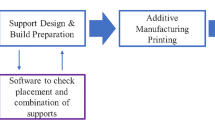
The optimization process of the software works based on the previously described theoretical calculations. Depending on the user’s specifications, the software runs through different program steps. The input mask of the program contains mandatory fields (e.g. workpiece geometry, material specifications and support variant) which are always necessary for the calculation. Further inputs regarding the support geometries or the specification of a post-processing process influence the program run.

If the user does not specify any post-processing, then the software cannot optimize the support structure and the user must specify the support structure parameters himself. The program calculates the cross-section properties and the support volume using the specifications based on the theoretical calculation model. If information about a post-processing activity is available, then the software model can determine the required parameters of the support structures itself. The user has the possibility to control or limit the degree of optimization by entering his own data in the support parameters. Once the calculation process is complete, the results are displayed in an output window. In the software model, the optimization process takes place while passing through several loops. The user specifies the load occurring in the component or support structure by specifying the machining process. From this, the software can determine the required cross-sectional properties of the support elements. In the program loops, the variable support parameters are adjusted until the required values are reached. Figure 4 shows schematically the program flow for the optimization of a support structure of the type Rod-Support. In this example, the parameters grid spacing, thickness, and diameter are varied during the loop pass until the required cross-section properties are achieved. The boundary conditions for the run variables are defined by specifications such as the component geometry or support geometry. If the requirements are met, the software saves the parameter configuration. When several parameters meet the requirements, the software selects the best variant. One selection criterion for this is, for example, a minimum cross-sectional area or a minimum support volume.

Fig. 4
figure 4

Loop pass during the optimization process of a rod support structure

Full size image

Depending on the selected support type, there are different parameters that can be adjusted by the optimization model to achieve the required strength properties. Table 2 shows the variable parameters for the three different support structures.

TABLE 2 Optimization parameters for the selected support structures (block, rod, cross)
Full size table

4 Verification of the Calculation Model

In order to verify the suitability of the calculation model, practical machining tests [8] are carried out. The tests are performed on a 5-axis milling machine, and the cutting forces are measured using a Kistler Multicomponent Dynamometer (type 9129AA) in combination with a Kistler 5070A10100 charge amplifier. A 25 mm diameter face milling cutter with one cutting edge is used for face milling [8]. The cutting depth in the tests is between 0.1 and 1.5 mm. The parameters for the cutting force calculation can be taken from Table 3.

TABLE 3 Cutting parameters for the milling tests
Full size table

The support parameters (W, M, S) as shown in Table 1 are used as test structures [8]. The support height is 4 mm and the test components have a square cross-section (14 mm × 14 mm). Table 4 shows the theoretical cutting forces, based on the previously described calculation schema, at different cutting depths ap.

TABLE 4 Theoretical cutting force Fc at different cutting depths ap
Full size table

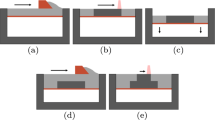
Figure 5 shows the measured cutting forces at different cutting depths. When machining the rod support, the support structure fails at the configuration “W” of a cutting depth ap of 1 mm. The cross support (configuration “W”) already fails at a cutting depth of 0.5 mm.

Fig. 5
figure 5

Measured cutting forces for the different support structures

Full size image

Figure 6 shows the comparison between the measured cutting force from the cutting tests and the calculated theoretical cutting force. The curves show the calculated cutting force matches the measured values very well.

Fig. 6
figure 6

Theoretical cutting force curve compared to maximum measured cutting forces

Full size image

The results from the machining tests show that the selected support configurations are not ideally designed for the corresponding machining. With the help of the developed calculation model, the parameters of the support structures are optimized. Table 5 shows the results of the optimization for the rod support structure. The values in bold type are the parameters that are available to the program for optimization.

TABLE 5 Example of a support structure optimization for a given finishing operation (face milling)
Full size table

The optimization software selects the support parameters so that the structures can withstand the loads that occur. The findings from the machining tests [8] performed are used for the dimensioning.

5 Conclusion

In its current form, the optimization software forms a rough model for support structure design in combination with direct machining. Optimization of the support structure offers several advantages, such as shortening the build time, reducing powder consumption, and optimizing post-processing. The goal is to implement the optimization software in existing AM programs, in order to integrate the Direct Machining process already during job preparation. The calculation model represents a first prototype. However, there are still some development steps necessary to be able to integrate the software into industrial applications. In particular, the creation of the load model for various reworking processes requires further development work.

Nevertheless, the optimization model of support structures has great potential in the field of additive manufacturing and can contribute not only to improvements in post processing but also to the optimization of the actual manufacturing process (Fig. 7).

Fig. 7
figure 7

Input window and possible implementation of the “Support Optimizer” optimization software

Full size image