1 Introduction

Safe tunnel construction and operation is a key challenge in a wide range of engineering disciplines as the safety and comfort of the people remain the priority in various conditions. During tunnel construction, the detonation of explosives and the use of diesel engines generate toxic emissions that can seriously endanger the health and safety of construction workers. Road tunnel ventilation systems aim to limit the concentration of air pollutants under normal tunnel operation providing fresh air and then removing the exhaust fumes from the tunnel. And, of course, ventilation is the most common measure to mitigate fire effects and remove smoke, heat, and contaminants from tunnels [1].

The dynamically changing environment, techniques, and machinery constantly produce new challenges for researchers in the area of tunnel ventilation. Computational fluid dynamics (CFD) provides effective solutions to a wide range of problems in many fields of study and industries, including aerodynamics, fluid dynamics, heat transfer, environmental engineering, and industrial system design and analysis. As of today, computer numerical simulations are integral for studying the efficiency of multiple engineering methods due to a cost-effective approach and available amount of data [2].

Recent research shows great value in the use of CFD models in assessing tunnel ventilation objectives under diverse scenarios [3,4,5,6,7]. A variety of CFD software packages is available to resolve the whole range of emerging issues, whereas Ansys Fluent is the most used fluid flow simulation module [8]. Fire Dynamics Simulator (FDS) is an alternative open-source CFD program designed to deal with problems in the field of fluid dynamics and heat transfer.

Ansys Fluent is a general-purpose CFD software that contains comprehensive modelling capabilities needed to model fluid flow, turbulence, heat and mass transfer, and reactions for industrial applications. This program is based on a finite volume method and solves the partial differential equations that define the energy, mass, and momentum conservation. Thus, Fluent converts the general transport equations to a system of linear equations that are solved numerically by a point implicit (Gauss-Seidel) algorithm in conjunction with an algebraic multigrid (AMG) method [9]. The availability of the different turbulence models, e.g. Reynolds Time-Averaged Navier-Stokes Equations (RANS), Large Eddy Simulation (LES) and others allows studying general questions of aerodynamics phenomena and occasionally occurring tasks such as optimization of tunnel ventilation systems.

Ansys Fluent is commonly applied for numerical simulations and further analysis of tunnel ventilation operations because of the enhanced possibility of geometry modelling and available physical models [10]. Theoretical and experimental results were obtained for various tunnel operation scenarios where the airflow of jet fans and ventilation ducts was simulated and validated by field measurements providing the background for optimization recommendations [11,12,13,14,15].

The second program used in the area under discussion is Fire Dynamics Simulator. It is a computational fluid dynamics model that solves numerically a form of the Navier-Stokes equations appropriate for low-speed, thermally-driven flow with an emphasis on smoke and heat transport from fires [16]. FDS is a large eddy simulation (LES) model that uses an explicit second-order predictor/corrector scheme within the Cartesian coordinate system where the turbulent viscosity is obtained from the Deardorff eddy viscosity model. All the details of the FDS mathematical model are comprehensively described in the FDS Technical Reference Guide (Volume 1) [17].

Despite the initially indicated purpose, this forensic tool was gradually improved, and now it can be successfully applied to analyse different fluid dynamics problems of various complexity. Several FDS models with a focus on ventilation issues in tunnels are evaluated within the verification and validation procedures and given in the FDS Technical Reference Guide (Volumes 2 and 3) [18, 19], acknowledging the possibility of obtaining reliable and accurate results. Furthermore, many examples of the FDS model implementation in the design and performance assessment of ventilation and air conditioning systems, optimization of tunnel ventilation and other areas have been published in academic journals or presented at scientific conferences [20,21,22]. The relatively limited adoption of FDS in tunnel applications is largely due to the requirement of a rectilinear mesh whereas other CFD modules may support unstructured grids to better reflect the actual tunnel structure. However, studies show that even in the case of replacing the original arch-shaped tunnel cross-section with a rectangular one, it is possible to obtain results with sufficient accuracy by taking into consideration the corresponding hydraulic (equivalent) diameter [23, 24].

Reverse or backflow is a feature of jet fan ventilation that requires special attention in underground infrastructure systems due to the presence of harmful gases and particulate matter on-site during construction or the generation of combustion products by vehicles under normal tunnel operation, as well as the emergence of heat and smoke in a case of fire [25]. In all cases, harmful contaminants pose a real danger to people and can cause serious health issues and even death, since air backflow is able to prevent the removal of pollutants from the underground space. Recent research is mainly focused on the investigation of backflow features during the tunnel construction phase or in the event of an emergency in an operating tunnel [26, 27]. But there are also a number of studies that review the potential impact of backflow in forced ventilated tunnels [28,29,30,31].

Therefore, this study aims to evaluate the performance of the two most popular software packages (Ansys Fluent and FDS) regarding the backflow investigation in the western railway tunnel of the research facility “Zentrum am Berg” by comparing it with experimental observations.

2 Research Approach and Methodology

2.1 Full-scale Experiment

2.1.1 Experimental Setup

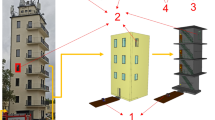
The experimental part of the study was conducted at the Zentrum am Berg (ZaB) in Eisenerz, Austria. This facility represents an independent research infrastructure for a wide variety of purposes. It consists of a two-tube road tunnel and two parallel railway tunnel tubes as well as a test tunnel enabling research, development, education, and training under real underground conditions (Fig. 1a).

Fig. 1
figure 1

Tunnel scheme at the Zentrum am Berg (a) and the portal of the western railway tunnel (b)

Full size image

A series of measurements were carried out in the western railway tunnel (despite the name, there are no railways in the tunnel, and the ground surface represents an asphalt road). The tunnel is slightly curved and has a length of 403 m, a width of 8.27 m, and a height of 7.55 m. Shotcrete is used as a lining for the tunnel walls and ceiling. The considered tunnel section (170 m long) has an elevation of 1084 m a. s. l. Two jet fans are installed on the tunnel ceiling at a distance of 50 m from the tunnel portal. According to the manufacturer’s documentation, the fans are fully reversible and have a nominal diameter of 1.12 m and a length of 3.0 m. The main fan characteristics are given in Table 1.

TABLE 1 Jet fan parameters
Full size table

Air velocity measurements were performed in two stages. The detailed measuring scheme is given in Fig. 2. For clarity and convenience, it is assumed that the fan outlets are positioned at the 0‑meter mark. The first phase included the evaluation of the naturally developed flow inside the tunnel. For this reason, the velocity values were measured at different points on several cross-sections within the considered tunnel part, including two outermost cross-sections (NV-Us and NV-Ds). During the second phase, 10 cross-sections at 10 m to 100 m from the fan outlets (10 m between the adjacent planes) were studied under the operating jet fans. To cover an entire tunnel cross-section, measurements were held for 9 points—3 rows (1, 2, 3) and 3 columns (A, B, C). As a result, air velocity was recorded for 90 points along the 100-meter tunnel section.

Fig. 2
figure 2

Overlay of the tunnel (a) and the arrangement of measuring points at each cross-section (b)

Full size image

The air velocity was recorded by Voltcraft PL-130 AN anemometer. This device is designed to measure the temperature, velocity, and volume flow of gases. Effective velocity (average speed), maximum or minimum speed can also be displayed during the measuring process. The main technical parameters of the anemometer are as follows: air velocity measuring range 0.4 … 30 m/s, resolution 0.01 m/s, basic accuracy ±3%; temperature measuring range −10 … +60 °C, resolution 0.1 °C, accuracy 2 °C; working humidity less than 80% RH.

The anemometer was additionally fitted out with a tuft of short flexible paper strips to be used as a flow direction indicator [32]. This helped to observe the backflow development since in turbulent conditions the directional changes occur so quickly that the measuring device (for example, a vane anemometer) is not always capable of recording them.

The pressure measurements were also performed to determine its effect on the development of natural conditions inside the tunnel. For this reason, one point in front of the tunnel entrance (“Ambient” area in Fig. 2) and four points within the first 150 m of the tunnel were assessed. The DP-Calc Micromanometer 5825 was used to estimate the pressure difference between the ambient and tunnel locations. This device has a −3735 to +3735 Pa measuring range with a reading accuracy of ±1% and a resolution of 0.1 Pa.

2.1.2 Experimental Results

The natural ventilation in the ZaB tunnels is defined by the pressure differential between the tunnel portals created by differences in elevation, ambient temperatures and wind. During the tests, the naturally developing airflow was measured at and in between the upstream (NV-Us) and downstream (NV-Ds) cross-sections (Fig. 2). The majority of results were in the range between 0 and 0.5 m/s. This low (under 0.4 m/s on average) natural flow was directed inside the tunnel (similar to the direction of the flow from the operating fans) and can be mostly explained by the favourable ambient conditions (partly cloudy, southeast wind under 6 km/h).

The main measuring session started after the fans were switched on and the air flow inside the tunnel became quasi-stable. During the measurements, three areas with distinctive flow structures were observed.

The first “initial” region (0 … ~40 m) is characterised by the non-uniformity of the airflow, vortexes, and constant directional changes of the local airstreams. An extremely turbulent vortex area is formed in the immediate vicinity (0 … ~20 m) of the fans. The backflow presence in the first zone was repeatedly confirmed by the observations.

The second “transitional” region (~40 … ~60 m) represents a transition area where the air flow is more balanced though high magnitude fluctuations appear recurrently. Negative velocity values indicating the backflow existence were monitored occasionally.

In the third “developed” region (~60 … ~100 m), the flow velocity gradually decreases, and the flow field distribution tends to be stable and uniform.

Preliminary tests showed a big difference in measured velocity values during a 3-minute spell at the first and the second regions due to the flow complexity. For this reason and considering the sequenced measurements, it was decided to record maximal and minimal values of air velocity at every point during the 30 s period. It allowed us to establish the velocity ranges for every measuring point and analyse the backflow development. The experimental results of full-scale ventilation tests are given in Table 2.

TABLE 2 Measured ventilation velocities in the tunnel
Full size table

The points from the same row (1, 2, or 3) have a sufficiently identical pattern, especially when considering areas limited by the maximum-minimum lines. Negative and positive velocities denote the flow direction. The flow generated by the fans as well as the naturally developed airflow is assumed to be positive, while the backflow gusts are defined as negative. The cells with values in italics and bold in Table 2 indicate the flow directions observed with the marker technique during the tests.

Air velocities were also measured at four points (locations similar to A1, B1, B2, and C1) at the “NV-Us” cross-section (−25 m) to provide data on the flow behaviour in the upstream part of the tunnel. The obtained results are given in Table 3.

TABLE 3 Measured air velocities at the upstream cross-section
Full size table

Air temperature (with an average value of 11.5 °C) inside the tunnel was also recorded during the tests.

The average difference of 1.1 Pa between air pressure outside and inside the tunnel based on the total of 2 min measuring period has been detected. It indirectly supports the assumption of the low positive natural flow existence that was observed during the velocity measurements.

Atmospheric pressure, considering the altitude of the tunnel, is defined as [33]:

$$P=P_{0}\cdot exp\left(-\frac{gMh}{RT}\right)$$
(1)

Where P0 is the standard atmospheric pressure (101,325 Pa), g is the gravitational acceleration (9.81 m/s2), M is the molar mass of air (0.029 kg/mol), h is the altitude of the tunnel (1084 m), R is the universal gas constant (8.314 N·m/(mol · K)), and T is the temperature at the altitude (284.65 K). Thus, the atmospheric pressure during the tests assumed as 88,946 Pa.

2.2 FDS Simulation Setup

2.2.1 Model Settings and Boundary Conditions

Fire Dynamic Simulator (version 6.7.9) is adopted to carry out numerical simulations. The Large Eddy Simulation (LES) mode and the Deardorff turbulence model with the default parameters are used in this study to compute the vortices and fluctuations of relatively large scale in the flow field.

Environmental conditions (ambient temperature and pressure) are set according to the observations (see Sect. 2.1.2).

The ambient in front of the tunnel portal is modelled as a zone where its side and top surfaces are set as “OPEN” to indicate a passive opening to the outside, the bottom surface denotes the ground (road area), and the surface adjacent to the tunnel contains an opening (tunnel gate) connecting the ambient and tunnel spaces. The dynamic pressure of 1.1 Pa is specified here at the “OPEN” boundary to determine the pressure difference between the outside and inside of the tunnel. The “OPEN” property is also applied to the cross-section (parallel to the portal) on the opposite side of the tunnel as it represents the exterior boundary of the computational domain.

The total simulation time is set to 270 s. The jet fans are switched on after 150 s when the stable ventilation mode inside the tunnel is reached in accordance with the applied boundary conditions. During the period between 150 and 210 s, a quasi-stable state of the longitudinal airflow is achieved and the data from 210 to 270 s are considered for the subsequent analysis.

A number of measuring planes, devices and tracing massless particles allow to control the airflow development and record values for velocity, volume flow and pressure. Point gas-phase devices determine air velocity at the locations corresponding to the experimental setup (Fig. 2). At the exact cross-sections, the mean velocity values are defined. Additionally, longitudinal and cross-sectional 2D slices are used to monitor the pattern of flow distribution in terms of pressure and velocity.

2.2.2 The Tunnel

A full-scale numerical model is established according to the project documentation and physical dimensions of the tunnel. A Cartesian coordinate system is assigned along X (length), Y (width), and Z (height) directions. The total length of the tunnel model is 163.2 m, including a 10-meter space in front of the tunnel entrance recreating the ambient (Fig. 2a). The length of the tunnel section is 153.2 m and the distance between the tunnel entry gate and the fan outlets is 50 m. The most distant from the portal a 3-meter long area is used as an extension (additional computational region) to minimize the influence of the model openings while recording the data at the last cross-section (100 m from fan outlets). The importance of the tunnel portal in the model is worth noting as it significantly affects the process of air supply from the outside, ensuring a given local resistance. In addition, a straight tunnel model is adopted based on the assumption that the bending radius of a real tunnel is sufficiently large.

The cross-section of the modelled tunnel has a width of 8.8 m and a height of 7.6 m (Fig. 3). The curved ceiling is simplified and constructed using rectangular obstructions. The difference in the cross-sectional areas and wetted perimeters between the real and modelled tunnels is less than 1% (for a mesh with a cell side of 0.2 m) which allows to assume their hydraulic similarity. The material of the tunnel surfaces including walls, ceilings, and floor is set as concrete with a thickness of 0.5 m (other properties specified according to [34]). The tunnel walls are assumed to have a uniform sand roughness height of 0.02 m.

Fig. 3
figure 3

The parameters of the cross-section (a) and general view of the tunnel (b)

Full size image

The phenomenon of a “zigzag tunnel wall” in FDS is inevitable when modelling horseshoe-shaped tunnel sections. However, previous studies showed that it is possible to obtain satisfactory results when the numerical grid is fine and the serrated obstruction is small enough [35].

2.2.3 Jet Fans

Two similar tunnel jet fans are modelled in this study. Their geometry is close to the real size (length, width, and height are 3.0, 1.2, and 1.2 m, respectively) and matches the adopted computational mesh. The fans are located under the tunnel ceiling at a height of 5.6 m above the ground (Fig. 3).

The HVAC sub-model is used to simulate the jet fans. It allows air to pass through the fan in a particular direction with a specified volumetric flow rate across two connected nodes thereby simulating a jet fan’s intake and outlet. The fan flow is directed inside the tunnel (positive value) and has the following attributes added via the HVAC properties: the circular diameter of 1.12 m and the volume flow of 31.4 m3/s (according to Table 1). The fan start up is based on the FDS default ramp up time.

2.2.4 Meshes

The most sensitive numerical parameter in FDS modelling is the mesh (grid cell) size, which affects the accuracy, computational costs and efficiency [36]. A mesh sensitivity analysis is conducted to verify whether the obtained results were influenced by the selection of mesh size during the modelling.

In this study, the computational domain is divided into 6 rectilinear meshes of the same size (27.2 × 8.8 × 7.6 m) enabling multiple processor calculations for time efficiency. Five mesh sizes are reviewed in the process. To reduce computing time, an unevenly distributed grid is obtained by stretching the mesh along the X‑direction maintaining the recommendation that mesh cells should not possess an aspect ratio larger than 2 to 1. A summary of grid systems and their characteristics for the mesh sensitivity study is given in Table 4.

TABLE 4 Details of the meshes adopted in the grid sensitivity analysis
Full size table

Volume flow generated by a jet fan and developing longitudinal velocity (mean value for a tunnel cross-section) caused by the pressure difference between the outer and inner spaces of the tunnel are used to assess the sensitivity of the simulation results to the mesh resolution. The dependency of the selected parameters on time using variant mesh types is shown in Fig. 4 while the relative difference in average values for a steady period is given in Table 4. The initial input value of fan volume flow and the calculated velocity for the smallest mesh (Type A) are used as reference quantities.

Fig. 4
figure 4

Influence of grid resolution on volume flow from the jet fan (a) and natural air flow (b)

Full size image

It can be observed that the difference between the mesh types A, B, and C is not sufficient as a deviation under 7.5% could be regarded as acceptable in a CFD simulation. Furthermore, during the mesh sensitivity analysis, it became evident that grid resolution (within the considered range) barely affects the velocities at points located at a distance of 50 m and further from the jet fans. This observation keeps up with the outcomes obtained in the research of multiscale modelling of tunnel ventilation flows [37,38,39].

On this basis, it can be assumed that mesh type C with a cell size of 0.4 × 0.2 × 0.2 m would be the most suitable option. In this case, the relative difference is less than 5% while the CPU time is about 6% of that required for the finest mesh.

However, mesh resolution heavily impacts the accuracy of results for the areas in the vicinity of jet fans. Thereby, the mesh type B with a cell size of 0.2 × 0.2 × 0.2 m is applied in the model as a balanced solution between efficiency and simulation accuracy. Additionally, the opted mesh resolution corresponds well with the findings in recent publications on tunnel ventilation [40, 41].

2.3 ANSYS Simulation Setup

2.3.1 Model Settings and Boundary Conditions

The Ansys Fluent software (release 2022 R1) is used for numerical modelling. It is assumed that air is an incompressible, isothermal, homogeneous fluid and obeys the law of conservation of mass and momentum.

The simulated boundary conditions followed the actual experimental environment in terms of atmospheric pressure and temperature (see Sect. 2.1.2). Air density and dynamic viscosity are taken as 1.225 kg/m3 and 1.802 × 10−5 kg/(m · s), respectively.

In the computational domain, the planes normal to the fan flow are defined as pressure boundary conditions. The tunnel portal has a square gate (Fig. 1b) representing a surface that is defined as a pressure inlet with a gauge total pressure of 1.1 Pa. The tunnel cross-section from the opposite side of the domain is considered as a pressure outlet with a gauge pressure of 0 Pa. The rest of the planes (tunnel walls, ceiling and floor as well as fan housing) are specified by a non-slip stationary wall boundary condition. The equivalent roughness height of 0.03 m is applied for the tunnel surfaces.

The pair of jet fans are assumed to be represented by fan outlet surfaces for which a pressure jump is defined according to the fan properties (Table 1). The swirl velocity is negligible in the model.

The adopted turbulence model is the standard k‑ε two equation model, and the coupling of pressure and velocity is solved via the SIMPLE algorithm. A transient time model is applied and the total simulation time is 100 s.

2.3.2 The Tunnel

The full-scale Fluent model is established based on the tunnel dimensions. The adopted shape of the cross-section is given in Fig. 2b. The computational domain length corresponds to the experimental scheme where the most distant investigated cross-section is situated at 100 m from the fan outlets (Fig. 5). Thus, the total length of the model is 150 m, and the distance between the tunnel portal and the fans is 50 m.

Fig. 5
figure 5

Overview of the model established in Fluent

Full size image

2.3.3 Meshes

The mesh study is performed to ensure the accuracy of the numerical simulation. Several built-in mesh statistic tools are available in Ansys to quantify the overall grid quality during and after the mesh generation phase. In this research, one of the most commonly used mesh metrics (Orthogonal Quality) is used for the grid evaluation.

The general recommendation on mesh quality states that the minimum orthogonal quality should be more than 0.1 [42]. The “Orthogonal Quality” value for the adopted mesh with the element size of 0.5 m is 0.216, which corresponds to “Good” quality in the mesh metrics spectrum.

An additional mesh size survey is conducted in regard to the jet fan’s performance. The predicted values of centerline velocity generated by a fan are compared to the mathematical model. Namely, for a round jet in the decay phase, the centreline velocity Ux with the increasing distance from the fan outlet follows the formula [43]:

$$U_{x}=\frac{kU_{o}D}{x}$$
(2)

Where k is a constant (between 3 and 10), Uo is the outlet discharge velocity (31.8 m/s), D is the outlet diameter (1.12 m) and x is the distance from the outlet. Equation 2 is valid for the case when x  = (5 … 75) D.

The comparison of the predicted in Fluent with theoretically calculated values of the centreline velocity for the distance from 15 to 80 m is given in Fig. 6.

Fig. 6
figure 6

Dependency of centerline velocities on the distance from the fan outlet

Full size image

Good convergence is observed between the modelled curve and the considered theoretical range while the best agreement is feasible when k = 4.

The conducted analysis shows that the adopted grid allows to obtain adequate data in terms of the addressed tasks and thereby is selected for the further numerical study.

2.4 Model Validation

2.4.1 Validation of the FDS Model

The FDS model is validated using data obtained in full-scale tests. A comparison of average velocities along the tunnel length from the experiment and numerical simulation for the randomly chosen measuring point (B2) is given in Fig. 7a. For greater clarity, maximal and minimal measured values and standard deviations (error bars) determined from modelling results are added to the graph. The standard deviation here demonstrates the magnitude of the calculated velocity fluctuations.

Fig. 7
figure 7

Comparison of the measured and calculated velocities in the frame of distance (a) and time (b)

Full size image

The calculated velocity values are significantly close to the measured ones, especially when a dataset’s variability (dispersion) is considered.

Good agreement between the test and modelled data is also observed for the upstream locations. The time-dependent velocity profile for two (B1 and C1) of the assessed points at a “−25 m” position is given in Fig. 7b. The simulated velocity curves lie inside the measured range through much of the considered period.

Additionally, the mesh sensitivity analysis described earlier suggests the adequacy of the proposed FDS model providing sufficient reliability in both cases: for naturally developed airflow and mechanical fan ventilation.

2.4.2 Validation of the Fluent Model

The results from the conducted tests are used in the validation process of the Fluent model. The measured velocities are compared with the simulated values along the tunnel length and height. For example, the calculated average velocities for the examined point A1 are presented within the experimentally obtained maximal and minimal bounds in Fig. 8a. Despite some discrepancies, the similarity in the trend and values are clearly visible.

Fig. 8
figure 8

Comparison of the measured and calculated velocities along the tunnel length (a) and by the tunnel height (a)

Full size image

A similar situation is observed when considering the velocity profile along the height of the tunnel (Fig. 8b). The modelled curve for the points in the row (B) at a distance of 30 m from the fan outlets falls in the middle of the measured range and follows its outline.

The discussed findings, coupled with the results of the grid study, lead to the conclusion that the developed Fluent model possesses the required qualities in relation to the current study.

3 Results and Discussion

3.1 Comparison of Experimental and Numerical Data

The development of the flow field regarding its velocity along the tunnel is presented in Fig. 9. These data also contain information about the velocity changes within the assessed tunnel cross-sections. Experimental findings and calculated results are shown together for each measurement point to simplify the comparison process and further analysis. The area bounded by thin lines indicates the longitudinal velocity range between maximal and minimal measured values, while average velocities are shown with a black dashed line. The calculated FDS (round markers) and Ansys (square markers) curves are coloured in dark red and green, respectively.

Fig. 9
figure 9

Comparison of the experimental data and simulation results

Full size image

The calculated results indicate good congruence with the field measurements for the majority of the examined spots. Although for some survey points experimental data differ from numerical results, velocity variation trends are consistent between measurements and simulations. The Fluent and FDS models show acceptable conformity with measured maximum-minimum range, especially at cross-sections from 30 to 100 m.

In distant areas (60–100 m), the numerical models slightly overestimate the velocity values, wherein the FDS results are closer to the observations. The adopted straight shape of the tunnel part under study may cause this behaviour as the flow velocities are not additionally affected by occurring local resistance from flow interaction with tunnel walls.

3.2 Backflow Development

The simulation results (FDS and ANSYS) are in good agreement with the field observations regarding the length of the backflow area and its behaviour within the three defined regions (see Sect. 2.1.2). The obtained negative velocities suggest the reverse flow existence within a certain distance from the fan outlets (Fig. 9). It is worth noting that, even when the average value presented in graphs is positive (or negative) for some locations in the fan vicinity, there is a high probability of time-dependent transformation in flow direction due to chaotic changes in pressure and flow velocity.

The same situation concerns the highlighted by font styles quantities in Table 2, where, despite the positive maximum, average, and minimum values for several locations the negative flow was observed (e.g. points A1 at 40 m, A2 at 30 m, etc.). For example, at point B1 at a distance of 40 m from the fan outlets, we see a minimal velocity of 0.13 m/s and the bold font marking of the reverse flow presence. It can be assumed that the “wavy” flow development affected by turbulence causes this behaviour. The FDS simulation results support this assumption as velocity fluctuations of a changing magnitude and direction are predicted during a quasi-stable flow state (Fig. 10a). The same applies to points (e.g., A1 at 10 m, B1 at 20 m, etc.) with negative measured values where the positive air flow was observed (Fig. 10b).

Fig. 10
figure 10

Velocity development in time at points B1 (a) and A1 (b)

Full size image

The obtained results also show the dependency of the backflow existence and its intensity on the height and distance from the fan outlets. Two layers with opposite flow directions can be distinguished at the velocity profile (Fig. 11). The presented flow fields are obtained for the middle tunnel longitudinal section after the air flow reached its quasi-stable state.

Fig. 11
figure 11

Velocity profile for the tunnel longitudinal section modelled by FDS (a) and Fluent (b)

Full size image

It can be assumed that a stable backflow zone occurs within a 30-meter distance from the fan outlets. However, local airstreams of a negative direction may occasionally appear in the region up to 50 m.

Similar flow patterns show a velocity distribution in the vicinity of the fans. The moderate difference in terms of velocity magnitude may be caused by the difference in the applied turbulence models (LES and k‑ε for FDS and Fluent, respectively) as well as grid resolution (the FDS model has a finer mesh).

4 Conclusions

In this study, two CFD models were developed using Fire Dynamic Simulator and Ansys Fluent for the investigation of the ventilation issues regarding the backflow development in the tunnel of the “Zentrum am Berg” facility. A full-scale experiment for the evaluation of the ventilation conditions in the western railway tunnel was carried out. The results obtained were used for the assessment of the numerical models by comparing the predicted velocities with their measured values. The main results are as follows:

  • The simulated with both CFD packages velocity variation trends are in good agreement with field measurements.

  • Predictably, the greatest discrepancies in the data are observed in areas close to the fans due to high turbulence and the backflow presence.

  • Good convergence of results is observed for the quasi-stable state of the airflow at distances from 30 to 100 m though the simulated velocities are slightly overestimated at the more distant cross-sections. In this area, the FDS results were closer to the experimental data.

  • The simulated backflow development corresponds to that observed concerning the three specified regions (initial, transitional and developed) with distinctive flow structures.

  • The observed spontaneous changes in flow direction for points with a prevailed flow direction (positive or negative) were confirmed by the FDS-simulated velocity curves.

The comparative analysis of two numerical models shows their applicability in the backflow study. Depending on the tasks to be solved further adjustment of the numerical models could improve the congruence between the predicted and experimental results providing reliable and efficient solutions.