1 Introduction

Resonant sensors can be used in a wide range of applications, e.g. as microbalances, chemical sensors in liquid and gaseous environments, and for physical property sensing of liquid and viscoelastic media [1]. Sensor elements with direct linear relation between the measured quantity and a processable output signal are desired in measurement practice but are often not available, especially when high accuracy and suppression of cross influences are required. For a viscosity and mass density sensor, the utilization of a measurement principle which evaluates the frequency response of an electroacoustic resonator in contact with the fluid under test is advantageous. The frequency response of such a resonant sensor is related to the fluid properties by a nonlinear function but is also affected by several other – in most cases spurious – influences [2].

The most commonly known example for such an influence is the electrode capacitance of quartz crystal resonators (QCR). An established electrical model for this resonator type is the Butterworth - Van Dyke (BVD) circuit as shown in Fig. 1, comprising a series resonant RLC circuit, representing the electromechanical (motional) properties of the resonator. An extension to this simple second order resonant system has to be considered in form of the capacitance C 0 between the electrodes.

Fig. 1
figure 1

Left: Butterworth - Van Dyke model for QCR. The simple damped resonant circuit is in parallel with the electrode capacitance C0 of the QCR. Right: The liquid loading affects the QCR mechanically by mass-drag (Lf), and viscous losses (Rf), but also electrically by fluid conductivity (Re) and permittivity (Ce)

Full size image

For alternative sensor concepts, e.g. using Lorentz-force excitation and inductive readout [3], similar extensions to a resonant circuit are required to model inductive crosstalk or wire resistances, for instance. It can be shown that these sensors can be described by circuits similar to the BVD model [4], and thus the approach described here is also applicable to a wider class of sensors. For the sake of convenience, this contribution focuses on piezoelectric resonators as an illustrative example.

2 Readout of Resonant Sensors

The use of oscillator circuits detuned by the measurement parameters is one of the most common approaches for the readout of resonant sensors and is particularly suitable for sensors with high quality factors or when the damping of the resonance remains constant. This is the case for, e.g. quartz crystal microbalances (QCM) monitoring the deposed metal layer in vapor deposition lines. One of the major advantages of oscillators is that this approach allows for very cost-efficient implementations yielding a frequency as output parameter which, in principle, can be measured very accurately.

For operating conditions where increased damping of the resonator is expected, e.g. when electromechanical resonators are exposed to liquid environments, additional effort has to be made to separate the behavior of the motional branch from parasitic effects like the parallel capacitance and the fluid’s permittivity and conductivity (Fig. 1).

Several variations of locked loop circuits were reported to consider these influences (e.g. [5],[6]), but, with this approach, spurious influences that are changing during operation can be addressed only to a very limited extent (e.g. compensation of changes in parallel capacitance as shown in [5]). With increasing demands for measurement accuracy or with higher damping of the resonator (viscous liquids), the only practicable solution is to record the behavior of the resonator in vicinity of the resonance and to shift the extraction of desired parameters to a post processing step in the digital domain. In this context several dedicated analyzer systems based on measurement methods like those implemented in gain-phase/network/impedance analyzers were reported (e.g. [7],[8]).

In our previous work, we addressed numerous details in order to improve the performance of these compact analyzer systems. This concerns data acquisition concepts for minimal signal processing effort [8], approaches to reduce parasitic signal components [9], numerical methods for separating motional from parasitic behavior [10], and improvements in sensor modeling [11].

The latest development in this respect is a highly universal evaluation system for interfacing resonant sensors, which utilizes and combines various approaches that are required or simply beneficial for a high performance measurement system. This system is developed by the university spin-off Micro Resonant Technologies and tested in collaboration with the Institute for Microelectronics and Microsensors at the Johannes Kepler University Linz.

3 Tuning Fork Resonator as Sensor for Viscosity and Density of Fluids

Various publications address the use of tuning fork resonators for determination of physical fluid properties such as viscosity and mass density (e.g. [12],[13]). In contrast to resonators with dominant shear oscillation (like torsional resonators or thickness shear mode QCR), the tuning fork resonator allows better separation of mass density and viscosity [4],[11],[13].

For the experiments presented below, a commercial off-the-shelf 32.768 kHz clock crystal with removed housing was used (Fig. 2). No electrical insulation of the resonator against the fluid is required due to the implemented compensation of spurious effects, which efficiently eliminates cross-sensitivity to liquid permittivity and conductivity (see Fig. 1 right) as well as spurious phase shifts and propagation delays.

Fig. 2
figure 2

Commercial off-the-shelf 32.768 kHz clock crystal with removed housing. With the electrodes on the tines of the tuning fork a low voltage signal can be used to excite the oscillation

Full size image

4 Experimental Setup

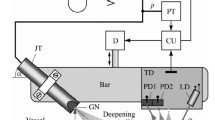
The tuning fork is connected to a low noise amplification stage and is mounted on the cap of a small glass bottle (as used for gas chromatography) and immersed in about 1 ml of the sample liquid (Fig. 3). The bottle is inserted in a holder connected to a refrigerated and heated circulating bath system in order to accurately set the temperature of the sample within an accuracy of ±0.01°C.

Fig. 3
figure 3

The liquid sample (1 ml) is contained in a small glass bottle connected to a circulating bath for temperature stabilization (right). The sensor is immersed into this bottle and connected to an amplifier circuit in order to achieve low noise signals. For the evaluation of the sensor signal, a signal processor based universal evaluation system for resonant sensors (left) is used. The acquired results are sent to a PC via USB connection

Full size image

The evaluation system is based on a digital signal processor (DSP) generating the excitation signal for the resonator and calculating the resonance frequency \(f_{r}\) and the quality factor \(Q\) from the recorded response signals. This is achieved by compensating for parasitic influences and fitting the admittance Y of a series resonant circuit

$$Y(f)=\frac{Y_{\max }}{1+jQ\left (\frac{f}{f_{\mathrm{r}}}-\frac{f_{\mathrm{r}}}{f}\right )}$$
(1)

to the remaining data [10]. From these parameters viscosity and density of the sample are determined by applying a fluid-mechanical sensor model of the tuning fork [11]. Finally the results are transferred to a host PC via USB port.

Reference measurements for comparison purposes as well as for calibration of the resonator model were performed with a Stabinger Viscometer (SVM3000), which nominally provides an accuracy of ±0.35% for viscosity and ±0.5 kg/m³ for mass density.

5 Results

For demonstration purposes, two experiments are shown below: one to determine the achievable accuracy when monitoring liquid properties of fuels (Diesel) and a second one on the condition monitoring of engine oil, where the dilution with fuel is a severe issue for engine manufactures. Previous results of similar experiments were reported in [15] and [16].

5.1 Fuel Analysis

In the first experiment, various test liquids with viscosities and densities similar to Diesel were measured with the reference instrument and the resonant sensor setup. The resonator was immersed in the sample and placed in the holder sufficiently long (for temperature stabilization) before a sequence of 300 measurement points was acquired in about 5 minutes, exemplarily shown in Fig. 4.

Fig. 4
figure 4

Measurement in Diesel fuel after stabilization of temperature. With a measurement rate of about one measurement per second, 300 data points were acquired in approximately 5 minutes

Full size image

From the acquired sequences, mean values and standard deviations were derived and compared to the reference measurements. The standard deviations of frequency and quality factor and subsequently of viscosity and density results are in close agreement with the theoretically predicted error propagation [14].

A comparison of reference data and the mean values of the measurement results obtained with the tuning fork are shown in Tab. 1. As depicted in Fig. 5, these results deviate from the reference measurements less than 0.2 % for viscosity and less than 0.1 % for density.

TABLE 1 Measured values for viscosity and mass density compared to reference data (obtained with an Anton Paar SVM3000)
Full size table
Fig. 5
figure 5

Tested sample liquids with different density and viscosity. Relative errors and standard deviations of viscosity and density are given for each sample

Full size image

5.2 Fuel Dilution of Engine Oil

The second experiment was conducted to demonstrate the measurement of fuel dilution by means of viscosity change of engine oil. For this test a series of various dilutions (0, 0.2, 0.5, and 1 % mass fraction of Diesel in 5W30 oil) was prepared and measured with the resonant sensor system. For each liquid sample, data were recorded for one hour after temperature stabilization at 90 °C (Fig. 6).

Fig. 6
figure 6

Measurements of 5W30 engine oil with different contents of Diesel fuel at 90°C. The sampling rate was 1/s, for each dilution ratio a series of one hour duration (3600 samples) was acquired. For this measurement rate the noise level is about the same as a change of 0.1 % fuel content, for slower data acquisition a much lower noise level can be achieved

Full size image

The results show that a change of fuel content in the range of 0.1 % can be reliably determined within seconds even at elevated temperatures as expected in a running engine. In order to obtain a high absolute accuracy of the diesel content ratio, the implementation of a mixing model for the specific oil is recommended.

6 Conclusions

A viscosity and density measurement system based on a resonant sensor has been presented. For demonstration purposes, the system was evaluated using a commercial off-the-shelf resonator as sensor. The signal processor based system for evaluating the resonant behavior of the sensor can be used with virtually any kind of resonator from small quartz crystal tuning forks up to rugged resonators made from stainless steel.

The results obtained with this setup have been compared to an accurate top-grade lab bench viscosity and density meter and show outstanding trueness and precision at a significantly higher measurement speed, ideally suited for a large range of applications, such as online process monitoring, condition monitoring of lubricants, low fluid volume measurements, hand-held devices, laboratory use, and more.