Principal Factors of Contact Charging of Minerals for a Successful Triboelectrostatic Separation Process – a Review

Abstract

Triboelectrostatic separation is a promising method used to separate non-conductive minerals. However, the knowledge about the underlying triboelectrification mechanisms is still very limited. Thus, predicting the separation results and finding proper separation parameters are challenging tasks.

This article presents a comprehensive summary of phenomena and factors which play a decisive role in the charging behavior of non-conductors and, by implication, the efficiency of the separation process, such as water and adsorbents layers on the surface, surface roughness, humidity, type of contact, etc. The authors hope that this article opens a way for a systematic approach through basic experiments dedicated to a better understanding of triboelectrification processes.

Zusammenfassung

Die Elektroscheidung nach Triboaufladung stellt eine vielversprechende Methode zur Trennung nicht leitfähiger Mineralphasen dar. Das begrenzte Wissen über die zugrundeliegenden Mechanismen der Triboaufladung macht die Vorhersage von über einzustellende Prozessparameter zu erzielenden Trennergebnissen zu einer herausfordernden Aufgabe.

Diese Veröffentlichung gibt einen umfassenden Überblick über Phänomene und Faktoren, die eine entscheidende Rolle beim Aufladeverhalten von Nichtleitern spielen oder spielen können und die damit Einfluss auf die Effizienz der Trennung nehmen. Solche Faktoren können sein: Wasser- und Adsorbatschichten, Oberflächenrauigkeit, Luftfeuchtigkeit, Kontaktart, usw. Die Autoren hoffen, dass dieser Artikel Wege für einen systematischen Ansatz durch grundlegende Experimente aufzeigt und damit zu einem besseren Verständnis der bei der Triboaufladung wirkenden Faktoren beiträgt.

1 Introduction

Triboelectrostatic separation is an inexpensive environmentally friendly separation technique, which has a potential to take over a greater significance of mineral processing and polymer recycling. It has been successfully applied for the separation of salts [1–3], calcite – quartz [4], feldspar – quartz [5], carbon – ash-coal [6], and even for the purification of secondary materials like plastic [7, 8]. In general it is based on triboelectrification, which is the generation of net charges on insulating powder materials by bringing powder grains into contact with each other and the device walls. The grains, differently charged upon contact, are separated in a strong electric field depending on the sign and amount of the charge they carry. However, an application as a widespread separation method is limited due to the complexity of the involved interactions, which make it technologically difficult to adjust the proper process parameters. Different factors like the behavior of the powder stream, the environmental conditions (humidity, temperature, etc), the mechanical and electrical properties of the individual grains as well as the design of the equipment have to be considered simultaneously. Especially triboelectrification/contact charging is a highly non-trivial phenomenon. So far no universal model for a quantitative or even qualitative description is available. Therefore, a main focus of this work is set on contact charging phenomena.

We start with a brief description of the state-of-the art triboelectrostatic separation technologies in Sect. 2. The discussion is continued with reviewing factors, which determine charging behavior of insulators in Sect. 3. There the focus is set on triboelectric charging models, charge transfer mechanisms, influences like type of contact and environment. In Sect. 4 we provide a short overview of experimental approaches for the investigations of electrification of minerals both at macro- and microscale. The authors hope that the article presents the complexity of the topic and will intensify systematic interdisciplinary investigations to a better understanding of triboelectrification processes.

The considerations to follow are an integral part of the first author’s PhD thesis, which is in the final stage.

2 Triboelectrostatic Separation

Triboelectrostatic separation, invented about 100 years ago [9, 10], has been utilized in mineral processing [1–6, 11], as well as in waste treatment [7, 8, 12] industries to separate nonconducting materials of similar densities from each other. This process is based on the different charging behavior of the materials to be separated and thus, on the difference in their effective work functions between materials separated. Since the charge exchange occurs via the surface, tribocharging is a surface sensitive technique. This relatively cheap and environmentally friendly concentration technique has a realistic potential to gain in importance and become a dry alternative to flotation processes [13]. Detailed reviews about the triboelectrostatic separation are given in [12, 14–24].

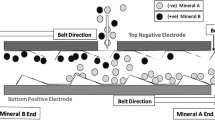
Generally, the process proceeds as follows. At first, fine grained materials (for minerals, particle size is between hundred micrometers and few millimeters) are fed into the triboelectric charging unit, where they are electrically charged upon contact. Next, charged particles are separated in a sorting unit under the influence of a strong electric field, depending on the sign and the amount of their surface charge. A simplified scheme of the phenomena occurring during triboelectrostatic separation is presented in Fig. 1.

Fig. 1

Schematic representation of the triboelectrostatic separation [16] via particle – particle interaction (top panel) and particle – charger wall interaction (bottom panel)

Charging is realized by (frictional) contact through particle - particle and/or particle - charger wall interaction. During contact, charge transfer occurs, and after parting two oppositely charged objects are obtained. Details of the (tribo)electrification phenomenon are described in Sect. 3. Separation is carried out in a strong electric field where charged particles are attracted to the electrode with opposite bias and collected thereupon.

In mineral processing industry, this concentration technique is commercially applied in separating salts [1–3], feldspar from quartz [5], carbon from ash-coal [11], calcite from quartz [4], talc from magnesite [4] and various other material combinations [25].

Potentially, triboelectrostatic separation can be employed for separating nonconductors from conductors. In this case, electrodes have to be electrically isolated from the stream of charged particles preventing discharging/charging of particles by contact with the attracting electrode. In general, electrically isolated electrodes are a good practice, which hinders the particles to change their charged state when they come in contact with the electrodes [26], (own observations).

The technical advantages of triboelectrostatic separation include easy operation, low energy and water consumption, little usage of chemicals. However, the process of charging behavior of mineral particles is poorly understood, which makes it difficult to select proper process parameters without intense lab work. This calls for investigating the system empirically in a pilot plant which is both time and cost intensive. Furthermore, triboelectrostatic separation has in general a low throughput rate and suffers from the high sensitivity towards the surface properties of the feed material.

2.1 Equipment

A triboelectrostatic separation apparatus is usually divided into feeding, charging, and sorting zones. Fig. 2 and 3 show examples of two main types of triboelectrostatic separators: free-fall separator and belt separator and their corresponding working principles.

Fig. 2

Free-fall triboelectrostatic separator a hamos EMS 500 [27, 28]; left: overview scheme, right: inside view, b schematic drawing (after hamos EMS 500)

Fig. 3

Belt triboelectrostatic separator: a ST separator [25], b schematic drawing of the belt triboelectrostatic separator (after [4])

It is worth to note that there is a great diversity in the realization of the free-fall separators, starting from applying chemical conditioning chambers in the case of separation of salts [1, 2], using different charging units [6, 8, 28–34] up to varying the shape of electrodes [35]. As a tribocharging unit, conveyer belt [29, 30], cyclone [8, 31, 32], drum [6, 28], and others can be employed. Also the separation units can vary; electrodes can have plate shapes or rotary shapes. The variety of devices manifests itself in plenty of patents that are still valid [36–41].

The main difference between free-fall and belt separators lies in the different flow of charged particles in the separation zone. In the free-fall unit charged particles fall freely due to gravitational force and are simultaneously subjected to attracting/repelling electrostatic forces from the electric field of the electrodes. Whereas in belt triboelectrostatic separators free fall of particles is limited by the short distance between electrodes, once particles reach the attracting electrode, they are dragged by a belt to the collecting bins.

Generally, free-fall separators are designed for beneficiation of mineral particles with grain sizes in range of 0.1–2 mm. Too heavy particles are not sufficiently deflected by the electric field of the electrodes, whereas too light particles tend to stick to the electrodes and/or disturb the laminar flow of the falling particles. In both cases, the separation becomes inefficient [13]. Otherwise, due to the small distance between electrodes, belt separators are used for the concentration of smaller mineral particles with grain sizes in the range of 1–300 µm which allows to process deposits of lower quality and/or to increase the quality of obtained products. Additionally, contact electrification between particles also occurs in the separation zone in a strong electric field, which significantly improves the efficiency of the process. The only limitations of belt triboelectrostatic separation are the necessity of periodic service caused by belt wear and blocking of the belt movement due to too high powder amount in the belt caused by a wrong selection of the separation conditions. Triboelectrostatic separation is usually a dry process; however, there are also applications involving chemical conditioning of the mineral particles [1, 2].

Choosing proper equipment which adequately fulfills the requirements is essential to achieve the presumed efficiency of the separation process. It is worth to mention here that rotating electrodes with brushes at the bottom should be utilized for the separation of shredded plastics (unpublished data), whereas a belt separator should be employed to achieve good results in the separation of very fine minerals [4, 25]. Other factors which can have an influence on the separation results are described in Sect. 2.3.

2.2 Principles

In general, triboelectrostatic separation employs tribocharging to get different materials charged with opposite polarities. Herein, during separation, two main forces act on charged particles, i.e., the gravitational force F_g and the electrostatic force F_e. Separation occurs when electrostatic forces are strong enough to shift the trajectory of a charged particle sufficiently to the electrodes with opposite charge.

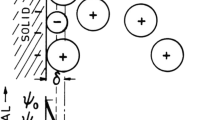
The simplest model applies a spherical grain of uniform charge Q and mass m in an uniform electric field E generated between two vertical-plate electrodes parted by a distance d and a potential difference ΔV between them [8] (Fig. 4). The particle is deflected forward towards the electrode with opposite sign during its free-fall.

Fig. 4

Forces acting on a particle falling in a uniform electric field [8]

In an industrial separation process, air resistance has to be considered [42], especially for flat and/or very light objects with a long falling distance. Furthermore, a uniform charge on the particle surface occurs only for conductive particles, whereas nonconductive particles are characterized by locally charged surface areas which correspond to the contact areas. Therefore, multiple bouncing events during charging play a significant role.

In separators with additional air flow, for instance generated by cyclone or fluid bed chargers, additional shear forces [13] occur, which can act with or against the gravitational force. Moreover, any turbulence in the air flow disturbs the “electrical” path of particles, thus introducing additional forces into the system and probably reducing the separation effect. This shows that the phenomenological behavior of the powder should also be taken into account.

So far, only a few authors have simulated free-fall processes [26, 43] or the behavior of granular systems during charging [44–46].

2.3 Influencing Factors

The factors influencing the separation process can be divided into four groups:

• material characteristics,

• powder particle characteristics,

• equipment design,

• environmental conditions.

An effort has been made to establish a detailed list of factors belonging to each group (Table 1) by compiling theoretical consideration and experimental investigations [6, 12, 13, 21, 24, 28, 31, 46–58, 60]. Those parameters influence individual phenomena such as type of contact, contact stress, time of contact, single and multiple contacts (saturation), charge transport, charge distribution, charge decay and forces within the system. Those individual phenomena are directly related to the final surface potential (surface charge) of the particles and therefore to the process efficiency.

Table 1 List of factors taking into account during the triboelectrostatic separation (partially after [62])

For instance, properties of a water layer on the surface of the particle which can change the lateral distribution of charge on the particle surface from local to uniform can be caused by storing conditions, wet milling of materials, atmospheric conditions, or by additional conditioning of the material.

Examples for the influence of some individual factors on the triboelectric charging of the particles can be found in [28, 47–52, 57–59]. The impact of factors, such as contact time, contact area, number of contacts, material of charger and environmental conditions is shown. Experimental results of triboelectrification and its effect on the triboelectrostatic separation are presented in Sect. 4.

The long list of presented factors simply demonstrates that the separation process is a nontrivial task. First of all, the separation process is sensitive to environmental conditions. Therefore, controlling the process atmosphere plays a decisive role. Secondly, the separation performance depends on actions taken before the process itself, such as: aging, storing, transporting, crushing, milling of materials, and others. Milling, for example, can cause both, precharging of the surface (strong multiple contacts between particle – particle and particle – mill walls) and changing electrical properties of the particles by introducing foreign ions on the particle surface (from chemicals and water used during wet milling). By implication, experiments in a pilot plant should take into consideration the whole production line. Thirdly, proper selection of the separator, especially the charger unit is crucial. Finally, it turns out that even small changes in the powder materials or in particle size and shape distribution can strongly influence the efficiency of the separation [58].

3 Triboelectrification

Contact electrification or contact charging is a phenomenon characterized by charge transfer from one material to another when these two materials are brought into contact and then separated again. Triboelectric charging or frictional electrification is a particular case of contact electrification when materials rub against each other [60], whereas impact charging occurs for short contact of high contact force during collision [61]. In practice, it is usually not easy to distinguish the processes for charging, and therefore the term ‘triboelectric charging’ is used in a broad sense [54].

Charge transfer may occur by electrons, ions and/or mass transport [54, 55, 60]. It is not clear which of those three transport mechanisms is dominant. It is rather well accepted that more than one mechanism of charge transport is active during a single process [54, 55, 62–65].

3.1 Charge Transport, Models and Mechanisms

3.1.1 Electron Transport, Surface State Theory and Effective Work Function

The electron transfer mechanism is well understood for metal – metal contact, wherein a difference in work function is the main driving force. When two metals come in contact, electron transfer happens until their conduction bands are filled to the same level and their Fermi levels equalize (work function theory). For metals, the work function is defined as “the minimum energy needed to remove one electron from the interior of a solid to a position just outside. >Just outside< means a distance from the surface that is large at the atomic scale, but small (in macroscopic sense)” [66]. It can be, more formally, expressed as the difference between Fermi level and (local) vacuum level. Upon contact, the body with lower work function acts as a donor of electrons and the body with higher work function acts as an acceptor. In 1951, Harper [67] introduced the concept of contact potential difference (V_CPD), which is defined by Eq. 1.

$$V_{CPD}=\, -\frac{\left (\phi _{1}\, -\phi _{2}\right )}{e}$$

(1)

where e is the elementary charge, and ϕ₁ and ϕ₂ are work functions of metal 1 and metal 2, respectively.

For insulators, work function theory is not applicable, since their conduction bands are empty and there are practically no ‘free electrons’ available in them. In general, energetically the surface of solids differs from its bulk properties, whereby accessible states for electrons exist in the electronic structure of the surface that are not available in the bulk (surface states theory). Taking surface states into account, electron transport occurring during insulators contact might be explained with the difference of effective work functions of the two surfaces as the driving force for the charge transfer [68]. A definition of the effective work function is given below.

When the insulators come into contact, electrons move from the filled surface states of one insulator to the empty surface states of the other insulator. Thus, electron transfer takes place until the Fermi levels of the two materials coincide with each other through changing it by a value ∆ (Fig. 5b). Due to the charge transfer, a potential difference (E z) is created between the surfaces (Eq. 2), where E is the electric field that exists between insulators at tunneling separation distance z [54]. Fig. 5 presents a scheme for electron transfer for the contact of two insulators. This surface state model of insulator contact has been discussed in details by Gutman et al. [69], and Anderson [70].

Fig. 5

Model of electron potential energy for an insulator–insulator contact a before, and b during contact (surface states theory) [54, 68]. E_L is local vacuum level, and E_F is the Fermi level, ∆₁ and ∆₂ are changes of the Fermi levels due to contact, and ϕ₁ and ϕ₂ are effective work functions of the insulator 1 and insulator 2, respectively

$$V_{CPD}=E\, z=\, \frac{\left (\phi _{1}-\phi _{2}\right )-\left (\Updelta _{1}+\Updelta _{2}\right )}{e}$$

(2)

where ∆₁ and ∆₂ are changes of the Fermi levels due to contact, and ϕ₁ and ϕ₂ are effective work functions of the insulator 1 and insulator 2, respectively.

For generalization, this electronic potential created between the touching surfaces in the following will be referred to as the contact potential difference (V_CPD).

Surface states: Although the surface state theory was developed to explain the behavior of a semiconductor in contact with a metal or another semiconductor, it can also be applied to describe insulators as they can be considered as semiconductors with a large band gap. The band gap corresponds to the energy difference between the bottom of the conduction band E_c and the top of the valence band E_v. In this region, no electronic bulk states exist. Additional electron surface states can only be present on the free surface of an insulator. These states, i.e., the available energy levels that electrons can occupy, can possess energies which lie within the band gap. The electronic surface states are induced by the interruption of the bulk periodic structure (dangling bonds), impurities or defects on the surface and contact with a new phase (e.g. atmosphere) [21]. This modifies the electronic structure of the insulator near the surface. These surface states can be occupied by charge carriers resulting in a surface charge. The charge accumulation generates an electric field which can be simply described as a “bending” of the electronic bands near the surface (Fig. 6). Also surface dipoles can be included in the band diagrams as a sudden jump (∆δ_S) in the local vacuum level of the surface.

Fig. 6

Schematic diagram of the electronic band structure of insulator bulk and surface [72]. E_L is local vacuum level, E_C - bottom of conduction band, E_F - Femi level, E_V - top of valence band, χ - bulk electron affinity, χ_e - effective electron affinity, Δδ_S - the surface dipole, V_S - surface potential, and ϕ_e – effective work function

Consequently, the value of the work function at the surface, i.e. the effective work function (ϕ_e), differs from the work function of a bulk material [71, 72], and can be expressed by Eq. 3. Thus, the contact potential difference (V_CPD) between two insulators can be interpreted as the difference between their effective work functions: e V_CPD = ϕ_e1 – ϕ_e2.

$$\phi _{e}=E_{LS}-E_{F}=\left (E_{C}-E_{F}\right )_{B}-eV_{S}+\, \chi \, -\, \Updelta \delta _{S}\, \equiv \left (E_{C}-E_{F}\right )_{B}-eV_{S}+\, \chi _{e}$$

(3)

where E_L is the local vacuum level, E_C - bottom of conduction band, E_F - Fermi level, E_V - top of valence band, χ - bulk electron affinity, χ_e - effective electron affinity, Δδ_S - the surface dipole, V_S - surface potential. Index S is referred to surface and B to bulk material, respectively.

The surface potential (V_S) is created as a result of the different charge carrier density (accumulation/depletion) at the surface with respect to the bulk. By definition, the lower the energy band, the higher is the electrical potential, whereby a positive V_S corresponds to downward-bent bands [72]. In other words, any change in the surface potential causes a change of equal magnitude in the effective (surface) work function.

As shown in Fig. 6 and Eq. 3, the work function can be defined by the difference between Fermi (E_F) and vacuum (E_L) levels, or alternatively by the difference in conduction band edge (E_C), Fermi level, and electron affinity (χ). The electron affinity (χ) is the energy required to remove an electron from the bottom of the conduction band (E_C) to the vacuum level (E_L). Therefore, some authors prefer to refer alternatively to electron affinity differences instead of work functions as driving force of triboelectrification.

It is worth to note that the surface state theory has two limitations: (a) finite number of high energy electrons present on the surface (the low density limit), (b) electric field generated during charge transfer limits further transfers (the high density limit). However, it has been reported that not all data agree with limits of the surface state density [68].

Moreover, any modification of the surface, as for instance induced by the presence of adsorbates, has a local influence on the surface band bending [73]. However, adsorbate layers on mineral surfaces should be considered as a new substance with its own electronic structure. The thickness of the adsorbed layer plays a significant role in the behavior of the surface. A single layer of adsorbents performs quite differently than a thick multi-layer. An important example is the behavior of water, which is described in details later in this chapter.

Furthermore, the presence of an external electric field, illumination and temperature can have a substantial effect on the occupation of surface states. Thus, the effective work function can differ locally, making it difficult to assign a representative value.

Bulk dopants and impurities: Although the electronic structure of the surface plays a dominant role in the electron transfer during contact charging, the bulk structure and its changes cannot be neglected. Generally, impurities or dopants, present in the bulk of the crystal, create additional energetically available levels within the band gap. This can drastically change the electric behavior of the material. As an example, the effect of slightly varying chemical composition on the average work functions for natural minerals from different sources (mines) is presented in Table 2; [21]. Additionally, Lowell and Rose-Innes report on the increase of the contact charge density with increasing doping level for octadecanol-doped polyethylene and for solid argon doped with chlorine [60].

Table 2 Influence of slight differences in chemical composition (presence of impurities) on a value of the work function for chosen minerals [21]

Surface dipoles: In addition to surface states, a double layer of charges, known as a surface dipole (∆δ_S) may form on the surface. As illustrated in Fig. 6, a surface dipole causes a ’step’ in the local vacuum level. The dipole is described as positive if the local vacuum level drops when passing from the material into vacuum. The ’tail’ of the surface-localized electron wave functions passes through the surface into the vacuum. Therefore, the region just outside the surface has a net negative charge, and the region just inside the surface is left with a net positive charge. The separation of positive and negative charges over atomic distances is a microscopic dipole and creates an additional electric field which opposes further electron transfer into the vacuum [72].

In summary, electron transfer between two insulators or an insulator and a conductor in contact can occur only locally and is mainly determined by the local surface properties. In general, the electronic surface properties of solids differ from their corresponding bulk properties. As a result of the termination of the periodic bulk structure at the surface, the presence of adsorbates and the contact with different phases, localized electronic states are created. This can lead to the formation of local electrically non-neutral regions on the surface [72]. However, quantitative predictions of the band structure at the surface of real materials and therefore the electron transfer during their contact, are complex.

Three important concepts of direct electron transfer are briefly presented below.

Difference in effective work functions: Assuming that the introduced charge is confined in a surface-near layer with thickness x and constant charge density q_S, the local contact potential difference (V_CPD) can be correlated with q_S [72, 74] via:

$$q_{S}=2\, \varepsilon _{O\, }\varepsilon \, \left (\frac{V_{CPD}}{x}\right )$$

(4)

where ε is the dielectric permittivity of the insulator.

Several authors [75–77] state that the density of charge introduced by contact depends on the difference between the effective work functions. Estimations show that the maximum depth at which the charge is introduced into the surface by triboelectrification can be several tens of nanometers [76, 77]. Conversely, all additional phenomena which occur on the surface and subsurface can have influence on the density of the introduced charge. However, the model presented does not explain accumulation and saturation of charge in the contact area due to repetitive contact [74].

“Quantum-mechanical model” of electron transfer: In the “quantum-mechanical model”, Lewis (after [74]) claims that contact between nonconductor and conductor leads to the creation of temporary additional donor and/or acceptor states around the contact area. After breaking the contact, the introduced charges can be transported further to other existing available states and then stay trapped there. This process can proceed until the electric field generated by the trapped charges around the contact area is strong enough to prevent further charge uptake. This model explains both, the saturation effect upon repetitive contact, and the long-term charge decay.

Condenser model: In the condenser model [54, 78], the charge exchanging bodies are considered to form a capacitor. A schematic illustration of particle charging on the wall by contact is shown in Fig. 7. The transferred charge (∆q) is proportional to the capacitance (C) and the total potential difference (V) between the two bodies in contact (Eq. 5). The capacity depends on the contact area (S) and the contact distance, called ‘critical gap’ (z₀) between the two bodies. At separation below the critical gap, electron transport can take place between the two bodies.

Fig. 7

Schematic illustration of the condenser model. From [54]

$$\Updelta q=k_{C}\, C\, V=k_{C}\, \frac{\varepsilon _{O}\, S}{z_{0}}\, V$$

(5)

where k_c is the charging efficiency and ε₀ is the absolute permittivity of free space.

The total potential difference at the contact (V) is the sum of following contributions: the differences in the effective work functions (V_c), precharging (V_e), space charge caused by electric field from the surrounding (V_b) (e.g. charged particles), and externally applied electric field (V_ex). This can be expressed as: V = V_c – V_e – V_b +V_ex. Within this approach, several influences can be described. Firstly, precharging of the tribocharger walls causes an electric field, changing the total potential difference. Secondly, repetitive contact causes charge accumulation, and therefore the total potential difference between the contacting bodies decreases with increasing surface charge reducing further charge transfer.

A very similar model, the “ohmic charging model”, was presented by Ireland [45]. There, the charge accumulation and saturation effects due to repetitive charging are taken into account. The model assumes that the contact between a neutral particle A (q_A0) and a neutral surface B (q_B0) results in an exchange of charges. Each of the objects has an equal and opposite charge on the surface (q_A1 = - q_B1) after separation. This process was called “charge separation”. A second type of process – “charge transfer” – takes place during contact between a charged particle A (q_A2) and a neutral surface B (q_B0). As a consequence, the charge is transferred from the charged particle to the neutral body, thus ending up with a neutralized particle A (q_A0) and a charged surface B (q_B2).

3.1.2 Ion Transport

Ions present on the surface are not only a source of surface bands bending, but also transport charge when transferred to another body. Generally, upon contact, the bigger ions preferentially remain on the surface, while the smaller ions with greater mobility get transferred. Therefore, chemicals with big cationic and small anionic groups (e.g. crystal violet dye) tend to create a positive charge at the surface of their host, whereas those with big anionic and small cationic groups (e.g. sulfonated azo dyes) result preferentially in a negative charge [54, 55]. In fact, as it was shown by Diaz and Fenzel-Alexander [79], all ions can be transferred but the transfer of the larger ions is harder, so they remain behind in greater amounts. On the contrary, for chemicals where both ions are mobile, the resulting magnitude of the contact charge is relatively low [79]. Moreover, only dissociated ions are taking part in the charge transport due to contact, while ions which are associated in ion pairs do not impart charge even upon transfer. Ion pairs usually remain paired and only contaminate the other surface due to transfer [79]. Contamination, however, might also change charging behavior by facilitating electron transfer.

In general, the role of ions during contact charging is complex. The result of triboelectrification depends on the type and concentration of the ions on the surface and on their mobility. Also, the presence of water at the surface has a significant influence on contact charging. Depending on its thickness, water layers can facilitate charging or discharging processes. The impact of a water layer is described in more detail below. Furthermore, ion transport can also be activated thermally [55] by increasing ion dissipation. For example, the concentration of H⁺ and OH^– ions in the adsorbed water layer increases at higher temperatures [80].

Several models of triboelectrification due to ion transfer were proposed, including works of Harper (after [55]), Diaz and Fenzel-Alexander [79], McCarty and Whitesides [55] and Knorr [64]. A brief overview of them is presented below. Unfortunately, none of them provides a quantitative description of triboelectrification by ion transport.

Harper ion-transfer model adapted by McCarty and Whitesides [55]: The Harper ion-transfer model [55] focuses on the behavior of a single ion during the contact–separation process. When the two surfaces are in contact, the mobile ion between them moves within a single potential well (Fig. 8). While separating, the potential energy evolves into an asymmetric double-well potential. For a small distance, the double-well potential has a sufficiently small barrier, and the ion can move freely between the two surfaces. At a greater distance, the ion is trapped on one of the surfaces.

Fig. 8

Scheme of the ion-transfer mechanism according to Harper. a Contact: The mobile ion between the surfaces moves into a single potential well. b–d Separation: Evolution of a double potential well. b The ion still can move between surfaces (small distance between the surfaces – potential barrier is small); c It resides on one of the surfaces (the intermediate distance – the probability of jumping of the ion to the opposite surface is very low); d ion is trapped on one of the separated surfaces (surfaces far from each other – potential barrier is high). From [55]

The potential energy of a mobile ion between two surfaces is the sum of two short-range interactions (one for each surface) and a long-range Coulombic interaction. The energy difference ∆E, given in Fig. 8, is the electrostatic contribution, which also includes local interactions between the ion and the proximal interface.

Furthermore, within this model, the ion transfer is enhanced by the presence of water. This is illustrated in Fig. 10.

Ions can originate from: atmospheric ions which interact with the surface, water present on the surface, and chemical agents added to the mineral powder in earlier treatments or for tuning the tribocharging behavior. Charge control agents (CCAs) applied to toners of laser printers are good examples of additives changing the contact charging behavior. Materials themselves can intrinsically possess mobile ions on the surface on account of their specific chemical/crystal structure (i.e. ionic electrets), or due to trapping of ions from the ambient. Furthermore, adsorbed water from the ambient can play a decisive role in ion-based charge transfer [55].

Charge control agents and charge stabilizers : Experiments with electrophotographic toners [81–84] showed that the contact charging process can be controlled by chemical modification of the toner composition and/or the toner surface (surface agents). The additives, known as ‘charge control agents’, are applied to enable the required charging (sign and magnitude) through contact. ‘Charge stabilizing’ agents are able to prolong charge stability (both negative as well as positive charges) when used in combination with CCAs. Examples of surface CCAs are fumed silica and polyvinylidene fluoride, whereas polyester salt is an example of a charge stabilizer. Another example involves the presence of a water layer on the insulator surface; acidic or basic functional groups (negatively or positively charged, respectively) of the CCA facilitate water adsorption on the surface, which supplies H⁺ and OH^– ions that are exchanged between the materials in contact (after [83]).

Water on the surface: Almost all surfaces are covered by a water layer when exposed to ambient conditions. Generally, electrostatic interactions in water are different from those in air or vacuum because water contains mobile ions (H⁺, OH^–, and other electrolyte ions), and has a high permittivity (ε_r ≅ 80 at RT) [55]. Thus, the presence of water influences the contact charging results by enhancing the charging process if the water layer is thin, or facilitating discharging if the water layer is thick (bulk).

To illustrate the difference between thin and bulk water layers, a schematic of the interface between a charged insulating surface and an aqueous solution is shown in Fig. 9. An electrical double layer is created at the phase interface. In the case of a solid with a positive electrostatic charge at the surface, some anions accumulate close to the surface charge areas in the so called Stern layer. The remaining ions form the Gouy–Chapman layer that extends into the electrolyte. As a rule, the ions in the Gouy–Chapman layer are mobile, whereas those in the Stern layer are immobile. The plane of shear divides the Stern layer with immobile ions from the Gouy–Chapman layer containing mobile ions, and the zeta potential is the electrical potential at the plane of shear. The sign of the zeta potential indicates the net charge of the immobile ions at the surface. As a consequence of the ion distribution, the electrostatic potential reduces with increasing distance from the solid surface. The so-called Debye length is defined as the distance at which the potential is reduced to 1/e (with Euler’s number e) of its value at the surface; for 0.01M electrolyte at RT, the Debye length is 3 nm [55]. A thin water layer has a thickness of less than the Debye length, while bulk water is considerably thicker.

Fig. 9

a The interface between a charged solid and an aqueous solution. b The electrostatic potential corresponding to the model shown in (a). After [55]

The complicated role of water in the contact electrification of insulators manifests itself in several effects: A bulk layer with a thick Gouy–Chapman layer increases the surface conductivity, thus leading to surface discharging. For thin water layers, the contact creates a water bridge between the surfaces in contact, facilitating ion charging by improving the ion dissipation. Additionally, a separation of hydroxide and hydron ions during contact can also occur (hydroxide adsorption model [55] and bipolar tribocharging model [64]). Many articles, such as [85, 86] discuss a structure of the water layer on the flat mineral surfaces.

Formation of a water bridge allows mobile ions to diffuse easily between surfaces. Fig. 10 shows a schematic of the ion contact transfer modified by the presence of a water bridge. For materials which contain covalently bonded ions and mobile counterions, the mobile ions can distribute themselves across the entire water bridge when diffusion forces are comparable to the electrostatic forces. The electrostatic forces tend to accumulate the mobile ions at the charged interface, whereas entropy tends to cause a spread of the ions into the solvent. During separation, a part of the mobile ions is kinetically trapped on the second surface, thus leading to the creation of two charged surfaces. This is possible because the increasing distance and the high dielectric constant of water reduce the electrostatic cost of separating mobile ions from their bounded counterions [55]. This mechanism does not require a continuous water layer and therefore should be valid also for highly hydrophilic surfaces.

Fig. 10

The role of water in the ion-transfer mechanism of triboelectrification for insulators that contain covalently bound ions and mobile counterions. From [55]

Furthermore, the role of water in triboelectrification seems to be more complex when the following aspects are considered:

• creation of a water hydrogen bonded network and the auto-dissipation of water (creation of hydronium H₃O⁺ and hydroxide OH^– ions) [87],

• influence of mechanical stress on water ionization [64],

• different adsorption properties of water on different surfaces (e.g., on calcite [88], quartz [89], a comparison for different minerals [85]),

• increasing the effective area of contact due to formation of a water bridge [55],

• reduction of the water layer thickness and, simultaneously, decreasing water permittivity (due to higher ion dissipation) with temperature,

• influence of an external electric field on the surface wettability [90],

• presence of other ions (HCO₃ ⁻, CO₃ ²⁻, Na⁺, Cl⁻) typically dissolved in water [64].

It needs to be noted that the water layer present on the surface may have an influence on the charging not only by ion transfer but also by electron transfer. Water ions can neutralize charge through screening or redistribution of charges on an area bigger than the actual contact area. Also, like other adsorbents, water ions change the electronic surface structure of the host insulator. Table 3 contains the experimentally determined work functions of selected minerals in dry and humid air [21].

Table 3 Work function for different minerals in dry and humid air. From [21]

Hydroxide adsorption model: Based on Diaz’s considerations [91], their own works and extended literature analysis, McCarty et al. [55] proposed the hydroxide ion transfer mechanism (Fig. 11) which explains contact charging of a non-ionic insulator with a water layer on its surface. The model is based on the observation that hydroxide ions (OH^–) from the water preferentially accumulate in the immobile Stern layer, leaving protons (H⁺) in the solution. It is important to mention that the tendency to accumulate OH^– ions at the interface, although experimentally observed, is not well understood.

Fig. 11

Hydroxide adsorption model. a Before contact OH^– ions preferentially accumulate on the insulator surface, whereas H⁺ ions remains in the solvent. b Due to contact, a water bridge is formed and OH^– ions are collected mostly on the surface with higher chemical affinity. c Separation results in two oppositely charged surfaces. From [55]

During contact, when the water bridge is formed, hydroxide ions redistribute and stabilize on the insulator surface with the greater chemical affinity, whereas H⁺ ions remain evenly spread in the solution. Finally, when surfaces are separated, the material with more hydroxide ions acquires a negative charge. And oppositely, the material with lesser hydroxide ions on the surface shows a positive total charge, since protons predominate. Additionally, other ions – present in the water layer – can also contribute to the proposed process, which makes final results difficult to predict.

However, by simple analogy, this model can be applied to explain the successful triboelectrostatic separation of different minerals functionalized by the same additives (e.g. conditioning of salts increases the efficiency of the triboelectrostatic separation [1, 2]).

Bipolar tribocharging model: An ion transport model involving frictional forces, proposed by Knorr [64], is based on two assumptions. Firstly, the hydroxide ions are more strongly bonded to the insulator surface than the protons. Secondly, the charge separation is driven by the rubbing forces as suggested by the strong dependence of tribocharging results on the rubbing load. Interestingly, based on observations, the spontaneous dissociation of bulk water is actually insufficient to provide a high enough amount of OH^– ions for the process. However, the dissociation rate might be significantly enhanced in the presence of a surface. When a capillary bridge is formed, the separation of water ions occurs by preferential dragging of protons in front of the moving asperity of one of the surfaces in contact with the second. The hydroxide ions underneath the asperity may be squeezed into the uppermost layers of the surface or into abraded particles. As a result, bipolarly charged surface is obtained; the positively charged area is created by accumulation of protons, and the negatively charged by depletion of protons.

Knorr [64] also suggested that the contact path of the asperity is much shorter than the total path of rubbing. This can explain the differently charged areas within the charging surface. Moreover, the roughness of the surfaces and the shape of the rubbing asperity have an impact on the charging characteristics. Unfortunately, the bipolar tribocharging model does not elucidate different values of net contact charging acquired by different materials.

3.1.3 Mass Transport

Mass transport as a mechanism of charging is similar to the processes in ion transport. The main difference lies in the type of the charge carriers. Unlike in the case of ion transport where charging occurs by the exchange of ionized surface adsorbates, here, surface atoms of one body are transferred onto the surface of the copartner body due to contact.

Experiments by Baytekin et al. [92] showed that material transfer depends on the mechanical properties of the materials, such as hardness and cohesive energy. Harder materials remove pieces of a softer surface, and materials with higher cohesive energy are less susceptible to having pieces ripped off. Also, the roughness of the material’s surface can influence material transfer. Rough and smooth samples of the same material can vary in their charging behavior [60]. A rough surface of a hard material is more effective at tearing (abrading) another surface than a smooth surface of the same material. In some cases, exchange of mass can be so strong that the initial properties of materials change dramatically up to the point of emulating charging behavior of the counterpart materials [92, 93]. This is an inherent feature of charging by mass transport. Surprisingly, Baytekin et al. [92] report exchange of atoms in both directions. After bringing polydimethylsiloxane (PDMS) into contact with polytetrafluoroethylene (PTFE), fluorine atoms were found on the PDMS surface whereas silicon and oxide atoms where detected on PTFE.

Moreover, material transfer strongly depends on the mode of contact, whereby normal and shear contact forces differ in their effect from each other [94]. Recent results [92, 93] indicate that material transfer is more significant in some types of contact electrification. In this concept, authors hypothesized that mass transport is supported by the presence of air or water molecules on the insulator surface. These adsorbents cause local heterolysis of the surface material. This is the cleavage of chemical bonds of a neutral molecule which generates a cation and an anion, i.e. or . The created ions are weakly bound and mass-charge transport can occur due to contact with other objects.

Moreover, Lacks [94] suggested that the very contact leads to material transfer which causes surface contamination that can never be avoided in contact charging experiments. However, it is difficult to establish whether this mass transfer is the primary cause of the charge separation or simply a side effect.

Lowell and Rose-Innes [60] argue that charge transfer occurs due to electron transport and ions present on the surface. Material exchange during contact only influences the electronic structure of the insulator and therefore enhances or reduces the amount of electrons which can be available during triboelectrification.

Finally, based on density functional theory (DTF) calculations for polymeric materials, Sakaguchi et al. [95] propose that charge transfer is simply a combination of electron, ion and mass transport. The frictional contact between two polymeric materials induces macroscopic and microscopic fracture of material (mass transport). This results in the creation of mechano ions (ion transport) which change the energetic structure of the materials in contact and thus facilitate electron transport.

Mosaic charge model – ion/mass transport: The mosaic charge model [92] describes the evolution of a net charge on insulating surfaces due to a light contact. Charging manifests itself as a random network (“mosaic”) of nanoscopic regions with opposite charges (positive and negative polarity). The mosaic can accommodate a significant amount of charge per unit area, but the total charge on the electrified surface remains relatively low due to the compensation between charged regions of different polarities. Moreover, the charging process is accompanied by changes in the surface composition. Therefore, contact charging properties can be derived from the chemical and micromechanical properties at and near the involved surfaces. Furthermore, material transport can occur during contact and can even play a role in the charging process.

In Fig. 12a, a schematic of the charging process according to the mosaic charging model is presented. Due to the light contact (touching), a mosaic charge structure is created on the surface of two neutral insulators with alternating positive and negative regions within the contact area. Kelvin probe force microscopy (KPFM) [96] measurements (Fig. 12b) reveal two characteristic length scales of the mosaic structure that can be distinguished: (a) bigger regions with diameters of several hundreds of nanometers, and (b) smaller regions, inside bigger ones, with a diameter of tens of nanometers.

Fig. 12

a Scheme of the mosaic charge model. Upon contact charging, the regions with different charge polarities are developed on the contact area. b A set of typical KPFM scans of surface potential of PDMS (A) before and (B, C) after contact. The map in (B), corresponds to PDMS surface potential after charging PDMS against PDMS, and in (C), to PDMS surface potential after PDMS against PC contact, featuring a mosaic of (+) and (–) regions. From [92]

In summary, as shown above, there is no consensus on the tribocharging mechanism. However, it is obvious that the insulator charging behavior is determined by the surface properties of the materials in contact. And also, the complex charging behavior indicates that more than one mechanism is active. (Nonetheless, creation of a tribocharging model post factum, i.e. based on experimental observations, does not guarantee that a universal model, properly applicable to industrial applications, can ever be built.)

3.2 Contact of Two Bodies

3.2.1 Non-frictional and Frictional Contact

Depending on the behavior of the charging materials, a contact which causes charging is categorized as (light) touching, rubbing, rolling, sliding, bouncing, or impact contact. Generally, contacts can be divided into two types, i.e. non-frictional and frictional. In the case of non-frictional contact, the contact force is purely normal to the contact interface. On the contrary, in frictional contacts, in addition to the normal force, lateral shear and frictional forces also act. Apart from the non-frictional contact of two smooth surfaces, frictional contact is a highly non-equilibrium situation [97].

Also, other distinctions for the contact can be made, as follow:

• contact without mechanical deformation vs. contact with elastic or plastic deformation,

• contact of smooth surfaces vs. multiple asperity contact.

Hertzian contact: Hertzian contact [98, 99] is the classical model to describe the contact of two solids. The Hertzian contact model defines a static, point or linear, and non-frictional contact between two homogenous, smooth bodies at rest and in equilibrium [99]. Rolling and sliding can also be considered as a sequence of consecutive static point contacts (but not in equilibrium). In Fig. 13, stresses which appear during a Hertzian contact of two bodies at a smooth interface are illustrated.

Fig. 13

Stresses during Hertzian contact: a static and b sliding; σ₁, σ₃ are the main stresses, p is the hydrostatic pressure, k – the shear yield stress of the material, μ – the coefficient of friction, q – the stress normal to the interface or compressive stress due to load, ϕ – the angle by which the principal planes are rotated from the corresponding zero friction positions to balance the frictional stress. From [99]

Under a static load and without a relative movement between the bodies, shearing does not occur. If the contact load is sufficiently high, i.e. in the elastic deformation regime, the material slips along the line of action of maximum shear stress, which is at 45° to the plane on which the shear stress is zero (the principal plane). Further increase in the load leads to plastic deformation [99] under the surface of the material. Interestingly, the maximum shear stress also occurs at the same depth as the maximum depth of the plastic deformation for a given load and this value is related to the contact area (the Hertzian stress field – Fig. 14a). In a circular static contact, for instance, the maximum shear stress occurs at a depth of approximately 0.6 times the radius of the contact area [99]. This may have implications for tribocharging mechanisms, in terms of an active region of charging which comprises of the contact area at the surface and the “active depth” of contact.

Fig. 14

Subsurface stress field for a static contact of two cylinders, and b sliding of a cylinder on a plane; b is the half width of the contact area. From [103]

For rolling or sliding, additional shear stress acts at the contact interface due to the frictional forces. Moreover, the contact area increases during frictional contacts as compared to static contacts and the additional shear modifies the Hertzian stress field (Fig. 14b). This can be the origin of the frequently observed higher tribocharging efficiency of frictional contacts compared to non-frictional contacts.

3.2.2 Mechanical Deformation Due to Contact

Mechanical deformation may occur under compressive stresses, caused by the contact load, and result in a rearrangement of the object atoms [100]. The interlayer spacing of the atoms are reduced along the direction of the contact load and expanded in the other directions. Changing the lattice parameters of the crystal unit cell alters the electronic properties of the deformed area of the object, such as band gap, work function and surface conductance, etc. Thus, the magnitude of the transferred charge may increase with deformation, as it was shown by Zhang and Shao [101] for metals. Their calculations based on density functional theory (DFT) indicate that the crystal deformation causes an increase in the concentration of nearly free electrons and a decrease in the energy barrier for the charge transfer. Thus, mechanical deformation promotes electron transfer during contact. Moreover, according to Zhang and Shao [101], the “classical” model of metal tribocharging based on work function differences can only be applied to very light contacts (contact without deformation).

It seems that the differences in tribocharging with respect to elastic and plastic contact deformation can just be attributed to the number of the introduced structural changes in the material and the durability of these changes. It will also be interesting to compare the tribocharging abilities of textured and undeformed materials.

3.2.3 Multi-asperity Contact

Surface roughness limits the contact between bodies to small areas of true contact between the highest spots of the surfaces – a multi-asperity contact. There are several differences between the contacts through asperities and the contact of flat surfaces. Firstly, the contact path of the asperity may be much shorter than the total path of rubbing [64]. Thus, the true contact area may be very different from the macroscopic contact area. Secondly, the contact pressure is much higher than that calculated by simple division of the contact load by the total contact area, which can cause stronger deformation of the asperities (flattening) in softer material than expected [77, 99]. Thirdly, the electric field is enhanced at the asperities. Thus, a stronger charging might occur as described above [101]. Usually, after an initial plastic deformation, the asperities keep their shape. Therefore, the contact between them occurs mostly in an elastic regime [99].

The local contact pressure between asperities which are constantly coming in and out of contact during shearing can vary significantly. According to Urbakh [97], the value fluctuates between 1 Pa and 1 GPa within microseconds and depends only [99] on the Young’s modulus of the materials and the asperity geometry.

There are several models describing multi-asperity contacts based on both statistical methods and fractal geometry. An overview is given in [99].

3.2.4 Friction, Adhesion and Wear

Friction, adhesion and wear are strongly correlated with each other. Wear can be considered as mass transport and will not be taken into account here. However, local adhesion can be a reason for stick-and-slip contact of two bodies in relative motion [97]. Fig. 15 shows schematically areas of local adhesion during the contact of two rough surfaces.

Fig. 15

Schematic of local adhesion during contact of two rough bodies. From [99]

In the stick–slip motion, adhering areas are successively formed and broken, which is the reason for the discontinuous movement of two bodies in frictional contact. Stick–slip processes are observed for even very low friction forces [99] and a general relation between the driving velocity and the height of stick–slip spikes (the frequency and the occurrence time) was found [97].

During contact, adhesion of two dissimilar materials in dry atmosphere is much higher than the adhesion of similar materials. A change of humidity can modify the interaction of the surfaces. This is due to the formation of a water layer which modifies the adhesion and friction. Furthermore, the shear stress decreases dramatically with increasing humidity [102]. This alteration in the mechanics of contact can be, besides increasing the number of mobile ions on the surface, another reason for the different tribocharging behavior observed in the presence of a water layer on the surface.

The contact theories developed by Johnson, Kendall, and Roberts (JKR theory) and Derjaguin, Muller, and Toporov (DMT theory) adapt the Hertzian theory by including adhesive forces and elastic deformation which occur during contact between two smooth surfaces (after [102]). JKR theory is usually applied to high adhesion and large radii of contact, whereas DMT theory is used to describe systems with low adhesion and small radii of contact. None of the theories take into account the long-range electrostatic interactions which occur during contact electrification [102].

Friction, defined as the dissipation of energy between sliding bodies, obeys two empirical rules: There is proportionality between the maximum tangential force and the normal force and the frictional forces do not depend on the contact area and the sliding speed [99].

3.2.5 Differences Between Static and Sliding (Dynamic) Contacts

It is believed that the fundamental differences in structure and physical processes occur for static and sliding contacts [99].

A static contact between rough surfaces can be seen as a random distribution of point contacts. For sliding contacts, contact areas are larger and less numerous (Fig. 16). If surfaces are in motion, the distance between individual contact points is larger than in the static contact. Only the larger asperities survive mechanically during sliding and additionally their areas in contact increase due to the movement [99]. Therefore, despite of the same total load and number of asperities, the local contact pressure for a single asperity can differ between static and sliding contacts. Thus static and sliding contacts can behave quite differently.

Fig. 16

A comparison between a static contact and b sliding. From [99]

The latter considerations show that the final result of tribocharging does not only depend on the electronic structure of the materials and the presence of ions on the surfaces, but also depends on surface roughness and mechanical properties of the materials in contact. Especially the contact through asperities is the most probable type of contact [103], since all surfaces exhibit some roughness.

3.3 Further Considerations

A collection of factors which have an impact on triboelectrification has already been listed in Table 1. Those factors involve a set of basic physical and chemical material properties and the influence of environmental conditions. The most important factors are described in more detail below.

3.3.1 Influence of Pretreatment – Surface Modification

Since surface impurities or defects in the crystal lattice influence the electronic surface states, any surface treatment can change the ability of a material for contact charging [104]. Fig. 17 illustrates the impact of different grinding procedures and radiation treatment on the position of the Fermi level (effective work function) of calcite.

Fig. 17

Position of Fermi level as a function of temperature for calcite at different a grinding, and b X-ray irradiation (wavelength λ was 2.29 Å) conditions. From [104]

In a mill the mineral grains are continuously crushed and nascent and highly reactive surfaces are exposed to the ambient grinding atmosphere. The effect of wet or dry comminution on the calcite Fermi level is shown in Fig. 17a. Calcite behaves as an n‑type semiconductor when wet-ground, and as a p‑type when dry-ground. Also X‑ray radiation (Fig. 17b) causes a shift in the Fermi level with respect to the natural mineral. Thus calcite turns from being an n‑type semiconductor in its natural mineral state to p‑type semiconductor after irradiation.

Additionally, Lindley and Rowson [105] report that comminution produces charges on the surface of the crystals both with and without cleavage planes. For example, on a quartz (the crystal without cleavage planes) surface a continuous array of charges exists. “A positive charge is linked with the electropositive atom (silicon) and a negative charge with the electronegative atom (oxygen) for each rupture site”. For materials with natural cleavage planes, each face opened by grinding or crushing can vary in the number of ions, which influences the surface charge. Also, performing comminution in moist air leads to adsorption of water molecules on the fracture surfaces. Those water molecules ionize and thus surface charging by ion transport and/or ion segregation can occur.

3.3.2 Discharging, Decay and Evolution of the Introduced Charge

In principle, the contact charging process can be divided into a charging and a discharging step [106]. First, during the contact, charge transfer takes place (charging). Thereupon, during separation, tunneling of electrons, field emission of electrons, and dielectric breakdown of the surrounding gas lead to charge recombination and partial discharge of the surface. Additionally, charged objects can be discharged during the next contact [107]. Finally, the charge remaining on the surface decays slowly. In the following, phenomena such as (i) dielectric breakdown of the gas environment, (ii) discharge during separation caused by the electric field created between charged surfaces, (iii) accumulation and saturation of the charges on the insulator surface by repetitive charging of the same area, and (iv) long-term charge decay on the insulator surface are described briefly.

Dielectric breakdown of the gas environments: The density of charge locally stored on the insulator surface is limited due to the dielectric breakdown in the atmosphere. Paschen’s law [108] defines the breakdown limit as the potential V between electrodes placed against each other under specific environmental conditions at which electric breakdown occurs (density of gas molecules, which depends on type of atmosphere, atmospheric pressure p and temperature, etc.) and is given by Eq. 6:

$$V=\, \frac{a\left (pd\right )}{\ln \left (pd\right )+b}$$

(6)

Here d is the distance between the electrodes and a, b are constants which depend on the atmosphere and the electrode material [109, 110].

Charge carriers are accelerated in the electric field between the electrodes. If the carriers gain sufficient kinetic energy to create further electrons and ions upon collision with gas molecules, the number of free charge carriers multiplies causing an avalanche ionization of the surrounding which is discharging the objects. The sharp rise in the breakdown voltage on the left side in Fig. 18 (red line) occurs as the electrode spacing is too small for ionization. (However, it is known that Paschen’s law fails at micrometer distances due to electron field emission, which results in the creation of modified Paschen’s curves [111, 112].) On the right side the slow rise in breakdown voltage with increasing electrode distance (and/or higher pressures) arises because charge carriers cannot gain enough energy between generation and collision to cause impact ionization. Thus high potentials are needed for breakdown [110].

Fig. 18

Schematic of the separation discharge process. Paschen’s breakdown curve depends on electric field and distance between two electrodes or charged objects under specific environmental conditions. After [109]

For breakdown at the microscale [112] field emission might serve as a significant source of free electrons and causes discharging and charge recombination between charged bodies.

Matsuyama and Yamamoto [106, 109] proposed that the limitation of contact charging is caused due to discharging during separation (Fig. 18). After contact the potential between highly charged particles increases with increasing distance until it reaches the left side of the minimum in the Paschen’s discharge curve (beginning point of charge relaxation). This discharge lowers the charge of the particles to the level which corresponds to the terminal point of charge relaxation on the Paschen’s curve.

Discharge during separation of charged bodies: Discharge between contact charged bodies is often observed as they are separated [107, 109, 113] and is associated with both tunneling back-flow of charge carriers [55, 60] and breakdown in the atmosphere [55, 113] due to the electric field existing between charged bodies. In the separation process, the potential difference between the charged surfaces increases with increasing distance between them to eventually reach a value for the atmospheric breakdown limit. However, before breakdown is reached, charge back-flow can occur by tunneling. Back-flow by tunneling is a quantum mechanical effect and is practically restricted to small distances between surfaces (less than a few nanometers).

Charge accumulation and saturation by repetitive charging: First Matsuyama and Yamamoto [109] and then Ireland [113] identified the experimentally observed charge accumulation and saturation effects to be a result of separation discharging. They distinguished two possible cases (Fig. 19). In the first case the saturation is reached after a certain number of contacts (discharge limit). After that the discharge during every next separation event limits further building up of charge (Fig. 19a). In the second case single discharging events reduce the formerly accumulated charge to such an extent that several contact – separation cycles are necessary to reach the discharge limit again (Fig. 19b). In this case, the charge oscillates between a maximum value, the discharge limit, and a minimum value, the extinction limit.

Fig. 19

Separation discharge scheme: a after reaching the discharge limit, discharge occurs during every separation compensating an increase of contact charge [109] (experimentally observed as a saturation), b charge builds up over several contact – separation cycles before discharge occurs [113] (experimentally observed as dropping and building up charge due to repetitive contact with the same area)

Long-term decay of charged insulators: A comparison of the temporal decay of contact charge on a polymer surface in humid air (relative humidity 40 % r.H.) and in water-free environment (in paraffin oil) [114] showed that the decay kinetics is of first-order, and that the corresponding charge decay rates vary with environmental conditions (10^-3 s^-1 and 10^-2 s^-1 in air and oil, respectively). This suggests that the charge decay is associated with a different stability of the introduced charges under humid air and paraffin oil. Another model assumes impingement of the surrounding molecules onto the charged surface as a way of charge neutralization. The probability of collisions with the liquid molecules is much higher than with the molecules/ions of the air (about 3 x 10²¹ molecules per cm³ in paraffin oil and 2 x 10¹⁹ in air). Thus, the charge can be transferred more readily to the liquid. The experimentally observed complete discharge of a moving sample within 1 s supports the later model.

3.3.3 Bipolar Charge Distribution of Granular Materials with Different Grain Size

In a polydisperse powder of the same material, the transferred charge depends on the particle size [115, 116]. After contact of two particles of different size (but same material), it is experimentally observed that the smaller will be charged negatively whereas the bigger one exhibits a positive net charge.

Several contrary ideas have been discussed in literature to explain this phenomenon [46, 64, 80, 115, 117]. Inculet et al. [115] imply that there are differences in the effective work functions between fine and coarse particles, which can be caused by differences in their surface energy, microscopic surface structure and/or selective adsorption on the surface. Moreover, the work function is generally assumed to be inversely proportional to the particle size [118, 119]. Thus, more energy is required to extract an electron from the surface of a small particle than from a larger one. Optionally, as a result of repetitive fracturing or grinding, the fine particles are usually more subjected to mechanical treatment than the coarser ones. This yields differences in shape and surface roughness, which also can be related to changes of the effective work function. Finally, adsorbents or additives have usually higher surface densities on finer particles as the surface energy increases with decreasing particle size [115]. Therefore, adsorbed air ions, for instance, can change the value of the effective work function of the finer particles more strongly compared to the coarser ones.

Asymmetrical contact between particles of different size is also considered as origin of bipolar charge distribution. Asymmetrical contact can either mean the asymmetrical transfer of electrons [46, 117] or size dependent differences in the number of repeated contacts [80].

The larger particles have a larger number of electrons to transfer, so compared to the smaller particles they are more likely to lose electrons as multiple collisions occur. Therefore they charge positively. During initial collisions both small and large particles drop similar amounts of electrons; however, lost electrons remain a larger part of all available electrons for smaller particles. Thus the loss of electrons at further collisions is reduced for smaller particles as compared to larger particles, which effects in final diversification of charge between larger positively and smaller negatively charged particles [46]. A model of asymmetrical in-transferred electrons for a granular system of identical insulators was proposed by Kok and Lacks [46]. It was further extended by Zheng et al. [117] to account for the influence of a water layer.

Contrarily, Gu et al. [80] suggest that the difference in charging occurs as the probability of repeated collisions at the same contact area is higher for finer particles. This is owing to the difference in the surface areas, whereby the same part of the small particle surface is brought into contact more often than that of a bigger particle. As a result of intensive friction, the temperature of finer grains increases faster, which in turn has an influence on the concentration of OH^– and H⁺ ions. Hydroxide ions are trapped on the surface of the finer particles, while hydroxyl ions transfer due to contact onto the surface of coarser particles.

Finally, both the coexistence of nano- and micro-bipolar areas on flat charged insulators [64, 120, 121], and the opposite charging of small and large particles can be explained by the bipolar tribocharging model [64]. The fine grain in contact with the coarse grain acts as the appendix which collects the hydroxide ions and leaves the dragged protons on the surface of the large object.

3.3.4 Other Influences

Electric permittivity: It should be mentioned that in earlier publications differences in the electric permittivity were also discussed as a driving force of triboelectrification. However, due to large scattering of the measured values of electric permittivity [20], a definitive statement on the influence of permittivity is still missing.

Saturation effect: The well-known saturation effect, originally defined as limited accumulation of charge on the surface [47], can also be caused by:

• gradual charging of different parts of the particle surface with increasing number of contacts [122],

• nano-mass transport when each contact causes exchange of atoms between the two bodies, up to a certain level of mass transport when the top layer of the surface shows different electric properties compared to the rest of the body [92, 93],

• complicated interaction between neutral and partially charged particles, which can be described as fluctuation of an external electric field [123],

• discharging during separation (as already mentioned earlier).

Surface behavior under mechanical stress: Another important phenomenon which can impact on tribocharging results, is the mechanoemission of ions, low-energy electrons, etc. (Fig. 20). Electrons with energies typically between 1 and 4 eV are emitted from the insulating surface by chemical bond scission (during contact) and rapidly react with the surface material to form free radicals and ions [124]. Thus, the rubbed surface is highly reactive. With higher contact loads (∼1 N or more ) a higher degree of surface damage will occur and thus the quantity of emitted charge carriers increases [125]. Nakayama and Martin [100] even observed the creation of a triboplasma due to the sliding of a diamond sphere with a radius of 0.3 mm on a sapphire disc. The normal force was 0.9 N, while the sliding velocity was 30 cm/s at 30–40 % r.H., which are conditions that can essentially occur in technical separators. The existence of a triboplasma is accompanied by an increasing chemical reactivity of the surface. An example of a dry tribochemical reaction is the creation of thin lamellar graphitic structures on silicon carbide surfaces sliding against each other in ultra-high vacuum [100]. The authors suggest that the top layers of the silicon carbide transforms into graphite due to friction induced evaporation of silicon atoms.

Fig. 20

Schematic of triboemission [125], which involves emission of particles (gas atoms, surface molecules, molecular clusters, ions, radicals, electrons) and energy (electromagnetic radiation, magnetic and electric field, heat, sound and vibrations) [124]

Mechanoemission implies that ion, electron and mass transport can occur during contact. Moreover, mechanical forces intensify the dissociation of adsorbed water. According to simulations, adsorbed water may enhance the heterolytic mechanical breaking of chemical bonds at the surface [64]. The rapid point increase of the temperature due to rubbing (flash temperature) [124] might also play a role in the resulting tribocharge. Therefore mechanochemistry and especially tribochemistry should also be considered for a general description of tribocharging.

4 Experiments of Triboelectrification

4.1 Triboelectrification at the Macroscale

Knowledge of the triboelectrostatic separation behavior of a particular system of insulating powders/particles is derived from empirical studies, mostly based on trial-and-error experiments. The lack of a comprehensive model is attributed to the complexity of the tribocharging process and the variety of basic phenomena which facilitate triboelectrostatic separation.

Triboelectric series: The first triboelectric series was determined experimentally by Shaw in 1917 (after [126]). He rubbed various materials together and used an electroscope to measure the charge on their surfaces. The empirical “triboelectric series” is simply a row which arranges materials according to their ability to gain/acquire a negative or a positive charge due to contact. And thus it helps to predict charging behavior of materials since the relative position of any two materials in the series determines the direction of charge transfer when these materials come into contact. However, the concept of the triboelectric series, although technically useful, is challenged by the existence of a cyclic triboelectric series [55]. Additionally, the order in the triboelectric series is not always reproducible and there exist several variants of the triboelectric series with different material orderings, since many additional factors influence the triboelectrification process (as shown earlier).

Charging of a single particle: The tribocharging behavior of a single particle is the basis for understanding the charging of powders [54]. For this purpose, investigations of the changes in the surface charge for single particles caused by a collision with a still target were performed. Several studies have been reported, a few among the newest can be found in [61, 78, 127, 128]. A particle is accelerated, which then collides with a target in a collection chamber. The charge on the particle is measured before and after impact using a Faraday cage.

Watanabe et al. [127] showed that the impact charge increases with the impact velocity. Additionally, Ema et al. [128] studied the influence of the impact angle on the triboelectric charging upon the contact of a particle stream with rotating or inclined target system. The results suggest that the contact charge depends on the effective contact area. Also the results presented in [127] confirm that increasing the contact area and the impact angle increases the impact charge. Moreover, an initial charge (before contact) of the particle and its distribution on the particle surface influences the final charge after contact [61].

Repetitive contact: Another important group of experiments focuses on the influence of repetitive contacts, which are expected to occur typically during contact charging of powders [49, 65, 78, 93].

Matsusaka et al. [78], for instance, measured the influence of repetitive contacts of a rubber sphere with a metal plate. The results indicate an accumulation – saturation mechanism. They also showed that the impact velocity determines the contact area which in turn can influence the resulting charge due to contact repetition. Ciccu et al. [49] investigated the accumulation – saturation process for single grains of different minerals (coal, limestone) by changing time and type of contact with the steel walls of a tribocharging unit. No simple relationship of the charging as a function of energy added to the system was observed. For a given experimental time, the introduced charge was higher in the case of lighter contacts (sliding vs. rubbing). The authors related this observation mainly to the short time of experiments (maximum 160 s), which showed only the early stage of accumulation and did not allow to reach saturation. Kwetkus and Sattler [65] studied repetitive charging of different systems such as particles of quartz, calcite, graphite particles, teflon, etc. with a metal plate (aluminum, nickel, copper, gold) in vacuum. These systems showed accumulation and saturation effects depending on the number of contacts. However, further investigations revealed that the sign of the charge can change with increasing number of contacts. For example, when calcite particles are brought into contact with a copper plate, initially they are charged negatively, and after about 25 charging cycles they become positively charged. Also quartz particles in contact with a copper plate charge negatively during the first 150 charging cycles and beyond that showed a positive total surface charge. As shown by X‑ray fluorescence analysis, this behavior can be explained by material transfer since copper, a soft material, is abraded due to contact with the relatively hard calcite and quartz particles. Similar charge reversal due to material transport was recently reported by Baytekin et al. [93] for contact between two insulators in air. Teflon beads were rolled in a polystyrene dish. After about a minute, the Teflon beads charged negatively, however, if rolling was continued for more than a few minutes, the Teflon beads charged positively. Independently, Raman spectroscopy and X‑ray photoelectron spectroscopy confirmed the mass transfer.

Charging of powders: There are at least three main types of methods used to measure tribocharging of powders. The first one involves using a real or a laboratory triboelectrostatic free-fall separation system with many collecting bins. Mass and chemical analysis of the product from each collecting bin combined with a selection of the process parameters allows finding the best separation procedure for a chosen mineral system. Sometimes, the collecting bins are Faraday cups which measure the total charge for each product, and thus the specific charge can be determined. However, these measurements have to be repeated for each powder composition and each charging – separation set-up; therefore they are time consuming and are actually more useful for analyzing the separation equipment than for the characterization of the tribocharging behavior of the powders. Exemplary applications of this type of method are presented in [8, 32, 52, 129].

The second technique used to characterize the tribocharging of particles is to measure the specific charge of powders of only one material with a Faraday cage. Charging is realized in different triboelectrostatic charging units, for instance by sliding particles on a plate [48], on a rotating drum [28, 42, 57], or a cyclone [59], etc. A prime disadvantage of the latter method lies in the weak predicting value of the behavior of powder mixtures. It is caused by the fact that charging occurs not only due to contact with the charger walls but also due to contact between the particles.

The third group of methods is dedicated to determine the charge distribution in powders [54]. Tribocharged particles are dragged by a laminar air flow between parallel electrodes of opposite electrical potential. The position where they are deposited on the electrode walls indicates the charge distribution and the amount of charge in the powder. An interesting review of further measurement techniques for powder systems can be found in.[54].

4.2 Triboelectrification by Atomic Force Microscopy

Measuring triboelectrification charge using classic macroscale methods is not appropriate to explore single charging events since they just deliver average values over large areas. As an alternative, measuring at micro- and nanoscale can be applied. The main advantages of studying triboelectrification phenomena at the microscale are: (i) information from very small areas is provided, (ii) the system can be simplified to the maximum extent, thus giving scope for investigating influences separately. These features present an opportunity to describe complex tribocharging phenomena and, finally, to build a comprehensive model of triboelectrification.

The development of AFM by Binning and Quate [130], followed by the introduction of a vibrating cantilever technique (non-contact mode) with the light-lever read out technique by Martin et al. [131] and finally the elaboration of KPFM by Nonnenmacher et al. [96] allow to study electrostatic interactions on very small scale and thus triboelectrification phenomena at the microscale. Especially over the recent few years, several publications [120, 121, 132–143] dealt with the local triboelectrification on thin insulating layers. Hence there is a need for a review article solely dedicated to this topic.

5 Summary

In this article triboelectrification phenomena that occur during the industrially applied triboelectrostatic separation have been briefly reviewed. It has been shown that for good separation results a precise adjustment of a number of system parameters is necessary. Mechanic and electrical properties of the powder have to be considered as well as the properties of the charging unit, the type of separator and environmental conditions.

Special attention has been payed to the contact charging of solids, because the controlled generation and conservation of charge on the powder particles is the most important factor for a successful separation.

We hope that we could show that contact charging and triboelectrification is a very complex topic that so far is not well understood. In order to push forward the technological application of the conceptually cheap and environmentally friendly method, a deeper understanding of the basic physical mechanisms is inevitable. Therefore, research on the basic processes involved in tribocharging has to be intensified in the future.