Statistical inference on quantiles of two independent populations under uncertainty

Abstract

Statistical inference is the process of drawing conclusions about underlying population(s) using sample data to either confirm or falsify hypotheses. However, the complexity of real-life problems often makes the underlying statistical models inadequate, as information is often imprecise in many respects. To address this common problem, some papers have been published on modifications and extensions of test concepts by employing tools of fuzzy statistics. In this paper, we present a non-parametric test for the difference between quantiles of two independent populations based on fuzzy random variables. For this purpose, we consider the fuzzy quantile function and its estimation based on $\alpha$-values of fuzzy random variables. We then provide a fuzzy test based on the fuzzy empirical distribution function for the difference of fuzzy order statistics from these independent populations. We also suggest a specific degree-based criterion to compare the fuzzy test statistics at a specific significance level to decide whether the underlying fuzzy null hypothesis can be rejected or not. The effectiveness of the proposed two-sample test on quantiles is investigated via numerical examples.

1 Introduction

Hypothesis testing regarding an assumption about the probability distribution of one random variable or a set of random variables is a main field of statistical inference. Those tests demand a well-defined modeling of the tested hypothesis, i.e., precisely stated requirements in relation to the distribution of the underlying random variable(s) (Chukhrova and Johannssen 2020a). In many practical applications, it is necessary to compare two independent populations concerning their central tendencies or other distribution-related criteria (O’Gorman 2004; Shi and Tao 2008; Taff 2018). With the aim to conclude whether the difference of interest between both these populations is significant or not, techniques of statistical inference are employed. Considering two-sample hypothesis tests, the populations are usually compared in terms of their central tendency measures (like the means) to conclude if there are significant differences in these populations. Although comparing two populations concerning their means is a common problem, there are situations where one needs to compare other characteristics of the populations such as quantiles (see, e.g., Hutson 2009; Viertl 2006; Kosorok 1999). When using quantiles (e.g., quartiles) instead of the means, the test decision is based on robust location parameters and outliers have no impact on the test decision (Chukhrova and Johannssen 2021b).

Further, censoring or truncation can complicate estimation of entire distribution functions and an examination of a collection of quantiles is a reasonable alternative (Gözde and Özdemir 2018). In addition, in many real-life applications (like psychology, biology, medicine, economics), the quantiles of the underlying characteristic variables are important boundaries for decision-making (Wang and Hettmansperger 1990; Farrell et al. 1997). For instance, the determination of the differences in the tails (by employing quantiles) is often of interest in such cases. But, the main advantage of non-parametric testing on quantiles compared to common tests such as Student’s t-test is that there is no need for additional assumptions related to homoscedasticity or normality of two population distributions, which are often not fulfilled in practical applications (for instance, when the distributions are asymmetric or irregularly shaped). That is, the results of Student’s t-test can be misleading when the assumptions are not satisfied. For these reasons, several non-parametric two-sample quantile-based tests have been developed (Heinzl and Mittlboeck 2017; Hutson 2009).

However, in situations, where point- or interval-valued formulations of hypotheses appear too rigid for real-life problems, the above limitations make the practitioner do decision procedures in a non-reasonable way. In this case, common statistical inference techniques are inappropriate for testing a hypothesis. Moreover, there are many situations in practical applications where the observations cannot be measured as crisp quantities, because information is often imprecise, incomplete, linguistic, noisy, qualitative, or vague (Chukhrova and Johannssen 2019). In contrast, fuzzy hypothesis testing provides a more realistic framework for such hypothesis testing problems, as fuzzy set theory is a natural tool for modeling and analyzing subjective and imprecise concepts. A fuzzy hypothesis allows for a more appropriate treatment of the unknown parameter(s), i.e., instead of specifying its (their) hypothesized values over a crisp interval, it allows, for example, specifying a smooth transition from “preferred” to “non-preferred” or from “possible” to “impossible” values in terms of an appropriate modeled membership function (Chukhrova and Johannssen 2020a). Furthermore, hypothesis testing in fuzzy environments facilitates to add available expert knowledge to the test procedure, taking into consideration the economic context or possibilistic aspects. Therefore, fuzzy modeling approaches provide appropriate techniques for dealing with those various types of uncertain information (Chukhrova and Johannssen 2021a).

Through the years, various techniques have been developed for testing hypotheses based on fuzzy information. Such methods can be decomposed in parametric tests (Arnold 1998; Filzmoser and Viertl 2004; Chen and Chang 2020; Haktanir and Kahraman 2019; Hesamian and Akbari 2021; Hryniewicz 2006b; Mylonas and Papadopoulos 2021; Parchami 2020; Rodríguez et al. 2006; Viertl 2006; Wu 2005; Akbari and Rezaei 2010; Chukhrova and Johannssen 2020a, b, c; Hesamian and Shams 2016; Montenegro et al. 2004; Kahraman et al. 2004) and non-parametric tests (Chukhrova and Johannssen 2021b, c, 2022; Grzegorzewski 2000; Denoeux et al. 2005; Gil et al. 2006; Grzegorzewski 2004, 2009, 2020; Hesamian and Chachi 2015; Hesamian and Taheri 2013; Hryniewicz 2006a; Lin et al. 2010; Hesamian and Taheri 2013; Kahraman et al. 2004). Further, Akbari and Rezaei (2010); Chukhrova and Johannssen (2020a, 2020b, 2020c, 2021b, 2021c, 2022, 2023); Denoeux et al. (2005); Filzmoser and Viertl (2004); Grzegorzewski (2000); Hesamian and Shams (2016); Hesamian and Taheri (2013); Hryniewicz (2006b); Montenegro et al. (2004); Rodríguez et al. (2006); Viertl (2006); Wu (2005); Kahraman et al. (2004) proposed one-sample tests, while Denoeux et al. (2005); Gajivaradhan and Parthiban (2015); Grzegorzewski (2005); Hesamian and Chachi (2015); Montenegro et al. (2001); Kahraman et al. (2004) discussed two-sample tests. Some of these approaches mainly rely on fuzzy data and exact hypotheses (Hesamian and Akbari 2021; Parchami 2020; Kahraman et al. 2004; Grzegorzewski 2000; Denoeux et al. 2005; Grzegorzewski 2004, 2009; Filzmoser and Viertl 2004; Chen and Chang 2020; Haktanir and Kahraman 2019; Hryniewicz 2006b; Mylonas and Papadopoulos 2021; Rodríguez et al. 2006; Viertl 2006; Akbari and Rezaei 2010; Chukhrova and Johannssen 2020a, b; Montenegro et al. 2004; Grzegorzewski 2020; Hryniewicz 2006a; Lin et al. 2010), fuzzy data and fuzzy hypotheses (Wu 2005; Hesamian and Shams 2016; Gil et al. 2006; Hesamian and Chachi 2015; Hesamian and Taheri 2013) or crisp data and fuzzy hypotheses (Arnold 1998; Chukhrova and Johannssen 2020a, b, c, 2021c). In addition, several studies rely on univariate hypothesis testing with parametric or non-parametric intuitionistic fuzzy information (Akbari and Hesamian 2019a, b; Hesamian and Akbari 2017; Zainali et al. 2014). For a comprehensive review on the topic of fuzzy hypothesis testing, we refer to Chukhrova and Johannssen (2021a).

Considering previous fuzzy non-parametric tests for the two-sample case, they essentially rely on comparing fuzzy medians. As comparing any quantiles of two populations is an important issue, it is necessary to develop a methodology to compare quantiles of two populations based on fuzzy data. In this study, therefore, we introduce a new idea of non-parametric testing for comparing fuzzy quantiles of two independent populations based on fuzzy random variables. Since the observed data are fuzzy quantities, it is a natural step to consider the components of the population such as distribution function, order statistics and quantile functions as fuzzy quantities as well. In this regard, we extend the concept of the fuzzy quantile function of fuzzy random variables and their empirical estimation based on fuzzy data. We also construct the respective hypotheses to compare fuzzy quantiles of the populations via ranking criteria and introduce a test statistic that employs the $\alpha$-cuts of fuzzy numbers. Then, a procedure for constructing a fuzzy test function to reject or not reject the underlying null hypothesis related to the comparison of fuzzy quantiles is presented. Therefore, besides testing on the medians of both populations, the introduced method can be applied for any fuzzy quantile functions of two populations related to, e.g., percentiles or deciles. For practical reasons, the proposed method is illustrated via some application examples.

The rest of this paper is organized as follows. Section 2 reviews essential concepts related to fuzzy numbers and fuzzy random variables. Section 3 introduces the notion of fuzzy quantiles and discusses their empirical estimation considering fuzzy random variables. In Sect. 4, the non-parametric hypothesis test for comparing fuzzy quantiles of two independent populations is developed. In Sect. 5, practical applications of the proposed test are illustrated. Finally, conclusions are provided in Sect. 6.

2 Preliminaries

This section reviews some necessary basic definitions of fuzzy numbers and fuzzy random variables.

2.1 Fuzzy sets and fuzzy numbers

A fuzzy set $\widetilde{A}$ on the real line $\mathbb {R}$ is defined by the membership function $\mu _{\widetilde{A}}:\mathbb {R}\rightarrow [0,1]$ (Lee 2005). The subset $\{x\in \mathbb {R} \mid \mu _{\widetilde{A}}(x)\ge \alpha \}$, $\alpha \in (0,1]$, is referred to as $\alpha$-cut of $\widetilde{A}$, i.e., $\widetilde{A}[\alpha ]$. The set $\widetilde{A}[0]=$ $\overline{\{x\in \mathbb {R}:\mu _{\widetilde{A}}(x)>0\}}$ is the support of $\widetilde{A}$, while $\overline{A}$ is the closure of A. The lower and upper bounds of $\widetilde{A}[\alpha ]$, $\alpha \in [0,1]$, are denoted by $\widetilde{A}^L[\alpha ]$ and $\widetilde{A}^U[\alpha ]$, respectively. Further, a fuzzy set $\widetilde{A}$ is a fuzzy number (FN) when $\widetilde{A}[\alpha ]$ is a non-empty, bounded interval in $\mathbb {R}$ for all $\alpha \in [0,1]$. As for the practical handling of FNs, they are often modeled via a functional parametric form called LR-FN $\widetilde{A} = (a; l_a, r_a)_{LR}$. The membership function of an LR-FN $\widetilde{A}$ is given by

$$\begin{aligned} \mu _{\widetilde{A}}(x)=\left\{ \begin{array}{lll} L\left( \dfrac{a-x}{l_a}\right) &{}\text { if}\quad &{} a-l_a\le x\le a,\\ R\left( \dfrac{x-a}{r_a}\right) &{}\text { if}\quad &{} a \le x\le a+r_a, \end{array} \right. \end{aligned}$$

where $l_a>0$ is the left spread, $r_a>0$ is the right spread, and L and R are reference functions defining the left and the right shapes of the FN, respectively, where $L,R:[0,1]\rightarrow [0,1]$ should satisfy the following conditions:

• 1. $L(1) = R(1) = 0$,

• 2. $L(0) =R(0) = 1$, and

• 3. L(x) and R(x) are continuous and monotone-decreasing functions on [0, 1].

The set of all LR-FNs is represented by $\mathcal {F}(\mathbb {R})$. Furthermore, the most commonly used (unimodal) LR-FNs (with $L(x)=R(x)=\max \{0,1-x\}$) are triangular FNs (TFNs). The membership function of a TFN, denoted by $\widetilde{A}=(a;l_a,r_a)_{T}$, is given by:

$$\begin{aligned} \mu _{\widetilde{A}}(x)=\left\{ \begin{array}{ll} \frac{x-(a-l_a)}{l_a} \quad &{}\text {if } a-l_a \le x \le a\\ \frac{a+r_a-x}{r_a} \quad &{}\text {if } a < x \le a+r_a\\ 0 \quad &{} \text {otherwise}.\\ \end{array} \right. \end{aligned}$$

Remark 1

(Hesamian and Shams 2016) For a given $\widetilde{A}\in \mathcal {F}(\mathbb {R})$, the mapping $\widetilde{A}_{\alpha }:[0,1]\rightarrow \mathbb {R}$ is called $\alpha$-cut of $\widetilde{A}$ defined by

$$\begin{aligned} \widetilde{A}_{\alpha }=\left\{ \begin{array}{ll} \widetilde{A}^L[2\alpha ] &{}\quad \text {if }\alpha \in [0,0.5],\\ \widetilde{A}^U[2(1-\alpha )] &{}\quad \text {if } \alpha \in , (0.5,1],\end{array}\right. \end{aligned}$$

where $\widetilde{A}^L[\alpha ]$ and $\widetilde{A}^U[\alpha ]$ denote the lower and upper limits of $\alpha$-cuts of $\widetilde{A}$, respectively. Then, it follows:

$$\begin{aligned} \widetilde{A}[\alpha ]=[\widetilde{A}^L[\alpha ],\widetilde{A}^U[\alpha ]]=[\widetilde{A}_{\alpha /2}, \widetilde{A}_{1-\alpha /2}]. \end{aligned}$$

For instance, $\alpha$-cuts of an LR-fuzzy number $\widetilde{A} = (a;l_a,r_a)_{LR}$ can be calculated as:

$$\begin{aligned} \widetilde{A}_{\alpha }=\left\{ \begin{array}{ll} a-l_aL^{-1}(2\alpha ) \qquad &{} \text {if }\alpha \in [0,0.5]\\ a+r_aR^{-1}(2(1-\alpha )) \qquad &{} \text {if }\alpha \in (0.5,1]. \end{array} \right. \end{aligned}$$

Specifically, if $\widetilde{A}=(a;l_a,r_a)_T$ is a TFN, then:

$$\begin{aligned} \widetilde{A}_{\alpha }=\left\{ \begin{array}{ll} (a-l_a)+2l_a\alpha \qquad &{} \text {if }\alpha \in [0,0.5]\\ a+r_a-2r_a(1-\alpha ) \qquad &{} \text {if }\alpha \in (0.5,1]. \end{array} \right. \end{aligned}$$

Remark 2

(Hesamian et al. 2019) Note that for all $\widetilde{A}, \widetilde{B}\in {{\mathcal {F}}}({\mathbb {R}})$, $\lambda \in {\mathbb {R}}$ and $\alpha \in [0,1]$, the following arithmetic operations on fuzzy numbers can be defined:

$$\begin{aligned} (\widetilde{A}\oplus \widetilde{B})_{\alpha }= & {} \widetilde{A}_{\alpha }+\widetilde{B}_{\alpha },\\ (\lambda \otimes \widetilde{A})_{\alpha }= & {} \left\{ \begin{array}{ll} \lambda \widetilde{A}_{\alpha } &{}\text{ if }\ ~~\lambda > 0,\\ 0&{}\text{ if }\ ~~\lambda =0, \\ \lambda \widetilde{A}_{1-\alpha }&{}\text{ if }\ ~~\lambda <0,\\ \end{array}\right. \end{aligned}$$

where $\oplus$ and $\otimes$ denote common arithmetic operators of fuzzy numbers.

Definition 1

(Yuan 1991) For two FNs $\widetilde{A}$ and $\widetilde{B}\in \mathcal {F}(\mathbb {R})$, let

$$\begin{aligned} \varDelta _{\widetilde{A}\widetilde{B}}=\int _{\{\alpha :\widetilde{A}_{\alpha }\ge \widetilde{B}_{\alpha }\}}(\widetilde{A}_{\alpha }-\widetilde{B}_{\alpha })d\alpha . \end{aligned}$$

The preference degree “$\widetilde{A}$ is larger than $\widetilde{B}$” is defined by:

$$\begin{aligned} P_d(\widetilde{A}\succ \widetilde{B})=\left\{ \begin{array}{ll} 0.5 &{} ~~~~~~~~~ \widetilde{A}=\widetilde{B}\\ \frac{\varDelta _{\widetilde{A}\widetilde{B}}}{\varDelta _{\widetilde{A}\widetilde{B}}+\varDelta _{\widetilde{B}\widetilde{A}}} &{} ~~~~~~~~~\widetilde{A}\ne \widetilde{B}.\\ \end{array} \right. \end{aligned}$$

Definition 2

For two FNs $\widetilde{A}$ and $\widetilde{B}$, it holds that:

• 1. $\widetilde{A}$ is larger than $\widetilde{B}$, denoted by $\widetilde{A}\succ _{P_d}\widetilde{B}$, if $P_d(\widetilde{A}\succ \widetilde{B})> 0.5$.

• 2. $\widetilde{A}$ is equivalent to $\widetilde{B}$, denoted by $\widetilde{A}\simeq _{P_d}\widetilde{B}$, if $P_d(\widetilde{A}\succ \widetilde{B})=P_d(\widetilde{B}\succ \widetilde{A})= 0.5$.

The preference criterion $P_d$ meets the following properties:

Proposition 1

Let $\widetilde{A}$, $\widetilde{B}$, $\widetilde{C}$ be three FNs in $\mathcal {F}(\mathbb {R})$. Then, it holds:

• (1) $P_d$ is reciprocal, i.e., $P_d(\widetilde{A}\succ \widetilde{B})=1-P_d(\widetilde{B}\succ \widetilde{A})$.

• (2) $P_d$ is reflexive, i.e., $\widetilde{A}\succ _{P_d}\widetilde{A}$.

• (3) $P_d$ is transitive, i.e., $\widetilde{A}\succ _{P_d}\widetilde{B}$ and $\widetilde{B}\succ _{P_d} \widetilde{C}$ imply $\widetilde{A}\succ _{P_d}\widetilde{C}$.

• (4) $P_d(\widetilde{A}\succeq \widetilde{B})=1$ if and only if $\widetilde{B}_{\alpha }\le \widetilde{A}_{\alpha }$ for all $\alpha \in [0,1]$.

Proof

See Yuan (1991). $\square$

Definition 3

(Hesamian and Akbari 2018) The absolute error distance between two FNs $\widetilde{A}$ and $\widetilde{B}$ is defined as follows:

$$\begin{aligned} D(\widetilde{A},\widetilde{B})=\sup _{\alpha \in [0,1]}|\widetilde{A}_{\alpha }-\widetilde{B}_{\alpha }|. \end{aligned}$$

The TFNs $\widetilde{A}$, $\widetilde{B}$, $\widetilde{C}$ satisfy the following conditions:

• (1) $D(\widetilde{A},\widetilde{B})=0$, if and only if $\widetilde{A}=\widetilde{B},$

• (2) $D(\widetilde{A},\widetilde{B})=D(\widetilde{B},\widetilde{A}),$

• (3) $D(\widetilde{A},\widetilde{C})\le D(\widetilde{A},\widetilde{B})+ D(\widetilde{B},\widetilde{C}).$

2.2 Fuzzy random variables

In the following, we briefly give common definitions of fuzzy random variables, fuzzy cumulative distribution function and its estimator.

Definition 4

(Hesamian and Shams 2016) Let $(\varOmega ,\mathcal {A},P)$ be a probability space. The fuzzy-valued mapping $\widetilde{X}: \varOmega \rightarrow \mathcal {F}(\mathbb {R})$ is called a fuzzy random variable (FRV), if for any $\alpha \in [0,1]$ the real-valued mapping $\widetilde{X}_\alpha : \varOmega \rightarrow \mathbb {R}$ is a real-valued random variable.

Definition 5

Two FRVs $\widetilde{X}$ and $\widetilde{Y}$ are called identically distributed and independent, if $\widetilde{X}_{\alpha }$ and $\widetilde{Y}_{\alpha }$ are identically distributed and independent for all $\alpha \in [0,1]$. Similarly, it can be said that $\widetilde{X}_1,\ldots ,\widetilde{X}_n$ is a fuzzy random sample (FRS) of size n if all $\widetilde{X}_i$ are independent and identically distributed FRVs. An observed fuzzy random sample can denoted by $\widetilde{x}_1,\ldots ,\widetilde{x}_n$.

Definition 6

(Hesamian et al. 2019) Let $\widetilde{X}$ be a FRV and $\{\widetilde{X}_n\}_{n=1}^{\infty }$ a collection of FRVs defined on the same probability space. Then, $\widetilde{X}_n$ converges almost surely to $\widetilde{X}$, denoted by $\widetilde{X}_n{\mathop {\rightarrow }\limits ^{a.s.}} \widetilde{X}$. For every $\varepsilon >0$, it holds

$$\begin{aligned} P\left( \lim _{n\rightarrow \infty }D(\widetilde{X}_n,\widetilde{X})>\varepsilon \right) =0. \end{aligned}$$

Definition 7

Let $\widetilde{X}_1,\ldots ,\widetilde{X}_m$ be a FRS of $\widetilde{X}$. The $j^{th}$ order statistic of $\widetilde{X}_1,\ldots ,\widetilde{X}_m$ is defined to be a FN with $\alpha$-cuts $(\widetilde{X}_{(j)})_{\alpha }=(\widetilde{X}_{\alpha })_{(j)}$.

Lemma 1

Let $\widetilde{X}_1,\ldots ,\widetilde{X}_m$ be a FRS of $\widetilde{X}$. Then, $\widetilde{X}_{(j+1)}\succ _{P_d} \widetilde{X}_{(j)}$ for every $j=1,2,\ldots ,m-1$.

Definition 8

(Hesamian and Chachi 2015) The fuzzy number $\widetilde{F}_{\widetilde{X}}(x)$ is said to be a fuzzy cumulative distribution function (FCDF) of $\widetilde{X}$, if its $\alpha$-cuts are defined by $(\widetilde{F}_{\widetilde{X}}(x))_{\alpha }=P(\widetilde{X}_{1-\alpha }\le x)$.

Definition 9

(Hesamian and Chachi 2015) Let $\widetilde{x}_1,\ldots ,\widetilde{x}_n$ be a FRS of $\widetilde{X}$. The fuzzy number $\widetilde{\widehat{F}}_{n}(x)$ is said to be a fuzzy empirical cumulative distribution function, if its $\alpha$-cuts are defined by $(\widetilde{\widehat{F}}_{n}(x))_{\alpha }=\frac{1}{n}\sum _{i=1}^{n}I((\widetilde{x}_i)_{1-\alpha }\le x)$.

Lemma 2

Suppose that $\widetilde{X}_1,\ldots ,\widetilde{X}_n$ is a fuzzy random sample with FCDF $\widetilde{F}_{\widetilde{X}}(x)$. Then,

$$\begin{aligned} P\left( \sup _{x\in \mathbb {R}}D(\widetilde{\widehat{F}}_{n}(x),\widetilde{F}_{\widetilde{X}}(x))\rightarrow 0\right) =1. \end{aligned}$$

Proof

See Hesamian and Chachi (2015). $\square$

3 Fuzzy quantile function

In this section, the notions of fuzzy quantile function and fuzzy empirical quantile are introduced and discussed.

Definition 10

Let $\widetilde{X}$ be a FRV. The fuzzy quantile function (FQF) of $\widetilde{X}$ at level $\tau$ is defined by a FN with the following $\alpha$-cuts:

$$\begin{aligned} (\widetilde{Q}_{\widetilde{X}}(\tau ))_{\alpha }=\inf \{x:(\widetilde{F}_{\widetilde{X}}(x))_{\alpha }>\tau \}. \end{aligned}$$

Example 1

Consider the FRV $\widetilde{X}=(0.99X,X,1.1X)_T$, where $X\sim \exp (\lambda )$. Then, it holds that $\widetilde{Q}_{\widetilde{X}}(\tau )=-\ln (1-\tau )/\lambda \otimes (0.99,1,1.1)_T$.

Example 2

Let $\widetilde{X}$ be a (normal) FRV (Puri and Ralescu 1985) with $\widetilde{X}=\widetilde{\mu }\oplus \epsilon$, where $\epsilon \sim N(0,\sigma ^2)$. Then, it holds that $(\widetilde{Q}_{\widetilde{X}}(\tau ))_{\alpha }=\inf \{x:(\widetilde{F}_{\widetilde{X}}(x))_{1-\alpha }>\tau \}=F^{-1}_{\widetilde{X}_{\alpha }}(\tau )=\widetilde{\mu }_{\alpha }+Z_{\tau } \sigma$, where $Z_{\tau }$ denotes the $\tau ^{th}$ quantile of the standard normal distribution. Therefore, the FQF of $\widetilde{X}$ can be evaluated by $\widetilde{Q}_{\widetilde{X}}(\tau )=\widetilde{\mu }\oplus Z_{\tau } \sigma$.

Definition 11

Let $\widetilde{x}_1,\ldots ,\widetilde{x}_m$ be a FRS of $\widetilde{X}$. The fuzzy empirical quantile function (FEQF) of $\widetilde{X}$ at level $\tau$ is defined by a FN with the following $\alpha$-cuts:

$$\begin{aligned} (\widetilde{\widehat{Q}}(\tau ))_{\alpha }=\inf \{x:(\widetilde{\widehat{F}}_n(x))_{\alpha }>\tau \}. \end{aligned}$$

Lemma 3

Let $\widetilde{X}_1,\ldots ,\widetilde{X}_n$ be a FRS of $\widetilde{X}$. Then, $\widetilde{\widehat{Q}}_{n}(\tau )=\widetilde{X}_{([n\tau ]+1)}$, where [k] represents the integer part of k.

Proof

The claim is immediately verified via

$$\begin{aligned} (\widetilde{\widehat{Q}}_n(\tau ))_{\alpha }=\inf \{x:(\widetilde{\widehat{F}}_n(x))_{\alpha }>\tau \}=(\widetilde{X}_{\alpha })_{([n\tau ]+1)}. \end{aligned}$$

$\square$

Table 1 Data set in Example 3

Example 3

Consider the data set given in Table 1 with $L(x)=1-x^3$ and $R(x)=\sqrt{1-x^5}$. From Definition 9, first note that

$$\begin{aligned} (\widetilde{\widehat{F}}_{n}(x))_{\alpha }=\frac{1}{30}\sum _{i=1}^{30}I((\widetilde{x}_i)_{1-\alpha }\le x), \end{aligned}$$

where

$$\begin{aligned} (\widetilde{x}_i)_{\alpha }=\left\{ \begin{array}{ll} x_i-l_{x_i}\root 3 \of {1-2\alpha } \qquad &{} \text {if }\alpha \in [0,0.5],\\ x_i+r_{x_i}\root 5 \of {1-4(1-\alpha )^2} \qquad &{} \text {if }\alpha \in (0.5,1]. \end{array} \right. \end{aligned}$$

Therefore, at quantile level $\tau \in (0,1)$, the FEQF of $\widetilde{X}$ is given as follows:

$$\begin{aligned} (\widetilde{\widehat{Q}}_{n}(\tau ))_{\alpha }=\inf \left\{ x:\frac{1}{30}\sum _{i=1}^{30}I((\widetilde{x}_i)_{1-\alpha }\le x)>\tau \right\} . \end{aligned}$$

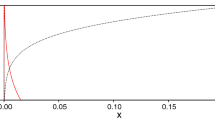
Table 2 shows the lower and upper bounds of $\widetilde{\widehat{Q}}_{n}(\tau )[\alpha ]$ for $\tau =0.25,0.50$ and 0.75 and some values of $\alpha$. The plots of $\widetilde{\widehat{Q}}_{n}(0.25),\widetilde{\widehat{Q}}_{n}(0.5)$ and $\widetilde{\widehat{Q}}_{n}(0.75)$ are presented in Fig. 1.

Table 2 Some $\alpha$-cuts of $\widetilde{\widehat{Q}}_{n}(0.25)$, $\widetilde{\widehat{Q}}_{\widetilde{X}}(0.50)$ and $\widetilde{\widehat{Q}}_{\widetilde{X}}(0.75)$ in Example 3

Fig. 1

Plots of $\widetilde{\widehat{Q}}_{n}(\tau )$ for $\tau =0.25,0.50$ and 0.75 in Example 3

Lemma 4

Suppose that $\widetilde{X}_1,\ldots ,\widetilde{X}_n$ is a fuzzy random sample with FQF $\widetilde{Q}_{\widetilde{X}}(\tau )$. Then, $\widetilde{\widehat{Q}}_n(\tau ){\mathop {\rightarrow }\limits ^{a.s.}}\widetilde{Q}_{\widetilde{X}}(\tau )$.

Proof

As

$$\begin{aligned} (\widetilde{\widehat{Q}}_n(\tau ))_{\alpha }=\inf \{x:(\widetilde{\widehat{F}}_n(x))_{\alpha }>\tau \}{\mathop {\rightarrow }\limits ^{a.s.}}(\widetilde{Q}_{\widetilde{X}}(\tau ))_{\alpha }, \end{aligned}$$

holds for every $\alpha \in [0,1]$, it follows that

$$\begin{aligned}{} & {} P\left( \lim _{n\rightarrow \infty }D(\widetilde{\widehat{Q}}_n(\tau ),\widetilde{Q}_{\widetilde{X}}(\tau ))>\varepsilon \right) \le \\{} & {} P\left( \lim _{n\rightarrow \infty }|(\widetilde{\widehat{Q}}_n(\tau ))_{\alpha }-(\widetilde{Q}_{\widetilde{X}}(\tau ))_{\alpha }|>\varepsilon \right) =0 \end{aligned}$$

is satisfied for every $\varepsilon >0$, which completes the proof. $\square$

4 Hypothesis test for comparing fuzzy quantiles of two populations

Let $X_1,\ldots ,X_m$ and $Y_1,\ldots ,Y_n$ be random samples from two independent populations with absolutely continuous distribution functions $F_X$ and $G_Y$, respectively. Also, let $X_{(1)},\ldots ,X_{(m)}$ and $Y_{(1)},\ldots ,Y_{(n)}$ be the corresponding order statistics. The null hypothesis of interest is $H_0:Q_X(\tau )=Q_Y(\nu )$, where $\tau$ and $\nu$ are two quantile levels. A test statistic for the difference of the empirical quantile functions $\widehat{Q}_X(\tau )=X_{([m\tau +1])}$ and $\widehat{Q}_Y(\tau )=Y_{([n\tau +1])}$ from different populations can be defined by Heinzl and Mittlboeck (2017); Hutson (2009)

$$\begin{aligned} T^{m,n} =&({[}m\tau ]+1){\left( {\begin{array}{c}m\\ {[}m\tau ]+1\end{array}}\right) }\\&\sum _{k=1}^{n}\varvec{\beta }(\widehat{F}_X(Y_{(k)})),{[}m\tau ]+1,m-{[}m\tau ])w_{{[}m\tau ]+1}(k) \end{aligned}$$

with

$$\begin{aligned} \varvec{\beta }(x,p,q)= & {} \int _{0}^{x}s^{p-1}(1-s)^{q-1}ds,\\ w_{{[}n\nu ]+1}(k)= & {} ({[}n\nu ]+1){\left( {\begin{array}{c}n\\ {[}n\nu ]+1\end{array}}\right) }\left( \varvec{\beta }\bigg (\frac{k}{n},{[}n\nu ]+1,n-{[}n\nu ]\right) \\{} & {} -\varvec{\beta }\left( \frac{k-1}{n},{[}n\nu ]+1,n-{[}n\nu ]\right) \bigg ), \end{aligned}$$

where

$$\begin{aligned} \widehat{F}_X(Y_{(k)})=\frac{1}{m}\sum _{i=1}^{m}I(X_i\le Y_{(k)}). \end{aligned}$$

Now, let $\tilde{X}_1,\ldots ,\tilde{X}_m$ and $\tilde{Y}_1,\ldots ,\tilde{Y}_n$ be two independent FRSs from two populations with FCDFs $\widetilde{F}_{\widetilde{X}}$ and $\widetilde{F}_{\widetilde{Y}}$. In the following, a procedure is established for comparing fuzzy quantiles of two populations. For this purpose, consider the following fuzzy hypotheses concerning quantiles of two populations:

Definition 12

Let $\widetilde{X}$ and $\widetilde{Y}$ be two FRVs. The hypotheses of interest are defined as

$$\begin{aligned}{} & {} H_0: \widetilde{Q}_{\widetilde{X}}(\tau )=_{P_d} \widetilde{Q}_{\widetilde{Y}}(\nu )~\text {with}~ P_d(\widetilde{Q}_{\widetilde{X}}(\tau )\succ \widetilde{Q}_{\widetilde{Y}}(\nu ))\\{} & {} \quad =P_d(\widetilde{Q}_{\widetilde{Y}}(\nu )\succ \widetilde{Q}_{\widetilde{X}}(\tau ))=0.5 \end{aligned}$$

versus

$$\begin{aligned} H^A_1: \widetilde{Q}_{\widetilde{X}}(\tau )\succ _{P_d} \widetilde{Q}_{\widetilde{Y}}(\nu )~\text {with}~ P_d(\widetilde{Q}_{\widetilde{X}(\tau )}\succ \widetilde{Q}_{\widetilde{Y}(\nu )})>0.5, \end{aligned}$$

or

$$\begin{aligned} H^B_1: \widetilde{Q}_{\widetilde{Y}}(\nu )\succ _{P_d} \widetilde{Q}_{\widetilde{X}}(\tau )~\text {with}~ P_d(\widetilde{Q}_{\widetilde{Y}(\nu )}\succ \widetilde{Q}_{\widetilde{X}(\tau )})>0.5. \end{aligned}$$

For testing the above hypotheses, we employ the following test statistic.

Definition 13

Let $\tilde{X}_1,\ldots ,\tilde{X}_m$ and $\tilde{Y}_1,\ldots ,\tilde{Y}_n$ be two independent FRS from two FCDFs $\widetilde{F}_{\widetilde{X}}$ and $\widetilde{F}_{\widetilde{Y}}$. The $\alpha$-cuts of the fuzzy test statistic are defined by

$$\begin{aligned} \widetilde{T}^{m,n}[\alpha ]= \left[ \inf _{\beta \in I_{\alpha }}\widetilde{T}^{m,n}_{\beta },\sup _{\beta \in I_{\alpha }}\widetilde{T}^{m,n}_{\beta }\right] , \end{aligned}$$

where

$$\begin{aligned} (\widetilde{\widehat{F}}_{\widetilde{X}})_{\beta }((\widetilde{Y}_{\beta })_{(k)})=\frac{1}{m}\sum _{i=1}^{m}I((\widetilde{X}_i)_{1-\beta }\le (\widetilde{Y}_{\beta })_{(k)}). \end{aligned}$$

The test decision on rejecting or non-rejecting $H_0$ can be made as follows:

Definition 14

Let us consider the problem of testing the fuzzy hypothesis $H_0$ versus $H_1^A$ or $H_1^B$ based on two independent FRS $\tilde{x}_1,\ldots ,\tilde{x}_m$ and $\tilde{y}_1,\ldots ,\tilde{y}_n$. Then, at significance level $\delta$, the fuzzy test is defined as a fuzzy set:

• 1. As for testing $H_0$ versus $H_1^A$, we use

  $$\begin{aligned} \widetilde{\varphi }^A_{\delta }[(\widetilde{x}_1,\ldots ,\widetilde{x}_m),(\tilde{y}_1,\ldots ,\tilde{y}_n)]= \bigg \{\frac{Reject}{\widetilde{\varphi }^A_{\delta }(Reject)},\frac{Accept}{\widetilde{\varphi }^A_{\delta }(Accept)}\bigg \}, \end{aligned}$$

  where $\widetilde{\varphi }^A_{\delta }(Reject)=P_d(\widetilde{T}^{m,n}\succ 1-\delta /2)$ is called the degree of rejection of $H_0$ and $\widetilde{\varphi }^A_{\delta }(Accept)=1-\widetilde{\varphi }^A_{\delta }(1)$ is the degree of non-rejection of $H_0$.

• 2. As for testing $H_0$ versus $H_1^B$, we use

  $$\begin{aligned} \widetilde{\varphi }^B_{\delta }[(\widetilde{x}_1,\ldots ,\widetilde{x}_m),(\tilde{y}_1,\ldots ,\tilde{y}_n)]= \bigg \{\frac{Reject}{\widetilde{\varphi }^B_{\delta }(Reject)},\frac{Accept}{\widetilde{\varphi }^B_{\delta }(Accept)}\bigg \}, \end{aligned}$$

  where $\widetilde{\varphi }^B_{\delta }(Reject)=P_d(\delta /2\succ \widetilde{T}^{m,n})$ is called the degree of rejection of $H_0$ and $\widetilde{\varphi }^B_{\delta }(Accept)=1-\widetilde{\varphi }^B_{\delta }(Reject)$ is the degree of non-rejection of $H_0$.

Here, “Accept” and “Reject” stand for non-rejection and rejection of $H_0$, respectively. Since $\widetilde{\varphi }_{\delta }(Reject)+\widetilde{\varphi }_{\delta }(Accept)=1$, at significance level $\delta$, one cannot reject the null hypothesis if $\widetilde{\varphi }_{\delta }(Accept)>\widetilde{\varphi }_{\delta }(Reject)$ or $\widetilde{\varphi }_{\delta }(Accept)\ge 0.5$.

Remark 3

Since the decision to reject or non-reject $H_0$ versus $H_1^A$ or $H_1^B$ is made via a fuzzy test, this motivates to defuzzify the decision in order to get an exact decision similar to classical statistical hypothesis testing. For this purpose, note that $\widetilde{A}\succ _{P_D}k$ if and only if $M_{\widetilde{A}}=0.5\int _0^1(\widetilde{A}_{\alpha }+\widetilde{A}_{1-\alpha })>k$. As for the interpretation of the test decision, it can be done similar to the classical approach as follows:

• 1. Testing $H_0$ versus $H_1^A$: if $M_{\widetilde{T}^{m,n}}> 1-\delta /2$, then $H_0$ is rejected; otherwise it cannot be rejected

• 2. Testing $H_0$ versus $H_1^B$: if $M_{\widetilde{T}^{m,n}}<\delta /2$, then $H_0$ is rejected; otherwise, it cannot be rejected

Remark 4

As a special case of the proposed method, it can be employed for comparing the fuzzy medians of two populations. In this regard, Grzegorzewski (2005) and Grzegorzewski (2009) introduced a fuzzy test for comparing two and k (crisp) population medians based on fuzzy random variables, respectively. He developed a fuzzy test statistic by employing fuzzy random variables and proposed a fuzzy test based on the necessity ranking criterion. However, the method presented in this paper follows a different strategy for comparing fuzzy quantiles of two populations based on fuzzy random variables. The proposed fuzzy quantile technique includes the following procedure:

• 1. Extending the quantile of a FRV as a FN

• 2. Extending the empirical estimator of a fuzzy quantile based on a FRS

• 3. Investigating the relationship between a fuzzy quantile and its corresponding estimator for large sample cases

Then, a non-parametric statistical hypothesis test was developed for comparing any fuzzy quantiles of two populations based on two independent fuzzy random samples.

5 Numerical examples

In this section, the feasibility and effectiveness of the proposed non-parametric two-sample test on quantiles are examined via numerical examples. Note that there is no method for a reasonable comparison, as other two-sample fuzzy tests rely on comparing the means or medians (or variances) of two populations.

Table 3 Data set in Example 4

Example 4

A random sample of 30 identical twins underwent psychological tests to measure their aggressiveness. We are interested in comparing the twins to see if the firstborn twin tends to be more aggressive than the other one. Assume that, due to limitations in psychological measurements, the results of the evaluations are reported as TFNs for the first born as $(x; 0.02x)_L$ and the second born as $(y;0.02y)_L$ with $L(x)=1-x^2$, where the observations $x_i$ and $y_i$, $i=1,\ldots ,30$, are shown in Table 3. At significance level $\delta =0.05$ we intend to test:

$$\begin{aligned} \begin{array}{ll} H_0: &{} \widetilde{Q}_{\widetilde{X}}(0.5)\simeq _{P_d} \widetilde{Q}_{\widetilde{Y}}(0.5),\\ H^A_1: &{} \widetilde{Q}_{\widetilde{X}}(0.5)\succ _{P_d} \widetilde{Q}_{\widetilde{Y}}(0.5). \end{array} \end{aligned}$$

The fuzzy test statistic can be determined based on Definition 13. The lower and upper bounds of $\widetilde{T}^{30,30}$ are shown in Table 4 based on various values of $\alpha \in (0,1)$. The plot of $\widetilde{T}^{30,30}$ is shown in Fig. 2. According to Definition 14, the fuzzy test can be performed via

$$\begin{aligned}{} & {} \widetilde{\varphi }^A_{0.05}[(\widetilde{x}_1,\ldots ,\widetilde{x}_{30}),(\tilde{y}_1,\ldots ,\tilde{y}_{30})]\\{} & {} =\bigg \{\frac{Reject}{\widetilde{\varphi }^A_{0.05}(Reject)},\frac{Accept}{\widetilde{\varphi }^A_{0.05}(Accept)}\bigg \}, \end{aligned}$$

where $\widetilde{\varphi }^A_{0.05}(Reject)=P_d(\widetilde{T}^{30,30}\succ 0.975)=0.72$. Therefore, at significance level 0.05, the fuzzy null hypothesis is rejected with a degree of 0.72 and non-rejected with a degree of 0.28. As for the defuzzification of this test decision, note that it holds $M_{\widetilde{T}^{30,30}}=0.984>1-\delta /2=0.975$. Following this approach, the final decision is to reject the null hypothesis at level $\delta = 0.05$.

Table 4 Some $\alpha$-cuts of $\widetilde{T}^{30,30}$ in Example 4

Fig. 2

The observed fuzzy test statistics in Example 4

Table 5 Data set in Example 5

Example 5

Let us consider the rocket-motor experiment data set based on Weerahandi and Johnson (1992). It is of interest to make inference on the reliability of the rocket motor at the highest operating temperature of 59$^oC$. At this temperature, the distribution of the operating pressure Y tends to be closest to the distribution of the chamber burst strength X. It is assumed that the observations can be reported as TFNs via $\widetilde{x}_i=(x_i;0.05x_i)_T$ and $\widetilde{y}_i=(y_i;0.1y_i)_T$, where the observations $x_i$ and $y_i$ are given in Table 5. At significance level $\delta =0.05$, we test the following pair of hypotheses:

$$\begin{aligned} \begin{array}{ll} H_0: &{} \widetilde{Q}_{\widetilde{X}}(0.10)\simeq _{P_d} \widetilde{Q}_{\widetilde{Y}}(0.90),\\ H^B_1: &{} \widetilde{Q}_{\widetilde{X}}(0.10)\prec _{P_d} \widetilde{Q}_{\widetilde{Y}}(0.90). \end{array} \end{aligned}$$

According to Definition 13, the plot of $\widetilde{T}^{17,23}$ is shown in Fig. 3. Table 6 also shows the lower and upper bounds of $\widetilde{T}^{17,23}$ based on specific values of $\alpha \in (0,1)$. According to Definition 14, the fuzzy test can be conducted via

$$\begin{aligned}{} & {} \widetilde{\varphi }^B_{0.05}[(\widetilde{x}_1,\ldots ,\widetilde{x}_{17}),(\tilde{y}_1,\ldots ,\tilde{y}_{23})]\\{} & {} =\bigg \{\frac{Reject}{\widetilde{\varphi }^B_{0.05}(Reject)},\frac{Accept}{\widetilde{\varphi }^B_{0.05}(Accept)}\bigg \}, \end{aligned}$$

where $\widetilde{\varphi }^B_{0.05}(Reject)=P_d(\widetilde{T}^{17,23}\prec 0.025)=0.21$ and $\widetilde{\varphi }^B_{0.05}(Accept)=0.79$. Thus, at significance level 0.05, the fuzzy null hypothesis is not rejected with a degree of 0.79 and rejected with a degree of 0.21. Furthermore, the defuzzified value related to $\widetilde{T}^{17,23}$ ($M_{\widetilde{T}^{17,23}}=0.057$) is larger than $\delta /2=0.025$, so the decision will be to non-reject the null hypothesis at level $\delta = 0.05$.

Fig. 3

The observed fuzzy test statistics in Example 5

Table 6 Some $\alpha$-cuts of $\widetilde{T}^{17,23}$ in Example 5

6 Conclusions

In this article, an inferential procedure was developed for comparing fuzzy quantiles of two independent populations. For this purpose, the notion of the fuzzy quantile of a fuzzy random variable was introduced. Then, an estimator of the proposed fuzzy quantile function was developed according to a fuzzy random sample. The estimation procedure was illustrated based on some numerical examples. Further, the large sample property of the proposed fuzzy empirical quantile function was analyzed based on an absolute error distance for fuzzy numbers. In addition, the concept of the fuzzy test statistic was introduced based on fuzzy order statistics of two fuzzy random samples. To test the fuzzy hypotheses on quantiles of two populations, the obtained fuzzy test statistic and the crisp significance level were compared using an criterion called preference degree. As the proposed fuzzy test leads to a degree of rejection or non-rejection of the underlying fuzzy null hypothesis, we also proposed an approach to defuzzify the fuzzy test decision in order to reach a crisp test decision that is important for practical usage.

The results of the practical applications indicate that the proposed method is effective for comparing fuzzy quantiles of two independent populations. One of the advantages of the proposed method is that it can be applied to all kind of fuzzy numbers. As for potential future investigations, employing the proposed method to other types of imprecision such as intuitionistic fuzzy data and/or intuitionistic fuzzy hypotheses could be a promising direction. As another idea for future research, the presented methodology could also be extended to the case when more than two populations need to be compared in terms of their quantiles.