1 Introduction

Multi-objective optimisation problems (MOPs) need to consider more than one conflicting objective simultaneously, and they are ubiquitous in many real-world engineering applications. Unlike single-objective optimisation problems (SOPs), MOPs are more challenging and difficult to solve because the objectives in MOPs are often conflicting and/or incommensurable with each other, and improvement of one objective deteriorates other objectives. Hence, finding a set of equally-optimal solutions, i.e. the Pareto optimal set (PS), is necessary, since there is no single solution that can fulfill all objectives simultaneously (Akbari et al. 2012; Li et al. 2011).

Evolutionary algorithms (EAs) have become popular in recent years, mainly due to their population-based search capabilities that can approximate the PS. The applicability of EAs, however, is not always as good as that of other metaheuristics (Khan et al. 2016, 2019). Metaheuristic algorithms are flexible and easy to implement for solving SOPs and MOPs because they do not rely on gradient information of the objective landscape. While metaheuristic algorithms have been widely used to tackle various SOPs and MOPs, one key limitation is that the user-defined parameters of each metaheuristic algorithm require accurate tuning to realise its full potential. Another downside is the slow or premature convergence towards the global optimum solution (Talbi 2009; Heidari et al. 2019).

Two main types of metaheuristic algorithms are single solution-based and population-based models. Simulated Annealing (SA) (Van Laarhoven and Aarts 1987) and Variable Neighbourhood Search (VNS) (Mladenović and Hansen 1997) are examples of single solution-based metaheuristics, while Genetic Algorithm (GA) (Holland 1992b) and Differential Evolution (DE) (Price 1996; Storn and Price 1997) are examples of population-based metaheuristics (p-metaheuristic) (Talbi 2009). Single solution-based metaheuristics methods only solve one solution at a time during the optimisation process, while p-metaheuristics methods process a set of solution in each iteration. As expected, p-metaheuristics methods are more efficient than single solution-based metaheuristic and can often find an optimal solution, or suboptimal solutions that are located in the neighbourhood of the optimal solution space. By maintaining a population of solutions, these algorithms can avoid local optima and explore new regions of the search space.

Heidari et al. (2019) presents the four main types of p-metaheuristics methods, namely EAs, physics-based, human-based, and swarm intelligence (SI) models. The first types of p-metaheuristics methods are EAs. GA and DE are the most popular EAs, and many enhancements have been introduced (Holland 1992b; Price 1996). The algorithms use a variety of operators, such as mutation, crossover, and selection in the GA, to generate new solutions and improve the quality of the population. The search process involves the evaluation of multiple solutions simultaneously, and the selection of a pool of good solutions for the next generation. Genetic Programming (GP) and Biogeography-Based Optimiser (BBO) are other examples of EAs (Kinnear et al. 1994; Simon 2008). The physics-based metaheuristics methods include Big-Bang Big-Crunch (BBBC) (Erol and Eksin 2006), Central Force Optimisation (CFO) (Formato 2007) and Gravitational Search Algorithm (GSA) (Rashedi et al. 2009).

As the name suggests, these metaheuristics methods are based on the physics principles of a system. Human-based metaheuristics methods imitate human behaviours such as Teaching Learning-Based Optimisation (TLBO) (Rao et al. 2011), Tabu Search (TS) (Glover and Laguna 1998) and Harmony Search (HS) (Geem et al. 2001). SI algorithms have been the current trend for solving MOPs. SI algorithms are generally based on the social behaviours of organisms and social interactions of the population, e.g. the Particle Swarm Optimisation (PSO) algorithm that simulates the bird clustering behaviours (Kennedy and Eberhart 1995).

Recently, many new nature-inspired SI models have been proposed, such as Grey Wolf Optimisation (GWO) algorithm (Mirjalili et al. 2014), Whale Optimisation Algorithm (WOA) (Mirjalili and Lewis 2016), Grasshopper Optimisation Algorithm (GOA) (Mirjalili et al. 2018), Moth-flame optimisation (MFO) (Mirjalili 2015), Artificial Bee Colony (ABC) (Karaboga and Basturk 2008), and Harris’ Hawk Optimisation (HHO) (Heidari et al. 2019). The general procedure of these SI models can be summarised as follows:

  • Generate a set of individuals (population), where each individual represents a solution

  • Each individual in the population is updated using a metaheuristic algorithm

  • The newly generated population replaces the current population on an iterative manner

The above procedure continues for every iteration until a termination condition is satisfied, e.g. the maximum number of iterations. In accordance with the ’no free lunch’ theorem (NFL), there is no universal optimisation methods for solving all possible problems (Wolpert and Macready 1997). Many new optimisation methods and their enhanced variants have been introduced, since no single algorithm is effective for solving all classes of optimisation problems.

SI models have been used to solve various optimisation problems in different fields. Nonetheless, there is room for further research to improve their performance and extend their applications. Several enhancements of metaheuristic algorithms have been proposed to improve the efficiency of an algorithm. In general, four categories of enhancements are: (i) hybrid metaheuristic algorithms, (ii) modified metaheuristic algorithms, (iii) integration with chaos theory, and (iv) multi-objective metaheuristic algorithms. Note that hybrid metaheuristic algorithms integrate two or more algorithms for performance enhancement, while modified metaheuristic algorithms change the search process to improve the performance of an algorithm.

One major problem of all metaheuristic algorithms is pre-mature convergence and local optima, particularly in large-scale optimisation problems. Hybrid metaheuristic algorithms are used to solve optimisation problems with more efficient characteristics and with higher flexibility (Bettemir and Sonmez 2015; Li and Gao 2016). The GA and SA models are useful stochastic search algorithms for solving combinatorial optimisation problems. GA has been developed based on the principle of the survival-of-the-fittest and natural selection principles while SA is inspired by the physical process of annealing (Kirkpatrick et al. 1983; Van Laarhoven and Aarts 1987; Holland 1992a). SA often is coupled with GA to avoid local optima by irregularly allowing the acceptance of non-improving solutions. Hybrid Genetic Algorithm and Simulated Annealing (HGASA) is good at tackling optimisation problems, such as project scheduling with multiple constraints and railway crew scheduling (Chen and Shahandashti 2009; Hanafi and Kozan 2014; Bettemir and Sonmez 2015). Leveraging the capability of DE in searching for good and diverse solutions, many researchers have proposed integration of DE and other p-metaheuristics algorithms. Wang and Li (2019) enhanced the solution diversity by combining DE and GWO. An adaptive DE model was combined with GOA for multi-level satellite image segmentation (Jia et al. 2019). The resulting hybrid algorithm was evaluated with a series of experiments using satellite images, demonstrating search efficiency and population diversity.

Modification methods in metaheuristic algorithms refer to the process of changing the search process to improve the performance of an algorithm. One such method is the use of local search techniques to improve the solution quality. Local search techniques involve searching the local neighbourhood of a solution to find a better solution. Another modification method is the use of diversity mechanisms to prevent an algorithm from converging prematurely. Diversity mechanisms involve maintaining a diverse population of solutions to explore different regions of the search space. As an example, Gao et al. (2008) employed a logarithm decreasing inertia weight and chaos mutation with PSO to improve the convergence speed and diversity of solutions. In Gao and Zhao (2019), a variable weight was assigned to the leader of grey wolves, and a controlling parameter was introduced to decline exponentially and alter the transition pattern between exploration and exploitation. Moreover, Xie et al. (2020) enhanced GWO by integrating a nonlinear exploration factor to increase exploration in the early stage and improve exploitation in the second half of the search process.

This paper proposes enhancements to the HHO algorithm. Specifically, the nonlinear exploration factor, DE scheme, chaos strategy, and mutation mechanism from EAs are leveraged, leading to the proposed enhanced HHO (EHHO) model and its extension to multi-objective EHHO for solving SOPs and MOPs, respectively. A nonlinear exploration factor is introduced to replace the linear exploration factor in the original HHO algorithm. This nonlinear exploration factor aims to improve the exploration capability in the early search stage and facilitate the transition from exploration to exploitation. The DE scheme is then used to generate new, diverse individuals through mutation, crossover and selection. A chaos strategy is adopted to replace the DE mutation factor, in order to increase the randomness and find more valuable search areas. In MO-EHHO, a mutation mechanism is introduced to increase diversity of individuals in the external archive. The fast non-dominated sorting and crowding distance techniques from NSGA-II are also employed to select the optimal solution in each iteration and to maintain diversity of the non-dominated solutions.

Benchmark SOPs and MOPs are used to evaluate the effectiveness of EHHO and MO-EHHO (Yao et al. 1999; Digalakis and Margaritis 2001). The benchmark suite of SOPs includes the following tasks: unimodal (UM) functions F1–F7, multimodal (MM) functions F8–F23, and composition (CM) functions F24–F29. On the other hand, MO-EHHO is applied to tackling high-dimensional bi-objective problems without equality or inequality constraints and scalable tri-objective problems without equality or inequality constraints for performance evaluation. These include ZDT benchmark functions (ZDT1-4,6) (Deb et al. 2002; Deb and Agrawal 1999) and DTLZ benchmark functions (DTLZ1-DTLZ7) (Deb et al. 2005). The statistical sign test with a 95% confidence level is used for performance comparison. Four performance indicators are used, namely convergence, diversity, generational distance (GD), and inverted generational distance (IGD). The average ranking method (Yu et al. 2018) is leveraged to rank the performance of MO-EHHO against its competitors on each performance indicator.

This study introduces enhanced HHO-based models for solving SOPs snd MOPs. The organisation of this paper is as follows. In Sect. 2, a review on HHO, chaos theory, and DE is provided. In Sect. 3, the HHO algorithm and the proposed enhancements, namely EHHO and MO-EHHO, are explained in detail. The effectiveness of EHHO and MO-EHHO for solving SOPs and MOPs is evaluated, compared, analysed and discussed in Sect. 4. Concluding remarks and suggestions for future work are presented in Sect. 5.

2 Literature review

This section provides the concepts of multi-objective optimisation and current methods in meta-heuristics for solving MOPs.

2.1 Harris’ Hawks optimisation algorithm

Proposed by Heidari et al. (2019), the HHO algorithm is a swarm-based, nature-inspired metaheuristic model. It imitates the collaboration behaviours of Harris’ hawks working together to search and chase for a prey in different directions. A variety of hunting strategies are performed by Harris’ hawks based on the prey’s escaping energy. The mathematical model pertaining to the behaviours of Harris’ hawks are formulated for solving optimisation problems. The HHO algorithm has received extensive interest from researchers due to its effectiveness and fast convergence speed; however, the HHO algorithm suffers from the following problems:

  1. 1.

    greatly affected by the tuning parameters;

  2. 2.

    weak transition between exploration and exploitation;

  3. 3.

    easily fall into local optima;

  4. 4.

    poor convergence for high-dimensional problems and multimodal problems; and

  5. 5.

    limited diversity of the solutions.

Enhancements of HHO have been proposed, e.g. hybridisation of HHO, modification of HHO and chaotic HHO (Alabool et al. 2021). Hybridisation is a popular method to improve the performance of an algorithm. HHO has been integrated with other optimisation methods to find the solution faster, avoid falling into local optima, provide better solution quality, and improve algorithm stability (Chen et al. 2020a; Gupta et al. 2020; Ewees and Abd Elaziz 2020). Chen et al. (2020a) integrated the DE algorithm and a multi-population strategy into HHO to overcome its convergence issue and prevent HHO from being trapped in local optima. In addition, opposition-based learning was applied to HHO by Gupta et al. (2020) to reduce the number of opposite solutions and increase the convergence speed. HHO has also been used to improve the performance of other algorithms, e.g. accelerating the search process of multi-verse optimisation (MVO) and maintaining the MVO population (Ewees and Abd Elaziz 2020).

Other HHO modifications include improving the convergence speed, increasing the population diversity, and enhancing the transition from exploration to exploitation (Alabool et al. 2021). HHO was integrated with a chaotic map to improve the balance between exploration and exploitation (Zheng-Ming et al. 2019; Qu et al. 2020). Specifically, Zheng-Ming et al. (2019) used a tent map in the exploration phase to identify the optimal solution rapidly, while Qu et al. (2020) employed a logistic map in the escaping energy factor to balance global exploration and local exploitation. The use of HHO for solving MOPs was investigated in Islam et al. (2020) and Jangir et al. (2021). Table 1 summarises the main enhancement methods of HHO.

Table 1 Recent popular enhancement methods of HHO for solving SOPs and MOPs
Full size table

2.2 Differential evolution (DE)

Introduced by Price (1996) and Storn and Price (1997), DE is well-known for its simplicity, fewer control parameters and superior performance in optimisation. Storn and Price (1997) employed DE to solve global optimisation problems. However, one major problem of all metaheuristics algorithms is the potential of early convergence and local optima. Leveraging on DE’s capability in finding better and diverse solutions, many researchers have proposed integration of DE and other p-metaheuristics algorithms. As an example, Wang and Li (2019) enhanced the solution diversity by integrating DE and the GWO algorithm. An adaptive DE was combined with GOA by Jia et al. (2019) for multi-level satellite image segmentation. The hybrid algorithm was evaluated with a series of experiments using satellite images. It was able to increase search efficiency and population diversity through iterations. In addition, hybrid models of DE and HHO can elevate the performance of the original HHO algorithm. Birogul (2019) introduced HHODE, which blends HHO and DE, which uses mutation operators from DE to harness its exploration strengths. The hybridisation manages to strike a balance between exploratory and exploitative tendencies. It was tested on an altered IEEE 30-bus test system for optimal power flow problem and proved to be more effective than other optimisation algorithms. Besides, DE is used by Chen et al. (2020a) in HHO to boost its local search capability and exploit the DE operations, such as mutation, crossover and selection, to discover better and more diverse solutions. A new HHO variant was introduced by Islam et al. (2020) to solve the power flow optimisation problem. Multiple researchers conducted studies to demonstrate hybridisation of DE with HHO for improving the HHO performance. Table 1 summarises the main publications in this topic (Birogul 2019; Bao et al. 2019; Wunnava et al. 2020; Abd Elaziz et al. 2021; Abualigah et al. 2021; Liu et al. 2022). In short, DE is useful for maintaining a more diverse and quality individual without losing the convergence speed in HHO.

2.3 Chaos theory

Chaos theory helps enhance the population diversity and cover wider search areas that an algorithm may miss. As mentioned before, HHO has a poor changeover from exploration to exploitation; hence, its susceptibility to local optima. Besides, HHO exhibits a poor performance in tackling high-dimensional and multimodal problems. In this respect, chaos theory is often applied to an optimisation algorithm to enhance their global search capability (Ewees and Abd Elaziz 2020; Chen et al. 2020b; Liu et al. 2020; Dhawale et al. 2021; Hussien and Amin 2022). A variety of chaotic maps are available: Chebyshev, circle, intermittency, iterative, Leibovich, logistic, piecewise, sawtooth, sine, singer, sinusoidal and tent map. Researchers popularly use logistic and tent maps to improve the HHO performance (Zheng-Ming et al. 2019; Menesy et al. 2019; Chen et al. 2020a). Chen et al. (2020a) introduced chaotic sequence into the escaping energy of the rabbit in HHO to enhance the global searchability and cover broader search areas. A chaotic map was incorporated into the adaptive mutation strategy and integrated into the external archive by Liu et al. (2020) to attain a set of diverse non-dominated solutions. Moreover, Xie et al. (2020) employed a chaotic strategy to assign weights for the leader wolf in GWO to increase the diversity of the leader wolves. Barshandeh and Haghzadeh (2021) integrated a chaos strategy to initialise the population and improve the solution diversity, allowing a larger search space to be covered. Table 1 Chaos shows the key publications on the use of chaos theory for improvement of the HHO algorithm.

2.4 Multi-objective optimisation

MOPs are similar to SOPs in terms of problem definition, but with multiple objective functions that cannot be efficiently solved by a single-objective algorithm. A set of equilibrium solutions exists for solving an MOP, i.e. a set of non-inferior solutions or Pareto optimal solutions (Fonseca and Fleming 1998). An MOP can be formulated as follows:

$$\begin{aligned} \begin{aligned} \text {Minimise} \, F(\textbf{x})&=f_{1}(\textbf{x}), f_{2}(\textbf{x}), \cdots , f_{k}(\textbf{x}) \\ \text {subject to:}&\\ g_{j}(\textbf{x})&\ge 0, \quad j=1,2, \ldots , r \\ h_{j}(\textbf{x})&=0, \quad j=r+1, r+2, \ldots , s \\ Lb_{i}&\le x_{i} \le Ub_{i}, i = 1,2,\ldots ,n \end{aligned} \end{aligned}$$
(1)

where n is the number of design variables, o is the number of objective functions, r is the number of inequality constraints, s is the number of equality constraints, \(g_{j}\) and \(h_{j}\) are the j-th inequality and equality constraints, respectively, and \(Lb_{i}\) and \(Ub_{i}\) are the lower and upper bounds of the i-th design variables.

In a single-objective function, solution \(\mathbf {x_1}\) is better than \(\mathbf {x_2}\) if \(f(\mathbf {x_1}) < f(\mathbf {x_2})\); however, this definition cannot be used in a MOP that has two or more objective functions. Using the Pareto dominance concept in solving MOP, solution \(\mathbf {x_1}\) is better than (dominates) \(\mathbf {x_2}\) if all objective functions \(f(\mathbf {x_1}) < f(\mathbf {x_2})\) (Fonseca and Fleming 1998). Two solutions are denoted as non-dominated if, for at least one objective function, but not all of them, \(f(\mathbf {x_1}) \nless f(\mathbf {x_2})\).

Recently, p-metaheuristics algorithms have been utilised to solve MOPs due to their population-based search capabilities in yielding multiple solutions in a single run. The Pareto dominance concept is used to determine the PS. Most p-metaheuristics algorithms employ non-dominated ranking and Pareto strategy to ensure the diversity of PS. Several useful p-metaheuristics algorithms that store the best PS when there are multiple optimum solutions are: NSGA-II (Deb et al. 2002), SPEA2 (Zitzler et al. 2001), and MOPSO with an archive (Coello et al. 2004). Mirjalili et al. (2016) discussed several multi-objective p-metaheuristics algorithms, such as multi-objective grey wolf optimiser (MOGWO) (Mirjalili et al. 2016), multi-objective ant lion optimiser (MOALO) (Mirjalili et al. 2017b), multi-objective multi-verse optimisation (MOMVO) (Mirjalili et al. 2017a) and multi-objective grasshopper optimisation algorithm (MOGOA) (Mirjalili et al. 2018), to solve MOPs. Jangir and Jangir (2018) embedded the non-dominated sorting into GWO to solve several multi-objective engineering design problems and apply it to a constraint multi-objective emission dispatch problems with economic constrained and integration of wind power. Liu et al. (2020) modified a MOGWO with multiple search strategies to solve MOPs. Hence, this paper extended the EHHO to a multi-objective EHHO that incorporated the non-dominated sorting from NSGA-II to sort and rank the non-dominated solution by calculating the crowding distance between solution sets to ensure a diverse PS. An external archive with a mutation strategy is utilised to diversify the obtained PS.

3 The proposed enhanced Harris’ Hawk optimiser

3.1 Harris’ Hawk optimisation

Fig. 1
figure 1

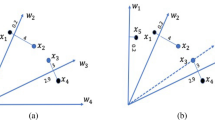
Different stages of HHO (Heidari et al. 2019)

Full size image

HHO was originally proposed by Heidari et al. (2019) to solve SOPs. It mimics the hunting strategy of harris’ hawks, focusing on their "surprise pounce" and "seven kills" to catch a prey (e.g. a rabbit). The hawks collaborate with each other in chasing or attacking the prey, and change their attack mode dynamically based on the escaping pattern of the prey. The hawk’s behaviour is modelled in three main stages: exploration, the transition from exploration to exploitation, and exploitation. Figure 1 presents the different stages of HHO, while the pseudocode of the HHO algorithm is presented in Algorithm 1.

The HHO algorithm begins by initialising a fixed number of randomised individuals (population), in which every individual represents a candidate solution. The individuals are random within the lower and upper boundaries of the problems. The fitness value of each individual is calculated every iteration until the stopping criteria are satisfied.

The key mathematical formulation of each HHO stage is as follows:

\({\textbf {Exploration stage:}}\):
$$\begin{aligned}{} & {} X(t+1)= {\left\{ \begin{array}{ll} X_\textrm{rand}(t)-r_1 |X_\textrm{rand}(t)\\ -2r_2X(t) |&{} q \ge 0.5\\ (X_\textrm{rabbit}(t)-X_m(t))\\ -r_3(LB+r_4(UB-LB))) &{} q < 0.5 \end{array}\right. }\nonumber \\ \end{aligned}$$
(2)
$$\begin{aligned}{} & {} X_m(t+1)=\frac{1}{N} \sum _{i=1}^{N} X_i(t) \end{aligned}$$
(3)
\({\textbf {Transition stage:}}\):
$$\begin{aligned}{} & {} e = 2 (1-\frac{t}{T}) \end{aligned}$$
(4)
$$\begin{aligned}{} & {} E_0 = 2rand()-1 \end{aligned}$$
(5)
$$\begin{aligned}{} & {} E = E_0 \times e \end{aligned}$$
(6)

Exploitation stage: Soft besiege (\(r \ge 0.5 \text {and} |E |\ge 0.5\))

$$\begin{aligned}{} & {} X(t+1) = \Delta X(t) - E|JX_\textrm{rabbit}(t)-X(t) |\end{aligned}$$
(7)
$$\begin{aligned}{} & {} \Delta X(t) = X_\textrm{rabbit}(t)-X(t) \end{aligned}$$
(8)
$$\begin{aligned}{} & {} J= 2(1-r_5) \end{aligned}$$
(9)

Hard besiege (\(r \le 0.5\) and \(|E |< 0.5\))

$$\begin{aligned} X(t+1) = X_\textrm{rabbit}(t) - E |\Delta X(t) |\end{aligned}$$
(10)

Soft besiege with progressive rapid dives(\(r < 0.5\) and \(|E |\ge 0.5\))

$$\begin{aligned}{} & {} Y = X_\textrm{rabbit}(t) - E|JX_\textrm{rabbit}(t)-X(t) |\end{aligned}$$
(11)
$$\begin{aligned}{} & {} Z = Y + S \times LF(D) \end{aligned}$$
(12)
$$\begin{aligned}{} & {} \begin{array}{l} L F(D)=0.01 \times \frac{\mu \times \sigma }{|v |^{\frac{1}{\beta }}}, \\ \sigma =\left( \frac{\Gamma (1+\beta ) \times \sin \left( \frac{\pi \beta }{2}\right) }{\Gamma \left( \frac{1+\beta }{2}\right) \times \beta \times 2\left( \frac{\beta -1}{2}\right) }\right) ^{\frac{1}{\beta }}, \beta =1.5 \end{array} \end{aligned}$$
(13)
$$\begin{aligned}{} & {} X(t+1) = {\left\{ \begin{array}{ll} Y &{} if \, F(Y)< F(X(t))\\ Z &{} if \, F(Z) < F(X(t)) \end{array}\right. } \end{aligned}$$
(14)

Hard besiege with progressive rapid dives (\(r < 0.5\) and \(|E |\le 0.5\))

$$\begin{aligned}{} & {} Y' = X_\textrm{rabbit}(t) - E |JX_\textrm{rabbit}(t)-X_m(t) |\end{aligned}$$
(15)
$$\begin{aligned}{} & {} Z' = Y + S \times LF(D) \end{aligned}$$
(16)
$$\begin{aligned}{} & {} X(t+1) =\left\{ \begin{array}{ll} Y' &{} \quad {\text {if }} \, F(Y')< F(X(t))\\ Z' &{} \quad {\text {if }} \, F(Z') < F(X(t)) \end{array} \right. \end{aligned}$$
(17)

where \(X(t+1)\) is the position vector of an individual in the next iteration t, \(X_\textrm{rabbit}(t)\) is the best position of a prey, X(t) is the current position of the individual, \(X_\textrm{rand}(t)\) is the random position of the individual, \(X_m(t)\) is the average position of the population, \(r_1\),\(r_2\), \(r_3\), \(r_4\), \(r_5\), q, v and \(\beta \) are random factors within [0,1], while LB and UB are the lower and upper bounds of the search space, respectively. In addition, E denotes the escaping energy of the prey, \(E_0\in (-1,1)\) is the initial state of the prey’s energy, \(e\in (2,0)\) is the exploration factor, and T is the maximum number iterations (e.g. 100 iterations). Besides, J is the jumping strength of the prey and \(\Delta X(t)\) denotes the difference between the position of an individual with the best position of the prey, while LF, D and S represent the dimensions of the search space (Heidari et al. 2019; Chen et al. 2020a). The detailed processes of the original HHO algorithm are shown in Algorithm 1 (Heidari et al. 2019).

Algorithm 1
figure a

Harris’ Hawk Optimiser

Full size image

3.2 Nonlinear exploration factor

A nonlinear exploration factor is introduced to replace the linear version from the original HHO algorithm. In the HHO algorithm, the exploration factor, e controls the transition pattern from exploration to exploitation as defined in Eq. (4), which decreases linearly from 2 to 0, resulting in an acute shrinkage of the search space and insufficient search attention. Multiple studies in the literature have explored adaptive control of diverse search operations to improve the conversion between exploration and exploitation. Trigonometric (Mirjalili 2016; Gao and Zhao 2019), exponential (Mittal et al. 2016; Long et al. 2018a), and logarithmic-based functions (Gao et al. 2008; Long et al. 2018b) functions are useful for controlling the exploration factor nonlinearly. In this research, we use a nonlinear exploration factor proposed by Xie et al. (2020), which is a combination of the trigonometric functions, i.e. cos and sin, and a hyperbolic function, i.e tanh. This nonlinear exploration factor aims to amplify the diversification capabilities in the early exploration phase and smoothen the changeover from exploration to exploitation. The proposed nonlinear exploration factor and newly proposed escaping energy are defined as follows:

$$\begin{aligned}{} & {} e' = 2 \times \Big (\cos \Big (\frac{(\tanh \theta )^2+(\theta \sin \pi \theta )^k}{(\tanh 1)^2}\times \frac{\pi }{2} \Big )\Big )^2 \end{aligned}$$
(18)
$$\begin{aligned}{} & {} \theta = \frac{t}{Max\_iter} \end{aligned}$$
(19)
$$\begin{aligned}{} & {} E' = E_0 \times e' \end{aligned}$$
(20)

where \(e'\) is the newly proposed exploration factor to govern the switch between exploration to exploitation, t and Max\(_\textrm{iter}\) are the current iteration and maximum iteration of each iteration, respectively. Coefficient k controls the descending slope of the exploration factor, \(e'\), while \(k = 5\) is adopted, as used in Xie et al. (2020). The new exploration factor and escaping energy descending pattern are presented in Fig. 2a, b, respectively. As shown in Fig. 2a, the proposed nonlinear exploration factor decreases with a descending slope. The first half of the search path has a more effective exploration rate, while the second half has a lower exploration rate. The search space is significantly expanded in the first half, which helps EHHO to focus on exploration and finish the search with exploitation.

Fig. 2
figure 2

Proposed enhancements of the exploration and exploitation of EHHO

Full size image

3.3 Differential evolution (DE)

Developed by Price (1996), Storn and Price (1997), DE is a robust yet straightforward EA for optimising real-valued, multi-modal functions. DE is utilised in EHHO to enhance its searchability and solution quality. Three primary processes exist in DE, namely mutation, crossover and selection (Price 1996; Storn and Price 1997). They are described in the following subsection.

3.3.1 Mutation

Following the DE process, three random solutions are selected from the population for mutation. A constant mutation factor is applied to the difference between two individuals. The third individual is combined with the mutated difference vector to produce a new individual, as follows:

$$\begin{aligned} V_i(t) = X_{r1}(t) + F \times (X_{r2}(t) - X_{r3}(t)) \end{aligned}$$
(21)

where \(X_{r1}\), \(X_{r2}\), \(X_{r3}\) are three random solutions selected from the population, \(V_i\) is the new individual, F is the mutation factor \(\in [0.5,1]\), which is generated by a sinusoidal mapping defined in Eq. (22). The sinusoidal mapping is a chaotic sequence, as shown in Fig. 3. In accordance with chaos theory, a chaotic sequence has three important features, i.e. its initilisation condition, ergodicity, and randomness. The chaotic mutation factor can avoid local optima and premature convergence by exploiting randomness of the chaotic sequence.

$$\begin{aligned} ch_{i+1}&= ach^2_i \sin (\pi ch_i), \quad a =2.3 \,, \, ch_0 =0.7 \nonumber \\&\quad {\text {and }} \, i = 1,2,\ldots ,N \end{aligned}$$
(22)
Fig. 3
figure 3

A sinusoidal chaotic map is used in the DE mutation factor

Full size image

3.3.2 Crossover

The crossover operation is modelled as follows:

$$\begin{aligned}{} & {} U_ i,j,g \left\{ \begin{array}{ll} V_ i,j,g &{}\quad \hbox {if rand}_j(0,1)\le Cr \,\hbox {or}\, j = {\text {rand}}_j \\ X_i,j,g &{}\quad \text{ if } \text{ otherwise } \end{array} \right. \end{aligned}$$
(23)
$$\begin{aligned}{} & {} Cr=Cr_l+{\text {rand}}\times (Cr_u-Cr_l) \end{aligned}$$
(24)

where \({\text {rand}}_j\) is randomised between [0, 1] and Cr is the crossover ratio. The solution from the mutation process will replace the current solution if Cr is higher than \({\text {rand}}_j\) in Eq. 23. The \(Cr_l\) and \(Cr_u\) are the lower and upper boundaries of Cr.

3.3.3 Selection

The selection operation is modelled as follows:

$$\begin{aligned} \begin{aligned} X_i,g+1 \left\{ \begin{array}{ll} U_{i,g} &{}\quad \text {if}\, f(U_{i,g})\le f(X_{i,g}) \\ X_i,g &{}\quad \text {otherwise} \end{array} \right. \\, i = 1,2,\ldots ,N \end{aligned} \end{aligned}$$
(25)

where \(X_ {i,g} \) is the original individual, \(U_{i,g}\) is the individual from crossover, and \(X_{i,g+1}\) is the new individual for the next iteration. Following crossover, DE determines the solution using equation 25. In this regard, f is the fitness function before and after mutation and crossover. The new solution with lower fitness value will replace the current solution with higher fitness lower in a minimisation problem.

3.4 EHHO for multi-objective optimisation

3.4.1 Mutation strategy

A mutation strategy is employed in the external archive to increase the chance of generating better non-dominated solutions when the mutation probability is smaller than the mutation factor. An adaptive mutation factor is applied and modelled as follows:

$$\begin{aligned} m=m_l+{\text {rand}}\times (m_u-m_l) \end{aligned}$$
(26)

where \(m_l\) and \(m_u\) are the lower and upper boundaries of the mutation factor (m). Generally, \(m_l=0.1\) and \(m_u=0.9\). A set of new solutions is obtained after the mutation operation is completed (Fig. 4).

Fig. 4
figure 4

Flowchart of the proposed multi-objective enhanced Harris’ Hawks Optimiser (MO-EHHO)

Full size image

3.4.2 External archive

Zhang and Sanderson (2009) proposed an adaptive DE algorithm with an optimal external archive to solve MOPs. The external archive is a solution set, Arc, that acts as a storage unit to keep historical PS obtained from each iteration. When a new and better solution is found, the existing solution is replaced by the new non-dominated solution. Moreover, other non-dominated solutions are removed based on the crowding distance when the maximum capacity q is reached. Note that q is denoted as the maximum number of solutions can be stored in the external archive, which has the same size of that of the population.

3.4.3 Fast non-dominated sorting

The fast non-dominated sorting method is integrated into the multi-objective p-metaheuristics algorithm for finding non-dominated solutions. Developed by Deb et al. (2002), it is used to sort the Pareto optimal solutions according to their degree of dominance in NSGA-II. The non-dominated solution is assigned as rank 1, the solution that is dominated by only one solution is assigned as rank 2, and so on. The solutions are chosen based on their ranks, in order to preserve quality of the solution base.

3.4.4 Crowding distance

The crowding distance is computed as follows (Deb et al. 2002):

$$\begin{aligned} X = {\left\{ \begin{array}{ll} \infty &{} \hbox {if }\; i=1 \hbox {or} j=1 \\ \sum _{j=1}^{n} \frac{{\text {obj}}_j (S_ i+1 )-{\text {obj}}_j (S_ i-1 )}{{\text {obj}}_j^\text {max}-{\text {obj}}_j^\text {min}} &{} \text {otherwise} \end{array}\right. } \end{aligned}$$
(27)

where q is the size of solution set, \(i\in q\). n is the number of objectives; \({\text {obj}}_j (S_ i+1)\) is the value of the jth objective of solution \(S_i\), and \({\text {obj}}_j^\text {max}\) and \({\text {obj}}_j^\text {min}\) are the maximum and minimum values of the jth objective of the solution set. Specifically, the crowding distance is the distance between two adjacent solutions on the same front; the larger the crowding distance, the closer the two adjacent solutions.

Algorithm 2
figure b

Multi-objective Enhanced Harris’ Hawk Optimiser

Full size image

4 Experimental results and analysis

4.1 Evaluation with single-objective optimisation problems

4.1.1 Experimental setup and compared algorithms

A set of diverse benchmark problems (Yao et al. 1999; Digalakis and Margaritis 2001) is used to evaluate the proposed EHHO algorithm. The benchmark suite includes the following problems: unimodal (UM) functions F1–F7, multimodal (MM) functions F8–F23, and composition (CM) functions F24–F29. The UM functions evaluate the exploitative capabilities of optimisers with respect to their global best. The MM functions are designed to assess the diversification or exploration capabilities of optimisers. The characteristic and mathematical formulation of the UM and MM functions are presented in Tables 22, 23 and 24 in the Appendix. The CM functions are selected from the IEEE CEC 2005 competition (García et al. 2009), which include rotated, shifted and multi-modal hybrid composition functions. Details of the CM functions are presented in Table 25 in the Appendix. These functions are beneficial to investigate the interchange from exploration to exploitation and the capabilities of an optimiser in escaping from the local optima of an optimiser.

EHHO is implemented in Python and executed on a computer with Windows 10 64-bit professional and 16 GB RAM. The population size and maximum iterations of EHHO are set to 30 and 500, respectively, as proposed in the original HHO (Heidari et al. 2019) and HHODE (Birogul 2019). The EHHO results are documented and compared with other algorithms across the average performance over 30 independent runs. The results of other algorithms are extracted from the original HHO publication (Heidari et al. 2019) and HHODE publication (Birogul 2019). The average (AVG) and standard deviation (STD) of EHHO are compared with those of the following algorithms: GA (Simon 2008), BBO (Simon 2008), DE (Simon 2008), PSO (Simon 2008), FPA (Yang et al. 2014), GWO (Mirjalili et al. 2016), BAT (Yang and Gandomi 2012), FA (Gandomi et al. 2011), CS (Gandomi et al. 2013), MFO (Mirjalili 2015), TLBO (Rao et al. 2012) and DE (Simon 2008). These include commonly utilised optimisers, such as GA, DE, PSO and BBO, and also newly emerged optimisers such as FPA, GWO, BAT, FA, CS, MFO and TLBO. Additionally, EHHO is compared with a modified version of HHO, i.e. HHODE, from Birogul (2019).

A statistical hypothesis test, i.e. the non- parametric sign test at the 95% confidence level, is used for performance assessment from the statistical perspective. The sign test results at the 95% confidence interval and the associated p-values are presented in Tables 6, 7, 8 and 9. Symbol "+/=/-" indicates a better/equal/worse performance between two compared algorithms. The \(\checkmark \) indicates the target algorithm has significant difference in performance with the compared algorithm, \(\times \) is vice versa, and \(\approx \) depicts no significant difference in performance between the two algorithms.

To compare an algorithm with others in a more general form, lexicographic ordering and average ranking are used. Lexicographic ordering has been adopted to obtain the final ranking for all algorithms in the CEC 2009 competition (Yu et al. 2018). The average ranking method is used to reveal accuracy and stability of an algorithm against other competitors. All algorithms are ranked based on their average results pertaining to the total number of benchmark functions, N. To measure accuracy of the target algorithm, the mean rank \(\mu _r\) is used, i.e.

$$\begin{aligned} \mu _{r}=\frac{\sum _{i=1}^{n} R_{i}}{N} \end{aligned}$$
(28)

where \(R = \{ R_1,R_2,\ldots ,R_n \}\) is a rank set of the target algorithm. The lower the mean rank \(\mu _r\), the better the performance of the target algorithm.

4.2 Quantitative results of EHHO and discussion

By observing the quantitative results from different classes of benchmark functions, the AVG and STD measures from 30 independent runs indicate the performance and stability of EHHO. The EHHO results versus those from other competitors in dealing with UM and MM functions (F1–F13) on 30, 100, 500 and 1000 dimensions are tabulated in Tables 2, 3, 4 and 5. Table 8 shows the EHHO results versus those from competitors in dealing with MM and CM functions. The best AVG and STD scores of EHHO are in bold. The statistical results of UM, MM, and CM benchmark functions are tabulated in Tables 6, 7, 8 and 9. The average ranking results are tabulated in Tables 7, 8, 9 and 10.

From Table 2, EHHO generates superior results on F2, F4–F7, and F9–F13. From the statistical evaluation veiwpoint, EHHO outperforms its competitors in all 30-dimensional UM functions at the 95% confidence level, as indicated by \(p < 0.05\) in Table 6. Moreover, EHHO achieves better results than other models on F1, F2, F4–F6, and F9–F13 on 100-dimensional UM functions, as shown in Table 3. As indicated in Table 6, EHHO performs significantly better than its competitors at the 95% confidence level. It can be noticed that EHHO yields the best results on 9 out of 13 500-dimensional benchmark problems, as presented in Table 4. In addition, Table 6 shows EHHO performs statistically better than its competitors, achieving comparable results than those of HHODE/rand/1, HHODE/best/1, HHODE/current-to-best/2, and HHODE/best/2. From Table 5, EHHO depicts its superior performance with 10 out of 13 best results on the benchmark problem with 1000-dimension. Comparing with other models statistically, EHHO performs significantly better than its competitors at the 95% confidence level, and no statistically difference with HHODE/current-to-best/2. From the results, integrating DE can certainly achieve more diverse solutions, leading to the attainment of the global optimum solution. In summary, EHHO proves to be highly effective in solving the F4–F6 and F9–F13 benchmark functions. Furthermore, EHHO outperforms other algorithms in almost all instances, and achieves the most optimal global solution for F9 and F11 in search spaces ranging from 30 to 1000 dimensions.

According to the results presented in Table 8, EHHO outperforms other models on several functions, including F14–F17, F19, F21–F22, and F25–F27. It also depicts similar performance to other models on F23 and F29. However, when it comes to hybrid composition functions F18, F20, F24, and F28, EHHO has a relatively lower performance on those hybrid composition functions. From Table 10, the average ranking results reinforce the findings from the statistical analysis, providing additional insights into the comparative performance of algorithms on benchmark functions F14–F29. EHHO is inferior to HHODE/current-to-best/2, HHODE/rand/1, HHODE/best/1, HHODE/best/2, and HHO, but it outperforms GA, PSO, BBO, FPA, GWO, BAT, FA, CS, MFO, TLBO, and DE. These findings provide valuable insights into the strengths and weaknesses of the EHHO algorithm on specific benchmark functions.

Based on the results, it can be seen that using a hybrid of HHO and DE method can enhance the diversity of solutions and prevent local optima. By incorporating a chaotic mutation rate in DE, the population diversity can be further improved while avoiding stagnation. Additionally, the ergodicity and randomness of the chaotic mutation assist EHHO in avoiding premature convergence. The nonlinear escaping factor further enhances EHHO in transitioning from exploration to exploitation, which enabling its attainment of the global optimum solution. Overall, EHHO outperforms the original HHO algorithm in solving SOPs. However, there are certain composition functions, such as F18, F20, F24, and F28, where HHODE performance proposed by Birogul (2019) is superior to that of EHHO.

Table 2 Comparative analysis of EHHO and other published algorithms in Heidari et al. (2019) and Birogul (2019) for benchmark functions (F1–F13) with 30 dimensions
Full size table
Table 3 Comparative analysis of EHHO and other published algorithms in Heidari et al. (2019) and Birogul (2019) for benchmark functions (F1–F13) with 100 dimensions
Full size table
Table 4 Comparative analysis of EHHO and other published algorithms in Heidari et al. (2019) and Birogul (2019) for benchmark functions (F1–F13) with 500 dimensions
Full size table
Table 5 Comparative analysis of EHHO and other published algorithms in Heidari et al. (2019) and Birogul (2019) for benchmark functions (F1–F13) with 1000 dimensions
Full size table
Table 6 Statistical test results with 95% confidence interval for EHHO on benchmark functions (F1–F13) with varying dimensions as compared with those published in Heidari et al. (2019) and Birogul (2019)
Full size table
Table 7 Final rankings of each algorithm in Heidari et al. (2019) and Birogul (2019) for benchmark function F1–F13 with dimension of 30–1000
Full size table
Table 8 Results of benchmark functions (F14–F29) for EHHO vs its competitors in Heidari et al. (2019) and Birogul (2019)
Full size table

4.2.1 Runtime analysis

Table 11 presents the runtime (seconds) of EHHO for different benchmark functions and dimensions (30D, 100D, 500D, and 1000D), providing information into its computational efficiency and scalability. It takes more time to solve most benchmark functions as the number of dimensions increases, implying that the computational complexity of EHHO increases with larger problem dimensions. From Table 11, functions F1, F4, F5, F6, F8, F9, and F10 have lower runtimes across different dimensions. On the other hand, functions F3, F7, F11, F12, and F13 experience significant increases in runtimes with higher dimensions. This suggests that these functions may face scalability issues, as the algorithm takes longer to reach optimal solutions in higher-dimensional spaces. It is therefore essential to evaluate the scalability of the EHHO algorithm and find ways to improve its performance for higher-dimensional optimisation problems.

From Table 12, functions F15, F16, F17, F18, F19, and F20 have shorter completion times, which indicates that the algorithm can find satisfactory solutions for these functions rapidly. However, functions F14, F21, F22, and F23 take longer to complete, indicating that EHHO needs more computational power to find optimal solutions for these functions.

In addition, Table 12 presents the average runtime for functions F24–F29, which comprise rotated, shifted, and hybrid composition functions from the IEEE CEC 2005 competition (García et al. 2009). Function F29 has the shortest runtime, indicating that the algorithm is able to find satisfactory solutions faster for this function. F24 and F25–F27 have similar runtimes, with each run taking 47 s and 49 s, respectively. Function F28 takes the longest time to run, suggesting that it has more difficult optimisation properties that slow down the convergence of EHHO (Table 13).

To obtain a comprehensive understanding of the computational efficiency of EHHO, it is valuable to compare its runtimes with other competing algorithms on the same benchmark functions and dimensions. Unfortunately, the authors of these algorithms did not disclose their computational times. Nevertheless, this study has employed the same maximum iterations as those published in Heidari et al. (2019) and Birogul (2019).

4.3 Evaluation with multi-objective optimisation problems

4.3.1 Experimental setup and compared algorithms

MO-EHHO is applied to high-dimensional bi-objective problems without equality or inequality constraints and scalable tri-objective problems without equality or inequality constraints for performance evaluation. A total of 12 test functions are available, as follows:

  • ZDT benchmark functions (ZDT1-4,6) (Deb et al. 2002; Deb and Agrawal 1999)

  • DTLZ benchmark functions (DTLZ1-DTLZ7) (Deb et al. 2005).

The MO-EHHO performance is compared with those reported in Liu et al. (2020), Xiang et al. (2015), and Yang et al. (2022). The evaluation constitutes a comprehensive analysis of MO-EHHO to ascertain its effectiveness. A summary of performance comparison is as follows:

Table 9 Statistical test results with 95% confidence interval for EHHO on benchmark functions (F14–F29) as compared with those published in Heidari et al. (2019) and Birogul (2019)
Full size table
Table 10 Final rankings of each algorithm in Heidari et al. (2019) and Birogul (2019) for benchmark function F14–F29
Full size table
Table 11 Average runtime of EHHO for benchmark function F1–F13 on 30, 100, 500, 1000-dimension
Full size table
Table 12 Average runtime of EHHO for benchmark function F14–F23
Full size table
Table 13 Average runtime of EHHO for benchmark function F24–F29
Full size table

  • Comparison with a variety of MOEAs reported in Yang et al. (2022), i.e. CMPMOHHO (Yang et al. 2022), NSGA-II, SPEA2, NSGA-III (Deb and Jain 2013), PESA-II (Corne et al. 2001), CMOPSO (Zhang et al. 2018), CMOEA/D (Asafuddoula et al. 2012), MOEA/D-FRRMAB (Li et al. 2013), hpaEA (Chen et al. 2019), PREA (Yuan et al. 2020), ANSGA-III (Cheng et al. 2019), ar-MOEA (Yi et al. 2018), RPD-NSGA-II (Elarbi et al. 2017), and PICEA-g (Wang et al. 2012).

  • Comparison with a variety of MOEAs reported in Liu et al. (2020), i.e. MMOGWO (Liu et al. 2020), SPEA2 (Zitzler et al. 2001), NSGA-II (Deb et al. 2002), MOPSO (Coello et al. 2004), MOGWO (Mirjalili et al. 2016), MOALO (Mirjalili et al. 2017b), MOMVO algorithm (Mirjalili et al. 2017a), MOGOA (Mirjalili et al. 2018) and Multi-objective artificial bee colony (MOABC) algorithm (Akbari et al. 2012).

  • Comparison with a variety of MOEAs reported in Xiang et al. (2015) and Liu et al. (2020), i.e. PAES, SPEA2, NSGA-II, IBEA (Zitzler and Künzli 2004), OMOPSO (Lin et al. 2015), AbYSS (Nebro et al. 2008), CellDE (Durillo et al. 2008), MOEA/D, SMPSO (Lin et al. 2015), MOCell (Nebro et al. 2009), GDE3 (Kukkonen and Lampinen 2009) and eMOABC (Xiang et al. 2015).

Table 14 Mean values, standard deviation and ranking of MO-EHHO variants and other enhanced models in Yang et al. (2022) in terms of IGD for all test problems
Full size table

4.3.2 Performance metrics

Three common objective functions for evaluating the performance of a multi-objective algorithm in solving MOPs are as follows:

  • minimise the distance between the true PF and the obtained PS

  • maximise the spread of the obtained PS along with the true PF

  • maximise the extent of the obtained PS in covering the true PF

Based on these objectives, the following performance metrics are used to assess the MO-EHHO efficacy.

Convergence metric (\(\gamma \)): the distance between the PF and the obtained PS (Deb et al. 2002), i.e.

$$\begin{aligned} Y=\frac{\sum _{i=1}^{n}d_i}{n} \end{aligned}$$
(29)

Diversity metric (\(\Delta \)): the degree of spread achieved by the obtained PS (Deb et al. 2002), i.e.

$$\begin{aligned} \Delta =\frac{d_\textrm{min}+d_\textrm{max}+\sum _{i=1}^{n-1}|d_i-\bar{d}|}{d_\textrm{min}+d_\textrm{max}+(n-1)\bar{d}} \end{aligned}$$
(30)
Table 15 Statistical comparison of MO-EHHO and other enhanced models in Yang et al. (2022) with 95% confidence interval on each metric
Full size table
Table 16 Final rankings of each algorithm on IGD metric with other enhanced models in Yang et al. (2022)
Full size table

Generational distance (GD): the distance between the true PF and the obtained PS (Van Veldhuizen and Lamont 1998), i.e.

$$\begin{aligned} GD=\frac{\sqrt{\sum _{i=1}^{n}d_i^2}}{n} \end{aligned}$$
(31)

Inverted generational distance (IGD): the distance between each solution composing the true PF and the obtained PS (Zitzler and Thiele 1999), i.e.

$$\begin{aligned} IGD=\frac{\sqrt{\sum _{i=1}^{m}(d_i)^2}}{m} \end{aligned}$$
(32)

where i the index of a solution set, \(d_i\) is the Euclidean distance between the ith solution in the non-dominated set and the ith solution in the true PF. n is the number of obtained PS, m is the number of solutions in the true PF. In addition, \(d_\textrm{min}\) and \(d_\textrm{max}\) are the minimum and maximum Euclidean distances of the extreme non-dominated solution, respectively, in the objective space, \(\bar{d}\) is the mean of all \(d_i\).

Table 17 Statistical test results with 95% confidence interval for each MO-EHHO variant on each metric as compared with those published in Liu et al. (2020)
Full size table
Table 18 Final rankings of each algorithm on each metric with algorithms in Liu et al. (2020)
Full size table
Table 19 Mean values, standard deviation and ranking of MO-EHHO and several improved MOEAs in Liu et al. (2020) and Xiang et al. (2015) in IGD for all test problems
Full size table

4.4 Quantitative results of MO-EHHO and discussion

4.4.1 Comparison between MO-EHHO and other enhanced models in Yang et al. (2022)

MO-EHHO and other enhanced models presented in Yang et al. (2022) are compared using the ZDT and DTLZ functions. In accordance with the experimental procedure in Yang et al. (2022), the population size and external archive are set to 100. The number of maximum function evaluations of ZDT is 30,000, i.e. the same as that in Yang et al. (2022). However, the number of maximum function evaluations of DTLZ is 300,000 in Yang et al. (2022), as compared with only 50,000 for MO-EHHO in this research. In this comparison, 18 algorithms are compared with MO-EHHO, i.e. CMPMO-HHO, NSGA-II, SPEA2, NSGA-III, PESA-II, CMOPSO, C-MOEA/D, MOEA/D- FRRMAB, hpaEA, PREA, ANSGA-III, ar-MOEA, RPD-NSGA-II, PICEA-g, MOHHO/SP (multiobjective HHO algorithm with single population), CMPMOHHO/NoP (CMPMO-HHO without LCSDP) and CMPMOHHO/SES (CMPMO-HHO with single elite selection), and CMPMO-GA which is a CMPMO/des-based many-objective GA.

The average results and standard deviation of MO-EHHO and those presented in Yang et al. (2022) are depicted in Table 14. MO-EHHO generates the best or second-best scores on 9 out of 12 test problems in terms of IGD. Table 15 presents the sign test results of all MO-EHHO in terms of IGD as compared with those in Yang et al. (2022). MO-EHHO achieves comparable IGD results as compared with those of CMPMO-HHO, NSGA-III, NSGA-II, SPEA2, ANSGA-III, and ar-MOEA, but outperforms others at the 95% confidence interval with \(p<0.05\). Table 16 summarises the ranking outcomes of all algorithms. MO-EHHO is ranked in the top 1 position as the overall best performer in solving the ZDT and DTLZ problems. Note that the number of maximum function evaluations of MO-EHHO is lower than that in Yang et al. (2022), i.e. 50,000 versus 300,000, indicating the effectiveness of MO-EHHO in tackling MOPs.

4.4.2 Comparison between MO-EHHO and other algorithms published in Liu et al. (2020)

The performance of MO-EHHO is evaluated using the ZDT and DTLZ benchmark functions. The obtained results are compared with those published in Liu et al. (2020). In accordance with the experimental procedure in Liu et al. (2020), the maximum numbers of function evaluations are set to 25,000 and 50,000 for ZDTs and DTLZ problems, respectively; the population size and external archive size are set to 100; while the maximum numbers of iterations of each run are set to \(25,000 / 100 = 250\) for ZDT problems and \(50,000 / 100 = 500\) for DTLZ problems. The experiment is conducted in a Python environment. The obtained results are tabulated in Tables 27, 28, 29 and 30 in the Appendix. Besides, Table 17 presents the sign test results of MO-EHHO as compared with those of MMOGWO, SPEA2, NSGA-II, MOPSO, MOGWO, MOALO, MOMVO, MOGOA, and MOABC.

From Table 17, MO-EHHO outperforms SPEA2, NSGA-II and MOABC in terms of both \(\gamma \) and GD. In addition, MO-EHHO achieves better results than those of MOGOA in terms of GD. It should be noted that the \(\Delta \) metric evaluates the spread among the non-dominated solutions obtained by an algorithm, indicating the diversity property of the solutions. In terms of \(\Delta \), MO-EHHO achieves comparable results with those of SPEA2, NSGA-II, MOGWO, and MOABC. It yields better results as compared with those of MMOGWO, MOPSO, MOALO, MOMVO, and MOGOA at the 95% significance level (\(\alpha = 0.05\)). MO-EHHO depicts a superior performance as compared with those of its competitors. MO-EHHO results show a statistically significant difference in performance at the 95% confidence level as compared with those of MMOGWO, SPEA2, NSGA-II, MOPSO, MOGWO, MOALO, MOMVO, MOGOA, and MOABC, indicating a better balance between diversity and convergence by MO-EHHO.

From the analysis above, MO-EHHO outperforms their competitors at the 95% confidence interval in terms of IGD. The IGD metric evaluates both the convergence and diversity properties of an algorithm. Hence, the solutions produced by MO-EHHO have a good balance between convergence and diversity. Besides that, Table 18 depicts the ranking outcome of the algorithms on each metric. MO-EHHO ranks the first in terms of \(\gamma \), GD and IGD. Moreover, MOPSO occupies the top rank in terms of \(\Delta \), which is the diversity metric. In summary, MO-EHHO has a good overall performance in terms of convergence, but is inferior in diversity as compared with NSGA-II and MOPSO.

4.4.3 Comparison between MO-EHHO and several improved MOEA models in Liu et al. (2020)

MO-EHHO is compared with a variety of MOEA models presented in Liu et al. (2020) and Xiang et al. (2015), namely MMOGWO, PAES, SPEA2, NSGA-II, IBEA, OMOPSO, AbYSS, CellDE, MOEA/D, SMPSO, MOCell, GDE3, and eMOABC. The ZDTs and DTLZs benchmark functions are used for performance evaluation and comparison. In accordance with the experimental procedure in Liu et al. (2020) and Xiang et al. (2015), the number of maximum function evaluations is set to 50,000 for all problems, and the population size and external archive are set to 100, respectively. As such, the number of maximum iteration is \(50,000/100 = 500\) for each of the 30 independently runs. Only the IGD metric is used for performance evaluation, as per the results presented in Liu et al. (2020) and Xiang et al. (2015). This experiment is performed in a Python environment.

The mean IGD results of MO-EHHO over 30 independent runs are shown in Table 19. MO-EHHO is the best algorithm, producing the best scores on 10 out of 12 test problems. Table 20 presents the sign test outcomes of MO-EHHO against those of other algorithms. MO-EHHO demonstrates a superior performance as compared with those from its competitors in a statistical context. From Table 21, MO-EHHO is the best in ranking against its competitors. In short, MO-EHHO is the best among other MOEA models.

Table 20 Statistical comparison of MO-EHHO and several improved MOEAs in Liu et al. (2020) and Xiang et al. (2015) with 95% confidence interval on each metric
Full size table
Table 21 Final rankings of each algorithm on IGD metric with several improved MOEAs in Liu et al. (2020) and Xiang et al. (2015)
Full size table

5 Conclusions

In this study, we have proposed enhancements to the HHO algorithm, namely EHHO and MO-EHHO to solve SOPs and MOPs, respectively. Both EHHO and MO-EHHO models have been evaluated with 29 SOPs and 12 MOPs. Specifically, EHHO has been evaluated using a variety of single-objective benchmark problems, including unimodal functions F1–F7, multimodal functions F8–F23, and composition functions F24–F29. Two sets of well-known multi-objective benchmark functions, i.e. ZDT and DTLZ, have been employed to evaluate MO-EHHO. Four performance metrics, i.e. \(\gamma \), \(\Delta \), GD, and IGD, have been utilised to measure the convergence and diversity properties of MO-EHHO. In addition, the sign test is employed to deduce a statistical conclusion for the performance comparison between two compared algorithms at the significance level of \(\alpha =0.05\). The average ranking method has also been adopted to reveal accuracy and stability of an algorithm against other competitors. All algorithms have ranked based on their average results pertaining to the total number of benchmark functions.

The DE scheme has been integrated into EHHO, while the chaos theory has been utilised to formulate its mutation factor. It leverages the DE/best/1 mutation scheme, where the "best" indicates that the non-dominated solution is stored in the external archive, while "1" represents one mutated vector is used. The nonlinear exploration factor contributes towards the diversification capability in the early exploration phase, which facilitates a smooth changeover from exploration to exploitation. Additionally, the incorporation of DE into EHHO and the mutation strategy in the population are useful to prevent EHHO from falling into local optima. Despite its strengths, EHHO struggles in certain benchmark problems that involve higher dimensions and more complex search landscapes in comparison with those from the HHODE variants. For MOPs, the non-dominated sorting strategy from NSGA-II has been employed in MO-EHHO. MO-EHHO is able to exploit the Pareto optimal solutions while preserving its diversity.

The results of EHHO and MO-EHHO are compared with those from popular optimisation algorithms published in the literature. The results indicate that in most SOPs and MOPs, EHHO and MO-EHHO perform better than their competitors, as presented in Sect. 4. For further work, several research directions can be pursued. Firstly, the proposed models still have room for improvement. In particular, MO-EHHO can be combined with other multi-objective algorithms to attain more diverse solutions. Secondly, the proposed models can be applied to various optimisation tasks, including job-shop scheduling and other real-world problems.