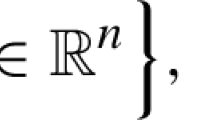1 Introduction

Machine learning is concerned with developing computer techniques and algorithms that can learn (Weston et al. 2000). Machine learning algorithms can essentially be divided into Supervised learning, Unsupervised and Data clustering (Forman et al. 2003; Nolfi et al. 1994).

All learning algorithms perform model selection and parameter estimation based on one or multiple criteria; in such a framework numerical optimization plays a significant role (Gambella et al. 2021). In this paper, we focus on Classification, a supervised learning area based on the separation of sets in finite-dimensional spaces (the Feature ones) by means of appropriate separation surfaces. The most popular approach to classification is the Support Vector Machine (SVM) model, where one looks for a hyperplane separating two given sample sets (Cristianini et al. 2000).

Optimization methods that seek sparsity of solutions have recently received considerable attention (Bach et al. 2011; Bauschke and Combettes 2011; Bertsimas et al. 2016), mainly motivated by the need of tackling Feature selection problems, defined as ”the search for a subset of the original measurements features that provide an optimal tradeoff between probability error and cost of classification” Swain and Davis (1981). The Feature selection methods are discussed in Al-Ani et al. (2013); Cervante et al. (2012).

In this paper, we tackle Feature Selection (FS) in the general setting of sparse optimization, where one is faced to the problem (Gaudioso et al. 2018a):

$$\begin{aligned} \begin{aligned}&\underset{\textbf{x} \in {\mathbb {R}}^{n} }{\text {Minimize}}{} & {} f(x)+\Vert x\Vert _{0} \\ \end{aligned} \end{aligned}$$
(1)

where \( f: {\mathbb {R}}^{n} \rightarrow {\mathbb {R}} \) and \( \Vert .\Vert _{0} \) is the \( l _{0} \) pseudo-norm, which counts the number of nonzero components of any vector. Sometimes sparsity of the solution, instead of acting on the objective function, is enforced by introducing a constraint on the \( l _{0} \) pseudo-norm of the solution, thus defining a cardinality-constrained problem (Gaudioso et al. 2018b, 2020; Chen et al. 2010; Pilanci et al. 2015).

In many applications, the \( l _{0} \) pseudo-norm in (1) is replaced by the \( l _{1} \)-norm, which is definitely more tractable from the computational point of view, yet ensuring sparsity, to a certain extent (Wright 2012).

In the seminal paper (Watson 1992), a class of polyhedral norms (the \( k \)-norms), intermediate between \( \Vert .\Vert _{1} \) and \( \Vert .\Vert _{\infty } \), is introduced to obtain sparse approximation solutions to systems of linear equations. Some other norms have been used in different applications (Jafari-Petroudi and Pirouz 2016; Petroudi et al. 2022; Jafari-Petroudi and Pirouz 2015b, a; Petroudi and Pirouz 2015). The use of other norms to recover sparsity is described in Gasso et al. (2009). In more recent years the use of \( k \)-norms has received much attention and has led to several proposals for dealing with \( l _{0} \) pseudo-norm cardinality constrained problem (Gotoh et al. 2018; Hempel and Goulart 2014; Soubies et al. 2017; Wu et al. 2014).

An alternative way to deal with Feature selection is the multi-objective approach discussed in the Hamdani et al. (2007). Multi-objective optimization is a basic process in many fields of science, including mathematics, economics, management, and engineering applications (Ehrgott 2005). In most real situations, the decision-maker needs to make tradeoffs between disparate and conflicting design objectives rather than a single one. Having conflicting objectives means that it is not possible to find a feasible solution where all the objectives could reach their individual optimal, but one must find the most satisfactory compromise between the objectives. These compromise solutions, in which none of the objective functions can be improved in value without impairing at least one of the others, are often referred to as Pareto optimal or Pareto efficient (Neshatian and Zhang 2009). The set of all objective function values at the Pareto and weak Pareto solutions is said to be the Pareto front (or efficient set) of the multi-objective optimization problem (MOP) in the objective value space (Dolatnezhadsomarin et al. 2019). In general, solving a MOP is associated with the construction of the Pareto frontier. The problem of finding the whole solution set of a MOP is important in applications (Ceyhan et al. 2019). Many methods have been proposed to find the Pareto front of the multi-objective optimization problems (See Ghane-Kanafi and Khorram (2015); Pirouz and Khorram (2016); Pirouz and Ramezani Paschapari (2019); Das and Dennis (1998); Dutta and Kaya (2011); Fonseca et al. (1993); Pirouz et al. (2021)).

In this paper, we have specifically emphasized the application of sparse optimization in Feature Selection for SVM classification. We propose a novel model for sparse optimization based on the polyhedral k-norm. Also, to demonstrate the advantages of considering SVM classification models as multi-objective optimization problems, we propose some multi-objective reformulation of these models. In these cases, a set of Pareto optimal solutions is obtained instead of one in the single-objective cases.

The rest of the paper is organized as follows. Section 2 contains some basic concepts and notations about binary classification, the Support Vector Machine model and Feature Selection as a sparse optimization problem. Our approach to sparse optimization via k-norms is presented in Sect. 3, together with a discussion on possible relaxation and algorithmic treatment. In Sect. 4 some basic concepts and notations of multi-objective optimization problems (MOPs) are resumed and a reformulation of the feature selection model in the form of MOPs is given. The results of some numerical experiments on benchmark datasets are in Sect. 5. Section 6 is devoted to conclusions.

2 Basic concepts and notations

This section presents some basic concepts and notations that make more accessible the understanding of this paper. We start by giving a brief description of the classification problem (especially binary classification) in supervised learning. We then focus on a specific task: support vector machine, feature selection, and sparse optimization.

2.1 Binary classification

In this paper, we consider the classification task in the basic form of binary classification. In binary classification we have the representation of two classes of individuals in the form of two finite sets \( {\mathcal {A}} \) and \( {\mathcal {B}} \subset {\mathbb {R}}^{n} \), such that \( {\mathcal {A}} \cap {\mathcal {B}} =\emptyset \), and we want to classify an input vector \( x \in {\mathbb {R}}^{n} \) as a member of the class represented by \( {\mathcal {A}} \) or that by \( {\mathcal {B}} \). The training set for binary classification is defined as follows (Rinaldi 2009):

$$\begin{aligned} T= & {} \bigl \{ \left( x_{i}, y_{i}\right) : x_{i} \in {\mathbb {R}}^{n} , \quad y_{i} \in \left\{ \pm 1\right\} , \quad \mathrm{{and}} \nonumber \\{} & {} \quad i=1,\ldots ,m \bigr \} \end{aligned}$$
(2)

with the two sets \( {\mathcal {A}} \) and \( {\mathcal {B}} \) labelled by \( +1 \) and \( -1 \), respectively. The functional dependency \( f: {\mathbb {R}}^{n} \rightarrow \left\{ \pm 1\right\} \), which determines the class membership of a given vector \( x \), assumes the following form Rinaldi (2009); Rumelhart et al. (1986); Haykin and Network (2004):

$$\begin{aligned} f\left( x\right) = \left\{ \begin{array}{ll} +1, &{} if \quad x \in {\mathcal {A}} \\ -1, &{} if \quad x \in {\mathcal {B}} \\ \end{array} \right. \end{aligned}$$

Assume that the two finite point sets \( {\mathcal {A}} \) and \( {\mathcal {B}} \) in \( {\mathbb {R}}^{n} \) consist of \( m \) and \( k \) points, respectively. They are associated with the matrices \( A \in {\mathbb {R}}^{m \times n} \) and \( B \in {\mathbb {R}}^{k \times n} \), where each point of a set is represented as a row of the corresponding matrix. In the classic SVM method, we want to construct a separating hyperplane:

$$\begin{aligned} \begin{aligned} P = \left\{ x: x \in {\mathbb {R}}^{n} , \quad x^{T}w=\gamma \right\} \end{aligned} \end{aligned}$$
(3)

with normal \( w \in {\mathbb {R}}^{n} \) and distance (Rinaldi 2009):

$$\begin{aligned} \begin{aligned} \dfrac{\mid \gamma \mid }{\Vert w\Vert _{2}} \end{aligned} \end{aligned}$$
(4)

to the origin. The separating plane P determines two open halfspaces:

  • \( P_{1} = \left\{ x: x \in {\mathbb {R}}^{n} , \quad x^{T}w>\gamma \right\} \) it is intended to contain most of the points belonging to \( {\mathcal {A}} \).

  • \( P_{2} = \left\{ x: x \in {\mathbb {R}}^{n} , \quad x^{T}w<\gamma \right\} \) it is intended to contain most of the points belonging to \( {\mathcal {B}} \).

Therefore, letting e be a vector of ones of appropriate dimension, we want to satisfy the following inequalities:

$$\begin{aligned} \begin{aligned} A w > e\gamma , \hspace{0.2cm} B w < e\gamma \end{aligned} \end{aligned}$$
(5)

to the possible extent. The problem can be equivalently put in the form.

$$\begin{aligned} \begin{aligned} Aw \ge e\gamma +e, \quad Bw \le e\gamma -e \end{aligned} \end{aligned}$$
(6)

Conditions (5) and (6) are satisfied if and only if the convex hulls of \( {\mathcal {A}} \) and \( {\mathcal {B}} \) are disjoint (the two sets are linearly separable) (Rinaldi 2009).

Application of Feature Selection to SVM, as we will see next, amounts to suppressing as many of the components of w as possible.

2.2 Support vector machine and feature selection

In real-world classification problems based on supervised learning, the information available are the vectors \(a_i\)’s and \(b_l\)’s (the rows of A and B, respectively) defining the (labelled) training set. Nothing is known about the mapping function \( f \) (John et al. 1994). A separating plane is generated by minimizing a weighted sum of distances of misclassified points to two parallel planes that bound the sets and which determine the separating plane midway between them. In the Support Vector Machine (SVM) approach in addition to minimizing the error function, that is the weighted sum of distances of misclassified points to the bounding planes, we also maximize the distance (referred to as the separation margin) between the two bounding planes that generate the separating plane (Bradley and Mangasarian 1998).

The standard formulation of SVM is the following, where variables \(y_i\) and \(z_l\) represent the classification error associated with the points of \({\mathcal {A}}\) and \({\mathcal {B}}\), respectively:

$$\begin{aligned} \begin{aligned}&{\text {Min}} \quad C \left( \sum _{i=1} ^{m_{1}} y_{i} + \sum _{l=1} ^{m_{2}} z_{l} \right) + \Vert w \Vert _{2}^{2} \\&\quad \text {subject to}\\&\quad -a_{i}^{T}w+\gamma +1 \le y_{i}, \quad i=1, \ldots , m_{1} \\&\quad \quad b_{l}^{T}w-\gamma +1 \le z_{l}, \quad l=1, \ldots , m_{2} \\&\quad \quad y_{i}, z_{l} \ge 0. \\ \end{aligned} \end{aligned}$$
(7)

Positive parameter C defines the trade-off between the objectives of minimizing the classification error and maximizing the separation margin.

Feature selection is primarily performed to select informative features (Rinaldi 2009), and has become one of the most important issues in the field of machine learning (Rinaldi et al. 2010).

Referring to the above model, the goal is to construct a separating plane that gives good performance on the training set while using a minimum number of problem features. This objective can be pursued by a looking for a normal w to the separating hyperplane characterized by the smallest possible number of nonzero components. This can be achieved by adding a sparsity enforcing term to the objective function (Rinaldi 2009; Rinaldi et al. 2010).

As we will see next, a companion model aimed at suppressing as many elements of w as possible, known as LASSO approach, is obtained by replacing \( l_{2} \)-norm with the \( l_{1}\) (Rinaldi 2009; Bradley and Mangasarian 1998).

2.3 Sparse optimization

As previously mentioned, in sparse SVM the objective is to control the number of nonzero components of the normal vector to the separating hyperplane while maintaining satisfactory classification accuracy (Gaudioso et al. 2020). Therefore, the following two objectives should be minimized (Rinaldi 2009):

  • The number of misclassified training data;

  • The number of nonzero elements of vector w.

We tackle Feature Selection in SVM as a special case of sparse optimization by stating the following problem (Gaudioso et al. 2020; Rinaldi et al. 2010):

$$\begin{aligned} \begin{aligned}&{\text {Min}} \quad C \left( \sum _{i=1} ^{m_{1}} y_{i} + \sum _{l=1} ^{m_{2}} z_{l} \right) + \Vert w \Vert _{0} \\&\quad \text {subject to}\\&\quad -a_{i}^{T}w+\gamma +1 \le y_{i}, \quad i=1, \ldots , m_{1} \\&\quad \quad b_{l}^{T}w-\gamma +1 \le z_{l}, \quad l=1, \ldots , m_{2} \\&\quad \quad y_{i}, z_{l} \ge 0 \\ \end{aligned} \end{aligned}$$
(8)

where \( \Vert . \Vert _{0} \) is the \( l_{0} \)-pseudo-norm, which counts the number of nonzero components of any vector. This problem is equivalent to the following parametric program (Rinaldi 2009):

$$\begin{aligned} \begin{aligned}&{\text {Min}} \quad C \left( \sum _{i=1} ^{m_{1}} y_{i} + \sum _{l=1} ^{m_{2}} z_{l} \right) + \sum _{i=1} ^{n} s\left( v_{i} \right) \\&\quad \text {subject to}\\&\quad -a_{i}^{T}w+\gamma +1 \le y_{i}, \quad i=1, \ldots , m_{1} \\&\quad \quad b_{l}^{T}w-\gamma +1 \le z_{l}, \quad l=1, \ldots , m_{2} \\&\quad \quad -v \le w \le v \\&\quad \quad y, z \ge 0 \\ \end{aligned} \end{aligned}$$
(9)

Where \( s: {\mathbb {R}} \rightarrow {\mathbb {R}}^{+} \) is the step function such that \( s\left( t\right) =1 \) for \( t>0 \) and \( s\left( t\right) =0 \) for \( t \le 0 \). This is the fundamental feature selection problem in the general setting of sparse optimization, as defined in Mangasarian (1996).

A simplification of the models (8) and (9) can be obtained by replacing the \( l_{0} \)-pseudo-norm with the \( l_{1} \)-norm, thus obtaining:

$$\begin{aligned} \begin{aligned}&{\text {Min}} \quad C \left( \sum _{i=1} ^{m_{1}} y_{i} + \sum _{l=1} ^{m_{2}} z_{l} \right) + e^{T} v \\&\quad \text {subject to}\\&\quad -a_{i}^{T}w+\gamma +1 \le y_{i}, \quad i=1, \ldots , m_{1} \\&\quad \quad b_{l}^{T}w-\gamma +1 \le z_{l}, \quad l=1, \ldots , m_{2} \\&\quad \quad -v \le w \le v \\&\quad \quad y, z \ge 0 \\ \end{aligned} \end{aligned}$$
(10)

It has been demonstrated that model (10) exhibits in practice good sparsity properties of the solution.

Our approach to feature selection based on sparse optimization is presented in the next section.

3 A new approach to feature selection

This section introduces a new Feature Selection approach based on the use of k-norm in Sparse Optimization (see Gaudioso et al. (2020) and Gaudioso and Hiriart-Urruty (2022)). Then a relaxation for the model is provided. Finally, some differential properties and some algorithms for solving the proposed nonlinear model are introduced.

We consider, in a general setting, the following sparse optimization problem:

$$\begin{aligned} \begin{aligned}&\underset{\textbf{x} \in {\mathbb {R}}^{n} }{\text {Minimize}} \quad f(x)+\Vert x\Vert _{0} \\&\quad \text {subject to}\\&\quad \quad x \in P, \\ \end{aligned} \end{aligned}$$
(11)

where we assume that \( f: {\mathbb {R}}^{n} \rightarrow {\mathbb {R}} \) is convex and \( f\left( x\right) \ge 0 \) for all \( x \in {\mathbb {R}}^{n} \), as it is the case when f is the error function in the SVM model. We introduce now the k-norm.

Definition 1

. (k-norm). Gaudioso et al. (2020). The k-norm is defined as the sum of k largest components (in modulus) of the vector X:

$$\begin{aligned} \begin{aligned}&\Vert x\Vert _{\left[ k\right] }=\mid x_{i1} \mid + \mid x_{i2} \mid + \ldots + \mid x_{ik} \mid \\&\quad where \quad \mid x_{i1} \mid \ge \mid x_{i2} \mid \ge \ldots \ge \mid x_{in} \mid \\ \end{aligned} \end{aligned}$$
(12)

The k-norm is polyhedral, it is intermediate between \( \Vert .\Vert _{1} \) and \( \Vert .\Vert _{\infty } \) and enjoys the fundamental property linking \( \Vert .\Vert _{\left[ k\right] } \) to \(\Vert .\Vert _0\), \(1 \le k\le n\):

$$\begin{aligned} \Vert x\Vert _0 \le k \Leftrightarrow \Vert x\Vert _1-\Vert x\Vert _{[k]} =0. \end{aligned}$$
(13)

The property above is used to define the following Mixed Integer Nonlinear Programming (MINLP) formulation of problem (11), where we have introduced the set of binary variables \(y_k\), \(k=1,\ldots ,n\).

$$\begin{aligned} \begin{aligned}&\underset{\textbf{x} \in {\mathbb {R}}^{n} }{\text {Minimize}} \quad f(x)-\sum _{k=1}^{n} y_{k} \\&\quad \text {subject to}\\&\quad \quad \Vert x\Vert _{\left[ k\right] } \ge \Vert x\Vert _{1} y_{k},\quad k=1, \ldots , n \\&\quad \quad x \in P, \\&\quad \quad y_k=0, 1,\quad k=1,\ldots ,n. \\ \end{aligned} \end{aligned}$$
(14)

Note that, at the optimum of (14), the following hold:

$$\begin{aligned} y_{k} = \left\{ \begin{array}{ll} 0, &{} \quad if \quad \Vert x\Vert _{\left[ k\right] } < \Vert x\Vert _{1} \\ 1, &{} \quad if \quad \Vert x\Vert _{\left[ k\right] } = \Vert x\Vert _{1}, \\ \end{array} \right. \end{aligned}$$
(15)

thus, taking into account (13), \(y_k=1\) if \(\Vert x\Vert _0 \le k\). Summing up we have:

$$\begin{aligned} \begin{aligned} \sum _{k=1}^{n} y_{k} = n - \Vert x\Vert _{0} + 1 \Rightarrow \Vert x\Vert _{0} = n - \sum _{k=1}^{n} y_{k} + 1, \end{aligned} \end{aligned}$$
(16)

from which we obtain that maximization of \(\displaystyle \sum _{k=1}^{n} y_{k}\) implies minimization of \(\Vert x\Vert _{0}\).

We can relax the integrality constraint on \( y_{k} \) in problem (14) by setting \( y_{k} \in \left[ 0, 1\right] \) for \( k=1, \ldots , n \). We observe that at the optimum of the relaxed problem all constraints \(\Vert x\Vert _{\left[ k\right] } \ge \Vert x\Vert _{1} y_{k}\) are satisfied by equality, which implies that for variables \(y_k\) it is \(y_k = \dfrac{\Vert x\Vert _{\left[ k\right] }}{\Vert x\Vert _{1}}\) and, consequently, they can be eliminated, obtaining:

$$\begin{aligned} \begin{aligned}&\underset{\textbf{x} \in {\mathbb {R}}^{n} }{\text {Minimize}} \quad f(x)- \frac{1}{\Vert x\Vert _{1}} \sum _{k=1}^{n} \Vert x\Vert _{\left[ k\right] } \\&\quad \text {subject to}\\&\quad \quad x \in P \\ \end{aligned} \end{aligned}$$
(17)

From now on, we will consider problem (17) as our main problem and call it “Our Model”. We rewrite it in following fractional programming form:

$$\begin{aligned} \begin{aligned}&\underset{\textbf{x} \in {\mathbb {R}}^{n} }{\text {Minimize}} \quad \dfrac{f\left( x\right) \Vert x\Vert _{1} - \sum _{k=1}^{n} \Vert x\Vert _{\left[ k\right] }}{\Vert x\Vert _{1}} \\&\quad \text {subject to}\\&\quad \quad x \in P \\ \end{aligned} \end{aligned}$$
(18)

Problem above can be tackled via Dinkelbach’s method (Rodenas et al. 1999), which consist in solving the scalar nonlinear equation \( F\left( p\right) = 0 \) where:

$$\begin{aligned} \begin{aligned} F\left( p\right) = \underset{x \in P \subset {\mathbb {R}}^{n} }{\text {Min}} \hspace{0.2cm} \underbrace{f(x) \Vert x\Vert _{1} - \sum _{k=1}^{n} \Vert x\Vert _{\left[ k\right] } - p \Vert x\Vert _{1}}_{f_p(x)}. \\ \end{aligned} \end{aligned}$$
(19)

Remark 1

Calculation of \( F\left( p\right) \) amounts to solving an optimization problem in DC (Difference of Convex) form. Observe, in fact, that function \(f(x) \Vert x\Vert _{1}\) is convex, being the product of two convex and non-negative functions. Thus function \(f_p(x)\) can be put in DC form \(f_p(x)=f^{(1)}_p(x)- f^{(2)}_p(x)\) by letting:

$$\begin{aligned} \left\{ \begin{array}{cll} f^{(1)}_p(x)= &{} f(x) \Vert x\Vert _{1}, \\ f^{(2)}_p(x)= &{} \displaystyle \sum _{k=1}^{n} \Vert x\Vert _{\left[ k\right] } + p \Vert x\Vert _{1}, \end{array} \right. \end{aligned}$$
(20)

\( \text{ if } \,\, p \ge 0 \), and:

$$\begin{aligned} \left\{ \begin{array}{cll} f^{(1)}_p(x) = &{} f(x) \Vert x\Vert _{1}- p \Vert x\Vert _{1}, \\ f^{(2)}_p(x) = &{} \displaystyle \sum _{k=1}^{n} \Vert x\Vert _{\left[ k\right] }, \end{array} \right. \end{aligned}$$
(21)

\( \text{ if } \,\, p< 0 \).

Remark 2

Function \(f_p(x)\) is nonsmooth. Thus the machinery provided by the literature on optimization of nonsmooth DC functions can be fruitfully adopted to tackle (19) (see Gaudioso et al. (2018a, 2018b) and the references therein). We recall some differential properties of the k-norm. In particular, given any \( x \in {\mathbb {R}}^{n} \), and denoting by \( J_{\left[ k\right] } \left( {\bar{x}}\right) = \left\{ j_{1}, \ldots , j_{k} \right\} \) the index set of k largest absolute-value components of \( {\bar{x}} \), a subgradient \( g^{\left[ k\right] } \in \partial \Vert {\bar{x}}\Vert _{\left[ k\right] } \) can be obtained as Gaudioso et al. (2020, 2017):

$$\begin{aligned} g^{\left[ k\right] }_{j} = \left\{ \begin{array}{ll} 1, &{} \quad if \quad j \in J_{\left[ k\right] } \left( {\bar{x}}\right) \quad \mathrm{{and}} \quad {\bar{x}}_{j} \ge 0 \\ -1, &{} \quad if \quad j \in J_{\left[ k\right] } \left( {\bar{x}}\right) \quad \mathrm{{and}} \quad {\bar{x}}_{j} < 0 \\ 0, &{} \quad \mathrm{{otherwise}} \\ \end{array} \right. \end{aligned}$$
(22)

Note that the subdifferential \( \partial \Vert .\Vert _{\left[ k\right] } \) is a singleton (i.e. the vector k-norm is differentiable) any time the set \( J_{\left[ k\right] } \left( .\right) \) is uniquely defined.

In the next section, we will first introduce some basic concepts in the field of multi-objective optimization problems and then we will present the previous models in the form of multi-objective optimization problems.

4 Multi-objective optimization problem and reformulated feature selection problems

A Multi-objective optimization problem (MOP) is given as follows (Ehrgott 2005):

$$\begin{aligned} \begin{aligned}&{\text {Min}} \quad f\left( x\right) =\left( f_{1}\left( x\right) , \ldots , f_{p}\left( x\right) \right) \\&\quad \text {subject to}\\&\quad \quad x \in X \\ \end{aligned} \end{aligned}$$
(23)

where \( X \subseteq {\mathbb {R}}^{n} \), and the objective functions \( f_{k}: {\mathbb {R}}^{n} \rightarrow {\mathbb {R}} \), \( k=1, \ldots ,p \) are continuous. The image of the feasible set X under the objective function mapping f is denoted as \( Y = f\left( X\right) \). Assuming that at least two objective functions are conflicting in (23), no single \( x \in X \) would generally minimize all \( f_{k}\)’s simultaneously. Therefore, Pareto optimality or Pareto efficiency come into play (Ehrgott 2005).

In Pirouz and Khorram (2016) the following computational algorithm based on the \( \epsilon \)-constraint method has been proposed for MOP.

In Phase I, solve the following single-objective optimization problems for \( k=1, \ldots ,p \):

$$\begin{aligned} \begin{aligned}&{\text {Min}} \quad f_{k}\left( x\right) \\&\quad \text {subject to}\\&\quad \quad x \in X, \\ \end{aligned} \end{aligned}$$
(24)

and let \( x_{1}^{*}, \ldots , x_{p}^{*} \) be the optimal solutions of these problems, respectively. Then in the space of objective functions the restricted region is defined as follows, for \( k=1, \ldots ,p \):

$$\begin{aligned} \begin{aligned}&f_{k}\left( x_{k}^{*}\right) \le f_{k}\left( x\right) \le \left( \underset{i=1,\ldots , p; i \ne k }{\text {Max}} \quad \left\{ f_{k}\left( x_{i}^{*}\right) \right\} \right) \end{aligned} \end{aligned}$$
(25)

Pareto optimal solutions will be searched only inside this restricted region. Note that, according to the definition of the Pareto optimal solution, there is no any Pareto solution outside this restricted region (Pirouz and Khorram 2016).

In Phase II, the following steps are performed in order:

Step 1: For arbitrary values \( d\in {\mathbb {N}} \), the step length \( \Delta _{k} \) determine as follows:

$$\begin{aligned} \begin{aligned} \Delta _{k}&= \frac{(\max _{i=1,\ldots , p; i\ne k} \{f_{k}(x^{*}_{i})\})-f_{k}(x^{*}_{k})}{d}, \end{aligned} \end{aligned}$$
(26)

Step 2: In each stage, for any arbitrary \( j \in \{1,\ldots , p\} \) the following single-objective optimization problems will solve for \( l=0,1,\ldots , d \):

$$\begin{aligned} \begin{aligned}&{\text {Min}} \quad f_{j}\left( x\right) \\&\quad \text {subject to}\\&\quad \quad f_{k}\left( x\right) \le \left( \max _{i=1,\ldots , p; i\ne k} \{f_{k}(x^{*}_{i})\}\right) \\&\quad -l*\Delta _{k}, \quad k=1,\ldots , p; k \ne j \\&\quad \quad x \in X \\ \end{aligned} \end{aligned}$$
(27)

According to the following theorem, this method can give the approximation of the Pareto frontier. For more details, refer to Pirouz and Khorram (2016).

Table 1 The results of Test problem 1 for \( C = 10 \)
Full size table
Fig. 1
figure 1

The Result of Separator Hyperplanes for Test Problem 1, (\( {C = 10} \))

Full size image

Theorem 1

Pirouz and Khorram (2016). If \( x^{*} \) is an optimal solution of (27), then it is clear that: 1. \( x^{*} \) is a weakly efficient solution of multi-objective optimization (23), and, 2. Let \( x^{*} \) be a unique optimal solution of (27), then \( x^{*} \) is a strictly efficient solution of multi-objective optimization (23) (and therefore is an efficient solution of multi-objective optimization (23)).

4.1 Multi-objective optimization problem for feature selection

The MOP reformulations of the problems \( l_{1} \), \( l_{2} \) in Sect. 2.2, are as follows, respectively:

$$\begin{aligned} \begin{aligned}&{\text {Min}} \quad \sum _{i=1} ^{m_{1}} y_{i} + \sum _{l=1} ^{m_{2}} z_{l} \\&{\text {Min}} \quad \Vert w \Vert _{1} \\&\quad \text {subject to}\\&\quad -a_{i}^{T}w+\gamma +1 \le y_{i}, \quad i=1, \ldots , m_{1} \\&\quad \quad b_{l}^{T}w-\gamma +1 \le z_{l}, \quad l=1, \ldots , m_{2} \\&\quad \quad y_{i}, z_{l} \ge 0 \\ \end{aligned} \end{aligned}$$
(28)
$$\begin{aligned} \begin{aligned}&{\text {Min}} \quad \sum _{i=1} ^{m_{1}} y_{i} + \sum _{l=1} ^{m_{2}} z_{l} \\&{\text {Min}} \quad \Vert w \Vert _{2}^{2} \\&\quad \text {subject to}\\&\quad -a_{i}^{T}w+\gamma +1 \le y_{i}, \quad i=1, \ldots , m_{1} \\&\quad \quad b_{l}^{T}w-\gamma +1 \le z_{l}, \quad l=1, \ldots , m_{2} \\&\quad \quad y_{i}, z_{l} \ge 0 \\ \end{aligned} \end{aligned}$$
(29)

Our FS model, formulated according to (17) in section 3 is reformulated as the following MOP:

$$\begin{aligned} \begin{aligned}&{\text {Min}} \quad \sum _{i=1} ^{m_{1}} y_{i} + \sum _{l=1} ^{m_{2}} z_{l} \\&{\text {Min}} \quad - \frac{1}{\Vert x\Vert _{1}} \sum _{k=1}^{n} \Vert x\Vert _{\left[ k\right] } \\&\quad \text {subject to}\\&\quad -a_{i}^{T}w+\gamma +1 \le y_{i}, \quad i=1, \ldots , m_{1} \\&\quad \quad b_{l}^{T}w-\gamma +1 \le z_{l}, \quad l=1, \ldots , m_{2} \\&\quad \quad y_{i}, z_{l} \ge 0 \\ \end{aligned} \end{aligned}$$
(30)

To solve these multi-objective optimization problems, we can use a modified algorithm based on the Epsilon constraint method which was introduced in Sect. 4. The methods presented in Jaggi (2013) and Sivri et al. (2018) can be used as well.

5 Numerical experiments

In this section, some numerical experiments are presented to compare the results of different models. We will take at first the results of single-objective problems for all of our numerical experiments. Then we will consider the results of MOP reformulations for two of our numerical experiments. To solve the test problems in this paper, we used the Global Solve solver of the global optimization package in MAPLE v.18.01. The algorithms in the Global Optimization toolbox are global search methods, which in this method systematically search the entire feasible region for a global extremum (see Pintér et al. (2006)). To compare the results, we ran all the models for C=1 and C=10. However, we did not report the results of the models with C = 1 in Test Problems 1 to 3, because the error of some models was not equal to zero for this value.

Test Problem 1. (Single objective testing). The following two sets are given:

$$\begin{aligned} A= & {} \left\{ (1, 4, 1), (1.5, 6, 1), (3.5, 5, 1) \right\} ,\\ B= & {} \left\{ (2, 6, 3), (3, 5, 2), (6, 3, 1.7) \right\} \end{aligned}$$

In this example, the number of samples is 6 and the number of features is 3. We have set \( C = 10 \). All models provide the correct separator of the sets (the error of all models is equal to zero). But \( l_{1} \) and \( l_{2} \) return a vector w where components are all nonzero, whereas the vector w returned by our sparse optimization method has just one nonzero component. The results of this example are depicted in Table 1 and Fig. 1.

Test Problem 2. (Single objective testing). In this example, the number of samples is 14, and the number of features is 3. Suppose that we have the following two sets:

$$\begin{aligned} \begin{aligned} A&= \left\{ [2,5,1],[1.7,4,1.5],[3,5.5,1.6],[2.5,5.3,1.3],\right. \\&\quad \left. [1.5,1.5,0.8],[2.5,3.5,1.4],[2.8,4,1.2]\right\} \\ B&= \left\{ [3.2,6,2],[3.5,5.8,2.4],[5,4.1,1.9],[4,6.5,3],\right. \\&\quad \left. [3.8,8,2],[6,6,2],[4.2,6.1,1.8] \right\} \end{aligned} \end{aligned}$$

The results are similar to those obtained for Test problem 1 (See Fig. 2 and Table 2).

Fig. 2
figure 2

Data set and the Result of Separator Hyperplanes for Test Problem 2, (\( {C = 10} \))

Full size image
Table 2 The results of Test problem 2 for \( C = 10 \)
Full size table
Table 3 The results of Test problem 3 for \( C = 10 \)
Full size table

Test Problem 3. (Single objective testing). In this example, the number of samples is 6, and the number of features is 4. Suppose that we have the following two sets:

$$\begin{aligned} \begin{aligned} A&= \left\{ [1.5,4.2,1,2],[1.9,4.6,1.5,1.5],\right. \\&\quad \left. [1.8,4.5,1.6,1.9] \right\} \\ B&= \left\{ [2.2,6,3,2.1],[2.6,5,2,2.3],[4,4.7,1.7,2.5]\right\} \end{aligned} \end{aligned}$$

We have set \( C = 10 \), and in this test problem also all models provide the correct separator of the sets. Models \( l_{1} \) and \( l_{2} \) return a vector w where components are all nonzero, but the vector w returned by our method has just one nonzero component. The results of this test problem is shown in Table 3.

Test Problem 4. (Single objective testing for Benchmark Problems). We have performed our experiments on a group of five datasets adopted as benchmarks for the feature selection method described in Gaudioso et al. (2018a). These datasets are available at (https://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/). They are listed in Table 4, where m is the number of samples and n is the number of features.

Table 4 Description of the datasets
Full size table
Table 5 The results of \( l_{1} \) model for two values of C
Full size table

A standard tenfold cross-validation has been performed in datasets. The results are in Tables 5, 6 and 7, where the Average Training Correctness (ATC) column is expressed as the average percentage of samples correctly classified.

Columns \( \Vert w\Vert _{1} \) report the average \( l_{1} \) norm of w. Finally, columns “\( \%ft(0) \)” “\( \%ft(-8) \)” report the average percentage of components of w whose modulus is greater than or equal to \( 10^{0}-10^{-8} \), respectively. Note that, assuming, conventionally, to be equal to “zero” any component \( w_{j} \) of w such that \( w_{j} < 10^{-8} \), the percentage of zero-components is \( (100-\%ft(-8)) \). Two different values of parameter C have been adopted for all datasets, \( C=1 \) and 10.

As shown in column \( \%ft(-8) \) of Tables 5, 6 and 7, our model resets the number of more components of the w vector equal to zero in all datasets. Also, our model results in a smaller error value compared to the \( l_{1} \) and \( l_{2} \) methods. In comparison, the correctness of our model classification is better for the whole datasets. For \( c = 10 \), the value of \( \Vert w\Vert _{1} \) in our model results in a smaller value in all datasets.

In the next two test problem, our goal is to demonstrate the benefits of considering the model as a multi-objective optimization problem. In this case, we can obtain a set of Pareto optimal solutions instead of one optimal solution. We consider the \( l_{1} \), \( l_{2} \) and our model as two-objective optimization problems described in Section 4.

Table 6 The results of \( l_{2} \) model for two values of C
Full size table
Table 7 The results of our model for two values of C
Full size table

Test Problem 5. (MOP Testing). We used the dataset of Test problem 2 for MOP models. The Algorithm introduced in section 4 has been used to solve these MOPs. Here we have set \( d=100 \). Out of 100 Pareto solutions that were obtained for each model we have considered only 2 Pareto solutions for more consideration. The results are displayed in Tables 8, 9 and 10.

For the \( l_1 \) MOP model, as shown in Table 8, for the first Pareto solution with an error value equal to zero, a smaller value for the \( \Vert w\Vert _{1} \) has been achieved compared to the results of the single-objective problem \( l_{1} \), presented in Table 2. For second Pareto solution we have obtained the smallest value for \( \Vert w\Vert _{1} \), where one of the components of w equal to zero, but the error value is nonzero.

Table 8 The results of 2 Pareto solutions of \( l_{1} \) MOP model for the dataset of Test problem 2
Full size table
Table 9 The results of 2 Pareto solutions of \( l_{2} \) MOP model for the dataset of Test problem 2
Full size table

For the \( l_2 \) MOP model, as shown in Table 9, for the first Pareto solution with an error value equal to zero, a smaller value for the \( \Vert w\Vert _{1} \) has been achieved compared to the results of the single-objective problem \( l_{2} \) presented in Table 2. For second Pareto solution we have obtained the smallest value for \( \Vert w\Vert _{1} \), but the error value is nonzero.

For our MOP model, as shown in Table 10, for the first Pareto solution with an error value equal to zero, a smaller value for \( \Vert w\Vert _{1} \) has been achieved compared to the results of our single-objective model presented in Table 2. Also, in this Pareto solution, similar to the solution obtained in the single-objective case, two components of the vector w are equal to zero. In the second Pareto solution, a smaller value for \( \Vert w\Vert _{1} \) has been achieved, and the vector w has only one nonzero component, but the error value is nonzero.

Test Problem 6. (MOP Testing). In this example we used the dataset of Test problem 3 for MOP models. We have used the algorithm introduced in section 4 to solve these MOPs, and in this algorithm, we have set \( d=100 \). Out of 100 Pareto solutions that were obtained for each model we have considered only 2 Pareto solutions that seemed interesting for more consideration that are displayed in Tables 11, 12 and 13.

For the \( l_1 \) MOP model, as shown in Table 11, for the first Pareto solution with an error value equal to zero we have obtained a smaller value for \( \Vert w\Vert _{1} \), compared to the results of the \( l_1 \) single-objective model presented in Table 3. For the second Pareto solution, we have obtained a solution where one of the components of w is equal to zero, but the error value is nonzero.

Table 10 The results of 2 Pareto solutions of our MOP model for the dataset of Test problem 2
Full size table
Table 11 The results of 2 Pareto solutions of \( l_{1} \) MOP model for the dataset of Test problem 3
Full size table
Table 12 The results of 2 Pareto solutions of \( l_{2} \) MOP model for the dataset of Test problem 3
Full size table
Table 13 The results of 2 Pareto solutions of Our MOP model for the dataset of Test problem 3
Full size table

For the \( l_2 \) MOP model, as shown in Table 12, for the first Pareto solution with an error value equal to zero a smaller value for \( \Vert w\Vert _{1} \) is obtained, compared to the results of the \( l_2 \) single-objective model presented in Table 3. For the second Pareto solution we have obtained smallest value for \( \Vert w\Vert _{1} \), but the error value is nonzero.

For our MOP model, as shown in Table 13, the first Pareto solution is similar to the solution that was obtained in the single-objective model in which the vector w returned only one nonzero component. For the second Pareto solution also three components of vector w are equal to zero while \( \Vert w\Vert _{1} \) has decreased but the error value is nonzero .

6 Conclusion

In this paper, we emphasized the application of sparse optimization in Feature Selection for Support Vector Machine classification. We have proposed a new model for sparse optimization based on the polyhedral k-norm. Due to the advantages of using multi-objective optimization models instead of single-objective models, some multi-objective reformulation of Support Vector Machine classification was proposed. The results of some test problems on classification datasets are reported for both single-objective and multi-objective models.