An enhanced efficient optimization algorithm (EINFO) for accurate extraction of proton exchange membrane fuel cell parameters

Abstract

In order to assure accurate modelling, this study presents a new technique for appropriately modelling and simulating a proton exchange membrane fuel cell (PEMFC) system. The PEMFC is a cleaner and more sustainable energy source as compared to fossil fuels. The fundamental idea is to minimize the sum of squared error (SSE) between the estimated and measured output voltage for the Ballard Mark V model in order to identify the model parameters of PEMFC stacks as efficiently as possible using a newly developed meta-heuristic called enhanced efficient optimization algorithm (EINFO). The proposed optimizer is considered an enhanced version of the original INFO algorithm. By balancing the exploration and exploitation phases better, the EINFO algorithm is intended to improve the performance of the original INFO approach and prevent local optima. The new method was tested on 23 benchmark functions and compared to the original INFO algorithm as well as other recently evolved optimizers. The algorithm is examined and compared with some literature meta-heuristics, including the particle swarm optimization, sine cosine algorithm, dragonfly algorithm, atom search optimization, Harris hawks optimization, and efficient optimization algorithm, using 50 independent runs, in terms of convergence speed and least SSE. When compared to other methods, the final findings show that, the suggested technique achieves the fastest convergence speed.

1 Introduction

Given the rising need for power, ongoing depletion of fossil fuels, and greenhouse gas emissions, researchers and scientists must concentrate on creating innovative technologies that efficiently utilize available renewable energy supplies. Fuel cells have become popular energy sources in recent years due to their high efficiency, robustness, dependability, and simplicity of application in a number of industries. A fuel cell is an electrochemical device that uses hydrogen fuel to produce electricity. The cathode and the anode are the two electrodes that make up this device. Between the positive electrode and the negative electrode, there is an electrolyte that allows oxygen to travel through the negative electrode and hydrogen to pass through the positive electrode, assisting the passage of electrons along the external circuit to generate electricity (Yang and Wang 2012).

Due to their high levels of efficiency and resilience, fuel cells are often employed in commercial, industrial, and residential settings (Askarzadeh and Rezazadeh 2011). The electrolyte used and the startup time needed are used to classify fuel cells. For instance, a solid oxide (SO) fuel cell starts up in 10 min as opposed to 1 s for a proton exchange membrane (PEM) fuel cell. A fuel cell typically generates an output voltage of 0.5–0.9 V. For real-time applications, this low output voltage is inadequate, hence numerous fuel cells are linked in series to produce the necessary voltage (Kadjo et al. 2007). The PEM fuel cell is the most commonly used fuel cell. Popularity stems from its distinctive features such as low temperatures, low pressures, and no waste generated (Oliveira et al. 2007).

Ideally, fuel cell models should be built before proceeding to the installation of the system, so that testing and design can be made easier (Ohenoja and Leiviskä 2010). Researchers have been interested in modelling the characteristics of fuel cells over the past decade since it helps them to better understand how the cell operates. Fuel cell characteristics must be accurately modelled by researchers and practitioners since its behaviour is highly dependent on both a fuel cell's predicted characteristics and its model parameters. The values of each model parameter needed for fuel cell modelling are not included in the manufacturer's datasheet. As a result, using any appropriate optimization approach makes it simpler to determine the values of the unknown parameters.

Therefore, the last few years have seen development of multiple techniques and implementation for finding the optimal parameter set of PEMFC beginning with conventional algorithms and moving to meta-heuristic algorithms. PEMFC parameter estimation was done by developing black widow optimization (BWO) (Singla et al. 2021) along with the comparison of its results with other different meta-heuristic algorithms under various operating temperatures. Various other meta-heuristic algorithms developed are slime mould (SM) based optimization algorithm (Gupta et al. 2021), Harris Hawks’ optimization (HHO) and atom search optimization (ASO) (Mossa et al. 2021), bald eagle search (BES) algorithm (Rezk et al. 2022a), particle swarm optimization (PSO) (Ye et al. 2009), genetic algorithms (GA) (Mohamed and Jenkins 2004), cuckoo search algorithm (CSA) (Chen and Wang 2019), grey wolf optimizer (GWO) (Ali et al. 2017), hybrid artificial bee colony differential evolution optimizer (HABCDEO) (Hachana and El-Fergany 2022), multi-verse optimizer (MVO) (Fathy and Rezk 2018), effective informed adaptive PSO (EIA-PSO) (Li et al. 2010), gradient-based optimizer (GBO) (Rezk et al. 2022b), enhanced transient search optimization algorithm (Hasanien et al. 2022), cuckoo search ant colony optimization (Mahato et al. 2020), and bio-inspired algorithm (Rani et al. 2022). Bird mating optimizer (BMO) (Askarzadeh and Rezazadeh 2013) was created to estimate the PEMFC's parameters based on the intelligent behaviour of birds. Several of these algorithms have some merits and demerits i.e. either algorithm tends to get stuck in local minima but has great memorizing capability about previous best result, whereas some algorithm has poor memorizing capability about previous best result but provide optimal solution for simpler mathematical problems. The algorithm also faces failure in obtaining optimal solution with increase in high number of iterations, increase in parameter adjustment complexity, frequent tuning of parameters, and finally, inadequate randomness. Since several of the techniques described have the aforementioned drawbacks, initiatives are continuously needed to either strengthen the current algorithm or to implement a novel one. The key purpose of this article is to establish a new parameter extraction approach for PEMFC model. The weighted mean approach is used by the INFO algorithm, a metaheuristic optimization method, to migrate populations in the direction of a better place. This primary aim of INFO highlights its performance qualities to address several optimization issues. The enhanced INFO (EINFO) approach is a modified version of the INFO algorithm suggested in this article and is used to avoid the local solutions while addressing complex issues. This modification is based on the exploitation phase of the marine predator algorithm (MPA) (Faramarzi et al. 2020). This modification can improve the solution efficiency as well as the rate of convergence for the EINFO algorithm. This paper's main objective is to provide a proposed algorithm for estimating PEMFC's parameters. The major contributions are listed as follows:

• 1. A new algorithm i.e. EINFO based upon Enhanced Efficient Optimization Algorithm is proposed in order to estimate the parameters of PEMFC.

• 2. Using 23 test functions, it will be demonstrated that the proposed EINFO algorithm is valid when compared to the original INFO and other recently created optimizers such the grey wolf optimizer (GWO), tunicate swarm algorithm (TSA), and jellyfish search (JS) optimizer.

• 3. For evaluation of consistency, robustness of the proposed algorithm, convergence graph, I–V, and P–I characteristic curves are obtained.

• 4. Nonparametric statistical test i.e. Friedman Ranking Test, Wilcoxon’s Rank Sum Test, and Anova Kruskal–Wallis Test is done for finding the significance of parameter estimation of PEMFC with proposed algorithm.

2 PEMFC mathematical modelling

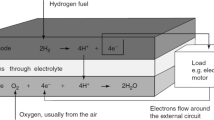
Anode and cathode are two electrodes in PEMFC segregated by membrane having polymer electrolyte as illustrated in Fig. 1. Hydrogen is injected by anode, whereas oxygen is injected by cathode and thin membrane forms the electrolyte which conducts ions and prevents passage of electrons. Output voltage is generated when the flow of ions takes place through electrolyte, whereas the outside circuit allows the passage of electrons.

Fig. 1

PEMFC diagram (Fan et al. 2013)

Electrochemical reactions occurring in PEMFC are shown in the following equations, where the anode and cathode side chemical reaction is represented in (1) and (2), respectively, and (3) shows the total chemical reaction or electrical energy generation (Singh et al. 2022).

$$ {\text{H}}_{2} \to 2{\text{H}}^{ + } + 2_{e}^{ - } $$

(1)

$$ \frac{1}{2}{\text{O}}_{2} + 2{\text{H}}^{ + } + 2_{e}^{ - } \to {\text{H}}_{2} {\text{O}} $$

(2)

$$ {\text{H}}_{2} + \frac{1}{2}{\text{O}}_{2} \to {\text{H}}_{2} {\text{O}} $$

(3)

$$ V_{{\text{c}}} = E_{{{\text{Nernst}}}} - V_{{{\text{activation}}}} - V_{{{\text{ohmic}}}} - V_{{{\text{concentration}}}} $$

(4)

There are three types of voltages constituted in fuel cell Terminal voltage ($V_{{\text{c}}}$) as illustrated in (4), where, $E_{{{\text{Nernst}}}}$ represents reversible open circuit voltage, $V_{{{\text{activation}}}}$ represents activation voltage drop, $V_{{{\text{ohmic}}}}$ represents ohmic voltage drop, $V_{{{\text{concentration}}}}$ represents concentration voltage drop.

$$ E_{{{\text{Nernst}}}} = E_{{\text{r}}} + \frac{{RT_{{\text{c}}} }}{ZF}\left[ {\ln \left( {P_{{{\text{H}}_{2} }} } \right) + \ln \left( {\sqrt {P_{{{\text{O}}_{2} }} } } \right)} \right] $$

(5)

The Nernst equation, which is illustrated in (5), defines the reversible thermodynamic potential of the oxygen and hydrogen reactions. In this equation $E_{{\text{r}}}$ stands for the reference voltage, R for the universal gas constant, $T_{{\text{c}}}$ for the cell’s temperature (in Kelvin), z for the number of electrons transferred, F for the faraday constant, $P_{{{\text{H}}_{2} }}$ and $P_{{{\text{O}}_{2} }}$ for hydrogen and oxygen pressure, respectively. After expansion, Eq. (5) is re-written in the following form,

$$ E_{{{\text{Nernst}}}} = 1.229 - 8.5 \times 10^{ - 4} \left( {T_{{\text{c}}} - 298.15} \right) + 4.385 \times 10^{ - 5} T_{{\text{c}}} \times \left( {\ln \left( {P_{{{\text{H}}_{2} }} } \right) + \ln \left( {\sqrt {P_{{{\text{O}}_{2} }} } } \right)} \right) $$

(6)

$$ P_{{{\text{H}}_{2} }} = 0.5\left( {PH_{{\text{anode }}} \times P_{{{\text{H}}_{2} {\text{O}}}} } \right)\left[ {\left( {\exp \left( {\frac{{1.635\left( {\frac{{i_{{\text{c}}} }}{A}} \right)}}{{T_{{\text{c}}}^{1.334} }}} \right) \times \frac{{\left( {PH_{{\text{anode }}} \times P_{{{\text{H}}_{2} {\text{O}}}} } \right)}}{{P_{{\text{anode }}} }}} \right)^{ - 1} - 1} \right] $$

(7)

$$ P_{{{\text{O}}_{2} }} = \left( {PH_{{{\text{cathode}}}} \times P_{{{\text{H}}_{2} {\text{O}}}} } \right)\left[ {\left( {\exp \left( {\frac{{4.192\left( {\frac{{i_{{\text{c}}} }}{A}} \right)}}{{T_{{\text{c}}}^{1.334} }}} \right) \times \frac{{\left( {PH_{{\text{anode }}} \times P_{{{\text{H}}_{2} {\text{O}}}} } \right)}}{{P_{{{\text{cathode}}}} }}} \right)^{ - 1} - 1} \right] $$

(8)

$P_{{{\text{H}}_{2} }}$ and $P_{{{\text{O}}_{2} }}$ are shown in (7) and (8), respectively, where $P_{{{\text{anode}}}}$ represents anode pressure of input side, $P_{{{\text{cathode}}}}$ represents cathode pressure of input side, relative humidity of vapour about cathode and anode side of PEMFC is represented by $PH_{{{\text{cathode}}}}$ and $PH_{{{\text{anode}}}}$, respectively, $i_{{\text{c}}}$ represents generated current by PEMFC, surface area of membrane is represented by A, $P_{{{\text{H}}_{2} {\text{O}}}}$ is the pressure at water saturation, as represented in (9) (Singla et al. 2022).

$$ P_{{{\text{H}}_{2} {\text{O}}}} = 2.95 \times 10^{ - 2} \left( {T_{{\text{c}}} - 273.15} \right) - 9.18 \times 10^{ - 5} \left( {T_{{\text{c}}} - 273.15} \right)^{2} + 1.44 \times 10^{ - 2} \left( {T_{{\text{c}}} - 273.15} \right)^{2} - 2.18 $$

(9)

$$ V_{{{\text{activation}}}} = \frac{{RT_{{\text{c}}} }}{z\alpha F}\ln \left( {\frac{{i_{{\text{c}}} }}{{i_{O} }}} \right) $$

(10)

Activation process leads to voltage loss which is shown in (10), where $\alpha$ represents transfer coefficient, $i_{O}$ represents exchange current density and it can be expanded as shown below.

$$ V_{{{\text{activation}}}} = - \left[ {\varepsilon_{1} + \varepsilon_{2} T_{{\text{c}}} + \varepsilon_{3} T_{{\text{c}}} \ln \left( {C_{{{\text{O}}_{2} }} } \right) + \varepsilon_{4} T_{{\text{c}}} \ln \left( {i_{{\text{c}}} } \right)} \right] $$

(11)

where $\varepsilon_{1} ,\varepsilon_{2} ,\varepsilon_{3} ,\varepsilon_{4}$ represent semi-empirical coefficients on the cathode side of PEMFC. The concentration of oxygen ($C_{{{\text{O}}_{2} }}$) is calculated as shown in (12).

$$ C_{{{\text{O}}_{2} }} = \frac{{P_{{{\text{O}}_{2} }} }}{{5.08 \times 10^{6} \exp^{{\left( {\frac{ - 498}{{T_{{\text{c}}} }}} \right)}} }} $$

(12)

The resistive ohmic voltage drop ($V_{{{\text{ohmic}}}}$) is illustrated in (13), in which $R_{{{\text{MR}}}}$ represents the membrane surface resistance, and $R_{{{\text{CR}}}}$ represents the contact resistance.

$$ V_{{{\text{ohmic}}}} = i_{{\text{c}}} \left( {R_{{{\text{MR}}}} + R_{{{\text{CR}}}} } \right) $$

(13)

$$ R_{{{\text{MR}}}} = \frac{{\rho_{{\text{M}}} l}}{A} $$

(14)

The membrane resistance ($R_{{{\text{MR}}}}$) is calculated using (14), where $\rho_{{\text{M}}}$ represents the membrane resistivity and $l$ represents the membrane thickness. Further, $\rho_{{\text{M}}}$ can be expressed as follows:

$$ \rho_{{\text{M}}} = \frac{{181.6\left( {1 + 0.03\left( {\frac{{i_{{\text{c}}} }}{A}} \right) + 0.0062\left( {\frac{{T_{{\text{c}}} }}{303}} \right)\left( {\frac{{i_{{\text{c}}} }}{A}} \right)^{2.5} } \right)}}{{\left( {\lambda - 0.634 - 3\left( {\frac{{i_{{\text{c}}} }}{A}} \right)} \right) \exp \left( {418\left( {\frac{{T_{{\text{c}}} - 303}}{{T_{{\text{c}}} }}} \right)} \right)}} $$

(15)

where adjustable empirical variable is denoted by $\lambda$. The value of voltage concentration loss ($V_{{{\text{concentration}}}}$) is calculated as shown in (16).

$$ V_{{{\text{concentration}}}} = \frac{{RT_{{\text{c}}} }}{z\alpha F}\ln \left( {\frac{{i_{{\text{d}}} }}{{i_{{\text{d}}} - i_{{\text{c}}} }}} \right) $$

(16)

where i_d is the current density when reactant concentration is zero. It can be re-written as shown below.

$$ V_{{{\text{concentration}}}} = - b\ln \left( {i_{{\text{c}}} - \frac{{\frac{{i_{{\text{c}}} }}{A}}}{{i_{\max } }}} \right) $$

(17)

where b represents the constant and $i_{\max }$ represents the maximum current density. The value of b can be evaluated as shown in (18).

$$ b = \frac{{RT_{{\text{c}}} }}{z\alpha F} $$

(18)

In order to generate the sufficient energy, multiple stacks need to be combined as well as connected in series or parallel as the value of single stack PEMFC current and output voltage is small. The output voltage ($V_{{{\text{stack}}}}$) of the stack of fuel cell in case of series connection is shown in (19) (Outeiro et al. 2008).

$$ V_{{{\text{stack}}}} = n \cdot V_{{\text{c}}} $$

(19)

where n is the quantity of cells that are linked together in series. The equation can be rewritten as seen as follows:

$$ V_{{{\text{stack}}}} = n\left( {E_{{{\text{Nernst}}}} - V_{{{\text{activation}}}} - V_{{{\text{ohmic}}}} - V_{{{\text{concentration}}}} } \right) $$

(20)

As per equations mentioned above, seven parameters of PEMFC i.e. $\varepsilon_{1} ,\varepsilon_{2} ,\varepsilon_{3} ,\varepsilon_{4} ,\lambda ,R_{{{\text{CR}}}} ,b$ are to be estimated with accuracy and precision for controlled operation and adequate modelling of fuel cell. Proposed algorithm as well as other meta-heuristic algorithms i.e. PSO, SCA, DA, ASO, HHO, INFO have been used to do parameter estimation of PEMFC.

3 Problem formulation

To estimate the PEMFC's parameters, a new approach called EINFO is proposed in this study. Utilizing optimization methods, output voltage is predicted for each input of current density. The SSE (sum of square error) assessment metric between the estimated output voltage and observed output voltage values is illustrated along with its objective function shown in Eq. (21).

$$ {\text{SSE}} = {\text{MIN}}\left( {F = \mathop \sum \limits_{i = 1}^{N} \left( {V_{{{\text{actual}}}} - V_{i} } \right)^{2} } \right) $$

(21)

where N stands for the number of data points V_actual is the experimental output voltage and ${V}_{i}$ is the output voltage anticipated using different optimization algorithms. The major objective of this article is to achieve higher performance, more accuracy, and greater precision for PEMFC parameter estimation.

4 Algorithm

In this part, the suggested improved INFO (EINFO) algorithm is provided after a brief description of the weighted mean of vectors (INFO) methodology.

4.1 Efficient optimization algorithm (INFO)

In 2022, the INFO method was presented (Ahmadianfar et al. 2022). Using four key stages—initialization, updating rule, vector combining, and lastly local search—this technique's concept relies on a strong structure and updating the vectors' positions.

Step 1 Initialization Stage: A population of n vectors in a D-dimensional search space compensate the INFO approach. The following Eq. (22) produces a random beginning population:

$$ X_{n} = X_{\min } + {\text{rand}}\left( {0,1} \right) \cdot \left( {X_{\max } - X_{\min } } \right) $$

(22)

where $X_{n}$ is the nth vector, $X_{\min } , X_{\max }$ are the limits of the solution domain in each problem and ${\text{rand}}\left( {0,1} \right)$ is a random number defined in the range of [0, 1].

Step 2 Updating Rule: Through the search process, this step broadens the population. This operation produces new vectors by using the weighted mean of the vectors. The following Eq. (23) is the updating rule's key formulation:

$$ \begin{aligned} & {\varvec{if}} \,{\text{rand}} < 0.5 \\ & \quad \quad \quad z1_{l}^{{{\text{iter}}}} = x_{l}^{{{\text{iter}}}} + \sigma \times {\text{MeanRule}} + {\text{rand}}\,n \times \frac{{\left( {x_{bs} - x_{a1}^{{{\text{iter}}}} } \right)}}{{\left( {f\left( {x_{bs} } \right) - f\left( {x_{a1}^{{{\text{iter}}}} } \right) + 1} \right)}} \\ & \quad \quad \quad z2_{l}^{{{\text{iter}}}} = x_{bs} + \sigma \times {\text{MeanRule}} + {\text{rand}}\,n \times \frac{{\left( {x_{a1}^{{{\text{iter}}}} - x_{b}^{{{\text{iter}}}} } \right)}}{{\left( {f\left( {x_{a1}^{{{\text{iter}}}} } \right) - f\left( {x_{a2}^{{{\text{iter}}}} } \right) + 1} \right)}} \\ & {\varvec{else}} \\ & \quad \quad \quad z1_{l}^{{{\text{iter}}}} = x_{a}^{{{\text{iter}}}} + \sigma \times {\text{MeanRule}} + {\text{rand}}\,n \times \frac{{\left( {x_{a2}^{{{\text{iter}}}} - x_{a3}^{{{\text{iter}}}} } \right)}}{{\left( {f\left( {x_{a2}^{{{\text{iter}}}} } \right) - f\left( {x_{a3}^{{{\text{iter}}}} } \right) + 1} \right)}} \\ & \quad \quad \quad z2_{i}^{{{\text{iter}}}} = x_{bt} + \sigma \times {\text{MeanRule}} + {\text{rand}}\,n \times \frac{{\left( {x_{a1}^{{{\text{iter}}}} - x_{a2}^{{{\text{iter}}}} } \right)}}{{\left( {f\left( {x_{a1}^{{{\text{iter}}}} } \right) - f\left( {x_{a2}^{{{\text{iter}}}} } \right) + 1} \right)}} \\ & {\varvec{end}} \\ \end{aligned} $$

(23)

where $z1_{l}^{{{\text{iter}}}}$ and $z1_{l}^{{{\text{iter}}}}$ denote the new vectors in the gth generation; and $\sigma$ is the scaling rate of a vector, as shown in Eq. (24) as:

$$ \sigma = 2\alpha \times {\text{rand}} - \alpha $$

(24)

Step 3 Vector combining: The two vectors generated in the preceding section ($z1_{l}^{{{\text{iter}}}}$ and $z2_{l}^{{{\text{iter}}}}$) (and) are merged with vector $x_{l}^{{{\text{iter}}}}$ based on the INFO method to build the population's diversity as shown in Eqs. (25.1 to 25.3):

if rand < 0.5

if rand < 0.5

$$ u_{l}^{{{\text{iter}}}} = z1_{l}^{{{\text{iter}}}} + \mu \cdot \left| {z1_{l}^{{{\text{iter}}}} - z2_{l}^{{{\text{iter}}}} } \right| $$

(25.1)

else

$$ u_{l}^{{{\text{iter}}}} = z2_{l}^{{{\text{iter}}}} + \mu \cdot \left| {z1_{l}^{{{\text{iter}}}} - z2_{l}^{{{\text{iter}}}} } \right| $$

(25.2)

end

else

$$ u_{l}^{{{\text{iter}}}} = x_{l}^{{{\text{iter}}}} $$

(25.3)

end

where $\mu$ is equal to $0.05 \times {\text{rand}}\,n$.

Step 4 Local Search: The capability of this stage prevents the algorithm to drop into local minima. The local operator is considered using the global location ($x_{best}^{iter}$). According to this operator, a novel vector can be produced around global position ($x_{best}^{iter}$) as shown in Eqs. (26.1 to 26.4):

if rand < 0.5

if rand < 0.5

$$ u_{l}^{{{\text{iter}}}} = x_{bs} + {\text{rand}}\,n \times \left( {{\text{MeanRule}} + {\text{rand}}\,n \times \left( {x_{bs}^{{{\text{iter}}}} - x_{a1}^{{{\text{iter}}}} } \right)} \right) $$

(26.1)

else

$$ u_{l}^{{{\text{iter}}}} = x_{{{\text{rnd}}}} + {\text{rand}}\,n \times \left( {{\text{MeanRule}} + {\text{rand}}\,n \times \left( {\upsilon_{1} \times x_{bs} - \upsilon_{2} \times x_{{{\text{rnd}}}} } \right)} \right) $$

(26.2)

end

end

$$ x_{{{\text{rnd}}}} = \phi \times x_{{{\text{avg}}}} + \left( {1 - \phi } \right) \times \left( {\phi \times x_{bt} + \left( {1 - \phi } \right) \times x_{bs} } \right) $$

(26.3)

$$ x_{{{\text{avg}}}} = \frac{{\left( {x_{a} + x_{b} + x_{c} } \right)}}{3} $$

(26.4)

where $\phi$ is a random number in the range of (0, 1); and x_rnd is a new solution that combines the components of the three solutions (x_avg, $x_{bt}$ and $x_{bs}$) randomly. This increases the randomness nature of the proposed algorithm to better search in the solution space. $\upsilon_{1}$ and $\upsilon_{2}$ are two random numbers given by the following Eqs. (26.5 to 26.6):

$$ \upsilon_{1} = \left\{ {\begin{array}{*{20}l} {2 \times {\text{rand}}} \hfill & {\quad {\text{if}}\;p > 0.5} \hfill \\ 1 \hfill & {\quad {\text{otherwise}}} \hfill \\ \end{array} } \right. $$

(26.5)

$$ \upsilon_{2} = \left\{ {\begin{array}{*{20}l} {{\text{rand}}} \hfill & {\quad {\text{if}}\;p < 0.5} \hfill \\ 1 \hfill & {\quad {\text{otherwise}}} \hfill \\ \end{array} } \right. $$

(26.6)

where p refers to a random number in the range of (0, 1).

4.2 Proposed enhanced efficient optimization (EINFO) algorithm

The development is called the high and low velocity ratios based on the Marine predator algorithm (MPA) (Faramarzi et al. 2020; Hassan et al. 2022). This way was proposed to solve the possibility of the optimal value may drop into a local minima. This modification depends on two stages. The first stage is the high-velocity ratio situation. This stage's mathematical model is shown in Eqs. (27.1 to 27.3):

$$ {\text{iter}} < \frac{1}{3}{\text{iter}}_{\max } $$

(27.1)

$$ S = \overrightarrow {{R_{B} }} \otimes \left( {E - \overrightarrow {{R_{B} }} \otimes X_{n} \left( {{\text{iter}}} \right)} \right) $$

(27.2)

$$ X_{n} \left( {{\text{iter}} + 1} \right) = X_{n} \left( {{\text{iter}}} \right) + P \cdot \overrightarrow {{R_{B} }} \otimes S $$

(27.3)

where $\overrightarrow {{R_{B} }}$ is a vector of random integers from the Normal distribution that reflect Brownian motion. The notation $\otimes$ depicts entry-by-entry multiplications. The new position is simulated by multiplying $\overrightarrow {{R_{B} }}$ by previous position, $P$ = 0.5 is a constant, and $\overrightarrow {{R_{B} }}$ is a vector of uniform random values in the range [0, 1]. This situation occurs during the first third of iterations when the step size is large, indicating a high level of exploratory ability. Iter is the current iteration while ${\text{iter}}_{\max }$ is the maximum one. The fittest solution (E) is designated as a best position to form a matrix as shown in Eq. (28):

$$ E = \left[ {\begin{array}{*{20}c} {Xb_{1.1}^{{{\text{iter}}}} } & {\quad \cdots } & {\quad Xb_{1.d}^{{{\text{iter}}}} } \\ \vdots & {\quad \ddots } & {\quad \vdots } \\ {Xb_{n.1}^{{{\text{iter}}}} } & {\quad \cdots } & {\quad Xb_{n.d}^{{{\text{iter}}}} } \\ \end{array} } \right] $$

(28)

where $Xb{ }$ denotes the best solution, which is copied n times to create the E matrix. n denotes the number of search agents, whereas d denotes the number of dimensions.

The second stage is the low velocity ratio. This stage occurs near the end of the optimization process, which is typically associated with high exploitation capability. Lévy is the best approach for low-velocity ratios. This stage is depicted as shown in Eqs. (29.1 to 29.3):

$$ {\text{iter}} > \frac{1}{3}{\text{iter}}_{\max } $$

(29.1)

$$ S = \overrightarrow {{R_{{\text{L}}} }} \otimes \left( {\overrightarrow {{R_{{\text{L}}} }} \otimes E - X_{n} \left( {{\text{iter}}} \right)} \right) $$

(29.2)

$$ X_{n} \left( {{\text{iter}} + 1} \right) = E + P \cdot CF \otimes S $$

(29.3)

In the Lévy method, multiplying $R_{{\text{L}}}$ and E, whereas adding the step size to position to aid in the updating of location. Additional feature of EINFO is increasing the chances of escape from local optima. Figure 2 depicts the flow chart of proposed algorithm. The place of high and low velocity ratios in the proposed algorithm is presented in this figure. This modification leads to enhance the exploration of the proposed EINFO algorithm.

Fig. 2

Proposed algorithm flow chart

5 Results and discussion

5.1 Benchmark test functions

By statistically measuring the best values, mean values, median values, worst values, and standard deviation (STD) for the optimum solutions obtained by the proposed EINFO algorithm and the other well-known optimization algorithms, the capability and proficiency of the proposed EINFO algorithm are validated on the various benchmark functions. Four contemporary methods the grey wolf optimizer (GWO) (Mirjalili et al. 2014), tunicate swarm algorithm (TSA) (Kaur et al. 2020), jellyfish search (JS) optimizer (Chou and Truong 2021), and the traditional INFO algorithm (Ahmadianfar et al. 2022) were used to compare the results obtained with the proposed EINFO algorithm. The same limit number of feature evaluations (i.e. maximum iteration = 200 and population size = 50) is set for a fair comparison of twenty-three benchmark test functions and other rest of the compared algorithms. Each technique was run 20 times independently, and all codes were programmed in MATLAB 2016a on a laptop with Intel(R) Core i5-4210U CPU 2.40 GHz with an 8 GB RAM environment. Figure 3 displays the Qualitative metrics on F1, F2, F4, F7, F8, F12, F15, and F18: 2D views of the functions, convergence curve, average fitness history, and search history.

Fig. 3

Qualitative metrics of eight benchmark functions: 2D views of the functions, search history, average fitness history, and convergence curve using EINFO algorithm

The suggested EINFO approach and four optimization algorithms' statistical analysis results for three different benchmark functions are shown in Tables 1, 2, and 3 (unimodal, multimodal, and composite, respectively). The bolded EINFO, INFO, JS, TSA, and GWO approaches were successful in obtaining the ideal values. It can be observed that for the majority of these benchmark functions, the EINFO approach yields the best result. Figure 4 depicts the convergence curves for all approaches for those functions, and Fig. 5 depicts the boxplots for these techniques.

Table 1 Unimodal statistical results

Table 2 Multimodal statistical results

Table 3 Results of composite benchmark functions

Fig. 4

The convergence curves of all optimization algorithms for 23 benchmark functions

Fig. 5

Boxplots for all optimization algorithms for 23 benchmark functions

5.2 Parameter estimation

Table 4 shows parametric values of the compared algorithms. Table 5 displays the parameter search range for calculating the PEMFC parameter, while Table 6 displays the Ballard Mark V specification datasheet. Each programme was coded in MATLAB 2020a, and each programme was performed 20 times. The population size feature evaluation limit for estimating PEMFC parameters is 50 and 1000, respectively. The proposed algorithm is used to estimate PEMFC parameters, and its performance and efficiency are compared to that of other algorithms such as PSO, SCA, DA, ASO, HHO, and INFO. PEMFC parameter estimation at STC (Standard Temperature Condition), i.e. 343.15 K is shown in Table 7. Table 7 also shows the sum of square error and computation time and from this table it is concluded that the proposed algorithm has minimum error and as well as computation time. Table 8 shows the statistical results of PEMFC, from this table it is also clear that the proposed algorithm error is less as compared to other meta-heuristic algorithms. Figure 6 shows the convergence curve of PEMFC, and it clearly shows that the proposed hybrid algorithm has higher pace of convergence than other meta- heuristic algorithms, thus proving it to have more accuracy and precision. The values of power, absolute error and voltage are calculated and represented in Table 9. Further, P–I and V–I characteristic curves of PEMFC are illustrated in Figs. 7 and 8, respectively, which justifies the accuracy of proposed algorithm.

Table 4 Parametric values of the compared algorithms

Table 5 Parameter search range

Table 6 Data sheet for the parameter estimation

Table 7 PEMFC parameter estimation

Table 8 Statistical results of PEMFC model

Fig. 6

Convergence curve

Table 9 Voltage, power and absolute error calculated values

Fig. 7

I–V curve

Fig. 8

P–I curve

5.3 Nonparametric test

Table 10 shows the result of the Friedman ranking test. The Friedman ranking test clearly shows that the proposed algorithm is significantly more exact and accurate than the other algorithms. In the data sheet of Ballard Mark V, it is apparent that proposed algorithm has earned first rank, INFO has secured second rank, and DA has gained third rank, with HHO, ASO, SCA and PSO to follow. It is obvious that proposed algorithm is a superior approach for parameter estimation of the PEMFC model when compared to the other algorithms in Ballard Mark V data sheet.

Table 10 Friedman ranking test

Additionally, the nonparametric Wilcoxon rank sum test is employed. This test appears to be a straightforward but safe and reliable nonparametric strategy for integrated statistical analysis when samples are independent, and it is widely used in dynamic programming. Wilcoxon's rank sum test is used to compare the proposed method against other algorithms, as shown in Table 11 for the PEMFC data sheet. With a 95% level of significance in the probability range, this test reveals that the suggested algorithm performs better than the other methods.

Table 11 p values for Wilcoxon’s rank test

After that, the Kruskal–Wallis nonparametric test is used to compare the statistical differences between the methods. The list of graph acquired from the test, as well as the mean rank of EINFO, is given in Fig. 9. EINFO has a considerably different mean rank than the other categories. The list of graph acquired from the test, as well as the median rank of EINFO, is displayed in Fig. 10. EINFO's median rank is likewise much better than that of other groupings. Table 12 displays the outcomes of the Anova Kruskal–Wallis test. To evaluate the significance of probability, the chi square is employed. The recommended method, EINFO, beat the comparable algorithms in terms of precision and accuracy, according to the findings of the preceding nonparametric tests.

Fig. 9

Mean ranking multiple comparisons

Fig. 10

Median ranking multiple comparisons

Table 12 Anova Kruskal–Wallis test

6 Conclusions and future research

A new suggested method, EINFO, is proposed to handle global optimization concerns and extract the parameters of multiple PEMFCs models at varying temperature. On 23 benchmark functions, the suggested EINFO method has been evaluated. These are composite, multimodal, and unimodal functions. The outcomes of EINFO have been compared to those of the original INFO algorithm and other more current algorithms in every function. Additionally, all functions solved using all researched strategies have undergone statistical analysis. In this study, the Ballard Mark V PEMFC model was examined. The mathematical equivalent model of PEMFCs was examined in this work. The following conclusions have been reached based on the findings.

• 1. A newest algorithm is developed i.e. EINFO for the extraction of PEMFC model.

• 2. EINFO outperforms the other algorithms in terms of precision and convergence speed for solving global optimization problems.

• 3. EINFO surpasses the other algorithms under comparison based on equivalent efficiency on the PEMFCs model, the solution consistency findings, the I–V and P–I characteristic curves, the Friedman ranking test, the Wilcoxon's rank sum test results, and the Annova Kruskal–Wallis test.

• 4. According to the statistical findings, EINFO has improved its parameter extraction efficiency for both PEMFC models.

• 5. Convergence curves reveal that EINFO converges faster than the other methods under consideration.

In the future work, authors will try to solve the more complex mathematical problems. Moreover, the obtained results of EINFO technique motivate the application of it in complex power system optimization problems like energy management in smart grid considering electrical vehicles and renewable energy such as PV and wind energy.