Cellular automaton created as an m-ary product of algebraic quasi-multiautomata

Abstract

In this work, we follow the construction of an n-ary system of Cartesian composition of multiautomata with internal links, where we define the internal links to the homogeneous and heterogeneous products of multi-automata. While the introduction of an internal link is rectilinear in the Cartesian composition, it requires a new approach in product construction for the other two automata products. In this way, it is possible to focus on multiple options for creating these systems. More specifically, we combine automata and multi-automata with binding according to the basic definitions given by Dörfler. This approach shows new connections to cellular automata, which allow for the modeling of phenomena in many areas. At the end of the work, we discuss the advantages of these individual schemes for quasi-multiautomata connections.

1 Introduction

In the past, algebraic automata were considered to be systems for the transmission of information of a specific type, i.e., an input is transformed into an output by transition functions. The methods by which the input is transferred to the output necessarily depend on the specific type of automaton. Although there is a close connection between automata from the theory of formal languages and theory of algebraic automata, the requirements for the transition function are different, for detail see Novák et al. (2020) and Křehlík et al. (2022). In the theory of formal languages, emphasis is placed on the concatenation of input symbols and the acceptance of the language, i.e., for all strings that lead to the final state, see Massouros (1994a), Jing et al. (2015) and Massouros and Massouros (2020). However, algebraic automata are studied from a structural point of view, see Chvalina (2009), Chvalina and Chvalinová (1996), Gécseg and Peák (1972), Ginzburg (1968).

With the development of nondeterminism, algebraic structures were generalized to multivalued structures, also called hypercompositional structures (e.g., hypergroups, hyperrings, hypermodules etc), see Marty (1934) and Dresher and Ore (1938). Similarly, automata were generalized to multi-automata, see Ashrafi and Madanshekaf (1998), Chvalina (2009), Chvalina and Chvalinová (1996), Massouros (2013), Chvalina et al. (2018).

Note that in the algebraic theory of automata, we distinguish between an automaton and a quasi-automaton, where the free monoid is the input structure in the automaton and the monoid is the input structure in the quasi-automaton. The formal definition is introduced in the following section. Details about these terms can be found in Křehlík et al. (2022) and Novák et al. (2020).

The description of real systems that use basic algebraic automata, quasi-automata and quasi-multiautomata shows weakness. These structures cannot affect the complexity of today’s systems. Therefore, combinations of these structures were created. They were introduced by W. Dörfler in Dörfler (1978, 1976) in their basic form, and further studied and generalized in papers (Dutta et al. 2020; Chvalina et al. 2006; Ashrafi and Madanshekaf 1998; Chvalina 2009; Chvalina et al. 2016, 2018; Taş et al. 2021). The next step in the development of combining automata was the introduction of internal links. This tool provided a better description and modeling for the systems in the context of L. Bertalanffy’s system definition. The principle of this definition is that the system as a whole is more than a simple sum of its parts, and is instead a complex system of interacting elements therefore, the constitutive properties of the system cannot be explained by the characteristics of its isolated parts.

By adding an internal link to various combinations of the automaton, i.e., the ability of some internal element of the system to influence other internal elements, or even itself, we get a structure that more closely corresponds to the definition of the basic system according to L. Bertalanffy.

At present, there are already well - described constructions for the combination of quasi-automata or quasi-multiautomata into one unit automaton or quasi-multiautomaton, i.e., a heterogeneous product, a homogeneous product, a Cartesian composition of (quasi-multi)automata.

In the (n-ary) Cartesian composition, the internal links were introduced are straightforward, see Křehlík (2020) and Křehlík and Novák (2019). We present the principle internal links in Cartesian composition: Consider $S=(s_1, s_2, s_3, \ldots , s_n)$ as a state of n-ary Cartesian composition. The input word can change only one component of $S=(s_1, s_2, s_3, \ldots , s_n)$, e.g., input $i_2$ can change component $s_2$ to $s_2'$, this results is a new state. $S'=(s_1, s_2', s_3, \ldots , s_n)$. All other components $s_1, s_3, \ldots , s_n$ are influenced by internal, which are triggered by the change from $s_2$ to $s_2'$. This process is possible in homogenous nor heterogenous product straightforward.

The addition of internal links is not clear for the homogeneous and heterogeneous products of quasi-automata or quasi-multiautomata. In the above-mentioned case of the two products, the input symbols are specifically determined so that each one is applied to the corresponding state of n-tuple-states at the same time. It is necessary to specify the conditions under which the states in the n-tuple are to be influenced by their neighbors. This offers several cases for establishing internal links. These cases are presented in Sect. 3. The possibility of influencing the states of the n -tuple build by using selected neighbors leads us to study the connections between the algebraic automata and the cellular automata.

In Sect. 4, we study one of the proposals for the construction of an internal link in both homogeneous and heterogeneous products. This special design for the internal link construction is similar to a cellular automaton. John von Neumann is the founder of the cellular automaton. His model of a cellular automaton, which corrects itself, was published in 1964, see von Neumann (1963). In physics, it is common to describe the time evolution of particles with differential equations. If any solution exists, it is often sensitive to initial conditions. The study of cellular automata offers a different approach to the study of dynamic systems. Its great advantage lies in its simplicity, thanks to which dynamic systems can be analyzed. In addition, their numerical solution does not simplify approximations, which lead to an accurate result because cellular automata are considered to be dynamical discrete systems, which contain a set of cells. Each cell can contain one of K possible states. Often there are only two conditions: 0—a dead cell, 1—a living cell. State 0 is referred to as an empty field. State 1 is sometimes referred to as a cell. This enables the effective modeling of biological processes and especially, transport systems (Ding et al. 2011). First, we would observe that traffic model that uses a one-dimensional cellular automaton was presented by Nagel and Schreckenberg, see Nagel and Schreckenberg (1992). Second, the use of cellular automata is known from physics and image processing. A concise review of cellular automata with their applications, is presented in the paper (Fomina et al. 2018). The current state of urban transport leads to problems in the form of traffic jams, which are mainly related to the growth of the population and the increase in the number of car. This arouses interest in the creation of simulation tools that can contribute to a deeper understanding of the issue. There are many concepts for modeling dynamic systems in traffic with cellular automata, for e.g. Ruskin and Wang (2002), Wu et al. (2005), Cruz-Piris et al. (2019), Li et al. (2020) and Shi et al. (2021).

2 Basic terminology of multi-automata

Note that the theory of algebraic automata has a close connection to the theory of formal languages of computer science, see Massouros (2013) and Massouros and Massouros (2020). If, in the following definition, we consider a free monoid instead of a monoid, then we call the structure $\mathbb {A}=(I,S,\delta )$ an automaton that corresponds to the automaton from theory of formal languages, see Massouros (1994a).

The definition of an automaton without output and where the input structure is a monoid, i.e., a non-empty set I enriched with an associative composition which has a unit element. This definition is used in papers (Chvalina et al. 2013; Chvalina 1995; Chvalina et al. 2016; Gécseg and Peák 1972; Ginzburg 1968).

Definition 1

(Chvalina et al. 2016) A quasi-automaton is a structure $\mathbb {A}=(I,S,\delta )$ such that $I\not =\emptyset$ is a monoid, $S\not =\emptyset$ and $\delta :I\times S \rightarrow S$ satisfies the following conditions:

• 1. There exists an element $e\in I$ such that $\delta (e,s)=s$ for any state $s\in S$.

• 2. $\delta (y,\delta (x,s))=\delta (xy,s)$ for any pair $x,y\in I$ and any state $s\in S.$

The set I is called the input set or input alphabet, the set S is called the state set and the mapping $\delta$ is called next-state or transition function. Condition 1 is called the unit condition (UC) while condition 2 is called the Mixed Associativity Condition (MAC).

The development of nondeterminism led to the generalization of single-valued algebraic structures, to multi-valued algebraic structures, which are called hypercompositional structures. Frederic Marty introduced the first such structure, the hypergroup, which is the generalization of the group (Marty 1934).

Recall some terms from the theory of Hypercompositional Algebra.

A hypergroupoid is a pair $(H,*)$, where H is a nonempty set and the mapping $*:\textit{H} \times \textit{H}\longrightarrow \mathcal {P}^*(H)$ is a binary hyperoperation (or hypercomposition) on $\textit{H}$ (here $\mathcal {P}^*(H)$ denotes the system of all nonempty subsets of $\textit{H}$). If $a*(b*c)=(a*b)*c$ holds for all $a,b,c\in \textit{H}$, then $(H,~*)$ is called a semihypergroup. If moreover the reproductive axiom, i.e., the relation $a*H=H=H*a$ for all $a\in H$, is satisfied, then the semihypergroup $(H,*)$ is called hypergroup. For further reference see, e.g., books (Corsini and Leoreanu 2003; Davvaz and Leoreanu-Fotea 2007; Chvalina 1995) or papers (Al Tahan et al. 2018; Cristea et al. 2019; Massouros and Massouros 2020, 2021)

The generalization groups to the concepts of hypergroups was followed by quasi-automata. Under a certain perspective, automata can be thought of as actions of operators or hyperoperators on specific sets. (e.g., see (Ashrafi and Madanshekaf 1998; Massouros 1994b)). For the terminology convenience the following definition of the quasi-multiautomata was introduced, see Chvalina and Chvalinová (1996), Chvalina (2009), Chvalina et al. (2016) and Novák et al. (2020):

Definition 2

(Chvalina et al. 2016) A quasi–multiautomaton is a triad $\mathbb{M}\mathbb{A}=(I,S,\delta )$, where $(I,*)$ is a semihypergroup, S is a non–empty set and $\delta :~I \times S\rightarrow S$ is a transition function satisfying the condition:

$$\begin{aligned} \delta (b, \delta (a,~s))\in \delta (a*b,~s)\text { for all } a,b\in I,~s\in S. \end{aligned}$$

(1)

The semihypergroup $(I,*)$ is called the input semihypergroup of the quasi–multiautomaton $\mathbb {A}$ (I alone is called the input set or input alphabet), the set S is called the state set of the quasi–multiautomaton $\mathbb {A}$, and $\delta$ is called next-state or transition function. The elements of the set S are called states and the elements of the set I are called input symbols or letters. Condition (1) is called Generalized Mixed Associativity Condition (abbr. as GMAC).

Next, we recall that all compositions (i.e., homogeneous, heterogeneous and Cartesian composition) of automata, were introduced by w. Dörfler in Dörfler (1978). In the following definition, we use our notations opportunity the original definition. In teh other words, input set is on the first position and state set is on second position, i.e., $(I, S, \delta )$. Note that the input set and state set have a reversed order in original, i.e $(S, I, \delta )$. The definition with our notations is used in Chvalina et al. (2018), Chvalina et al. (2016), Novák et al. (2020) and Křehlík and Novák (2019).

Definition 3

(Chvalina et al. 2018) Let $\mathbb {A}_1=(I, S, \delta )$, $\mathbb {A}_2=(I, R, \tau )$ and $\mathbb {B}=(J, T, \sigma )$ be quasi–automata. The homogeneous product $\mathbb {A}_1\times \mathbb {A}_2$ is the quasi-automaton $(I,S\times R, \delta \times \tau )$, where $\delta \times \tau : I\times (S\times R)\rightarrow S\times R$ is a mapping satisfying, for all $s\in S, r\in R, a\in I$,

$$\begin{aligned} (\delta \times \tau )(a,(s,r))=(\delta (a,s),\tau (a,r)), \end{aligned}$$

(2)

while the heterogeneous product $\mathbb {A}_1\otimes \mathbb {B}$ is the quasi-automaton $(I\times J,S\times T, \delta \otimes \sigma )$, where $\delta \otimes \tau :(I\times J)\times (S\times T)\rightarrow S\times T$ is a mapping satisfying, for all $a\in I, b\in J, s\in S, t\in T$,

$$\begin{aligned} \delta \otimes \sigma ((a,b),(s,t))=(\delta (a,s),\sigma (b,t)). \end{aligned}$$

(3)

For I, J disjoint we by $\mathbb {A}\cdot \mathbb {B}$ denote Cartesian composition of $\mathbb {A}$ and $\mathbb {B}$, i.e., the quasi–automaton $(I\cup J, S\times T,\delta \cdot \sigma )$, where $\delta \cdot \sigma :(I\cup J)\times (S\times T)\rightarrow S\times T$ is defined, for all $x\in I\cup J$, $s\in S$ and $t\in T$, by

$$\begin{aligned} (\delta \cdot \sigma )\left( x,(s,t)\right) ={\left\{ \begin{array}{ll} (\delta (x,s),t) &{}\quad \text {if}~ x\in I,\\ (s,\sigma (x,t)) &{}\quad \text {if}~ x\in J. \end{array}\right. } \end{aligned}$$

(4)

Fig. 1

Three cases combination

The generalization of homogeneous and heterogeneous products on the quasi-multiautomata was straightforward.

Definition 4

If in Definition 3 we consider quasi–multiautomata with inputs (semi)hypergroup and satisfying the condition:

$$\begin{aligned}{} & {} (\delta \times \tau )(a,(\delta \times \tau )(b,(s,r)))\in (\delta \times \tau )(a*b (s,r)),\nonumber \\{} & {} \quad \text{ for } \text{ all } s\in S, r\in R, a\in I, \end{aligned}$$

(5)

and

$$\begin{aligned}{} & {} (\delta \otimes \sigma )((a,b),(\delta \otimes \sigma )((c,d),(s,t)))\nonumber \\{} & {} \quad \quad \in (\delta \otimes \sigma )((a,b)*(c,d),(s,t)),\nonumber \\{} & {} \qquad \hbox { for all } a\in I, b\in J, s\in S, t\in T, \end{aligned}$$

(6)

we call $\mathbb {A}_1\times \mathbb {A}_2$ homogeneous product of quasi-multiautomata and $\mathbb {A}_1\otimes \mathbb {B}$ heterogeneous product of quasi–multiautomata.

Note that the GMAC condition failed in the case generalizing Cartesian composition and it had to be expanded to E-GMAC, more (Chvalina et al. 2016). Thanks to unique input symbols, which operate on only the component from state n-tuple, was included a internal links co Cartesian composition, more (Křehlík and Novák 2019; Křehlík 2020). However, adding internal links is not clear for the homogeneous and the heterogeneous products of quasi-multiautomata.

3 Some conditions for internal links in the homogeneous and heterogeneous products of multi-automata

In this section, we present the problem with adding internal links to the homogeneous and heterogeneous products of quasi-multiautomata for n-quasi-multiautomata. First, we consider two quasi-multiautomata, then we develop the following definitions.

Definition 5

Let $\mathbb {A}=(I,S,\delta _\mathbb {A})$ and $\mathbb {B}=(I,T,\delta _\mathbb {B})$ be two quasi–multiautomata $\delta _\mathbb {A}:I\times S\rightarrow S, \delta _{\mathbb {B}}:I\times T\rightarrow T$. By the homogeneous product with internal link $\mathbb {A}\times _{il} \mathbb {B}$ we mean the quasi–multiautomaton $(I,S\times T, \delta _\mathbb {A}\times \delta _\mathbb {B})$, where $\delta _\mathbb {A}\times \delta _\mathbb {B}: I\times (S\times T)\rightarrow S\times T$ is mapping satisfying, for all $s\in S, r\in T, a\in I$,

$$\begin{aligned}{} & {} (\delta _\mathbb {A}\times \delta _\mathbb {B})(a,(s,r))=\left[ \delta _\mathbb {A}\left( \varphi (\delta _\mathbb {B}(a,r)), \delta _\mathbb {A}(a,s)\right) , \right. \nonumber \\{} & {} \qquad \left. \delta _\mathbb {B}(\psi ( \delta _\mathbb {A}(a,s)),\delta _\mathbb {B}(a,r))\right] , \end{aligned}$$

(7)

where $\varphi : T\rightarrow I$, $\psi : S\rightarrow I$.

Definition 6

Let $\mathbb {A}=(I,S,\delta _\mathbb {A})$ and $\mathbb {C}=(J,T,\delta _\mathbb {C})$ be two quasi–multiautomata $\delta _\mathbb {A}:I\times S\rightarrow S, \delta _{\mathbb {C}}:J\times T\rightarrow T$. By the heterogeneous product with internal link $\mathbb {A}\otimes _{il} \mathbb {C}$ we mean the quasi–multiautomaton $(I\times J,S\times R, \delta _\mathbb {A}\times \delta _\mathbb {C})$, where $\delta _\mathbb {A}\times \delta _\mathbb {C}: I\times (S\times R)\rightarrow S\times R$ is mapping satisfying, for all $s\in S, r\in R, a\in I, b\in J$,

$$\begin{aligned}{} & {} (\delta _\mathbb {A}\times \delta _\mathbb {C})((a,b),(s,r))=\left[ \delta _\mathbb {A}\left( \varphi (\delta _\mathbb {C}(b,r)), \delta _\mathbb {A}(a,s)\right) , \right. \nonumber \\{} & {} \qquad \left. \delta _\mathbb {C}(\psi ( \delta _\mathbb {A}(a,s)),\delta _\mathbb {C}(b,r))\right] , \end{aligned}$$

(8)

where $\varphi : S\rightarrow J$, $\psi : T\rightarrow I$.

The combining two quasi-multiautomata by adding internal links is not problematic. In one iteration, the calculation of both components of the state set takes place in parallel, then at the same time the first component affects the second component and the second component affects the first, such that the calculation of the new state is completed. In other words, the order is interchangeable.

For a combination of more than two quasi-multiautomata, we must precisely define the order of the internal links to the individual components of the n-tuple. Consider the quasi-multiautomata $\mathbb {A}_1=(I_1,S_1,\delta _1), \mathbb {A}_2=(I_2,S_2,\delta _2), \mathbb {A}_3=(I_3,S_3,\delta _3)$ and its internal links $\varphi _{12}: S_2\rightarrow I_1$, $\varphi _{13}:S_3\rightarrow I_1, \ldots$

Then, for the first component of state triplet we have two possible calculations:

$$\begin{aligned}{} & {} \left[ \delta _1\left( \varphi _{13}(\delta _3(c,t)),\delta _1\left( \varphi _{12}(\delta _2(b,s)), \delta _1(a,r)\right) \right) ,\right. \nonumber \\{} & {} \qquad \left. \delta _2(\ldots ) \delta _3(\ldots )\right] \end{aligned}$$

(9)

or

$$\begin{aligned}{} & {} \left[ \delta _1\left( \varphi _{12}(\delta _2(b,s)),\delta _1\left( \varphi _{13}(\delta _3(c,t)), \delta _1(a,r)\right) \right) ,\right. \nonumber \\{} & {} \qquad \left. \delta _2(\ldots ) \delta _3(\ldots )\right] \end{aligned}$$

(10)

for $a\in I_1, b\in I_2, c\in I_3, r\in S_1, s\in S_2, t\in S_3$. It is obvious that the state triplet (9) and (10) are different for the confused ordered internal links, then

$$\begin{aligned}{} & {} \left[ \delta _1\left( \varphi _{13}(\delta _3(c,t)),\delta _1\left( \varphi _{12}(\delta _2(b,s)), \delta _1(a,r)\right) \right) , \delta _2(\ldots ) \delta _3(\ldots )\right] \ne \nonumber \\{} & {} \quad \left[ \delta _1\left( \varphi _{12}(\delta _2(b,s)),\delta _1\left( \varphi _{13}(\delta _3(c,t)), \delta _1(a,r)\right) \right) ,\delta _2(\ldots ) \delta _3(\ldots )\right] \end{aligned}$$

(11)

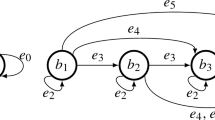
Note that we show problems with the ordered internal link on the heterogeneous product but the same problem occurs in the homogeneous product of quasi-multiautomata with internal links. In the second part of this section, we suggest the same idea to clarify problems with the order of internal links, where the graphical representation of the first three items is shown in Fig. 1:

• (1) all quasi-multiautomata in combination are abelian;

• (2) internal links are a strictly ordered;

• (3) the state component $s_i$ influences only the next state component $s_{i+1}$,

• (4) the special composition of internal links.

3.1 Combination of abelian quasi-multiautomata

Before we show the ordered internal links for the combination of the homogeneous and heterogeneous products of quasi-multiautomata, we will introduce the definition of an abelian quasi-multiautomaton.

Definition 7

The quasi-multiautomaton $\mathbb {A}=(I,S,\delta )$ is called abelian, if for every state $s\in S$ and for every input $a,b\in H$, it holds that

$$\begin{aligned} \delta (a,\delta (b,s))=\delta (b,\delta (a,s)). \end{aligned}$$

(12)

It is obvious from the (12) that ordering the internal links in (9) and (10) does not affect on the final state for abelian quasi-multiautomata.

Lemma 1

The order of the internal links does not matter in homogenous and heterogenous products of abelian quasi-multiautomata.

Proof

The proof is obvious. $\square$

3.2 Strictly ordered internal links

In the second case, we have to define the order of the internal links. This leads to the extension of Definition 5 and Definition 6 for n quasi-multiautomata in the form of the addition of a matrix, where the matrix defines according to the order of the internal links and the elements of the matrix are natural numbers. For example, we present a matrix:

$$\begin{aligned} \begin{bmatrix} 0 &{} \quad 2 &{} \quad 1\\ 2 &{} \quad 0 &{} \quad 1\\ 1 &{} \quad 0 &{}\quad 2\\ \end{bmatrix}, \end{aligned}$$

where the first row corresponds to the first component from (10). The internal link $\varphi _{13}$ is applied first to the first state of the state triple, then the internal link $\varphi _{12}$ is applied. Similar for other rows.

3.3 State influences only its follower by internal link

In Case 3, we can use the matrix the similarly in the case above. However, for an influencing state component by only one internal link, we can define it by a rule, e.g., the following equation

$$\begin{aligned}{} & {} (\delta _\mathbb {A}\times \delta _\mathbb {\mathbb {B}}\times \delta _\mathbb {C}\times \ldots )((a,b,c,\ldots ),(s,r,t,\ldots ))=\nonumber \\{} & {} \quad \left[ \delta _\mathbb {A}(a,s), \delta _\mathbb {B}(\varphi _{21}( \delta _\mathbb {A}(a,s)),\delta _\mathbb {B}(b,r)),\right. \nonumber \\{} & {} \quad \left. \delta _\mathbb {C}(\varphi _{32}( \delta _\mathbb {B}(b,r)),\delta _\mathbb {C}(c,t)), \ldots \right] . \end{aligned}$$

(13)

Consider the following model situation for intelligent traffic management. At a crossroads, autonomous cars wait in a row for a signal. The intelligent transport system (ITS) sends a “free” signal, which means that the vehicles can start moving and cross the intersection safely. Because this is the same input for all of the cars in the considered direction, this is a case of a homogeneous automaton. However, a vehicle can be in the second position of the line and move only after the vehicle in front of it frees the space into which the other vehicle is about to pass (Fig. 1). In other words, the free signal alone is not sufficient; another input must be provided. Other similar real-life examples can be found in Křehlík (2020) and Novák et al. (2019).

This model case corresponds exactly to Case 3, i.e., changing the components of the $s_i$ state n-tuple will only affect the next component from the state n-tuples $s_ {i + 1}$ to which the input symbol has already been applied. Such types of homogeneous/heterogeneous products, with internal links, are offered for modeling cases for real use, where the order of state n-tuples has dependency.

The last case is comprehensive so we will process it in a new section.

4 Homogeneous and heterogenous products with internal links correspondence with cellular automaton

The idea n-ary homogenous and heterogenous product of quasi-automata or quasi-multiatomata with special internal links corresponds with cellular automata (CA). In other words, a cellular automaton can be created from n-ary homogeneous or heterogenous product of quasi-multiautomata with internal links. Recall that CA is discrete and abstract computing systems, that have proven to be useful in various scientific disciplines.

We will show CA and focus on its model results. Although the field of systems that can be found in the CA literature is huge, all CAs can be defined through four properties that define their structure, see Karafyllidis (1999).

• Discrete n-dimensional structure of cells: We can have one-dimensional, two-dimensional,..., n-dimensional CA. The atomic components of the structures can be differently shaped: for example, a 2D lattice can be composed of triangles, squares, or hexagons. Usually, homogeneity is assumed: all cells are qualitatively identical:

• Discrete states: At each discrete time step, each cell is in one and only one state, $\sigma \in \Sigma$, $\Sigma$ being a set of finite cardinality $\vert \Sigma \vert =k$.

• Local interactions: Each cell’s behavior depends only on what happens within its local neighborhood of cells (which may or may not include the cell itself). Lattices with the same basic topology may have different definitions of the neighborhood, as we will see below. It is crucial, however, to note that “actions at a distance” are not allowed.

• Discrete dynamics: At each time step, each cell updates its current state according to a deterministic transition function $\phi :\Sigma ^n\rightarrow \Sigma$ that maps neighborhood configurations (n-tuples of states of $\Sigma$) to $\Sigma$. It is also commonly, though not necessarily, assumed that (1) the update is synchronous, and (2) $\phi$ takes as input at time step t of the neighborhood states at the previous time step $t-1$.

For the construction n-ary homogenous or heterogenous products of quasi-multiautomata we need a quasi-automaton that has hypergroups as an input structure.

Frequently, the values in cells are numbers 0 and 1 therefore, we will lead the construction with similar values. We start with a hyperstrgroupoid $(\mathcal {I},\odot )$, where $\mathcal {I}=\{-1, 0, 1\}$ and hyperoperation $\odot$ is defined $\odot :\mathcal {I}\times \mathcal {I}\rightarrow \mathcal {P}^*(\mathcal {I})$ by the following Table 1.

Table 1 Hyperoperation,,$\odot$”

Lemma 2

The hypergroupoid $(\mathcal {I}, \odot )$ is hypergroup.

Proof

The proof is obvious thanks to Corollary 1. and Section 3.4. of the paper (Křehlík and Novák 2016). $\square$

With respect to the Game of Life, introduced by John H. Conway Berlekamp et al. (2001), we consider only two states for the set of state S, which $S = \{0, 1 \}$. Notis that, we use function signum in connect with GMAC condition, i.e., signum of a set. If A is non–empty subset of $\mathbb {R}$, then ${\text {sgn}}\, A = \bigcup \limits _{a\in A} {\text {sgn}}\,a$.

Now, we can formulate the first theorem.

Theorem 1

The structure $\mathbb{M}\mathbb{A}=(\mathcal {I}, S, \delta )$, where the transition function is defined $\delta : \mathcal {I}\times S\rightarrow S$ by

$$\begin{aligned} \delta \left( i,s\right) = {\text {sgn}}\,(s+i+\vert i+s\vert ) \end{aligned}$$

(14)

is a quasi-multiautomaton.

Proof

We have to show that GMAC condition is valid. In other words, the following holds true:

$$\begin{aligned}{} & {} {\text {sgn}}\,\left( {\text {sgn}}\,(s+b+\vert b+s\vert )+ a + \vert a \right. \nonumber \\{} & {} \quad \left. + {\text {sgn}}\,(s+b+\vert b+s\vert )\vert \right) \nonumber \\{} & {} \qquad \in {\text {sgn}}\,(s+b\odot a +\vert b\odot a +s\vert ). \end{aligned}$$

(15)

The valid GMAC condition is presented in the following Table 2

For all $a, b\in \mathcal {I}$, the states included in the third column are in the sets of the fourth. Thu condition GMAC is satisfied and $\mathbb{M}\mathbb{A}=(\mathcal {I}, S, \delta )$ is a quasi-multiautomaton. $\square$

Table 2 The valid GMAC condition

From the table of proof of the Theorem 1, we can describe the working of the quasi-multiautomaton $\mathbb{M}\mathbb{A}$. If quasi-multiautomaton has input symbols 0, then its state is not changed, i.e., $\delta (0,s)=s$ for all $s\in S$. Input symbol 1 sets value of the state on 1, i.e., $\delta (1,s)=1$ for all $s\in S$ and the input symbol $-1$ sets value of the state on 0, i.e. $\delta (-1,s)=0$ for all $s\in S$.

Without respect to the logical structure of the one-dimensional cellular automata, the two-dimensional cellular automata were more often to discussed as solution for philosophical problems. Next, the two dimensional cellular automata are suitable for modeling a lot of physical phenomena, and even biological and human phenomena. The movement of birds in a storm, the movement of soldiers on a battlefield, and gas dynamics can be modeled with a two dimensional cellular automaton. Configuration CAs are often square or hexagonal cells that show their translational or rotational symmetry. Two dimensions of CA make interesting and wider possibilities for the creation of different rules based on the neighborhood of cells. The most used rules are for a neighborhood introduced by von Neumann and another neighborhood introduced by Moore, where every cell interacts only with two horizontal and two vertical neighbors, and every cell interacts with all eight neighbors, respectively.

For two dimensions, cells are ordered into square structures (call field from information science) $n\times n$. For construction CA, we will need m quasi-multiautomaton which are going to combine as m-ary homogeneous or m-ary heterogeneous products with internal links. In the information sciences, the two-dimensional field $n\times n$ is considered to be a series $\underbrace{1, 2, \ldots n}_{1.~row}, \underbrace{n + 1, \ldots n + n}_{2.~row}, \ldots \underbrace{(n-1) n + 1, \ldots , n^2}_{n~row}$, so that the cell array is not indexed with two numbers but only one. For example, when $n=6$, the cell in the third row and the fourth column is indexed by the number $2*6+4 = 14$.

It is thus obvious that the construction of a cellular automaton will be formed from m quasi-multiautomata, where $m=n^2$ and every quasi-multiautomaton will represent one cell of a cellular automaton.

In the following theorem, we consider m quasi-multiautomata from Theorem 1 with the index $i\in \{1, 2,\ldots m\}$. Moreover, every quasi-multiautomaton has the same input set $\mathcal {I}$ and state $S_i$ is the i-th the cell of the CA with corresponding transition function $\delta _i$.

Theorem 2

Let $\mathbb{M}\mathbb{A}_i$ be quasi-multiautomata for all index $i\in \{1, 2, \ldots , m\}$ form Theorem 1, then the homogeneous product $\mathbb{M}\mathbb{A}_{\textrm{hom}}^m=(\mathcal {I}, \bigotimes \nolimits _{i=1}^m S_i, \prod \nolimits _{i=1}^m \delta _i)$ is a quasi-multiautomaton with the transition function:

$$\begin{aligned}{} & {} (\delta _1,\ldots , \delta _m)(a, (s_1, \ldots , s_m))\nonumber \\ {}{} & {} =\left( \delta _1\left( a, s_1\right) ,\ldots , \delta _m\left( a, s_m\right) \right) \nonumber \\{} & {} =\left( {\text {sgn}}\,(s_1\!+\!a\!+\!\vert a\!+\!s_1\vert ),\ldots , {\text {sgn}}\,(s_m\!+\!a\!+\!\vert a\!+\!s_m\vert )\right) ,\nonumber \\ \end{aligned}$$

(16)

where $a\in \mathcal {I}$ and $s_i\in S_i$ for all $i\in \{1, 2, \ldots , m\}$.

Proof

We show, that the GMAC condition is valid, i.e. $\left( \delta _1,\ldots , \delta _m\right) \left( a, \left( \delta _1,\ldots , \delta _m\right) \left( b,(s_1, \ldots , s_m)\right) \right) \in \left( a\odot b, (s_1,\ldots , s_m)\right)$. We calculate the left hand side as follows:

$$\begin{aligned}{} & {} \left( \delta _1,\ldots , \delta _m\right) \left( a, \left( \delta _1,\ldots , \delta _m\right) \left( b,(s_1, \ldots , s_m)\right) \right) \\{} & {} \quad =\left[ \left( \delta _1,\ldots , \delta _m\right) \left( a, \left( \delta _1 (b, s_1), \ldots ,\delta _m (b, s_m)\right) \right) \right] \\{} & {} \quad =\left[ \delta _1(a, \delta _1(b, s_1), \ldots , \delta _m(a, \delta _m(b, s_m)\right] . \end{aligned}$$

We calculate the right hand side as follows:

$$\begin{aligned}{} & {} (\delta _1, \ldots \delta _m) \left( a\odot b, (s_1, \ldots , s_m) \right) = (\delta _1, \ldots \delta _m)\\{} & {} \quad \left( \bigcup \limits _{c\in a\odot b} c, (s_1, \ldots , s_m)\right) \\{} & {} \quad =\bigcup \limits _{c\in a\odot b} (\delta _1, \ldots \delta _m)\left( c, (s_1, \ldots , s_m)\right) \\{} & {} \quad = \bigcup \limits _{c\in a\odot b} \left( \delta _1(c, s_1),\ldots , \delta _m(c, s_m)\right) . \end{aligned}$$

Next, we want to show that the m-tuple on the left-hand side is an element of the set on the right-hand side. The table in the proof of Theorem 1 shows the valid GMAC condition for one component, i.e., $i=1$. It is obvious that homogeneous product of quasi-multiautomata holds the order of m-tuple state. Thus, the GMAC condition is satisfied and the m-ary homogenous product $\mathbb{M}\mathbb{A}_{\textrm{hom}}^m=(\mathcal {I}, \bigotimes \nolimits _{i=1}^m S_i, \prod \nolimits _{i=1}^m \delta _i)$ is a quasi-multiautomaton. $\square$

We can construct an m-ary heterogeneous product of quasi-multiautomata in the same way, but we use an input m-tuple as introduced above: $\bigotimes \nolimits _{i=1}^m \mathcal {I}=\underbrace{\mathcal {I} \times \mathcal {I} \times \ldots }_m$.

Theorem 3

Let $\mathbb{M}\mathbb{A}_i$ be quasi-multiautomata for all index $i\in \{1, 2, \ldots , m\}$ from Theorem 1, then the triple $\mathbb{M}\mathbb{A}_{het}^m=(\bigotimes \nolimits _{i=1}^m \mathcal {I}, \bigotimes \nolimits _{i=1}^m S_i, \prod \nolimits _{i=1}^m \delta _i)$ is a quasi-multiautomaton where transition function $\prod \nolimits _{i=1}^m \delta _i$ is defined

$$\begin{aligned}{} & {} (\delta _1,\ldots , \delta _m)((a_1,\ldots , a_m), (s_1, \ldots , s_m))\nonumber \\ {}{} & {} =\left( \delta _1\left( a_1, s_1\right) ,\ldots , \right. \nonumber \\{} & {} \quad \left. \delta _m\left( a_m, s_m\right) \right) \nonumber \\{} & {} \quad = \left( {\text {sgn}}\,(s_1+a_1+\vert a_1+s_1\vert ),\ldots , \right. \nonumber \\{} & {} \quad \left. {\text {sgn}}\,(s_m+a_m+\vert a_m+s_m\vert )\right) , \end{aligned}$$

(17)

. for all $a_i\in \mathcal {I}$ ans $s_i\in S$ where $i\in \{1, 2, \ldots , m\}$.

Proof

The proof is similar to the proof for Theorem 2. $\square$

For the m-ary products above, we will define internal links where every state component $s\in S_i$ is influenced by the states in its neighborhood for all $i\in \{1, \ldots , m\}$, i.e., values of the i-th component of the m-tuple state will be corrected by $\overline{s_i}$ for all $i\in \{1, 2, \ldots , m\}$, where

$$\begin{aligned} \overline{_{m}s_i}=\sum \limits _{j=-1}^1(s_{i-n+j} + s_{i+j} + s_{i+n+j}) - s_{i} \end{aligned}$$

(18)

for the Moore neighborhood and

$$\begin{aligned} \overline{_{n}s_i}=s_{i-n} + s_{i+n} + s_{i-1} + s_{i+1} \end{aligned}$$

(19)

for the von Neumann neighborhood.

Note that some indexes are negative in calculating $\overline{_{n}s_i}$ or $\overline{_{m}s_i}$, for the first row in particular. Therefore we set:

$$\begin{aligned} s_{i-n+j}= & {} s_{i+j}= s_{i-n} = s_{i-1}=0 \quad \text{ for }\quad i-n+j\\\le & {} 0, i+j\le 0, i-n\le 0, i-1\le 0 \end{aligned}$$

In other words, if a cell does not have a neighboring cell, then we consider it a non-existent as a dead cell. Recall, that the notion of living and dead cells is from Conway’s Game of Life, where value 1 represents a living cell and value 0 represents a ded cell. Next, we will define mapping $\varphi : ~_MS_i\rightarrow \mathcal {I}$ by:

$$\begin{aligned} \varphi (\overline{_{n}s_i})= {\text {sgn}}\,\left( (-\overline{_{n}s_i}+m_1)\left( \overline{_{n}s_i}-m_2-\frac{1}{2}\right) \right) , \end{aligned}$$

(20)

where $\overline{_{m}s_i}\in ~_MS_i=\{0,1,\ldots , 8\}$, for all $i\in \{1, 2, \ldots \}$ and $m_1, m_2\in \{0, 1,\ldots , 8\}$. Parameters $m_1$ and $m_2$ set a condition in the Games of Life.

Example 1

Consider the following rules for a specific Game of Life:

• if the cell has a neighborhood with 0–1 living neighbor, then the cell dies,

• if the cell has a neighborhood with 4–8 living neighbors, then the cell dies,

• if the cell has a neighborhood with 3 living neighbors, then the cell is born,

• if the cell has a neighborhood with 2 living neighbors, the original state remains.

For these rules, we set $m_1=2$ and $m_2=3$, then we show all of the possible values for mapping (20) in the following Table 3.

In the case of similar rules for the Game of Life, the parameters $m_1, m_2$ can be set to suit specific purposes, i.e., if the cell was born with 4 living neighbors, then we set $m_2 = 4$. For more specialized rules for the Game of Life, it is necessary to modify the polynomial in the argument of the signum function, e.g., increase the degree of the polynomial.

Table 3 Values of function $\varphi (\overline{_{n}s_i})$

Here, we have introduced everything necessary for the construction of m-ary homogeneous product of a quasi-multiautomaton with internal links, which works as cellular automata. This construction combines the quasi-multiautomata from Theorem 2 and the internal links defined by (18) and (20).

Theorem 4

m- ary homogenous product qusi-multiautomata $_{il}\mathbb{M}\mathbb{A}_{\textrm{hom}}^m=(\mathcal {I}, \bigotimes \nolimits _{i=1}^m S_i, \prod \nolimits _{i=1}^m \delta _i, \varphi (\overline{_ms_i}))$ with internal link $\varphi (\overline{_ms_i})$ and transition function

$$\begin{aligned}{} & {} (\delta _1,\ldots , \delta _m)\left( a, (s_1, \ldots , s_m)\right) \nonumber \\ {}{} & {} =\left[ \delta _1\left( \varphi (\overline{_ns_1}), \delta _1(a, s_1)\right) , \ldots , \right. \nonumber \\{} & {} \quad \left. \delta _m\left( \varphi (\overline{_ns_m}), \delta _m(a, s_m)\right) \right] , \end{aligned}$$

(21)

where $a, b\in \mathcal {I}, s_i\in S_i$ for all $i\in \mathbb {N}$, then $_{il}\mathbb{M}\mathbb{A}_{\textrm{hom}}^m$ is a quasi-multiautomaton.

Proof

We have to show that the GMAC condition is valid, i.e. $\left( \delta _1,\ldots , \delta _m\right) \left( a, \left( \delta _1,\ldots , \delta _m\right) \left( b, (s_1, \ldots , s_m)\right) \right) \in \left( \delta _1,\ldots , \delta _m\right) \left( a\odot b, (s_1, \ldots , s_m)\right)$. Thanks to (21) we have

$$\begin{aligned}{} & {} {[}\delta _1\left( \varphi (\overline{_ns_1}), \delta _1\left( a, \delta _1\left( \varphi (\overline{_ns_1}), \delta _1(b, s_1)\right) \right) \right) ,\ldots ,\\{} & {} \quad \delta _m\left( \varphi (\overline{_ns_m}), \delta _m\left( a, \delta _m\left( \varphi (\overline{_ns_m}), \delta _m(b, s_m)\right) \right) \right) ]\in \\{} & {} \quad \bigcup \limits _{c\in a\odot b} \left[ \delta _1\left( \varphi (\overline{_ns_1}), \delta _1(c, s_1)\right) ,\ldots , \delta _m\left( \varphi (\overline{_ns_m}), \delta _m(c, s_m)\right) \right] \end{aligned}$$

We recall, that $\delta _i(1, s_i)=1, \delta _i(0, s_i)=s_i$ and $\delta _i(-1, s_i)=0$ for all $i\in \{1, 2, \ldots , m\}$. In every component of the m-tuple state, the last calculation depends on the value $\varphi (\overline{_Ms_i})$, and it is the same for both the left and right sides. It is obvious, that the GMAC condition is valid for $\varphi (\overline{_Ms_i})-=1$ and $\varphi (\overline{_Ms_i})=1$.

Next we show, that GMAC holds for $\varphi (\overline{_Ms_i})=0$ for all $i\in \{1, 2, \ldots , m\}$. We calculate the left hand side as follows:

$$\begin{aligned}{} & {} {[}\delta _1\left( \varphi (\overline{_ns_1}), \delta _1\left( a, \delta _1\left( \varphi (\overline{_ns_1}), \delta _1(b, s_1)\right) \right) \right) ,\ldots ,\\{} & {} \quad \delta _m\left( \varphi (\overline{_ns_m}), \delta _m\left( a, \delta _m\left( \varphi (\overline{_ns_m}), \delta _m(b, s_m)\right) \right) \right) ]\\{} & {} \quad =\left[ \delta _1\left( 0, \delta _1\left( a, \delta _1\left( 0, \delta _1(b, s_1)\right) \right) \right) ,\ldots ,\right. \\{} & {} \quad \left. \delta _m\left( 0, \delta _m\left( a, \delta _m\left( 0, \delta _m(b, s_m)\right) \right) \right) \right] \\{} & {} \quad =\left[ \delta _1\left( 0, \delta _1\left( a, \delta _1(b, s_1)\right) \right) ,\ldots , \delta _m\left( 0, \delta _m\left( a, \delta _m(b, s_m)\right) \right) \right] \\{} & {} \quad =\left[ \delta _1\left( a, \delta _1(b, s_1)\right) ,\ldots , \delta _m\left( a, \delta _m(b, s_m)\right) \right] . \end{aligned}$$

Now, we calculate right hand side as follows:

$$\begin{aligned}{} & {} \bigcup \limits _{c\in a\odot b} \left[ \delta _1\left( \varphi (\overline{_ns_1}), \delta _1(c, s_1)\right) ,\ldots , \delta _m\left( \varphi (\overline{_ns_m}), \delta _m(b, s_m)\right) \right] \\{} & {} \quad =\bigcup \limits _{c\in a\odot b} \left[ \delta _1\left( 0, \delta _1(c, s_1)\right) ,\ldots , \delta _m\left( 0, \delta _m(b, s_m)\right) \right] \\{} & {} \quad =\bigcup \limits _{c\in a\odot b} \left[ \delta _1(c, s_1),\ldots , \delta _m(c, s_m)\right] . \end{aligned}$$

Thus the left hand side is included in right hand side, i.e.

$$\begin{aligned} \left[ \delta _1\left( a, \delta _1(b, s_1)\right) ,\ldots , \delta _m\left( a, \delta _m(b, s_m)\right) \right] \nonumber \\\in \bigcup \limits _{c\in a\odot b} \left[ \delta _1(c, s_1),\ldots , \delta _m(c, s_m)\right] . \end{aligned}$$

(22)

Indeed, (22) is provided as proof of the Theorem 2. Thus $_{il}\mathbb{M}\mathbb{A}_{\textrm{hom}}^m$ is a quasi-multiautomaton. $\square$

The quasi-multiautomaton from Theorem 5 is actually a cellular automaton. We describe the principle for the m-ary quasi-multiautomata. When the quasi-multiautomaton has the input value 1, then all states of the m-tuple state are set to value 1. This is means that $\overline{_ns_i}=8$ for all $i\in \{1, \ldots , m\}$. Then, internal links set all states to the value 0. Thus, the input symbol 1 resets all of the states in the cellular automaton.

The same holds for the input symbol $-1$. If the quasi-multiautomaton from Theorem 5 accepts the value 0, the setting of the states is not changed and the new values for the states are created as internal links. This construction has one weakness. We cannot set each component of the m-tuple state separately. To separate the effects of each component, we need to construct m-ary heterogeneous product of quasi-multiatuomata.

Theorem 5

m- ary heterogenous product qusi-multiautomata $_{il}\mathbb{M}\mathbb{A}_{het}^m=(\bigotimes \nolimits _{i=1}^m\mathcal {I}_i, \bigotimes \nolimits _{i=1}^m S_i, \prod \nolimits _{i=1}^m \omega _i, \varphi (\overline{_ns_i}))$ with internal link $\varphi (\overline{_ns_i})$ and transition function

$$\begin{aligned}{} & {} (\omega _1,\ldots , \omega _m)\left( (a_1,\ldots , a_m), (s_1, \ldots , s_m)\right) \nonumber \\{} & {} \quad =\left[ \omega _1\left( \varphi (\overline{_ns_1}), \omega _1(a_1, s_1)\right) , \ldots , \omega _m\left( \varphi (\overline{_ns_m}), \omega _m(a_m, s_m)\right) \right] , \end{aligned}$$

(23)

where $(a_1,\ldots , a_m)\in \bigotimes \nolimits _{i=1}^m\mathcal {I}_i, s_i\in S_i$ for all $i\in \mathbb {N}$, then $_{il}\mathbb{M}\mathbb{A}_{het}^m$ is a quasi-multiautomaton.

Proof

The proof is similar to the proof for Theorem 5. $\square$

This construction will allow better regulation of the cellular automaton through the input symbols. Values 1 and -1 reset the states, thanks to internal links, as in the case of a homogeneous product. However, after the reset of the m-tuple state, we can set the same cells on the value 1, i.e., input $(1,1,\ldots , 1)$ and resets all cellular automaton.

Example 2

We consider $_{il}\mathbb{M}\mathbb{A}_{het}^m$ as CA, where all of the states (i.e., cells) are set to the value 0. We make inputs $(\underbrace{0,\ldots , 0}_{n}, \underbrace{0, 0, 1, 1, 1, \ldots }_{n} \underbrace{0,\ldots , 0}_{m-2n} )$ with the traditional function (23). We obtain a new state, where the third, fourth and fifth cell of the second row has value 1, see Fig. 2.

For every state (i.e., cell), a quasi-multiautomaton with internal links calculates values $\overline{_{M}s_i}$ by (18). In this example, we calculate the values only for the important cells from Fig. 3.

We have $\overline{_{M}s_{2}}=\overline{_{M}s_{6}}=\overline{_{M}s_{n+2}}=\overline{_{M}s_{n+3}}=\overline{_{M}s_{n+5}}=\overline{_{M}s_{n+6}}=\overline{_{M}s_{2n+2}}=\overline{_{M}s_{2n+6}}=1, \overline{_{M}s_{3}}=\overline{_{M}s_{5}}=\overline{_{M}s_{n+4}}=\overline{_{M}s_{2n+3}}=\overline{_{M}s_{2n+5}}=2, \overline{_{M}s_{4}}=\overline{_{M}s_{2n+4}}=3$. For parameters $m_1=2, m_2=3$ and rules from Example 1, cells with value $\overline{_{M}s_{i}}=1$ are dead, cells with value $\overline{_{M}s_{i}}=2$ do not change state, and cells with value $\overline{_{M}s_{i}}=3$ will be born. See Fig. 4.

Fig. 2

Application input $(\underbrace{0,\ldots , 0}_{n}, \underbrace{0, 0, 1, 1, 1, \ldots }_{n} \underbrace{0,\ldots , 0}_{m-2n} )$ after reset cellular automaton

Fig. 3

Selected cells to demonstrate the application of internal links

Fig. 4

Application $\omega (\overline{_{M}s_{i}})$ from Fig. 2

5 Conclusions and future work

In this paper, we defined an internal link to the homogeneous and heterogeneous products of quasi-multiautomata. We presented some ways to introduce these internal links because it is not straightforward. Next, we chose one possible way, which is interesting from the view of cellular automata. The introduction of an internal link to these products does not require the use of decisive functions. The iteration process of homogeneous and heterogeneous quasi-multiautomata is based on the numerical calculation of the value in the cells. This principle has a weakness for border cells, which are valid but can influence the internal link with an inaccurate value, see Fig. 5. This problem can be eliminate by the input of suitable symbols for the next iteration, i.e., $(\underbrace{-1,\ldots , -1}_n, \underbrace{ -1, 0,\ldots , 0, -1}_n, \underbrace{-1, 0,\ldots , 0, -1}_n, \ldots )$. This input sets the values in border cells to 0, then the modeling of the arbitrary process can be realized with only the internal cells of the grid, thus avoiding the effect around the yellow cell in Fig. 5. The process, which controls the edge values, is standard in information sciences. We remark that the use of input $(\underbrace{-1,\ldots , -1}_n, \underbrace{ -1, 0,\!\ldots , 0, -1}_n, \underbrace{-1, 0,\!\ldots , 0, -1}_n, \!\ldots )$ is not possible for the homogeneous product of quasi-multiautomata, which require new measures.

Another important interesting aspect is the expansion of the neighbors who affect the situation such that distant neighbors affect the situation less. Constructions of this type could then have a wide application, for example, in models for obtaining data from underwater sensors, Křehlík and Novák (2019).

Fig. 5

Internal link for border calls