1 Introduction

The historical Emden–Fowler (EF) system is considered very important for the research community because of singularity at the origin and has various applications in wide-ranging fields of applied science and engineering. Some well-known applications are catalytic diffusion reactions using the error estimate models (Burdyny and Smith 2019), stellar configuration (Abbas et al. 2019), density profile of gaseous star (Bacchini et al. 2019), spherical annulus (Soliman 2019), isotropic continuous media (Adel and Sabir 2020), extrinsic thermionic maps (Barilla et al. 2020), the theory of electromagnetic (Guirao et al. 2020) and morphogenesis (Dridi and Trabelsi 2022). Due to the specialty of the singular point and extensive applications, the researcher has always shown keen interest to solve these models all the time. These models are not easy to solve due of this singular model, nonlinearity and stiff nature, and only a few techniques are available in the literature to solve these models. Few of them are Legendre spectral wavelets scheme (Dizicheh et al. 2020), Adomian decomposition scheme (Abdullah Alderremy et al. 2019), Haar quasilinearization wavelet scheme (Singh et al. 2020; Verma and Kumar 2019), an analytic algorithm approach (Arqub et al. 2020), rational Legendre approximation scheme (Dizicheh et al. 2020), modified variational iteration scheme (Verma et al. 2021), differential transformation scheme (Xie et al. 2019), fourth-order B-spline collocation scheme (Roul and Thula 2019), Chebyshev operational matrix scheme (Sharma et al. 2019) and variation of parameters scheme with an auxiliary parameter (Khalifa and Hassan 2019). Beside these, the numerical methodologies introduced in (Abdelrahman and Alharbi 2021; Alharbi et al. 2020; Almatrafi et al. 2021; Lotfy 2019; Sabir 2022a, Sabir et al. 2022c) can be exploited for EF equations-based systems.

All these mentioned schemes have their specific merits/advantages and demerits/imperfections, whereas soft computing stochastic solver is used to manipulate the artificial neural networks (ANNs) strength optimized by global/local search proficiencies of particle swarm optimization (PSO) and interior-point method (IPM), i.e., ANNs-PSO-IPM, have not been implemented for the nonlinear coupled EF model of second kind. The researchers have been generally practiced the numerical computing meta-heuristic schemes along with the neural network strengths for solving the various mathematical linear/nonlinear models (Guerrero-Sánchez et al. 2021; Guirao et al. 2022; Lu et al. 2019, 2021; Mehmood et al. 2020; Sabir et al. 2020a, e). Few recent applications of the stochastic solvers are financial market forecasting (Bukhari et al. 2020), food chain model (Sabir 2022b), nonlinear smoking models (Saeed et al. 2022), nonlinear fractional Lane–Emden systems (Sabir et al. 2022d), nonlinear second-order Lane–Emden pantograph delay differential systems (Nisar et al. 2021), peristaltic motion of a third-grade fluid involving planar channel (Mahmood et al. 2022), nonlinear predator–prey system (Umar et al. 2019), elliptic partial differential model (Fateh et al. 2019), mathematical form of the Leptospirosis system (Botmart et al. 2022), HIV mathematical models (Sabir et al. 2021c, 2022a), nonlinear multiple singularity-based systems (Raja et al. 2019), singular Thomas–Fermi equation (Sabir et al. 2018), heartbeat dynamics (Malešević et al. 2020), a corneal model for eye surgery (Umar et al. 2019; Wang et al. 2022) and heat conduction model of the human head (Raja et al. 2018). These proposed stochastic solvers verified the values of the exactness, convergence, and accurateness of the ANNs-PSO-IPM.

Keeping in view all the consequences of above proposals, authors are interested to exploit the numerical stochastic solvers for consistent, stable, and efficient scheme for nonlinear second-order coupled EF system. The literature form of the coupled EF model of second kind is written as (Sabir et al. 2020b):

$$ \left\{ {\begin{array}{*{20}l} {\frac{{d^{2} U}}{{d\Psi^{2} }} + \frac{\alpha }{\Psi }\frac{dU}{{d\Psi }} + H_{1} (\Psi )G_{1} (U,V) = F_{1} (\Psi ),} \hfill & {U(0) = A,} \hfill & {\frac{dU(0)}{{d\Psi }} = 0,} \hfill \\ {\frac{{d^{2} V}}{{d\Psi^{2} }} + \frac{\beta }{\Psi }\frac{dV}{{d\Psi }} + H_{2} (\Psi )G_{2} (U,V) = F_{2} (\Psi ),} \hfill & {V(0) = B,} \hfill & {\frac{dV(0)}{{d\Psi }} = 0,} \hfill \\ \end{array} } \right. $$
(1)

where \(G_{1}\) and \(G_{2}\) are the nonlinear functions, \(\alpha\) and \(\beta\) are the constants, while \(F_{1}\) and \(F_{2}\) are designated as a source functions. The aim of this current study is to solve the model given in Eq. (1) through intelligent computing schemes based on ANN-PSO-IP scheme. Some inventive inspiration of the current study is presented as:

  • A neuro-swarm novel intelligent computing ANNs-PSO-IPM is designed and presented to solve second-order nonlinear coupled EF model.

  • The overlapping results of the proposed ANNs-PSO-IPM with the exact solutions for four different examples of the nonlinear-coupled EF-based model of second kind establish the consistency, exactness and convergence.

  • Ratification of the precise performance is authenticated via statistical calculations/observations on multiple runs of ANN-PSO-IP scheme in terms of root mean square error, Variance Account For, Semi Interquartile Range and Theil’s inequality coefficient metrics.

  • Beside essentially precise continuous results on whole interval, ease in the concept, stability, the smooth implementable practice and extendibility are well-intentioned declarations for the presented ANNs-PSO-IPM.

The remaining forms of the present work are shown as; Sec 2 presents the detailed methodology of the neural networks using the optimization process ANNs-PSO-IP scheme. Sec 3 presents the performance measures. Sec 4 indicates the numerical measures of the ANNs-PSO-IPM together with the statistical measures. Finally, some concluding remarks along with future work plans are described.

2 Methodology

This section presents the design of ANNs-PSO-IPM for second-order nonlinear coupled EF model in two stages as given below:

Stage 1: A mean square error-based objective/fitness function is constructed for nonlinear coupled EF model

Stage 2: The training/learning of the networks is presented with the help of hybrid PSO-IPM.

2.1 ANNs modeling

The neural networks are extensively applied to solve the diverse applications arising in sundry domains of engineering and applied sciences (Nasirzadehroshenin et al. 2020; Sabir et al. 2021b, 2022e; Umar et al. 2020). The proposed results are indicated as \(\hat{U}(\Psi )\) and \(\hat{V}(\Psi )\), while \(\frac{{d^{n} \hat{U}}}{{d\Psi^{n} }}\) and \(\frac{{d^{n} \hat{V}}}{{d\Psi^{n} }}\) are the derivatives of nth order, respectively, and are given as follows:

$$ \begin{aligned} \left[ {\hat{U}(\Psi ),\hat{V}(\Psi )} \right] & = \left[ {\sum\limits_{i\, = \,1}^{m} {\phi_{U,i} P(w_{U,i} \Psi + a_{U,i} )} ,\,\,\sum\limits_{i\, = \,1}^{m} {\phi_{V,i} P(w_{V,i} \Psi + a_{V,i} )} } \right], \\ \left[ {\frac{{d^{n} \hat{U}}}{{d\Psi^{n} }},\frac{{d^{n} \hat{V}}}{{d\Psi^{n} }}} \right] & = \left[ {\sum\limits_{i\, = \,1}^{m} {\phi_{U,i} \frac{{d^{n} }}{{d\Psi^{n} }}P(w_{U,i} \Psi + a_{U,i} )} ,\,\,\sum\limits_{i\, = \,1}^{m} {\phi_{V,i} \frac{{d^{n} }}{{d\Psi^{n} }}P(w_{V,i} \Psi + a_{V,i} )} } \right], \\ \end{aligned} $$
(2)

where \(\phi ,\) \(w\) and \(a\) are the unknown weight vectors, while m and n are the number of neurons and the order of derivative, respectively.

\({\varvec{W}} = [{\varvec{W}}_{U} ,\,{\varvec{W}}_{V} ]\), for \({\varvec{W}}_{U} = [{\varvec{\phi}}_{U} ,{\varvec{w}}_{U} ,{\varvec{\alpha}}_{U} ]\) and \({\varvec{W}}_{V} = [{\varvec{\phi}}_{V} ,{\varvec{w}}_{V} ,{\varvec{\alpha}}_{V} ]\). The weight vector components are shown as:

$$ \begin{array}{*{20}l} {{\varvec{\phi}}_{U} = [\phi_{U,1} ,\phi_{U,2} ,\cdots,\phi_{U,m} ],} \hfill & {{\varvec{w}}_{U} = [w_{U,1} ,w_{U,2} ,\cdots,w_{U,m} ],} \hfill & {{\varvec{a}}_{U} = [a_{U,1} ,a_{U,2} ,\cdots,a_{U,m} ],} \hfill \\ {{\varvec{\phi}}_{V} = [\phi_{V,1} ,\phi_{V,2} ,\cdots,\phi_{V,m} ],} \hfill & {{\varvec{w}}_{V} = [w_{V,1} ,w_{V,2} ,\cdots,w_{V,m} ],} \hfill & {{\varvec{a}}_{V} = [a_{V,1} ,a_{V,2} ,\cdots,a_{V,m} ].} \hfill \\ \end{array} $$

The log-sigmoid \(P(\Psi ) = \frac{1}{{\left( {1 + {\text{e}}^{ - \Psi } } \right)}}\) is as an activation function and the simplified form of the network (2) using the \(\hat{U}(\Psi )\) and \(\hat{V}(\Psi )\) along with their derivatives are shown as:

$$ \begin{aligned} \left[ {\hat{U}(\Psi ),\,\hat{V}(\Psi )} \right] & = \left[ {\sum\limits_{i = 1}^{m} {\frac{{\phi_{U,\,i} }}{{1 + e^{{ - \left( {w_{U,\,i} \Psi + a_{U,\,i} } \right)}} }},\,\,} \sum\limits_{i = 1}^{m} {\frac{{\phi_{V,\,i} }}{{1 + e^{{ - \left( {w_{V,\,i} \Psi + a_{V,\,i} } \right)}} }}} } \right], \\ \left[ {\frac{{d\hat{U}}}{d\Psi },\frac{{d\hat{V}}}{d\Psi }} \right] & = \left[ {\sum\limits_{i = 1}^{m} {\frac{{\phi_{U,\,i} w_{U,\,i} e^{{ - \left( {w_{U,\,i} \Psi + a_{U,\,i} } \right)}} }}{{\left( {1 + e^{{ - \left( {w_{U,\,i} \Psi + a_{U,\,i} } \right)}} } \right)^{2} }},\,\,\sum\limits_{i = 1}^{m} {\frac{{\phi_{V,\,i} w_{V,\,i} e^{{ - \left( {w_{V,\,i} \Psi + a_{V,\,i} } \right)}} }}{{\left( {1 + e^{{ - \left( {w_{V,\,i} \Psi + a_{V,\,i} } \right)}} } \right)^{2} }}} } } \right], \\ \left[ {\frac{{d^{2} \hat{U}}}{{d\Psi^{2} }},\frac{{d^{2} \hat{V}}}{{d\Psi^{2} }}} \right] & = \left[ \begin{gathered} \sum\limits_{i = 1}^{m} {\phi_{U,\,i} w_{U,\,i}^{2} \left\{ {\frac{{2e^{{ - 2\left( {w_{U,\,i} \Psi + a_{U,\,i} } \right)}} }}{{\left( {1 + e^{{ - \left( {w_{U,\,i} \Psi + a_{U,\,i} } \right)}} } \right)^{3} }} - \frac{{e^{{ - \left( {w_{U,\,i} \Psi + a_{U,\,i} } \right)}} }}{{\left( {1 + e^{{ - \left( {w_{U,\,i} \Psi + a_{U,\,i} } \right)}} } \right)^{2} }}} \right\}} ,\, \hfill \\ \sum\limits_{i = 1}^{m} {\phi_{V,\,i} w_{V,\,i}^{2} \left\{ {\frac{{2e^{{ - 2\left( {w_{V,\,i} \Psi + a_{V,\,i} } \right)}} }}{{\left( {1 + e^{{ - \left( {w_{V,\,i} \Psi + a_{V,\,i} } \right)}} } \right)^{3} }} - \frac{{e^{{ - \left( {w_{V,\,i} \Psi + a_{V,\,i} } \right)}} }}{{\left( {1 + e^{{ - \left( {w_{V,\,i} \Psi + a_{V,\,i} } \right)}} } \right)^{2} }}} \right\}} \hfill \\ \end{gathered} \right]. \\ \end{aligned} $$
(3)

The mean square error-based objective/fitness formulation is formulated as follows:

$$ E_{Fit} = E_{Fit - 1} + E_{Fit - 2} + E_{Fit - 3} , $$
(4)
$$ E_{Fit - 1} = \frac{1}{N}\sum\limits_{m = 1}^{N} {\left( {\Psi_{m} \frac{{d^{2} \hat{U}}}{{d\Psi_{m}^{2} }} + \alpha \frac{{d\hat{U}}}{{d\Psi_{m} }} + \Psi_{m} H_{1} G_{1} (\hat{U},\hat{V}) - \Psi_{m} F_{1} } \right)^{2} ,\,} $$
(5)
$$ E_{Fit - 2} = \frac{1}{N}\sum\limits_{m = 1}^{N} {\left( {\Psi_{m} \frac{{d^{2} \hat{V}}}{{d\Psi_{m}^{2} }} + \beta \frac{{d\hat{V}}}{{d\Psi_{m} }} + \Psi_{m} H_{2} G_{2} (\hat{U},\hat{V}) - \Psi_{m} F_{2} } \right)^{2} ,\,} $$
(6)
$$ E_{Fit - 3} = \frac{1}{6}\left( {\left( {\hat{U} - A_{1} } \right)^{2} + \left( {\frac{{d\hat{U}}}{{d\Psi_{m} }}} \right)^{2} + \left( {\hat{V} - A_{2} } \right)^{2} + \left( {\frac{{d\hat{V}}}{{d\Psi_{m} }}} \right)^{2} } \right), $$
(7)

where \(hN = 1\,,\,\,\Psi_{m} = mh,\,\,\,F_{1} (\Psi ) = F_{1}\) and \(F_{2} (\Psi ) = F_{2}\). The objective functions \(E_{Fit - 1}\) and \(E_{Fit - 2}\) are linked with coupled differential systems, and \(E_{Fit - 3}\) is used for the initial conditions.

2.2 Optimization: PSO-IPM

The optimization to solve the second-order nonlinear-coupled EF system is ratified by the hybrid-computing of PSO-IPM.

PSO is a well-organized search algorithm used as a global search methodology like genetic algorithms (GAs). The PSO algorithm introduced by Eberhart and Kennedy (Hussain and Ismail 2020; Sibalija 2019) and works as an easy procedure that needs minor memory. In search space, an applicant single solution of decision variables by applying optimization is known as a particle and these particles set formulate a swarm. The PSO operates via local \({\varvec{P}}_{LB}^{\rho - 1}\) and global \({\varvec{P}}_{GB}^{\rho - 1}\) best particle positions in a swarm. The position Xi and velocity Vi are mathematical expressed as follows:

$$ {\varvec{X}}_{i}^{\chi } = {\varvec{V}}_{i}^{\chi - 1} + {\varvec{X}}_{i}^{\chi - 1} , $$
(8)
$$ {\varvec{V}}_{i}^{\chi } = \sigma {\varvec{V}}_{i}^{\chi - 1} + \xi_{1} ({\varvec{P}}_{LB}^{\chi - 1} - {\varvec{X}}_{i}^{\chi - 1} ){\varvec{\gamma}}_{1} + \xi_{2} ({\varvec{P}}_{GB}^{\chi - 1} - {\varvec{X}}_{i}^{\chi - 1} ){\varvec{\gamma}}_{2} , $$
(9)

here \(\chi\) stands for iteration/flight index, \(\sigma\) is for inertia weight vector varying between [0. 1], \(\xi_{1}\) and \(\xi_{2}\) are the cognitive/social constant accelerations, while, \({\varvec{\gamma}}_{1}\) and \({\varvec{\gamma}}_{2}\) are the vectors lie between [0, 1]. Some recent applications of PSO are parameter estimation (Özsoy et al. 2020), robotics (Mai et al. 2019; Yang et al. 2019), nonlinear electric circuits (Qu et al. 2020), systems of equation-based physical models (Kuntoji et al. 2020), and optimization of permanent magnets synchronous motor (Mesloub et al. 2020).

The convergence performance of PSO quickly achieved by using the combination with local search procedure by taking the global best particle of PSO as an initial weight. Consequently, an operative and quick local search approach named as interior-point method (IPM) is oppressed for rapid refinement of the outcomes obtained via PSO scheme. The integrated heuristics of PSO-IPM is exploited to train the networks, while the essential parameter settings of importance elements for PSO-IPM are given in Table 1. Few recently IP scheme applications are power flow security constraint optimization (Casacio et al. 2019), image processing (Chouzenoux et al. 2020), multistage nonlinear nonconvex problems (Zanelli et al. 2020) and nonlinear benchmark models (Wambacq et al. 2021). The PSO-IP scheme is used to train the networks as per process and parameter settings provided in Table 1.

Table 1 Comprehensive pseudocode of PSO-IP scheme for solving the second-order nonlinear coupled EF model
Full size table

3 Performance indices/metrics

The performances is measured using RMSE, VAF, TIC indices along their globals, i.e., mean values. The mathematical forms of these statistical operatives are given as:

$$ \left[ {{\text{RMSE}}_{U} ,{\text{RMSE}}_{V} } \right]{ = }\left[ {\sqrt {\frac{1}{n}\sum\limits_{k = 1}^{n} {\left( {U_{k} - \hat{U}_{k} } \right)^{2} } } ,\sqrt {\frac{1}{n}\sum\limits_{k = 1}^{n} {\left( {V_{k} - \hat{V}_{k} } \right)^{2} } } } \right], $$
(10)
$$ {\text{[TIC}}_{U} {\text{,TIC}}_{V} {] = }\left[ {\frac{{\sqrt {\frac{1}{n}\sum\limits_{k = 1}^{n} {\left( {U(\Psi_{k} ) - \hat{U}(\Psi_{k} )} \right)}^{2} } }}{{\left( {\sqrt {\frac{1}{n}\sum\limits_{k = 1}^{n} {U^{2} (\Psi_{k} )} } + \sqrt {\frac{1}{n}\sum\limits_{k = 1}^{n} {\hat{U}^{2} (\Psi_{k} )} } } \right)}},\frac{{\sqrt {\frac{1}{n}\sum\limits_{k = 1}^{n} {\left( {V(\Psi_{k} ) - \hat{V}(\Psi_{k} )} \right)}^{2} } }}{{\left( {\sqrt {\frac{1}{n}\sum\limits_{k = 1}^{n} {V^{2} (\Psi_{k} )} } + \sqrt {\frac{1}{n}\sum\limits_{k = 1}^{n} {\hat{V}^{2} (\Psi_{k} )} } } \right)}}} \right], $$
(11)
$$ \left\{ \begin{gathered} {\text{[VAF}}_{U} ,{\text{VAF}}_{V} ] = \left[ {\left( {1 - \frac{{{\text{var}} \left( {U(\Psi_{k} ) - \hat{U}(\Psi_{k} )} \right)}}{{{\text{var}} \left( {U(\Psi_{k} )} \right)}}} \right) \times 100,\left( {1 - \frac{{{\text{var}} \left( {V(\Psi_{k} ) - \hat{V}(\Psi_{k} )} \right)}}{{{\text{var}} \left( {V(\Psi_{k} )} \right)}}} \right) \times 100} \right] \hfill \\ \left[ {{\text{EVAF}}_{U} ,{\text{EVAF}}_{V} } \right] = \left[ {\left| {VAF_{U} - 100} \right|,\left| {VAF_{V} - 100} \right|} \right]. \hfill \\ \end{gathered} \right., $$
(12)

4 Results and discussions

The detail for presenting the solving the four examples of second-order coupled EF model is presented in this section.

Problem I

Consider the second-order nonlinear-coupled EF model is given as:

$$ \left\{ \begin{gathered} \frac{{d^{2} U}}{{d\Psi^{2} }} + \frac{1}{\Psi }\frac{dU}{{d\Psi }} - (4\Psi^{2} + 5)U = 0,\,\,\,\,U(0) = 1,\,\,\frac{dU(0)}{{d\Psi }} = 0, \hfill \\ \frac{{d^{2} V}}{{d\Psi^{2} }} + \frac{2}{\Psi }\frac{dV}{{d\Psi }} - (4\Psi^{2} - 5)V = 0,\,\,\,\,\,V(0) = 1,\,\,\frac{dV(0)}{{d\Psi }} = 0.\,\, \hfill \\ \end{gathered} \right. $$
(13)

The exact solutions of Eq. (13) are [\(e^{{\Psi^{2} }} ,\,\,e^{{ - \Psi^{2} }}\)], whereas the fitness function becomes as:

$$ E_{Fit} = \frac{1}{N}\sum\limits_{m = 0}^{N} {\left( \begin{gathered} \left( {\Psi_{m} \frac{{d^{2} \hat{U}}}{{d\Psi_{m}^{2} }} + \frac{{d\hat{U}}}{{d\Psi_{m} }} - \Psi_{m} (4\Psi_{m}^{2} + 5)\hat{U}} \right)^{2} + \hfill \\ \left( {\Psi_{m} \frac{{d^{2} \hat{V}}}{{d\Psi_{m}^{2} }} + 2\frac{{d\hat{V}}}{{d\Psi_{m} }} - \Psi_{m} (4\Psi_{m}^{2} - 5)\hat{V}} \right)^{2} \hfill \\ \end{gathered} \right)} + \frac{1}{4}\left( \begin{gathered} \left( {\hat{U} - 1} \right)^{2} + \left( {\frac{{d\hat{U}}}{{d\Psi_{m} }}} \right)^{2} \hfill \\ + \left( {\hat{V} - 1} \right)^{2} + \left( {\frac{{d\hat{V}}}{{d\Psi_{m} }}} \right)^{2} \hfill \\ \end{gathered} \right), $$
(14)

here N =20, 25 and 30 for input span [0, 1], [0, 1.25] and [0, 1.5], respectively.

Problem II

Consider the second-order nonlinear-coupled EF system is written as:

$$ \left\{ \begin{gathered} \frac{{d^{2} U}}{{d\Psi^{2} }} + \frac{2}{\Psi }\frac{dU}{{d\Psi }} - U^{2} + V^{2} + 6V = 6\Psi^{2} + 6,\,\,\,\,U(0) = 1,\,\,\frac{dU(0)}{{d\Psi }} = 0, \hfill \\ \frac{{d^{2} V}}{{d\Psi^{2} }} + \frac{2}{\Psi }\frac{dV}{{d\Psi }} + U^{2} - V^{2} - 6V = - 6\Psi^{2} + 6,\,\,\,\,\,V(0) = - 1,\,\,\frac{dV(0)}{{d\Psi }} = 0.\,\, \hfill \\ \end{gathered} \right. $$
(15)

The exact solutions of Eq. (15) are \(\left[ {\Psi^{2} + e^{{\Psi^{2} }} ,\Psi^{2} - e^{{\Psi^{2} }} } \right]\), and the error function is given as:

$$ \begin{gathered} E_{Fit} = \frac{1}{N}\sum\limits_{m = 0}^{N} {\left( \begin{gathered} \left( {\Psi_{m} \frac{{d^{2} \hat{U}}}{{d\Psi_{m}^{2} }} + 2\frac{{d\hat{U}}}{{d\Psi_{m} }} - \Psi_{m} \hat{U}^{2} + \Psi_{m} \hat{V}^{2} + 6\Psi_{m} \hat{V} = 6\Psi_{m}^{3} + 6\Psi_{m} } \right)^{2} + \hfill \\ \left( {\Psi_{m} \frac{{d^{2} \hat{V}}}{{d\Psi_{m}^{2} }} + 2\frac{{d\hat{V}}}{{d\Psi_{m} }} + \Psi_{m} \hat{U}^{2} - \Psi_{m} \hat{V}^{2} - 6\Psi_{m} \hat{V} = - 6\Psi_{m}^{3} + 6\Psi_{m} } \right)^{2} \hfill \\ \end{gathered} \right)} \hfill \\ \,\,\,\,\,\,\,\,\,\, + \frac{1}{4}\left( {\left( {\hat{U} - 1} \right)^{2} + \left( {\frac{{d\hat{U}}}{{d\Psi_{m} }}} \right)^{2} + \left( {\hat{V} + 1} \right)^{2} + \left( {\frac{{d\hat{V}}}{{d\Psi_{m} }}} \right)^{2} } \right), \hfill \\ \end{gathered} $$
(16)

here, N =20, 25 and 30 for input span [0, 1], [0, 1.25] and [0, 1.5], respectively.

Problem III

Consider the second-order nonlinear-coupled EF model is given as:

$$ \left\{ \begin{gathered} \frac{{d^{2} U}}{{d\Psi^{2} }} + \frac{3}{\Psi }\frac{dU}{{d\Psi }} - 4(U + V) = 0,\,\,\,\,U(0) = 1,\,\,\frac{dU(0)}{{d\Psi }} = 0, \hfill \\ \frac{{d^{2} V}}{{d\Psi^{2} }} + \frac{2}{\Psi }\frac{dV}{{d\Psi }} + 3(U + V) = 0,\,\,\,\,\,V(0) = 1,\,\,\frac{dV(0)}{{d\Psi }} = 0.\,\, \hfill \\ \end{gathered} \right. $$
(17)

The exact solutions of Eq. (17) are \(\left[ {1 + \Psi^{2} ,\,\,1 - \Psi^{2} } \right]\), and the fitness/objective function is given as follows:

$$ E_{Fit} = \frac{1}{N}\sum\limits_{m = 0}^{N} {\left( \begin{gathered} \left( {\Psi_{m} \frac{{d^{2} \hat{U}}}{{d\Psi_{m}^{2} }} + 3\frac{{d\hat{U}}}{{d\Psi_{m} }} - 4\Psi_{m} (\hat{U} + \hat{V})} \right)^{2} + \hfill \\ \left( {\Psi_{m} \frac{{d^{2} \hat{V}}}{{d\Psi_{m}^{2} }} + 2\frac{{d\hat{V}}}{{d\Psi_{m} }} + 3\Psi_{m} (\hat{U} + \hat{V})} \right)^{2} \hfill \\ \end{gathered} \right)} + \frac{1}{4}\left( \begin{gathered} \left( {\hat{U} - 1} \right)^{2} + \left( {\frac{{d\hat{U}}}{{d\Psi_{m} }}} \right)^{2} \hfill \\ + \left( {\hat{V} - 1} \right)^{2} + \left( {\frac{{d\hat{V}}}{{d\Psi_{m} }}} \right)^{2} \hfill \\ \end{gathered} \right). $$
(18)

here N =20, 25 and 30 for input span [0, 1], [0, 1.25] and [0, 1.5], respectively.

Problem IV

Consider the second-order nonlinear-coupled EF model is given as:

$$ \left\{ {\begin{array}{*{20}l} {\frac{{d^{2} U}}{{d\Psi^{2} }} + \frac{1}{\Psi }\frac{dU}{{d\Psi }} - (1 + U^{2} )V^{3} = 0,} \hfill & {U(0) = 1,} \hfill & {\frac{dU(0)}{{d\Psi }} = 0,} \hfill \\ {\frac{{d^{2} V}}{{d\Psi^{2} }} + \frac{3}{\Psi }\frac{dV}{{d\Psi }} + (3 + U^{2} )V^{5} = 0,} \hfill & {V(0) = 1,} \hfill & {\frac{dV(0)}{{d\Psi }} = 0.} \hfill \\ \end{array} } \right. $$
(19)

The exact solutions of Eq. (17) are \(\left[ {\sqrt {1 + \Psi^{2} } ,\,\,\frac{1}{{\sqrt {1 + \Psi^{2} } }}} \right]\), and the fitness/objective function is given as follows:

$$ E_{Fit} = \frac{1}{N}\sum\limits_{m = 0}^{N} {\left( \begin{gathered} \left( {\Psi_{m} \frac{{d^{2} \hat{U}}}{{d\Psi_{m}^{2} }} + \frac{{d\hat{U}}}{{d\Psi_{m} }} - \hat{V}^{3} \Psi_{m} (\hat{U}^{2} + 1)} \right)^{2} + \hfill \\ \left( {\Psi_{m} \frac{{d^{2} \hat{V}}}{{d\Psi_{m}^{2} }} + 3\frac{{d\hat{V}}}{{d\Psi_{m} }} + \hat{V}^{5} \Psi_{m} (\hat{U}^{2} + 3)} \right)^{2} \hfill \\ \end{gathered} \right)} + \frac{1}{4}\left( \begin{gathered} \left( {\hat{U} - 1} \right)^{2} + \left( {\frac{{d\hat{U}}}{{d\Psi_{m} }}} \right)^{2} \hfill \\ + \left( {\hat{V} - 1} \right)^{2} + \left( {\frac{{d\hat{V}}}{{d\Psi_{m} }}} \right)^{2} \hfill \\ \end{gathered} \right), $$
(20)

here N =20, 25 and 30 for input span [0, 1], [0, 1.25] and [0, 1.5], respectively.

To calculate/determined the proposed numerical outcomes for the Problems I to IV based on the second-order nonlinear-coupled EF model using the proposed PSO-IPM executed for 50 multiple runs to attain the adjustable weights. The numerical values of the weights are presented in Fig. 1 for \(\hat{U}\) and \(\hat{V}\). These parameters are applied to get the estimated results for all four variants based on the second-order nonlinear-coupled EF model and the mathematical representations becomes as:

$$ \hat{U}_{P - I} = \frac{1.6758}{{1 + e^{{ - (1.425\Psi + {1}{\text{.998}})}} }} - \frac{3.8309}{{1 + e^{{ - ( - 4.376\Psi + {5}{\text{.970}})}} }} + \frac{2.3451}{{1 + e^{ - (1.5452\Psi - 3.003)} }} + \cdots - \frac{6.8234}{{1 + e^{{ - ( - 7.387\Psi + 11.{211})}} }}, $$
(21)
$$ \hat{U}_{P - II} = \frac{6.0315}{{1 + e^{{ - (0.578\Psi + 0.{192})}} }} + \frac{9.0343}{{1 + e^{ - (6.155\Psi - 9.503)} }} + \frac{1.297}{{1 + e^{ - ( - 2.206\Psi - 1.560)} }} + \cdots + \frac{4.6126}{{1 + e^{{ - ( - 2.220\Psi - 1.9{21})}} }}, $$
(22)
$$ \hat{U}_{P - III} = \frac{ - 6.8663}{{1 + e^{{ - ( - 1.574\Psi + 3.{654})}} }} - \frac{1.0189}{{1 + e^{ - ( - 0.492\Psi - 1.299)} }} - \frac{2.1697}{{1 + e^{ - ( - 0.194\Psi - 4.339)} }} + \cdots + \frac{2.6387}{{1 + e^{ - ( - 0.331\Psi + 2.246)} }}, $$
(23)
$$ \hat{U}_{P - IV} = \frac{ - 0.2821}{{1 + e^{ - ( - 0.533\Psi + 2.368)} }} + \frac{0.3969}{{1 + e^{ - (2.391\Psi + 1.929)} }} - \frac{3.3036}{{1 + e^{ - ( - 0.038\Psi - 3.927)} }} + \cdots - \frac{2.1545}{{1 + e^{ - ( - 2.484\Psi - 2.701)} }}, $$
(24)
$$ \hat{V}_{P - I} = \frac{ - 4.3366}{{1 + e^{{ - ( - 1.990\Psi - 0.338{)}}} }} + \frac{4.8079}{{1 + e^{ - ( - 0.598\Psi - 3.336)} }} - \frac{2.9912}{{1 + e^{ - (0.600\Psi + 2.518)} }} + \cdots + \frac{1.1862}{{1 + e^{ - ( 2.928\Psi + 1.879)} }}, $$
(25)
$$ \hat{V}_{P - II} = \frac{ - 1.2095}{{1 + e^{{ - (1.812\Psi - 1.701{)}}} }} - \frac{1.4677}{{1 + e^{ - ( - 3.875\Psi - 2.842)} }} - \frac{5.4743}{{1 + e^{ - ( - 0.276\Psi + 2.736)} }} + \cdots - \frac{4.5921}{{1 + e^{ - ( 1.927\Psi + 2.108)} }}, $$
(26)
$$ \hat{V}_{P - III} = \frac{2.237}{{1 + e^{{ - (0.454\Psi - 0.035{)}}} }} - \frac{0.825}{{1 + e^{ - (1.564\Psi + 0.541)} }} - \frac{0.249}{{1 + e^{ - (1.204\Psi - 0.301)} }} + \cdots - \frac{0.7721}{{1 + e^{ - ( - 1.792\Psi + 0.440)} }}, $$
(27)
$$ \hat{V}_{P - IV} = \frac{ - 0.6548}{{1 + e^{{ - (2.202\Psi + 2.856{)}}} }} + \frac{3.6090}{{1 + e^{ - (5.003\Psi + 2.080)} }} - \frac{1.4197}{{1 + e^{ - (5.548\Psi + 1.859)} }} + \cdots + \frac{3.1940}{{1 + e^{ - ( - 0.815 + 2.385)} }}. $$
(28)
Fig. 1
figure 1

Best weight sets and results comparison for all the Problems of second-order nonlinear-coupled EF model

Full size image

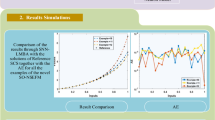
The optimization is performed for all the problems of the nonlinear-coupled EF system with ANNs-PSO-IPM for 50 independent runs. A set of the best weights along with proposed and exact outcomes are shown in Fig. 1. It is stated that all the problems of the nonlinear-coupled EF system of second kind, the exact/reference solution and ANNs-PSO-IPM results overlapped consistently for \(\hat{U}(\Psi )\) and \(\hat{V}(\Psi )\). This overlapping of the outcomes depicts the correctness/exactness of the proposed ANNs-PSO-IP scheme. Figure 2 shows the absolute error (AE), comparison of the proposed results and exact solutions as well as analysis on different performance metrics. The approximate solutions for N = 25 and N = 30 are plotted in Figs. 3 and 4 along with the reference exact values. One may see that results are consistently overlapping for small as well as large interval. The AE plots for \(\hat{U}(\Psi )\) and \(\hat{V}(\Psi )\) are drawn in Fig. 2a and b for N = 20, while the performance measures for \(\hat{U}(\Psi )\) and \(\hat{V}(\Psi )\) are provided in Fig. 2c and d for N = 20. It is observed that the AE values of \(\hat{U}(\Psi )\) lie around 10−05–10−06, 10−04–10−05, 10−06–10−08 and 10−06–10−07 for Problem I, II, III and IV in case of N = 20, 25 and 30. While the AE values of \(\hat{V}(\Psi )\) lie around 10−05–10−06, 10−04–10−05, 10−06–10−09 and 10−06–10−07 for Problems I–IV for N = 20. The performance measures of \(\hat{U}(\chi )\) and \(\hat{V}(\Psi )\) based on FIT, RMSE, TIIC and EVAF are plotted in Fig. 2c and d. It is seen that the FIT for \(\hat{U}(\Psi )\) and \(\hat{V}(\Psi )\) lie close to 10−08–10−10, for problems I, III and IV, and similarly the FIT for Problem II lies around 10−06–10−08. The RMSE and TIC for \(\hat{U}(\Psi )\) and \(\hat{V}(\Psi )\) lie around to 10−04–10−06, for all the problems. The TIC values lie around 10−06–10–08 for both indexes of all the Problems. The values of the EVAF for both indices of all the problems lie around 10–10–10–12. The convergence measures for the Problems I–IV based on the second-order nonlinear-coupled EF model using the fitness values, boxplots and histograms with 10 neurons are plotted in Fig 5. It is seen that the fitness lies around 10−04–10−08 for the Problems I–IV.

Fig. 2
figure 2

Absolute error and performance measures for all Problems of second-order nonlinear-coupled EF model

Full size image
Fig. 3
figure 3

Comparison of proposed solutions for all Problems of second-order nonlinear-coupled EF model in case of input interval [0, 1.25]

Full size image
Fig. 4
figure 4

Comparison of proposed solutions for all Problems of second-order nonlinear-coupled EF model in case of input interval [0, 1.5]

Full size image
Fig. 5
figure 5

Convergence indices for all the Problems of second-order nonlinear-coupled EF model using the Fitness, boxplots and boxplots for 10 neurons

Full size image

For more satisfaction, accuracy and precision examination of the ANNs-PSO-IP scheme, statistical measures are made based on minimum (MIN), mean, standard deviation (SD), median and semi interquartile range (S-IR). S-IR range is 0.5 times of the difference of the third quartile, i.e., Q3 = 75% data and first quartile, i.e., Q1 = 25% data, is calculated for 50 runs of ANNs-PSO-IP scheme to solve four different examples of the nonlinear-coupled EF system of second kind. These statistical results for Problems I–IV are provided in Tables 2 as well as 3 for \(\hat{U}\) and \(\hat{V}\), respectively. It is perceived that both \(\hat{U}(\Psi )\) and \(\hat{V}(\Psi )\) for Problems I–IV lie in the good range. The global performance, i.e., G-FIT, G-EVAF, G-RMSE and G-TIC of \(\hat{U}(\Psi )\) and \(\hat{V}(\Psi )\) for Problems I–IV is provided in Table 4. In the said Table, the presentations of the global performance for all problems based on second-order nonlinear-coupled EF model for 50 independent executions are provided. The magnitude as well as median values of each Problems based on the second-order nonlinear-coupled EF model using the indexes \(\hat{U}(\Psi )\) and \(\hat{V}(\Psi )\) proven good. The time complexity of the proposed scheme ANNs-PSO-IPM for all four problems in terms of time consume for learning of weights of neural network is around 50 ± 25 for N = 20, while in case of N = 25 and 30 time consumed are around 55 ± 25 and 60 ± 20, respectively.

Table 2 Statistics on \(\hat{U}(\Psi )\) for all the Problems of second-order nonlinear-coupled EF model using the ANNs-PSO-IP approach
Full size table
Table 3 Statistics on \(\hat{V}(\Psi )\) for all Problems of second-order nonlinear-coupled EF model using the ANNs-PSO-IP approach
Full size table
Table 4 Results for global performance on both \(\hat{U}(\Psi )\) and \(\hat{V}(\Psi )\) in case of Problems I to IV
Full size table

5 Conclusion

In this investigation, a reliable, stable, consistent and precise numerical ANNs-PSO-IPM is presented for solving the nonlinear-coupled EF system by using the ANNs strength. The objective function is optimized of these networks using the global as well as local search competences of PSO-IPM. The suggested ANNs-PSO-IPM is viably executed to solve four different examples of the nonlinear-coupled EF system. The detailed, precise and particular presentation is obtained for ANNs-PSO-IPM in terms of AE with steadfast precision that is measured around 4–7 decimals of accurateness of the present reference solutions for all four problems of the nonlinear-coupled EF system of second kind. Furthermore, the statistical clarifications achieved good measures using the Min, standard deviation, Mean, S-IR and Median to check the convergence, robustness and accuracy of the ANNs-PSO-IPM for solving the second-order nonlinear-coupled EF model-based problems I–IV.

6 Future research directions

In the future, one can exploit/explore the knacks of ANNs-PSO-IPM to solve the singular higher order models (Sabir et al. 2020c, d; 2021a), fractional order models (İlhan and Kıymaz 2020; Sabir et al. 2022b; Sulaiman et al. 2019; Touchent et al. 2020; Yokuş and Gülbahar 2019; Ziane et al. 2019) and many other applications of utmost importance (Kouider and Polat 2020; Xie et al. 2020; Xue et al. 2021; Yao 2021).