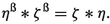Abstract
In this paper, the notions of maximal GE-filter and prime GE-filter of a GE-algebra are introduced and the relation between them is given. Some characterizations of prime GE-filters of a transitive GE-algebra are given in terms of the GE-filter generated by a subset of a transitive GE-algebra. We generalized Stone’s theorem to transitive GE-algebras. The notion of elitable GE-filter of a bordered GE-algebra is introduced and investigated its properties. We observed that the class of all elitable GE-filters of a transitive bordered GE-algebra is a complete distributive lattice. Equivalent conditions for a GE-filter of a transitive bordered GE-algebra to be elitable GE-filter are given. We provided conditions for a subset of a transitive bordered GE-algebra to be elitable GE-filter.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Imai and Iséki introduced BCK-algebras (see Imai and Iséki 1966; Iséki 1966) in 1966 as the algebraic semantics for a non-classical logic with only implication. Various researchers have examined the generalised concepts of BCK-algebras since then. Henkin and Skolem introduced Hilbert algebras in the 1950 s to investigate intuitionistic and other non-classical logics. A. Diego established that Hilbert algebras form a locally finite variety (see Diego 1966). Later several researchers extended the theory on Hilbert algebras. S. Celani given a representation theorem for Hilbert algebras by means of ordered sets and characterized the homomorphisms of Hilbert algebras in terms of applications defined between the sets of all irreducible deductive systems of the associated algebras (see Celani 2002). Chajda et al. considered the properties of deductive systems in Hilbert algebras which are upper semi-lattices as posets and shown that every maximal deductive system is prime. They have given a condition for a deductive system to be prime and shown that the annihilator of any non-empty subset of a Hilbert algebra is a deductive system which is an annihilator of the induced upper semilattice(see Chajda et al. 2002). Hong et al. introduced the concept of maximal deductive systems and shown that every bounded Hilbert algebra with at least two elements contains at least one maximal deductive system (see Hong and Jun 1996). Jun et al. introduced the concept of Hilbert filter in Hilbert algebras and studied how to generate a Hilbert filter by a set (see Jun and Kim 2005). The notion of BE-algebra was introduced by H.S. Kim and Y.H. Kim as a generalization of a dual BCK-algebra (see Kim and Kim 2006). Rezaei et al. discussed relations between Hilbert algebras and BE-algebras (see Rezaei et al. 2013). Borumand Saeid et al. introduced the notions of implicative filter, positive implicative filter, normal filter, fantastic filter, obstinate filter and maximal filter in a BE-algebra and obtained the related properties (see Borumand Saeid et al. 2013). Dudek et al. introduced the notion of poor and crazy filters in BCK-algebras and studied their properties in different types of BCK-algebras (see Dudek and Jun 2007).
The generalisation process is another important topic in the study of algebraic structures. Bandaru et al. introduced the concept of GE-algebras as a generalisation of Hilbert algebras and studied several properties (see Bandaru et al. 2021). Rezaei and colleagues introduced and discussed the concept of prominent GE-filters in GE-algebras (see Rezaei et al. 2021). Bandaru et al. introduced and investigated the concept of bordered GE-algebra (see Bandaru et al. 2021). Later, Ozturk et al. introduced and investigated the concept of Strong GE-filters, GE-ideals of bordered GE-algebras (see Ozturk et al. 2021). Song et al. introduced and discussed the concept of Imploring GE-filters of GE-algebras (see Song et al. 2021).
In this paper, we introduce and investigate the concepts of maximal GE-filter and prime GE-filter of a GE-algebra. We define prime GE-filter as the GE-filter produced by a subset of a transitive GE-algebra. We define and investigate the properties of an elitable GE-filter of a bordered GE-algebra. The class of all elitable GE-filters of a transitive bordered GE-algebra is a complete distributive lattice, as we observe. We describe an elitable GE-filter in a transitive bordered GE-algebra. In addition, we define the conditions under which a subset of a transitive bordered GE-algebra is an elitable GE-filter.
2 Preliminaries
Definition 2.1
(Bandaru et al. 2021) A GE-algebra is a non-empty set \(R\) with a constant 1 and a binary operation \(*\) satisfying the following axioms:
-
(GE1)
\(\mu *\mu = 1\),
-
(GE2)
\(1 *\mu =\mu \),
-
(GE3)
\(\mu *(\nu *\tau )=\mu *(\nu *(\mu *\tau ))\)
for all \(\mu ,\nu ,\tau \in R\).
In a GE-algebra \(R\), a binary relation “\(\le \)” is defined by
Definition 2.2
(Bandaru et al. 2021) A GE-algebra \(R\) is said to be
-
transitive if it satisfies:
$$\begin{aligned} (\forall \beta ,\gamma ,\alpha \in R)\left( \beta *\gamma \le (\alpha *\beta )*(\alpha *\gamma )\right) . \end{aligned}$$(2.2) -
antisymmetric if the binary relation “\(\le \)” is antisymmetric.
-
commutative if it satisfies:
$$\begin{aligned} (\forall \beta ,\gamma \in R)\left( (\beta *\gamma )*\gamma = (\gamma *\beta )*\beta \right) . \end{aligned}$$(2.3)
Theorem 2.3
(Bandaru et al. 2021) Every self-distributive BE-algebra is a GE-algebra.
The following proposition gives the equivalent conditions for a GE-algebra to be implication algebra, dual implicative BCK-algebra and commutative Hilbert algebra.
Proposition 2.4
(Bandaru et al. 2021) Let \((R, *, 1)\) be a GE-algebra. Then, the following are equivalent.
-
(i)
\(R\) is commutative,
-
(ii)
\(R\) is implication algebra,
-
(iii)
\(R\) is dual implicative BCK-algebra,
-
(iv)
\(R\) is commutative Hilbert algebra.
Definition 2.5
(Bandaru et al. 2021) If a GE-algebra \(R\) has a special element, say \(0\), that satisfies \(0\le \beta \) for all \(\beta \in R\), we call \(R\) the bordered GE-algebra.
For every element \(\beta \) of a bordered GE-algebra \(R\), we denote \(\beta *0\) by  , and
, and  is denoted by
is denoted by  .
.
Definition 2.6
(Bandaru et al. 2021) If a bordered GE-algebra \(R\) satisfies the condition (2.2), we say that \(R\) is a transitive bordered GE-algebra.
Definition 2.7
(Bandaru et al. 2021) A bordered GE-algebra \(R\) is said to be antisymmetric if the binary operation “\(\le \)” is antisymmetric.
Proposition 2.8
(Bandaru et al. 2021) Every GE-algebra \(R\) satisfies the following items.
If \(R\) is transitive, then
Lemma 2.9
(Bandaru et al. 2021) The following are equivalent to each other in a GE-algebra \(R\).
Definition 2.10
(Bandaru et al. 2021) A subset \(K\) of a GE-algebra \(R\) is called a GE-filter of \(R\) if it satisfies:
Lemma 2.11
(Bandaru et al. 2021) In a GE-algebra \(R\), every GE-filter \(K\) of \(R\) satisfies:
Proposition 2.12
(Bandaru et al. 2021) The following assertions are true in a bordered GE-algebra \(R\).





If \(R\) is a transitive bordered GE-algebra, then


If \(R\) is an antisymmetric bordered GE-algebra, then

If \(R\) is a transitive and antisymmetric bordered GE-algebra, then

Definition 2.13
(Bandaru et al. 2021) A duplex bordered element in a bordered GE-algebra \(R\) is defined as an element \(\beta \) of \(R\) that satisfies  .
.
The set of all duplex bordered elements of a bordered GE-algebra \(R\) is denoted by \({0}^{2}(R)\) and is referred to as the \(R\) duplex bordered set. It is clear that \(0, 1\in {0}^{2}(R)\).
Definition 2.14
(Bandaru et al. 2021) A bordered GE-algebra \(R\) is said to be duplex if every element of \(R\) is a duplex bordered element, that is, \(R= {0}^{2}(R)\).
Definition 2.15
(Ozturk et al. 2021) Let \(R\) be a bordered GE-algebra. If a subset \(G\) of \(R\) meets the following conditions for all \(\beta , \gamma \in R\), it is termed a GE-ideal of \(R\):
-
(1)
\(0\in G\),
-
(2)
\(\beta \in G\) and
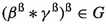 imply that \(\gamma \in G\).
imply that \(\gamma \in G\).
Clearly, \(\{0\}\) is a GE-ideal of \(R\).
Proposition 2.16
(Ozturk et al. 2021) Let \(G\) be a GE-ideal of \(R\). Then, for any \(\eta ,\zeta \in R\), we have
-
(1)
\(\eta \in G\) and \(\zeta \le \eta \) imply \(\zeta \in G.\)
-
(2)
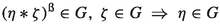 .
.
3 Maximal and prime GE-filters
Definition 3.1
(Ozturk et al. 2021) Let \(K\) be a subset of a GE-algebra \(R\). The GE-filter of \(R\) generated by \(K\) is denoted by \(\langle K\rangle \) and is defined to be the intersection of all GE-filters of \(R\) containing \(K\).
Example 3.2
Let \(R=\{1, e, f, g, h, a, b\}\) be a set with the binary operation “\(*\)” in the following Cayley Table.
Then, \((R, *, 1)\) is a GE-algebra. If we take a subset \(G=\{1,e\}\) of \(R\), then the GE-filter of \(R\) generated by \(G\) is \(\langle G\rangle =\{1,e,f,b\}\).
The next theorem shows how the elemental structure of \(\langle K\rangle \) is constructed.
Theorem 3.3
Let \(K\) be a non-empty subset of a transitive GE-algebra \(R\). Then, \(\langle K\rangle \) consists of \(\beta \)’s that satisfies the following condition:
that is, \(\langle K\rangle =\{\beta \in R\mid \beta _n*(\cdots *(\beta _2*(\beta _1*\beta ))\cdots )=1\text {for some} ~\beta _1, \beta _2, \cdots , \beta _n\in K\}\).
Proof
Let
Obviously, \(1\in G\). Let \(\mu , \nu \in R\) be such that \(\mu *\nu \in G\) and \(\mu \in G\). Then, there is \(\beta _1, \beta _2, \cdots , \beta _m, \gamma _1, \gamma _2,\cdots , \gamma _n\in K\) such that
By (GE3), (3.2) and (GE1), we can observe that,
that is,
By (2.12), we get
If we repeat this process n times, we have
By (2.8), it follows that
Hence, \(\nu \in G\). Thus, \(G\) is a GE-filter of \(R\). It is obvious that \(K\subseteq G\). Let \(M\) be a GE-filter for \(R\) that includes \(K\). If \(\beta \in G\), then \(\alpha _n*(\cdots *(\alpha _2*(\alpha _1*\beta ))\cdots )=1\in M\) for some \(\alpha _1, \alpha _2,\cdots ,\alpha _n\in K\subseteq M\). It follows that \(\beta \in M\). Therefore, \(G\subseteq M\). This shows that \(G= \langle K\rangle \). \(\square \)
Corollary 3.4
For every element \(\gamma \) in a transitive GE-algebra \(R\), we have
that is, \(\langle \gamma \rangle =\{\beta \in R\mid \gamma \le \beta \}\) which is called principal GE-filter generated by \(\gamma \).
We construct the smallest GE-filter containing \(K\) and \(\eta \), given a GE-filter \(K\) and an element \(\eta \) in a transitive GE-algebra \(R\).
Theorem 3.5
Let \(K\) be a GE-filter of a transitive GE-algebra \(R\) and \(\eta \) be any element of \(R\). Then,
Proof
Let \(K_{\eta }:=\{\zeta \in R\mid \eta *\zeta \in K\}.\) Since \(\eta *\eta =1\in K\), \(\eta \in K_{\eta }\). For any \(\zeta \in K\), we have \(\zeta \le \eta *\zeta \) by (2.6). Hence, \(\eta *\zeta \in K\) by Lemma 2.11. Thus, \(\zeta \in K_{\eta }\), which shows that \(K\subseteq K_{\eta }\). Hence, \(K\cup \{\eta \}\subseteq K_{\eta }\). Since \(\eta *1= 1\in K,\) we get \(1\in K_{\eta }.\) Let \(\zeta , \alpha \in R\) be such that \(\zeta \in K_{\eta }\) and \(\zeta *\alpha \in K_{\eta }\). Then, \(\eta *(\zeta *\alpha ) \in K\) and \(\eta *\zeta \in K.\) Using (2.7), (2.12) and (2.5), we have
and so \(\eta *\alpha \in K\) by Lemma 2.11 and (2.17). Hence, \(\alpha \in K_{\eta }\), and thus, \(K_{\eta }\) is a GE-filter of \(R\). Let \(G\) be a GE-filter of \(R\) containing \(K\cup \{\eta \}\) and \(\zeta \in K_{\eta }\). Then, \(\eta \in G\) and \(\eta *\zeta \in K\subseteq G\). Hence, \(\zeta \in G\) since \(G\) is GE-filter of \(R\). Therefore, \(K_{\eta } \subseteq G\). Hence, \(K_{\eta }=\langle K\cup \{\eta \}\rangle \). \(\square \)
Proposition 3.6
Let \(K\) and \(G\) be two GE-filters of a transitive GE-algebra \(R\). Then,
Proof
Let \(J= \{\beta \in R\mid \eta *(\zeta *\beta ) = 1\text { for some }\eta \in K\text { and } \zeta \in G\}\) and \(\beta \in J\). Then, \(\eta *(\zeta *\beta ) = 1\text { for some }\eta \in K\text { and } \zeta \in G.\) Hence, \(\beta \in \langle K\cup G\rangle \) by Theorem 3.3. Therefore, \(J\subseteq \langle K\cup G\rangle .\) Conversely, assume that \(\beta \in \langle K\cup G\rangle .\) Then, there are \(\gamma _1,\gamma _2,....,\gamma _i,...,\gamma _n\in K\cup G\) such that \(\gamma _n *(...*(\gamma _1*\beta )...) = 1.\) By (GE3), we can get that
such that \(\gamma _1, \gamma _2,...,\gamma _i\in K\) and\(\gamma _{i+1},...,\gamma _n\in G\). Since \(\gamma _n\in G\) and \(G\) is a GE-filter, we have
By repeating this, we get \(\gamma _i*(...*(\gamma _1*\beta )....)\in G.\) Take \(c=\gamma _i*(...*(\gamma _1*\beta )....).\) By repeating (GE3), we get that
Since \(\gamma _i\in K\) and \(K\) is a GE-filter of \(R\), we get \(c*\beta \in K\). Put \(\eta =\zeta *\beta \). Then, \(\eta *(\zeta *\beta ) = (\zeta *\beta ) *(\zeta *\beta ) = 1\) and hence \(\beta \in J\). Therefore, \(J=\langle K\cup G\rangle \). \(\square \)
The intersection of two GE-filters \(K\) and \(G\) of a GE-algebra is a GE-filter of \(R\), as can be seen. Also, \(K\cap G\) is the infimum of both \(K\) and \(G\), as can be shown. The class of all GE-filters in a GE-algebra \(R\) is designated by \({\mathfrak {O}}(R)\). The following theorem is now established.
Theorem 3.7
Let \(R\) be a transitive GE-algebra. Then, \({\mathfrak {O}}(R)\) forms a complete distributive lattice.
Proof
For any two GE-filters \(K_1\) and \(K_2\) of a transitive GE-algebra, define
Then, it is obvious that \(({\mathfrak {O}}(R), \cap ,\vee )\) is a complete lattice with respect to set inclusion. Let \(K_1,K_2,K_3\in {\mathfrak {O}}(R).\) Then, obviously, \(K_1\cap (K_2 \vee K_3) \supseteq (K_1 \cap K_2) \vee (K_2 \cap K_3).\) Conversely, assume that \(\beta \in K_1 \cap (K_2 \vee K_3).\) Then, \(\beta \in K_1\) and \(\beta \in K_2 \vee K_3.\) Then, there are \(c\in K_2\) and \(d\in K_3\) such that \(c*(d*\beta ) = 1.\) Let \(\alpha _1 = d*\beta \) and \(\alpha _2 = \alpha _1 *\beta \). It can be observed that \(\alpha _1\in K_1\) and \(\alpha _2\in K_1.\) Now, \(c*\alpha _1 = c*(d*\beta ) = 1\in K_2\) which implies that \(\alpha _1=d*\beta \in K_2\). Hence, \(\alpha _1\in K_1 \cap K_2\). Also, \(d*\alpha _2 = d*(\alpha _1 *\beta ) = d*((d*\beta ) *\beta ) = d*((d*\beta ) *(d*\beta )) = d*1= 1\in K_3\). Then, \(\alpha _2\in K_3\) and hence \(\alpha _2\in K_1 \cap K_3.\) Now, by (GE3), \(\alpha _1 *(\alpha _2 *\beta ) = (d*\beta ) *((\alpha _1 *\beta )*\beta ) = (d*\beta ) *(((d*\beta ) *\beta )*\beta ) = 1\). Hence, \(\beta \in (K_1 \cap K_2) \vee (K_1 \cap K_3).\) Hence, \(K_1 \cap (K_2 \vee K_3) \subseteq (K_1 \cap K_2) \vee (K_1 \cap K_3).\) Thus, \(({\mathfrak {O}}(R), \cap ,\vee )\) is a complete distributive lattice. \(\square \)
Corollary 3.8
Let \(R\) be a GE-algebra with transitivity. Then, with regard to the inclusion ordering \(\subseteq \), the class \({\mathfrak {O}}(R)\) of all GE-filters of \(R\) is a complete lattice in which for any class \(\{K_{\zeta }\}_{\zeta \in \Delta }\) of GE-filters of \(R\), inf\(\{K_{\zeta }\}_{\zeta \in \Delta } =\cap _{\zeta \in \Delta } K_\alpha \) and sup\(\{K_{\zeta }\}_{\zeta \in \Delta } =\langle \cup _{\zeta \in \Delta } K_\alpha \rangle .\)
A GE-filter \(K\) of a GE-algebra \(R\) is said to be proper if \(K\ne R\).
Definition 3.9
A proper GE-filter \(N\) of a GE-algebra \(R\) is said to be maximal if \(\langle N\cup \{\beta \}\rangle = R\) for any \(\beta \in R\setminus N\), where \(\langle N\cup \{\beta \}\rangle \) is the GE-filter generated by \( N\cup \{\beta \}\).
Example 3.10
Let \(R=\{1, e, f, g, h, a, b\}\) be a set with the binary operation “\(*\)” in the following Cayley Table.
Then, \((R, *, 1)\) is a GE-algebra and \(H:=\{1,e,f,a,b\}\) is a proper GE-filter of \(R\). Moreover, we have \(\langle H\cup \{g\}\rangle =R=\langle H\cup \{h\}\rangle \), and so \(H\) is a maximal GE-filter of \(R\).
We now have a necessary and sufficient condition for any proper GE-filter to be maximal.
Theorem 3.11
Let \(R\) be a transitive GE-algebra. Then, a proper GE-filter \(K_1\) of \(R\) is maximal if and only if \(K_1 \subseteq K\subseteq R\) implies \(K_1 =K\) or \(K=R\) for any GE-filter \(K\) of \(R\).
Proof
Suppose \(K_1\) is a maximal GE-filter of \(R.\) Let \(K\) be a GE-filter of \(R\) such that \(K_1\subseteq K\subseteq R.\) Suppose \(K\ne R\). Then, we have to show that \(K_1 =K\). Suppose \(K_1 \ne K.\) Then, there exists \(\beta \in K\) such that \(\beta \notin K_1\). Since \(K_1\) is a maximal GE-filter of \(R\), we have \(\langle K_1\cup \{\beta \}\rangle = R\). Let \(\gamma \in R\). Then, \(\gamma \in \langle K_1 \cup \{\beta \}\rangle .\) Then, \(\beta *\gamma \in K_1 \subseteq K\) and hence, \(\gamma \in K\). Therefore, \(K=K_1\). Conversely, assume that the condition holds. Let \(\beta \in R{\setminus }K_1\). Suppose \(\langle K_1\cup \{\beta \}\rangle \ne R.\) Chose \(\gamma \notin \langle K_1 \cup \{\beta \} \rangle \) and \(\gamma \in R\). Hence, \(K_1 \subseteq \langle K_1 \cup \{\beta \}\rangle \subset R.\) Then by assumption, we get \(K_1 =\langle K_1 \cup \{\beta \}\rangle .\) Hence, \(\beta \in K_1\) which is a contradiction. Thus, \(K_1\) is a maximal GE-filter of \(R.\) \(\square \)
Definition 3.12
A proper GE-filter \(P\) of a GE-algebra \(R\) is said to be prime if \(Q\cap H\subseteq P\) implies \(Q\subseteq P\) or \(H\subseteq P\) for any two GE-filters \(Q\) and \(H\) of \(R\).
Example 3.13
Consider the GE-algebra \(R\) in Example 3.10. It is easy to verify that the set \(K:=R\setminus \{a\}\) is a prime GE-filter of \(R\).
Theorem 3.14
A proper GE-filter \(P\) of a GE-algebra \(R\) is prime if and only if \(\langle \beta \rangle \cap \langle \gamma \rangle \subseteq P\) implies \(\beta \in P\) or \(\gamma \in P\) for all \(\beta ,\gamma \in R.\)
Proof
Assume that \(P\) is a prime GE-filter of \(R\). Let \(\beta ,\gamma \in R\) be such that \(\langle \beta \rangle \cap \langle \gamma \rangle \subseteq P\). Since \(P\) is prime, it implies that \(\beta \in \langle \beta \rangle \subseteq P\) or \(\gamma \in \langle \gamma \rangle \subseteq P\). Conversely, assume that the condition holds. Let \(K\) and \(G\) be two GE-filters of \(R\) such that \(K\cap G\subseteq P.\) Let \(\beta \in K\) and \(\gamma \in G\). Then, \(\langle \beta \rangle \subseteq K\) and \(\langle \gamma \rangle \subseteq G.\) Hence, \(\langle \beta \rangle \cap \langle \gamma \rangle \subseteq K\cap G\subseteq P.\) Then, \(\beta \in P\) or \(\gamma \in P\). Thus, \(K\subseteq P\) or \(G\subseteq P\). Therefore, \(P\) is a prime GE-filter of \(R\). \(\square \)
Theorem 3.15
Let \(K\) be a GE-filter of a transitive GE-algebra \(R\). Then, \(P\cap L\subseteq K\) if and only if \(\langle K\cup P\rangle \cap \langle K\cup L\rangle = K,\) for any GE-filters \(P\) and \(L\) of \(R\).
Proof
Let \(\langle K\cup P\rangle \cap \langle K\cup L\rangle =K\). Since \(P\subseteq \langle K\cup P\rangle \) and \(L\subseteq \langle K\cup L\rangle \), we get that \(P\cap L\subseteq \langle K\cup P\rangle \cap \langle K\cup L\rangle =K.\) Therefore, \(P\cap L\subseteq K.\) Conversely, assume that \(P\cap L\subseteq K\). Clearly, \(K\subseteq \langle K\cup P\rangle \cap \langle K\cup L\rangle .\) Let \(t\in \langle K\cup P\rangle \cap \langle K\cup L\rangle .\) Since \(K\) is a GE-filter of \(R\), we get \((\beta _n*(...*(\beta _1*t)..))\in K,\) for some \(n\in {\mathbb {N}}\) and \(\beta _1,\beta _2,....\beta _n\in P\). It follows that, there exists \(b_1\in K\) such that \(\beta _n*(...*(\beta _1*t)..) = b_1\). By the similar argument, we have \(\gamma _m*(...*(\gamma _1*t)..) = b_2\), for some \(m\in {\mathbb {N}}, \gamma _1,\gamma _2,...,\gamma _m\in L\) and \(b_2\in K.\) Hence, by repeating (GE3) and by (2.4), we get \(\beta _n*(...*(\beta _1*(b_1*t))..)= 1\). Hence, \(b_1*t\in P\). By the similar argument, we can show that \(b_2*t\in L.\) Since \(b_1,b_2\in K\), \(b_1*t\le b_2 *(b_1 *t)\) and \(b_2*t\le b_2 *(b_1 *t)\), we get \(b_2*(b_1*t) \in P\cap L\subseteq K\). Hence, \(t\in K\). Therefore, \(\langle K\cup P\rangle \cap \langle K\cup L\rangle \subseteq K.\) Thus, \(\langle K\cup P\rangle \cap \langle K\cup L\rangle =K\) \(\square \)
Corollary 3.16
Let \(Q\) be a GE-filter of a transitive GE-algebra \(R\). Then, for any \(\eta ,\zeta \in R\),
Theorem 3.17
In a transitive GE-algebra, every maximal GE-filter is a prime GE-filter.
Proof
Let \(Q\) be a maximal GE-filter of a transitive GE-algebra \(R\). Let \(\langle \mu \rangle \cap \langle \nu \rangle \subseteq Q\) for some \(\mu ,\nu \in R.\) Suppose \(\mu \notin Q\) and \(\nu \notin Q\). Then, \(\langle Q\cup \{\mu \} \rangle = R\) and \(\langle Q\cup \{\nu \} \rangle = R.\) Hence, \(\langle Q\cup \{\mu \} \rangle \cap \langle Q\cup \{\nu \} \rangle = R.\) Hence, by Corollary 3.16, \(\langle \mu \rangle \cap \langle \nu \rangle \nsubseteq Q\), which is a contradiction. Hence, \(\mu \in Q\) or \(\nu \in Q\). Therefore, \(Q\) is a prime GE-filter of \(R\). \(\square \)
Corollary 3.18
Let \(R\) be a transitive GE-algebra. If \(Q_1,Q_2,...Q_n\) and \(Q\) are maximal GE-filters of \(R\) such that \(\bigcap \limits ^n_{j=1} Q_j\subseteq Q.\) There exists \(i\in \{1,2,...,n\}\) such that \(Q_i=Q\).
The following example shows that the converse of Theorem 3.17 is not valid.
Example 3.19
Let \(R=\{1, e, f, g, h, a, b\}\) be a set with the binary operation “\(*\)” in the following Cayley Table.
Then, \((R,*, 1)\) is a transitive GE-algebra. It is routine to verify that \(L:=\{1,e,f,g,h\}\) is a prime GE-filter of \(R\). Note that \(P:=\{1,f,g,h\}\) is a GE-filter of \(R\) such that \(P\subsetneq L\subsetneq R\). Hence, \(L\) is not a maximal GE-filter of \(R\).
Theorem 3.20
Let \(R\) be a transitive GE-algebra and \(G\) be a nonempty subset of \(R\) such that \(G\) is closed under \(``\partial \)”, where \(\beta \partial \gamma := (\gamma *\beta )*\beta \), for any \(\beta ,\gamma \in G\). If \(K\) is a GE-filter of \(R\) such that \(K\cap G=\emptyset \), then there exist a prime GE-filter \(M\) of \(R\) such that \(K\subseteq M\) and \(M\cap G=\emptyset .\)
Proof
Let \(K\) be a GE-filter of \(R\) such that \(K\cap G=\emptyset .\) Consider
Clearly \(K\in {\mathfrak {G}}\). Then, by Zorn’s lemma, \({\mathfrak {G}}\) has a maximal element, say \(M\). Then, \(K\subseteq M\) and \(M\cap G=\emptyset .\) We prove that \(M\) is a prime GE-filter of \(R\). Suppose there are GE-filter \(K,Q\) of \(R\) such that \(K\cap Q\subseteq M, K\nsubseteq M\) and \(Q\nsubseteq M.\) By maximality of \(M\), we have \(\langle M\cup K\rangle \cap G\ne \emptyset \) and \(\langle M\cup Q\rangle \cap G\ne \emptyset \). Let \(t\in \langle M\cup K\rangle \cap G\) and \(r\in \langle M\cup Q\rangle \cap G\). Since \(t*(t\partial r) = t*((r*t) *t) = 1\) and \(r*(t\partial r) = r*((r*t)*t) = 1\), we have \(t\partial r\in \langle M\cup K\rangle \cap \langle M\cup Q\rangle .\) Also, \(t,r\in G\) and \(G\) is a GE-filter of \(R\) implies that \(t\partial r\in G\). Hence, \(t\partial r\in (\langle M\cup K\rangle \cap \langle M\cup Q\rangle )\cap G.\) Therefore, \(M\ne \langle M\cup K\rangle \cap \langle M\cup Q\rangle .\) Hence, by Theorem 3.15, \(K\cap Q\nsubseteq M\) which is a contradiction. Therefore, \(M\) is a prime GE-filter of \(R\). \(\square \)
Corollary 3.21
Let \(R\) be a transitive GE-algebra. Then, the following holds:
-
(1)
For any \(\beta \in R\setminus \{1\},\) there exists a prime GE-filter \(M\) such that \(\beta \notin M\).
-
(2)
\(\bigcap \{M\mid M\text { is a prime GE-filter of } \)R\(\} =\{1\}.\)
-
(3)
Any proper GE-filter \(K\) of \(R\) can be expressed as the intersection of all prime GE-filters of \(R\) containing \(K\).
Theorem 3.22
If a GE-algebra \(R\) is transitive, then \({\mathfrak {G}}(X)\) is a chain if and only if every proper GE-filter of \(R\) is a prime GE-filter.
Proof
Suppose that \({\mathfrak {G}}(X)\) is a chain. Let \(P\) be a proper GE-filter of \(R\). Let \(\mu ,\nu \in R\) be such that \(\langle \mu \rangle \cap \langle \nu \rangle \subseteq P.\) Since \(\langle \mu \rangle \) and \(\langle \nu \rangle \) are GE-filters of \(R,\) we get either \(\langle \mu \rangle \subseteq \langle \nu \rangle \) or \(\langle \nu \rangle \subseteq \langle \mu \rangle \). Hence, \(\mu \in P\) or \(\nu \in P\). Therefore, \(P\) is a prime GE-filter of \(R\).
Conversely, suppose that every proper GE-filter of \(R\) is a prime GE-filter of \(R\). Let \(P\) and \(L\) be two proper GE-filters of \(R\). Since \(P\cap L\) is a proper GE-filter of \(R\), we get \(P\subseteq P\cap L\) or \(L\subseteq P\cap L.\) Hence, \(P\subseteq L\) or \(L\subseteq P\). Therefore, \({\mathfrak {G}}(X)\) is a chain. \(\square \)
4 Elitable GE-filters
In this section, the concept of elitable GE-filters is introduced and characterized. Some basic properties of elitable GE-filters are observed in terms of maximal GE-filters.
Definition 4.1
Let \(K\) be a nonempty subset of a bordered GE-algebra \(R\). Then, the elitable of \(K\) is denoted by \(K^{\otimes }\) and is defined as 
Example 4.2
Let \(R=\{0,1, e, f, g, h, a, b\}\) be a set with the binary operation “\(*\)” in the following Cayley Table.
Then, \((R, *, 1)\) is a bordered GE-algebra. Given a nonempty subset \(K\) of \(R\), we have:
Given a nonempty subset \(K\) in a bordered GE-algebra \(R\), the elitable of \(K\) may not be a GE-filter of \(R\) as seen in the following example.
Example 4.3
In Example 4.2, if we take \(K:=\{1,g,h\}\), then \(K^{\otimes }=\{1, e, f, a\}\) and it is not a GE-filter of \(R\) since \(e*h=1\) and \(e\in K^{\otimes }\) but \(h\notin K^{\otimes }\).
Lemma 4.4
Let \(R\) be a bordered GE-algebra and consider two elitable subsets \(K\) and \(G\) of \(R\). Then, the following holds:
Proof
Suppose \(K\subseteq G\) and \(\beta \in K^{\otimes }\). Then,  and hence, \(\beta \in G^{\otimes }\). Thus, (4.1) holds. Let \(\beta \in (K\cap G)^{\otimes }\). Then,
and hence, \(\beta \in G^{\otimes }\). Thus, (4.1) holds. Let \(\beta \in (K\cap G)^{\otimes }\). Then,  . Hence,
. Hence,  and
and  . Therefore, \(\beta \in K^{\otimes }\cap G^{\otimes }\). Hence, \((K\cap G)^{\otimes }\subseteq K\cap G\). Suppose \(\beta \in K^{\otimes }\cap G^{\otimes }\). Then, \(\beta \in K^{\otimes }\) and \(\beta \in G^{\otimes }\). Hence,
. Therefore, \(\beta \in K^{\otimes }\cap G^{\otimes }\). Hence, \((K\cap G)^{\otimes }\subseteq K\cap G\). Suppose \(\beta \in K^{\otimes }\cap G^{\otimes }\). Then, \(\beta \in K^{\otimes }\) and \(\beta \in G^{\otimes }\). Hence,  and
and  . Therefore,
. Therefore,  and hence, \(\beta \in (K\cap G)^{\otimes }\). Therefore, \(K^{\otimes }\cap G^{\otimes }\subseteq (K\cap G)^{\otimes }.\) Thus, (4.2) holds. \(\square \)
and hence, \(\beta \in (K\cap G)^{\otimes }\). Therefore, \(K^{\otimes }\cap G^{\otimes }\subseteq (K\cap G)^{\otimes }.\) Thus, (4.2) holds. \(\square \)
Lemma 4.5
Let \(R\) be a bordered GE-algebra which is transitive. Then, for any \(\beta , \gamma \in R\), we have
-
(1)
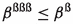 ,
, -
(2)
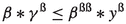 ,
, -
(3)
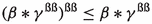 ,
, -
(4)
 ,
, -
(5)
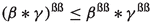 .
.
Proof
(1). Let \(\beta \in R\). Then, by (GE1), (2.7) and (2.25),

Hence,  , which gives
, which gives  .
.
(2). Let \(\beta , \gamma \in R\). Then, by (2.21) and (2.25),  .
.
(3). Let \(\beta , \gamma \in R\). We can observe that  . By (2.12), we get
. By (2.12), we get  and so
and so  . Hence, by (GE1),(2.7), (2.20) and (2.21), we get
. Hence, by (GE1),(2.7), (2.20) and (2.21), we get

Thus,  . Therefore,
. Therefore,  .
.
(4). By (2.21), we have  . Hence, by (2.25), (3) and (2.21), we get
. Hence, by (2.25), (3) and (2.21), we get

(5). By (2.25), we get  . Hence,
. Hence,  . Also, by (4), we can observe that
. Also, by (4), we can observe that  . Hence, (5) follows, since \(R\) is transitive. \(\square \)
. Hence, (5) follows, since \(R\) is transitive. \(\square \)
Theorem 4.6
Let \(R\) be a bordered GE-algebra which is transitive. Then, for any GE-filter \(K\) of \(R\), we have the following:
-
(1)
\(K^{\otimes }\) is a GE-filter of \(R.\)
-
(2)
\(K\subseteq K^{\otimes }.\)
-
(3)
\((K^{\otimes })^{\otimes } = K^{\otimes }.\)
Proof
(1). Since  , we have \(1\in K^{\otimes }\). Let \(\eta \in K^{\otimes }\) and \(\eta *\zeta \in K^{\otimes }.\) Then,
, we have \(1\in K^{\otimes }\). Let \(\eta \in K^{\otimes }\) and \(\eta *\zeta \in K^{\otimes }.\) Then,  and
and  . Since
. Since  by Lemma 4.5(5) and
by Lemma 4.5(5) and  , we have
, we have  . Therefore,
. Therefore,  and hence, \(\zeta \in K^{\otimes }\). Thus, \(K^{\otimes }\) is a GE-filter of \(R\).
and hence, \(\zeta \in K^{\otimes }\). Thus, \(K^{\otimes }\) is a GE-filter of \(R\).
(2). Let \(\eta \in K\). Since  and \(\eta \in K\), we have
and \(\eta \in K\), we have  . Hence, \(\eta \in K^{\otimes }\). Thus, \(K\subseteq K^{\otimes }\).
. Hence, \(\eta \in K^{\otimes }\). Thus, \(K\subseteq K^{\otimes }\).
(3). Clearly \(K^{\otimes } \subseteq (K^{\otimes })^{\otimes }\) by (2). Let \(\eta \in (K^{\otimes })^{\otimes }\). Then,  and hence,
and hence,  . Since
. Since  implies that
implies that  by (2.24), and \(K\) is a GE-filter of \(R\), we have
by (2.24), and \(K\) is a GE-filter of \(R\), we have  . Therefore, \(\eta \in K^{\otimes }\). Thus, \(K^{\otimes }= (K^{\otimes })^{\otimes }.\) \(\square \)
. Therefore, \(\eta \in K^{\otimes }\). Thus, \(K^{\otimes }= (K^{\otimes })^{\otimes }.\) \(\square \)
The following example shows that if \(R\) is a bordered GE-algebra which is not transitive, then the elitable of a GE-filter \(K\) of \(R\) may not be a GE-filter of \(R\).
Example 4.7
Let \(R=\{0,1,e,f,g,h\}\) be a set with a binary operation \(*\) given in the following table:
Then, \(R\) is a bordered GE-algebra which is not transitive. Let \(K=\{1\}\). Then, \(K\) is a GE-filter of \(R\) and its elitable is \(K^{\otimes }=\{1,e,f\}\). But \(K^{\otimes }\) is not a GE-filter of \(R\) since \(e*h=1\in K^{\otimes }\) and \(e\in K^{\otimes }\) but \(h\notin K^{\otimes }\).
Definition 4.8
Let \(R\) be a bordered GE-algebra. Then, a nonempty subset \(K\) of \(R\) is called an elitable GE-filter of \(R\) if it is a GE-filter of \(R\) and its elitable is \(K\) itself.
Example 4.9
Consider a \(4-\)element Boolean algebra \(R:= \{0, 1, e, e'\}\) with the partial order \(\le \). If we define
then \((R, *, 1)\) is a bordered GE-algebra. Let \(K=\{1,e,e'\}\). Then, it can be easily verified that \(K\) is an elitable GE-filter of \(R\).
Example 4.10
In Example 4.2, we can observe that \(G=\{1,e,f,a\}\) is an elitable GE-filter of \(R\).
Theorem 4.11
Let \(R\) be a bordered GE-algebra. Then, the intersection of two elitable GE-filters of \(R\) is also an elitable GE-filter of \(R\).
Proof
Let \(K_1\) and \(K_2\) be two elitable GE-filters of \(R\). Then, \(K_1^{\otimes }=K_1\) and \(K_2^{\otimes }=K_2\) which imply from (4.2) that
Hence, \(K_1\cap K_2\) is an elitable GE-filter of \(R\). \(\square \)
In the following example, we can find two elitable GE-filters of \(R\) whose union is not an elitable GE-filter of \(R\).
Example 4.12
Let \(R=\{0,1,e,f,g,h\}\) be a set with a binary operation \(*\) given in the following table:
Then, \(R\) is a bordered GE-algebra. Let \(K_1=\{1,e,f\}\) and \(K_2=\{1,g,h\}\). Then, it is routine to verify that \(K_1\) and \(K_2\) are elitable GE-filters of \(R\). But \(K_1\cup K_2=\{1,e,f,g,h\}\) is not an elitable GE-filter of \(R\) since \(f*0=g\in K_1\cup K_2\) and \(f\in K_1\cup K_2\) but \(0\notin K_1\cup K_2\).
Theorem 4.13
For any transitive bordered GE-algebra \(R\), the class \({\mathfrak {O}}^{\otimes }(R)\) of all elitable GE-filters of \(R\) is a complete distributive lattice.
Proof
For any two elitable GE-filters \(K\) and \(G\) of \(R\), define a relation \(\le \) on \({\mathfrak {O}}^{\otimes }(X)\) by \(K\le G\Leftrightarrow K\subseteq G\). Then, it can be observed that \(({\mathfrak {O}}^{\otimes }(X),\le )\) is a partially ordered set. Consider \(K\cap G=(K\cap G)^{\otimes }\) and \(K\sqcup G= (K\vee G)^{\otimes },\) where
Obviously \((K\cap G)^{\otimes }\) is infimum of \(K\) and \(G\) in \({\mathfrak {O}}^{\otimes }(X)\). Also, \((K\vee G)^{\otimes }\) is the upper bound of \(K^{\otimes }\) and \(G^{\otimes }\). Let \(M\) be any elitable GE-filter of \(R\) such that \(K\subseteq M\) and \(G\subseteq M\). Let \(\beta \in (K\vee G)^{\otimes }\). Then,  , and hence, there exist \(t\in K\) and \(r\in G\) such that
, and hence, there exist \(t\in K\) and \(r\in G\) such that  . Since \(K\subseteq M\) and \(G\subseteq M\), we get
. Since \(K\subseteq M\) and \(G\subseteq M\), we get  . Hence, \(\beta \in M.\) Therefore, \((K\vee G)^{\otimes }\) is supremum of \(K\) and \(G\) in \({\mathfrak {O}}^{\otimes }(X)\). Hence, \(({\mathfrak {O}}^{\otimes }(X),\cap , \sqcup )\) is a lattice. We can observe that the set theoretical intersection of an arbitrary set of elitable GE-filters of \(R\) is an elitable GE-filter of \(R\) again by (4.2). Hence, the set \({\mathfrak {O}}^{\otimes }(X)\) forms a complete lattice with respect to set inclusion. The least and greatest element of \({\mathfrak {O}}^{\otimes }(X)\) are \(\{1\}\) and \(R\), respectively. Now, for any \(K, G, M\in {\mathfrak {O}}^{\otimes }(X)\), we obtain
. Hence, \(\beta \in M.\) Therefore, \((K\vee G)^{\otimes }\) is supremum of \(K\) and \(G\) in \({\mathfrak {O}}^{\otimes }(X)\). Hence, \(({\mathfrak {O}}^{\otimes }(X),\cap , \sqcup )\) is a lattice. We can observe that the set theoretical intersection of an arbitrary set of elitable GE-filters of \(R\) is an elitable GE-filter of \(R\) again by (4.2). Hence, the set \({\mathfrak {O}}^{\otimes }(X)\) forms a complete lattice with respect to set inclusion. The least and greatest element of \({\mathfrak {O}}^{\otimes }(X)\) are \(\{1\}\) and \(R\), respectively. Now, for any \(K, G, M\in {\mathfrak {O}}^{\otimes }(X)\), we obtain
Therefore, \(({\mathfrak {O}}^{\otimes }(R),\sqcup , \cap ,\{1\},R)\) is a distributive lattice. \(\square \)
Theorem 4.14
Given a GE-filter \(K\) of a transitive bordered GE-algebra \(R\), the following are equivalent:
-
(1)
\(K\) is an elitable GE-filter.
-
(2)
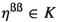 implies \(\eta \in K,\) for all \(\eta \in R\).
implies \(\eta \in K,\) for all \(\eta \in R\). -
(3)
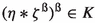 implies \(\zeta \in K\), for all \(\eta ,\zeta \in R.\)
implies \(\zeta \in K\), for all \(\eta ,\zeta \in R.\)
Proof
(1) \(\Rightarrow \) (2) Assume (1) and  . Then, \(\eta \in K^{\otimes }=K\). Thus, (2) follows.
. Then, \(\eta \in K^{\otimes }=K\). Thus, (2) follows.
(2) \(\Rightarrow \) (3) Assume (2) and \(\eta ,\zeta \in R\) such that  . We can observe that
. We can observe that  and hence,
and hence,  . Since \(K\) is an GE-filter of \(R\) and
. Since \(K\) is an GE-filter of \(R\) and  , we get
, we get  . Therefore, \(\zeta \in K\) by (2). Thus, (3) follows.
. Therefore, \(\zeta \in K\) by (2). Thus, (3) follows.
(3) \(\Rightarrow \) (1) Assume (3). Let \(\eta \in K^{\otimes }\). Then,  . Therefore,
. Therefore,  and hence, \(\eta \in K\) by (3). Thus, \(K^{\otimes }\subseteq K\), and hence, \(K\) is an elitable GE-filter of \(R\). \(\square \)
and hence, \(\eta \in K\) by (3). Thus, \(K^{\otimes }\subseteq K\), and hence, \(K\) is an elitable GE-filter of \(R\). \(\square \)
Theorem 4.15
If \(K\) is an elitable GE-filter of a transitive bordered GE-algebra \(R\), then for  and \(\beta \in K\) imply that \(\gamma \in K\).
and \(\beta \in K\) imply that \(\gamma \in K\).
Proof
Let \(K\) be an elitable GE-filter of \(R\) and \(\beta ,\gamma \in R\) be such that  and \(\beta \in K\). Then,
and \(\beta \in K\). Then,  and hence,
and hence,  since \(K\) is GE-filter of \(R\). Therefore, \(\gamma \in K\) by Theorem 4.14. \(\square \)
since \(K\) is GE-filter of \(R\). Therefore, \(\gamma \in K\) by Theorem 4.14. \(\square \)
Theorem 4.16
Every maximal GE-filter of a transitive bordered GE-algebra \(R\) is an elitable GE-filter of \(R\).
Proof
Let \(H\) be a maximal GE-filter of \(R\). Clearly, \(H\subseteq H^{\otimes }\) by Theorem 4.6(2). Now, we prove that \(H^{\otimes }\subseteq H\). Suppose \(H^{\otimes }\nsubseteq H\). Then, there exists \(\beta \in H^{\otimes }\) such that \(\beta \notin H\). Hence,  and \(\langle H\cup \{\beta \}\rangle =R\). Since \(0\in R\), we have
and \(\langle H\cup \{\beta \}\rangle =R\). Since \(0\in R\), we have  Since \(0\le \beta \), we have \((\beta *0)*0\le (\beta *0) *\beta \) by (2.12). That is
Since \(0\le \beta \), we have \((\beta *0)*0\le (\beta *0) *\beta \) by (2.12). That is  . Since
. Since  and \(H\) is a GE-filter of \(R\), we get \(\beta \in H\) which is a contradiction. Hence, \(H^{\otimes }\subseteq H\). Thus, \(H\) is an elitable GE-filter of \(R\). \(\square \)
and \(H\) is a GE-filter of \(R\), we get \(\beta \in H\) which is a contradiction. Hence, \(H^{\otimes }\subseteq H\). Thus, \(H\) is an elitable GE-filter of \(R\). \(\square \)
The following example shows that the converse of Theorem 4.16 is not valid.
Example 4.17
Let \(R=\{0,1, e, f, g, h, a\}\) be a set with the binary operation “\(*\)” in the following Cayley Table.
Then, \((R, *, 1)\) is a transitive bordered GE-algebra. Consider two GE-filters \(K=\{1,e,f\}\) and \( G=\{1,e,f,g,a\}\) of \(R\). Then, we can observe that \(K\) is an elitable GE-filter of \(R\), but \(K\) is not maximal GE-filter of \(R\) since \(K\subseteq G\subseteq R\) but \(K\ne G\) and \(G\ne R\).
We provide conditions for a subset of a transitive bordered GE-algebra to be an elitable GE-filter.
Theorem 4.18
Let \(K\) be a nonempty subset of a transitive bordered GE-algebra \(R\) such that its elitable is \(K\) itself. If \(K\) satisfies (2.18) and

then \(K\) is an elitable GE-filter of \(R\).
Proof
Suppose \(K^{\otimes }=K\) and satisfies (2.18) and (4.3). Since \(K\ne \emptyset \), there exists \(\eta \in K\). As \(\eta \le 1\), we have \(1\in K\) by (2.18). Let \(\eta , \zeta \in R\) be such that \(\eta \in K\) and \(\eta *\zeta \in K\). Then,  and
and  by (2.10) and (2.18), which induces
by (2.10) and (2.18), which induces  by (4.3). Since
by (4.3). Since  and
and  , we have
, we have  by (2.18). Now,
by (2.18). Now,  by (2.21). Hence, it follows from (2.24) and (2.18) that
by (2.21). Hence, it follows from (2.24) and (2.18) that  . Since
. Since  by (2.2), we have
by (2.2), we have  by (2.24) and hence
by (2.24) and hence  by (2.18). Thus, \(\zeta \in K\), and so \(K\) is a GE-filter of \(R\). Therefore, \(K\) is an elitable GE-filter of \(R\). \(\square \)
by (2.18). Thus, \(\zeta \in K\), and so \(K\) is a GE-filter of \(R\). Therefore, \(K\) is an elitable GE-filter of \(R\). \(\square \)
Corollary 4.19
If \(R\) is antisymmetric, then, for all \(\eta ,\zeta \in R\), the following are equivalent.
-
(1)
\(R\) is duplex.
-
(2)
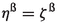 implies \(\eta =\zeta .\)
implies \(\eta =\zeta .\) -
(3)
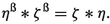
Corollary 4.20
If \(R\) is antisymmetric, then the conditions below are equivalent.
-
(1)
\(R\) is duplex.
-
(2)
Every GE-filter is an elitable GE-filter.
-
(3)
Every principal GE-filter is an elitable GE-filter.
Open Problem. We were unable to identify an example of an elitable GE-filter for an infinite GE-algebra. Is it possible to construct an elitable GE-filter for an infinite GE-algebra?
5 Conclusion
In this paper, we have introduced the notions of maximal GE-filter and prime GE-filter in a GE-algebra and studied the relation between them. We have characterized prime GE-filter in terms of the GE-filter generated by a subset of a transitive GE-algebra. We generalized Stone’s theorem to transitive GE-algebras. We have introduced the notion of elitable GE-filter of a bordered GE-algebra and investigated its properties. We have observed that the class of all elitable GE-filters of a transitive bordered GE-algebra is a complete distributive lattice. We have given equivalent conditions for a GE-filter of a transitive bordered GE-algebra to be elitable GE-filter. We have provided conditions for a subset of a transitive bordered GE-algebra to be elitable GE-filter.
Data Availability
No data were used to support this study.
References
Bandaru RK, Borumand Saeid A, Jun YB (2021) On GE-algebras. Bull Sect Logic 50(1):81–96. https://doi.org/10.18778/0138-0680.2020.20
Bandaru RK, Öztürk MA, Jun YB (2021) Bordered GE-algebras, J Algeraic Syst (submitted)
Celani S (2002) A note on homomorphisms of Hilbert algebras. Int J Math Math Sci 29(1):55–61. https://doi.org/10.1155/S0161171202011134
Chajda I, Halas R, Jun YB (2002) Annihilators and deductive systems in commutative Hilbert algebras. Comment Math Univ Carol 43(3):407–417
Diego A (1966) Sur les algebres de Hilbert. Collection de Logique Mathematique, Edition Hermann, Serie A, XXI
Dudek WA, Jun YB (2007) Poor and crazy filters of BCK-algebras. Int J Pure Appl Math Sci 4:25–38
Hong SM, Jun YB (1996) On deductive systems of Hilbert algebras. Commun Korean Math Soc 11(3):595–600
Imai Y, Iséki K (1966) On axiom system of propositional calculi, XIV. Proc Japan Acad Ser A Math Sci 42(1):19–22
Iséki K (1966) An algebra related with a propositional calculus. Proc Japan Acad Ser A Math Sci 42(1):26–29
Jun YB, Kim KH (2005) H-filters of Hilbert algebras. Sci Math Japonicae e–2005:231–236
Kim HS, Kim YH (2006) On BE-algebras. Sci Math Japonicae Online e–2006:1299–1302
Ozturk MA, Lee JG, Bandaru RK, Jun YB (2021) Strong GE-filters and GE-ideals of bordered GE-algebras, J Math, Volume 2021, Article ID 5520023, 9 p. https://doi.org/10.1155/2021/5520023
Rezaei A, Borumand Saeid A, Borzooei RA (2013) Relation between Hilbert algebras and BE-algebras. Appl Appl Math Int J 8(2):573–584
Borumand Saeid A, Rezaei A, Borzooei RA (2013) Some types of filters in BE-algebras. Math Comput Sci 7:341–352. https://doi.org/10.1007/s11786-013-0157-6
Rezaei A, Bandaru RK, Borumand Saeid A, Jun YB (2021) Prominent GE-filters and GE-morphisms in GE-algebras. Afrika Matematika 32:1121–1136. https://doi.org/10.1007/s13370-021-00886-6
Song SZ, Bandaru RK, Jun YB (2021) Imploring GE-filters of GE-algebras, J Math, Volume 2021, Article ID 6651531, 7 pages. https://doi.org/10.1155/2021/6651531
Acknowledgements
This paper was supported by Wonkwang University in 2022.
Funding
Funding was provided by Wonkwang University.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
The authors declare that they have no conflicts of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lee, JG., Shaik, M.K., Bandaru, R. et al. Elitable GE-filters of bordered GE-algebras. Soft Comput 26, 8987–8996 (2022). https://doi.org/10.1007/s00500-022-07306-2
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-022-07306-2



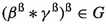 imply that
imply that 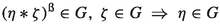 .
.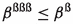 ,
,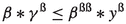 ,
,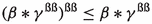 ,
, ,
,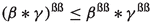 .
.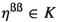 implies
implies 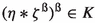 implies
implies 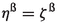 implies
implies