Price of robustness optimization through demand forecasting with an application to waste management

Abstract

Robust optimization can be effectively used to protect production plans against uncertainties. This is particularly important in sectors where variability is inherent the process to be planned. The drawback of robust optimization is the chance of producing over-conservative solutions with respect to the real occurrences of the stochastic parameters. Information can be added in order to better control the extra cost resulting from considering the parameter variability. This work investigates how demand forecasting can be used in conjunction with robust optimization in order to achieve an optimal planning while considering demand uncertainties. In the proposed procedure, forecast is used to update uncertain parameters of the robust model. Moreover, the robustness budget is optimized at each planned stage in a rolling planning horizon. In this way, the parameters of the robust model can be dynamically updated tacking information from the data. The study is applied to a reverse logistics case, where the planning of sorting for material recycling is affected by uncertainties in the demand, consisting of waste material to be sorted and recycled. Results are compared with a standard robust optimization approach, using real case instances, showing potentialities of the proposed method.

1 Introduction

Robust optimization approaches are commonly applied in solving mathematical programming problems where a certain set of parameters are subject to uncertainty. Considering either production or procurement planning problems, these are dealing with the stochastic nature of demand, and a deterministic approach would definitely fail to provide concrete decision support when modeling those kind of scenarios. Therefore, demand variability across the planning time horizon should be properly addressed. This can be done by introducing a protection function in each constraint according to the probabilistic robust approach presented in Bertsimas and Sim (2004). This approach ensures deterministic and probabilistic guarantees on constraints satisfaction, and it does so in a linear framework.

In order to trade-off between optimality and level of robustness, a risk parameter has to be set to formulate the robust counterpart of the nominal model and its level of conservatism. At the same time, the level of conservatism of robust solutions can be such to constitute a significant cost in terms of optimality reduction, also known as price of robustness. This is often the case of over-conservative robust solutions which consider demand values perturbations with low probability of occurrence. In a production planning, setting these solutions leads to extra costs resulting from additional production and storage.

Either risk-averse or risk-taking decision makers will struggle to deal with the challenging trade-off of risk management by setting the robustness control parameter only, besides its odd interpretation. This topic is studied by the literature of robust approaches aiming at producing models better supporting the reality of decision making in uncertain scenarios. Adjustable robust models, for example, are a branch of robust optimization introduced in Ben-Tal et al. (2004) where some of the decision variables can be adjusted after some portion of the uncertain data reveals itself. This approach offers increased flexibility and produces less conservative solutions with respect to static robust optimization. An interesting application of this approach in scheduling problems is presented in Bruni et al. (2017). In the aforementioned paper, the authors present an adjustable robust formulation where sequencing decisions are taken in a first stage, and scheduling decisions are made in a second stage. We refer the reader to the survey in Yanıkoğlu et al. (2019) for a substantial knowledge of adjustable robust optimization (ARO) literature. Other approaches are soft robust optimization (Ben-Tal et al. 2010), light robustness (Fischetti and Monaci 2009), scenario-based robust optimization (Goerigk and Schöbel 2011) and the one proposed in (Roos and den Hertog 2020).

Demand is the most critical information input of production planning and the main source of uncertainty as well. Addressing demand forecasting with proper time series analysis and regression models plays an important role in the overall decision processes. Features such as fitness of demand regressions models should be taken into account along with their parameters setting and forecast accuracy metrics.

Supply chain management is one of the most used scenario to prove the potentialities of robust optimization. Some fundamental supply chain and inventory management models are revised using robust optimization theory in Bertsimas and Thiele (2004); Bertsimas and Thiele (2006). The authors develop robust models for the optimization of the inventory in different settings and policies, such as the (s, S) case, allowing to control the level of conservatism of the solution, without assuming a specific demand distribution. The models are applied to a multi-period planning problem for single or networked warehouses, and for the uncapacitated and capacitated cases. The networked capacitated case is similar to the model studied in our work as an application case. Multi-period inventory management is addressed in detail in See and Sim (2010) where the concept of budget of uncertainty proposed in Bertsimas and Thiele (2004); Bertsimas and Thiele (2006) is extended for controlling the demand. This is done considering demand descriptive information such as standard deviation, seasonality and autoregressive aspects. The inventory policy introduced by the authors is solved by means of Second-Order Cone Programming (SOCP).

In real-case applications, robust optimization could induce over conservatism. The problem is addressed in Daneshvari and Shafaei (2021) where correlation between uncertain parameters is taken into account in the definition of uncertainty sets in order to mitigate over conservatism. Another methodology used to shape the uncertainty sets based on data analysis has been proposed in Qiu et al. (2020). The authors propose a data-driven robust approach of modeling the multi-product inventory problem with demand uncertainties. Basically, they construct an uncertainty set using historical demand data which are estimated not via demand descriptors but using a support vector clustering (SVC) model.

In this paper, we aim to provide a mechanism for setting the level of conservatism of robust solutions according to accurate estimates of robustness costs. Thus, a framework integrating both a forecasting model and two extensions of the nominal multi-period planning model is proposed.

The central idea is to iteratively solve planning and forecasting problems with the goal of finding the best configuration of robust parameters that minimizes the costs that result from overestimating or underestimating risk. These costs are the so-called price of robustness (Pr) as described in Bertsimas and Sim (2004) and the potential extra cost resulting from overtime production (Po) whenever demand is underestimated. In the considered setting, the way of dealing with demand underestimation errors is indeed the activation of overtime production, while demand overestimation contributes to Pr costs.

In order to study the performance of the proposed method, a robust optimization problem arising from waste management and inverse production planning with demand uncertain coefficients is solved and variants of the model with different protection strategies are compared with real-case instances.

The remainder of the paper is organized as follows: Sect. 2 is dedicated to the definition of the planning problem formulations; the proposed framework aimed at the optimization of the risk considering parameters is presented in Sect. 3; Sect. 4 presents the experimental results, while Sect. 5 gives some conclusions, research perspectives and reports acknowledgments.

2 Problems definition and modeling

This section presents the formulations of the problems used in the proposed framework which is detailed in Sect. 3.

Let $\tau$ be a planning period made of T time slots. Each time slot is indexed by $t \in {\mathscr {T}} = \{1, \ldots , T \}$ and corresponds to a working shift where production can be activated. Thus, the planning consists of defining the production lot sizes and the schedules in order to meet the demand quantity $d_t$ of each time slot t. Therefore, each planning period $\tau$ is given with a foreseen demand vector $d_T \in {\mathbb {R}}^T_+$.

Considering a deterministic planning problem ${{\mathscr {D}}}$, we refer to ${{\mathscr {R}}}$ as its robust counterpart, while a third model ${{\mathscr {E}}}$ replicates the same deterministic formulation of ${{\mathscr {D}}}$ and includes some additional decision variables regarding overtime production. Overtime production is the assumed strategy to counteract, with an extra cost, the uncovered demand.

The formulations of problems ${{\mathscr {D}}}$, ${{\mathscr {R}}}$ and ${{\mathscr {E}}}$ are presented in Sects. 2.1, 2.2, and 2.3, respectively.

2.1 Deterministic model ${{\mathscr {D}}}$

Dealing with a production planning setting, ${{\mathscr {D}}}$ is a mixed-integer linear programming model to schedule and lot-size production operations. To better introduce a general formulation of ${{\mathscr {D}}}$, model notation for parameters and indexes is set out in the following.

• T : time horizon length;

• $t \in {\mathscr {T}} = \{1, \ldots , T \}$ : index of working shifts across time

• $f_t$ : setup cost of working shift at time t;

• $d_t$ : production demand at time t;

• $k_t$ : production capacity at time t;

• $c_t$ : unitary production cost at time t;

• $h_t$ : unitary inventory holding cost at time t;

• $I_0$ : initial inventory level.

The model considers the following variables.

• $y_{t} \in \{0,1\}$ : equal to 1 if production is activated at time t, 0 otherwise

• $u_{t} \in {\mathbb {R}}^+$ : production quantity at time t

• $I_{t} \in {\mathbb {R}}^+$ : inventory level at time t

The model minimizes the sum of production, setup and holding costs and is detailed as follows:

$$\begin{aligned}&\min \, Z = \sum _{t \in T} c_t u_{t} +\sum _{t \in T} f_t y_{t} +\sum _{t \in T} h_t I_{t} \end{aligned}$$

(1)

$$\begin{aligned}&\mathrm {s.t.} \nonumber \\&u_{t} \le k_t y_{t} \quad \forall t \in {\mathscr {T}} \end{aligned}$$

(2)

$$\begin{aligned}&I_t = I_{t-1} - d_t + u_{t} \quad \forall t \in {\mathscr {T}}\end{aligned}$$

(3)

$$\begin{aligned}&I_{t} \in {\mathbb {R}}^+ \quad \forall t \in {\mathscr {T}} \end{aligned}$$

(4)

$$\begin{aligned}&u_{t} \in {\mathbb {R}}^+ \quad \forall t \in {\mathscr {T}} \end{aligned}$$

(5)

$$\begin{aligned}&y_{t} \in \{0,1\} \quad \forall t \in {\mathscr {T}} \end{aligned}$$

(6)

The objective function (1) defines the minimization of the sum of the three cost terms, which are production, setup and inventory costs, respectively. Constraints (2) bound the production quantity for each time period, and constraints (3) define the inventory.

2.2 Robust model ${{\mathscr {R}}}$

The mixed-integer linear programming model ${{\mathscr {R}}}$ defines the robust counterpart of ${{\mathscr {D}}}$ according to the robust approach presented in Bertsimas and Sim (2004). We first consider the parameters $d_t, \, t \in {\mathscr {T}} = \{1, \ldots , T \}$, which are subject to uncertainty to take values according to a symmetric distribution with mean equal to the nominal value $d_t$ in the interval $[d_t - \sigma _t,d_t + \sigma _t]$. Indeed, $\sigma _t$ is the maximum deviation allowed for $d_t$. In order to meet the standard formulation of the nominal problem presented in Bertsimas and Sim (2004), where parameters subject to uncertainties belong to inequality constraints only, the equality constraints (3) of ${{\mathscr {D}}}$ regarding demand quantities $d_t$ are reformulated to turn them into inequality constraints. This is performed considering, for each period t, the sum of all demanded quantities up to that period, as in constraints (7) and (8) of the formulation of ${{\mathscr {R}}}$ presented in this section. According to the robust approach presented in Bertsimas and Sim (2004), a parameter $\Gamma _i$ is introduced for each constraint i holding one or more uncertainty coefficients. $\Gamma _i$ is not necessarily integer and takes values in the interval $[0,|J_i |]$ where $J_i$ is the set of the coefficients of constraint i being subject to uncertainty. The nominal problem ${{\mathscr {D}}}$ presents only one set of T constraints considering the coefficients $d_t$, and these are the ones reformulated as inequality constraints. Therefore, we get $\Gamma \in R^T_{+}$, and because of this reformulation $|J_t |= t \ \forall t \in \{1,\ldots , T\}$. For each period t, $\Gamma _t$ represents the number of coefficients that we consider as allowed to vary within their interval. In practice, we consider nature behaving like only a subset of the coefficients will change with respect to their nominal value. Indeed, as affirmed in Bertsimas and Sim (2004), it is unlikely that all $|J_t |$ will change; so the idea of conservative robustness is to be protected against all cases that up to $\lfloor {\Gamma _t}\rfloor$ of these coefficients are allowed to change, and one coefficient $d_t$ changes by $(\Gamma _t - \lfloor \Gamma _{t}\rfloor )\hat{d_t}$. Note that when $\Gamma _t = 0 \ \forall t \in \{1,\ldots , T\}$, we get the nominal deterministic scenario, while setting $\Gamma _t = |J_t |= t \ \forall t \in \{1,\ldots , T\}$ represents solving the problem of the worst case scenario. It is clear that by varying $\Gamma$ the level of robustness can be flexibly adjusted against the level of conservatism of the solution. Considering the structure of the constraints including $d_t$ is important: Because of the telescopic expansion of each set $J_t$ as t goes from 1 to T (i.e., $|J_{t+1} |= |J_t |+ 1$), we consistently constraint $\Gamma _t$ to be bigger than or equal to $\Gamma _{t-1}$.

In the following, we present all the additional variables and parameters that are required to introduce the robustness protection functions presented in Bertsimas and Sim (2004) and formulate the robust counterpart of ${{\mathscr {D}}}$:

• $\epsilon _t \in {\mathbb {R}}^+$ : extra variables multiplying $d_t$ for $t \in T$. These variables are introduced in order to have a variable multiplying the only set of parameters that are affected by uncertainty. These are indeed constrained to be equal to 1 for $t \in T$ as in constraint (11) of ${{\mathscr {R}}}$.

• $z_{t} \in {\mathbb {R}}^+$ : variables resulting from duality within Bertsimas and Sim’s robustness theory; when multiplied by $\Gamma _t$, these variables provide their overall contribution to the protection function of constraint t.

• $p_{t,k} \in {\mathbb {R}}^+$ : variables resulting from duality within Bertsimas and Sim’s robustness theory; they contribute to the protection function of constraint t with respect to the specific coefficient $d_k$.

• $s_{t} \in {\mathbb {R}}^+$ : variables resulting from duality and Bertsimas and Sim’s robustness theory; multiplied by $\sigma _t$, they set the lower bound of the protection function contribution in each constraint t.

• $\Gamma _t$ : parameter to adjust the level of robustness of each period t.

The robust counterpart ${{\mathscr {R}}}$ of ${{\mathscr {D}}}$ is introduced as follows:

$$\begin{aligned}&\min \, (1) \nonumber \\&\mathrm {s.t.} \nonumber \\&(2) , (4) , (5) , (6)\nonumber \\&I_{0} - \sum _{k=0}^t d_k \epsilon _k + \sum _{k=0}^t u_{k} + z_t \Gamma _t + \sum _{k=0}^t p_{t,k} \ge 0 \quad \forall t \in {\mathscr {T}} \nonumber \\ \end{aligned}$$

(7)

$$\begin{aligned}&I_{t} = I_{0} - \sum _{k=0}^t d_k \epsilon _k - \sum _{k=0}^t u_{k} + z_t \Gamma _t + \sum _{k=0}^t p_{t,k} \quad \forall t \in {\mathscr {T}} \nonumber \\ \end{aligned}$$

(8)

$$\begin{aligned}&z_{t} + p_{t,k} \ge \sigma _t \ s_t \quad \forall t \in {\mathscr {T}}, k \in \{ 0,...,t\} \end{aligned}$$

(9)

$$\begin{aligned}&-s_t \le \epsilon _t \le s_t \quad \forall t \in {\mathscr {T}} \end{aligned}$$

(10)

$$\begin{aligned}&\epsilon _t = 1 \forall t \in {\mathscr {T}} \end{aligned}$$

(11)

Constraint (7) defines inventory considering the cumulative demand $d_t$ up to period t, the overall produced quantity $u_{t}$ up to period t, and the uncertainties protection function made of the joint contribution of $z_t \Gamma _t$ and the sum of $p_{t,k}$ for $k \in \{1,\ldots , t\}$. Constraint (7) sets the lower bound of the inventory for each period. Equality constraint (8) allows the inventory to be considered within the cost function. Constraints (9) and (10) resulted from duality in Bertsimas and Sim (2004) robustness theory, where (9) sets the lower bound of the protection function contribution in constraints (7) and (8).

Solving model ${{\mathscr {R}}}$ allows us to evaluate the price of robustness (Pr) resulting from a specific protection $\Gamma$. This is done by computing the difference between the optimal objective function value of ${{\mathscr {R}}}$ and the optimal objective function value of $\mathcal D$.

Table 1 Notation

2.3 Overtime production model ${{\mathscr {E}}}$

In our approach, overtime production is to be activated whenever standard scheduled production is not enough to meet the entire demand across the time horizon. For this reason, the third model ${{\mathscr {E}}}$ replicates the same deterministic formulation of ${{\mathscr {D}}}$ and includes some additional decision variables regarding overtime production. This additional production has of course a higher unitary cost with respect to standard scheduled production. Solving model ${{\mathscr {E}}}$ is intended to evaluate the need and the cost of overtime production (Po).

Considering the main decision variables of ${{\mathscr {D}}}$, such as $y_{t} \in \{0,1\}$ and $u_{t} \in {\mathbb {R}}^+$, the formulation of ${{\mathscr {E}}}$ incorporates also $y_{t}^{\prime } \in \{0,1\}$ and $u_{t}^{\prime } \in {\mathbb {R}}^+$ which correspond to the overtime production equivalent of the previous ones. These additional variables allow ${{\mathscr {E}}}$ to capture the extra costs resulting whenever the robust solution of ${{\mathscr {R}}}$ is not feasible when the true demand vector $\bar{d}$ is observed. Indeed, while both $\mathcal D$ and ${{\mathscr {R}}}$ are solved considering the predicted demand vector ${\hat{d}}$, instances of ${{\mathscr {E}}}$ are solved w.r.t. the true demand vector $\bar{d}$ and its set of standard production variables (i.e., $y_{t}$ and $u_{t}$) are fixed to the values of the robust solution of ${{\mathscr {R}}}$ for the same corresponding scheduling time window. The corresponding unitary costs of these overtime production variables are $f_{t}^{\prime } > f_{t}$ and $c_{t}^{\prime } > c_{t}$, respectively. Therefore, the formulation of ${{\mathscr {E}}}$ is the following:

$$\begin{aligned}&\min \, (1) + \sum _{t \in T} f_{t}^{\prime } y_{t}^{\prime } +\sum _{t \in T} c_{t}^{\prime } u_{t}^{\prime } \end{aligned}$$

(12)

$$\begin{aligned}&\mathrm {s.t.} \nonumber \\&u_{t}^{\prime } \le k_t y_{t}^{\prime } \quad \forall t \in {\mathscr {T}} \end{aligned}$$

(13)

$$\begin{aligned}&I_{t} = I_{t-1} - \bar{d} + u_{t} + u_{t}^{\prime } \quad \forall t \in {\mathscr {T}} \end{aligned}$$

(14)

$$\begin{aligned}&y_{t}^{\prime } \in \{0,1\} \quad \forall t \in {\mathscr {T}}\end{aligned}$$

(15)

$$\begin{aligned}&u_{t}^{\prime } \in {\mathbb {R}}^+ \quad \forall t \in {\mathscr {T}}\end{aligned}$$

(16)

$$\begin{aligned}&I_{t} \in {\mathbb {R}}^+ \quad \forall t \in {\mathscr {T}} \end{aligned}$$

(17)

Solving ${{\mathscr {E}}}$ allows the evaluation of the cost of overtime production (Po) as the difference between the optimal objective function value of ${{\mathscr {E}}}$ and the optimal objective function value of ${{\mathscr {D}}}$. Thus, the sum P of the price of robustness (Pr) and overtime production (Po) can be computed according to a specific protection $\Gamma$ (i.e., $P(\Gamma ) = Pr(\Gamma ) + Po(\Gamma )$). We introduce a procedure, which we call Eval_P, that generates a single evaluation of $P(\Gamma )$. This procedure is part of the routine, detailed later in Sect. 3, aimed at the optimization of the robustness control vector $\Gamma$. The pseudo-code of Eval_P is set out below.

Eval_P $\left( \Gamma ,\bar{d},{\hat{d}},\sigma \right) :$

• 1. Solve ${{\mathscr {R}}}$ $\left( {\hat{d}},\sigma ,\Gamma \right)$ to get $y^* , u^*$, $Obj_{{{\mathscr {R}}}}^*$

• 2. Solve ${{\mathscr {D}}}$ $\left( {\hat{d}}\right)$ to obtain $Obj_{{{\mathscr {D}}}}^*$

• 3. $Pr(\Gamma ) = Obj_{{{\mathscr {R}}}}^* - Obj_{{{\mathscr {D}}}}^*$

• 4. Solve ${{\mathscr {E}}}$ $\left( {\bar{d}}\right)$ where y and u are fixed to $y^*$ and $u^*$, respectively, to obtain $Obj_{{{\mathscr {E}}}}^*$

• 5. $Po(\Gamma ) = Obj_{{{\mathscr {E}}}}^* - Obj_{{{\mathscr {D}}}}^*$

• 6. Return $P(\Gamma ) = Pr(\Gamma ) + Po(\Gamma )$

3 Robustness control optimization

The main notation used in the proposed framework is defined in Table 1.

The forecasting model ${{\mathscr {F}}}$ employed in the framework to evaluate the expected demand is presented in Taylor (2017); its implementation is available as open source software and is called Prophet, and it uses a decomposable time series model Harvey and Peters (1990) with three main model components: trend, seasonality and holidays.

The robustness control vector $\Gamma$ is learned by a routine properly built in order to achieve this parameter tuning objective. The optimization of $\Gamma$ is to find the value that minimizes the sum $P(\Gamma )$ of the price of robustness $Pr(\Gamma )$ and the potential extra costs resulting from overtime production $Po(\Gamma )$. We present a routine that seeks for the best configuration of $\Gamma$ for a considered planning period $\tau$ with its corresponding demand forecast ${\hat{d}}(\tau )$ and its true observations $\bar{d}(\tau )$. Its pseudo-code is set out below. We refer to this routine as Optimize_$\Gamma$ $\left( \Gamma _0,\Gamma _{step},\bar{d}(\tau ),{\hat{d}}(\tau ),\sigma (\tau )\right)$:

• 1. Set $\Gamma _0 \in R^T_+$ : the starting configuration of $\Gamma$

• 2. Set $\Gamma _{step} \in R^T_+$ : a vector of the updating step sizes of each component $\Gamma _t$ of $\Gamma$

• 3. Set $max_k$ = $floor\left( 1/\Gamma {step}\right)$ : maximum number of iterations k for a complete search over the space of $\Gamma \in R^T_+$

• 4. Set $k = 0$ ; $\Gamma _k = \Gamma _0$

• 5. $P\left( \Gamma _k\right) = \textit{Eval}\_{P} \left( \Gamma _k,\bar{d}(\tau ),{\hat{d}}(\tau ),\sigma (\tau )\right)$

• 6. Set $P^* = P\left( \Gamma _k\right)$ ; $\Gamma ^* = \Gamma _k$

• 7. While $k \le max_k$

  • (a) $k = k+1$

  • (b) $\Gamma _k = \Gamma _{k-1} + \Gamma _{step}$

  • (c) $P_k = \textit{Eval}\_{P} \left( \Gamma _k,\bar{d}(\tau ),{\hat{d}}(\tau ),\sigma (\tau )\right)$

  • (d) if $P_k \le P^*$

    • $P^* = P_k$

    • $\Gamma ^* = \Gamma _k$

Whatever setting of $\Gamma _0$ and $\Gamma _{step}$ is made, this must be done according to the peculiar structure of constraints (7), (8) of the formulation of ${{\mathscr {R}}}$. Indeed, as stated in Sect. 2, before introducing model ${{\mathscr {R}}}$, the telescopic expansion of each set $J_t$ (i.e., $|J_{t+1} |= |J_t |+ 1$) constrains each component $\Gamma _t$ of the protection vector $\Gamma$ to be bigger than or equal to the component $\Gamma _{t-1}$ and smaller than t. The setting of both $\Gamma _0$ and $\Gamma _{step}$ must be consistent with these constraints. Given a scalar $\gamma _{step} \in \{0 \ldots 1 \}$, we propose a rule for setting each component $\Gamma _{step}(t)$ of $\Gamma _{step}$ such that the previous constraints are satisfied:

$$\begin{aligned}&\Gamma _{step}(t) = \gamma _{step} \ t&\,\, \forall t \in \{1 \ldots T \} \end{aligned}$$

This Optimize_$\Gamma$ routine can be embedded in the proposed framework for solving the multi-period planning problem under uncertainties. The purpose of this framework is to provide automated decision support to implement an appropriate robustness control vector that minimizes the aforementioned costs of over- or underestimating risk in this class of planning problems.

Referring to the most recent demand realizations, and to its corresponding time series $D(\rho ,\tau )$, we consider $\tau$ planning period as the latest T time slots part of $D(\rho ,\tau )$. This demand time series $D(\rho ,\tau )$ can be used along with Optimize_$\Gamma$ to mine what would have been the best robustness control vector $\Gamma ^*$ for the planning period $\tau$. This is indeed described in the following:

• 1. Set $\rho$ and $\tau$, then consider $D(\rho ,\tau )$ and get $\bar{d}\left( \tau \right)$

• 2. Solve ${{\mathscr {F}}}$ $\left( D(\rho , \tau )\right)$ to forecast ${\hat{d}}(\tau )$ and ${\hat{\sigma }}(\tau )$

• 3. Set $\Gamma _0$ and $\Gamma _{step}$

• 4. $\Gamma ^*$ = Optimize_$\Gamma$ $\left( \Gamma _0,\Gamma _{step},\bar{d}(\tau ),{\hat{d}}(\tau ),\sigma (\tau )\right)$

The rationale of the proposed framework is the use of $D(\rho ,\tau )$ and its corresponding best configuration $\Gamma ^*$ to solve the planning problem of the future planning period $\tau + 1$. Therefore, for each observed demand time series $D(\rho ,\tau )$, the corresponding $\Gamma ^*$ impact in term of $P(\Gamma ^*)$ is evaluated when $\Gamma ^*$ is used to protect against the uncertainties of the very immediate future period $\tau + 1$. Considering a sequence of framework implementations, at each of these it is reasonable to set $\Gamma _0$ starting configuration to $\Gamma _{\tau - 1}^*$. The experimental results of both Optimize_$\Gamma$ and its implementation framework are presented in Sect. 4. Performances in terms of P costs are compared with P resulting from either the deterministic and worst-case scenario approaches that we refer to as $P(\Gamma _{nominal})$ and $P(\Gamma _{worstcase})$, respectively.

4 Application to waste management

This section holds the experimental results obtained by applying the proposed methodology to a waste management (WM) setting.

With respect to the problem addressed, while it is possible to find several applications of robust optimization to supply chain and production problems, fewer research works address circular economy and reverse logistics related cases. Stochastic-based approaches in waste flow optimization have been addressed in Sun and Huang (2015) and Zhu and Huang (2011). The work of Kim et al. (2018) develops a robust model where box uncertainty and robustness budget are used to control uncertainty in a closed loop supply chain in the textile industry. The paper considers recycling operations in a networked environment and considers the over conservatism problem but does not consider demand characteristics. In Hatefi and Jolai (2014), p-robust constraints are used to control disruption events. In Entezaminia et al. (2017), a multi-objective multi-period multi-product multi-site aggregate production planning model is solved with reverse flow considerations. In this case, the robust approach is pretty standard. In Pinto and Stecca (2020), the same problem addressed in this work is treated with classical robust theory.

In WM, the planning consists of scheduling and lot sizing each phase of a recycling material sorting process. The planning model presented in Pinto et al. (2021) is considered as the deterministic model ${{\mathscr {D}}}$ for testing the proposed framework. The formulation of ${{\mathscr {D}}}$ is reported in Sect. A of the appendix. This model supports several strategic decisions that are critical in the considered WM application. It can be described as a variant of a lot sizing model with nonlinear costs (approximated by mean of piecewise linear functions) with the additional features of scheduling the operations and allocating the appropriate workforce dimension. The aim of the model is finding the best allocation of operators to each working shift in order to process the recycling material quantity $d_t$ arriving at each time slot t. In this scenario, a time slot is indeed a working shift where teams of operators may be allocated. The robust counterpart of ${{\mathscr {D}}}$ is newly introduced in Pinto and Stecca (2020) and is considered as ${{\mathscr {R}}}$ for what concerns the experimental results. The formulation of ${{\mathscr {R}}}$ is reported in Sect. B of the appendix. Model ${{\mathscr {E}}}$ is derived from model ${{\mathscr {D}}}$ in Pinto et al. (2021) as illustrated in Sect. 2.3, and its formulation is reported in Sect. C of the appendix.

Optimize_$\Gamma$ routine is supposed to densely explore the search space of $\Gamma$ for an exhaustive search aimed at the optimization of P. In order to validate its performances, some preliminary experiments are performed over a set of subsequent planning periods: For each planning period $\tau$, performances in terms of P costs resulting from applying $\Gamma ^*$ found by Optimize_$\Gamma$ are compared with P resulting from the deterministic (i.e., nominal) and worst-case scenario approaches. The results are illustrated in Table 2 and discussed below. The accuracy of the forecast model is reported in terms of symmetric mean absolute percentage error (i.e., SMAPE), an accuracy measure based on percentage errors which is usually defined as follows:

$$\begin{aligned} \mathrm {SMAPE} = \frac{1}{n} \sum _{t=1}^{N} \frac{ |F_t - A_t |}{\left( |A_t |+ |F_t |\right) / 2} \end{aligned}$$

where $A_t$ is the actual value and $F_t$ is the forecast value. The absolute difference between these values is divided by half the sum of absolute values of the actual value $A_t$ and the forecast value $F_t$. Then, the value of this calculation is summed for every fitted point t and divided by the number of fitted points n.

Table 2 Optimize_$\Gamma$ validation results

The table’s columns present the reduction of robustness and overtime production costs P achieved by $P(\Gamma ^*)$ with respect to the deterministic $P(\Gamma _{nominal})$ and worst-case $P(\Gamma _{worstcase})$ approaches. The presented values of costs reduction result from the following expressions:

$$\begin{aligned}&wrt \ nominal = \frac{P(\Gamma ^*) - P(\Gamma _{nominal})}{P(\Gamma _{nominal})} \quad \\&wrt \ worstcase = \frac{P(\Gamma ^*) - P(\Gamma _{worstcase})}{P(\Gamma _{worstcase})} \end{aligned}$$

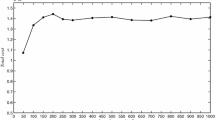
The following columns of Table 2 present the percentage of protection guaranteed by each $\Gamma ^*$ considered, obtained as the ratio between the sum of the components of $\Gamma ^*$ and the sum of the components of the vector $\Gamma$ corresponding to the worst case, the SMAPE accuracy metrics of the forecasting model, while the last column presents the sum of all the forecasting residuals of the planning period to consider forecast bias, that is overestimating (a positive value of bias) or underestimating (a negative value of bias) the future demand. Indeed, the forecast model is implicitly introducing robustness to the planning solution whenever is overestimating the demand realization. At the same time, the model ${{\mathscr {F}}}$ is incautiously fostering the importance of robust planning solutions whenever is underestimating the demand realization. Indeed, considering systematical biased behavior of forecast models is crucial for a proper planning. Results of Table 2 show how $\Gamma ^*$ moderate its robustness contribution with respect to forecast bias over the planning period: its percentage protection remains minimal (or close to zero) for positively biased prediction in order to produce solutions close or equal to a deterministic (nominal) solution, while it provides a stronger protection to uncertainties when dealing with underestimating demand forecasts. However, for both types of biased prediction scenarios, Optimize_$\Gamma$ routine produces configurations of $\Gamma$ minimizing risk costs with respect to either deterministic and worst-case approaches. Figure 1 shows an example of Optimize_$\Gamma$ instance solving.

Fig. 1

Example of an Optimize_$\Gamma$ instance solving

Table 3 Framework results in real-case application

4.1 Analysis of results

As described at the end of Sect. 3, considering an observed demand time series $D(\rho ,\tau )$, the proposed framework essence is using the very close past best configuration $\Gamma ^*$ to protect against the uncertainties of the very immediate future, that is, solving the robust planning problem ${{\mathscr {R}}}$ $\left( {\hat{d}},\sigma ,\Gamma ^* \right)$ of the subsequent future planning problem $\tau + 1$. Therefore, a new set of experiments is performed to test the performance relative to the observed costs P of robustness and overtime production of the very next future. All instances are created by a real-world case study from a waste sorting plant located next to Rome, Italy. Results are shown in Table 3. As in Table 2, performances in terms of $P(\Gamma ^*)$ costs are compared with P resulting from either the deterministic $P(\Gamma _{nominal})$ and worst-case $P(\Gamma _{worstcase})$ scenario approaches. Demand arising from the considered real-case study is particularly unstable, and it seems reasonable to consider this adverse feature of the time series D particularly challenging for the proposed framework. Indeed, no autocorrelations are present either for small or larger seasonal lagged values of D. Therefore, the larger the planning period $\tau + 1$ towards the future, the smaller the chances of a good performance of $\Gamma ^*$ learned over the immediate past planning period $\tau$. Experiments presented in this section consider 50 instances of subsequent planning periods of two weeks (i.e., 12 time slots considering 6 weekly working days of 2 working shifts each). Table 3 highlights two main important results: The framework provides stronger protections to uncertainties (as featured in $\Gamma ^*$ column) for most of the occasions of underestimation of demand realization, and it does so while guaranteeing a lower cost P of robustness and eventual overtime production with respect to the deterministic and worst-case approaches. Indeed, out of the 30 instances where ${{\mathscr {F}}}$ underestimates the demand, 21 of these reveal a valuable P cost reduction, that is about 70% of the occasions. At the same time, costs reduction are also observed for 7 of the remaining 20 occasions (35%) where ${{\mathscr {F}}}$ overestimates the demand. Moreover, 42 of all 50 instances (84%) prove how the framework is providing protection vectors $\Gamma ^*$ with smaller associated $P(\Gamma ^*)$ with respect to $P(\Gamma _{worstcase})$.

5 Conclusions

In this paper, we addressed the problem of controlling the extra costs resulting from considering demand uncertainties in planning problems. Robust optimization theory is applied to both a general production planning model in the general discussion and to a waste management use case regarding recycling operations planning. An optimization procedure determining the best possible robustness budget to use in successive planning stages is proposed. In this way, it is possible to dynamically update both the estimated demand and the robustness budget, helping to balance the extra costs of robustness and extra costs due to overtime production. The framework is tested in a real-case environment where demand does not follow a specific probability distribution. The results show that, most of the time, the classical robust approach is over-conservative. Moreover, when the forecasts overestimate the observed demand, the robustness budget $\Gamma$ can be effectively optimized. Forecasting model features and their overall effect over the protection cost are not addressed by this study, and they will be done in a future work. Moreover, the proposed approach can be applied to different planning problems and tested against different scenarios in future works.

Appendices

Appendices

: Model ${{\mathscr {D}}}$

Dealing with a waste management setting, ${{\mathscr {D}}}$ is a mixed-integer linear programming model scheduling the sorting operations of each phase of a waste sorting process. The model can be described as a variant of a lot sizing model with nonlinear costs (approximated by mean of piecewise linear functions) with the additional features of scheduling the operations and allocating the appropriate workforce dimension. To better introduce the formulation of ${{\mathscr {D}}}$, model notation for parameters and indexes is set out in the following.

• $j \in \{1,\ldots , J\}$ : index of the J sorting stages

• $p \in \{1,\ldots , P\}$ : index of the P time shifts

• T : time horizon partitioned into time shifts with $t \in {\mathscr {T}} = \{1, \ldots , T \}$

• C : hourly cost of each operator

• $b_t$ : working hours for time t determined by the corresponding shift p

• $C_t = C*b_t$ : cost of each operator at time t

• $f_j$ : setup cost of sorting stage j

• $d_t$ : quantity of material in kg unloaded from trucks at time t

• $\alpha _j$ : percentage of waste processed in stage $j-1$, received in input by buffer j

• $S_j$ : maximum inventory capacity of the sorting stage buffer j

• $LC_j$ : critical inventory-level threshold of buffer j

• $n_j$ : fraction of material allowed to be left at buffer j at the end of time horizon

• $K_j$ : single operator hourly production capacity [kg/h] of sorting stage j

• $SK_{j,t} = K_j*b_t$ : operator sorting capacity in sorting stage j, at time t

• M : maximum number of operators available in each time shift

• $E_j$ : minimum number of operators to be employed in each time shift of stage j

• $\partial h_j^i$ : slope of the i-th part of linearization of the buffer j inventory cost curve

• $I_{j,0}$ : initial inventory level in buffer j

The model considers the following variables.

• $x_{j,t} \in {\mathbb {Z}}^+$ : operators employed in the sorting stage j at time t

• $u_{j,t} \in {\mathbb {R}}^+$ : processed quantity at stage j at time t

• $y_{j,t} \in \{0,1\}$ : equal to 1 if stage j is activated at time t , 0 otherwise

• $I_{j,t} = I_{j,t}^{\ '} + I_{j,t}^{\ ''} \ge 0$: inventory level of material in buffer j at time t; for each stage j the corresponding $I'_{j,t}$ and $I''_{j,t}$ represent the inventory level before and after reaching the critical threshold, respectively.

• $w_{j,t} \in \{0,1\}$ : equal to 1 if $I_{j,t}^{\ ''} > 0$, 0 otherwise. Indeed, these binary variables are used to model the piecewise linear functions of the buffer inventory costs.

The model minimizes the sum of sorting and holding costs and is detailed as follows:

$$\begin{aligned}&\min \, Z = \sum _{j \in J} \sum _{t \in T} C_t x_{j,t} +\sum _{j \in J} \sum _{t \in T} f_j y_{j,t} \nonumber \\&\qquad \qquad \quad +\sum _{j \in J} \sum _{t \in T}\left( \partial h_j^1 I_{j,t}^{'} + \partial h_j^2 I_{j,t}^{''} \right) \end{aligned}$$

(18)

$$\begin{aligned}&\mathrm {s.t.} \nonumber \\&E_j \; y_{j,t} \le x_{j,t} \le M \; y_{j,t} \quad \forall j \in J , t \in {\mathscr {T}} \end{aligned}$$

(19)

$$\begin{aligned}&\sum _{j \in J} x_{j,t} \le M \quad \forall t \in {\mathscr {T}} \end{aligned}$$

(20)

$$\begin{aligned}&u_{j,t} \le SK_{j,t}\ x_{j,t} \quad \forall j \in J , \in {\mathscr {T}} \end{aligned}$$

(21)

$$\begin{aligned}&I_{1,t} = I_{1, t-1} + d_t - u_{1,t} \quad \forall t \in {\mathscr {T}}\end{aligned}$$

(22)

$$\begin{aligned}&I_{j,t} = I_{j, t-1} - u_{j,t} + \alpha _j\ u_{j-1,t} \quad \forall t \in {\mathscr {T}}, j \in J \setminus 1\end{aligned}$$

(23)

$$\begin{aligned}&I_{j,t} = I_{j,t}^{\ '} + I_{j,t}^{\ ''} \quad \forall j \in J,t \in {\mathscr {T}}\end{aligned}$$

(24)

$$\begin{aligned}&LC_j\ w_{j,t} \le I_{j,t}^{\ '} \le LC_j \quad \forall j \in J, t \in {\mathscr {T}}\end{aligned}$$

(25)

$$\begin{aligned}&0 \le I_{j,t}^{\ ''} \le (S_j - LC_j)\ w_{j,t} \quad \forall j \in J, t \in {\mathscr {T}}\end{aligned}$$

(26)

$$\begin{aligned}&I_{j,T} \le n_j\ LC_j \quad \forall j \in J\end{aligned}$$

(27)

$$\begin{aligned}&x_{j,t} \in {\mathbb {Z}}^+ \quad \forall j \in J,t \in {\mathscr {T}}\end{aligned}$$

(28)

$$\begin{aligned}&u_{j,t} \in {\mathbb {R}}^+ \quad \forall j \in J,t \in {\mathscr {T}}\end{aligned}$$

(29)

$$\begin{aligned}&y_{j,t} \in \{0,1\} \quad \forall j \in J,t \in {\mathscr {T}} \end{aligned}$$

(30)

The objective function (18) defines the minimization of the sum of the three cost terms, which are sorting, setup and inventory costs, respectively. Constraints (19) and (20) bound the number of workers that can be assigned to each sorting station and to each time shift. Constraints (21) limit the quantity sorted $u_{j,t}$ to the sorting capacity dependent on the number of workers $x_{j,t}$. The remaining constraint sets define and limit the inventories: Constraint set (22) defines the inventory for the first buffer, considering the inbound material $d_t$ and the sorted material $u_{1t}$, while (23) defines the inventory for the other buffers corresponding to $j > 1$. Indeed, constraints (23) describe the waste flow across the sorting stages that follow one another: Each subsequent inter-operational buffer j receives by the previous sorting stage $j-1$ a quantity of waste equal to a $\alpha _j$ percentage of the waste processed in stage $j-1$. Constraint sets (24), (25), and (26) define the piecewise linear functions for inventories; in these constraints, level $S_j$ and maximum capacity $LC_j$ are connected with the inventory levels through the variable $w_{j,t}$. The last constraint set (27) imposes the maximum unsorted material allowed to be left at the end of the planning period for each buffer.

: Model ${{\mathscr {R}}}$

The robust counterpart ${{\mathscr {R}}}$ of ${{\mathscr {D}}}$ is introduced as follows:

$$\begin{aligned}&\min \, (18) \nonumber \\&\mathrm {s.t.} \nonumber \\&(19)-(21) , (23)-(30)\nonumber \\&I_{1,0} + \sum _{k=1}^t d_k \epsilon _k- \sum _{k=1}^t u_{1,k} + z_t \Gamma _t\nonumber \\&\quad + \sum _{k=1}^t p_{t,k} \le S_1 \qquad \forall t \in {\mathscr {T}} \end{aligned}$$

(31)

$$\begin{aligned}&I_{1,0} + \sum _{k=1}^t d_k \epsilon _k - \sum _{k=1}^t u_{1,k} + z_t \Gamma _t\nonumber \\&\quad + \sum _{k=1}^t p_{t,k} \ge 0 \qquad \forall t \in {\mathscr {T}} \end{aligned}$$

(32)

$$\begin{aligned}&I_{1,0} + \sum _{k=1}^T d_k \epsilon _k - \sum _{k=1}^T u_{1,k} + z_T \Gamma _T + \sum _{k=1}^T p_{T,k}\le n_1\ LC_1&\end{aligned}$$

(33)

$$\begin{aligned}&I_{1,t} = I_{1,0} + \sum _{k=1}^t d_k \epsilon _k - \sum _{k=1}^t u_{1,k} + z_t \Gamma _t\nonumber \\&\qquad \quad + \sum _{k=1}^t p_{t,k} \qquad \forall t \in {\mathscr {T}} \end{aligned}$$

(34)

$$\begin{aligned}&z_{t} + p_{t,k} \ge \sigma _t \ s_t \end{aligned}$$

(35)

$$\begin{aligned}&\forall t \in {\mathscr {T}}, k \in \{ 0,...,t \} \nonumber \\&-s_t \le \epsilon _t \le s_t \end{aligned}$$

(36)

$$\begin{aligned}&\forall t \in {\mathscr {T}} \nonumber \\&\epsilon _t = 1 \nonumber \\&\forall t \in {\mathscr {T}} \end{aligned}$$

(37)

Constraint sets (31)(32)(33)(34) define and limit the inventories: Constraint (31) defines the inventory for the first buffer, considering the cumulative inbound material $a_t$ up to period t, the overall sorted material $u_{1t}$ up to period t and the uncertainties protection function made of the joint contribution of $z_t \Gamma _t$ and the sum of $p_{t,k}$ for $k \in \{1,\ldots , t\}$. Constraint (32) sets the lower bound of the inventory for each period, and (33) imposes the maximum unsorted material allowed to be left at the end of the planning period for the first buffer, as constraint (27) does for all other subsequent buffers. Equality constraint (34) allows the inventory of the main buffer (i.e., buffer no. 1) to be considered in the corresponding piece-wise linear part of the cost function. Constraints (35) and (36) resulted from duality in Bertsimas and Sim (2004) robustness theory, where (35) sets the lower bound of the protection function contribution in constraints (31) and (33).

: Model ${{\mathscr {E}}}$

Model ${{\mathscr {E}}}$ replicates the same deterministic formulation of ${{\mathscr {D}}}$ and introduces some additional decision variables to model overtime production. Consider the following set of main decision variables of ${{\mathscr {D}}}$:

• $y_{j,t} \in \{0,1\}$ : equal to 1 if production stage j is activated at time t, 0 otherwise

• $x_{j,t} \in {\mathbb {Z}}^+$: operators employed in the production stage j at time t

• $u_{j,t} \in {\mathbb {R}}^+$: processed quantity at production stage j at time t

The formulation of ${{\mathscr {E}}}$ incorporates also the variables $y_{j,t}^{\prime }$, $x_{j,t}^{\prime }$ and $u_{j,t}^{\prime }$ which correspond to the overtime production equivalent of the previous ones. The corresponding unitary cost of these overtime production capacity variables (i.e., $y_{j,t} \in \{0,1\}$ and $x_{j,t} \in {\mathbb {Z}}^+$) is $f_{j}^{\prime }$ and $C_{t}^{\prime }$, respectively, while $M^{\prime }$ is the maximum number of operators available for overtime production. Therefore, the formulation of ${{\mathscr {E}}}$ is the following:

$$\begin{aligned}&\min \, (18) +\sum _{j \in J} \sum _{t \in T} f_{j}^{\prime } y_{j,t}^{\prime } + \sum _{j \in J} \sum _{t \in T} C_{t}^{\prime } x_{j,t}^{\prime } \end{aligned}$$

(38)

$$\begin{aligned}&\mathrm {s.t.} \nonumber \\&(19) , (20) , (21) , (24) , (25) , (26) , (27)\nonumber \\&\sum _{j \in J} x_{j,t}^{\prime } \le M^{\prime } \quad \forall t \in {\mathscr {T}} \end{aligned}$$

(39)

$$\begin{aligned}&u_{j,t}^{\prime } \le SK_{j,t}\ x_{j,t}^{\prime } \quad \forall j \in J , t \in {\mathscr {T}}\end{aligned}$$

(40)

$$\begin{aligned}&I_{1,t} = I_{1, t-1} + d_t - u_{1,t} - u_{1,t}^{\prime } \quad \forall t \in {\mathscr {T}}\end{aligned}$$

(41)

$$\begin{aligned}&I_{j,t} = I_{j, t-1} - u_{j,t} + \alpha _j\ u_{j-1,t}\nonumber \\&\qquad \quad + \alpha _j\ u_{j-1,t}^{\prime }\quad \forall t \in {\mathscr {T}}, j \in J \setminus 1\end{aligned}$$

(42)

$$\begin{aligned}&x_{j,t}^{\prime } \in {\mathbb {Z}}^+ \quad \forall j \in J,t \in {\mathscr {T}}\end{aligned}$$

(43)

$$\begin{aligned}&u_{j,t}^{\prime } \in {\mathbb {R}}^+ \quad \forall j \in J,t \in {\mathscr {T}}\end{aligned}$$

(44)

$$\begin{aligned}&y_{j,t}^{\prime } \in \{0,1\} \quad \forall j \in J,t \in {\mathscr {T}} \end{aligned}$$

(45)