Periodic event-triggered modified repetitive control with equivalent-input-disturbance estimator based on T-S fuzzy model for nonlinear systems

Abstract

In this paper, the periodic signal tracking and the disturbance rejection problems are considered for a class of time-varying delay nonlinear systems with unknown exogenous disturbances under limited communication resources. The Takagi–Sugeno (T-S) fuzzy model is used to approximate the nonlinear system. The developed scheme achieves periodic reference tracking and improves the performance of periodic and aperiodic unknown disturbances rejection effectiveley. This can be operated by incorporating the equivalent-input-disturbance (EID) estimator with the modified repetitive controller (MRC) scheme. Moreover, a fuzzy periodic event-triggered feedback observer (FPETFO) is proposed for the purpose of reducing the computational burden, energy consumption and saving communication resources. The periodic event-triggered technique is designed to observe the occurrence of an event which is described by an error signal. When this error signal exceeds a prescribed threshold, the event occurs and the current data are transmitted; otherwise, there is a zero-order hold to keep data unchanged. The overall system consists of MRC, EID and FPETFO based on a T-S fuzzy model. Then, some sufficient conditions are derived to gurantee the asymptotic stability of the overall system subjected to unknown disturbances using the Lyapunov–Krasovskii functional (LKF) stability theory and linear matrix inequalities (LMIs). The fuzzy state feedback controller and observer gains are designed using the LMI and matrix decomposition approaches. Simulation results illustrate the effectiveness and feasibility of the proposed scheme with comparative study.

1 Introduction

In control engineering, the nonlinearities have been appeared in most of the physical plant and practical applications such as robots, power systems and in other more systems (Zhou et al. 2013; Hamdy and Hamdan 2015; Su et al. 2018; Yousef et al. 2019; Cheng et al. 2020; Hamdy et al. 2020). Hence, many control approaches had been developed to deal with these nonlinearities. One of these approaches is the well-known Takagi–Sugeno (T-S) fuzzy model, which has the good ability of describing the nonlinear systems (Hamdy and Hamdan 2015). T-S fuzzy model can approximate such nonlinearities with an effective way based on the universal approximation property (Tanaka et al. 1996). In addition, it has the capability to approximate the nonlinear systems with less rules than other types of fuzzy models (Tanaka and Wang 2001; Hamdy and Hamdan 2015). Recently, there are a great works of control and analysis of T-S fuzzy systems which deals with different control approaches (Kole 2015; Abid and Toumi 2016; Aslam and Li 2019; Lian et al. 2019; Kien et al. 2020; Li, et al. 2020a, b; Sakthivel et al. 2020).

On the other hand, the unknown disturbance rejection and the periodic signal tracking are two main important issues. The repetitive control (RC) is one of the effective control algorithms which is used to compensate for the unknown periodic disturbances and track exogenous periodic signals via repeated learning actions (She et al. 2012; Teo et al. 2016). Due to its ability to achieve an improved performance, RC has been widely implemented in numerous applications such as robotic manipulators, hard disk drives, rotary servo motors, inverted pendulum, power systems and a lot of systems which require tracking or rejection for the periodic signals (Fujimoto 2009; Na et al. 2014; Cui and Zhang 2019; Liu et al. 2019; Li, et al. 2020a, b; Sun et al. 2020). A low-pass filter (LPF) has been incorporated with RC to construct a modified RC (MRC) to stabilize a strictly proper plants, which it was difficult for RC to stabilize them (Zhou et al. 2013). The LPF in MRC can be used in rejection the high frequency signals and hence reduce the control effort significantly as well as the stability improvement of the system can be achieved. This ensures that the steady state tracking error of the MRC systems is less than to that of the RC systems and so improve the tracking performance (Na et al. 2014; Sakthivel et al. 2020). The design of the LPF reflects the tradeoff between the stability and the tracking performance. MRC scheme cannot reject the aperiodic disturbance effects as good as it does with the periodic one because it cannot be realized using the RC feedback loop (Sakthivel et al. 2018a, b). MRC is an effective algorithm with T-S fuzzy model and there are a lot of researches have taken this topic in concern such as (Sakthivel et al. 2018a, b; Wang et al. 2020a, b, c; Zhang et al. 2020).

In practice, disturbances are usually mixed between periodic and aperiodic components and often unknown with different frequencies. Hence, more attention has been paid to overcome this drawback by developing several control schemes with RC or MRC technique (T. Miyazaki, K. Ohishi, I. Shibutani 2006; Pipeleers et al. 2008; Wu et al. 2014) and the references therein. In (Miyazaki 2006), the disturbance observer is used to estimate the disturbances on the output. However, the LPF design in the disturbance observer is complicated because it needs to achieve both the overall system stability and the causality of the disturbance observer. A robust high order RC technique is introduced to handle the both types of disturbances in (Pipeleers et al. 2008). Although the controller gives optimal performance balance for the two types of disturbances, it can suffer from reduced control performance for one of them. In (Wu et al. 2014), the solution is focused on constructing an equivalent-input-disturbance (EID) estimator-based MRC system for rejecting the aperiodic disturbance. Because of its robustness to compensate for the disturbances, this technique can be implemented in practice easily. As a result of the practical advantages of the EID estimator, a great number of control methodologies which depend on EID have been presented for different types of control systems (Liu et al. 2014; Yu et al. 2019; Zhou et al. 2020). Furthermore, MRC based on an EID estimator is proposed for various nonlinear systems such as in (Susana Ramya et al. 2018; Sakthivel et al. 2019; Sweety et al. 2020). Also, the EID based MRC through T-S fuzzy model for nonlinear systems has been presented (Sakthivel et al. 2019; Sweety et al. 2020). It is known that the state observer can be used to estimate the system states and the EID estimator depends on the state observer. The design of the observer has been introduced for various nonlinear systems such as (Afaghi et al. 2020; Liang et al. 2020, Pan et al. 2021).

Most of the previous literature on the MRC systems depend on continuous states, output, or observer feedback, which can cause heavy communication burden on the sensors and controller. Therefore, more studies have been presented for event triggered control (ETC) (Ma, et al. 2018a, Su et al. 2019, Zhang et al. 2020, Wang, et al. 2020a, b, c). The ETC is distinguished by its high effect to save the communication resources and its control flexibility compared with the timing triggered control in which the data are updated periodically regardless of whether it is needed or not (Hamdy et al. 2017a, 2017b, 2018). Particularly, in the control systems over a network, the signals from the controller to actuator and from the sensors to controller are transmitted through communication channels. To avoid the network congestion and data dropout or loss, the signals over network must be as infrequent as possible. To achieve that, the event triggered mechanism (ETM) is inserted in the data communication channels to decide that the control inputs will be updated or not based on an event which is usually designed as the error signal overtakes a predetermined limit. If the event is not achieved, the data will be unchanged using a zero-order hold (ZOH) (Ma et al. 2018a). However, most ETC approaches depend on a continuous ETM, which cause the unwanted Zeno behavior as a result of continuous sampling (Dolk et al. 2017). This problem has been solved by designing a periodic ETM (PETM) at which the event-triggering condition is being checked periodically at fixed sampling time instants to decide sending a new control signal or not (Garcia et al. 2017, Li and Fu 2017, Ma et al. 2018b, Ma and Pagilla 2019, Abd-Elhaleem et al. 2021). In (Abd-Elhaleem et al. 2021), the MRC based on EID with two PETM transmission channels has been designed for a linear system subjected to periodic and aperiodic disturbances. Although the control design achieved a good tracking performance and saved the communication resources, this design cannot deal with the nonlinear systems. Over the past few years, there has been an interest in PETM for nonlinear systems (Dolk et al. 2017; Yang et al. 2018; Wang, et al. 2020a, b, c). Moreover, it is noticed that the previous work on MRC based on PETM approach has not taken the nonlinearity and the aperiodic disturbances in concern which motivates this study.

Based on the above mentioned results and shortcomings, this paper introduces the design of the MRC with fuzzy periodic event-triggered feedback observer (FPETFO) based on EID estimator for a class of time-varying delay nonlinear system. The EID based MRC is used to track the exogenous periodic signals and compensate for the unknown periodic and aperiodic disturbances.The T-S fuzzy model is used to approximate the time-varying delay nonlinear system subjected to unknown periodic and aperiodic disturbances. The system states are assumed to be unmeasurable; hence, a full fuzzy state observer (FSO) is utilized to estimate these states. The PETM based on FSO is considered for the purpose of reducing the computational burden, energy consumption and saving the communication resources. The PETM is located between the FSO and the fuzzy state feedback control to detect the occurrence of an event via a certain condition. The PET condition is described by exceeding the designed error signal to a predetermined value. The current data are transmitted only when the event occurs; otherwise, a ZOH keeps the data unchanged. The proposed scheme improves the control performance for the periodic signal tracking and the rejection for both types of unknown disturbances under limited communication resources. Furthermore, the proposed scheme reduces the computational burden, energy consumption and saves the communication resources. One of the difficulties is the guaranteed stability of the overall system (FPETFO-MRC based on EID esitmator with time-varying delay T-S fuzzy model) especially in case of the time-varying delays systems and periodic and aperiodic disturbances. However, in this paper, the stability of the closed-loop system is guaranteed in the presence of periodic and aperiodic disturbances and time-varying delay using an LMI-based stability criterion which is derived by using Lyapunov–Krasovskii functional (LKF) stability theory. In addition, the fuzzy observer and controller gains are designed using the LMI and the matrix decomposition approaches. The synthesis of the proposed scheme design and its effectiveness can be illustratived through a simulation example of a modified truck-trailer model with time-varying delay with comparative study. The main contributions of this paper can be summarized as follow:

• The proposed controller achieves a good control performance for periodic signal tracking and actively compensates for the periodic and aperiodic disturbances for a class of time-varying nonlinear systems with comparative results.

• The PETM depends on FSO is proposed to reduce the computational burden, energy consumption and saves communication resources.

• The EID estimator is designed independently from MRC. So, the procedure of the design is simple and the system can be implemented in practice easily.

• The overall system stability is guaranteed using LKF candidate via LMIs stability criterion. Moreover, the proposed controller is robust to the unknown disturbances and the structure uncertainties.

This paper can be classed as: Sect. 2 includes the system structure and problem setup. Section 3 discusses the main results. The simulation results are presented in Sect. 4. Finally, Sect. 5 contains the conclusions.

Notations: ${\mathbb{R}}^{n}$: $n$ dimensional Euclidean space, ${\mathbb{R}}^{p\times n}$ the $p\times n$ real matrices, ${\mathbb{R}}^{+}$ stands for the sets of positive real numbers, ${\mathbb{N}}$ represents the sets of natural numbers, ${M}^{-1}$ and ${M}^{T}$ are the inverse and the transpose of the matrix $M$, respectively. $M>0(<0)$ matrix $M$ is positive(negative) definite, $sym\{M\}$ denotes $M+{M}^{T}$ and ${}^{*}$ denotes symmetric term in a matrix.

2 System structure and problem setup

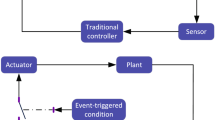
The proposed FPETFO-MRC based on EID technique for time-varying delay nonlinear systems subjected to unknown periodic and aperiodic disturbances is studied in this section. The structure of the overall system as shown in Fig. 1 consists of: the T-S fuzzy model with external disturbance, the MRC system, the FPETFO and the EID estimator.

Fig. 1

The structure of the proposed FPETFO-MRC based on EID technique for time-varying delay nonlinear systems

2.1 T-S fuzzy model

Consider a single–input–single–output nonlinear system with time-varying delay subjected to disturbance input. T-S fuzzy modeling approach can represent the time-varying delay nonlinear system using the sector nonlinearity concept into IF–THEN rules as $R$ fuzzy plant rules as following (Sakthivel et al. 2020):

Model Rule $i:$ IF $\theta_{1} \left( t \right)$ is $M_{1i} ,\theta_{2} \left( t \right)$ is $M_{2i} \left( t \right),...,$ and $\theta_{p} \left( t \right)$ is $M_{pi} \left( t \right)$ THEN

$$ \begin{gathered} \dot{x}( t ) = A_{i} x( t) + A_{di} x( {t - d( t )} ) + B_{i} u( t ) + B_{wi} w( t ), \hfill \\ y( t ) = C_{i} x( t ) + D_{\vartheta i} \vartheta ( t ), \hfill \\ x( t ) = \phi ( t ),t \in [ { - \tau ,0} ]. \hfill \\ \end{gathered} $$

(1)

where $x(t)\in {\mathbb{R}}^{n}$ is the system state vector, $y(t)\in {\mathbb{R}},u(t)\in {\mathbb{R}}$ are the system output and the control input, respectively, $w(t)\in {\mathbb{R}}^{q},\vartheta (t)\in {\mathbb{R}}^{q}$ are the external disturbance input and the noise of the output signal, respectively, $d(t)$ is the time-varying delay and satisfies the following conditions: $0\le d(t)\le \tau$ and $\dot{d}(t)\le \lambda ,$ where $\tau ,\lambda$ are positive constants. Moreover, $\phi (t)$ is the continuous initial state function on $[-\tau ,0]$. Furthermore, ${A}_{i}$ and ${A}_{di}\in {\mathbb{R}}^{n\times n}, {B}_{i}\in {\mathbb{R}}^{n\times 1}, {B}_{wi}\in {\mathbb{R}}^{n\times q}, {C}_{i}\in {\mathbb{R}}^{n},$ and ${D}_{\vartheta i}\in {\mathbb{R}}^{q}$ are known matrices. In addition, ${\theta }_{1}(t),{\theta }_{2}(t),...,{\theta }_{p}(t)$ are the premise variables which can be denoted as θ(t);${M}_{1i}(t),{M}_{2i}(t),...,{M}_{pi}(t)$ are the fuzzy sets which can be denoted as ${M}_{mi}(t)$, where $i=\mathrm{1,2},3,...,R$. The overall T-S fuzzy model (1) using the product inference, singleton fuzzifier and center average defuzzifier can be inferred as follow:

$$ \begin{gathered} \dot{x}\left( t \right) = \mathop \sum \limits_{i = 1}^{R} h_{i} \left( {\theta \left( t \right)} \right)\left[ {A_{i} x\left( t \right) + A_{di} x\left( {t - d\left( t \right)} \right) + B_{i} u\left( t \right) + B_{wi} w\left( t \right)} \right] \hfill \\ y\left( t \right) = \mathop \sum \limits_{i = 1}^{R} h_{i} \left( {\theta \left( t \right)} \right)\left[ {C_{i} x\left( t \right) + D_{\vartheta i} \vartheta \left( t \right)} \right] \hfill \\ \end{gathered} $$

(2)

where ${h}_{i}(\theta (t))=({\zeta }_{i}(\theta (t))/{\sum }_{i=1}^{R}{\zeta }_{i}(\theta (t))$ represents the fuzzy weighting function with ${\zeta }_{i}(\theta (t))={\prod }_{m=1}^{p}{M}_{mi}({\theta }_{m}(t));(m=\mathrm{1,2},...,p,i=\mathrm{1,2},...,R)$. And ${h}_{i}(\theta (t)$ satisfies the following conditions:$0\le {h}_{i}(\theta (t))\le 1$,${\sum }_{i=1}^{R}{h}_{i}(\theta (t))=1$, and ${\dot{h}}_{i}(\theta (t))\le {\Upsilon }_{i}$,$\forall t>0$, where ${\Upsilon }_{i}$ are positive scalers. Furthermore, ${M}_{mi}({\theta }_{m}(t))$ is the grade of the membership of ${\theta }_{m}(t)$ in ${M}_{mi}.$

2.2 MRC system

The MRC system is used for the periodic signal tracking and/or for the periodic disturbances rejection. In particular, the MRC block contains an LPF $l(s)$ before a time-delay ${e}^{-sT}$ in the positive feedback as shown in Fig. 2, where $T$ is the period of the desired reference signal ${x}_{r}(t)$. To make the MRC system easy in design and implementation, a first-order LPF is considered (Liu et al. 2014). Hence, $l(s)={w}_{a}/(s+{w}_{a})$, such that $l(s)$ satisfies, $|l(jw)|\approx 1 \forall w\in [0,{\overline{w} }_{a}]$ where ${w}_{a}$ and ${\overline{w} }_{a}$ are the LPF cutoff angular frequency and the highest angular frequency of the input signal of the RC, respectively. Hence, the state-space of the MRC can be described as:

$$ \begin{gathered} \dot{x}_{a} \left( t \right) = - w_{a} x_{a} \left( t \right) + w_{a} x_{a} \left( {t - T} \right) + w_{a} \varepsilon \left( t \right) \hfill \\ \upsilon \left( t \right) = x_{a} \left( {t - T} \right) + \varepsilon \left( t \right) \hfill \\ \end{gathered} $$

(3)

where ${x}_{a}(t)\in {\mathbb{R}}^{n}$ is the LPF state, $\upsilon (t)$ is the MRC system output and $\upvarepsilon (t)$ is the tracking error which is described as:

Fig. 2

The configuration of MRC system

$$\varepsilon (t)={x}_{r}(t)-y(t)$$

(4)

2.3 FSO

Since the system states are assumed to be unmeasurable, a FSO is introduced to estimate the states of the system. Based on the parallel distributed compoensation (PDC) scheme, the dynamics of the observer of system (2) can be obtained as follow:

Observer rule $i:$ IF ${\theta }_{1}(t)$ is ${M}_{1i},{\theta }_{2}(t)$ is ${M}_{2i}(t),...,$ and ${\theta }_{p}(t)$ is ${M}_{pi}(t)$ THEN

$$ \begin{gathered} \dot{\hat{x}}\left( t \right) = A_{i} \hat{x}\left( t \right) + A_{di} \hat{x}\left( {t - d\left( t \right)} \right) + B_{i} u_{f} \left( t \right) + L_{i} \left( {y\left( t \right) - \hat{y}\left( t \right)} \right), \hfill \\ \hat{y}\left( t \right) = C_{i} \hat{x}\left( t \right), \hfill \\ \hat{x}\left( t \right) = \hat{\phi }\left( t \right),t \in \left[ { - \tau ,0} \right] \hfill \\ \end{gathered} $$

(5)

where $\widehat{x}(t),\widehat{y}(t),{u}_{f}(t)$ and ${L}_{i}$ are the observer state vector, observer output, fuzzy feedback control input and observer gain of the $i$ th model, respectively.

The overall FSO can be inferred using the product inference, singleton fuzzifier and center average defuzzifier as following:

$$ \begin{gathered} \dot{\hat{x}}\left( t \right) = \mathop \sum \limits_{i = 1}^{R} h_{i} \left( {\theta \left( t \right)} \right)\left[ {A_{i} \hat{x}\left( t \right) + A_{di} \hat{x}\left( {t - d\left( t \right)} \right) + B_{i} u_{f} \left( t \right) + L_{i} \left( {y\left( t \right) - \hat{y}\left( t \right)} \right)} \right], \hfill \\ \hat{y}\left( t \right) = \mathop \sum \limits_{i = 1}^{R} h_{i} \left( {\theta \left( t \right)} \right)\left[ {C_{i} \hat{x}\left( t \right)} \right] \hfill \\ \end{gathered} $$

(6)

Remark 1

The designed FSO has a simple structure and less number of tuning parameters. The simplicity structure is due to the simplicity design procedure of the PDC structure which offers a procedure to design a fuzzy controller from a given T-S fuzzy model. In addition, it can be seen from Eq. (6) that, it is only one parameter $({ L}_{i})$ to be designed, which will be designed using the LMI approach in the main results section.

2.4 FPETFO-MRC

In this subsection, the PETM is firstly discussed then the FPETFO based on MRC is handled. From Fig. 2, there is an event detector to sample the observer states $\widehat{x}(t)$ with a constant period ${T}_{1}$ to observe the occurrence of an event. The event-triggering instants $({t}_{n})$ can be described by ${t}_{n}={i}_{n}{T}_{1}$, where ${t}_{n},{T}_{1}\in {\mathbb{N}}$ with ${i}_{0}=0$ and ${t}_{n}<{t}_{n+1}$. Furthermore, the periodic instants $({l}_{n,J})$ can be described by ${l}_{n,J}=({i}_{n}+J){T}_{1}$, $J=\mathrm{0,1},2,...,{d}_{n}$ with ${d}_{n}={i}_{n+1}-{i}_{n}-1$. Then $[{t}_{n},{t}_{n+1})={\bigcup }_{J=0}^{{d}_{n}}[{l}_{n,J},{l}_{n,J+1}).$ The observer error signal ${\upvarepsilon }_{o}(t)$ which is used to design the condition of ETM is defined (Ma et al. 2018a):

$${\upvarepsilon }_{\mathrm{o}}(t)=\widehat{x}({t}_{n})-\widehat{x}({l}_{n,J}) , t\in [{l}_{n,J},{l}_{n,J+1})$$

(7)

Based on ${\upvarepsilon }_{o}(t)$, the event-triggered fuzzy observer states condition is designed as:

$${\upvarepsilon }_{\mathrm{o}}^{T}(t){\psi }_{1}{\upvarepsilon }_{\mathrm{o}}(t)\le \sigma {\widehat{x}}^{T}({l}_{n,J}){\psi }_{2}\widehat{x}({l}_{n,J})$$

(8)

where ${\psi }_{1},{\psi }_{2}>0$ are symmetric positive definite matrices and $\sigma \in {\mathbb{R}}^{+}$ is an adjusting positive parameter. When the condition (8) is violated, an ‘event’ is triggered and the current signal is transmitted to the ZOH, at this instant $J=0$, so ${t}_{n}={l}_{n,J}$ and ${\upvarepsilon }_{\mathrm{o}}(t)$ is reset to zero according to (7); otherwise the ZOH keeps the last signal unchanged and the event detector continuous sampling the observer state$\widehat{x}(t)$. Furthermore, at the next periodic instant ${l}_{n,J+1}$ the condition (8) can be checked. Based on this ETM, ${i}_{n+1}$ is computed from:

$${i}_{n+1}=\underset{J\in {\mathbb{N}}}{\mathrm{min}}\{{l}_{n,J}|{\upvarepsilon }_{\mathrm{o}}^{T}(t){\psi }_{1}{\upvarepsilon }_{\mathrm{o}}(t)>\sigma {\widehat{x}}^{T}({l}_{n,J}){\psi }_{2}\widehat{x}({l}_{n,J})\}$$

(9)

Hence, the problem of Zeno behavior is canceled under the designed ETM. Define ${\tau }_{n}(t)=t-{l}_{n,J}$, $t\in [{l}_{n,J},{l}_{n,J+1})$, therefore, ${\tau }_{n}(t)$ is a time-varying delay satisfies ${\tau }_{n}(t)\in [0,{T}_{1})$ and ${\dot{\tau }}_{n}(t)=1$. Then $\widehat{x}({l}_{n,J})$ can be reformatted as $\widehat{x}(t-{\tau }_{n}(t))$. Moreover, from (7), $\widehat{x}({t}_{n})$ can be written as:

$$\widehat{x}({t}_{n})={\upvarepsilon }_{\mathrm{o}}(t)+\widehat{x}(t-{\tau }_{n}(t))$$

(10)

Based on PDC scheme, the system output $y(t)$ can track the reference signal ${x}_{r}(t)$ through the following fuzzy rule based on MRC (FPETFO-MRC law) which is constructed as:

Control rule $j:$ IF ${\theta }_{1}(t)$ is ${M}_{1j},{\theta }_{2}(t)$ is ${M}_{2j},...,$ and ${\theta }_{p}(t)$ is ${M}_{pj}$ THEN

$${u}_{f}(t)={k}_{cj}\upsilon (t)+{k}_{pj}\widehat{x}({t}_{n})$$

(11)

where ${M}_{1j}, {M}_{2j},\dots , {M}_{pj}$ are the control fuzzy sets, ${k}_{cj}$ and ${k}_{pj}$ are the designed fuzzy feedback controller gains, where $j=\mathrm{1,2},3,...,R$. Hence, the inferred output of the fuzzy controller can be defined as:

$${u}_{f}(t)=\sum_{j=1}^{R}{h}_{j}\left(\theta \left(t\right)\right)[{k}_{cj}\upsilon (t)+{k}_{pj}\widehat{x}({t}_{n})],$$

(12)

2.5 EID estimator

The incorporation of the EID estimator into the developed scheme can attenuate the aperiodic disturbance as well as the periodic one. As introduced in (Zhou et al. 2020), the expression of the EID estimation is as follow:

$$\widehat{w}(t)=\sum_{i=1}^{R}{h}_{i}\left(\theta \left(t\right)\right)[{B}_{i}^{+}{L}_{i}{C}_{i}(x(t)-\widehat{x}(t))+{u}_{f}(t)-u(t)]$$

(13)

where ${B}_{i}^{+}={B}_{i}^{T}/({B}_{i}^{T}{B}_{i})$. The output measurements noise may affect the estimated disturbance$\widehat{ w}(t)$. So an LPF $F(s)$ is used to filter the noise out of the estimate (Liu et al. 2014). To be easy for design and also for use, the LPF can be chosen as$F(s)={w}_{f}/(s+{w}_{f})$, such that $F(s)$ satisfies, $|F(jw)|\approx 1 \forall w\in [0,{\overline{w} }_{F}]$ where ${w}_{F}$ and ${\overline{w} }_{F}$ are the LPF cutoff angular frequency and the highest angular frequency of the input signal of the filter, respectively. The LPF state space can be written as:

$$ \begin{aligned} &\dot{x}_{f} \left( t \right) = A_{f} x_{f} \left( t \right) + B_{f} \hat{w}\left( t \right) \hfill \\& \tilde{w}\left( t \right) = C_{f} x_{f} \left( t \right) \hfill \\ \end{aligned} $$

(14)

where ${x}_{f}(t),\tilde{w }(t)$ are the state and the output of the filter, respectively. The state feedback control law and the output of the EID estimator can be combined to get the newest control law as:

$$u(t)={u}_{f}(t)-\tilde{w }(t)$$

(15)

The system (1) under the improved fuzzy feedback control law (15), EID-based MRC achieves the periodic signal tracking and the disturbance rejection effectively. Moreover, due to the PETM, the data are updated only at specified times and hence the communication resources are reduced.

Remark 2

MRC can track the periodic signal and/or reject the periodic disturbance only. But the EID-based MRC scheme has two degrees of freedom, it can improve the control performance for the periodic signal tracking and the periodic disturbance rejection and also it effectively compensates for the aperiodic disturbances.

3 Main results

In this section, the asymptotic stability of the closed-loop system is discussed. Some of sufficient conditions are derived based on the LKF stability theory and LMIs for the asymptotic stabilization of the T-S fuzzy system by using the proposed scheme. In order to ease the analysis, the modeling of the closed-loop system is first presented, and then, the stability analysis can be discussed through theorem 1.

3.1 Closed-loop system modeling

In the control design procedure, the external signals are set to zero for the sake of simplicity and due to the stability’s independency on exogenous signals. Therefore, let the external signals equal zero; ${x}_{r}(t)=w(t)=\vartheta (t)=0$, so (2) and (4) can be rewritten, respectively, as:

$$ \begin{aligned} &\dot{x}\left( t \right) = \mathop \sum \limits_{i = 1}^{R} h_{i} \left( {\theta \left( t \right)} \right)\left[ {A_{i} x\left( t \right) + A_{di} x\left( {t - d\left( t \right)} \right) + B_{i} u\left( t \right)} \right] \hfill \\& y\left( t \right) = \mathop \sum \limits_{i = 1}^{R} h_{i} \left( {\theta \left( t \right)} \right)\left[ {C_{i} x\left( t \right)} \right] \hfill \\ \end{aligned} $$

(16)

$$\upvarepsilon (t)=-\sum_{i=1}^{R}{h}_{i}\left(\theta \left(t\right)\right)[{C}_{i}x(t)]$$

(17)

Let the error between the plant state and the observer state be:

$${x}_{e}(t)=x(t)-\widehat{x}(t)$$

(18)

The closed-loop system can be represented using the following states: $x(t),{x}_{e}(t),{x}_{a}(t)$ and ${x}_{f}(t)$.

Substituting (12) and (14) into the control law (15) yields:

$$u(t)=\sum_{j=1}^{R}{h}_{j}\left(\theta \left(t\right)\right)[{k}_{cj}\upsilon (t)+{k}_{pj}\widehat{x}({t}_{n})-{C}_{f}{x}_{f}(t)]$$

(19)

Substituting (3),(4) and (10) into (19), one gets:

$$u(t)=\sum_{i=1}^{R}\sum_{j=1}^{R}{h}_{i}\left(\theta \left(t\right)\right){h}_{j}\left(\theta \left(t\right)\right)[{k}_{cj}{x}_{a}(t-T)-{k}_{cj}{C}_{i}x(t)+{k}_{pj}({\upvarepsilon }_{\mathrm{o}}(t)+\widehat{x}(t-{\tau }_{n}(t)))-{C}_{f}{x}_{f}(t)]$$

(20)

Applying (18) and (20) to (16) yields:

$$\dot{x}(t)=\sum_{i=1}^{R}\sum_{j=1}^{R}{h}_{i}(\theta (t)){h}_{j}(\theta (t))[({A}_{i}-{B}_{i}{k}_{cj}{C}_{i})x(t)+{A}_{di}x(t-d(t))+{B}_{i}{k}_{cj}{x}_{a}\left(t-T\right)+ {B}_{i}{k}_{pj}x(t-{\tau }_{n}(t))-{B}_{i}{k}_{pj}{x}_{e}(t-{\tau }_{n}(t))+{B}_{i}{k}_{pj}{\varepsilon }_{o}(t)-{B}_{i}{C}_{f}{x}_{f}(t)]$$

(21)

The time derivative of (18) will be

$${\dot{x}}_{e}(t)=\dot{x}(t)-\dot{\widehat{x}}\left(t\right)$$

(22)

Substituting (6) and (16) into (22) yields

$${\dot{x}}_{e}(t)=\sum_{i=1}^{R}\sum_{j=1}^{R}{h}_{i}(\theta (t)){h}_{j}(\theta (t))[({A}_{i}-{L}_{i}{C}_{i}){x}_{e}(t)+{A}_{di}{x}_{e}(t-d(t))-{B}_{i}{C}_{f}{x}_{f}(t)]$$

(23)

From (3) and (17), the MRC can be rewritten as:

$${\dot{x}}_{a}(t)=\sum_{i=1}^{R}{h}_{i}(\theta (t))[-{w}_{a}{x}_{a}(t)+{w}_{a}{x}_{a}(t-T)-{w}_{a}{C}_{i}x(t)$$

(24)

Then by substituting (13) and (15) into (14), one obtains:

$${\dot{x}}_{f}(t)=\sum_{i=1}^{R}{h}_{i}(\theta (t))[({A}_{f}+{B}_{f}{C}_{f}){x}_{f}(t)+{B}_{f}{B}_{i}^{+}{L}_{i}{C}_{i}{x}_{e}(t)]$$

(25)

So, the closed-loop system in Fig. 1 is described by Eqs. (21), (23), (24) and (25).

3.2 Stability analysis

The closed-loop system stability is studied using LKF stability theory, where the following assumptions are considered as:

Assumption 1

The system (1) is considered to be observable, controllable and the imaginary axis has no zeros to achieve the asymptotic stability and perfect performance tracking.

Assumption 2

(Zhou et al. 2020) Assume that the matrix ${B}_{i}\in {\mathbb{R}}^{n\times m}$ with rank $({B}_{i})=m$. Hence, the matrix ${B}_{i}$ has a singular value decomposition (SVD) is defined as:

$${B}_{i}=U\left[\begin{array}{l}\Delta \\ 0\end{array}\right]{V}^{T},$$

(26)

where $U\in {\mathbb{R}}^{n\times n}$ and $V\in {\mathbb{R}}^{m\times m}$ are unitary matrices, $\Delta \in {\mathbb{R}}^{m\times m}$ is a diagonal matrix and $0\in {\mathbb{R}}^{(n-m)\times m}$ is a zero matrix.

Lemma 1

(Ho and Lu 2003) For a symmetric matrix $X\in {\mathbb{R}}^{n\times n}$ and the SVD (26), there exists a matrix $\overline{X}\in {\mathbb{R} }^{m\times m}$ where $X{B}_{i}={B}_{i}\overline{X }$ holds if and only if.

$$X=Udiag\left\{{X}_{11},{X}_{22}\right\}{U}^{T},$$

(27)

where ${X}_{11}\in {\mathbb{R}}^{n\times m},{X}_{22}\in {\mathbb{R}}^{(n-m)\times (n-m)}$.

Lemma 2

(Protter and Morrey 1985) For a function $F\left(t\right)={\int }_{{\alpha }_{1}}^{{\alpha }_{2}}f(s,t)ds$, if ${\alpha }_{1}$ and ${\alpha }_{2}$ are differentiable for $t$ and $f(s,t)$ is continuous for $\mathrm{s}$ and partially derivation for $t$, then.

$$\frac{dF\left(t\right)}{dt}={\dot{\alpha }}_{2}f\left({\alpha }_{2},t\right)-{\dot{\alpha }}_{1}f\left({\alpha }_{1},t\right)+{\int }_{{\alpha }_{1}}^{{\alpha }_{2}} \frac{\partial f\left(s,t\right)}{\partial t} ds$$

The following theorem establishes the overall system stability condition in terms of LMIs.

Theorem 1

Given positive constant parameters $\alpha ,\beta ,\gamma ,T,{T}_{1},{w}_{a},{w}_{f}$ and $\sigma$, if there are positive definite matrices ${\rho }_{1},{\rho }_{2},{\rho }_{3},{\rho }_{4},{\eta }_{1},{\eta }_{2},\omega ,\mu ,\Lambda ,{\psi }_{1},{\psi }_{2},{\xi }_{1},{\xi }_{2},{\xi }_{3}$ and arbitrary matrices ${\widehat{O}}_{1},{\widehat{O}}_{2},{\widehat{O}}_{3},{\mathcal{Z}}_{1i},{\mathcal{Z}}_{2j},{\mathcal{Z}}_{3j},{\mathcal{Z}}_{4i}$ of appropriate dimensions, such that the following LMIs hold:

$$\begin{aligned} &{\Omega }_{1}=\left[\begin{array}{lll}{\xi }_{3}& {\widehat{O}}_{3}& 0\\ *& \beta {e}^{-\beta {T}_{1}}{\eta }_{2}& 0\\ *& *& \gamma {e}^{-\gamma {T}_{1}}\mu \end{array}\right]\ge 0,\\& { \Omega }_{2}=\left[\begin{array}{ll}{\Omega }_{2.1}& {\Omega }_{2.2}\\ *& {\Omega }_{2.3}\end{array}\right]\ge 0 \end{aligned} $$

(28)

${\rm {where}}\, {\Omega }_{2.1}= diag \{{\xi }_{1},{\xi }_{2}\}, {\Omega }_{2.2}= diag \{{\widehat{O}}_{1},\, {\widehat{O}}_{2}\}, {\Omega}_{2.3}= diag \{\alpha {e}^{-\alpha {T}_{1}}{\eta }_{1},0\}$

$$\Psi =\left[\begin{array}{ll}{\Psi }_{1}& {\Psi }_{2}\\ *& {\Psi }_{3}\end{array}\right]<0$$

(29)

where ${\Psi }_{1}=\left[\begin{array}{ll}{\Psi }_{1.1}& {\Psi }_{1.2}\\ *& {\Psi }_{1.3}\end{array}\right]{,\Psi }_{2}=\left[\begin{array}{ll}{\Psi }_{2.1}& {\Psi }_{2.2}\\ 0& {\Psi }_{2.3}\end{array}\right]$,${\Psi }_{3}=\left[\begin{array}{ll}{\Psi }_{3.1}& {\Psi }_{3.2}\\ *& {\Psi }_{3.3}\end{array}\right]$

$$ \Psi_{1.1} = \left[ {\begin{array}{*{20}l} {{\text{sym}}\left\{ {\rho_{1} A_{i} - B_{i} {\mathcal{Z}}_{2j} C_{i} } \right\}} \hfill & {{ }0} \hfill & { - \omega_{a} \rho_{3} C_{i} } \hfill \\ { *} \hfill & {{\text{sym}}\left\{ {\rho_{2} A_{i} - {\mathcal{Z}}_{1i} C_{i} } \right\}} \hfill & {{ }0} \hfill \\ { *} \hfill & { *} \hfill & { - 2\omega_{a} \rho_{3} + \Lambda } \hfill \\ \end{array} } \right] $$

$$ \Psi_{1.2} = \left[ {\begin{array}{*{20}l} { - \rho_{1} B_{i} C_{f} } \hfill & {B_{i} {\mathcal{Z}}_{3j} + \hat{O}_{1}^{T} } \hfill & { - B_{i} {\mathcal{Z}}_{3j} } \hfill \\ { - \rho_{2} B_{i} C_{f} + B_{f} B_{i}^{ + } {\mathcal{Z}}_{4i} C_{i} } \hfill & {{ }0} \hfill & {\hat{O}_{2}^{T} } \hfill \\ {{ }0} \hfill & {{ }0} \hfill & 0 \hfill \\ \end{array} } \right] $$

$$ \Psi_{1.3} = \left[ {{ }\begin{array}{*{20}l} {{\text{sym}}\left\{ {\rho_{4} A_{f} + \rho_{4} B_{f} C_{f} } \right\}} \hfill & {{ }0} \hfill & {{ }0} \hfill \\ { *} \hfill & { - {\text{sym}}\left\{ {\hat{O}_{1} } \right\} + T_{1} \xi_{1} + \sigma \psi_{2} } \hfill & {{ }0} \hfill \\ { *} \hfill & { *} \hfill & { - {\text{sym}}\left\{ {\hat{O}_{2} } \right\} + T_{1} \xi_{2} + \sigma \psi_{2} } \hfill \\ \end{array} } \right] $$

$$ \Psi_{2.1} = \left[ {\begin{array}{*{20}l} { - \rho_{2} A_{di} + \hat{O}_{3}^{T} } \hfill & {B_{i} {\mathcal{Z}}_{2j} } \hfill & {B_{i} {\mathcal{Z}}_{3j} } \hfill \\ { \rho_{2} A_{di} } \hfill & 0 \hfill & { 0} \hfill \\ { 0} \hfill & {\omega_{a} \rho_{3} } \hfill & { 0} \hfill \\ \end{array} } \right], \Psi_{2.2} = \left[ {\begin{array}{*{20}c} {\rho_{1} A_{i} - B_{i} {\mathcal{Z}}_{2j} C_{i} } & 0 & {\begin{array}{*{20}c} 0 & 0 \\ \end{array} } \\ 0 & {\rho_{2} A_{i} - {\mathcal{Z}}_{1i} C_{i} } & {\begin{array}{*{20}c} 0 & 0 \\ \end{array} } \\ 0 & 0 & {\begin{array}{*{20}c} 0 & 0 \\ \end{array} } \\ \end{array} } \right] $$

$$ \Psi _{{2.3}} = \left[ {\begin{array}{*{20}l} { - \rho _{1} B_{i} C_{f} } \hfill & { - \rho _{2} B_{i} C_{f} } \hfill & 0 \hfill & 0 \hfill \\ {B_{i} {\mathcal{Z}}_{{3j}} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ { - B_{i} {\mathcal{Z}}_{{2j}} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right] $$

$$ \Psi _{{3.1}} = \left[ {\begin{array}{*{20}l} { - sym\left\{ {\widehat{O}_{3} } \right\} + \tau \xi _{3} } \hfill & 0 \hfill & 0 \hfill \\ * \hfill & { - \wedge } \hfill & {0} \hfill \\ * \hfill & * \hfill & { - \psi _{1} } \hfill \\ \end{array} } \right] $$

$$ \Psi_{3.2} = \left[ {\begin{array}{*{20}c} {\rho_{1} A_{di} } & {\rho_{2} A_{di} } & {\begin{array}{*{20}c} 0 & 0 \\ \end{array} } \\ {B_{i} {\mathcal{Z}}_{2j} } & 0 & {\begin{array}{*{20}c} 0 & 0 \\ \end{array} } \\ {B_{i} {\mathcal{Z}}_{3j} } & 0 & {\begin{array}{*{20}c} 0 & 0 \\ \end{array} } \\ \end{array} } \right] $$

$$\Psi_{3.3} = \left[\matrix{ - {\text{sym}}\left\{ {\rho_{1} } \right\} + \xi_{1} + \xi_{2}&0&0&0\\ *& - {\text{sym}}\left\{ {\rho_{2} } \right\} + \mu &0&0\\ *&*&- \eta_{2} \left( {1 - \lambda } \right)e^{ - \beta \tau }&0\\ *&*&*&- \mu \left( {1 - \lambda } \right)e^{ - \gamma \tau }}\right]$$

Hence, the augmented system is asymptotically stable. Furthermore, if the previous LMIs are solvable, then the observer and the controller parameters can be obtained using the following equations:

$${L}_{i}={\rho }_{2}^{-1}{\mathcal{Z}}_{1i}$$

(30)

$${k}_{pj}={\overline{\rho }}_{1}^{-1}{\mathcal{Z}}_{3j}$$

(31)

$${k}_{cj}={\overline{\rho }}_{1}^{-1}{\mathcal{Z}}_{2j}$$

(32)

where the observer gain ${L}_{i}$ and the feedback controller gains ${k}_{pj}$ and ${k}_{cj}$ are obtained from the following proof.

Proof

By choosing an LKF candidate as follow:

$$V(t)=\sum_{i=1}^{4}{V}_{i}(t)$$

(33)

where

$$ V_{1} \left( t \right) = x^{T} \left( t \right)\rho_{1} x\left( t \right) + \mathop \int \limits_{{t - \tau_{n} \left( t \right)}}^{t} e^{{\alpha \left( {s - t} \right)}} \dot{x}^{T} \left( s \right)\eta_{1} \dot{x}\left( s \right)ds + \mathop \int \limits_{t - d\left( t \right)}^{t} e^{{\beta \left( {s - t} \right)}} \dot{x}^{T} \left( s \right)\eta_{2} \dot{x}\left( s \right)ds, $$

(34)

$$ V_{2} \left( t \right) = x_{e}^{T} \left( t \right)\rho_{2} x_{e} \left( t \right) + \mathop \int \limits_{t - d\left( t \right)}^{t} e^{{\gamma \left( {s - t} \right)}} \dot{x}_{e}^{T} \left( s \right)\mu \dot{x}_{e} \left( s \right)ds, $$

(35)

$$ V_{3} \left( t \right) = x_{a}^{T} \left( t \right)\rho_{3} x_{a} \left( t \right) + \mathop \int \limits_{t - T}^{t} x_{a}^{T} \left( s \right){\Lambda }x_{a} \left( s \right)ds, $$

(36)

$$ V_{4} \left( t \right) = x_{f}^{T} \left( t \right)\rho_{4} x_{f} \left( t \right) $$

(37)

Then, along the trajectory of the closed-loop system, taking the time derivative of $V(t)$ with considering lemma 2, we have:

$$\dot{V}(t)=\sum_{i=1}^{4}{\dot{V}}_{i}(t)$$

(38)

$${\dot{V}}_{1}\left(t\right)\le \sum_{i=1}^{R}\sum_{j=1}^{R}{h}_{i}\left(\theta \left(t\right)\right){h}_{j}\left(\theta \left(t\right)\right)\left[2{x}^{T}\left(t\right)\left({\rho }_{1}{A}_{i}-{\rho }_{1}{B}_{i}{k}_{cj}{C}_{i}\right)x\left(t\right)+2{x}^{T}\left(t\right){\rho }_{1}{A}_{di}x\left(t-d\left(t\right)\right)+2{x}^{T}\left(t\right){\rho }_{1}{B}_{i}{k}_{pj}x\left(t-{\tau }_{n}\left(t\right)\right)-2{x}^{T}\left(t\right){\rho }_{1}{B}_{i}{k}_{pj}{x}_{e}\left(t-{\tau }_{n}\left(t\right)\right)+2{x}^{T}\left(t\right){\rho }_{1}{B}_{i}{k}_{cj}{x}_{a}\left(t-T\right)+2{x}^{T}\left(t\right){\rho }_{1}{B}_{i}{k}_{pj}{\varepsilon }_{o}\left(t\right)-2{x}^{T}\left(t\right){\rho }_{1}{B}_{i}{C}_{f}{x}_{f}\left(t\right)+{\dot{x}}^{T}\left(t\right)\left({\eta }_{1}+{\eta }_{2}\right)\dot{x}\left(t\right)-(1-\lambda ){e}^{-\beta \tau }{\dot{x}}^{T}\left(t-d\left(t\right)\right){\eta }_{2}\dot{x}\left(t-d\left(t\right)\right)\right]- \alpha {\int }_{t-{\tau }_{n}(t)}^{t}{e}^{\alpha (s-t)}{\dot{x}}^{T}(s){\eta }_{1}\dot{x}(s)ds-\beta {\int }_{t-d(t)}^{t}{e}^{\beta (s-t)}{\dot{x}}^{T}(s){\eta }_{2}\dot{x}(s)ds,$$

(39)

where

$${\dot{V}}_{2}\left(t\right)\le \sum_{i=1}^{R}\sum_{j=1}^{R}{h}_{i}\left(\theta \left(t\right)\right){h}_{j}\left(\theta \left(t\right)\right)\left[2{x}_{e}^{T}\left(t\right)\left({\rho }_{2}{A}_{i}-{\rho }_{2}{L}_{i}{C}_{i}\right){x}_{e}\left(t\right)+2{x}_{e}^{T}\left(t\right){\rho }_{2}{A}_{di}{x}_{e}\left(t-d\left(t\right)\right)-2{x}_{e}^{T}\left(t\right){\rho }_{2}{B}_{i}{C}_{f}{x}_{f}\left(t\right)+ {\dot{x}}_{e}^{T}(t)\mu {\dot{x}}_{e}(t)-(1-\lambda ){e}^{-\gamma \tau }{{\dot{x}}_{e}}^{T}\left(t-d\left(t\right)\right)\mu {\dot{x}}_{e}\left(t-d\left(t\right)\right)\right] -\gamma {\int }_{t-d(t)}^{t}{e}^{\gamma (s-t)}{\dot{x}}_{e}^{T}(s)\mu {\dot{x}}_{e}(s)ds,$$

(40)

$${\dot{V}}_{3}\left(t\right)=\sum_{i=1}^{R}{h}_{i}\left(\theta \left(t\right)\right)\left[{x}_{a}^{T}(t)(-2{\omega }_{a}{\rho }_{3}+\Lambda ){x}_{a}(t)-2{\omega }_{a}{x}_{a}^{T}(t){\rho }_{3}{C}_{i}x(t)+2{\omega }_{a}{x}_{a}^{T}(t){\rho }_{3}{x}_{a}(t-T)-{x}_{a}^{T}(t-T)\Lambda {x}_{a}(t-T)\right] ,$$

(41)

$${\dot{V}}_{4}\left(t\right)=\sum_{i=1}^{R}{h}_{i}\left(\theta \left(t\right)\right)\left[2{x}_{f}^{T}(t)({\rho }_{4}{A}_{f}+{\rho }_{4}{B}_{f}{C}_{f}){x}_{f}(t)+2{x}_{f}^{T}(t){\rho }_{4}{B}_{f}{B}_{i}^{+}{L}_{i}{C}_{i}{x}_{e}(t)\right].$$

(42)

From Newton-Leibniz formula:

$$x(t)-x(t-{\tau }_{n}(t))-{\int }_{t-{\tau }_{n}(t)}^{t}\dot{x}(s)ds=0$$

(43)

Therefore, the following equalities are obtained

$$\begin{array}{l}2{x}^{T}(t-{\tau }_{n}(t)){\widehat{O}}_{1}[x(t)-x(t-{\tau }_{n}\left(t\right))-{\int }_{t-{\tau }_{n}(t)}^{t}\dot{x}(s)ds]=0,\\ 2{x}_{e}^{T}(t-{\tau }_{n}(t)){\widehat{O}}_{2}[{x}_{e}(t)-{x}_{e}(t-{\tau }_{n}\left(t\right))-{\int }_{t-{\tau }_{n}(t)}^{t}{\dot{x}}_{e}(s)ds]=0,\\ 2{x}^{T}(t-d(t)){\widehat{O}}_{3}[x(t)-x(t-d\left(t\right))-{\int }_{t-d(t)}^{t}\dot{x}(s)ds]=0,\end{array}$$

(44)

Also, from (21) and (23) we have:

$$\begin{aligned} &2{\dot{x}}^{T}(t){\rho }_{1}\sum_{i=1}^{R}\sum_{j=1}^{R}{h}_{i}\left(\theta \left(t\right)\right){h}_{j}\left(\theta \left(t\right)\right)[({A}_{i}-{B}_{i}{k}_{cj}{C}_{i})x(t)\\& \quad +{A}_{di}x(t-d(t))+{B}_{i}{k}_{cj}{x}_{a}(t-T)+{B}_{i}{k}_{pj}x(t-{\tau }_{n}(t))\\& \quad-{ B}_{i}{k}_{pj}{x}_{e}(t-{\tau }_{n}(t))+{B}_{i}{k}_{pj}{\varepsilon }_{o}(t)-{B}_{i}{C}_{f}{x}_{f}(t)-\dot{x}(t)]=0, \end{aligned} $$

(45)

$$\begin{aligned} & 2{\dot{x}}_{e}^{T}(t){\rho }_{2}\sum_{i=1}^{R}\sum_{j=1}^{R}{h}_{i}\left(\theta \left(t\right)\right){h}_{j}\left(\theta \left(t\right)\right)[({A}_{i}-{L}_{i}{C}_{i}){x}_{e}(t)\\& \quad+{A}_{di}{x}_{e}(t-d(t))-{B}_{i}{C}_{f}{x}_{f}(t)-{\dot{x}}_{e}(t)]=0. \end{aligned} $$

Furthermore,

$$\begin{array}{l}{\tau }_{n}\left(t\right){x}^{T}\left(t-{\tau }_{n}\left(t\right)\right){\xi }_{1}x\left(t-{\tau }_{n}\left(t\right)\right)-{\int }_{t-{\tau }_{n}\left(t\right)}^{t}{x}^{T}\left(t-{\tau }_{n}\left(t\right)\right){\xi }_{1}x\left(t-{\tau }_{n}\left(t\right)\right)ds=0,\\ {\tau }_{n}(t){x}_{e}^{T}(t-{\tau }_{n}(t)){\xi }_{2}{x}_{e}(t-{\tau }_{n}(t))-{\int }_{t-{\tau }_{n}(t)}^{t}{x}_{e}^{T}(t-{\tau }_{n}(t)){\xi }_{2}{x}_{e}(t-{\tau }_{n}(t))ds=0,\\ d(t){x}^{T}(t-d(t)){\xi }_{3}x(t-d(t))-{\int }_{t-d(t)}^{t}{x}^{T}(t-d(t){\xi }_{3}x(t-d(t))ds=0,\end{array}$$

(46)

Also, the event-triggering condition (8) can be written, respectively, as:

$$ \begin{gathered} - {\upvarepsilon }_{o}^{T} \left( t \right)\psi_{1} {\upvarepsilon }_{o} \left( t \right) + \sigma x^{T} \left( {t - \tau_{n} \left( t \right)} \right)\psi_{2} x\left( {t - \tau_{n} \left( t \right)} \right) + \sigma x_{e}^{T} \left( {t - \tau_{n} \left( t \right)} \right)\psi_{2} x_{e} \left( {t - \tau_{n} \left( t \right)} \right) - \hfill \\ 2\sigma x^{T} \left( {t - \tau_{n} \left( t \right)} \right)\psi_{2} x_{e} \left( {t - \tau_{n} \left( t \right)} \right) \ge 0 \hfill \\ \end{gathered} $$

(47)

Adding (39), (40), (41), (42), (44), (45), (46) and (47), the derivative of $V(t)$ can be obtained as

$$\begin{aligned} \dot{V}(t) &\le \sum_{i=1}^{R}\sum_{j=1}^{R}{h}_{i}\left(\theta \left(t\right)\right){h}_{j}\left(\theta \left(t\right)\right)[{\Pi }^{T}(t)\tilde{\Psi}\Pi (t)]\\& \quad-{\int }_{t-d(t)}^{t}{{\lambda }_{1}}^{T}(t,s){\Omega }_{1}{\lambda }_{1}(t,s)ds\\& \quad-{\int }_{t-{\tau }_{n}(t)}^{t}{{\lambda }_{2}}^{T}(t,s){\Omega }_{2}{\lambda }_{2}(t,s)ds,\end{aligned} $$

(48)

where

$${\Pi }^{T}(t)=[{x}^{T}\left(t\right),{x}_{e}^{T}\left(t\right),{x}_{a}^{T}\left(t\right),{x}_{f}^{T}\left(t\right),{x}^{T}\left(t-{\tau }_{n}\left(t\right)\right),{x}_{e}^{T}\left(t-{\tau }_{n}\left(t\right)\right),{x}^{T}\left(t-d\left(t\right)\right),{x}_{a}^{T}(\mathrm{t}-\mathrm{ T}),{\varepsilon }_{o}^{T}\left(t\right),{\dot{x}}^{T}\left(t\right),{{\dot{x}}_{e}}^{T}\left(t\right),{\dot{x}}^{T}(t-d\left(t\right)),{{\dot{x}}_{e}}^{T}(t-d\left(t\right))],$$

$${{\lambda }_{1}}^{T}(t,s)=[{x}^{T}(t-d(t)),{\dot{x}}^{T}(s),{{\dot{x}}_{e}}^{T}(s)],{{\lambda }_{2}}^{T}(t,s)=[{x}^{T}(t-{\tau }_{n}(t)),{x}_{e}^{T}(t-{ \tau }_{n}(t)),{\dot{x}}^{T}(s),{\dot{x}}_{e}^{T}(s)].$$

We can obtain $\tilde{\Psi}$ as follow:

$$\tilde{\Psi}=\left[\begin{array}{ll}{\tilde{\Psi}}_{1}& {\tilde{\Psi}}_{2}\\ *& {\tilde{\Psi}}_{3}\end{array}\right]<0$$

(49)

where

$$\tilde{\Psi}_{1}=\left[\begin{array}{ll}\tilde{\Psi}_{1.1} \;\;\tilde{\Psi}_{1.2}\\ *\; \quad\,\;\tilde{\Psi}_{1.3}\end{array}\right],\tilde{\Psi }_{2}=\left[\begin{array}{ll}\tilde{\Psi}_{2.1} \;\;\tilde{\Psi}_{2.2}\\ 0\; \;\quad\,\tilde{\Psi}_{2.3}\end{array}\right],\tilde{\Psi}_{3}=\left[\begin{array}{ll}\tilde{\Psi}_{3.1} \;\;\tilde{\Psi}_{3.2}\\ * \;\;\quad\,\tilde{\Psi}_{3.3}\end{array}\right]$$

$${\tilde{\Psi}}_{1.1}=\left[\begin{array}{lll}\mathrm{sym}\{{\rho }_{1}{A}_{i}-{\rho }_{1}{B}_{i}{k}_{cj}{C}_{i}\}& 0& -{\omega }_{a}{\rho }_{3}{C}_{i}\\ *& \mathrm{sym}\{{\rho }_{2}{A}_{i}-{\rho }_{2}{L}_{i}{C}_{i}\}& 0\\ *& *& -2{\omega }_{a}{\rho }_{3}+\Lambda \end{array}\right]$$

$${\tilde{\Psi}}_{1.2}=\left[\begin{array}{lll}-{\uprho }_{1}{\mathrm{B}}_{\mathrm{i}}{\mathrm{C}}_{\mathrm{f}}& {\uprho }_{1}{\mathrm{B}}_{\mathrm{i}}{\mathrm{k}}_{\mathrm{pj}}+{{\widehat{\mathrm{O}}}_{1}}^{\mathrm{T}}& -{\uprho }_{1}{\mathrm{B}}_{\mathrm{i}}{\mathrm{k}}_{\mathrm{pj}}\\ -{\uprho }_{2}{\mathrm{B}}_{\mathrm{i}}{\mathrm{C}}_{\mathrm{f}}+{\uprho }_{4}{\mathrm{B}}_{\mathrm{f}}{\mathrm{B}}_{\mathrm{i}}^{+}{\mathrm{L}}_{\mathrm{i}}{\mathrm{C}}_{\mathrm{i}}& 0& {{ \widehat{\mathrm{O}}}_{2}}^{\mathrm{T}}\\ 0& 0& 0\end{array}\right]$$

$${\tilde{\Psi}}_{1.3}=\left[ \begin{array}{lll}\mathrm{sym}\{{\uprho }_{4}{\mathrm{A}}_{\mathrm{f}}+{\uprho }_{4}{\mathrm{B}}_{\mathrm{f}}{\mathrm{C}}_{\mathrm{f}}\}& 0& 0\\ *& -\mathrm{sym}\{{\widehat{\mathrm{O}}}_{1}\}+{\mathrm{T}}_{1}{\upxi }_{1}+\upsigma {\uppsi }_{2}& 0\\ *& *& -\mathrm{sym}\{{\widehat{\mathrm{O}}}_{2}\}+{\mathrm{T}}_{1}{\upxi }_{2}+\upsigma {\uppsi }_{2}\end{array}\right]$$

$${\tilde{\Psi}}_{2.1}=\left[\begin{array}{lll}-{\rho }_{2}{A}_{di}+{{\widehat{O}}_{3}}^{T}& {\rho }_{1}{B}_{i}{k}_{cj}& {\rho }_{1}{B}_{i}{k}_{pj}\\ { \rho }_{2}{A}_{di}& 0& 0\\ 0& {\omega }_{a}{\rho }_{3}& 0\end{array}\right], {\tilde{\Psi}}_{2.2}=\left[\begin{array}{ccc}{\rho }_{1}{A}_{i}-{\rho }_{1}{B}_{i}{k}_{cj}{C}_{i}& 0& \begin{array}{cc}0& 0\end{array}\\ 0& {\rho }_{2}{A}_{i}-{\rho }_{2}{L}_{i}{C}_{i}& \begin{array}{cc}0& 0\end{array}\\ 0& 0& \begin{array}{cc}0& 0\end{array}\end{array}\right],{\tilde{\Psi}}_{2.3}=\left[\begin{array}{ccc}-{\rho }_{1}{B}_{i}{C}_{f}& -{\rho }_{2}{B}_{i}{C}_{f}& \begin{array}{cc}0& 0\end{array}\\ {\rho }_{1}{B}_{i}{K}_{pj}& 0& \begin{array}{cc}0& 0\end{array}\\ -{\rho }_{1}{B}_{i}{k}_{cj}& 0& \begin{array}{cc}0& 0\end{array}\end{array}\right],{\tilde{\Psi}}_{3.1}=\left[\begin{array}{lll}-sym\{{\widehat{O}}_{3}\}+\tau {\xi }_{3}& 0& 0\\ *& -\Lambda & 0\\ *& *& -{\psi }_{1}\end{array}\right]$$

$$ \tilde{\Psi} _{{3.2}} = \left[ {\begin{array}{*{20}l} {\rho _{1} A_{{di}} } \hfill & {\rho _{2} A_{{di}} } \hfill & 0 \hfill & 0 \hfill \\ {\rho _{1} B_{i} k_{{cj}} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ {\rho _{1} B_{i} k_{{pj}} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right],\;\tilde{\Psi}_{{3.3}} = \left[ {\begin{array}{*{20}l} { - sym\left\{ {\rho _{1} } \right\} + \xi _{1} + \xi _{2} } \hfill & \quad\quad0 \hfill & \quad\quad0 \hfill & \quad\quad0 \hfill \\ \quad\quad* \hfill & { - sym\left\{ {\rho _{2} } \right\} + \mu } \hfill & \quad\quad0 \hfill & \quad\quad0 \hfill \\ \quad\quad* \hfill & \quad\quad* \hfill & { - \eta _{2} (1 - \lambda )e^{{ - \beta t}} } \hfill & \quad\quad0 \hfill \\ \quad\quad * \hfill & \quad\quad* \hfill & \quad\quad* \hfill & { - \mu (1 - \lambda )e^{{ - \gamma t}} } \hfill \\ \end{array} } \right] $$

Therefore, if $\tilde{\Psi}<0,\mathrm{and }\,{\Omega }_{1},{\Omega }_{2}>0,$ then $\dot{V}(t)<0$, i.e., the closed-loop system is asymptotically stable. Then, the controller and the observer parameters can be obtained as follows:

Let ${\rho }_{2}{L}_{i}={\mathcal{Z}}_{1i}$ into matrix $\tilde{\Psi}$. After that by using lemma 1 and assumption 2, there is a matrix ${\overline{\rho }}_{1}$ satisfies:

$${\rho }_{1}{B}_{i}={B}_{i}{\overline{\rho }}_{1}$$

(50)

Also there is a matrix ${\overline{\rho }}_{4}$ satisfies:

$${\rho }_{4}{B}_{i}={B}_{i}{\overline{\rho }}_{4}$$

(51)

Assume ${\rho }_{1}=U$ diag $\{{\rho }_{11},{\rho }_{22}\}{U}^{T}$, then we have ${\overline{\rho }}_{1}=V{\Delta }^{-1}{\rho }_{11}\Delta {V}^{T}$ and assume ${\rho }_{4}=U$ diag $\{{\rho }_{41},{\rho }_{44}\}{U}^{T}$, then we have ${\overline{\rho }}_{4}=V{\Delta }^{-1}{\rho }_{41}\Delta {V}^{T}.$ Then substituting ${\mathcal{Z}}_{2j}={\overline{\rho }}_{1}{k}_{cj},$ ${\mathcal{Z}}_{3j}={\overline{\rho }}_{1}{k}_{pj}$ and ${\mathcal{Z}}_{4i}={\overline{\rho }}_{4}{L}_{i}$ into matrix $\tilde{\Psi}$, we can obtain (29). This completes the proof. Then ${L}_{i},{k}_{pj}$ and ${k}_{cj}$ are obtained as (30), (31) and (32), respectively. The design procedures are ordered in the following steps:

Step 1: Determine the period $T$ of the time delay ${e}^{-sT}$ using the period of the reference input. Also, determine the cutoff angular frequency ${w}_{a}$ of the LPF $l(s)$ such that $l(s)$ satisfies, $|l(jw)|\approx 1 \forall w\in [0,{\overline{w} }_{a}]$.

Step 2: Choose ${A}_{F},{B}_{F},$ and ${C}_{F}$ for the low-pass filter $F(s)$ so that $F(s)$ satisfies, $|F(jw)|\approx 1 \forall w\in [0,{\overline{w} }_{F}]$.

Step 3: Choose the sample time $({T}_{1})$ of PETM and the adjusting positive parameter $\sigma$.

Step 4: Determine the fuzzy rules for T-S fuzzy model and control. Then, the appropriate membership functions can be obtained.

Step 5: Calculate the SVD of ${B}_{i}$.

Step 6: For chosen positive constants $\alpha ,\beta$ and $\gamma$, find a feasible solution of LMI (29) using Matlab toolbox.

Step 7: Hence, the observer and controller gains ${L}_{i},{k}_{pj}$ and ${k}_{cj}$ can be obtained as (30), (31) and (32), respectively.

4 Simulation results

This section presents the verification of the proposed FPETFO-MRC based on EID scheme for T-S fuzzy systems through the following simulation example. Consider the following modified truck-trailer model with time-varying delay as provided in (Wu and Li 2007; Sakthivel et al. 2020):

$$ \begin{gathered} \dot{x}_{1} \left( t \right) = - b\frac{{\nu \overline{t}}}{{Lt_{0} }}x_{1} \left( t \right) - \left( {1 - b} \right)\frac{{\nu \overline{t}}}{{Lt_{0} }}x_{1} \left( {t - d\left( t \right)} \right) + \frac{{\nu \overline{t}}}{{lt_{0} }}u\left( t \right) + \frac{{\nu \overline{t}}}{{Lt_{0} }}w\left( t \right) \hfill \\ \dot{x}_{2} \left( t \right) = b\frac{{\nu \overline{t}}}{{Lt_{0} }}x_{1} \left( t \right) + \left( {1 - b} \right)\frac{{\nu \overline{t}}}{{Lt_{0} }}x_{1} \left( {t - d\left( t \right)} \right) \hfill \\ \dot{x}_{3} \left( t \right) = \frac{{\nu \overline{t}}}{{t_{0} }}sin\left( {x_{2} \left( t \right) + b\frac{{\nu \overline{t}}}{2L}x_{1} \left( t \right) + \left( {1 - b} \right)\frac{{\nu \overline{t}}}{2L}x_{1} \left( {t - d\left( t \right)} \right)} \right) \hfill \\ y\left( t \right) = \frac{{\nu \overline{t}}}{{Lt_{0} }}x_{1} \left( t \right) \hfill \\ \end{gathered} $$

(52)

where ${x}_{1}$ is the angle difference between the truck and trailer, ${x}_{2}$ is the angle of trailer, and ${x}_{3}$ is the vertical position of rear end of trailer. The model parameters are chosen as $l=2.8m,L=5.5m,v=-1m/s,{t}_{0}=0.5s,\overline{t }=2s,$ and $b=0.7$. The T-S fuzzy model with two fuzzy rules for the system (52) can be considered. We can asssume the angle $\varpi ={x}_{2}(t)+b\frac{\nu \overline{t}}{2L}{x }_{1}(t)+(1-b)\frac{\nu \overline{t}}{2L}{x }_{1}(t-d(t))$. Moreover, under the condition, $\varpi \in [-179.427{0}^{\circ },179.427{0}^{\circ }]$, the nonlinear term $\mathrm{sin}(\varpi (t))$ can be represented as (Wu and Li 2007):

$$\mathrm{sin}(\varpi (t))={h}_{1}(\varpi (t)).\varpi (t)+{h}_{2}(\varpi (t)).\overline{g }.\varpi (t),$$

(53)

where $\overline{g }=(1{0}^{-2}/\pi )$. Then, the membership functions can be obtained as follow:

$${h}_{1}(\varpi (t))=\left\{\begin{array}{ccc}\frac{sin(\varpi (t))-\overline{g }.\varpi (t)}{\varpi (t).(1-\overline{g })},& \varpi (t)\ne 0& \\ 1 ,& \varpi (t)=0& \end{array}\right.$$

(54)

and,

$${h}_{2}(\varpi (t))=\left\{\begin{array}{ccc}\frac{\varpi (t)-sin(\varpi (t))}{\varpi (t).(1-\overline{g })},& \varpi (t)\ne 0& \\ 0 ,& \varpi (t)=0& \end{array}\right.$$

(55)

The membership functions satisfies that ${h}_{1}(\varpi (t)),{h}_{2}(\varpi (t))\in [\mathrm{0,1}]$ and ${h}_{1}(\varpi (t))+{h}_{2}(\varpi (t))=1$. Then, the T-S fuzzy model of the nonlinear system (52) can be exactly represented as the two following rules:

Model Rule 1: IF $\varpi (t)$ is ′′ about 0 rad ′′,

THEN $\dot{x}(t)={A}_{1}x(t)+{A}_{d1}{x}_{p}(t-d(t))+{B}_{1}u(t)$

Model Rule 2: IF $\varpi (t)$ is ${^{\prime}}{^{\prime}}$ about $\pi$ rad or $-\pi$ rad ′′,

THEN $\dot{x}(t)={A}_{2}x(t)+{A}_{d2}x(t-d(t))+{B}_{2}u(t)$. where $x(t)=[{x}_{1}(t),{x}_{2}(t),{x}_{3}(t){]}^{T}$ and

$$ A_{1} = \left[ {\begin{array}{*{20}l} { - b\frac{{\nu \overline{t}}}{{Lt_{0} }}} \hfill & 0 \hfill & 0 \hfill \\ {b\frac{{\nu \overline{t}}}{{Lt_{0} }}} \hfill & 0 \hfill & 0 \hfill \\ {b\frac{{\nu^{2} \overline{t}^{2} }}{{2Lt_{0} }}} \hfill & {\frac{{\nu \overline{t}}}{{t_{0} }}} \hfill & 0 \hfill \\ \end{array} } \right],A_{d1} = \left[ {\begin{array}{*{20}l} { - \left( {1 - b} \right)\frac{{\nu \overline{t}}}{{Lt_{0} }}} \hfill & 0 \hfill & 0 \hfill \\ {\left( {1 - b} \right)\frac{{\nu \overline{t}}}{{Lt_{0} }}} \hfill & 0 \hfill & 0 \hfill \\ {\left( {1 - b} \right)\frac{{\nu^{2} \overline{t}^{2} }}{{2Lt_{0} }}} \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right],A_{2} = \left[ {\begin{array}{*{20}l} { - b\frac{{\nu \overline{t}}}{{Lt_{0} }}} \hfill & 0 \hfill & 0 \hfill \\ {b\frac{{\nu \overline{t}}}{{Lt_{0} }}} \hfill & 0 \hfill & 0 \hfill \\ {b\overline{g}\frac{{\nu^{2} \overline{t}^{2} }}{{2Lt_{0} }}} \hfill & {\overline{g}\frac{{\nu \overline{t}}}{{t_{0} }}} \hfill & 0 \hfill \\ \end{array} } \right] $$

$$ A_{d2} = \left[ {\begin{array}{*{20}l} { - \left( {1 - b} \right)\frac{{\nu \overline{t}}}{{Lt_{0} }}} \hfill & 0 \hfill & 0 \hfill \\ {\left( {1 - b} \right)\frac{{\nu \overline{t}}}{{Lt_{0} }}} \hfill & 0 \hfill & 0 \hfill \\ {\left( {1 - b} \right)\overline{g}\frac{{\nu^{2} \overline{t}^{2} }}{{2Lt_{0} }}} \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right],B_{1} = B_{2} = \left[ {\begin{array}{*{20}l} {\frac{{\nu \overline{t}}}{{lt_{0} }}} \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{array} } \right],D_{w1} = D_{w2} = \left[ {\begin{array}{*{20}l} {\frac{{\nu \overline{t}}}{{Lt_{0} }}} \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{array} } \right] $$

and ${C}_{1}={C}_{2}=\left[\begin{array}{lll}\frac{\nu \overline{t}}{L{t }_{0}}& 0& 0\end{array}\right]$

Let the periodic reference signal be ${x}_{r}(t)=10sin(\pi t)$ rad/sec with $T=2$ sec and the external disturbance be

$$w(t)=\left\{\begin{array}{l}400\,sin(\pi t)+\,450\,\mathrm{tanh}(t-27)+450\mathrm{tanh}\,(t-17),\quad 10\le t\le 25s \\ 50(sin\,(\pi t)+cos\,(\pi t)),\quad 30\le t\le 37s\\ 0\quad \mathrm{elsewhere}\end{array}\right.$$

(56)

Moreover, the time-varying delay can be assumed to be $d(t)=2+0.5sin(t)$. Choose ${w}_{a}=100$ rad/sec, and the state-space representation parameters of the EID filter F(s) can be chosen as ${A}_{f}=-101,{B}_{f}=100,{C}_{f}=1$. By taken other parameters values as $\alpha =0.2,\beta =0.1,\gamma =0.5,\sigma =0.01,$ and ${T}_{1}=1$ sec, ${\psi }_{1}={\psi }_{2}={I}_{3\times 3}$. From Theorem (1), the fuzzy feedback and observer gains can be obtained by solving the LMIs as ${k}_{p1}=[98.231 -0.872 1.743],{k}_{p2}=[102.134 -1.214 2.122],{k}_{c1}=1.112,{k}_{c2}=1.450,{L}_{1}=[-4.224 3.890 2.543{]}^{T},$ and ${L}_{2}=[-6.844 2.254 2.654{]}^{T}$. The controller gains which have been obtained in (Sakthivel et al. 2020) are ${k}_{p1}=\left[132.0069 -0.5463 0.1342\right],{k}_{p2}=\left[134.0783 -0.5136 0.1343\right],{k}_{c1}=0.9398,\mathrm{ and }\;{k}_{c2}=0.9843$. The initial condition $\phi (t)$ is choosen as ${\phi }^{T}(t)=[4,-\mathrm{1,2}]$ where $t\in [-\mathrm{3.5,0}].$ The external disturbance is shown in Fig. 3, which contains aperiodic and periodic components. The aperiodic component appears in the time interval 10–25 s and the periodic one in the interval 30–37 s. Moreover, we discuss the reference and the system output signals responses in the following cases.

Fig. 3

External periodic and aperiodic disturbance

4.1 System under the proposed controller (FPETFO-MRC based on EID) case

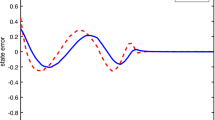
In this subsection, the tracking performance of truck-trailer system is investigated using the proposed controller and the controller one which is addressed in (Sakthivel et al. 2020). The periodic disturbance has been considered in (Sakthivel et al. 2020) only but in practice, disturbances are usually mixed between periodic and aperiodic components and unknown with different frequencies. The state responses of the reference ${x}_{r}(t)$ and the output $y(t)$ are shown in Fig. 4. From Fig. 4a, the control system in (Sakthivel et al. 2020) can well compensate the periodic disturbance in the absence of EID estimator and ETM but through the interval of the aperiodic disturbance, i.e., 10–25 s, it cannot compensate for the disturbance as good as the periodic one. Moreover, the stable state reached after that period as shown in Fig. 4b. On the other hand, in the presence of EID estimator, the proposed controller has achieved a good tracking performance, where the output $y(t)$ moves toward the reference ${x}_{r}(t)$ without steady state error and overshoot. Furthermore, the proposed controller has effectively succeeded in attenuation both the periodic and aperiodic disturbances. Thus, the steady state has been reached more faster and minimum tracking error with respect to the other scheme as shown in Fig. 4b.

Fig. 4

Tracking responses of system under FPETFO-MRC based on EID and (Sakthivel et al. 2020): a $y(t)$. b $\upvarepsilon (t)$

Moreover, the significance of the proposed controller appears in saving the communication resources as shown in Fig. 5. The intervals between two successive event triggering instants for the data transmission are provided, where the control actions are updated only at necessary instants which can save the communication and the computational resources unlike the other scheme, in which the control actions are updated continuously.

Fig. 5

The inter-event intervals

The proposed controller and the controller one of (Sakthivel et al. 2020) is compared in Table 1 using three performance indices: the root mean square of error (RMSE), the mean square of error (MSE) and the mean absolute error (MAE). These indices can be defined as:

$$ \begin{gathered} {\text{RMSE}} = \sqrt {\frac{1}{N}\mathop \sum \limits_{k = 1}^{N} (\varepsilon \left( k \right))^{2} ,} \hfill \\ {\text{MSE}} = \frac{1}{N}\mathop \sum \limits_{k = 1}^{N} (\varepsilon \left( k \right))^{2} , \hfill \\ {\text{MAE}} = \frac{1}{N}\mathop \sum \limits_{k = 1}^{N} \left| {\varepsilon \left( k \right)} \right| \hfill \\ \end{gathered} $$

(57)

where $N$ is the number of iterations. From Table 1, it is observed that the value of RMSE, MSE and MAE indices of the proposed controller are smaller than that of the scheme (Sakthivel et al. 2020). In addition, the rise time (${T}_{r}$) of the system under the proposed scheme is 579.213 m sec and under the other scheme is 591.677 m sec, which indicates that the proposed controller is more efficient. Hence, the proposed controller improves the system performance in the presence of time-varying delay and periodic and aperiodic disturbances.

Table 1 Comparison results

4.2 Applying external input and output disturbance case

To examine the robustness of the proposed scheme, an external disturbance is applied to the input and the output of the system.

4.2.1 External input disturbance

By adding a step signal with amplitude 10 at a time 28 s as an external input disturbance as shown in Fig. 6, the proposed controller is significantly fast to compensate for the disturbance and gives a good tracking performance.

Fig. 6

Tracking response under input disturbanc: a $y(t)$. b $\upvarepsilon (t)$

4.2.2 External output disturbance

The proposed controller compensates for the external output disturbance and a good tracking performance can be achieved by adding an external step with amplitude 10 at a time 28 s as shown in Fig. 7. It can be seen that the proposed controller effort is increased at a time 28 s to achieve the robustness of the FPETFO-MRC based on EID against the external disturbances.

Fig. 7

Tracking response under output disturbance: a $y(t)$. b $\upvarepsilon (t)$

4.3 Applying uncertainties case

In this paper, the uncertainty is utilized to check the robustness of the proposed scheme. In the stability analysis, this uncertainty is not considered. The structure of uncertainty addition will alter the system (1) parameters as the following:

$$\begin{aligned}\dot{x}(t)&=[{A}_{i}+\Delta {A}_{i}(t)]x(t)+[{A}_{di}+\Delta {A}_{di}]x(t-d(t))\\& \quad+[{B}_{i}+\Delta {B}_{i}(t)]u(t)+{B}_{wi}w(t)\end{aligned}$$

(58)

where $\Delta {A}_{i}(t),\Delta {A}_{di}(t)$ and $\Delta {B}_{i}(t)$ are time-varying parametric uncertainties can be described as follow (Sakthivel et al. 2018a, b):

$$[\Delta {A}_{i}(t)\quad\Delta {A}_{di}(t)\quad\Delta {B}_{i}(t)]=GF\left(t\right)\left[{\Xi }_{0} \quad{\Xi }_{1} \quad{\Xi }_{2}\right]$$

(59)

where $G,{\Xi }_{0},{\Xi }_{1}$ and ${\Xi }_{2}$ are known appropriate dimensions matrices and $F(t)\in {\mathbb{R}}^{n\times n}$ is an unknown real time-varying matrix with ${F}^{T}(t)F(t)\le I,\forall t>0$. Take the uncertain matrices as:

$$ \begin{gathered} G = \left[ {\begin{array}{*{20}l} 1 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 1 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill \\ \end{array} } \right],{\Xi }_{0} = {\Xi }_{1} = \left[ {\begin{array}{*{20}l} 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill \\ {0.8} \hfill & {0.4} \hfill & 1 \hfill \\ \end{array} } \right],{\Xi }_{2} = \left[ {\begin{array}{*{20}l} {0.1} \hfill \\ {0.2} \hfill \\ 1 \hfill \\ \end{array} } \right], \hfill \\ F\left( t \right) = \left[ {\begin{array}{*{20}l} {{\text{sin}}\left( {0.5\pi t} \right)} \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {{\text{sin}}\left( {0.5\pi t} \right)} \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {{\text{sin}}\left( {0.5\pi t} \right)} \hfill \\ \end{array} } \right]. \hfill \\ \end{gathered} $$

(60)

The proposed controller can achieve a good tracking performance under the parametric uncertainties in Fig.8.

Fig. 8

Tracking response under uncertainty structure: a $y(t)$. b $\upvarepsilon (t)$

5 Conclusions

This paper has investigated the tracking control and disturbance rejection problems for a class of time-varying delay nonlinear systems subjected to unknown exogenous disturbances. In particular, the proposed FPETFO-MRC based on the EID estimator has been constructed for T-S fuzzy model to achieve periodic reference tracking, disturbances rejection and communication resources saving. Based on the design of EID based MRC, both the periodic and aperiodic disturbances are compensated. Furthermore, in order to save communication resources and reduce energy consumption, the PETM has been incorporated to transmit the data at only necessary instants. Some of sufficient conditions have been used in terms of LMIs to guarantee the stability of the closed-loop system via LKF stability theorem. Moreover, the fuzzy observer and controller gains have been designed through the LMI and the matrix decomposition approaches. The simulation results of the modified truck-trailer model with time-varying delay have been provided to reveal the effectiveness of the proposed scheme with comparative study.