Abstract
In maritime container terminals, yards have a primary role in permitting the efficient management of import and export flows. In this work, a mixed 0/1 linear programming model and a heuristic approach are proposed for defining storage rules in order to minimize the space used in the export yard. The minimization of land space is pursued by defining the rules to allocate containers into the bay-locations of the yard, in such a way as to minimize the number of bay-locations used and the empty slots within them. The main aim of this work is to propose a solution approach for permitting the yard manager to compare yard storage strategies for different transport demands, in such a way to be able to evaluate and, eventually, modify the storage strategy when the characteristics of the transport demand change. Computational experiments, based on both real instances and generated ones, are presented. All instances are derived by a case study related to an Italian terminal.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
1 Introduction and literature review
Maritime container terminals are generally recognized as crucial intermodal change nodes in the logistic chains, managing the greater part of the world sea trade, i.e. about 80\(\%\) of the world one (UNCTAD, 2018).
The storage yards have a primary role in permitting the efficient management of import and export flows Carlo et al. (2014) and, in recent years, thanks to advancements in quayside equipment and technologies, seems the bottleneck of port operations has moved from quayside to yard side Tan et al. (2017). This means that the typical operations performed in the yard, such as the storage and the retrieval of containers, dispatching and routing of material handling equipment, must be managed improving their efficiency, in such a way not to compromise the efficiency of the whole terminal system and the competitiveness of the terminal in the whole logistic chain.
The yard, the intermediate area between the frontier and the backward of a terminal, is used to store, control and handle the containers and occupies a considerable part in a terminal. The yard is usually divided into some segmentation for the inbound and outbound containers based on the process of import and export, respectively.
The container yard is divided into numerous Blocks, each one composed by a given number of Bays. Each bay is formed by several Rows; containers are stacked in Tiers. The identification of a container position in the yard is based on these 3 indicators: Bay, Row and Tier. In modern container terminals, the maximum tier to stock a container in a block is 4 and the utilization ratio ranges from 70\(\%\) to 90\(\%\).
Blocks can be positioned either perpendicular or parallel to the quay, and the location of the input/output container points (i.e. points for the exchange of containers between transfer vehicles and yard cranes) can be either at the end of the blocks or in the middle; thus, two configurations of layout are possible and they are generally known as European and Asian layout, respectively. (More details can be found in Carlo et al. 2014; Wiese et al. 2010.)
As far as the storage strategies are considered, the most of literature is devoted to export containers. Many terminals store containers in the yard per their loading vessels. In this case, the terminal has to assign sub-blocks to vessels and then organize the storage of containers inside every sub-block. This problem is known as the yard template planning (Moorthy and Teo 2006; Zhen 2014), and it represents a tactical level decision problem. The yard template planning has been generally solved under deterministic assumptions (i.e. the number of containers to load on a vessel is known).
At the operational level, given a yard template, the terminal solves the storage allocation problem (Zhang et al. 2003; Lee and Tan 2006) generally based on the sub-blocks. Some authors refer to these sub-blocks as loading clusters. In Yu et al. (2020), the authors model the choice of loading clusters in such a way to obtain a more flexible allocation strategy for organizing the space in the export yard. They describe in detail the concept of loading cluster and loading operations, and the link between these two important activities. In He et al. (2020) and Tan et al. (2019), the authors try to develop more flexible yard management by determining simultaneously the size of the loading clusters and their allocation to specific blocks. A loading cluster is a stretch of bays in a specific yard block. The word loading is used to stress the importance of coordinating the bay configuration in the yard with the slots on the ship in a given bay. The ideal situation is to have the containers in the same yard stack to be put in the same ship bay. Thus, the yard manager has to optimize the choice of loading cluster while considering their loading operations. In Ambrosino and Sciomachen (2003), the authors evaluate the impact of the yard organisation on container loading operations by computing the total stowage time when different picking sequences are considered. In Han et al. (2008), the authors optimize the yard template and the yard storage allocation problems simultaneously.
More recent papers deal with the robust yard template facing uncertainty Zhen (2014). In Petering (2009), the authors evaluate how the block widths affect the terminal performances thanks to a discrete event simulation model, while Petering and Murty (2009) show how the length of the blocks in the storage yard affects.
The template of the terminal is organized following the handling equipment used. In the analysed literature, the terminals use Rubber Tyred Gantry (RTG) cranes. The template of a terminal using reach stackers for picking up export containers is quite different, since the blocks are operated from one side. The pickup operations and the number of re-handles to execute to pick up a container are affected by the type of terminal equipment used.
In this paper, we consider a terminal with blocks parallel to the quay, where import and export yards are independent, and we deal with export standard containers. Handling operations in the export yard are executed thanks to reach stackers.
The yard template is given, this means that the export yard is organized in blocks of different capacities and, for each vessel, there is a subset of dedicated blocks, that is the containers that will be loaded on that vessel must be stored in the dedicated subset of blocks. Containers can be stored in the dedicated blocks under different storage strategies. Since now we only consider the subset of blocks dedicated to a vessel and the containers that must be loaded on it.
Each container is characterized by its type, size, weight and destination; these characteristics are important when defining the storage strategy. The ideal rule is to store together containers having the same characteristics, to reduce the operation time and avoid a bottleneck in the terminal when loading the ship Zhang et al. (2003), Saanen and Dekker (2007). This strategy is known as consignment strategy. Note that this strategy requires large storage space (for example, more than random policies De Koster et al. 2007), but on the other hand permits to improve the storage yard operations during the vessel containers loading in terms of productivity of both pickup operations in the bays and movements of material handling equipment among bays. Note that when a random policy is used, another strategy follows to improve the efficiency in the loading process; this strategy can be either a pre-marshalling strategy that permits to reorganize the container stacking beforehand, in order to reduce reshuffles, or a re-marshalling strategy that permits to move containers from their current storage location to a location closer to their vessel. Generally this happens in European layout terminals.
Among the papers dealing with the storage allocation for export containers, in Kim et al. (2000) a consignment strategy, based on Light, Medium and Heavyweight classes, destination and size, is used to decide an exact slot for each container; Kim and Park (2003) try to increase the loading operation efficiency by considering the travel distances of equipment, while in the optimal storage location is determined taking into consideration the container handling schedules.
In Woo and Kim (2011), four rules to determine the number of blocks to allocate the groups of export containers are proposed. Rules are fixed, and the main aim is to optimize the movements of yard equipment and the distance between the yard and the quay. Moreover, the authors evaluate the influence of the yard size on the efficiency of loading operations.
In an optimization model for defining storage strategies for export containers is proposed. The authors focus on the definition of rules of the consignment strategy intending to minimize the space used.
Starting from the model proposed in the present paper a new formulation for defining the best allocation of containers to storage spaces is proposed, simultaneously defining the best consignment strategy to use.
The main purpose of this work is to propose a solution approach, based on a mathematical model, being able to determine the set of best rules for defining which containers to store together, while determining the loading cluster for each group of containers. From a managerial point of view, the proposed approach permits the yard manager to compare storage strategies, and in particular, it should be used by the yard manager to evaluate and, eventually, change the storage strategy when the characteristics of the transport demand change.
The remainder of this paper is organized as follows. The problem under investigation is described in Sect. 2. The 0-1 linear model is presented in Sect. 3, while the solution approach is described in Sect. 4. Finally, the experimental tests are reported in Sect. 5 and conclusions and future works are outlined in Sect. 6.
2 Problem under investigation
2.1 The general contest
Let us consider an export yard and the blocks dedicated to a particular vessel. Blocks are characterized by different capacities, depending on bays, rows and tiers. Generally, the number of rows ranges from 2 to 5, while 4 tiers are considered.
A bay-locations is a set of cells belonging to the same bay of a block. Thus, the capacity of each bay-locations varies according to the number of rows in the block; the capacities are 8, 12, 16 and 20 containers. Figure 1 represents two different blocks with several bays. The yellow part is a block composed of 4 bays, each one characterized by 2 rows, thus the capacity of each bay-locations is 8. Meanwhile, the blue part is a block composed of bay-locations with 3 rows, and thus, the capacity of each bay-locations is 12.
Note that we refer to 20’ bay-locations. For the storage of 40’ containers, two contiguous 20’ bay-locations are required. Figure 2 shows how it is possible to use a block composed of 6 bay-locations (Block1 in Fig. 2a), having both 20’ and 40’ containers to store. The block can be used for the storage of 20’ containers, e.g. 6 bay-locations are occupied by 20’ containers (Fig. 2b), for the storage of 40’ containers, e.g. 6 bay-locations are used as 40’bay-locations and only 40’ containers can be stored there (Fig. 2c), for storing both 20’ and 40’ containers. In this last case, either 4 bay-locations of 20’ containers and 1 40’bay-locations for 40’ containers (Fig. 2d) or 2 bay locations of 20’ containers and 2 40’bay-locations for 40’ containers (Fig. 2e) can be used.
Summarizing, the yard consists of a given number of 20’ bay-locations (here called simply bay-locations) of different capacities.
The yard manager assigns containers to the bay-locations following the storage rules adopted by the terminal. The storage rules consist of a list of characteristics that containers may have to be stored together. These rules permit to have homogeneous containers in each bay-locations, i.e. to be able to pick them up in sequence for their loading on board of the vessel and to optimize the work of the reach stackers during their pick-up in the yard. (It is generally preferred to complete the pick-up process in a bay-locations and empty it before moving the reach stacker to another bay-locations).
The most common characteristics used when defining a storage strategy are the following:
Size: 20 feet (20’) and 40 feet (40’) containers; only stacks (and bay-locations) of one size (i.e. either 20’ or 40’) are permitted.
Type: standard containers, 20’ and 40’ box and 40’ HC containers (special containers follow different rules derived directly from the particular requirements for their storage: plugs for reefers, special locations for hazardous and out of huge, etc.).
Destination: containers are grouped by their destination. Containers on board are generally grouped for homogeneous port of discharge, i.e. either a bay of the vessel or a part of it is dedicated to store containers for the same destination.
Weight: containers stored in the same bay have similar weights for respecting the requirement of safety, generally saying that the weight of the container stored in a given tier has to be no greater than the weight of the container stored in the tier below it, within a given tolerance. Many terminals group containers according to weight classes, i.e. containers belonging to the same weight class, can be stored together; the most common configuration used is based on three classes: Light, Medium and Heavy. For each class weight lower and upper limitations are given; for example the weight of containers in the Medium class ranges from 15 to 25 tons, those in the Light class have a weight less than 15 tons, while containers with a weight greater than 25 tons belong to the Heavy class.
It is easy to understand that the elements more impacting on the space utilization are the following:
-
the yard template and layout of blocks: the capacities of the bay-locations and the number of bay-locations of each capacity;
-
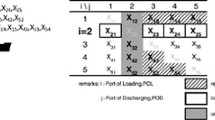
the consignment strategy: the rules adopted impact on the number of containers of each group, and the number of groups to manage (as shown in Fig. 3). The number of groups to manage corresponds to the required bay-locations’patterns.
In Fig. 3, containers are grouped by their destination, their type (Box or High Cube), their size and their weight class. For each destination, nine patterns must be managed. The higher is the number of patterns to manage, the higher is the yard space required. The required space is also a function of the bay-locations capacities. How it is possible to act on these elements to reduce the yard space without penalising the efficiency of loading operations?
The number of weight classes used for defining the storage rules has a direct impact on the number of patterns, while acting on the weight limitations of each class it is possible to modify the number of containers in each pattern, thus the number of the required bay-locations for each pattern. Hence, these two elements might have a great impact on the space used in the yard and we have decided to investigate the possibility to optimize both the number of weight classes to use and the weight lower and upper bounds of each class.
In the following, we will refer to the number of weight classes as Class configuration; that is, 3 class configurations can be chose when defining the storage strategy; containers can be grouped into 2 weight classes (i.e. Light and Heavy), 3 weight classes (i.e. Light, Medium and Heavy) or 4 weight classes (i.e. Light, Medium, Heavy and Extra). Then, the best set of lower and upper bounds for each weight class of the chosen class configuration must be adopted. This means that for each class configuration many weight limitations, here called Weight configurations, are possible and only one can be adopted in the storage strategy.
Let us give an example. Let us consider the more common class configuration based on three weight classes: Light, Medium and Heavy, with two alternative weight configurations, i.e. W1 and W2, each one characterized by three weight limits: W1(p1,p2,p3) and W2(p4,p5,p6). The weight limits for example can be as p1=(0,15), p2=(15,25), p3=(25,33) and p4=(0,12), p5=(12,25), p6 =(25,33). The yard manager has to decide the most appropriate lower and upper bounds for the weight limitations of the above mentioned 3 weight classes; that is, he can use either the weight limitations given in W1 or in W2.
2.2 The analysed contest
As explained above, the key elements of a storage strategy are the class configuration (i.e. the number of weight classes used to split containers) and the weight limitations associated to each class (lower and upper bounds), together with the characteristics of containers such as destination, type and size. In very general terms, the problem under investigation can be described as follows. Given the export yard blocks characterized by a set of bay-locations of different capacities dedicated to store the containers waiting for their loading on a specific vessel, given a set of containers representative of the average transport demand for the considered vessel, the problem consists in deciding the Class configuration and the Weight configuration to use for grouping the containers in order to minimize the space used in the export yard.
Let us now introduce the problem in more details. As far as the yard is considered, the following elements are given: the set of bay-locations of the blocks and the number of bay-locations having a given capacity; the set of the possible class configurations and weight configurations, together with the weight limits. Moreover, each container to store in the yard is characterized by its size, type, weight and destination.
The problem consists in deciding the assignment of each container to a specific bay-locations, while simultaneously determining the class configuration of the blocks dedicated to the vessel under investigation, and their weight limitations, the characteristics of each bay-locations in terms of destination, type, size, capacity (among the set of available capacities in the blocks of the yard) and the weight class among the set belonging to the chosen class configuration, in order to respect the yard capacity and minimize both the number of bay-locations and the total empty slots.
Note that this problem emerges at tactical level for defining rules to use in the operative contests. These rules are not fixed once and ever adopt; the idea is to modify them following the trend of the export flow demand. Consider, for example, a service served by the terminal, and suppose that the number of containers for a destination of this service increases; we are interested to observe which groups of containers increase (i.e. 20’ box containers or heavy 20’ ones, etc.). Only in this way, we are able to decide whether the existing rules are adequate or not, and in this latter case, how to modify them thanks to optimization approach. The model and the solution approach useful for performing that analysis are presented in the following sections.
3 The mathematical model
In this section, a basic 0-1 linear programming model to solve the problem described in Sect. 2.2 is presented. The useful notation is the following:
- B:
-
the set of bay-locations
- Q:
-
the set of bay-locations capacities (i.e. 8, 12, 16, 20)
- F:
-
the set of the possible class configurations
- W:
-
the set of weight configurations
- P:
-
the set of weight limits
- C:
-
the set of containers
- D:
-
the set of ports of destination
- H:
-
the set of types/heights (Box, High Cube)
- S:
-
the set of sizes (20, 40 feet)
- \(n_q\):
-
the number of 20’bay-locations having capacity \(q, \forall q\in Q\)
- \(d_i\):
-
destination of container \(i, \forall i\in C\)
- \(s_i\):
-
size of container \(i, \forall i\in C\)
- \(h_i\):
-
height of container \(i, \forall i\in C\)
- \(w_i\):
-
weight of container \(i, \forall i\in C\)
- \(u_p\):
-
weight upper bound of weight limit \(p, \forall p\in P\)
- \(l_p\):
-
weight lower bound of weight limit \(p, \forall p\in P\)
- \(\delta _{fw} \forall f\in F,\forall w\in W\), \(\delta _{fw}=1\):
-
if the weight configuration w belong to class configuration f, 0 otherwise
- \(\gamma _{wp} \forall w\in W,\forall p\in P\), \(\gamma _{wp}=1\):
-
if the weight limits p belong to configuration w, 0 otherwise
- \(\alpha \):
-
weight used in the objective function for penalising the empty slots in the bay-locations.
Let us introduce the following decision variables:
- \(x_{ij} \in \{0,1\}, \forall i\in C ,\forall j\in B\):
-
\(x_{ij}=1\) if container i is stored in bay-locations j
- \(y_{jdhsq}\in \{0,1\}, \forall j\in B, \forall d\in D, \forall h\in H, \forall s\in S,\forall q\in Q\):
-
\(y_{jdhsq}=1\) if in bay-locations j, with capacity q, are stored containers for destination d, with height h and size s
- \(c_{pj} \in \{0,1\}, \forall p\in P, \forall j\in B\):
-
\(c_{pj}=1\) if weight limits p are assigned to bay-locations j
- \(a_f \in \{0,1\}, \forall f\in F\) \(a_f=1\):
-
\(a_f=1\) if class configuration f is chosen for the yard storage
- \(b_w \in \{0,1\}, \forall w\in W\):
-
\(b_w=1\) if weight configuration w is chosen
- \(z_j \ge 0, \forall j\in B\):
-
number of empty slots in bay-locations j.
The resulting model is the following:
Subject to:
Equation (1) is the objective function that minimizes the number of bay-locations used and penalizes the empty slots in the bay-locations.
Thanks to constraints (2), each container must be stored in one bay-locations. Constraints (3) assign at most one destination, one size, one type and one capacity to each bay-locations. Constraints (4) verify the number of containers assigned to the bay-locations is less or equal to the capacity assigned to it.
The yard capacity, in terms of the number of bay-locations of the different capacities available (i.e. 8, 12, 16, 20 containers), is verified thanks to (5).
Constraints (6), (7) and (8) refer to the choice of a class configuration together with a weight configuration.
Only one couple of weight limits can be assigned to each bay locations (9), and thanks to (10), the weight limits are assigned to each bay-locations following the choice of the weight configuration chosen for the blocks of the yard. Thanks to (11) and (12), a container can be assigned to a bay-locations only if its weight is within the maximum and minimum weight limitations imposed to the bay-locations by the weight configuration assigned to it thanks to (9). In (13), the number of empty slots in each bay-locations is computed.
Model (1)-(13) can be solved up to optimally only for small instances (as shown in Sect. 5); in the following section, a heuristic procedure that can be used for solving real size instances is described.
4 Heuristic approach
For defining the best storage strategy rules for the real size problems, we propose a heuristic approach based on the model (1)-(13). From computational results (see Section 5), it is clear that the number of destinations and the different capacities of bay-locations have a great impact on the CPU time. Due to these considerations and to the fact that each consignment strategy groups containers for their destination and size, we propose a solution approach that decomposes the problem into sub-problems. In particular, we solve model (1)-(13) for each destination and for each size of containers (i.e. 20’ and 40’). Moreover, we relax the capacity constraints due to the layout of the yard; thus, we suppose to have an unlimited number of 16 and 20-capacity bay-locations. Thanks to the union of the sub-problem solutions, we have a solution for the original problem; unfortunately, this solution can be unfeasible for constraints (5) that verify the yard capacity. Moreover, the obtained solution should present different class configurations for the destinations (i.e. a violation of constraint (6)) and, as a consequence, different weight limitations. In the proposed heuristic, only the unfeasibility concerning the yard capacity is eliminated.
The main steps of the proposed heuristic procedure are the following:
Step1: construct a solution and verify its feasibility;
Step2: remove unfeasibility by new assignment of containers belonging to the bay-locations used in more quantities than available in the real yard layout.
Before describing the solution approach, let us introduce the following additional notation:
- \({\hat{x}}\):
-
complete current solution
- \(u_q\):
-
number of 20’bay-locations of capacity q used in the current solution
- \(E_q\):
-
number of bay-locations of capacity q used in excess with respect to the available ones (\(n_q\))
- \(A_q\):
-
number of bay-locations of capacity q left with respect to the available ones (\(n_q\))
- \(\beta \):
-
permits to manage the size of containers (20’ and 40’)
- \(L_q\):
-
list of bay-locations of capacity q used in the current solution
- \(m_j\):
-
number of containers stored in the bay-locations j
Step1: construct a solution and verify its feasibility
After having solved model (1)-(13) for each destination d and for each size s, we construct, by the union of the obtained solutions, the current solution \({\hat{x}}\), characterized by a given number of used 16 and 20-capacity bay-locations.
For verifying the feasibility of solution \({\hat{x}}\), it is necessary to compute the number of 20’ bay locations used for each capacity q (\(u_q\)) and compare them with \(n_q\).
This check is detailed in the following procedure described in c-like.
Check feasibility:

Step2: obtaining feasibility
When the current solution \({\hat{x}}\) does not respect the yard layout, i.e. there is at least one \(E_q >0\), and then, it is necessary to modify the usage of bay-locations in the yard.
Since one of the aims is to minimize the number of empty slots in the bay-locations, the idea is starting to replace the bay-locations with capacity q such that \(E_q >0\) with large numbers of empty slots, with bay-locations of different and more adequate capacities. Thus, all bay-locations with capacity q such that \(E_q >0\) are put in the list \(L_q\) in descendent order with respect to their empty slots (\(z_j\)) in such a way to try to reduce the number of bay-locations with capacity q used, starting from those having the largest number of empty slots.
For example, let us suppose to have a 20-capacity bay-locations with 9 empty slots. If in the yard is available a 12-capacity bay-locations, we can change them and reduce the number of empty slots from 9 to 1. In case there is no a bay-locations with a capacity greater than 11 containers, and we need to remove the 11 containers assigned to the 20-capacity bay-locations, we can try to split the 11 containers into two bay-locations, the most adequate among the available in the yard; for example, we can use two 8-capacity bay-locations.
These ideas, used to modify the current unfeasible solution in order to obtain feasibility while improving it, are detailed in the following procedure described in c-like.
Obtaining feasibility by removing bay-locations over used:

The search in the yard among the available bay-locations is realized by comparing the capacity of available bay-locations with \(m_{{\hat{j}}}\) that is the number of containers stored in bay-locations \({\hat{j}}\), to minimize the empty slots in the new selected bay-locations. If there is not a bay-location with capacity greater than \(m_{{\hat{j}}}\), the idea is to split \(m_{{\hat{j}}}\) in two bay-locations, and thus, it is necessary to select the two most adequate bay-locations, again with the aim of minimizing the number of empty slots. If it is not possible to split \(m_{{\hat{j}}}\), this means that we are not able to construct a feasible solution starting from the \({\hat{x}}\), for the current layout.
Remember that we are referring to the layout of the yard reserved for a vessel; thus, in the operative contest, the capacity of this yard does not represent a strong constraint. This does not mean that it is possible to modify the layout on request, but in case of critical situations, a part of a block dedicated to another vessel can be temporarily used (as sometimes in the terminal under investigation happens).
5 Computational experiments
To verify the effectiveness of the proposed model and to justify the choice of the heuristic approach, we conduct a series of numerical experiments. In the first campaign, we try to show the behaviour of the model in different circumstances, i.e. when permitting more freedom degree to choose the storage strategy, when considering different yard layouts, and increasing the size instances in terms of the number of containers. Moreover, we try to show the benefits for the terminal yard manager of having more freedom degree in choosing storage strategies, evaluating the impact on the space utilization. In the second campaign, we test the model by using a particular scenario (i.e. Scenario 3) by increasing both the number of containers and the number of destinations.
The model introduced in Sect. 3 and the solution approach described in Sect. 4 have been implemented in MPL (Mathematical Programming Language) and spreadsheet Excel and solved by the commercial solver GUROBI on a device with Intel Core i7, 2.6 G Hz, Memory 16G. All experiments have been conducted by using instances generated by having in mind the real cases solved by a container terminal of an Italian port. Also some instances derived by a case study are reported to validate the proposed approach.
5.1 First experimental campaign
In the first campaign, we use small-scale instances. In particular, we refer to instances SS, characterized by 86 containers to load on the same vessel, and instances MS with 320 containers. The main aim of this campaign is to investigate the behaviour of the model presented in Sect. 3 either with fixed and predetermined weight and class configurations or different weight and class configurations to choose. For this analysis, we investigate four scenarios of increasing difficulty and complexity. Details of parameters of each scenario are specified in Figure 9 reported in Appendix. In particular, in Scenario 1 only one fixed class configuration is used, with fixed weight limits. Scenario 2 permits to choose the weight limits for a given class configuration. Scenario 3 permits to choose among different class configurations, each one characterized by fixed weight limits. The last scenario, Scenario4, represents the larger degree of flexibility: it is possible to choose both the best class configuration and weight configuration. Note that the model proposed in Sect. 3 permits to face this problem, the more general case for defining the best storage strategy.
Moreover, in this analysis we suppose to have two different terminal layouts in terms of capacity of the bay-locations. In fact, thanks to an historical data analysis of the terminal under investigation, we know that bay-locations with capacity of 12, 16 and 20 are in common usage. Thus, we compare performances under two different situations, a capacity set 1 (named CS1) in which the blocks of the terminal are composed by bay-locations with a capacity of 16 and 20 containers, and a capacity set 2 (named CS2), in which bay-locations have capacity 12, 16 and 20 containers. In particular, the terminal layout characteristics in terms of quantity of bay-locations of each capacity are summarized in Table 1.
Model (1-13) has been solved with time limits that differ for the considered scenarios; in particular, for the first scenario, the maximum CPU time is set as 3600 seconds, for the second scenario is 10800 seconds, while for the last two scenarios, the time limit is fixed to 14400 seconds.
The detailed results of the different solved scenarios are reported in Appendix in Fig. 10 and in the following figures where some graphs are used for showing them easily. In particular, we can note from graph in Fig. 4 that all SS instances can be solved up to optimally in the four analysed scenarios. More flexibility in the class and weight configuration choice required more CPU time, and from the graph, it is easy to note that instances characterized by layout CS2 are more time-consuming. This conclusion is more clear in the second graph shown in Fig. 5.
In case of medium-sized instances MS, model (1-13) can be used to solve up to optimally only instances characterized by the simple layout (SC1) with both the class configuration and the weight configurations fixed. The trend of the CPU time and Gap are reported in the graph in Fig. 6.
Finally, we have investigated how the space is used in the yard when the different layouts are implemented. From the results reported in Fig. 10, we can obtain the graphs depicted in Figs. 7 and 8. From these graphs we can note that the number of empty slots are lower when in the yard are available bay-locations with 12, 16 and 20 container capacity.
By fixing a priori, either the number of classes to use or the weight limitations for each class can cause an inefficient usage of the space in the yard. In fact, if we consider SS instances, we can note that, without optimizing the storage strategy can be generated even 94 empty slots [126], while in the optimal solution only 14 empty slots [30] are present when layout CS2 [CS1] is used. These numbers grow for instances MS. We can also note that the number of empty slots increases more than 100 percent by passing from layout CS2 to CS1, in case of optimal solutions.
Obviously, small capacity is more attractive in order to reduce vacancy in every bay-locations. However, the number of bay-locations generated remains almost the same under two different capacity sets. The influence denoted by the variety of weight configuration can be deemed as small on the space and bay-locations utilization.
5.2 Second experimental campaign
This campaign is executed by using the proposed model for solving different instances for Scenario 3 with a particular layout of the yard, that is only one bay-locations capacity is present, i.e. 20 containers bay-locations capacity. The effectiveness of the proposed model is evaluated for increasing size instances in terms of both number of containers and destinations. We conduct experiments with 200, 400, 800 and 1600 containers.
CPU time limit is fixed 3600 seconds for instances with 200 and 400 containers, while it is 7200 seconds for instances with 800 containers and 14400 seconds for the largest instances with 1600 containers. Results and detailed information are listed in Table 2, where columns refer to the number of containers (Cntr), the number of destinations (D.), the CPU time (CPU), the number of bay-locations used (B-l) and the empty slots (E.s.), the class configuration chosen (Conf.) and the optimality gap (Gap).
Looking at Table 2, we can note that all instances with 200 and 400 containers have been solved up to optimality requiring an average CPU time of 77 and 311 seconds, respectively. Larger instances present high gaps even if the time limit has been increased up to 7200 and 14400 seconds. We can note that larger instances with only one destination present lower gaps than those with either 4 or 8 destinations.
Summarizing, from both the results shown in Table 2 and in Figs. 5 and 6 (where CS1 and CS2 were compared), we can say that the number of different capacities of bay-locations strongly affects the proposed model performances. Moreover, it is clear that the number of destinations is another impacting factor on the capability of the model to solve the real size instances. However, containers are generally (almost always) grouped according to their destination, implying that it is possible to decompose the storage problem. Thus, from the above considerations we have decided to implement the solution approach described in Sect. 4. In the next subsection, we compare the solution obtained by the proposed model and the heuristic approach, with the solution used by the terminal under investigation for some real instances.
5.3 Some real case instances
As final test, we present a comparison of the results obtained by model (1)-(13) and the proposed heuristic approach. We have solved some real instances, belonging to the set of SS and MS, and one larger instance characterized by 646 containers and 9 different destinations. For one instance of each size, we are able to compare the obtained solutions also with the storage strategy adopted by the terminal under investigation.
Data reported in Table 3 are the average of the results of three SS and MS instances and permit to compare the performances of the model and the heuristic method in terms of empty slots (E.s.) and bay-locations used (B-l). From this comparison, we can note that the heuristic approach is worst in terms of empty slots, while almost the some number of bay-locations is used.
In Table 4, we compare the obtained results with the solutions adopted by the terminal. This comparison shows that either proposed model or heuristic approach outperforms the current storage plan of the terminal under investigation in terms of empty space and bay-locations. The solutions obtained by using the proposed heuristic approach grant a saving that ranges from 7% to 56% of empty slots, and from 16% to 53% of bay-locations used.
The proposed approach seems to be promising and helpful for yard storage managers.
6 Conclusions
In this paper, we have tried to implement a solution approach for helping yard managers in defining the best storage strategy to use for minimizing the space used. We have shared the obtained results with the maritime terminal under investigation that, having lots of problems due to the lack of space in the yard, have appreciated this approach. The idea is to solve this problem each time there is a significant change in the transport demand that can require a change in the storage strategy. The number of classes and the weight limitations, defined thanks to the proposed approach, are inserted as parameters in the TOS (Terminal Operating System) of the terminal that manage the real-time storage of the flow of containers reaching the terminal by trains and by trucks. The proposed approach provides maximum freedom to terminal managers choosing different storage strategies in accordance with numerous requests. It permits to decide the most appropriate combination of characteristics and configurations for reorganizing the storage plan granting better space utilization.
As future work, it should be interesting to extend this problem in such a way as to consider it dynamically. A vessel of a service can visit the terminal for example once a week and can occur that containers arrive too early at the terminal, and since they have to be loaded on the vessel of the next week, they have to wait; thus, it is necessary to manage together containers that must be loaded in two different vessels of the same service. This is the new request of the terminal we are involved with.
Availability of Data and Material
Real data are not available for privacy reasons. Generated instances are available on request.
References
Ambrosino D, Sciomachen A (2003) Impact of yard organisation on the master bay planning problem. Maritime Econ Logist. 5(3):285–300
Ambrosino D, Xie H (2020) An optimization model for defining storage strategies for export yards in container terminals: a case study. In: Lalla-Ruiz E, Mes M, Voß (eds) Computational logistics - 11th International Conference, ICCL 2020, Enschede, The Netherlands, September 28–30, 2020, Proceedings, Lecture Notes in Computer Science, vol. 12433, pp. 119–132
Carlo HJ, Vis IF, Roodbergen KJ (2014) Storage yard operations in container terminals: Literature overview, trends, and research directions. Eur J Operational Res 235(2):412–430
De Koster R, Le-Duc T, Roodbergen KJ (2007) Design and control of warehouse order picking: a literature review. Eur J Operational Res 182(2):481–501
Han Y, Lee LH, Chew EP, Tan KC (2008) A yard storage strategy for minimizing traffic congestion in a marine container transshipment hub. OR spectrum. 30(4):697–720
He J, Tan C, Yan W, Huang W, Liu M, Yu H (2020) Two-stage stochastic programming model for generating container yard template under uncertainty and traffic congestion. Adv Eng Inform 43:101032
Kim KH, Park KT (2003) A note on a dynamic space-allocation method for outbound containers. Eur J Operational Res 148(1):92–101
Kim KH, Park YM, Ryu KR (2000) Deriving decision rules to locate export containers in container yards. Eur J Operational Res 124(1):89–101
Kozan E, Preston P (2007) Mathematical modelling of container transfers and storage locations at seaport terminals. In: Container terminals and cargo systems. Springer. pp. 87–105
Lee C, Tan H (2006) An optimization model for storage yard management in transshipment hubs. OR Spectr 04(28):539–561
Legato P, Canonaco P, Mazza RM (2009) Yard crane management by simulation and optimisation. Maritime Econ Logist 11(1):36–57
Moorthy R, Teo C (2006) Berth management in container terminal: the template design problem. OR Spectr 01(28):495–518
Petering ME (2009) Effect of block width and storage yard layout on marine container terminal performance. Transportation research part e: logistics and transportation review 45(4):591–610
Petering ME, Murty KG (2009) Effect of block length and yard crane deployment systems on overall performance at a seaport container transshipment terminal. Comput Op Res 36(5):1711–1725
Saanen YA, Dekker R (2007) Intelligent stacking as way out of congested yards? part 1. Port Technol Int 31:87–92
Tan C, He J, Wang Y (2017) Storage yard management based on flexible yard template in container terminal. Adv Eng Inform 34:101–113
Tan C, He J, Yu H (2019) Mathematical modeling of yard template regeneration for multiple container terminals. Adv Eng Inform 40:58–68
Wiese J, Suhl L, Kliewer N (2010) Mathematical models and solution methods for optimal container terminal yard layouts. OR Spectr 32(3):427–452
Woo YJ, Kim KM (2011) Estimating the space requirement for outbound container inventories in port container terminals. Int J Prod Econ 133(1):293–301
Yu H, Zhang M, He J, Tan C (2020) Choice of loading clusters in container terminals. Adv Eng Inform 46:101190
Zhang C, Liu J, Wan Y, Murty K, Linn R (2003) Storage space allocation in container terminals. Trans Res Part B: Methodol 37:883–903
Zhen L (2014) Container yard template planning under uncertain maritime market. Trans Res Part E: Logist Trans Rev 69:199–217
Open Access
This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funding
This research has been supported by MUR- Italy - project PRIN2015 research program: SPORT: Smart PORt Terminals
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest
Additional information
Communicated by Anna Sciomachen.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A Details on instances and computational tests
Appendix A Details on instances and computational tests
In Fig. 9, the details of the parameters characterizing each scenario are reported. The TestID identifies each type of solved instance, by indicating the status of both the class configuration and the weight configuration. In the last two columns, the different classes and the possible weight limitations are shown. In Fig. 10, the results of each solved scenario are reported.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ambrosino, D., Xie, H. Optimization approaches for defining storage strategies in maritime container terminals. Soft Comput 27, 4125–4137 (2023). https://doi.org/10.1007/s00500-022-06769-7
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-022-06769-7