A distorted copula-based evolution model: risks’ aggregation in a Bonus–Malus migration system

Abstract

In this paper, we put forward a new model to compute the loss distribution of an automobile insurance company’s portfolio evolving by a bonus–malus system. We allow for a continuous evolution of the demographic-economic system based on a migration’s rule which is refreshed in discrete time, i.e., at the monitoring times. Therefore, the migration’s probabilities are discretely updated through a technique based on the combinatorial distributions of claims’ arrival in the rating classes. This technique is hierarchical copula-based, a natural tool permitting us to represent the co-movement between claims’ arrivals and distorted due to the formalization of an arrival policy of claims, that restricts the set of combinatorial distributions to those representing the most probable scenarios, therefore distorting the loss function. At every monitoring date, the copula-based model computes the migration’s probabilities and the loss function which accommodates for a discrete-time dynamic of the claims’ reserving and the capital requirements. An empirical application, the evaluation of the claims’ reserving and the capital requirements for different kinds of hierarchies are analyzed, with real data originating with the General Insurance Association of Singapore.

1 Introduction

The aggregation of risks is without doubt a topic of paramount importance, particularly since the financial crisis of 2008 one was forced to pay extreme attention to decision-making approaches based on the minimization of a risk measure concerning a multivariate portfolio. Here we focus on the insurance business and particularly on the underwriting risk side, i.e., on quantifiable risks faced by an insurance company and entailed in his specific business. Hence, we do not concern ourselves with the risk-related concept of uncertainty. The Solvency II regulatory framework (see CEIOPS 2007; European Commission 2010) suggests a risk aggregation model resting on a standard formula for the computation of solvency capital requirements. This standard formula aggregates, at least in its original version, different risk’s modules, considering only the linear correlation of them, ignoring any kind of tails dependencies; this drawback is sometimes mitigated by a calibration of the correlations that takes into account also the empirical tail dependences in one year. However, the tails do indeed represent the most interesting part of the distribution for solvency reasons and consequently the standard formula has been under largely critical scrutiny (see e.g., Filipovic 2009; Ronkainen and Koskinen 2007; Sandström 2007).

As an alternative, the directive warrants insurers to adopt an internal model to calculate the solvency capital requirements which should depend on a value-at-risk approach. The risk measure proposed in the Solvency II directive is the one-year value-at-risk at the level 0.005. Strictly related to the capital requirement is the claims’ reserving that refers to the modeling of the discounted reward process. It is obvious that in order to define it, we need to specify a set of stochastic underlying assumptions and we have at our disposal a large selection of choices in the literature. The first application of a continuous time Markov reward process in life insurance field is attributed to Norberg (1995) while several applications of discrete time Markov reward processes can also be found in Janssen and Manca (2006).

In this paper, we concentrate on an automobile insurance company whose business rests on some form of merit-rating in third-party liability insurance that penalizes at-fault accidents by premium surcharges and rewards claim-free years by discounts. Such a rating system is called a bonus–malus system (BMS). This system is specified by a set of rules assigning premiums and penalties to insureds depending on the class they belong to and by a migration rule that governs the evolution of the system itself built on the actual rating and the experienced number of claims.

We therefore present here a new model to compute the loss distribution of an automobile insurance company’s portfolio evolving by a BMS. We admit a continuous evolution of the system depending on a migration rule which is refreshed in discrete time, i.e., at the monitoring times.

Therefore, the migration probabilities are discretely updated through a technique relying on the combinatorial distributions of the claims’ arrival in the rating classes. This technique, a development of Bernardi and Romagnoli (2016), is copula-based since the copula is the tool through which we can represent the co-movement between claims’ arrivals, and distorted due to the formalization of an arrival policy of claims, that restricts the set of combinatorial distributions to those representing the most probable scenarios and then impacts on and distorts the loss function. Moreover, we account for a possible hierarchy in the dependency structure which has a twofold impact, i.e., in the aggregation step and also in the definition of the random matrix that formalizes the arrival policy of claims. These features of the suggested monitoring technique enable us to set us apart from the well-known generalized linear models, where the frequency of claim is recovered for any single group by a regression on the risk’s factors (among them eventually the BM claim’s history). In our model, the dependences from the risk’s factors are taken into account in the clustering phase: this then leads to a reduction of the complexity corresponding to the number of homogeneous classes defined. Moreover, the novelty of the technique introduced here can be appreciated in the global vision of the computation as well, where the whole system, i.e., all the classes considered together and not individually, is analyzed: consequently also the contagion and the effects induced by the hierarchical dependences of groups have an important role in defining the set of possible scenarios.

In the advocated monitoring phase, the migration probabilities and the loss function are evaluated as functions of the copula volumes, a concept well-known in copula theory (see Nelsen 2006 and Joe 1997). In Cherubini and Romagnoli (2009) and in Bernardi and Romagnoli (2011), an algorithm was proposed to compute analytically such volume in particular copulas’ families.

Finally, an interesting feature of the proposed model is to join a continuous time evolution of the demographic-economic risk, i.e., the systemic risk of insurance market, with a discrete-time hierarchical copula-based representation of the idiosyncratic risk of the multivariate portfolio of the company whose top level of the hierarchy stands for the systemic dependency itself. The demographic-economic risk is modeled as an epidemic model (see Allen 2007) with demographic stochasticity formalized as a n-dimensional SDE dependent on the migration’s probabilities governing the BMS. On the other hand, the idiosyncratic risk, which is given by a complex network of the claims’ arrivals (as a matter of fact the idiosyncratic risk’s component depends on individual features of insureds which imply a number of connections among claims’ arrivals), is strictly linked to the copula function, representing the dependency structure of the network and potentially including any kind of tail dependency, that provides the inputs of the demographic-economic evolution system. It is exactly this connection of a copula-based model, that is essentially a static tool, and a dynamic demographic-economic environment, whose evolution depends on the output of the copula-based one, which justifies our claim of a completely new approach. The connection of idiosyncratic and systemic risk is circular, meaning that from the copula-based model we can recover at time t the migration’s probabilities: they will then in turn let the dynamic system to continuously evolve until the immediate next monitoring date $t+1$, thus producing the input to update the migration’s probabilities set through the copula-based model and so on and so forth. At every monitoring instant, the copula-based model computes the migration’s probabilities and the loss function which makes provision for a discrete-time dynamic of the claims’ reserving and the capital requirements.

Our presentation relies on a very general framework, whose range of applicability certainly extends well over and beyond the more specific target applications studied in detail in the subsequent subsections. We have deemed it nevertheless of some interest to be able to exhibit here this more comprehensive scheme, summed up in Eqs. (4) and (7), since it lays the foundational structure within which further more extensive results will be proved.

The paper is organized as follows: in Sect. 2, we put forward a discussion of the demographic-economic stochastic evolution and the idiosyncratic copula-based network to recover the migration’s probabilities. The risk aggregations problem and the claims’ reserving is also discussed; in Sect. 3, we present an empirical application grounded on real data coming from the General Insurance Association of Singapore. The model is then implemented considering different kind of hierarchy and the results are compared in terms of capital requirements; in Sect. 4, we finally draw a number of conclusions.

2 A new BMS with continuous-time evolution and discrete monitoring

The proposed model joins a continuous time evolution of the demographic-economic risk with a discrete-time hierarchical copula-based representation of the idiosyncratic risk of the multivariate portfolio of the company.

The demographic-economic risk is modeled as an epidemic model (see Allen 2007) and provides the evolution in continuous time of the insureds, aggregated in homogeneous classes of risk; it is formalized as a n-dimensional SDE, dependent on the migration’s probabilities governing the BMS.

On the other hand, the idiosyncratic risk, which is given by a complex network of the claims’ arrivals, is strictly linked to the copula function, representing the dependency structure of the network. The modeling of this risk is in discrete-time and provides the inputs of the demographic-economic evolution system.

At every monitoring time, the copula-based model computes the migration’s probabilities and the loss function which makes provision for a discrete-time dynamic of the claims’ reserving and the capital requirements. The migration’s probabilities let the dynamic system to continuously evolve until the immediate next monitoring date, thus producing the input to update the migration’s probabilities set through the copula-based model and so on and so forth.

A scheme of the model is proposed in Fig. 1. Here the four decorated circles stand for the classes of risk: their composition evolves as a function of the continuous dynamic of the population till the next monitoring date (represented by the black bullets at the bottom of the figure). The discrete monitoring allows to update the migration probabilities governing the continuous evolution of the population until the next monitoring date is reached and to evaluate the forecast figures concerning the risk’s management activities.

Fig. 1

Scheme of a migration’s system organized in 4 classes: continuous evolution of the population with discrete time updating of the inputs

2.1 The demographic-economic evolution system in continuous time

Having in mind a motor car insurance, we arrange N insureds within n classes of risk (also called rating classes) according to several characteristics such as age of the driver, sex, region, type of car, mileage and so on. A set of rules assigning premiums and penalties to insureds, depending on the class they belong to and the recorded claims, will be taken for granted.

Moreover, we presuppose that the system evolves because the insureds may modify their status by changing class. The rules governing the evolution are expressed by a migration’s function that associates the actual rating class and the experienced number of claims to the new rating class.

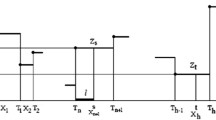
In order to describe our migration’s assumption, we review a general model system as presented in Allen (2007). Let $\varvec{X}(t)=[X_{1}(t), X_{2}(t), \dots X_{n}(t)]^T$ denote the vector whose j-th entry represents the number of insureds belonging to class j at time t and we consider a migration’s assumption sufficient to determine the evolution of the insureds’ population once the actual allocation of all the insureds at time $t=0$ is known. It is assumed that in a small time $\varDelta t$ every state $X_{j}$ can change by $-1$, 0 or $+1$. Let $\varDelta {\mathbf {X}}(t):=\varvec{X}(t+\varDelta t)-\varvec{X}(t)$ be the global change in the time interval $[t,t+\varDelta t]$. As illustrated in Fig. 2, for $j \in \{1, \ldots , n-1\}$ we denote by $\alpha _{2j-1}$ the probability per unit of time of the change $\varDelta {\mathbf {X}}(t) =-e_j+e_{j+1}$, where $\{e_1,...,e_n\}$ denotes the canonical bases of ${\mathbb {R}}^n$; more precisely,

$$\begin{aligned} \alpha _{2j-1}(t,x):={\mathbb {P}}(\varDelta \varvec{X}(t)=-e_j+e_{j+1}|\varvec{X}(t)=x)/\varDelta t. \end{aligned}$$

This corresponds to the case where the state j decreased of one unit, the state $j+1$ increased of one unit while all the other states remained unchanged. Similarly, we let $\alpha _{2j}$ denote the probability of the change $\varDelta {\mathbf {X}}(t) =-e_{j+1}+e_{j}$. In addition, we write $\beta _{2j-1}$ (resp. $\beta _{2j}$) for the probability of negative (resp. positive) interaction of state $X_{j}$ with the outside, $j\in \{1, \ldots , n\}$.

We observe that the extreme classes are characterized by modified probabilities to access from outside that include the upgrade/downgrade probabilities, respectively, i.e., ${\hat{\beta }}_{2}={\beta }_{2}+p_1^u$ and ${\hat{\beta }}_{2n}={\beta }_{2n}+p_n^d$ where $p_1^u$ stands for the upgrading probability of class 1 while $p_n^d$ is the downgrading probability of class n.

The probabilities associated to those changes not explicitly specified in Table 1 are assumed to be zero. We also remark that in order to reduce the complexity of the system, we are assuming to have a migration rule that admits movements only from the starting class to one of the two neighboring classes, depending on the revealed number of claims at the previous monitoring date, i.e., to have a downgrade in case of at least one recorded accident or an upgrade otherwise (in case of no recorded accidents). The two extreme classes constitute an exception, because they remain stable for the upgrade/downgrade, respectively. Therefore, we assume to penalize in the same measure for one or more than one accident. Nevertheless, we can imagine a different evolution rule where the penalty is double in case of more than one accident or any other different rule of migration.

Fig. 2

The representative n-state dynamical system

Table 1 Possible changes in the representative n-state system with the corresponding probabilities

The possible changes and the related probabilities of these changes are shown in Table 1. There are a total of $4n-1$ changes with positive probabilities.

Following (Allen 2007), we can now write

$$\begin{aligned}&{\mathbb {P}}({\mathbf {X}}(t+\varDelta t)=x)\\&\quad ={\mathbb {P}}({\mathbf {X}}(t+\varDelta t)=x|{\mathbf {X}}(t)=x){\mathbb {P}}({\mathbf {X}}(t)=x)\\&\qquad +\sum _{i=1}^n{\mathbb {P}}({\mathbf {X}}(t+\varDelta t)=x| {\mathbf {X}}(t)=x+e_i){\mathbb {P}}({\mathbf {X}}(t)=x+e_i)\\&\qquad +\sum _{i=1}^n{\mathbb {P}}({\mathbf {X}}(t+\varDelta t)=x| {\mathbf {X}}(t)=x-e_i){\mathbb {P}}({\mathbf {X}}(t)=x-e_i)\\&\qquad +\cdot \cdot \cdot \\&\quad =\left( 1-\varDelta t\left( \sum _{i=1}^{2n-2}\alpha _i(t,x)-\sum _{i=1}^{2n}\beta _i(t,x)\right) \right) {\mathbb {P}}({\mathbf {X}}(t)=x)\\&\qquad +\sum _{i=1}^n\beta _{2i-1}(t,x+e_i){\mathbb {P}}({\mathbf {X}}(t)=x+e_i)\\&\qquad +\sum _{i=1}^n\beta _{2i}(t,x-e_i){\mathbb {P}}({\mathbf {X}}(t)=x-e_i)\\&\qquad +\cdot \cdot \cdot . \end{aligned}$$

If we divide both sides by $\varDelta t$ and Taylor-expand in the variable x the functions $p(t,x):={\mathbb {P}}({\mathbf {X}}(t)=x)$ and the probabilities $\alpha$’s and $\beta$’s, we obtain a Fokker–Planck partial differential equation for the density p(t, x). Such equation is canonically associated to the stochastic differential equation

$$\begin{aligned} \left\{ \begin{array}{l} d{\mathbf {X}}(t) = {\mu }(t,\varvec{X}(t))dt + B(t,\varvec{X}(t))d{\mathbf {W}}(t)\\ {\mathbf {X}}(0) = {\mathbf {X}}_{0} \end{array}\right. \end{aligned}$$

(1)

where ${\mathbf {W}}(t) = [W_{1}(t),W_{2}(t), \ldots , W_{n}(t)]^{T}$ is an n-dimensional standard Brownian motion, B(t, x) is the unique symmetric square root of the covariance matrix

$$\begin{aligned} V(t,x) := {\mathbb {E}}((\varDelta \varvec{X}(t))(\varDelta \varvec{X}(t))^{T}|{\mathbf {X}}(t)=x)/\varDelta t, \end{aligned}$$

and

$$\begin{aligned} {\mu }(t,x): = {\mathbb {E}}(\varDelta \varvec{X}(t)|{\mathbf {X}}(t)=x)/\varDelta t. \end{aligned}$$

We refer the reader to Allen (2007) for more details on this procedure. Using the values from Table 1, we get that

$$\begin{aligned} {\mu }(t,x)= & {} (\alpha _{2} -\alpha _{1}+ {\hat{\beta }}_{2} -\beta _{1})e_{1}\nonumber \\&+\sum _{j=2}^{n-1}(\alpha _{2j} -\alpha _{2j-1}+\alpha _{2j-3}-\alpha _{2j-2}+\beta _{2j} -\beta _{2j-1})e_{j} \nonumber \\&+ (\alpha _{2n-3}-\alpha _{2n-2} +{\hat{\beta }}_{2n} -\beta _{2n-1})e_{n}. \end{aligned}$$

(2)

By the same token, denoting by $M_{j} = (e_{j} -e_{j+1})\otimes (e_{j} -e_{j+1})$, $1 \leqq j \leqq n-1$ we get:

$$\begin{aligned} V(t,x)= & {} \sum _{j=2}^{n-1}(\beta _{2j-1}+\beta _{2j})e_{j}\otimes e_{j} + (\beta _{1}+{\hat{\beta }}_{2})e_{1}\otimes e_{1}\nonumber \\&+(\beta _{2n-1}+{\hat{\beta }}_{2n})e_{n}\otimes e_{n}+ \sum _{j=1}^{n-1}(\alpha _{2j-1} + \alpha _{2j}) M_{j} .\nonumber \\ \end{aligned}$$

(3)

It is easy to see that $V_{11} = \gamma _{1} + \delta _{1}$, $V_{jj} = \gamma _{j} + \delta _{j} + \delta _{j-1}$, $2 \leqq j \leqq n-1$ and $V_{nn} = \gamma _{n} + \delta _{n-1}$, where we have put $\gamma _{j} := \beta _{2j-1} + \beta _{2j}$, $1< j < n$, $\gamma _{1}: = \beta _{1} + {\hat{\beta }}_{2}$, $\gamma _{n}: = \beta _{2n-1} + {\hat{\beta }}_{2n}$ and $\delta _{j}:= \alpha _{2j-1} + \alpha _{2j}$, $1 \leqq j \leqq n-1$.

We now aim to simplify the stochastic differential Eq. (1). For that, we recall another usual fact we will have a chance of using several times in the following. It is a consequence of the Martingale Representation Theorem (M.R.T.): namely, if $W_{j}$, $j=1,2$ are two independent Brownian motions then there exists another Brownian motion $W_{3}$ such that

$$\begin{aligned} \int _{0}^{t}f(s)dW_{1}(s) + \int _{0}^{t}g(s)dW_{2}(s) = \int _{0}^{t}\sqrt{f^{2}(s) + g^{2}(s)}~dW_{3}(s), \end{aligned}$$

for suitably regular Itô’s integrable functions f, g.

Let us now consider the j-th equation in system (1):

$$\begin{aligned} dX_{j}(t) = \mu _{j}(t,\varvec{X}(t))dt + \sum _{l=1}^{n}B_{jl}(t,\varvec{X}(t))dW_{l}(t). \end{aligned}$$

Applying the previous remark, we get that there exists a new Brownian motion $W_{j+n}$ such that the preceding equation becomes

$$\begin{aligned} dX_{j}(t) = \mu _{j}(t,\varvec{X}(t))dt + \sqrt{\sum _{l=1}^{n}B_{jl}(t,\varvec{X}(t))^{2}}dW_{j+n}(t). \end{aligned}$$

However, since V and B are symmetric and $B^{2} =V$ we have that

$$\begin{aligned} V_{jj}= \sum _{l=1}^{n}B_{jl}B_{lj} = \sum _{l=1}^{n}B_{jl}^{2}. \end{aligned}$$

Therefore, the system (1) reduces to

$$\begin{aligned} \left\{ \begin{array}{l} d{\mathbf {X}}(t) = {\mu }(t,\varvec{X}(t))dt + D(t,\varvec{X}(t))d{\tilde{\mathbf {W}}}(t)\\ {\mathbf {X}}(0) = {\mathbf {X}}_{0} \end{array}\right. \end{aligned}$$

(4)

where ${\tilde{\mathbf {W}}} = \{W_{j+n}\}_{1 \leqq j \leqq n }$ and $D =\mathrm {diag}(\sqrt{V_{jj}})$ (of course, the components of the new Brownian motion $\tilde{W}$ will be in general correlated). Here, we can notice how the system (4) reduces for $\alpha$ and $\beta$ being affine functions of $\varvec{X}$ to the system studied in Duffie and Kan (1996). A final remark is in order for the total number of insureds $N(t) := \sum _{j=1}^{n}X_{j}(t)$. From

$$\begin{aligned} dX_{j}(t) = \mu _{j}(t,\varvec{X}(t))dt +\sum _{l=1}^{n}B_{jl}(t,\varvec{X}(t))dW_{l}(t), \end{aligned}$$

which holds for every $j \in \{1,\ldots , n\}$, we get that

$$\begin{aligned} dN(t)= & {} d \left( \sum _{j=1}^{n}X_{j}(t) \right) = \left( \sum _{j=1}^{n}\mu _{j}(t,\varvec{X}(t))\right) dt\nonumber \\&+ \sum _{j=1}^{n}\sum _{l=1}^{n}B_{jl}(t,\varvec{X}(t))dW_{l}(t). \end{aligned}$$

(5)

From (5), we obtain

$$\begin{aligned} dN(t) = m(t,\varvec{X}(t))dt + \sum _{l=1}^{n} \left( \sum _{j=1}^{n} B_{jl}(t,\varvec{X}(t))\right) dW_{l}(t), \end{aligned}$$

(6)

where we set $m(t,x) := \sum _{j=1}^{n}\mu _{j}(t,x)$. Applying again the M.R.T., we have that there exists a Brownian motion ${\hat{W}}$ such that Eq. (6) becomes

$$\begin{aligned} dN(t) = m(t,\varvec{X}(t))dt + \sqrt{\sum _{l=1}^{n}\left( \sum _{j=1}^{n} B_{jl}(t,\varvec{X}(t))\right) ^{2}}d{\hat{W}}(t). \end{aligned}$$

But it is easy to verify that:

$$\begin{aligned} \sum _{l=1}^{n}\left( \sum _{j=1}^{n} B_{jl}(t,x)\right) ^{2}= & {} \sum _{j,h=1}^{n}V_{jh} = \sum _{j=1}^{n}\gamma _{j} \\= & {} \sum _{j=1}^{n}\beta _{2j-1} + \sum _{j=2}^{n-1}\beta _{2j}+{\hat{\beta }}_{2}+{\hat{\beta }}_{2n}, \end{aligned}$$

and

$$\begin{aligned} m(t,x) = -\sum _{j=1}^{n}\beta _{2j-1} + \sum _{j=2}^{n-1}\beta _{2j} +{\hat{\beta }}_{2}+{\hat{\beta }}_{2n}. \end{aligned}$$

As an aside, if we assume for instance that the net interaction of our system with the outside world is null also considering the stability of the extreme classes for the upgrading/downgrading, i.e., $\sum _{j=1}^{n}\beta _{2j-1} = \sum _{j=2}^{n-1}\beta _{2j}+{\hat{\beta }}_2+{\hat{\beta }}_{2n}$ and that the total incoming (or out-coming) only depends on N(t) , a not unreasonable assumption, we end up with

$$\begin{aligned} dN(t) = \sqrt{2\left( \sum _{j=2}^{n-1}\beta _{2j}(N(t))+{\hat{\beta }}_2(N(t))+{\hat{\beta }}_{2n}(N(t))\right) }d{\hat{W}}(t),\nonumber \\ \end{aligned}$$

(7)

for the evolution of N(t) . Suitable assumptions on

$$\begin{aligned} \sum _{j=2}^{n-1}\beta _{2j-1}(N) +{\hat{\beta }}_2(N)+{\hat{\beta }}_{2n}(N), \end{aligned}$$

as a function of N will guarantee strong existence, uniqueness and other features. For instance, if we assume the functions $\beta$ to be affine in N, then Eq. (7) becomes a so-called square root process (see e.g., Mao 2008 for its properties and applications).

We observe that, assuming the probabilities $\alpha$ and $\beta$ in Table 1 to be constant (i.e., independent of t and x), then the system (4) or equivalently (1) is explicitly solvable. More precisely, referring to the system (1) we can write in this case

$$\begin{aligned} \varvec{X}(t)=\varvec{X}_0+ \mu t + B\varvec{W}(t), \end{aligned}$$

where now $\mu$ and B are constant vector and matrix, respectively, obtained as before by the formulas (2), (3) and $B^2=V$. Therefore, $\{\varvec{X}_t\}_{t\ge 0}$ is a continuous n-dimensional Gaussian process starting at $\varvec{X}_0$ and with mean vector $t\mu$ and covariance matrix $tBB^T=tB^2=tV$. We remark that, in order to prevent possible negative values of the components of $\varvec{X}$, we implicitly work with $\max \{X_j(t),0\}$ instead of $X_j(t)$ for any $j\in \{1,...,n\}$.

In the following, we will focus on a special case represented by the assumption of a demographic-economic evolution in continuous time with a discrete monitoring. At every monitoring date (that will be defined in terms of a multiple of the evolution’s step), the inputs of the system will therefore be refreshed and the claims’ reserving evaluated. Hence, hinging on the updated system, the population will evolve until the next monitoring date,where the migration’s probabilities will be refreshed anew. The system then evolves continuously even if the information is checked and the network is refreshed discretely, in line with the periodic deadlines in matter of risk management and regulation concerning the claims’ reserving activity.

2.2 The discrete-time monitoring and the migration’s probabilities: the distorted copula-based approach

We point out that the continuous time dynamic model described above is coupled with a discrete monitoring assumption corresponding to the periodic deadlines $\{t_1,t_2,...,t_n\}$ where the claim reserving activity must be set. We thus assume to position ourselves at the starting time $t_0$ and to evaluate the risk with a time horizon $t_1$ by a forward looking approach.

At the future time $t_1$ and at every following monitoring date, given the historical frequencies distributions of accidents per class, we will retrieve the dependency structure of classes and utilize a sampling procedure to recover the inputs of our dynamic system, i.e., the migration’s probabilities per class according to a given migration rule R. Such a procedure corresponds to an advanced version of the Distorted Hierarchical Copula model (see Bernardi and Romagnoli 2016 and Bernardi and Romagnoli 2021). Nevertheless the model proposed here differs notably from its predecessor, since it deals with repeatable events, with a stochastic number of repetitions while in the cited paper one worked only with non-repeatable events. This is a combinatoric framework set up to recapture the distribution of a counting variable that considers the rule responsible for the arrival of claims (called arrival policy): the arrival looks like the attraction by a magnetic field, with an intensity proportional to a given probability (that is the probability of event’s occurrence) where the joint occurrences of events are described by a dependency structure possibly hierarchical. Thus, a hierarchical structure induces a twisting on the arrival of claims, which in turn characterizes the arrival policy together with the marginals. The main new feature of this approach resides in considering the impact of the hierarchy not only on the aggregation step, i.e., in the computation of the probability of every scenario, but also on the combinatorial distribution phase, i.e., in the claims’ arrival, thus allowing for contagious phenomena.

An arrival policy is formalized through a random matrix ${\mathbf {A}}$, called arrival matrix.

Definition 1

(Arrival matrix)

Given n groups with dependence structure represented by a copula function C and of cardinality $\{{X}_j,j=1,...,n\}$ at a given monitoring time, i.e., $t_1$, let k denote the maximum individual claim’s number and set $n_j:=kX_j$, i.e., the maximum claim’s number for the jth group. The arrival matrix is a random matrix ${\mathbf {A}}$ with components

$$\begin{aligned} A_{ij}=\sum _{s=1}^{X_j}a^s_{ij}, \end{aligned}$$

where $a^s_{ij}$ denote the i-th realization of dependent r.v.s standing for the number of claims recorded by the s-th individual who belongs to the j-th group, according to a copula $C^j$, such that

$$\begin{aligned}a^s_{ij}=\left\{ \begin{array}{ll} h\in {\mathbb {N}}\cap [1,k] &{}\quad \text {with probability } p^{h,s}_j\\ 0 &{}\quad \text {with probability } 1-\sum _{h=1}^{k}p^{h,s}_j \end{array}\right. \end{aligned}$$

where $h:\varOmega \rightarrow \{0,...,k\}$ is a r.v. representing the number of individual claims recorded in the period from $t_0$ to the monitoring time $t_1$, and $p^{h,s}_j$ are conditional probabilities of dependent events, hence decreasing in h.

We observe that every row of ${\mathbf {A}}$ identifies a possible scenario concerning the distribution of the random events in n groups. Moreover, we point out that the number of columns of ${\mathbf {A}}$ corresponds to the dimension of the r.v.s set, i.e., n, while the number of rows represents the number of distorted combinatorial distributions or the number of the combinatorial distributions of claims considered more probable.

As a matter of fact, the arrival policy distorts the matrix of the combinatorial distributions of claims, noted as ${\mathbf {E}}$, in such a way that some of these become negligible. Hence, the mass of probability is no longer equally distributed among the possible scenarios but turns out to be actually concentrated on the subset of the distorted combinatoric distributions. From a methodological point of view, in order to build the matrix ${\mathbf {A}}$ we need to sample from the copula function representing the dependency structure among variables.

Example 1

Assuming to have three BM classes, whose (between-groups) dependence structure is represented by copula C and whose cardinality at time $t_1$ (i.e., at the first monitoring date) turns out be $X_1=3,X_2=1$ and $X_3=2$, respectively, as output of the evolution system described in section refevo. Let be $k=3$ the max number of claims per insured and $C_1,C_2,C_3$ the within-groups dependences. Given the overall dependences and their hierarchy (the between-link can be on the top of the hierarchy, or we can imagine to connect the groups at different levels, realizing a nested structure as well), we figure out to implement a sampling tool, based on the migration probabilities and the groups’ cardinalities updated at time $t_1$, in order to define the arrival matrix at the same time $t_1$. Two possible realizations/scenarios (i.e., two rows of matrix ${\mathbf {A}}$ are going to be considered) might be the following:

$$\begin{aligned} \left\{ \begin{array}{ccc} {[}0\quad 0\quad 3]\rightarrow {A}_{11}=3 \quad &{} [0]\rightarrow {A}_{12}=0 \quad &{} [0\quad 0]\rightarrow {A}_{13}=0\\ {[}2\quad 1\quad 1]\rightarrow {A}_{21}=4 \quad &{} [2]\rightarrow {A}_{22}=2 \quad &{} [1\quad 0]\rightarrow {A}_{23}=1\\ \end{array}\right\} , \end{aligned}$$

where, for example the first entry, i.e., 3, corresponds to the sum of recorded claims $a_1^s$ of insureds $s=1,2,3$ in the first class, in the first scenario.

We assume to work with a copula belonging to the comprehensive Archimedean family, i.e., a family where any kind of tail dependence is permitted, by choosing different copulas in the same class. As far as the Hierarchical Archimedean family is concerned, we refer to the related large strand of the literature (see Okhrin et al. 2013a, b and Okhrin and Ristig 2014) and the sampling algorithm detailed in Bernardi and Romagnoli (2016) and in Hofert and Mächler (2011), for nested copulas, i.e., tree structures where the outermost Archimedean copula is called root copula. The basic idea of this procedure is to provide $2^n$ samples from the common dependency structure and transform the obtained variates to the multinomial margins $a_{ij}^s$. By this device, we create the arrival matrix ${\mathbf {A}}$, whose i-th row is given by vector $A_i$. Finally, we observe that the distortion function ${\mathcal {D}}$, represented by the sampling algorithm, which is a function of the set of copula’s generators $\{\phi _j, j=1,...,n-1\}$ and the set of margins’ means per class $\{p_j^h,j=1....,n\}$, gives the arrival matrix as a distorted version of the matrix ${\mathbf {E}}$, i.e., ${\mathbf {A}}={\mathcal {D}}({\mathbf {E}})$. The distortion function ${\mathcal {D}}$ is represented by the sampling algorithm developed in Hofert and Mächler (2011), in case of nested Archimedean copulas.

As seen before, the entries of the arrival matrix at time t are the discrete r.v.s $a_j^s$ with values in the natural numbers set $\forall j,s$, representing the number of success in k-dependent trials. Therefore, to recover this matrix we must consider the available information at this time, i.e., the probabilities ${\mathbb {P}}=\{p^{h}_j,h=0,...,k,j=1,...,n\}$ that coincide with the mean historical frequencies of the events for every class j (i.e., the event to record h claims in class j). The same holds true for every following monitoring dates. Then the dynamic system will evolve in accord to a given migration’s rule and the corresponding migration’s probabilities recovered through the distorted copula approach, whose pivotal input is the discussed current arrival matrix, as will be explained in more detail in the following.

In order to recover the migration’s probabilities given a migration’s rule R, we refer to the period $]t_0,t_1]$ and we define $H^{j+1}_{ij}=\sum _{s=1}^{X_j(t_1)}{\mathbf {1}}_{\{R^{j,j+1}(a^s_{ij})\}}$ where $R^{j,j+1}$ stands for the migration’s rule from class j to class $j+1$, which must depend on the number of claims recorded in the j-th class. Therefore, we assume to have a strictly ordered ranking among the classes, whatever it is but in line with the migration’s rule R. This is the i-th realization of a r.v. $H^{j+1}_{j}$ that counts the events in favor to an upgrade, from class j to class $j+1$, according to the migration’s rule $R^{j,j+1}$. Hence, the corresponding migration’s probability is given by $p^{j,j+1}(t_1)=\frac{{\mathbb {E}}^{{\mathbb {P}}}(H^{j+1}_{j}|{\mathcal {F}}_{t1})}{X_j(t_1)}$, where $H^{j+1}_{j}$ denotes the counting r.v. favoring an upgrade. For example, if we consider a particular migration’s rule granting to upgrade/downgrade (of one class) depending on the recorded claims’ arrival, it is useful to introduce a new matrix $\varvec{H}$, whose entries are $H_{ij}=\sum _{s=1}^{X_j(t_1)}{\mathbf {1}}_{\{a^s_{ij}=0\}}$. The corresponding r.v. $H_j$ counts the number of insureds in class j that have not recorded any claims in $]t_0,t_1]$. Hence, dependent on a migration’s rule complying with the upgrade iff no claims are recorded, the upgrading probability of class j at $t_1$ is given by $p_j^u(t_1)=\frac{{\mathbb {E}}^{{\mathbb {P}}}(H_{j}|{\mathcal {F}}_{t1})}{X_j(t_1)}$ while the downgrading one would be $p_j^d(t_1)=1-p_j^u(t_1)$. In case of an open system, we must take into account also a third probability, which is usually residual, corresponding to the event of an external entry or exit.

Example 2

Following Example 1, if the migration policy sets an upgrade in case of zero-recorded claims, the corresponding realizations of number of upgraded insureds are:

$$\begin{aligned}\left\{ \begin{array}{ccc} {H}_{11}^2=2 \quad &{} {H}_{12}^3=1 \quad &{} {H}_{13}^3=2\\ {H}_{21}^2=0 \quad &{} {H}_{22}^3=0 \quad &{} {H}_{23}^3=1\\ \end{array}\right\} ,\end{aligned}$$

where ${H}_{11}^2$ stands for the first realization of the number of upgrading from class 1 to class 2. We observe that there are no upgrading for the third class, since the BM structure foreseen only 3 classes. Therefore, matrix ${\mathbf {H}}$ is given as

$$\begin{aligned}{\mathbf {H}}=\left[ \begin{array}{ccc} 2 \quad &{} 1 \quad &{} 0\\ 0 \quad &{}0 \quad &{} 0\\ \end{array}\right] ,\end{aligned}$$

and the corresponding probabilities to upgrade are:

$$\begin{aligned}\left\{ \begin{array}{ccc} p_1^u=\frac{2}{3} \quad &{} p_2^u=1 \quad &{} p_3^u=0\\ p_1^u=0 \quad &{} p_2^u=0 \quad &{} p_3^u=0\\ \end{array}\right\} .\end{aligned}$$

Finally, assigning equal probability to the two scenarios, we recover the upgrading and downgrading probabilities at time $t_1$, i.e.,

$$\begin{aligned} p_1^u(t_1)= & {} \frac{1}{3}\rightarrow p_1^d(t_1)=\frac{2}{3}\\ p_2^u(t_1)= & {} \frac{1}{2}\rightarrow p_2^d(t_1)=\frac{1}{2}\\ p_3^u(t_1)= & {} 0\rightarrow p_3^d(t_1)=1. \end{aligned}$$

These probabilities will be the inputs of the evolution system in $(t_1, t_2)$.

We observe also that $H_{j}$ is a r.v. corresponding to the sum of $X_j$ dependent r.v.s. Therefore, in order to recover its cdf we recall that, given two dependent real-valued r.v.s X and Y defined on the same probability space with corresponding copula $C_{X,Y}(w,\lambda )$ and continuous marginals $F_X$ and $F_Y$, the cdf of $X+Y$ is given by the C-convolution aggregation formula (see e.g., Cherubini et al. 2011), i.e.,

$$\begin{aligned} F_{X+Y}(t)=\int ^{1}_0 D_1C_{X,Y}\left( w,F_Y(t-F_X^{-1}(w)) \right) dw, \end{aligned}$$

where $D_1C(u,v)=\partial _uC(u,v)$ stands for the conditional copula function. We are thus able to recover the cdf of $H_j$ as

$$\begin{aligned} F_{H_j}(t)= F_{a_j^1}(v_1^j) {\mathop {*}\limits ^{C^j}}F_{a_j^2}(v_2^j)...{\mathop {*}\limits ^{C^j}}...{\mathop {*}\limits ^{C^j}} F_{a_j^{X_j}}(v_{X_j}^j), \end{aligned}$$

where the operator ${\mathop {*}\limits ^{C^j}}$ stands for the $C^j$-convolution of $F_{a_j^s},\forall s$, i.e., it is the cdf of the r.v. given by the sum of a set of dependent (through $C^j$) r.v.s. whose cardinality is $X_j$. Therefore, under the exchangeable Archimedean assumption for $C^j$, we have $v_s^j=\frac{y_s}{\sum _{s=1}^{{X}_j}y_s}\,t$, where t is drown from $F_{H_j}$ while $y_s$ is one of the ${X}_j$ uncorrelated draws from a simple Poisson pdf. This works because the Poisson distribution has the property $\varPi _i P(x_i)=P(\sum _i x_i)$. Having so chosen a random value of t, we are then able to randomly select a set ${\mathbf {v}}^j$ with the constraint that their sum equals t (see Whelan 2004). Furthermore, in this case we have

$$\begin{aligned} p_j^u(t_1)=\frac{\sum _{s=1}^{X_j(t_1)}{\mathbf {1}}_{\{v^s_{j}=0\}}}{X_j(t_1)}. \end{aligned}$$

Finally, we point out that in order to recover the distribution of the counting variable $\sum _{j=1}^nA_j$, it is useful to decompose the arrival matrix into several random sub-matrices. In fact, each row i of ${\mathbf {A}}$ is associated to an integer $g\in {\mathbb {N}}$ equal to the sum by row, i.e., $g=\sum _{j=1}^nA_{ij},\forall i$. If we select the rows associated to the same integer g, i.e., to the same number of occurrences of the random event, we generate a sub-matrix ${\mathbf {p}}_{g,n}$ that is the random matrix of distorted combinatorial distributions of g claims into n classes. Indeed, the arrival matrix is the set of all the sub-matrices ${\mathbf {p}}_{g,n},\forall g,g\in {\mathbb {N}},g\le kN$, where $N=\sum _{j=1}^nX_j(t_1)$.

2.3 Risks aggregation and claims’ reserving: the distorted copula-based probability distribution valuation

The following procedure computes the probabilities assigned to the distorted combinatorial distributions of claims, representing the most probable scenarios, given an arrival policy of claims. These scenarios correspond to a set of samples drawn from the dependency structure of the insureds, grouped in a set of rating classes. These probabilities are computed as volumes of the copula that formalizes the dependency structure among variables, and that we assume here to be eventually hierarchical Archimedean (and then distorted by the arrival policy of claims induced by the hierarchy itself), DHC for short.

The following definition generalizes Proposition 2 in Bernardi and Romagnoli (2013) that refers to a non-hierarchical case where the arrival policy is assumed to be homogeneous, assigning the same probability to every scenario.

Definition 2

(DHC volume) Given a hierarchical Archimedean copula function of dimension n, and an arrival matrix ${\mathbf {A}}=\{{\mathbf {p}}_{g,n},g\in {\mathbb {N}},g\le kN\}$, where $N=\sum _{j=1}^nX_j(t)$, the volume of the DHC defined by the n-dimensional box ${\mathbf {S}}=[{\mathbf {u}}^{{\overline{h}}},{\mathbf {v}}]$ with ${\mathbf {u}}^{{\overline{h}}},{\mathbf {v}}\in [0,1]^n, {\mathbf {u}}^{{\overline{h}}}\le {\mathbf {v}}, {{\overline{h}}}=1,...,k\varvec{X}(t)$, may be represented as:

$$\begin{aligned} V_{DHC}({\mathbf {S}})=\sum _{g=0}^{kN}(-1)^{g}\sum _{i=1}^{{D}^d(g,n)} DHC({\mathbf {c}}({\mathbf {p}}_{g,n}(i))), \end{aligned}$$

where ${D}^d(g,n)$ denotes the number of distorted combinatorial distribution (d.c.d. ${D}^d(g,n)$ stands for the number of the combinatorial distributions of claims in the corresponding sub-arrival matrix ${\mathbf {p}}_{g,n}$, i.e., the most probable ways to distribute g claims into n rating classes) of g claims into n rating classes, ${\mathbf {p}}_{g,n}(i)$ is the i-th rows of the sub-arrival matrix ${\mathbf {p}}_{g,n}$ whose dimension is ${D}^d(g,n)\times n$, ${\mathbf {c}}({\mathbf {p}}_{g,n}(i))$ is a vector of dimension n such that $c_{i,j}=v_j$ if $p^{(i,j)}_{g,n}=0$ and $c_{i,j}=u_j^{{\overline{h}}}$ if $p^{(i,j)}_{g,n}={{\overline{h}}}$, where $u_j^{{\overline{h}}},v_j$ are the j-th element of the corresponding vectors and $c_{i,j}$ denotes the (i, j)-th element of the corresponding vector and $DHC({\mathbf {c}}({\mathbf {p}}_{g,n}(i)))$ is the hierarchical Archimedean copula computed for the i-th d.c.d. of the sub-arrival matrix ${\mathbf {p}}_{g,n}$.

Fig. 3

Graphical representation of V$_\mathrm {DHC}$(S) in three dimensions

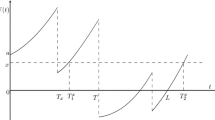
As pointed out previously, our approach is copula-based in the sense that, given a copula function representing the dependency structure of a given set of variables, we consider a random event, i.e., the claim’s arrival which may include such variables, and define a counting variable on this event. Moreover, we consider a particular kind of copula, i.e., the DHC one, which is defined through the arrival policy of claims formalized by the arrival matrix ${\mathbf {A}}$. The main tool of this technique is exactly the volume of such kind of copula that is represented in three dimensions in Fig. 3. As it is clear from the graphical representation of the volume, it is recovered through Definition 2, as a linear combination with sign of several sub-volumes of the 0–1 cube.

Definition 3

(Claims’ counting variable linked to a n-dimensional DHC) In the same setting of Definition 2, the claims’ counting variable linked to the copula function $DHC({\mathbf {c}}({\mathbf {p}}_{g,n}(i)))$ is given by

$$\begin{aligned} r(i) =\sharp ({\mathbf {p}}_{g,n}(i)), \end{aligned}$$

which counts the number of claims in the i-th row of the sub-arrival matrix ${\mathbf {p}}_{g,n}$. Clearly, we have $r(i)=g,\forall i, g\in {\mathbb {N}},g\le kN$ where $N=\sum _{j=1}^nX_j(t)$.

Our aim is to recover the probability distribution of the claims’ counting variable linked to a n-dimensional DHC. In order to achieve this, we consider the distorted setting where the claims’ arrival is studied through the set of scenarios having the greatest probability mass, in accord to a claims’ arrival policy assumption.

Definition 4

(Probability distribution of the claims’ counting variable linked to a n-dimensional DHC) In the same setting of Definition 2, the probability distribution of the claims’ counting variable linked to the n-dimensional DHC, with marginals ${\mathbf {u}}^{{\overline{h}}}\in [0,1]^n,{{\overline{h}}}=1,...,k{\mathbf {X}}(t)$ and arrival matrix ${\mathbf {A}}$, is the function $P_r:[0,kN]\rightarrow [0,1]$ where $N=\sum _{j=1}^nX_j(t)$, such that:

$$\begin{aligned} P_r(g)=\sum _{i=1}^{{D}^d(g,n)}V_{DHC}({\mathbf {S}}_i({\mathbf {p}}_{g,n}(i))),g\in {\mathbb {N}},g\le kN, \end{aligned}$$

where ${\mathbf {p}}_{g,n}(i)$ is the i-th row of the sub-arrival matrix ${\mathbf {p}}_{g,n}\in M({D}^d(g,n)\times n)$ (here $M(x\times y)$ stands for the set of matrices whose dimensions are x and y, respectively), representing the i-th d.c.d. of g claims into n rating classes and where $V_{DHC}({\mathbf {S}}_i)$ is the volume of the DHC computed for the box ${\mathbf {S}}_i=[{\mathbf {u}}_i,{\mathbf {v}}_i]\in {\mathbb {R}}^n \times {\mathbb {R}}^n$, determined for the i-th d.c.d. of g claims into n rating classes following the rule:

• if $p^{(i,j)}_{g,n}=0, u_{i,j}=\sum _{{\overline{h}}=1}^{kX_j}u_j^{{\overline{h}}}$ and $v_{i,j}=1$ for $j=1,...,n$ and $i=1,...,{D}^d(g,n)$;

• if $p^{(i,j)}_{g,n}={{\overline{h}}},{{\overline{h}}}>0, u_{i,j}=0$ and $v_{i,j}=u^{{\overline{h}}}_j$ for $j=1,...,n,{{\overline{h}}}=1,...kX_j(t)$ and $i=1,...,{D}^d(g,n)$,

where $u^{{\overline{h}}}_j,j=1,...,n,{\overline{h}}=1,...kX_j(t)$ are the historical claims’ frequencies for the j-th class.

We observe that the i-th d.c.d. of the sub-matrix ${\mathbf {p}}_{g,n}$ generates a pair of coordinates, i.e., the i-th d.c.d. generates the box ${\mathbf {S}}^i$ where we compute the corresponding DHC-volume. The sum of the volumes computed for all the coordinates generated by the d.c.ds of ${\mathbf {p}}_{g,n}$ represents the probability to count the more likely distributions of g claims, given a claims’ arrival hypothesis, i.e., given ${\mathbf {A}}$.

Example 3

Let us consider the arrival matrix at time $t_1$ of Example 1, i.e.,

$$\begin{aligned}{\mathbf {A}}=\left[ \begin{array}{ccc} 3 \quad &{} 0 \quad &{} 0\\ 4 \quad &{}2 \quad &{} 1\\ \end{array}\right] ,\end{aligned}$$

and be given ${\mathbf {u}}^{{\overline{h}}}$, where $u^{{\overline{h}}_1},{\overline{h}}_1=1,...,9$ gives the probability to record ${\overline{h}}_1$ claims in class 1, $u^{{\overline{h}}_2},{\overline{h}}_2=1,...,3$ gives the probability to record ${\overline{h}}_2$ claims in class 2 and $u^{{\overline{h}}_3},{\overline{h}}_3=1,...,6$ gives the probability to record ${\overline{h}}_3$ claims in class 3. We observe that we are considering only two possible scenarios that correspond to a total number of claims $g_1=3$ and $g_2=7$, respectively. Coherently with the notation of Definition 4, we have:

$$\begin{aligned} {\mathbf {p}}_{3,3}(1)= & {} [3\quad 0\quad 0]\\ {\mathbf {p}}_{7,3}(1)= & {} [4\quad 2\quad 1], \end{aligned}$$

where both the previous sub-matrices account for just one scenario. These sub-matrices must be connected with the corresponding probability of this scenario, evaluated as a volume of the copula which represents the dependence structure of the system; hence, we go on defining the boxes ${\mathbf {S}}_1({\mathbf {p}}_{3,3}(1))$ and ${\mathbf {S}}_1({\mathbf {p}}_{7,3}(1))$. We have:

$$\begin{aligned} p_{3,3}^{(1,1)}= & {} 3\rightarrow u_{1,1}=0,v_{1,1}=u_1^3\\ p_{3,3}^{(1,2)}= & {} 0\rightarrow u_{1,2}=\sum _{{\overline{h}}=1}^3 u_2^{{\overline{h}}},v_{1,2}=1\\ p_{3,3}^{(1,3)}= & {} 0\rightarrow u_{1,3}=\sum _{{\overline{h}}=1}^6 u_3^{{\overline{h}}},v_{1,3}=1, \end{aligned}$$

and ${\mathbf {S}}_1({\mathbf {p}}_{3,3}(1))=[{\mathbf {u}}_1,{\mathbf {v}}_1$], where:

$$\begin{aligned} {\mathbf {u}}_1= & {} [0\quad \sum _{{\overline{h}}=1}^3 u_2^{{\overline{h}}}\quad \sum _{{\overline{h}}=1}^6 u_3^{{\overline{h}}}]\\ {\mathbf {v}}_1= & {} [u^3_1\quad 1\quad 1]. \end{aligned}$$

Similarly, we have:

$$\begin{aligned} p_{7,3}^{(1,1)}= & {} 4\rightarrow u_{1,1}=0,v_{1,1}=u_1^4\\ p_{7,3}^{(1,2)}= & {} 2\rightarrow u_{1,2}=0,v_{1,2}=u_2^2\\ p_{7,3}^{(1,3)}= & {} 1\rightarrow u_{1,3}=0,v_{1,3}=u_3^1, \end{aligned}$$

and ${\mathbf {S}}_1({\mathbf {p}}_{7,3}(1))=[{\mathbf {u}}_1,{\mathbf {v}}_1$], where:

$$\begin{aligned} {\mathbf {u}}_1= & {} [0\quad 0 \quad 0]\\ {\mathbf {v}}_1= & {} [u^4_1\quad u_2^2\quad u_3^1]. \end{aligned}$$

Finally, the volumes $V_{DHC}({\mathbf {S}}_1({\mathbf {p}}_{3,3}(1)))$ and $V_{DHC}({\mathbf {S}}_1({\mathbf {p}}_{7,3}(1)))$, which stand for the probability of these two scenarios, respectively, can be evaluated.

Definition 5

(Cumulated probability distribution of the claims’ counting variable linked to a n-dimensional DHC)

In the same setting of Definition 2 and Definition 4, the cumulative probability distribution of the claims’ counting variable linked to the n-dimensional copula DHC with marginals ${\mathbf {u}}^{{\overline{h}}}\in [0,1]^n,{\overline{h}}=1,..,k{\mathbf {X}}$, is the function $F_r:[0,kN]\rightarrow [0,1]$, $F_r(j)={\mathbb {P}}(r\le j)=\sum _{g=0}^jP_r(g)$ where $P_r(g)={\mathbb {P}}(r=g)$, such that:

$$\begin{aligned} F_r(j)=\sum _{g=0}^i\sum _{i=1}^{{D}^d(g,n)}V_{DHC}({\mathbf {S}}_i({\mathbf {p}}_{g,n}(i))),g\in {\mathbb {N}},g\le kN, \end{aligned}$$

where $V_{DHC}({\mathbf {S}}_i)$ is the volume of the distorted hierarchical Archimedean copula computed in the box ${\mathbf {S}}_i=[{\mathbf {u}}_i,{\mathbf {v}}_i]\in {\mathbb {R}}^n \times {\mathbb {R}}^n$, determined for the i-th d.c.d. of g claims into n rating classes following the rule explained in Definition 4, where ${\mathbf {p}}_{g,n}(i)$ is the i-th row of the sub-arrival matrix ${\mathbf {p}}_{g,n}\in M({D}^d(g,n)\times n)$ corresponding to the i-th d.c.d. of g claims into n classes.

In order to provide the relevant information for risk management activities, we associate a sum of money to the state of the system; we pass then from the probability distribution of a counting variable, i.e., the number of claims at time t, to the definition of a reward process. This will be defined in discrete time corresponding to the set of monitoring dates and it will be characterized by amounts of money that will be positive if they are benefits or negative if they are costs for the insurer. The purpose of this model is to represent a generic insurance portfolio; hence, a useful tool for actuarial problems. Our approach is completely different from previous contributions in the literature because the premiums and benefits are jointly modeled in discrete time and associated to probabilities depending on a complex network where a hierarchical copula stands for the connections of the insureds and governs the happening of claims, making provision for a continuous evolution of the demographic-economic system between two monitoring dates. Therefore, the system evolves continuously even though the information is checked and the network is refreshed discretely: this induces us to overcome on the one hand the static nature of copula-based model and, on the other hand, to introduce a stochastic evolution of the insureds’ population related to the variations of the demographic-economic setting, i.e., the systemic risk of the insurance market.

With a particular kind of insurance with grounds on a BMS in mind, that is an incentive program designed to give a penalty in terms of greater premium to pay for poor performance, we then focus on automobile insurance where the insured’s claim corresponds to any car accident. Obviously this application is not restrictive and sure enough BMS has as of recent been studied with care by corporations for employees or executives unable to meet their goals for instance.

In a BMS automobile insurance the rating, indentified by the class identity, assigns to every insured both the premium to be paid, a function decreasing with the rating and increasing with the recorded claims at the previous monitoring date, and the benefit to receive. The net amount of money given by the difference of premium and benefit received or paid by the insurance company, which depends on the mean claim’s severity, i.e., on the entries of vector ${{\mathbf {P}}}{{\mathbf {r}}}$, and the mean premium per class, placed in vector ${\mathbf {C}}$, characterises the value of the reward process at time t.

Definition 6

(Cumulated probability distribution of the discounted Reward at the monitoring date t) In the same setting of Definition 5, the cumulative probability distribution of the discounted Reward whose single amount per class is given by the entries (which correspond to the difference of the class’s premium and the benefit paid by the insurance company) of the n-dimensional vector ${\mathbf {Y}}e^{-\int _0^t r(u) du}$ and where the short rate r(.) is assumed to be deterministic, is the ${\mathcal {F}}_t$-measurable function $F_{R,t}:[0,\hat{{\mathbf {Y}}}'{\mathbf {X}}(t)e^{-\int _0^t r(u) du}]\rightarrow [0,1]$ such that:

$$\begin{aligned} F_{R,t}(j)=\sum _{g,i:R_{g,n}(t,i)\le j}V_{DHC}({\mathbf {S}}_i({\mathbf {p}}_{g,n}(i))),g\in {\mathbb {N}},g\le kN, \end{aligned}$$

where $\hat{{\mathbf {Y}}}={{\mathbf {P}}}{{\mathbf {r}}}-k{\mathbf {C}}$, $R_{g,n}(t,i)={\mathbf {Y}}'{\mathbf {p}}_{g,n}(i)e^{-\int _0^t r(u) du}$ and as before $V_{DHC}({\mathbf {S}}_j)$ is the volume of the distorted hierarchical Archimedean copula computed for the box ${\mathbf {S}}_i=[{\mathbf {u}}_i,{\mathbf {v}}_i]\in {\mathbb {R}}^n \times {\mathbb {R}}^n$.

As noticed in Djehiche and Löfdahl (2014), the problem of risk aggregation is closely related to that of claims’ reserving. As far as the aggregation of risks and capital charges problems are concerned, the cumulative distribution of the Reward may be used as basic input for an internal model built on a value-at-risk approach over a specified horizon defined as a multiple of the monitoring step. For example, given the cumulative distribution of the discounted t-reward, his p-quantile can be used to compute the value-at-risk over the period [0, t] and recover the capital charge as to be the economic capital, i.e., the distance of the value at time 0 of the portfolio and the p-quantile of the discounted t-Reward. The discounted reward is, realistically, a r.v. representing the systemic risk, i.e., the risk related to the variations of the economic-demographic setting, and the idiosyncratic one, i.e., the risk related to the specific features of the company’s portfolio, at time t of the insurer and his expected value (at time 0) should correspond to the reserve at time 0 for the entire portfolio.

3 Empirical application

In this section, we apply our model to real data in order to consider the aptness of the dependency structure and of the distortion brought about by the arrival policy of claims linked to a portfolio of car’s insurances. The data originate from the General Insurance Association of Singapore, an organization consisting of a set of insurance companies in Singapore (see the organization’s website: www.gia.org.sg). It is a common practice to combine different experiences in a so-called intercompany database in order to glean important information about the competitors. From this database, which has been used in several research projects and publications as Frees and Valdez (2008) and Frees (2010), several characteristics are available to clarify and interpret automobile accident frequency. These characteristics contain vehicle-related variables, for instance age or type, and also person-related level characteristics, likes gender, age or previous driving experiences. We’ll restrict our analysis to data concerning the year 1993 where the documented rewards’ number permits to recover the claims’ frequency of the whole portfolio.

The first thing we must deal with is the classification of insureds in classes of risk. To this purpose, we report in Table 2 the description of the analyzed variables that will be used for clustering.

Table 2 Clustering variables description

The claim’s frequency concerning the period of observation is analyzed in the following tables. The result of 7483 observations, we report in Table 3 at the bottom the number of observations for every number of claims: we observe that the $93.5\%$of the observations didn’t reveal any claim while 487 register at least one claim. Moreover, the effects of the vehicle features concerning the recorded claims are demonstrated here: we notice how cars seem to have a slightly higher experience on claims with respect to other types of vehicles, and the age of vehicle does not seem to have a monotone dependance on the number of claims, showing the maximum impact for age between 1 and 5 years.

Table 3 Claim’s percentage versus vehicles’ features

In Table 4, we just consider the private car segment and report the claim’s frequency for every discussed insured features. We remark how gender doesn’t appear to impact on the claim’s frequency, while at the same time higher frequency is attributed to the class of insured of age between 46 and 65. Finally, the variable NoClaimsDiscount (NCD in the following) discloses an inverse relation of the claim’s frequency and the past experience: better past experience corresponds to lower claim’s frequency.

Table 4 Claim’s percentage versus insureds’ features

Reckoning on the variables described before and following a codification and a normalization toward a homogeneous scale for each and every one of them, we reduce the complexity of the problem by a clustering procedure. Here we decided to implement a semi-unsupervised self-organizing map (SOM for short in the following) which refers to a particular type of artificial neural network advanced by Kohonen (1982) and derived from the Euclidean metric, where the number of clusters is optimal in terms of a minimization of the clustering error defined as a sum of confusions (see Wang et al. 2006). More precisely our purpose is to separate the sample in rating classes as much homogeneous as possible, via a competitive layer for classification problems, composed of a topology function, calculating the neurons positions in a hexagonal pattern and a distance function (that in our application is the Euclidean distance) employed to find the distance between the layer’s neurons once their positions have been given. SOM is a single-layer characterized by a weight function and an input function corresponding to the vectors of the clustering variables described and detailed in Table 2. The layer takes up a weight (that is randomly initialized) from the input: subsequently the processes of adaptation and training renew the weights via the learning function. Training occurs until a maximum number of iterations (fixed on $10^3$ in this application) or until the performance goal is met. In the application at hand, the optimal number of classes turns out to be four.

Table 5 reports the main features defining the four rating classes. The reported percentage of the group’s complexity are particularly descriptive. The first cluster is made up by insured of not specified gender and mainly of age lower or equal than 21, that owned other types of vehicle as motorcycles in a past period whose length goes from 6 to 16 years; they have a medium-low NCD and therefore a quite high claims’ frequency in the past. The second cluster is composed by a population of insureds aged from 35 to 65, more male than female, owning a car whose age is at most 2 years; they have a medium-high NCD and thus a low claims’ frequency. The third cluster is constituted by insureds aged less or equal than 21, no specified gender and owning other types of vehicles of age between 3 and 5 years; they have a low NCD. Finally, the fourth cluster is mainly composed by insured of age from 35 and 65, they are more male than female and they own a car whose age is at most 2 years; they have a low NCD.

Table 5 Features of insureds per clusters

In order to implement the described model, we need to recover the inputs of the dynamic system, i.e., the migration’s probability, based on the available information concerning the risk’s profile of the policies’ holders. We arrive at this via the distorted-copula-based procedure, through which one recovers the needed inputs starting from the network of policies’ holders related by a copula function. The copula function is calibrated from data extrapolating information related to the marginal through an inverse procedure that includes possible contagious and tail dependence effects. Hence, from the clustering information depicted in Table 6, we retrieve the marginal probabilities of claim’s arrival via a Poisson model. The maximum likelihood estimates of the Poisson parameter and the corresponding frequencies are reported in Table 6. Here we have $k=3$ and the group’s cardinalities are detailed into Table 6.

We now move to consider the dependency structure that plays an important role at every level of the hierarchy. As we remarked previously, we choose to work with Archimedean copula functions which are a comprehensive family. In this family, we select three kinds of Archimedean copulas, i.e., Clayton, Gumbel and Frank: they are able to represent all possible kinds of tail dependency (but exclusive positive dependency). Given a decreasing and convex function $\phi :(0,1]\rightarrow [0,+\infty )$ such that $\phi (1)=0$, then the function

$$\begin{aligned} C^{(\phi )}({\mathbf {u}})=\phi ^{-1}\left( \sum _{i=1}^n\phi (u_i)\right) ,\quad \forall u_i\in (0,1],\forall i=1,...,n, \end{aligned}$$

where ${\mathbf {u}}$ stands for the vector of margins, is a n-dimensional Archimedean copula with generator $\phi$. Different choices of generator specify different families of Archimedean copulas. It is important to remark that this class of copulas is commonly used in multivariate applied sciences, because the dependency structure among variables can be explained only by means of a parameter $\alpha$, functionally related to the Kendall’s $\tau$ correlation measure.

To calibrate the dependency structure, we employed the Genest and Rivest (1993) procedure, detailed in Frees and Valdez (1998), and riding on the concordance/discordance of the clusters’ features.

Eventually a goodness-of-fit consideration permits to select the “closest” kind of copula function if compared to the empirical copula. The calibration technique is utilized here using a multistage procedure in the same spirit of Okhrin et al. (2013a); we advance with the estimate starting from the bottom, i.e., the lowest level of the hierarchy, then moving up, with the provision that the copula parameters at lower levels are known. By this token, at each level of this recursive estimation we compute a mean-squared error (MSE for short) that we call partial MSE (PMSE for short) and whose mean among all levels comes into what we call total MSE (TMSE for short). We estimate at first a unique dependency structure at the highest level, a dependency between classes, represented by a Kendall tau, $\tau _1=0.3526$ and a second level vector of dependency parameters representing the dependency within groups

$$\begin{aligned} {\tau _2}=\left[ \begin{array}{ccccc}0.3528&0.4094&0.4276&0.4179 \end{array}\right] . \end{aligned}$$

We observe that the first group seems to have a within dependency very similar to the between one; it might imply that we could improve the setting by increasing the number of clusters in order to identify subclasses with stronger connections. Nevertheless, in this case the increasing in complexity (we implemented two more splitting of the first class) happens to be not justified by the final output improvement; hence, we confirm the clustering in four classes.

We point out that Kendall tau of multivariate Archimedean copulas can be analytically recovered as a function of copula parameter or generator. Table 7 displays the copula parameters and the partial/total mean square errors for the first level of dependency, i.e., $\alpha _1$, and for the dependency within groups, i.e., $\mathbf {\alpha _2}$, estimated following the detailed procedure. The comparison of TMSEs prompts that Clayton copula, whose generator is $\phi (t)=\frac{1}{\alpha }\left( t^{-\alpha }-1\right)$, for $\alpha \in [-1,0)\cup (0,+\infty )$, is the Archimedean copula that best performs the calibration procedure.

Table 6 Marginal frequencies of claim’s arrival per clusters

Table 7 Copulas’ parameters and TMSEs/max PMSEs

Along with the described dependency with a unique level of aggregation between classes, we examine two different hierarchical structure: a partially exchangeable and a not exchangeable nested Archimedean copula function. These kinds of aggregations are depicted in Fig. 4 assuming a 4-dimensional setting. In Fig. 4a, the aggregations have been depicted as couples but they could be generalized positing a second level of aggregation within groups whose cardinality is not necessarily equal to 2. On the other hand, the not exchangeable aggregation is retrieved through a nested aggregation that progresses by a first group aggregation and by a series of single aggregations as shown in Fig. 4b supposing a 4-dimensional setting. In this example, we have a fully nested copula but we could devise also a partially nested case that proceeds by a nested aggregation by groups while by single ones.

Fig. 4

Partially exchangeable and Not exchangeable hierarchical aggregations

We consider the following Archimedean dependency structures:

• 1. One-level dependency structure, represented by a copula function with dependency parameter $\tau _1$.

• 2. Partially exchangeable hierarchical structure, with two dependency’s levels represented by $\tau _1$ and $\overline{{\tau _1}}=[0.4742;0.9069]$. Here the groups’ aggregation includes at first the clusters 1 and 2 and then clusters 3 and 4, whose dependencies are tidily placed in ${\hat{(\tau _1)}}$.

• 3. Not exchangeable partially nested hierarchical structure, whose nesting levels are given by ${\hat{(\tau _1)}}$ $=[0.9069; 0.4537; 0.3526]$. Here the aggregation proceeds starting by clusters 3 and 4, followed by cluster 2 and finally cluster 1, with dependencies tidily placed in ${\hat{(\tau _1)}}$.

We note how the dependency structure influences the claims’ arrivals through the arrival matrix ${\mathbf {A}}$, defining the distorted combinatorial distributions of claims as a determinant of the loss distribution. In our basic scenario, we resolved to compute an arrival matrix of dimension $d\times n$, where $d=2^{10}$ corresponds to the number of combinatorial distributions of the claims. Moreover, we choose to work with a number of trials $N=2^{11}$.

In what follows we shape the dependency structure using the best performing Archimedean copula, i.e., the Clayton one and then we study the listed cases of aggregation, i.e., the not hierarchical Clayton, and the partially/not exchangeable version of the hierarchical Clayton (PEClayton and NEClayton respectively) for the dependency parameters computed starting from the estimated Kendall $\tau _1$, $\varvec{\overline{\tau _1}}$ and $\varvec{\hat{\tau _1}}$. The sampling from the hierarchical Archimedean structures has been done with the algorithm proposed in Savu and Trede (2010). This algorithm is built upon the conditional inversion method.

The exercise we present in this section is assumed to start at the current monitoring time $t_0$; the dataset discussed before corresponds to time $t_0$-information and thanks to the distorted copula-based model we are able to compute the inputs of the evolution model, i.e., the upgrading/downgrading probabilities. We consider a BM system organized in four classes corresponding to the clusters identified before, whose rating level is decreasing from class 1 to class 4, and whose migration’s rule implies an upgrade (a shift of one class in the direction from class 4 to class 1) if no claims are recorded from the previous monitoring date and a downgrade (a shift of one class in the direction from class 1 to class 4) otherwise. In this migration’s rule, we assume that it is not possible to remain in the same class for two consecutive monitoring dates, except for the extreme classes which are stable for upgrading/downgrading, respectively. Obviously, this assumption is not restrictive like as the described migration’s rule. Nevertheless, we assume to work with an open system where all the insureds can leave the company or enter into every class at every time. The incoming/out-coming probability representing the connection of the company to the external insurance market is assumed to be a kind of systemic input that is residual and equal to $p^e=0.001$. Hence, given the downgrading probabilities $p^d_i(t_0),\forall i$, the upgrading probabilities will be $p_i^u(t_0)=1-p_i^d(t_0)-p^e$. They are reported in Table 8 for every case of aggregation detailed before.

3.1 Claim reserving and capital requirement: a forward-looking approach

Claims’ reserving is a very important topic in actuarial science. The most famous models are the chain-ladder method and the Bornhuetter–Ferguson method whose underlying stochastic assumptions are thoroughly discussed in Wüthrich and Merz (2008). Here we introduce an alternative stochastic claim-reserving method to assess the prediction uncertainty relying on the complex evolutionary approach discussed in the previous section. To this purpose, let us consider an horizon T equal to a multiple ${\hat{t}}$ of the monitoring period, i.e., $T=t_0+{\hat{t}}$, and let the system evolve according to the dynamics discussed in Sect. 2. However, the migration’s rule is left as calibrated at time t and put together via the contemplated dependency structure of the insurance company’s portfolio. At every monitoring date, the migration’s probabilities are recomputed using the new cardinalities and they will be used as inputs of the next evolution of the demographic-economic system. The procedure proceeds like this until the horizon is reached. In this way, we can have a forward-looking guess of the insureds’ grades ${\hat{t}}$ monitoring periods ahead. We are also able to evaluate the discounted reward distribution. We assume for simplicity to have a null interest rate, skipping the problem to pass from the forward to the spot evaluation, and we fix the insurance premium equal to euro 1000 in class 1 and increasing of euro 500 for every downgrading till class 4. Moreover, we assume to have the same benefit per claim in every class that is equal to euro 2500 (which is coherent with the mean cost per claim of 2017 IVASS report) and that corresponds to the mean’s claim severity at time t.

Due to the depicted evolution’s system, we recover the future cardinalities of the classes in three monitoring periods ahead, i.e., ${\hat{t}}=1,2,3$. They correspond to semestral periods, i.e., to 180 discretized (daily) steps of the Euler’s discretized version of the dynamic system. We implement 10.000 simulations. When every monitoring period is over, the migration’s probabilities are updated and resting on them the system is left to evolve until the next monitoring period (180 daily steps ahead). The evolution of the insureds’ population is described in Table 9 in terms of the variation of the group’s cardinalities in ${\hat{t}}=1,2,3$ monitoring periods ahead. We point out that the evolution of the extreme classes is comprehensive of both the insureds coming in/going out and those remaining in the same class. As it is clear from the experiment, the system appears to evolve toward a safer structure of the population since the first classes exhibit an increasing behavior while the riskiest one is decreasing. Moreover, the evolution concerning the future three monitoring periods is quite stable in time for all of the discussed aggregation models.

Table 8 Migration’s probabilities at time t: 1-class upgrade/downgrade open BMS with $p^e=0.001$

Table 9 Evolution of the BMS insureds’ population in three semestral monitoring periods

As far as the computation of the capital requirement is concerned , we assume to adopt an internal model organized along a value-at-risk approach. We compute it in terms of the solvency capital requirement, i.e., the amount of funds that EU insurance companies are required to hold, which corresponds to the 0.995-quantile of the loss distribution over one year (0.995-VaR). Moreover, we provide an alternative evaluation of it in terms of the economic capital, i.e., the difference of the value at time t of the portfolio and the 0.05-quantile of the discounted $(t_0+{\hat{t}})$-Reward (0.05-$\varDelta$P). The computation of both asks us to evaluate the cdf of the discounted $(t+{\hat{t}})$-reward and then to recover the value-at-risk over the period $[t_0,t_0+{\hat{t}}]$. We recover the requested cdf by the DHC method implemented on the forecast insureds’ portfolio, referring to the representation of the probabilities as linear combinations of copula’s volumes (see Definition 4). On the other hand, the expected value of the discounted $(t_0+{\hat{t}})$-reward stands for the value at time $t_0$ of the total claims’ reserve. In Table 10, we reported the percentage capital requirement (with respect to the $t_0$-value of the portfolio), assuming to have a null interest rate. Due the depicted evolution’s system, we recover the future cardinalities of the classes in three monitoring periods ahead, i.e., ${\hat{t}}=1,2,3$. They correspond to semestral periods, i.e., to 180 discretized (daily) steps of the Euler’s discretized version of the dynamic system. We implement 10.000 simulations. At the end of every monitoring period, the migration’s probabilities are updated and resting on them the system is left to evolve until the next monitoring period (180 daily steps ahead). The evolution of the insureds’ population is described in Table 9 in terms of the variation of the group’s cardinalities in ${\hat{t}}=1,2,3$ monitoring periods ahead. We point out that the evolution of the extreme classes is comprehensive of both the insureds coming in/going out and those remaining in the same class. As it is clear from the experiment, the system appears to evolve toward a safer structure of the population since the first classes exhibit an increasing behavior while the riskiest one is decreasing. Moreover, the evolution concerning the future three monitoring periods is quite stable in time for all of the discussed aggregation models.

Table 10 Percentage capital requirements in three semestral monitoring periods: 0.995-VaR versus 0.05-$\varDelta$P

We observe that in this experiment both models used to compute the capital requirements demonstrate a movement toward a safer scenario than the actual one; as a matter of fact, the 0.995-VaR is always decreasing with a huge fall in case of nested aggregation (which may be more sensitive to the contagious effect among the risk’s classes), like as the 0.05-$\varDelta$P is always positive, supporting the expected increasing value of the insurance portfolio. The showed pattern of 0.05-$\varDelta$P explains a not always monotone in time behavior but it can be considered quite stable in tendency. We further remark that the capital charges (evaluated at different confidence levels) are convergent after three monitoring periods for the hierarchical aggregation models: they are better in detecting the dependence structure than the non-hierarchical ones. Finally, we point out that the implemented models may represent useful tools for computing the capital requirements in terms of internal models or in the Solvency II framework. Moreover, the inclusion of the insurance risks in Pillar I places Solvency II straight in line to Basel’s requirement as far as the computation methods and the hedging of risks are concerned. As it happens, capital requirements are now approached in a more cautious way, as explained, e.g., by Basel III , where the minimum total capital level (minimum total capital + conservation buffer) is fixed at 10.5 level and by the Basel IV request on prudential reserves, to be expected higher as well (2% more on CET1 ratio). The copula-based models lead to a level that is not fixed within a scope, being flexible and depending on the noticed level of risk, originating from market data and taking into account any kind of dependencies’ effects as contagion and hierarchy on risks. Therefore, the previous empirical exercise enables us to align the copula-based approaches to the current more prudential approaches in capital requirements regulation.

4 Conclusions

The financial crisis of 2008 compelled one to pay much heed to decision-making approaches based on the minimization of a risk measure concerning a multivariate portfolio and highlighted as well the process of risks’ integration as an undeniable instrument of risk management. The main focus in this paper rests on the insurance business: a new model for the integration of risks is presented, making provision for the recovery of the loss distribution of an automobile insurance company’s portfolio, evolving by a BMS with n rating classes linked by a pure hierarchical Archimedean dependency structure. While a continuous evolution of the system is permitted, a migration rule refreshed at discrete time, i.e., at the monitoring times, will serve the dynamical system under study. Therefore, the migration probabilities are discretely updated through a technique based on the combinatorial distributions of claims’ arrival in the rating classes.

The model thus put forward reveals a circular connection of the systemic and the idiosyncratic component of risk:

• The systemic one is represented by the demographic-economic environment that develops continuously as a function of the migration’s probabilities governing the BMS;

• The idiosyncratic one is given by the complex network of the claims’ arrivals, whose dependency structure potentially includes any kind of tail dependency and hierarchy, thus providing the inputs of the demographic-economic system granting a refresh of the evolution in discrete time, depending on the updated migration’s probabilities.

The empirical example, making use of real data coming from the General Insurance Association of Singapore, concerns itself with the implementation of our model under different kinds of dependencies, entailing a different hierarchy on the rating classes: this in turn permits for different levels of contagion in the claims’ arrival. Under these assumptions, at every monitoring date taken into account, we compute the migration’s probabilities and the loss function through the copula-based model, which in turn enables a discrete-time dynamic of the claims’ reserving and of the capital requirements, evaluated by an internal model based on a value-at-risk approach. Therefore, this analysis makes visible how the flexibility of copula-based models can lead to a capital charge level that is not fixed within a range, thus being adaptable and depending on the perceived level of risk, coming from market data and taking into account any kind of dependency’s effects as contagion and hierarchy on risks. As a consequence, the previous empirical exercise enables us to align the copula-based approaches to the current more prudent approach in capital requirements regulation.