1 Introduction

There are a lot of uncertainties in the real world (Potyka et al. 2015; Atanassov 1999) and plenty of issues about uncertainty (Biró et al. 2019; Telcs et al. 2019). In order to deal with the uncertainties (Karci 2018; Abellan and Bosse 2018), many mathematical theories are proposed, such as fuzzy sets (Xue et al. 2020) and entropy (Tuğal and Karcı 2019). Beer et al. (2020) proposed the case of permutation-invariant criteria. Cao et al. (2019) proposed the multichannel EEG recordings under some uncertain environment. Du et al. (2019) proposed an improved Dempster–Shafer evidence theory under gray relational analysis. Jiang et al. (2019) proposed a novel probability transformation model based on a correlation coefficient of belief functions. Zhou et al. (2018) proposed a new multisensor data fusion method under modified Dempster–Shafer evidence theory. Yager et al. (2019) applied the fuzzy sets to linguistic data science by drawing on the iPad. Khan and Anwar (2019) proposed a new time-domain data fusion method by using weighted evidence and Dempster–Shafer combination rule and applied it to classify object. Kreinovich et al. (2021) studied how to reconcile maximum entropy approach with intuition. Jirousek and Shenoy (2018) proposed a novel entropy of belief functions in the Dempster–Shafer theory. Yager (2019) extended set measures to Pythagorean fuzzy sets.

Among these theories and models, a new belief entropy (Deng 2020), named as Deng entropy, is proposed to measure the uncertainty of mass function (Wang and Xiao 2019). The belief entropy is an extend of information entropy, which can evaluate uncertainties more flexible than information entropy (Huang et al. 2019). The belief entropy is based on the evidence theory, which means that the belief entropy can represent the uncertainties under the frame of discernment effectively (Mambé et al. 2018). Relying on the advantages on indicating vague information, the belief entropy has been widely studied by scholars at home and abroad (Liu et al. 2019). Some scholars has applied the belief entropy to deal with decision-making problems (Xiao 2019; Huang et al. 2019). Xiao (2019) proposed the evidential fuzzy multicriteria decision making based on belief entropy. Fan et al. (2020) proposed multisensor fusion method based on the belief entropy under evidential environment. Ozkan (2018) compared Shannon entropy with Deng entropy and improved Deng entropy for measuring biodiversity under an uncertain environment. Abellán (2017) has analyzed the properties of Deng entropy.

Recently, Yager proposed the interval-valued entropies for Dempster–Shafer structures (Yager 2018), which is based on Dempster–Shafer structure and has promising aspects (Deng and Jiang 2019). Dempster–Shafer structure is a mapping from the focal element to the interval [0,1] in a given space. It has a strong ability to represent unknown information. Through the focal elements of a given space, the possibility and certainty of each focal element can be obtained. The belief and plausibility of each focal element can be obtained through the possibility and certainty of each focal element and the Dempster–Shafer structure. The belief and plausibility of each focal element can determine the confidence interval of the corresponding focal element, which means that the Dempster–Shafer structure can express unknown information very efficiently. However, what is the corresponding interval-valued entropies for Dempster–Shafer structures under belief entropy is still an open issue to be addressed.

This paper proposes the interval-valued belief entropies for Dempster–Shafer structures, which is an interval-valued entropy. The proposed entropy is based on Dempster–Shafer structure and belief entropy, which is an efficient way to measure the uncertainty of location information. Through the focal elements in a given space, the proposed entropy can obtain the possibility and certainty of each focal element. Furthermore, the belief and plausibility of each focal element can be obtained. Based on the belief and plausibility and cardinality of each focal element, the proposed entropy can be obtained. The proposed entropy is based on the interval-valued entropies for Dempster–Shafer structures. When the belief entropy degenerates into the classic Shannon entropy, the proposed entropy will degenerate into the interval-valued entropies for Dempster–Shafer structures. And through a comparative experiment, we verified that the proposed entropy can obtain more information about an unknown object. At the same time, because the proposed entropy is an interval entropy model, it is more in line with human intuition, which provides a basis for practical applications.

The remaining of this paper is structured as follows. Section 2 introduces the preliminary. Section 3 presents the interval-valued belief entropies for Dempster–Shafer structures. Section 4 illustrates the flexibility and accuracy of the interval-valued belief entropies for Dempster–Shafer structures. Section 5 summarizes the whole paper.

2 Preliminaries

The world is full of unknowns, and the unknown world will have many unknown problems (Wang et al. 2019; Zhang and Deng 2021). Unknown information needs to be represented by tools that represent information (Turhan and Demirekler 2017; Wang et al. 2019). After the unknown information is expressed, many unknown means are needed to process it (Kern-Isberner and Rödder 2004; Pan and Deng 2020).

2.1 Dempster–Shafer structures

The real world is very uncertain and complex (Yager 1999; Zhang et al. 2017). Addressing uncertainty is an open issue (Prajapati and Saha 2019). Evidence theory is widely applied and generalized (Seiti and Hafezalkotob 2018; Jaunzemis et al. 2019). Dempster–Shafer structure is a very efficient tool for representing unknown information (Zhang et al. 2019). The performance of Dempster–Shafer structure is very powerful (Chao et al. 2019). Dempster–Shafer structure maps each non-empty crisp subset of a given space to a value in the [0,1] space (Vandoni et al. 2019). Through the Dempster–Shafer structure, we can get the belief and plausibility of each non-empty crisp subset in a given space (Jamal et al. 2019; Ferson et al. 2015). The belief and plausibility of each non-empty crisp subset in a given space can form an interval (Hurley et al. 2019; Zhang et al. 2019). This interval value is an important indicator for evaluating the reliability of a non-empty crisp subset (Wang 2018; Kuzemsky 2018). Given a space X consists of a collection \(F=\{F_1, \ldots , F_q\}\) of non-empty crisp subsets of X, the Dempster–Shafer structure is a mapping \(m(F_j)\in [0, 1]\) satisfying the following conditions:

Definition 1

(Dempster–Shafer structure) (Shafer 1976)

$$\begin{aligned}&m(F_j)>0 \end{aligned}$$
(1)
$$\begin{aligned}&\sum ^q_{j=1}m(F_j)=1 \end{aligned}$$
(2)

Two important measures that can be associated with a Dempster–Shafer structure m are the measures of plausibility and belief, Pl and Bel, as follows:

$$\begin{aligned}&\mathrm{Pl}\left( A\right) =\sum _{j, A\cap F_j\ne \emptyset }m(F_j) \end{aligned}$$
(3)
$$\begin{aligned}&\mathrm{Bel}\left( A\right) =\sum _{j, F_j\subseteq A}m(F_j) \end{aligned}$$
(4)

Assume A is a crisp subset of X, then the certainty and possibility of A is defined as follows:

$$\begin{aligned}&\mathrm{Pl}\left( A\right) =\sum _{j=1}^q \mathrm{Poss}(A/F_j)m(F_j) \end{aligned}$$
(5)
$$\begin{aligned}&\mathrm{Bel}\left( A\right) =\sum _{j=1}^q \mathrm{Cert}(A/F_j)m(F_j) \end{aligned}$$
(6)

where,

$$\begin{aligned}&\mathrm{Poss}(A/F_j)=1 \text { if } A\cap F_j\ne \emptyset \end{aligned}$$
(7)
$$\begin{aligned}&\mathrm{Poss}(A/F_j)=0 \text { if } A\cap F_j=\emptyset \end{aligned}$$
(8)
$$\begin{aligned}&\mathrm{Cert}(A/F_j)=1 \text { if } F_j\subseteq A \end{aligned}$$
(9)
$$\begin{aligned}&\mathrm{Cert}(A/F_j)=0 \text { if }F_j\nsubseteq A \end{aligned}$$
(10)

2.2 Interval-valued entropies for Dempster–Shafer structures

The interval-valued entropies for Dempster–Shafer structures proposed by Yager include Shannon-like interval-valued entropies and Gini entropy of Dempster–Shafer belief structure. Because Shannon entropy is the most classic entropy, the interval-valued entropies for Dempster–Shafer structures mentioned in this article are Shannon-like interval-valued entropies.

Assume m is a Dempster–Shafer structure on \(X=\{x_1,\ldots ,x_n\}\) with focal elements \(G=\{G_1,\ldots ,G_q\}\) and \(m\left( G_j\right) =\alpha _j\). where \(\alpha _j \in [0, 1]\) and \(\sum _{j=1}^{q}\alpha _j = 1\). The definition of Shannon-like interval-valued entropies is as follows:

Definition 2

(Shannon-like interval-valued entropies) (Yager 2018)

$$\begin{aligned} S\left( m\right) \in [S_L\left( m\right) , S_U\left( m\right) ] \end{aligned}$$
(11)

where,

$$\begin{aligned}&S_\mathrm{L}\left( m\right) =-\sum _{G_j\in G}{m\left( G_j\right) \log _2\left( \mathrm{Pl}_m\left( G_j\right) \right) } \end{aligned}$$
(12)
$$\begin{aligned}&S_\mathrm{U}\left( m\right) =-\sum _{G_j\in G}{m\left( G_j\right) \log _2\left( \mathrm{Bel}_m\left( G_j\right) \right) } \end{aligned}$$
(13)

where \(Pl_\mathrm{m}\left( A\right) \) and \(\mathrm{Bel}_\mathrm{m}\left( A\right) \) indicate the plausibility and belief of A with respect to the Dempster–Shafer structure m, respectively.

2.3 Tsallis entropy

The definition of Tsallis entropy under a probability distribution \(p_i\) is as follows:

Definition 3

(Tsallis entropy) (Tsallis 1988)

$$\begin{aligned} S_q=k\frac{1-\sum _{i=1}^{W}p_i^q}{q-1} \qquad q\in R \end{aligned}$$
(14)

When k is a conventional positive constant and \(\sum _{i=1}^{W}p_i=1\), it is obvious that \(\lim _{q\rightarrow 1}S_q=-k\sum _{i=1}^{W}p_i\ln p_i\). In this way, the Tsallis entropy is degenerated as classical information entropy.

2.4 Belief entropy

Given n is a mass function under frame of discernment Y, the definition of belief entropy is as follows:

Definition 4

(Belief entropy) (Deng 2020)

$$\begin{aligned} E_\mathrm{d} = -\sum _{C \subseteq Y}n(C)\log \frac{n(C)}{2^{|C|} - 1} \end{aligned}$$
(15)

where |C| is the cardinality of C.

Belief entropy is the generalization of Shannon entropy (Mambe et al. 2018; Khoshtinat et al. 2019). When the mass function is degenerated as a probability distribution, belief entropy is degenerated as Shannon entropy.

2.5 Golden rule method

Assume E is the any focal element of \(\Theta \). \(Pl\left( E\right) \) and \(Bel\left( E\right) \) are the plausibility and belief of E, respectively. The definition of E is as follows:

Definition 5

(Golden Rule Method) (Yager 2017)

$$\begin{aligned} \mathrm{Rep}\left( E\right) =m+\left( 0.5-m\right) r \end{aligned}$$
(16)

where,

$$\begin{aligned}&m=\left( Pl\left( E\right) +Bel\left( E\right) \right) /2 \end{aligned}$$
(17)
$$\begin{aligned}&r=Pl\left( E\right) -Bel\left( E\right) \end{aligned}$$
(18)

3 Interval-valued belief entropies for Dempster–Shafer structures

The unknown world is tens of thousands (Deng 2020; Deng and Deng 2021), and people cannot accurately judge the uncertainty of an unknown information (Pan et al. 2019; Jiang et al. 2019). But we can give an interval of the uncertainty of an object and then control the uncertainty of an object within a range, which is also a way of expressing unknown information. On this basis, it can help people deal with unknown information. Yager proposed the interval-valued entropies for Dempster–Shafer structures, which is an interval entropy model based on Dempster–Shafer structures and classic information entropy. Although the interval-valued entropies for Dempster–Shafer structures can solve the uncertainty interval of an object very efficiently, its scope of application is only a traditional probability space. If extended to the evidence environment, this is the interval value proposed in this article.

In this section, an interval-valued belief entropy for Dempster–Shafer structures is presented. Assume m is a Dempster–Shafer structure on \(X=\{x_1,\ldots ,x_n\}\) with focal elements \(G=\{G_1,\ldots ,G_q\}\) and \(m\left( G_j\right) =\alpha _j\). where \(\alpha _j \in [0, 1]\) and \(\sum _{j=1}^{q}\alpha _j = 1\). The definition of the interval-valued belief entropy for Dempster–Shafer structures is as follows:

Definition 6

(Interval-valued belief entropies for Dempster–Shafer structures)

$$\begin{aligned} S(m) = [S_{L}(m), S_{U}(m)] \end{aligned}$$
(19)

where

$$\begin{aligned}&S_{L}(m) = -\sum _{G_j\in G}m(G_j)\log _2\frac{\mathrm{Pl}_{m}(G_j)}{2^{|G_j|} - 1} \end{aligned}$$
(20)
$$\begin{aligned}&S_{H}(m) = -\sum _{G_j\in G}m(G_j)\log _2\frac{\mathrm{Bel}_{m}(G_j)}{2^{|G_j|} - 1} \end{aligned}$$
(21)

where

$$\begin{aligned}&\mathrm{Pl}_{m}(G_{j}) = \sum _{ k = 1 }^{q}\mathrm{Poss}(G_{j}/G_{k})m(G_{k}) \end{aligned}$$
(22)
$$\begin{aligned}&\mathrm{Bel}_{m}(G_{j}) = \sum _{ k = 1 }^{q}\mathrm{Cert}(G_{j}/G_{k})m(G_{k}) \end{aligned}$$
(23)

Hence,

$$\begin{aligned}&S_{L}(m) = -\sum _{ j = 1 }^{q}m(G_{j})\log _2\frac{\sum _{ k = 1 }^{q}\mathrm{Poss}(G_{j}/G_{k})m(G_{k})}{2^{|G_{j}|} - 1}\nonumber \\ \end{aligned}$$
(24)
$$\begin{aligned}&S_{U}(m) = -\sum _{ j = 1 }^{q}m(G_{j})\log _2\frac{\sum _{ k = 1 }^{q}\mathrm{Cert}(G_{j}/G_{k})m(G_{k})}{2^{|G_{j}|} - 1}\nonumber \\ \end{aligned}$$
(25)

The flowchart of the proposed entropy is shown in Fig. 1.

Fig. 1
figure 1

The flowchart of the proposed entropy

Full size image

Theorem 1

When the belief entropy degenerates into the classic Shannon entropy, the interval-valued belief entropies for Dempster–Shafer structures will degenerate into the interval-valued entropies for Dempster–Shafer structures.

Proof

Relying on Eqs. (20, 21), we have the equations as follows:

$$\begin{aligned} S_\mathrm{L}(m)= & {} -\sum _{G_j\in G}m(G_j)\log _2\frac{Pl_{m}(G_j)}{2^{|G_j|} - 1} \\ S_\mathrm{H}(m)= & {} -\sum _{G_j\in G}m(G_j)\log _2\frac{Bel_{m}(G_j)}{2^{|G_j|} - 1} \end{aligned}$$

When the belief entropy degenerates into the classic Shannon entropy, we can obtain the following equations:

$$\begin{aligned}&-\sum _{G_j\in G}m(G_j)\log _2\frac{Pl_{m}(G_j)}{2^{|G_j|} - 1}\\&\quad =-\sum _{G_j\in G}m(G_j)\log _2Pl_{m}(G_j) \\&-\sum _{G_j\in G}m(G_j)\log _2\frac{Bel_{m}(G_j)}{2^{|G_j|} - 1}\\&\quad =-\sum _{G_j\in G}m(G_j)\log _2Bel_{m}(G_j). \end{aligned}$$

The interval-valued belief entropies for Dempster–Shafer structures will degenerate into the interval-valued entropies for Dempster–Shafer structures.

Then, the interval-valued belief entropies for Dempster–Shafer structures will degenerate into the interval-valued entropies for Dempster–Shafer structures. \(\square \)

Theorem 2

Assume m is a Bayesian Dempster–Shafer structure with \(F_i=\{x_i\}\) and \(m\left( F_i\right) =p_i\) for \(i=1\) to n. For an interval-valued belief entropy for Dempster–Shafer structure, \(S(m) = [S_{L}(m), S_{U}(m)]\), on m, then \(S_{L}(m)=S_{U}(m)\).

Proof

Relying on the equations of Eqs. (24, 25), we have the equations as follows:

$$\begin{aligned}&S_\mathrm{L}(m) = -\sum _{ j = 1 }^{q}m(G_{j})\log \frac{\sum _{ k = 1 }^{q}\mathrm{Poss}(G_{j}/G_{k})m(G_{k})}{2^{|G_{j}|} - 1} \\&S_\mathrm{U}(m) = -\sum _{ j = 1 }^{q}m(G_{j})\log \frac{\sum _{ k = 1 }^{q}\mathrm{Cert}(G_{j}/G_{k})m(G_{k})}{2^{|G_{j}|} - 1} \end{aligned}$$

Since m is a Bayesian Dempster–Shafer structure, then \(\mathrm{Cert}(G_{i}/G_{k})=\mathrm{Poss}(G_{i}/G_{k})\).

Hence, the following equations hold:

$$\begin{aligned} \begin{aligned} S_\mathrm{L}(m)&= -\sum _{ i = 1 }^{q}m(G_{i})\log \frac{\sum _{ k = 1 }^{q}\mathrm{Poss}(G_{i}/G_{k})m(G_{k})}{2^{|G_{i}|} - 1}\\&= -\sum _{ i = 1 }^{n}m(G_{i})\log \sum _{ k = 1 }^{n}\mathrm{Poss}(G_{i}/G_{k})m(G_{k})\\&=-\sum _{ i = 1 }^{n}m(G_{i})\log m(G_{i})=-\sum _{ i = 1 }^{n}p_i\log p_i \\ S_\mathrm{U}(m)&= -\sum _{i = 1 }^{q}m(G_{i})\log \frac{\sum _{ k = 1 }^{q}\mathrm{Cert}(G_{i}/G_{k})m(G_{k})}{2^{|G_{i}|} - 1}\\&= -\sum _{ i = 1 }^{n}m(G_{i})\log \sum _{ k = 1 }^{n}Cert(G_{i}/G_{k})m(G_{k})\\&=-\sum _{ i = 1 }^{n}m(G_{i})\log m(G_{i})=-\sum _{ i = 1 }^{n}p_i\log p_i \end{aligned} \end{aligned}$$

So, we come to the conclusion that \(S_{L}(m)=S_{U}(m)\). \(\square \)

Example 1

Assume Dempster–Shafer structure m on the focal elements \(F=\{F_1,F_2,F_3\}\) of a given space \(X = \left\{ x_1, x_2\right\} \) with where \(F_1=\{x_1\}\) with \(m(F_1)=0.1\), \(F_2=\{x_2\}\) with \(m(F_2)=0.1\) and \(F_3=\{x_1, x_2\}\) with \(m(F_3)=0.8\).

Relying on Eqs. (24, 25), we have the equations as follows:

$$\begin{aligned} S_\mathrm{Y}(m)&=- 0.1\times \log _2\frac{Pl_{m}(F_1)}{2^{|1|} - 1} - 0.1\times \log _2\frac{Pl_{m}(F_2)}{2^{|1|} - 1} \\&\quad - 0.8\times \log _2\frac{Pl_{m}(F_3)}{2^{|2|} - 1}\\&=- 0.1\times \log _2\frac{0.1 + 0.8}{2^{|1|} - 1} - 0.1\times \log _2\frac{0.1 + 0.8}{2^{|1|} - 1} \\&\quad - 0.8\times \log _2\frac{0.1 + 0.1 + 0.8}{2^{|2|} - 1}\\&=1.298 \\ S_\mathrm{H}(m)&=- 0.1\times \log _2\frac{\mathrm{Bel}_{m}(F_1)}{2^{|1|} - 1} - 0.1\times \log _2\frac{\mathrm{Bel}_{m}(F_2)}{2^{|1|} - 1} \\&\quad - 0.8\times \log _2\frac{\mathrm{Bel}_{m}(F_3)}{2^{|2|} - 1}\\&=- 0.1\times \log _2\frac{0.1}{2^{|1|} - 1} - 0.1\times \log _2\frac{0.1}{2^{|1|} - 1} \\&\quad - 0.8\times \log _2\frac{0.1 + 0.1 + 0.8}{2^{|2|} - 1}\\&=1.932 \end{aligned}$$

Hence, we see that

$$\begin{aligned} S(m) = [1.298, 1.932] \end{aligned}$$

Here, [1.298, 1.932] is the interval-valued belief entropy for Dempster–Shafer structure on X. Through this example, we know that the proposed entropy can successfully calculate the belief interval of an unknown object.

Example 2

Assume Dempster–Shafer structure m on \(X = \left\{ x_1, x_2\right\} \) with focal elements \(F=\{F_1,F_2\}\) where \(F_1=\{x_1\}\) with \(m(F_1)=0.5\) and \(F_2=\{x_2\}\) with \(m(F_2)=0.5\).

Relying on the equations of Eqs. (24, 25), we have the equations as follows:

$$\begin{aligned} \begin{aligned} S_\mathrm{L}(m)&=- \,0.5\times \log _2\frac{}{\mathrm{Pl}_{m}(F_1)}{2^{|1|} - 1} - 0.5\times \log _2\frac{Pl_{m}(F_2)}{2^{|1|} - 1}\\&=- \,0.5\times \log _2\frac{0.5}{2^{|1|} - 1} - 0.5\times \log _2\frac{0.5}{2^{|1|} - 1}=1 \\ S_\mathrm{U}(m)&=- 0.5\times \log _2\frac{\mathrm{Bel}_{m}(F_1)}{2^{|1|} - 1} - 0.5\times \log _2\frac{\mathrm{Bel}_{m}(F_2)}{2^{|1|} - 1}\\&=-\, 0.5\times \log _2\frac{0.5}{2^{|1|} - 1} - 0.5\times \log _2\frac{0.5}{2^{|1|} - 1}=1 \end{aligned} \end{aligned}$$

Hence, we see that

$$\begin{aligned} S(m) = [1, 1]=1 \end{aligned}$$

Here, [1, 1] is the interval-valued belief entropy for Dempster–Shafer structure on X. In this example, m is a Bayesian Dempster–Shafer structure. From the calculation results, the upper and lower limits of the interval entropy that can be calculated by the proposed entropy are the same. That is, the proposed entropy can calculate the uncertainty of an unknown object accurately.

Example 3

Assume Dempster–Shafer structure m on the focal elements \(F=\{F_1,F_2\}\) of a given space \(X = \left\{ x_1, x_2, x_3\right\} \) where \(F_1=\{x_1\}\) with \(m(F_1)=0.6\), \(F_2=\{x_2,x_3\}\) with \(m(F_2)=0.4\).

Relying on the equations of Eqs. (24, 25), we have the equations as follows:

$$\begin{aligned} \begin{aligned} S_\mathrm{Y}(m)&=-\, 0.6\times \log _2\frac{\mathrm{Pl}_{m}(F_1)}{2^{|1|} - 1} - 0.4\times \log _2\frac{\mathrm{Pl}_{m}(F_2)}{2^{|2|} - 1}\\&=-\, 0.6\times \log _2\frac{0.6}{2^{|1|} - 1} - 0.4\times \log _2\frac{0.4}{2^{|2|} - 1}\\&=1.605 \\ S_\mathrm{H}(m)&=- 0.6\times \log _2\frac{\mathrm{Bel}_{m}(F_1)}{2^{|1|} - 1} - 0.4\times \log _2\frac{\mathrm{Bel}_{m}(F_2)}{2^{|2|} - 1}\\&=- \,0.6\times \log _2\frac{0.6}{2^{|1|} - 1} - 0.4\times \log _2\frac{0.4}{2^{|2|} - 1}\\&=1.605 \end{aligned} \end{aligned}$$

Hence, we see that

$$\begin{aligned} S(m) = [1.605, 1.605] \end{aligned}$$

Here, [1.605, 1.605] is the interval-valued belief entropy for Dempster–Shafer structure on X. In this example, the focal elements do not want to communicate with each other, indicating that this example is a special case. Through this example, we know that the proposed entropy can successfully calculate the belief interval of an unknown object under special case.

Example 4

A person is walking at a crossroads, and there are three roads to choose by the person. It means that three possible choices \(A_i\left( i = 1, 2, 3\right) \) can be chosen by the person and three attributes \(y_1\left( length\right) \), \(y_2\left( brightness\right) \) and \(y_3\left( humidity\right) \) are taken into account in the issue. From a traveler’s perspective, they tend to choose the path with the least uncertainty. According to the properties of belief entropy, the belief entropy can represent uncertainty effectively.

Assume the Dempster–Shafer structures \(m_1\), \(m_2\) and \(m_3\) based on the space \(Y=\{y_1, y_2, y_3\}\) represent alternatives \(A_1\), \(A_2\) and \(A_3\), respectively. According to experts, the alternative \(A_3\) is the best choice.

Assume Dempster–Shafer structures \(m_1\), \(m_2\) and \(m_3\) on the focal elements \(F_1=\{F_{11},F_{12},F_{13}\}\), \(F_2=\{F_{21}\}\) and \(F_3=\{F_{31},F_{32},F_{33}\}\) of a given space \(Y=\{y_1, y_2, y_3\}\), respectively, such that \(F_{11}=\{y_1\}\), \(F_{12}=\{y_2\}\), \(F_{13}=\{y_3\}\), \(F_{21}=\{Y\}\), \(F_{31}=\{y_1, y_2\}\), \(F_{32}=\{y_1, y_3\}\) and \(F_{33}=\{y_2, y_3\}\).

The Dempster–Shafer structures \(m_1\), \(m_2\) and \(m_3\) are as follows:

$$\begin{aligned} \begin{aligned}&m_1\left( \{y_1\}\right) = 1/3 \text { , }m_1\left( \{y_2\}\right) = 1/3 \text { , }m_1\left( \{y_3\}\right) = 1/3 \\&m_2\left( \{Y\}\right) = 1 \\&m_3\left( \{y_1, y_2\}\right) = 0.2 \text { , } m_3\left( \{y_1, y_3\}\right) = 0.4 \text { , }\\&m_3\left( \{y_2, y_3\}\right) = 0.4 \end{aligned} \end{aligned}$$

Relying on the equations of Eqs. (24, 25), we can obtain Table 1 as follows:

Table 1 The upper and lower limits of the proposed entropy of \(m_1\), \(m_2\) and \(m_3\)
Full size table

Hence, we can obtain the interval values of the proposed entropy of \(m_1\), \(m_2\) and \(m_3\) in Table 2:

Table 2 The interval values of the proposed entropy of \(m_1\), \(m_2\) and \(m_3\)
Full size table

According to Eq. (16), we can obtain the golden rule method values of the proposed entropy of \(A_1\), \(A_2\) and \(A_3\) in Table 3:

Table 3 The golden rule method values of the proposed entropy of \(m_1\), \(m_2\) and \(m_3\)
Full size table

From the discussion above, one get that \(\mathrm{Rep}(A_2)>\mathrm{Rep}(A_1)>\mathrm{Rep}(A_3)\). Then, we can find the choice \(A_3\) is the best choice in this problem, which is consistent with the experts’ judgment. It means that the proposed algorithm is validity in issue of decision making. This shows that the proposed entropy can successfully solve practical problems in life.

4 Application

The world is full of unknown information, and the uncertainty measurement of location information has always been an important issue of information fusion (Kang et al. 2019; Deng and Jiang 2019). Since the end of 2019, the new crown virus has raged, and the global economy and society are all in crisis. In order to effectively prevent infection by the new coronavirus, suppose we now have a vaccine, denoted as B. Before the vaccine is marketed, we need to use the relevant uncertainty measurement model to measure the vaccine. If the uncertainty of the vaccine is too large, then the vaccine is not suitable for injections to the relevant population, because we do not know whether the vaccine will eventually have a positive or negative impact on the person being injected.

Suppose that our uncertain evaluation of B is based on three attributes \(Y=\{y_1,y_2,y_3\}\). Because Dempster–Shafer structure is a recognized tool that can efficiently represent unknown information, we use Dempster–Shafer structure to express this issue. According to the suggestions of experts, the Dempster–Shafer structure based on Y is used in this example, m, as follows:

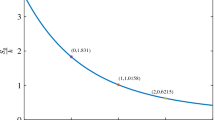
$$\begin{aligned}&m\left( \{y_1\}\right) = 0.2 \text { , } m\left( \{y_1, y_3\}\right) =x \text { , }\\&m\left( \{y_1, y_2, y_3\}\right) = 0.8-x \end{aligned}$$

We use Tsallis entropy and the proposed entropy to evaluate this problem. The comparison curve of the two entropies is shown in Fig. 2.

Fig. 2
figure 2

The comparison curve of two entropies

Full size image

In Fig. 2, when the non-extensive constant q is increased in increments of 0.5 from 0.5 to 2.5, the uncertainty of B calculated by Tsallis entropy is always less than the lower limit of the proposed entropy, which shows that the proposed entropy can obtain more information of Tsallis entropy. At the same time, because the uncertainty of an unknown information cannot be completely determined in practical applications, it is counterintuitive that Tsallis entropy obtains a certain uncertainty for an unknown object. The proposed entropy is an interval entropy model, and an interval of entropy can be obtained for an unknown information, which is also the reason why the proposed model is efficient.

5 Conclusion

This paper proposes interval-valued belief entropy for Dempster–Shafer structures, which is a new interval entropy model based on Dempster–Shafer structures and belief entropy. The proposed entropy can be based on the cardinality of the focal element in a given space and the belief and plausibility of the focal element of a given space to get an interval entropy value, which provides theoretical support for decision making. When belief entropy degenerates to classic information entropy, the proposed entropy degenerates to the interval-valued entropies for Dempster–Shafer structures. Numerical examples and comparative experiment are used to verify the efficiency of the proposed entropy in decision making. The experimental results show that the proposed entropy can be better applied to solve practical problems than some other entropy models.

Quantum theory is currently the most popular and important theory. Dempster–Shafer evidence theory and quantum theory have similarities in many aspects, and belief entropy is the most efficient entropy to measure the uncertainty of unknown information in the evidence environment. Therefore, we will later improve the proposed model to adapt to the quantum environment. In other words, we will use the proposed entropy in future work to measure the uncertainty of the unknown information in the quantum system.