1 Introduction

Sediment dynamics (transport and deposition) can cause environmental issues and concerns such as damage to aquatic ecosystems, declining quality of surface water and groundwater, and variations in reservoir recharge and river morphology (Afan et al. 2016; Shojaeezadeh et al. 2018; Gholami et al. 2016; Guo et al. 2020; Ren et al. 2020). Suspended sediment load (SSL) in watersheds is one of the most important hydraulic and hydrological parameters, which can impact the performance of hydraulic structures and water transfer projects. Additionally, sediments transported to reservoirs can reduce the reservoir capacity and affect operational policy, e.g., water supply, energy generation, and irrigation. Therefore, the estimation and prediction of SSL in rivers are vital tasks in the water resources management, and accurate results would help decision-making on river engineering, reservoir operation, watershed management, and sustainable water resources (Yang et al. 2009; Downs et al. 2009; Akrami et al. 2013; Himanshu et al. 2017; Haghighi et al. 2019). Prediction of daily sediment can lead to optimal decisions for dam’s outlet operation during the flood and conveying some part suspended sediment load to downstream area. Addressing short-term and long-term sediment dynamics is challenging owing to the heterogeneity of basins, the uncertainty in hydrological parameters, and the stochastic nature of flow and characteristics of sediment transport and deposition processes (Malmon et al. 2002; Pirnia et al. 2019b; Pizzuto 2020). Imprecise SSL modeling and prediction can reduce the amount of water stored by dam reservoirs, which can have an enormous negative impact on domestic and agricultural water supply, and also on dam structures (Lafdani et al. 2013; McCarney-Castle et al. 2017; Zhang et al. 2020; Zhao et al. 2020).

During recent decades, various approaches to improve the accuracy of SSL predictions have been introduced, including numerical and hydraulic, distributed and lumped models, statistics, empirical models, and machine learning models (Bezak et al. 2014; Merkhali et al. 2015; Kumar et al. 2016; Shamaei and Kaedi 2016; Choubin et al. 2018). Some studies have predicted SSL at daily scale using data-driven methods such as machine learning algorithms and soft computing models (Nourani and Andalib 2015; Choubin et al. 2018; Kaveh et al. 2020). Other studies worldwide seeking to enhance the precision of the SSL estimation have used machine learning techniques such as adaptive neuro-fuzzy system (ANFIS) (Rajaee et al. 2009; Cobaner et al. 2009; Kisi et al. 2012; Azamathulla et al. 2012; Vafakhah 2013; Choubin et al. 2018), artificial neural network (ANN) (Rajaee et al. 2009; Melesse et al. 2011; Kisi et al. 2012; Vafakhah 2013; Nourani and Andalib 2015; Wang et al. 2018; Halecki et al. 2018; Liu et al. 2019), support vector machine (SVM) (Kisi et al. 2012; Pektaş and Doğan 2015; Choubin et al. 2018), multilayer perceptron (MLP) (Cigizoglu 2004; Gholami et al. 2016; Romano et al. 2018), and radial basis function neural network (RBFNN) (Erol et al. 2008; Ahmad and Kumar 2016; Ibrahim et al. 2019). The soft computing models were widely applied for predicting SSL, e.g., Adib and Mahmoodi (2017) were applied GA method to optimize the structure of the ANN model predicting SSL, Talebi et al. (2017) estimated SSL using regression trees and ANN models, Salih et al. (2020) have illustrated that the attribute selected classifier performed better than the tree models in SSL prediction, Ehteram et al. (2020) have employed ANN and a multiobjective genetic algorithm to predict the SSL, and Samantary and Ghose (2020) estimated SSL using SVM, feed-forward neural network (FFN), and RBFNN and they have shown that the SVM had the highest performance.

Although the MLP, ANIFS, RBFNN, and SVM models have a high capability for estimating SSL, optimization of these algorithms is required to obtain more accurate results (Fiyadh et al. 2019). Classical model training algorithms, such as backpropagation and the gradient descent algorithm, may become trapped in local optimums, so researchers have begun to develop new optimization algorithms (Ehteram et al. 2017). One recent example is the sine–cosine algorithm (SCA), inspired by mathematical sine and cosine functions, which has high search accuracy, speed of convergence, and stability (Mirjalili 2016). Optimization algorithms can be utilized as training algorithms to set the internal parameters of the MLP, ANFIS, and RBFNN models.

In the present study, data-based approaches and soft computing models (stand-alone and hybridized with optimization algorithms) were used for predicting SSL in the Talar river basin in northern Iran, where sediment is mostly generated during high-severity, erosive precipitation events and where complex processes determine suspended sediment and precipitation in river systems at watershed scale. The innovation of the present study is the new soft computing hybrid models which have been employed in previous studies for predicting other hydrological variabels. Furthermore, the present study deals with using these soft computing models and optimization algorithms that can be linked to hydraulic and hydrological modeling. Additionally, the present study deals with the uncertainty of model parameters and its effect on the outcomes. ANFIS and ANN models are widely used models for predicting hydrological variables given their high potential, high accuracy, and easy learning for modelers. Furthermore, the extensive capability of soft computing models in other engineering fields makes the mentioned models be present as the models used in the study. However, the motivation behind of the study is to provide solutions to identify the parameters needed to estimate the SSL in different areas. Moreover, the optimization algorithms of the study, as will be stated, were selected for the study given their high search capability, fast convergence speed, and lack of computational complexity. The hybridization of the models makes the results more accurate. Likewise, the models are more able to simulate variables in more complex problems. Since the hybridized and optimized models performed better than individual models, the soft computing models are frequently optimized or hybridized to overwhelm the weakness of stand-alone models. However, it should be considered that the preparation of the structure of soft computing models and the selection of the best input scenario are the challenges of the current study.

The current study develops a low-cost estimation approach for accurately predicting SSL in developing regions where sediment loads in rivers are the main environmental concern. Specific objectives were to: (1) develop and implement optimization algorithms (SCA, particle swarm optimization (PSO), bat algorithm (BA) and firefly algorithm (FFA)) to improve model prediction of SSL; (2) investigate the capability of the four optimization methods in SSL prediction by applying widely used performance indices; and (3) compare outputs achieved using the stand-alone and hybrid ANFIS, MLP, and RBFNN models.

2 Material and methods

2.1 Study areas

This study was carried out in two case study including Talar river and Eagel Creek Basins located in Iran and USA with different types of climate and environmental conditions. In the following section, some characteristics of the two above-mentioned basins are presented.

2.1.1 Talar river basin

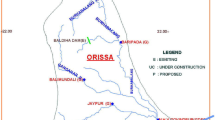
The Talar river watershed (2100 km2) is situated in Mazandaran region, northern Iran (52° 35′ 18′′–53° 23′ 35′′ E; 35° 44′ 19′′–36° 19′ 13′′ N) (Fig. 1). Based on its aridity index of 0.69 (Sahin 2012; Pirnia et al. 2019a), the region climate is semi-humid, with 552.7 mm yearly precipitation and mean yearly minimum and maximum temperatures of 7.7 and 21.1 °C (Kavian et al. 2018). The smaller Kasilian river also runs through the watershed, to discharge into the Caspian Sea to the north (Fig. 1). Landslides are an important sediment source to both the Talar and Kasilian river systems (Emamgholizadeh and Demneh 2019). The watershed is characterized by intense rainfall events accompanied by frequent floods (Kavian et al. 2018) and has mountainous terrain characterized by rugged topography (altitude ranging from approximately 200 to 4000 m asl) and sparse vegetation cover in headwater areas, leading to huge sediment flows to the river network (Kavian et al. 2018). Both rivers have hydrometric stations situated at their outlet, from which daily observed data on rainfall, discharge, and suspended sediment concentration (SSC) were obtained for this work. The data were randomly divided into two subsets, with 80% utilized to calibrate the models and the remaining 20% utilized to test the proposed models. The maximum suspended sediment concentrations in the training and testing datasets were, respectively, 40,000 and 39,200 ton/day at Talar station and 60,000 and 59,000 ton/day at Kasilian station (Table 1).

Fig. 1
figure 1

Location of the Talar watershed, Iran

Full size image
Table 1 Characteristics and range of suspended sediment load (SSL) at gauging stations
Full size table

2.1.2 Eagel Creek Basin

In addition of the Talar basin, we used our models to predicts the daily SSL in a temperate and humid continental climate named Eagel Creek Basin in the Indiana state, USA (Fig. 2). The models run based on the rainfall, temperature, and discharge data (Table 1) from 2015 to 2018 (data retrieved from https://www.usgs.gov/centers/oki-water). For this basin, THE data were randomly divided into two subsets, with 80% utilized to calibrate the models and the remaining 20% utilized to test the proposed models.

Fig. 2
figure 2

Location of Eagel Creek Basin, USA

Full size image

2.2 Models tested for SSL prediction

2.2.1 Adaptive neuro-fuzzy system (ANFIS)

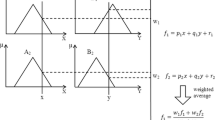
As an artificial neural network combined with fuzzy logical inference, ANFIS has a high ability for dealing with the imprecision and uncertainty of nonlinear environmental problems through its strong, effective learning techniques (Chang and Lai 2014; Choubin et al. 2018). Figure 3a shows a structure of the ANFIS model, which is a rule-based system comprising three parts: a rule base, a database, and an inference system that produces the system results by combining the fuzzy rules (Yurdusev and Firat 2009). The five layers in the ANFIS model are (1) input nodes, (2) rule nodes, (3) average nodes, (4) consequent nodes, and (5) output nodes, which employ different algorithms to produce fuzzy rules for training and testing (Park et al. 2012; Choubin et al. 2018). In ANFIS grid partitioning, fuzzy clustering and hybrid learning algorithms are applied to determine the input data structures in combination with the backpropagation gradient descent method (Cobaner et al. 2009; Kisi et al. 2012). The ANFIS model creates the following if–then rules using the pattern of input and output data:

$$ if\left( {x = A_{1} } \right)\;{\text{and}}\;\left( {y = B_{1} } \right) \to f = p_{1} x + q_{1} x + r_{1} $$
(1)
$$ if\left( {x = A_{2} } \right)\;{\text{and}}\;\left( {y = B_{2} } \right) \to f = p_{2} x + q_{2} x + r_{2} $$
(2)

where A1, B1, A2, and B2 are related membership functions (MFs), x and y are inputs, and p1, q1, r1, and r2 are consequent parameters. The ANFIS model has five computational layers:

Fig. 3
figure 3

Structure of the three models used: a adaptive neuro-fuzzy system (ANFIS), b multilayer perceptron (MLP), and c radial basis function neural network (RBFNN)

Full size image
  1. 1.

    The amount of input variable is fuzzified by the first layer:

    $$ O_{1,i} = - \mu_{{A_{i} }} \left( x \right) $$
    (3)

    where \(O_{1,i}\) is the MF of Ai and I is the linguistic label of node function. In the current work, the bell function was selected as the MF:

    $$ \mu_{{A_{i} }} \left( x \right) = \exp \left[ { - \left( {\frac{{x - c_{i} }}{{a_{i} }}} \right)^{2} } \right] $$
    (4)

    where ai and ci are premise parameters.

  2. 2.

    The second layer calculates the firing strength of each rule by product operation:

    $$ O_{2,i} = \mu_{Ai} \left( x \right) \times \mu_{Bi} \left( x \right) $$
    (5)

    where \(O_{2,i}\) is the second layer output and \(\mu_{Bi} \left( x \right)\) is the fuzzy MF of fuzzy set Bi.

  3. 3.

    The third layer is used to compute the normalized firing strength of every rule.

    $$ O_{3,i} = \frac{{\omega_{i} }}{{\sum {\omega_{i} } }} = \frac{{\omega_{i} }}{{\omega_{1} + \omega_{2} }} $$
    (6)

    where \(\omega_{i}\) is the fuzzy strength of each rule.

  4. 4.

    The fourth layer determines the output of each rule:

    $$ O_{4,i} = \overline{\omega } \times f_{i} $$
    (7)

    where \(f_{i}\) is the output of the fuzzy region and \(\overline{\omega }\) is the output of the third layer.

  5. 5.

    The fifth layer is defuzzification:

    $$ O_{5} = \sum {\overline{\omega }_{i} } \times f_{i} $$
    (8)

    where \(O_{5}\) is the output of all the rules.

2.2.2 Multilayer perceptron (MLP)

The MLP network is a model one or more hidden layers which can use various input sets by a set of suitable outputs (Choubin et al. 2018). In MLP (Fig. 3b), the major learning rule is the backpropagation algorithm, which comprises two stages, a feed-forward and a backward stage, with external input information and calculated and measured information signals at the output (Cigizoglu 2004). The MLP network can simulate 90% of processes related to environmental and nature problems (Kim and Valdes 2003). The MLP model employed in the present study was a three-layer learning network having a hidden, an input, and an output layer (Samanta et al. 2019; Bhowmik et al. 2019; Van Dao et al. 2020). The neurons at hidden layers use the nonlinear activation function to provide the output as follows:

$$ u_{j} = \sum\limits_{i = 1}^{p} {w_{ij} } .x_{i} $$
(9)
$$ x_{j} = \varphi \left( {u_{j} - \theta_{j} } \right) $$
(10)

where \(x_{i}\) is input, \(x_{j}\) is the output of the model, \(u_{j}\) is activation function, and \(\theta_{j}\) is a threshold function. Previous researchers have successfully utilized the logistic sigmoid function for the MLP model as follows:

$$ \varphi_{x} = \frac{1}{{1 + e^{ - x} }} $$
(11)

The training algorithms are introduced to search for the optimum value of weight connections. Classical training algorithms such as backpropagation algorithm and gradient descent algorithm are widely applied to calibrate the MLP parameters.

2.2.3 Radial basis function neural network (RBFNN)

The RBFNN model is a type of feed-forward neural network which consists of a number of artificial neurons (see Fig. 3c). It can be considered a general-purpose network that can be employed in different fields to achieve accurate predictions. The RBFNN is considered a good candidate for solving problems by faster learning potential (Erol et al. 2008; Han et al. 2012; Kong et al. 2016; Ibrahim et al. 2019). RBFNN has very powerful mathematical functions for organization of deep learning theory in solving problems (Sabour and Movahed 2017). In practical application, the learning algorithm for the RBFNN model employs different datasets for training and testing, so as to adapt itself rapidly to new factors or combinations (Sabour and Movahed 2017). RBFNN has the advantage over other types of neural networks of having a clustering stage in training and testing (Singh et al. 2014; Kumar et al. 2016). It uses symmetric basis functions as activation functions:

$$ \phi_{i} \left( x \right) = \exp \left( { - \frac{{\left\| {x - c_{i} } \right\|}}{{\sigma_{i}^{2} }}} \right) $$
(12)

where \(\phi_{i} \left( x \right)\) is the Gaussian function,\(\sigma_{i}\) is the width of the ith radial basis function node, and \(c_{i}\) is the center of hidden neuron i. The network output is computed as follows:

$$ y = \sum\limits_{i = 0}^{n} {\phi_{i} } w_{i} $$
(13)

where y is output and n is number of hidden neurons.

The training algorithms are used to set the RBFNN parameters such as center, width, and weight of the radial basis function node.

2.3 Optimization algorithms tested

2.3.1 Sine–cosine algorithm (SCA)

The SCA approach was first proposed by Mirjalili (2016). It updates the position of solutions using sine and cosine functions. The mathematical formulation of SCA is:

$$ X_{i}^{t + 1} = X_{i}^{t} + r_{1} \times \left( {\sin \left( {r_{2} } \right)} \right) \times \left| {r_{3} p_{i}^{t} - x_{i}^{t} } \right| $$
(14)
$$ X_{i}^{t + 1} = X_{i}^{t} + r_{1} \times \left( {\cos \left( {r_{2} } \right)} \right) \times \left| {r_{3} p_{i}^{t} - x_{i}^{t} } \right| $$
(15)

where \(X_{i}^{t}\) is the position of current solution at the ith iteration in the ith dimension, r2 and r3 are random values, pit is the destination solution, and r1 is a control parameter used to get a balance between exploration and exploitation. The two SCA functions (Eqs. 14, 15) are then integrated into one function:

$$ X_{i}^{t} = \left[ \begin{gathered} X_{i}^{t + 1} = X_{i}^{t} + r_{1} \times \left( {\sin \left( {r_{2} } \right)} \right) \times \left| {r_{3} p_{i}^{t} - x_{i}^{t} } \right|\quad \left( {{\text{if}}} \right)\;r_{4} < 0.5 \hfill \\ X_{i}^{t + 1} = X_{i}^{t} + r_{1} \times \left( {\cos \left( {r_{2} } \right)} \right) \times \left| {r_{3} p_{i}^{t} - x_{i}^{t} } \right|\quad \left( {{\text{if}}} \right)\;r_{4} \ge 0.5 \hfill \\ \end{gathered} \right] $$
(16)

The following equation is used to update the value of parameter r1:

$$ r_{1} = a - t\frac{a}{T} $$
(17)

where a is a constant and T is the maximum quantity of iterations. Parameter r2 is utilized to obtain the movement direction of the next solution. Parameter r3 is used to define a random weight for the destination with a stochastic influence emphasizing (r3 > 1) or decreasing distance (r3 < 1). Parameter r4 is used to switch between the cosine and sine functions. Figure 4 shows the sine–cosine effect on the next position and Fig. 5 shows a flowchart of SCA.

Fig. 4
figure 4

Sine–cosine effect on the next position in sine–cosine algorithm (SCA)

Full size image
Fig. 5
figure 5

Flowchart of optimization using sine–cosine algorithm (SCA)

Full size image

2.3.2 Bat algorithm (BA)

All bats have the echolocation characteristic to sense distance and use it to identify the difference between the food and obstacles (Yang et al. 2009). In the first step in BA, the initial population of bats is randomly initialized (Fig. 6). The BA uses the following equations to renew the bats’ velocity and position (Yang et al. 2009):

$$ \begin{aligned} f_{i} &= f_{\min } + \left( {f_{\max } - f_{\min } } \right)\beta \hfill \\ v_{i}^{t} &= v_{i}^{t - 1} + \left( {x_{i}^{t - 1} - x^{*} } \right)f_{i} \hfill \\ x_{i} &= x_{i}^{t - 1} + v_{i}^{t} \hfill \\ \end{aligned} $$
(18)

where \(f_{i}\) is frequency of bat i, \(f_{\max }\) is the maximum frequency, \(f_{\min }\) is the minimum frequency, \(v_{i}^{t}\) is velocity of agent i at iteration t, \(x_{i}^{t - 1}\) is position of agnet i at iteration t − 1, \(x^{t}_{i}\) is position of agnet i at iteration t, \(\beta\) is a random number, \(v_{i}^{t - 1}\) is velocity of agnet i at iteration t, \(x^{*}\) is the best solution, and xi is position of agnet i at iteration t. When the bat becomes closer to its prey, the rate of pulse emission and the loudness of the bat are renewed as:

$$ \begin{aligned} A_{i}^{t + 1} & = \alpha A_{i}^{t} \\ r_{i}^{t + 1} & = r_{i}^{o} \left[ {1 - \exp \left( { - \gamma t} \right)} \right] \\ \end{aligned} $$
(19)

where \(A_{i}^{t + 1}\) is loudness of bat i at iteration t + 1, \(\alpha\) is a constant value, \(\gamma\) is a constant value, \(r_{i}^{o}\) is the pulse emission’ initial rate, \(r_{i}^{t + 1}\) is the pulse emission rate of bat i at iteration t + 1, and \(A_{i}^{t}\) is the loudness of bat i at iteration t.

Fig. 6
figure 6

Flowchart of optimization using bat algorithm (BA)

Full size image

The bats use random walk to update their position:

$$ x_{new} = x_{old} + \varepsilon A_{i}^{t} $$
(20)

where \(x_{new}\) is the bat’s new position, \(x_{old}\) is the old position of the bat, and \(\varepsilon\) is a random number.

2.3.3 Firefly algorithm (FFA)

Firefly algorithm, introduced by Yang et al. (2009), is dependent on the firefly’s behavior (Fig. 7). The short, rhythmic flashes produced by fireflies are intended to attract other fireflies that have weaker flashes. The landscape of the objective function identifies the firefly brightness. For a problem of minimization, a brighter firefly has a smaller objective function. The fireflies update their position as follows:

$$ x_{i} \left( {t + 1} \right) = x_{i} \left( t \right) + \chi (r)\left( {x_{j} \left( t \right) - x_{i} \left( t \right)} \right) + \phi_{t} \upsilon $$
(21)

where \(x_{i} \left( {t + 1} \right)\) is position of firefly i at iteration t + 1, \(x_{i} \left( t \right)\) is position of firefly i at iteration t, \(x_{j} \left( t \right)\) is position of firefly j at iteration t, \(\chi (r)\) is attractiveness, \(\phi_{t}\) is a step factor, and \(\upsilon\) is a random number. The attractiveness is computed as follows:

$$ \chi \left( r \right) = \chi_{0} e^{{ - \gamma r^{2} }} $$
(22)
$$ r_{ij} = \left\| {x_{i} - x_{j} } \right\| = \sqrt {\sum\limits_{i = 1}^{D} {\left( {x_{id} - x_{jd} } \right)^{2} } } $$
(23)

where \(\chi_{0}\) is attractiveness at r = 0, D is number of dimensions, and \(r_{ij}\) is distance between two fireflies.

Fig. 7
figure 7

Flowchart of optimization using firefly algorithm (FFA)

Full size image

2.3.4 Particle swarm optimization (PSO)

Eberhart and Kennedy (1995) introduced PSO, which is inspired by the social behavior of particles (Fig. 8). The algorithm starts with initialization of random particles in the search space. The particles search for the optimal solution by updating generations. At each iteration, the two best values are used to update each particle. The first is the best solution found so far and the second is the best value found so far by any particle in the population. The following equations are utilized to renew the position and velocity of particles:

$$ x_{i} \left( t \right) = x_{i} \left( {t - 1} \right) + v_{i} \left( t \right) $$
(24)
$$ v_{i}^{t} = wv_{i}^{t - 1} + C_{1} r_{1} \left[ {P_{{{\text{best}}}} - x_{i} \left( t \right)} \right] + C_{2} r_{2} \left[ {G_{{{\text{best}}}} - x_{i}^{t} } \right] $$
(25)

where \(v_{i}^{t}\) is velocity of the particle at time t, w is inertia coefficient, \(C_{1}\) and \(C_{2}\) are acceleration coefficients, r1 and r2 are random numbers, \(P_{{{\text{best}}}}\) is the most promising position of the particle, \(G_{{{\text{best}}}}\) is the most promising position among the particles of the whole swarm, and \(x_{i} \left( t \right)\) is the position of particles at time t.

Fig. 8
figure 8

Optimal parameters of optimization algorithms based on signal-to-noise (S/N) ratio. a Sine –cosine algorithm (SCA), b firefly algorithm (FFA), c bat algorithm (BA), and d particle swarm optimization (PSO). PS population size, Lo loudness, Fr frequency. For explanation of parameters, see Sect. 2.2

Full size image

2.4 Hybridization of prediction models with optimization algorithms

2.4.1 ANFIS hybridization

Application of the ANFIS model starts with setting parameters to optimal values, commonly by using a hybrid learning method combining gradient descent (GD) and the least square estimate (LSE). However, the hybrid LSE-GE method may unable to achieve the rate of convergence for finding appropriate values of internal parameters in ANFIS, and therefore supporting algorithms are widely applied to optimize the internal parameters. The premise and consequent parameters in ANFIS are decision variables of the optimization algorithms that are optimized using these supporting algorithms. The main function of the optimization algorithms is then to update the initial values of the internal parameters in ANFIS, utilizing algorithm operators. An objective function, root mean square error (RMSE), is defined for hybrid ANFIS optimization algorithms. The optimization process tries to minimize the value of RMSE. When the ANFIS optimization algorithms converge to the lowest value of RMSE as a stopping criterion, the hybrid ANFIS model achieves the optimal value of its internal parameters.

2.4.2 MLP hybridization

The MLP parameters must be optimized to achieve the most accurate results. Training algorithms are required to set weight connections and threshold values. The initial threshold values and weight connections are defined as the initial population of algorithms. Each of the agents of the algorithms has two key parts: a set of weight connections and a set of threshold values. The values of MLP parameters are updated when the optimization algorithm tries to minimize the error function (RMSE). The convergence cycle of optimization continues until the hybrid MLP optimization algorithm model converges to a minimum objective function value.

2.4.3 RBFNN hybridization

Training algorithms are introduced to search for optimum parameters of the RBFNN model. Each of the agents of optimization algorithms has three key parts: center, width, and weight of the radial basis function node. The RBFNN parameters are defined as the initial population algorithms, which are entered into optimization algorithms to be updated by the operators of optimization algorithms. The optimal value of RBFNN parameters is found when the hybrid RBFNN optimization algorithm model converges to the lowest value of the target objective function.

2.5 Uncertainty analysis of soft computing models

Uncertainty in sequential uncertainty fitting (SUFI-2) is one of the best-known models for uncertainty analysis (Kumar et al. 2017). In SUFI-2, the parameter uncertainties account for uncertainty in model inputs and an objective function must be defined before the uncertainty analysis. Latin hypercube (LH) sampling is conducted, the objective function is assessed, and finally, the parameter covariance matrix is computed. In addition, 95% prediction uncertainty (95PPU) is computed at the 2.5% and 97% levels. Uncertainty analysis is required for the study as optimization algorithms try to find the exact values of the model parameters, as the input values may have include some sort of uncertainties. Thus, model uncertainty analysis can examine the effect of uncertainty related to model structure and parameter on the results. Two indices are used to quantify the uncertainty of models, observed data’s percentage bracketed by 95 PPU (p index) and an index r computed as follows:

$$ \begin{aligned} \overline{d} & = \frac{1}{n}\sum\limits_{t = 1}^{n} {\left( {y_{97.5\% } - y_{2.5\% } } \right)} \\ r & = \frac{{\overline{d}}}{\sigma } \\ \end{aligned} $$
(26)

where \(\sigma\) is standard deviation of the data, \(y_{97.5\% }\) is the upper boundary of 95PPU, \(y_{2.5\% }\) is the lower boundary of 95PPU, n is quantity of data, and r is average width of the confidence interval band. Other evaluation statistics utilized in this study were: RMSE (lower RMSE shows more accurate estimations), mean absolute error (MAE) (lower MAE shows more accurate estimation), percentage bias (PBIAS) (lower PBIAS shows more accurate estimations), and Nash–Sutcliffe efficiency (NSE) (NSE = 1 shows the ideal model):

$$ {\text{RMSE}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {Y_{{{\text{obs}}}} - Y_{{{\text{sim}}}} } \right)^{2} } } $$
(27)
$$ {\text{RMSE}} = \frac{1}{n}\sum\limits_{i = 1}^{n} {\left| {Y_{{{\text{obs}}}} - Y_{{{\text{sim}}}} } \right|} $$
(28)
$$ {\text{PBIAS}} = 100 * \left[ {\frac{{\sum\nolimits_{i = 1}^{n} {\left( {Y_{{{\text{obs}}}} - Y_{{{\text{sim}}}} } \right)} }}{{\sum\nolimits_{i = 1}^{n} {\left( {Y_{{{\text{obs}}}} } \right)} }}} \right] $$
(29)
$$ {\text{NSE}} = 1 - \left[ {\frac{{\sum\nolimits_{i = 1}^{n} {\left( {Y_{{{\text{obs}}}} - Y_{{{\text{sim}}}} } \right)}^{2} }}{{\sum\nolimits_{i = 1}^{n} {\left( {Y_{{{\text{obs}}}} - \overline{Y}_{{{\text{obs}}}} } \right)} }}} \right] $$
(30)

where n is quantity of observed data, \(Y_{{{\text{obs}}}}\) is observed data, \(Y_{{{\text{sim}}}}\) is simulated data, and \(\overline{Y}_{{{\text{obs}}}}\) is mean of observed data.

3 Results and discussion

3.1 Selection of appropriate inputs for soft computing models

In this study, the soft computing models are used to predict SSL (t) (a 1-day ahead forecast of SSL). Principal component analysis (PCA) is an effective method for identifying inputs of models and decreasing the number of input parameters required (Lu et al. 2019). PCA achieves parsimony by describing the maximum value of common variance in a correlation matrix using the smallest number of illustrative concepts. The Kaiser–Meyer–Melkin criterion (KMO) is used to investigate the adequacy of data as follows. The KMO is a measure of the proportion of variance among variables that might be common variance (Darabi et al. 2014).

$$ {\text{KMO}} = \frac{{\sum {\left( {{\text{correlation}}} \right)^{2} } }}{{\sum {\left( {{\text{correlation}}} \right)^{2} + \sum {\left( {{\text{partial}}\;{\text{correlation}}} \right)^{2} } } }} $$
(31)

According to the literature, the minimum value of KMO should be 0.5. In this study, KMO was 0.65. The correlation among variables should be checked, to avoid multicollinearity problems (Lu et al. 2019). In this study, all correlation values were below the threshold (0.9), and thus, there were no problems of multicollinearity. Table 2 shows the value of the contribution of principal components (PCs). The results indicated that the first three PCs included 60, 23, and 12% of input variables at Talar station, and 61, 20, and 11% of input variables at Kasilian station. Lagged data (one-day to nine-day lagged rainfall, one-day to nine-day lagged discharge, and one-day to nine-day lagged SSL) were regarded as the initial data. It was found that the first three PCs were affected more by one-day and two-day lagged SSL, one-day lagged R, and one-day lagged Q than by any other variables (Table 2). The direction of new future space was determined by the eigenvectors and the variance of data by the eigenvalues (Table 2). The PCs are the integration of the independent variable.

Table 2 Eigenvalues and eigenvectors obtained for principal components (PCs) describing the most influential variables (time (t)-lagged suspended sediment load (SSL), discharge (Q), rainfall (R))
Full size table

3.1.1 Tuning the random parameters in optimization algorithms

In the current work, the Taguchi model was utilized to set the random parameters of evolutionary algorithms. Population size and r2, r3, and r4 are regarded as the random parameters in SCA that can affect the accuracy of the proposed model. Four levels were defined for each of these four parameters. The total number of tests to be performed to find the optimum value of parameters was computed as:

$$ {\text{Number}} = 1 + N\left( {L - 1} \right) $$
(32)

where L is level number and N is parameter number. Hence, at least 13 experiments had to be conducted for SCA. In addition, the Taguchi model utilizes signal-to-noise ratio to select the optimal value of parameters (Mozdgir et al. 2013):

$$ \frac{S}{N}{\text{ratio}} = - 10\log \left( {{\text{objective}}\left( {{\text{function}}} \right)} \right)^{2} $$
(33)

where the optimal value of random parameters has the highest S/N ratio. Figure 8 depicts the computed S/N ratio for different parameters in the four optimization algorithms tested here.

3.2 Talar station

For Talar station, the best results with the training dataset were obtained when ANFIS-SCA was used (RMSE: 934.2 ton/day, MAE: 912.3 ton/day, NSE: 0.93, PBIAS: 0.14) and the worst results were obtained when RBFNN was used (RMSE: 1789.10 ton/day, MAE: 1765.2 ton/day, NSE: 0.77, PBIAS: 0.36) (Table 3). The MLP-SCA was the best second model, and the hybrid and stand-alone MLP outperformed the hybrid and stand-alone RBFNN models (Table 3). Comparison of results obtained using the optimization algorithms revealed that SCA provided the best results and FFA the worst results.

Table 3 Value of evaluation criteria (root mean square error (RMSE), mean absolute error (MAE), Nash–Sutcliffe efficiency (NSE), percentage bias (PBIAS)) obtained for the different hybrid and stand-alone models in the training and testing phases for the Talar and Kasilian stations
Full size table

The best results with the testing dataset for Talar station were also obtained with ANFIS-SCA (RMSE: 1423.2 ton/day, MAE: 1412.10 ton/day, NSE: 0.92, PBIAS: 0.16) (Table 3). Based on the RMSE, MAE, and PBIAS values, in the test stage the stand-alone ANFIS, MLP, and RBFNN models were more accurate than the hybrid ANFIS, MLP, and RBFNN models. Adding SCA decreased the RMSE of ANFIS, MLP, and RBFNN by 20%, 21%, and 22%, respectively. The testing results indicated that the hybrid and stand-alone MLP was better than the hybrid and stand-alone RBFNN models.

3.3 Kasilian station

For Kasilian station, in the training stage ANFIS-SCA was the best performing model (RMSE: 898.1 ton/day, MAE: 712.3 ton/day, NSE: 0.95, PBIAS: 0.12) and RBFNN was the worst (RMSE: 1655.6 ton/day, MAE: 1645.2 ton/day, NSE: 0.82, PBIAS: 0.39) (Table 3). The hybrid and stand-alone MLP models outperformed the stand-alone and hybrid RBFNN models during the training phase, while ANFIS-SCA outperformed MLP-SCA and RBFNN-SCA in terms of precision. Overall, the NSE, MAE, PBIAS, and NSE values for SCA proved its superiority among the optimization algorithms tested, while FFA gave the worst results. The performance of the hybrid ANFIS, MLP, and RBFNN models surpassed that of their stand-alone counterpart in the training stage.

In the testing phase, ANFIS-SCA again provided the best results (RMSE: 1412.10 ton/day, MAE: 1403.4 ton/day, NSE: 0.92; PBIAS: 0.14), and RBFNN again exhibited the worst results (RMSE: 1789.1 ton/day, MAE: 1767.2 ton/day, NSE: 0.65; PBIAS: 0.49) (Table 3). The hybrid ANFIS, MLP, and RBFNN models outperformed the stand-alone ANFIS, MLP, and RBFNN models. Based on the assessment statistics for Kasilian Station, it can be said that the SCA was the most accurate optimization algorithm and, as in the training phase, FFA gave the worst results) (Table 3). The evaluation criteria also confirmed the superiority of ANFIS-SCA, followed by the MLP-SCA, in comparison with RBFNN-SCA.

In order to visually summarize how closely the proposed models matching the observed values, Taylor diagrams were used to display the match between observed data and the output of the models in terms of their RMSE, standard deviation, and correlation. The Taylor diagram for Talar station, in which statistics for the 15 models (see Table 3) were calculated and a colored circle was assigned to each model, is shown in Fig. 8a. The position of each circle appearing in the diagram quantifies how that model’s estimated SSL matched measured data, where the centered RMSE is proportional to the distance from the reference point on the horizontal axis as observed data. The whole dataset was used to plot the Taylor diagrams. The results revealed that for ANFIS-SCA, MLP-SCA, and RBFNN-SCA, the centered RMSE was 1000, 1050, and 1189 m, respectively. The hybrid soft computing models resulted in lower RMSE than the stand-alone models (Fig. 9a).

Fig. 9
figure 9

Taylor diagram for the different hybrid and stand-alone models (using whole dataset) for a Talar station and b Kasilian station

Full size image

The Taylor diagram for Kasilian station is shown in Fig. 8b. It indicated that ANFIS-SCA and MLP-SCA predictions gave the best match with observed data and that the ANFIS-SCA model had a higher Taylor correlation and lower RMSE than the other models. The RBFNN model had the highest RMSE. When using the hybrid MLP, RBFNN, and ANFIS model, the Taylor correlation increased from 0.4 to 0.97. The highest RMSE was found for the stand-alone and hybrid MLP models (980–3000 ton/day) and the stand-alone and hybrid RBFNN models (1100 to 3300 ton/day) (Fig. 9b).

3.4 Uncertainty analysis of models and box plots

Comparison of models in terms of the selected indices (p and r) showed that ANFIS-SCA provided better r (0.12) and p (0.95) values for both Talar and Kasilian stations (Table 4). The hybrid ANFIS, MLP, and RBFNN models gave better p and r values than the stand-alone ANFIS, MLP, and RBFNN models. In addition, RBFNN-FFA had the lowest p (0.76) and highest r (0.39) among the hybrid models. For Talar station, the hybrid and stand-alone ANFIS models gave better r and p values than the hybrid and stand-alone MLP and RBFNN models (Table 4). Figure 10a, b shows the box plots for different models at Talar and Kasilian stations. The results indicated that ANFIS-SCA, MLP-SCA, and RBFNN-SCA most closely matched the observed SSL, outperforming the stand-alone ANFIS, MLP, and RBFNN models at both stations.

Table 4 Uncertainty results (r, p) for the different hybrid and stand-alone models
Full size table
Fig. 10
figure 10

Box plots of suspended sediment load (SSL) values obtained with the different hybrid and stand-alone models for a Talar and b Kasilian, c Eagel Creek Basin stations

Full size image

Overall, this study showed that the hybrid ANFIS-SCA model has good ability for predicting SSL in rivers. However, different climate parameters affected the SSL values obtained (Table 2), so follow-up studies should predict SSL for future periods using climate models and scenarios describing projected changes in meteorological parameters such as temperature and rainfall.

3.4.1 The analysis for the Eagel Creek river basin

Table 2 indicates that the first three components (PC1, PC3, and PC3) have greater values of participation. Furthermore, SSL (t − 1), R (t − 1), and Q (t − 1) data are more significant for all three components compared to other data. Thus, the first three components were selected as input to the models. Table 5 shows that the ANFIS-SCA model reduced RMSE by 15% and 21% compared to the MLP-SCA and RBFNN-SCA models in the training phase. Comparing models performance indicated that the ANFIS-SCA model could decrease MAE error compared to ANFIS-BA, ANFIS-PSO, ANFIS-FFA, and ANFIS models by 18%, 32%, 37%, and 49% in the training phase, respectively. Comparing the performance of the models showed that the ANFIS-SCA model with the highest value of p and the lowest value of r had less uncertainty than other models in the training phase. Moreover, the findings indicated that RBFNN model with 0.77 NSE had the weakest performance in the training phase. Examining the performance of the models in the training phase according to PBIAS value indicated that the MLP-SCA model had less PBIAS than other MLP models, showing better performance of the MLP-SCA model than other models. Comparing the performance of the models in the test phase indicated that the ANFIS-SCA model reduced RMSE value by 8.8%, 24%, 38%, and 45%, respectively, compared to the ANFIS-BA, ANFIS-PSO, ANFIS-FFA, and ANFIS in the test phase. Additionally, the results indicated that the RBFNN model with NSE and PBIAS of 0.62 and 0.55 has the weakest performance among the models in the test phase. One can see that the hybrid ANFIS models had higher and lower p and r values than the ANFIS model, showing less uncertainty of hybrid ANFIS models compared to the ANFIS model. Ultimately, Fig. 10c indicates that ANFIS-SCA box diagram was more in line with the observational data compared to other models. Figure 10c indicates that ANFIS, MLP, and RBFNN models are less accurate than models using optimization algorithms. Hence, the performance of the models for the second case study indicated that ANFIS-SCA model had better accuracy in the present study. In Table 5, the performance of the different hybrid and stand-alone models for the training and testing phases is presented for the Eagel Creek Basin.

Table 5 Performance of the different hybrid and stand-alone models for the training and testing phases for the Eagel Creek Basin
Full size table

4 Conclusions

The knowledge of suspended sediment load modeling in rivers is excessive, as it results from soil erosion and plays a key role in watershed management, river morphology, and the operation of hydraulic structures. The current research studied any possibility of evolutionary soft computing approaches in suspended sediment load modeling. However, soft computing approaches such as the ANFIS, MLP, and RBFNN models are widely used to estimate SSL, but their output is not sufficiently accurate for basin management. In this study, four optimization algorithms (SCA, PSO, BA, and FFA) were used to train the ANFIS, MLP, and RBFNN models for suspended sediment load prediction at the basin scale (Talar and Eagel Creek Basins located in northern Iran and central part of USA). The second case study demonstrated that the ANFIS-SCA model could decrease MAE error compared to ANFIS-BA, ANFIS-PSO, ANFIS-FFA, and ANFIS models by 18%, 32%, 37%, and 49% in the training phase, respectively. However, different climate parameters affected the SSL value, so future studies should predict SSL for future periods using models and scenarios describing future changes in climate. Each optimization algorithm in the study with high accuracy and appropriate convergence speed showed a very high capacity for solving optimization problems. The conclusions are as follows:

  • Novel optimized models had an important scientific contribution to the development of a powerful model for suspended sediment load prediction at the watershed scale. The sine–cosine algorithm (SCA) optimizer gave strong predictive capacities to the (multilayer perceptron (MLP), adaptive neuro-fuzzy system (ANFIS), and radial basis function neural network (RBFNN).

  • Among the optimized models, ANFIS-SCA showed the best performance in the training and testing phases for both stations, while RBFNN showed the lowest accuracy.

  • Optimization of the models using SCA has decreased the RMSE by 20%, 21%, and 22% for ANFIS, MLP, and RBFNN, respectively.

  • The uncertainty outputs (based on the uncertainty in sequential uncertainty fitting (SUFI-2)) indicated that the hybrid ANFIS, MLP, and RBFNN models were the most accurate (lowest r index, highest p index) of the models tested. Overall, ANFIS-SCA showed a good ability for predicting SSL.

  • This study can help as a basic research for future studies and other regions (other optimization algorithms or soft computing models) seeking suspended sediment load prediction in a watershed scale using optimized models.