Abstract
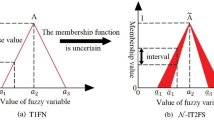
This paper focuses on the limit cycles prediction problem to discuss the stability analysis of dynamic nonlinear interval type-2 Takagi–Sugeno–Kang fuzzy control systems (NIT2 TSK FCSs) with adjustable parameters. First, in order to alleviate computational burden, a simple architecture of NIT2 TSK FCS using two embedded nonlinear type-1 TSK fuzzy control systems (NT1 TSK FCSs) is proposed. Then, describing function (DF) of NIT2 TSK FCS is obtained based on the DFs of embedded NT1 TSK FCSs. Subsequently, integrating the stability equation and parameter plane approaches provides a solution to identify the limit cycle and the asymptotically stable regions. Moreover, particle swarm optimization technique is applied to minimize the limit cycle region. Furthermore, for robust design, a gain-phase margin tester is utilized to specify the minimum gain margin (\(\hbox {GM}_{\mathrm{min}}\)) and phase margin (\(\hbox {PM}_{\mathrm{min}}\)) when limit cycles can arise. Finally, two simulation examples are considered to validate the advantages of the presented method.












Similar content being viewed by others
References
Antonio-Cruz M, Hernández-Guzmán VM, Silva-Ortigoza R (2018) Limit cycle elimination in inverted pendulums: furuta pendulum and pendubot. IEEE Access 6:30317–30332. https://doi.org/10.1109/ACCESS.2018.2839642
Aracil J, Gordillo F (2004) Describing function method for stability analysis of PD and PI fuzzy controllers. Fuzzy Sets Syst 143(2):233–249. https://doi.org/10.1016/S0165-0114(03)00162-3
Castillo O, Amador-Angulo L (2018) A generalized type-2 fuzzy logic approach for dynamic parameter adaptation in bee colony optimization applied to fuzzy controller design. Inf Sci 460:476–496. https://doi.org/10.1016/j.ins.2017.10.032
Dey A, Sen S (2018) Describing function-based approximations of biomolecular systems. IET Syst Biol 12(3):93–100. https://doi.org/10.1049/iet-syb.2017.0026
Enyinna N, Karimoddini A, Opoku D, Homaifar A, Arnold S (2015) Developing an interval type-2 TSK fuzzy logic controller. In: 2015 Annual conference of the North American fuzzy information processing society (NAFIPS) held jointly with 2015 5th world conference on soft computing (WConSC). IEEE, pp 1–6.https://doi.org/10.1109/NAFIPS-WConSC.2015.7284160
Eyoh I, John R, De Maere G, Kayacan E (2018) Hybrid learning for interval type-2 intuitionistic fuzzy logic systems as applied to identification and prediction problems. IEEE Trans Fuzzy Syst 26(5):2672–2685. https://doi.org/10.1109/TFUZZ.2018.2803751
Gao J, Yi J, Pu Z, Li C (2017) Interval type-2 TSK nominal-fuzzy-model-based sliding mode controller design for flexible air-breathing hypersonic vehicles. In: 2017 IEEE international conference on fuzzy systems (FUZZ-IEEE). IEEE, pp 1–6. https://doi.org/10.1109/FUZZ-IEEE.2017.8015601
Gaxiola F, Melin P, Valdez F, Castro JR, Castillo O (2016) Optimization of type-2 fuzzy weights in backpropagation learning for neural networks using GAs and PSO. Appl Soft Comput 38:860–871. https://doi.org/10.1016/j.asoc.2015.10.027
Hailemichael A, Behniapoor M, Karimoddini A (2018) Development of an interval type-2 TSK fuzzy logic attitude controller for a UAV. In: 2018 International conference on unmanned aircraft systems (ICUAS). IEEE, pp 1003–1009. https://doi.org/10.1109/ICUAS.2018.8453330
Hameed IA (2009) Simplified architecture of a type-2 fuzzy controller using four embedded type-1 fuzzy controllers and its application to a greenhouse climate control system. Proc Inst Mech Eng Part I J Syst Control Eng 223(5):619–631. https://doi.org/10.1243/09596518JSCE708
Hameed IA, Sorensen CG, Gree O (2011) Building an intelligent controller using simple genetic type-2 fuzzy logic system. Fuzzy Controllers, Theory and Applications, Dr Lucian Grigorie (Ed) pp 147–162. https://doi.org/10.5772/13376
Iannelli A, Marcos A, Lowenberg M (2018) Nonlinear robust approaches to study stability and postcritical behavior of an aeroelastic plant. IEEE Trans Control Syst Technol 27(2):703–716. https://doi.org/10.1109/TCST.2017.277911
Jafari P, Teshnehlab M, Tavakoli-Kakhki M (2018) Adaptive type-2 fuzzy system for synchronisation and stabilisation of chaotic non-linear fractional order systems. IET Control Theory Appl 12(2):183–193. https://doi.org/10.1049/iet-cta.2017.0785
Kabziński J, Kacerka J (2014) TSK fuzzy modeling with nonlinear consequences. In: IFIP international conference on artificial intelligence applications and innovations. Springer, pp 498–507. https://doi.org/10.1007/978-3-662-44654-6-49
Karakose M, Yetis H, Akin E (2018) Sine-square embedded fuzzy sets versus type-2 fuzzy sets. Adv Eng Inform 36:43–54. https://doi.org/10.1016/j.aei.2018.02.007
Kim E, Lee H, Park M (2000) Limit-cycle prediction of a fuzzy control system based on describing function method. IEEE Trans Fuzzy Syst 8(1):11–22. https://doi.org/10.1109/91.824762
Kw L, Choi H (2010) Analysis of FLC with changing fuzzy variables in frequency domain. Int J Control Autom Syst 8(3):695–701. https://doi.org/10.1007/s12555-010-0324-3
Maldonado Y, Castillo O, Melin P (2013) Particle swarm optimization of interval type-2 fuzzy systems for fpga applications. Appl Soft Comput 13(1):496–508. https://doi.org/10.1016/j.asoc.2012.08.032
Martínez-Soto R, Castillo O, Aguilar LT (2014) Type-1 and type-2 fuzzy logic controller design using a hybrid PSO–GA optimization method. Inf Sci 285:35–49. https://doi.org/10.1016/j.ins.2014.07.012
Martínez-Soto R, Castillo O, Aguilar LT, Rodriguez A (2015) A hybrid optimization method with PSO and GA to automatically design type-1 and type-2 fuzzy logic controllers. Int J Mach Learn Cybern 6(2):175–196. https://doi.org/10.1007/s13042-013-0170-8
Moodi H, Farrokhi M (2013) Robust observer design for Sugeno systems with incremental quadratic nonlinearity in the consequent. Int J Appl Math Comput Sci 23(4):711–723. https://doi.org/10.2478/amcs-2013-0053
Moodi H, Farrokhi M (2015) Robust observer-based controller design for Takagi–Sugeno systems with nonlinear consequent parts. Fuzzy Sets Syst 273:141–154. https://doi.org/10.1016/j.fss.2015.01.007
Moodi H, Farrokhi M, Guerra TM, Lauber J (2019) On stabilization conditions for T–S systems with nonlinear consequent parts. Int J Fuzzy Syst 21(1):84–94. https://doi.org/10.1007/s40815-018-0548-6
Namadchian Z, Zare A, Namadchian A (2014) Stability analysis of nonlinear dynamic systems by nonlinear Takagi-Sugeno-Kang fuzzy systems. J Dyn Syst Meas Control 136(2):021019-1. https://doi.org/10.1115/1.4025803
Oliveira N, Kienitz K, Misawa E (2012) A describing function approach to the design of robust limit-cycle controllers. Nonlinear Dyn 67(1):357–363. https://doi.org/10.1007/s11071-011-9983-8
Ontiveros E, Melin P, Castillo O (2018) Impact study of the footprint of uncertainty in control applications based on interval type-2 fuzzy logic controllers. In: Fuzzy Logic augmentation of neural and optimization algorithms: theoretical aspects and real applications. Springer, pp 181–197. https://doi.org/10.1007/978-3-319-71008-2-15
Perng JW (2012) Describing function analysis of uncertain fuzzy vehicle control systems. Neural Comput Appl 21(3):555–563. https://doi.org/10.1007/s00521-0110532-7
Perng JW (2013) Limit-cycle analysis of dynamic fuzzy control systems. Soft Comput 17(9):1553–1561. https://doi.org/10.1007/s00500-012-0971-9
Perng JW, Wu BF, Chin HI, Lee TT (2004) Gain-phase margin analysis of dynamic fuzzy control systems. IEEE Trans Syst Man Cybern Part B (Cybern) 34(5):2133–2139. https://doi.org/10.1109/TSMCB.2004.831772
Perng JW, Wu BF, Liao TY, Lee TT (2007) Robust stability analysis of a fuzzy vehicle lateral control system using describing function method. In: Theoretical advances and applications of fuzzy logic and soft computing. Springer, pp 673–682. https://doi.org/10.1007/978-3-540-72434-6-68
Perng JW, Ma LS, Wu BF (2010) Limit cycle prediction of a neurocontrol vehicle system based on gain-phase margin analysis. Neural Comput Appl 19(4):565–571. https://doi.org/10.1007/s00521-009-0319-2
Precup R, Preitl S (2006) On a class of control systems with Takagi–Sugeno PI-fuzzy controllers. Stud Inf Control 15(3):323
Prieto PJ, Cazarez-Castro NR, Aguilar LT, Cardenas-Maciel SL (2017) Chattering existence and attenuation in fuzzy-based sliding mode control. Eng Appl Artif Intell 61:152–160. https://doi.org/10.1016/j.engappai.2017.03.005
Rosales A, Shtessel Y, Fridman L, Panathula CB (2017) Chattering analysis of hosm controlled systems: frequency domain approach. IEEE Trans Autom Control 62(8):4109–4115. https://doi.org/10.1109/TAC.2016.2619559
Rosales A, Ibarra L, Ponce P, Molina A (2019) Fuzzy sliding mode control design based on stability margins. J Frankl Inst 356(10):5260–5273. https://doi.org/10.1016/j.jfranklin.2019.04.035
Sanchez MA, Castillo O, Castro JR (2015) Information granule formation via the concept of uncertainty-based information with interval type-2 fuzzy sets representation and Takagi–Sugeno–Kang consequents optimized with cuckoo search. Appl Soft Comput 27:602–609. https://doi.org/10.1016/j.asoc.2014.05.036
Sun X, Zhang H, Han J, Wang Y (2017) Non-fragile control for interval type-2 TSK fuzzy logic control systems with time-delay. J Frankl Inst 354(18):7997–8014. https://doi.org/10.1016/j.jfranklin.2017.08.025
Tavoosi J, Suratgar AA, Menhaj MB (2017) Stability analysis of recurrent type-2 TSK fuzzy systems with nonlinear consequent part. Neural Comput Appl 28(1):47–56. https://doi.org/10.1007/s00521-015-2036-3
Vander Velde WE (1968) Multiple-input describing functions and nonlinear system design. McGraw-Hill, New York
Xu B, Chen D, Zhang H, Zhou R (2015) Dynamic analysis and modeling of a novel fractional-order hydro-turbine-generator unit. Nonlinear Dyn 81(3):1263–1274. https://doi.org/10.1007/s11071-015-2066-5
Xun S, Huaguang Z, Yingchun W (2015) Stabilization algorithm for interval type-2 TSK fuzzy logic control systems with bounded time-varying delay. In: 2015 34th Chinese control conference (CCC). IEEE, pp 321–325. https://doi.org/10.1109/ChiCC.2015.7259657
Zhao T, Dian S (2017) Delay-dependent stabilization of discrete-time interval type-2 T–S fuzzy systems with time-varying delay. J Frankl Inst 354(3):1542–1567. https://doi.org/10.1016/j.jfranklin.2016.12.002
Zhao T, Dian S (2018) State feedback control for interval type-2 fuzzy systems with time-varying delay and unreliable communication links. IEEE Trans Fuzzy Syst 26(2):951–966. https://doi.org/10.1109/TFUZZ.2017.2699947
Zhao T, Liu J, Dian S (2019) Finite-time control for interval type-2 fuzzy time-delay systems with norm-bounded uncertainties and limited communication capacity. Inf Sci 483:153–173. https://doi.org/10.1016/j.ins.2019.01.044
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Communicated by V. Loia.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 A. Proof of Lemma 1:
\(\forall t_1\in R\), let \(x_1\equiv A\hbox {sin}\omega t_1\) and \({{\dot{x}}}_1\equiv \omega A\hbox {cos}\omega t_1\).
For LNT1 TSK FCS: As shown in Fig. 5, in the case
\( \Phi _{k} \le x_{1} <\Phi _{k+1} \) and \(\Psi _{l} \le {\dot{x}}_{1} <\Psi _{l+1} \), we have
where
As proved in Kim et al. (2000), for \(t_2\equiv t_1-({\pi }/{\omega })\), \(x_2=-x_1\) and \({{\dot{x}}}_2=-{{\dot{x}}}_1\). Therefore,
Therefore, \({\underline{u}}(t-\left( \frac{\pi }{\omega } \right) )=-{\underline{u}}(t).\) As shown in Fig. 4, in the case \(\Phi _{k} \le x<\Phi _{k+1} \) and \(\Psi _{l} \le {\dot{x}}<\Psi _{l+1} \), we have
where
The proof of \({\overline{u}}\left( t\right) =-{\overline{u}}\left( t-({\pi }/{\omega })\right) \) is similar to the proof of \({\underline{u}}\left( t\right) =-{\underline{u}}\left( t-({\pi }/{\omega })\right) \).
1.2 B. Proof of Lemma 2:
To obtain \({{\underline{a}}}_{r,k,l}\), \(\ {{\underline{b}}}_{r,k,l}\), \({{\underline{c}}}_{r,k,l}\), and \({{\underline{d}}}_{r,k,l}\) and \({\; }\Phi _{k} +\tau _{e} \le x<\Phi _{k+1} -\tau _{e} ,{\; \; }\Psi _{l} +\tau _{{\dot{e}}} \le {\dot{x}}<\Psi _{l+1} -\tau _{{\dot{e}}}\).
where for \(r=1,2,3,4\)
The proof of \({{\underline{a}}}_{r,k,l}\),\(\ {{\underline{b}}}_{r,k,l}\), \({{\underline{c}}}_{r,k,l}\), and \({{\underline{d}}}_{r,k,l}\) for other intervals and \({{\overline{a}}}_{r,k,l}\), \({{\overline{b}}}_{r,k,l}\), \({{\overline{c}}}_{r,k,l}\) and \({{\overline{d}}}_{r,k,l}\) is similar to this proof.
Rights and permissions
About this article
Cite this article
Namadchian, Z., Zare, A. Stability analysis of dynamic nonlinear interval type-2 TSK fuzzy control systems based on describing function. Soft Comput 24, 14623–14636 (2020). https://doi.org/10.1007/s00500-020-04811-0
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-020-04811-0