Abstract
This paper is aimed to make sense of the real effect of implement of social healthcare insurance on one’s medical expense in China. Due to previous studies drew various and inconsistent conclusions on this issue, this works intend to apply meta-analysis to the problem. For 31 related studies, we first implement an advanced conditional Dirichlet-based Bayesian semi-parametric model specific to meta-analysis, and come to a primary conclusion that healthcare possesses little probability reducing one’s medical expense in China. Further, the authors conduct random effects meta-regression and find that heterogeneity exists among the observed effect sizes. Mixed effects model shows that the age variation may is actually the heterogeneity source. The coefficients for Non-old and Old are respectively 0.29 and 0.54, implying that when researching on the medical expense for the elderly, it is more likely to conclude the medical insurance could increase medical spending. The coefficients for IV and OLS are both remarkably negative at 90% confidence level. This suggests when directly using Instrument Variable (IV) approach and OLS method to assess the implementation effect for the healthcare insurance, it is inclined to result in the reduced impact on medical expense. We deduce this is because this two methods can’t solve the sample-selection bias when compared with the Two-part model and difference-in-difference (DID) model. Based on the results and discussion, we finally propose suggests for the government.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
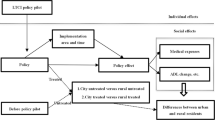
Since the Chinese economic reform in 1978, China has been experiencing rapid economic growth. However, the economic success is not translated into social welfare for citizens. The increasingly demands for medical services is not satisfied, what’s more, this situation is more aggravated on account of the rapid aging population. According to China National Bureau of Statistics, the out-of-pocket (OOP) medical expenses for citizens increase rapidly from 1980 to 2003, with the proportion rising from 21.19% to 55.87%, which increase the medical burden of households. According to National Bureau of Statistics, from 1995 to 2014, per capita health spending in urban areas averagely accounts for 4.6% of per capita disposable income, together with an increase speed of 3.24%; this proportion for rural areas is 4.79% and with 5.85% average annual growth rate. Besides, the income elasticity of health spending per capita for urban and rural households are respectively 1.51 and 2.18 from 1996-2014, manifesting the growth rate of residents’ per capita healthcare are separately 1.51 and 2.18 times of per capita disposable income in urban and rural areas. Until now, China has established relatively comprehensive healthcare system, including the Urban Employee Basic Medical Insurance (UEBMI) for the urban employed residents, initiated in 1998; the New Cooperative Medical Scheme (NCMS) for rural residents, established in 2003; and the Urban Resident Basic Medical Insurance (URBMI) in 2007, covering urban residents without formal employment. By the end of 2013, the insurance coverage has been over 95%. The three kinds of healthcare insurances are aimed at different groups with different social statuses, and the capital raising, government subsidies, compensation levels, etc are also different. Then, whether the health care make it easier and cheaper to get medical treatment? Whether it increases the utilization of healthcare services and reduces medical expenses for residents? These problems are deserved to attention.
This paper may provide the first attempt to contribute to examining the healthcare insurance impact from the perspective of meta-analysis. To date, a large body of literature has explored the implementing effect of the three types of healthcare insurances on medical expense. However, sometimes the results from the diverse studies are inconsistent: some studies are in favor of the reduced effect of the insurance, while others are neutral or negative. The goals of a meta-analysis is then to arrive at an overall conclusion regarding the benefits of the healthcare insurances, and also to figure out and explain the heterogeneity among the different studies. Thus, this method can make a substantial contribution to the focal relationship by highlighting more accurately the main factors behind the inconclusive results.
The organization of this paper is as follows. Section 2 provides a brief overview of the impact of healthcare on medical expenditure, and explains why using meta-analysis. Section 3 outlines the data and methods used in the paper. Section 4 presents the empirical results of two kinds of meta-analysis and related tests. Section 5 give a detailed discussion about the main empirical results. Finally, Sect. 6 presents the conclusions and policy suggestions.
2 Literature review
2.1 Impact of healthcare on medical expenditure
Internationally, a large body of literature has study the impact of different kinds of public healthcare systems. The general results suggest that the health insurance can improve access to hospital, but the impact on OOP health expenditure reduction is paradoxical. For example, for the developed counties in the United States, Canada, Australia and so on, the empirical results indicate that healthcare programme indeed increases healthcare utilization among the poor (Sinclair and Smetters 2004; Goldman et al. 2006,Kopecky and Koreshkova 2009,Pashchenko and Porapakkarm 2013), and crowds out medical spending for individuals with low wealth and low health status (Ariizumi 2008), but the OOP spending seems to have increased for the insured in urban areas (Suryahadi 2013). While in developing regions, most of the studies concluded the increasing coverage of health insurance has also increased hospital utilization (Cheng and Chiang 1997; Chen et al. 2007) and lowered outpatient and inpatient treatment costs in Vietnam and Mexico (Wagstaff and Pradhan 2006; Nguyen et al. 2012; Galárraga et al. 2010), particularly for the low-income households (Sheu and Lu 2014), However,Wagstaff (2010) found no impact of Vietnam’s recent healthcare fund for the poor and on hospital utilization, although it does seem to have reduced OOP health spending. Palmer and Nguyen (2012) found it no impact on inpatient-related costs for persons with disabilities, although improving access to the healthcare.
In light of the impact of China’s health insurances, the results are also mixed. For the effect of NCMS in rural China, Wagstaff et al. (2009) combines DID method with propensity score matching(PSM), and found positive effects on the outpatient and inpatient utilization between 2003 and 2005, but no reduced effect on OOP. Liu and Tsegai (2011) used the PSM to estimate and confirmed that the NCMS has indeed improved outpatient utilization for rural residents, but it also increased the incidence of one’s catastrophic expenditures in western regions. Wen and Song also found the new rural cooperation increase the old one’s total medical expense by19%. However, Bairoliya et al. (2017)developed a dynamic general equilibrium model evolving life-cycle, suggesting that introduction of rural health insurance in China results in large gains in social welfare, due to avoiding extreme OOP healthcare expenditures and reducing risk to households. Yu et al. (2010) found that the outpatient service utilization has not significantly changed under NCMS, when compared with the inpatient service.Su et al. (2013) built a two-part model and found that the NCMS not only enhance the rural residents’ probability to visit a doctor, but also reduced their medical expenses. Xue and Lu (2012), Zhang and Tong (2014) respectively applied Tobit model and Two-part model, and found that the NCMS can decrease the OOP medical expense for the aged.
For the UEBMI,Liu and Zhao (2006) adopted data from the pilot experiment conducted in Zhenjiang, and found the OOP expenditures for all groups increase (grouped by chronic disease, income, education, and job status). Wagstaff and Lindelow (2008) showed that the health insurance has in fact increased OOP and catastrophic payments, with IV, Poisson/Zrobit and FE Poisson/Logit panel data regression. However, Huang and Gan (2015) applied DID model using the China Health and Nutrition Survey (CHNS) data set from 1991-2006, and found that the probability of utilizing outpatient care and outpatient expenditures both declines due to the UEBMI reform, but insignificant and smaller for the inpatient. For the URBMI, Liu and Zhao (2014) explored the fixed effects approach with instrumental variable correction, used the CHNS data from 2006-2009, and found URBMI has significantly increased the utilization of formal medical services, but not reduced OOP health expense. While Huang and Gan (2012) demonstrated the outpatient total medical expense significantly declines 28.6%-30.6%, but insignificant in OOP healthcare spending.
By and larger, the implement of healthcare has a positive effect on outpatient and inpatient utilization, but the impact on medical cost is inconsistent. In summary, there are five methods used to examine the health insurance effectiveness, including DID model, Two-part model, Tobit model, ordinary least squares (OLS) regression involving IV, OLS. For the three types of social health insurances, some studies verify they are helpful in reducing medical burden, but others conclude they increase the medical expense. After a health programme is carried out, the policy makers are concerned about the outcomes. Nevertheless, the empirical results will be different even contradictory due to data selection, sample size, econometric models and so on, which makes people confused with the real impact. In this context, it is necessary to find out a method that could systematically consider and extract the characteristic variables of published literature, so as to reanalysis and reassess the estimated outcomes.
2.2 Why meta-analysis is used to re-examine the impact of healthcare insurance?
Since the findings of the impact of healthcare on medical expense are inconclusive, meta-analysis is a helpful tool in reconciling and clarifying the inconsistencies (Stanley 2005). There have been considerable studies investigating the impact of healthcare using meta-analysis (Gopalakrishnan and Ganeshkumar 2013; Costafont and Hernández-Quevedo 2015). Hughes et al. (1997) indexed 412 articles from 1964-1994 that examined the generic home care impact on hospital use/cost, effect sizes and homogeneity of variance measures were calculated to obtain the secondary data sources. Effect sizes indicate a small moderation will lead to positive impact of home care in reducing hospital days. Boland et al. (2013) carried out a systematic review and meta-analysis to assess the cost-effectiveness of Chronic Obstructive Pulmonary Disease Disease Management (COPD-DM) programs in Netherlands, suggesting that COPD-DM programs have favorable effects on both health outcomes and costs, but there was considerable heterogeneity depending on patient, intervention, and study-characteristics. Campanella et al. (2015) applied meta-analysis to assess the impact of electronic health record (EHR) on healthcare quality and the impact of Public Reporting on clinical outcomes (Campanella et al. 2016). Gallet and Doucouliagos (2017) applied meta-regression analysis (MRA), and examine the healthcare spending elasticity for the mortality rate and the spending elasticity for life expectancy. Shor et al. (2017)conducted meta-analyses and meta-regressions to examine the relationship between immigration and mortality from Latin American countries to OECD countries, and the overall results suggested no immigrant mortality advantage, and the relative risk of mortality largely depends on life course stages.
Broadly speaking, a meta-analysis can be defined as a systematic literature review supported by statistical methods where the goal is to aggregate and contrast the findings from several related studies (Glass 1976). Through the systematic collection of literature information, we determine the effect sizes, and conduct heterogeneity test for effect sizes, and finally use meta-regression to explore what moderators lead to the heterogeneity, i.e. the sample size and methods used in the studies and so on. Because various literature has disparate research conditions, data selection, methodologies, the outcomes for one research theme might be remarkably different. Meta-analysis exactly considers these difference, regards them as control variables, and reflects the real relationship among variables. In 1989, Stanley and Jarrel put forward meta-regression analysis (MRA), developing the economics branch for meta-analysis. As a kind of quantitative literature review method based on regression model, MRA is exactly appropriate for solving the problem mentioned above, which is able to combine the effect sizes, figure out the heterogeneity source, and finally achieve more comprehensive results. In the case, this paper intend to employ meta-analysis to re-examine the impact of healthcare insurance in China on medical expense.
3 Data and methods
3.1 Data
In essence, due to meta-analysis is a kind of quantitative literature summary method, that is, the meta-analysis is based on the published studies aiming at issues in the same scope. Therefore, firstly, we are supposed to extract data from related papers studying the impact of healthcare insurance on medical cost in China. In Google Scholar, China National Knowledge Infrastructure (CNKI), Wanfang Data, Elsevier Science Direct, Web of Science, under the options of “theme” or “keyword”, we input phrase like “healthcare insurance”, “health insurance”, “medical expense”, “hospitalization costs”, “medical costs” and so on, and finally download 237 papers from the database. Secondly, filtrate papers that do not meet the following criterions, (1) papers researching on commercial medical insurance rather than the three basic medical insurances; (2) papers written by the same authors, but published in different languages with approximately the same content; (3) papers without constructing statistic model and give regression outcomes with estimated coefficients, t-values, together with standard errors, or the estimation results is not significant; (4) if more than one models are adopted in one paper, we only extract the results from the more advanced model. Based on the four baselines, we ultimately pick out 31 fitted papers exploring the impact of basic health insurance on medical expense.
The data acquired from the 31 papers are showed in Table 1. LnRR denotes observed effect size in studies, which is the core factor in meta-analysis. According to Rosenberg et al. (1997),\(\ln RR=\ln ({X_{e} }/{X_{c} })=\ln (1+\beta )\), where RR is the abbreviation of Relative Risk, and \(\beta \) is the healthcare insurance elasticity for the medical spending, if \(\beta>0(RR>1)\), it denotes the implement of basic insurance have increased the medical expense for households, vice versa. SE is the estimated standard error presented in the literature. N is the sample size used in one’s study, the magnitude of sample data is assumed to introduce heterogeneity among studies. Studies examining the impact of health insurance always utilize the data from China Nutrition and Health Survey (CNHS), China Health and Retirement Longitudinal Survey (CHARLS), China Family Panel Studies (CFPS). Year is the implementing period of health insurance until the author utilize the data to research their implementation effect. The period for enforcement of a social insurance is deemed to generate different outcomes. Age denotes whether the study object is the elderly or not. The reason why we classify this is that the aged are more likely to suffer from disease, and the effect of medical insurance on this group probably is different. Model is the econometrical methodology used in the literature. Generally, six models are applied to examined the health insurance effect in the studies, including sample selection model, Two-Part model, Tobit model, DID model, OLS regression model (with instrument variable). Sample selection model, Two-Part model and Tobit model can deal with the zero health spending problem, so as to avoid sample selection bias. The DID model is widely developed to assess the implementation effect for a public policy or a program through control the ex-ante difference. The IV approach can solve the endogenous problem in estimation process to some extent. OLS neither consider the two kind of issues, so is the regarded as the most unreliable method to investigate the impact of health insurance. Type represents the class of healthcare insurance researched in the studies. NRC represents New Cooperative Medical Scheme (NCMS), UE denotes Urban Employee Basic Medical Insurance (UEBMI), UR is Urban Resident Basic Medical Insurance (URBMI). Different types of insurances are likely to exert discrepant impact.
3.2 Methods
3.2.1 Meta-analysis models
In this section, we briefly describe the meta-analytic fixed- and random/mixed models (Hedges and Olkin 1985; Berkey et al. 1995; Houwelingen et al. 2002). The fixed-effects model form is specified as:
where \(y_{i}\) is the observed effect size in the i-th study, \(\theta _{i}\) means the corresponding (unknown) true effect, \(\varepsilon _{i}\) is the sampling error, and \(\varepsilon _{i} \sim N(0,\upsilon _{i} )\). Therefore, \(y_i \) is hypothesized to be unbiased and normally distributed of their corresponding true effects.
In practice, most studies involved in the meta-analysis are not exactly identical in their methods and characteristics of the included samples. The differences are likely to result in heterogeneity among the true effects. One way to model the heterogeneity is to treat it as purely random. This leads to the random-effects model, given by
where \(\mu \) and \(\tau ^{2}\) are respectively the mean and variance of true effects \(\theta _{i}\), and \(u_{i} \sim N(0,\tau ^{2})\). The goal is then to estimate the average true effect \(\mu \), and the (total) amount of heterogeneity among the true effects \(\tau ^{2}\). If \(\tau ^{2}= 0\), then it implies true effects is homogenous (i.e., \(\theta _{1} =\ldots =\theta _{k} \equiv \theta )\), so that \(\mu =\theta \) denotes the true effect. Otherwise, the heterogeneity exists among the true effects.
Alternatively, we can incorporate one or more moderators (study-level variables, i.e. the variables show in Table 1) in the model, which may account for part of the heterogeneity in the true effects. This leads to the mixed-effects model, given by
where \(x_{ij} \) denotes the value of the j-th moderator variable for the i-th study, \(\beta _l \) is the estimated coefficients in meta regression, and we still assume \(u_i \sim N(0,\tau ^{2})\). Here, \(\tau ^{2}\) denotes the amount of residual heterogeneity among the true effects. The goal of mixed-effects model is to examine what moderators included in the model influence the heterogeneity of true effect.
3.2.2 Bayesian semi-parametric meta-analysis model
As described in Sect. 3.2.1, the true effects is specified as a normal distribution in usual frequentist meta-analysis. While in many situations, the true effect is not a normal distribution, e.g., it may have thick tails, be skewed, or be multi-modal. A Bayesian semi-parametric model based on mixtures of Dirichlet process priors is used in the literature to accommodate the non-normality, determine whether the overall effect is significant by allowing for a well-defined centrality parameter convenient. Note that the distribution of study effects in this paper seem to be multimodal, the author consider conditional Dirichlet process, proposed by Burr and Doss (2005), and a hierarchical model is presented as below:
In Eq. (4), \(D_i \) is summary statistic gathering an adjusted log odds ratio, that is, the true effects \(\psi _{i}\), and involves relevant standard error estimates \(\hat{{\sigma }}_{i}\). This distribution depends on \(\psi _i \) and also on other quantities, such as the sample size and methods specific to the i-th study. In Eq. (5) and Eq. (6), F is taken to be a Dirichlet process (Ferguson 1973, 1974), with parameter measure \(\alpha =M\cdot H\). For the conditional Dirichlet process, with probability one, the median of F is \(\mu \), so we denote it by \(D_{MN(\mu ,\tau ^{2})}^\mu \). In the context of meta-analysis model, Fis with triple parameters \((\{H_\theta \}_{\theta \in \Theta } ,M,\lambda )\), where M is precision parameter with positive number, determining the shape of posterior distribution, and large values of M correspond to a narrow tube, and small values of M correspond to a wide tube. H is a distribution function indicating the center parameter in Dirichlet process, and \(\{H_\theta \}_{\theta \in \Theta } \sim N(\mu ,\tau ^{2})\).
In Eq. (7) and Eq. (8),\(d_{2, } d_3 ,d_4 >0,d_1 \in {\mathbb {R}}\), and the prior on \((\mu ,\tau )\) is the normal/inverse gamma prior. As mentioned in Burr (2012), in order to get dispersed prior on\(\mu \) and \(\tau \), the default setting for hyper-parameters \(d_1 =0\), \(d_2 =1000\), \(d_3 =d_4 =0.1\).
\(\hbox {Burr and Doss (2005)}^{4444}\) gave a MCMC algorithm to estimate the posterior distribution of the vector \((\psi _{1} ,...,\psi _m,\mu ,\tau )\). The posterior density for \(\psi _i (i=1,...m)\) is presented as below,
where \(A=\frac{u\sigma _i^2 +D_i \tau ^{2}}{\sigma _i^2 +\tau ^{2}},B=\frac{\sigma _i^2 \tau ^{2}}{\sigma _i^2 +\tau ^{2}}\),
where, \(m_- =\mathop \Sigma \limits _{j\ne } I(\psi _j <\mu )\) and \(m_+ =\mathop \Sigma \limits _{j\ne } I(\psi _j >\mu )\)
The posterior distribution for \((\mu ,\tau )\) is expressed as follows:
where \(g_\psi (\mu ,\tau )\) is formed with Eq.(7) and Eq.(8). The updated hyper-parameters for \(d_{_1 }^{\prime } ,d_{_2 }^{\prime } ,d_{_3 }^{\prime } ,d_{_4 }^{\prime } \) is given by
where \(m^{*}\) denotes the number of distinct \(\psi _i \), and \(\bar{{\psi }}^{*}=(\sum {{ }^{dist}\psi _i } )/m^{*}\), in which “dist” indicates the sum only counts distinct values. Thus, the conditional probability density for \(\mu \) is
here, \(t(2d_{_3 }^{\prime } ,d_{_1 }^{\prime } ,d_{_4 }^{\prime } d_2^{\prime } /d_{_3 }^{\prime } )\)represents the t distribution with corresponding degree of freedom, location parameter and scale parameter. And the authors could generate random variables from the step function \(K(\psi ,\cdot )\). The conditional distribution of \(1/\tau ^{2}\) given \(\psi \) and \(\mu \) is Gamma \((d_{_3 }^{\prime } +1/2,d_{_4 }^{\prime } +{(\mu -d_{_1 }^{\prime } )^{2}}/2d_2^{\prime } )\).
4 Empirical results
4.1 Bayesian semi-parametric model for meta-analysis: conditional Dirichlet process
In the first place, we apply this model to examine the overall effect of healthcare. In the process of fitting Bayesian semi-parametric meta-analysis model based on conditional Dirichlet process, a proper precision parameter M should be find firstly to determine the shape of posterior distribution. Considering a conditional Dirichlet model, a Bayes choice for M is equivalent of maximizing \(m_{M}^{c} \), where \(m_{M}^{c} \) denotes the marginal likelihoods of the data under conditional Dirichlet process. In order to obtain more stable and accurate consequences, we set multiple Markov chains with several values of \(h_{1} =(M_{1} ,d_{1} )\). Thus, a nine Markov chains algorithm is carried out with the log of relative risks (lnRR) and standard errors (SE) in Table 1. The total iterations is 4000, 1000 iterations is to burn in, and the hyperparameter vector in the normal/inverse gamma prior on \((\mu ,\tau )\)is respectively \(d_1 =0\), \(d_2 =1000\), \(d_3 =d_4 =0.1\).
Through continuous trial and error, we obtain the M with maximal \(m_M^c \) equaling to 8, and \(m_M^c =1.7243\), as shown in Fig. 1. The Bayes factor forM=8 vs.\(M=\infty \) is 4.12, which suggests the Bayes semi-parameter model is considerably preferred to the usual frequentist for meta-analysis. Next, we fit the Bayesian semi-parametric model with the conditional Dirichlet MCMC process. The precision parameter value include \(M_{\min } =1\), \(M=8\), \(M_{\max } =1000\) (The value of \(M = 1000\) corresponds closely to a parametric model, whereas the value\( M = 8\) is a typical value that would be used in practice). Hyper-parameter vector d is still the default setting \(d=(0,1000,0.1,0.1)\).
Figure 2 presents the posterior distribution of posterior mean \(\mu \) and \(\tau \)with the three precision parameters. The posterior mean \(\mu \)under three precision parameters are respectively 0.123, 0.112 and 0.058, together with the three \(\tau \) values: 0.5, 0.45 and 0.34. Table 2 presents the posterior mean of conditional Dirichlet model for each value of lnRR. The conditional Dirichlet model as well as presents the posterior probability for \(\hbox {RR}<1\)(\(\hbox {RR}<1\) denotes the implement of basic insurance have reduced the medical expense of households, see Sect. 3.1), with probability respectively equal to 0.22, 0.16, and 0.19 for M=1, 8, 1000. The low probabilities imply the implement of healthcare is unlikely to reduce the medical expense of households. Therefore, we draw a preliminary conclusion that the implementation of healthcare has not contribute to alleviating burden of healthcare cost on thousands of families in China, which is against the original intention for the introduction of healthcare. This is perhaps for that, on the one hand, the considerable reimbursement proportion results in “adverse selection” among individuals, that is, the implement of healthcare improve the access to hospital, which generate more inpatient expense; on the other hand, the coming population aging society in China aggravate the healthcare cost for family with the elderly, and offset the benefits from the basic medical insurance. In this section, we conclude that the healthcare has not reduced the medial spending in the whole. Next, we will build random/mixed effect meta-analysis model to check if it exists heterogeneity of the effect sizes, and explore the source of heterogeneity.
4.2 Exploring sources of heterogeneity with meta-regression analysis
Although we have constructed Bayes semi-parameter model, obtained posterior probability with distinct precision parameter values, and finally drew a conclusion that basic medical insurance essentially is less helpful in decreasing family’s medical expense, there are still a lot of defects of this method. For instance, this model can not explore sources of heterogeneity, make sensitive analysis to inspect the quality of papers, test publication basis test, which are all indispensable parts for meta-analysis. In this way, it is of great necessity to conduct meta-regression analysis (Viechtbauer 2010) to deal with the questions mentioned above.
Plot of the externally standardized residuals, DFFITS values, Cook’s distances, covariance ratios, estimates of \(\tau ^{2}\) and test statistics for (residual) heterogeneity when each study is removed in turn, hat values, and weights for the 31 studies examining the effectiveness of the basic healthcare insurance for reducing medical expense
4.2.1 Heterogeneity examination
The premise for meta-regression is to figure out whether existing heterogeneity among true effects, only in this way, can we continue exploring what moderators account for part of the heterogeneity in the true effects. Therefore, heterogeneity examination is conducted and shown in Table 3. In this table, (1) Q statistic, whose null hypothesis is \(H_{0}\): \(ES_1 =ES_2 =\cdots ES_m \), denoting the effect sizes (namely variable lnRR) taken into this paper are homogeneous. Furthermore, it can be written as: \(Q=\sum \limits _{i=1}^{m} {w_{i} ES_{i}^{2} } -{(\sum \limits _{i=1}^{m} {w_{i} ES_{i }} )^{2}}/{\sum \limits _{i=1}^{m} {w_i } }\), where \(w_i \) is the weight for \(i-\)th study, represented by \(1/{SE^{2}}\)(SE is the standard error) . As seen in Table 3, Q statistic is 67.29, which is far greater than the critical value following\(\chi ^{2}\)distribution, and the corresponding p value is near to 0, smaller than 0.05. Thus, we reject the null hypothesis and build random effect model to combine effect size. (2)H statistic, an adjustment of Q statistic with degree of freedom, which can be described as: \(H=\sqrt{Q/{(k-1)}}\), where k stands for the number of literatures incorporated into in this paper. H=1.83>1.5, additionally, the 95% CI in Table 3 excludes one, illustrating heterogeneity among samples. (3)\(I^{2}=\frac{{\hat{\tau }^{2}}}{{\hat{\tau }^{2}}+{\hat{\sigma }^{2}}}\), here, \({\hat{\tau }^{2}}\) is the estimated between-sample variance,\({\hat{\sigma }^{2}}\) is the estimated in-sample variance, and the indicator \(I^{2}\) denotes the percentage of total variability due to heterogeneity, can also be described with H, that is \(I^{2}=\frac{H^{2}-1}{H^{2}}\). In this works, the value of \(I^{2}=70.15\%\) once again demonstrates the heterogeneity among studies. The judge standard can be found in Luo and Leng (2013). In addition, the combined effect size is 1.012, suggesting in the random-effects model, the medical spending for households with healthcare insurance is 1.012 times than the period without healthcare insurance.
4.2.2 Sensitivity diagnose
The relative low quality literatures may introduce unreliable outcomes in meta-analysis, therefore, it is indispensable to carry out sensitivity diagnose to remove inferior quality literatures. We exclude each study in turn to see if it leads to remarkable change in the fitted random effects model. If does, then the study may be considered to be influential; if not, then the study may impose little influence on the results. Case deletion diagnostics, namely leave-one-out test is adapted to identify the influential case.
Figure 3 displays the influential diagnostic outcomes, from which we can attain following information, (1) The rstudent function calculates externally standardized residuals (studentized deleted residuals) for i-th study, with the horizon reference line at -1.96, 0, 1.96. It is obvious that the standardized residuals for study 17 and 25 are beyond the critical value. (2)The DFFITS value essentially indicates how many standard deviations the predicted (average) effect for the i-th study changes after excluding the i-th study from the model fitting. The absolute DFFITS value larger than \(3\sqrt{p/{(k-p}})=2.07\), where \(p=10\) is the number of model coefficients and \(k =31\) is the number of studies, suggests that the i-th study is “influential”. From the second plot, study 17 and 25 introduce additional standard deviations for the predicted effect. (3) Cook’s distance means the Mahalanobis distance between the entire set of predicted values once with the i-th study included and once with the i-th study excluded from the model fitting. The lower tail area of a chi-square distribution with p degrees of freedom cut off by the Cook’s distance is larger than 50%, that is \(\chi _p^2 (a)=0.5\), where a is the horizon reference value. In this works, with \( p=10\), \(a=9.34\), and no study is above the baseline. (4)The value of covariance ratio lower than 1 indicates that removal of the i-th study yields more precise estimates of the model coefficients. The fourth plot shows that the covariance ratio for study 17, 24, 25 is markedly larger than 1. (5)The leave-one-out amount of (residual) heterogeneity is the estimated value of \(\tau ^{2}\)based on the dataset with the i-th study removed. A study may be considered “influential” if smaller \(\tau ^{2}\) is yielded when removing one study. Obviously, smaller \(\tau ^{2}\) is generated with the removal of 24, 25, 17. (6) The Q-statistic tests the degree of heterogeneity based on the dataset with the i-th study removed. Likewise, the Q-statistic is decreased below 30% once the study 25, 17, 24 is removed. (7) The diagonal elements of the hat matrix is given in picture 7 and the hat value larger than \(3(p/k) =0.97\) illustrates the study is “influential”. (8) On the plot of weights, a horizontal reference line is drawn at 100/k, corresponding to the value for equal weights (in %) for all k studies.
4.2.3 Publication basis test
The peculiarity that the meta-analysis is based on extractive data from literatures dominats possible publication basis in emprical results, so as to result in unreliable even nonsense conclusions. The so called publication basis may be drived from two aspects: (1) it seems impossible to collect all the same subject literatures in different dababase, and this may results in somewhat systemic bias of the quantitative analysis; (2) only those significnat statistic studies are more recommonded to be published, while those non-significant statistic factors in studies are tend to be ignored even if they are possioble latent influence factors.
Funnel plot ((Light and Pillemer 1984; Sterne and Egger 2001)is helpful for diagnosing publication bias. For the random effect model, Fig. 4 adresses the observed outcomes(effect sizes) on the horizontal axis against their corresponding standed error. A funnel plot has following features indicating publication bias does not exist in the effect sizes: most effect sizes are distributed centering on the vertical line and in the top of the funnel plot, and only small number of observations scatter in the bottom of funnel plot. If the funnel plot is antisymmetric, there exists publication bias. From Fig. 4, the funnel plot is almost symmetric and the acatter is surrounded the medial axis, thus we make premilimary judgement that there doesn’t exist publication basis in this works. Next, we will continue to verify the existence of publication bias with rank correlation test(Begg and Mazumdar 1994)and regression test (Egger et al. 1997). In Table 4, both p values for rank correlation test and regression test are above 0.05, which accept the null hypothesis(no publication bias), indicating that both test suggests asymmetry in the funnel plot. Therefore, the effect sizes in our works suggest nonexistence of publication bias.
4.2.4 Mixed effects meta-regression analysis
In this section, we will build mixed-effects meta-analysis model to find out what moderators account for part of the heterogeneity in the true effects. In this section, the authors explore the heterogeneous factors via adding moderators with the remaining 29 studies (study 17 and 25 are removed via sensitivity diagnose), consisting of five types of moderators to estimate the mixed -effects model, and the formula is presented as Eq. (9):
In Table 5, we can see that the coefficients of healthcare type (NRC, UR, and UW), implementing period of the insurance (Year), the sample size (N) are not significant at 90% confidence level, which indicate they can’t account for the heterogeneity, and they are may not the real moderators leading to heterogeneous outcomes for the true effects. The variables Non-old and Old stand for different age groups, and their estimates are respectively significant at 90% and 95% confidence interval, suggesting the age group is probably the real heterogeneity resource. The coefficients for Non-old and Old are respectively 0.29 and 0.54, implying that when researching on the medical expense for the elderly, it is more likely to conclude the medical insurance could increase medical spending. The coefficients for IV and OLS are both remarkably negative at 90% confidence level. This implies when directly using IV approach and OLS method to assess the implementation effect for the healthcare insurance, it will lead to the reduced impact on medical expense. We deduce this is because this two methods can’t solve the sample-selection bias when compared with the two-part model and difference-in-difference model. Additionally, the F-statistic for moderators is 2.1957, with P=0.0442, indicating the moderators in Table 5 are significant in general. The Q-statistic is 14.0264 (P=0.7822), \(\hbox {I}^{2}=0.00\%\), H=1, the three indexes indicate that the effect size combined with this mixed model are homogeneous, and our moderators account for part of the heterogeneity.
5 Discussion
In this paper, we employ two kinds of meta-analysis to estimate the causal effects of the healthcare insurances enrollment on healthcare spending. Our results suggest that heterogeneous effect in the effect sizes, and age variation is the main factors lead to the heterogeneity as well as the models used in the study. The conditional Dirichlet-based Bayesian semi-parametric model for meta-analysis examines the overall effect of healthcare insurances, and find that the implementation of healthcare insurances in China has not really alleviate citizens’ medical cost. For the three precision parameters \(M_{\min } =1\), \(M=8\), \(M_{\max } =1000\), the related posterior probability mean for \(\hbox {RR}<1\) are respectively 0.22, 0.16, and 0.19, which indicates it is of low probability that the healthcare insurance could reduce the households’ medical expense. From the literature review in Sect. 2, there are indeed many studies draw such conclusion. The meta-regression analysis consider five moderators of Age, Type, Model, N and Year, and we find the Age and Model may are the factors leading to the heterogeneous outcomes. Besides, when using the “Age” as a moderator, the medical spending for the elderly is more than the Non-old group. When directly using IV approach and OLS method to assess the implementation effect for the healthcare insurance, it is more likely to lead to a reduced impact on medical expense.
Our finding that the healthcare insurances have not reduced health spending is not surprising, and is consistent with many results of existing literature. (Lei and Lin 2009; Yip and Hsiao 2009; Sun et al. 2009, 2010). This may on account of the increased clinical rate and hospital utilization due to the involvement of healthcare insurances. Our healthcare service is operated under the “demand side-social health insurance-supply side” social co-payment model. On the one hand, in this mode, the outpatient expenses mainly consist of private medical account and out-of-pocket payment, and hospital costs by the social pool account and individual self-paid. Government and social medical insurance intervention makes the citizens generally incorporated into public health insurance, which breaks the price link relationship between supply side of medical services and consumers. People who can’t afford the medical cost before will get more access to medical care services due to reimbursement of insurance funds. In this way, we assume that the insurances make them more incline to seek care when they fall sick rather than make them more likely to fall sick, which results in overtreatment. Besides, the uneven allocation of medical resource also make people incline to high-level hospitals, which will also lead to more medical expense.
On the other hand, the supply side and demand side both have the impulse of expanding medical care demand as a result that the preference of each participant is not consistent. Medical institutions are concerned about own business development and cost compensation, and they are extremely incline to provide excessive medical care under opportunistic impulse. In recent years, the excessive treatment in the medical industry is common. Mainly including: relax the hospitalization and treatment standards, over-examination, high-grade drugs usage, excessive use of medical materials and excessive healthcare etc, which directly result in rising medical costs. According to China health statistics yearbook 2013, from 2008 to 2012, the total income for hospitals doubled in the past 5 years, and averagely increase 32.44% annually. The outpatient income and inpatient income respectively accounted for about 35 and 65% for total income, and drugs income accounted for a very large proportion, respectively, contributed 50 and 45% of outpatient and inpatient income. This indicates that China has not yet gotten rid of the “drug-maintaining-medicine” healthcare system, and drug sales is an important channel for hospital income. This seriously damage the entire image for medical workers, generate great waste of human, financial and medical resources, and even cause medical disputes. The demand for medical service is a kind of induced demand, derived from consumer’s preference for maintaining and improving one’s health status. Patients pay more attention to the quality and effectiveness of medical services, however, consumers can not only reckon the quantity of medical service demand, but also difficult to assess the quality of medical service. In this situation, they are insensitive to the medical price and spending, lack of bargaining power and decision-making power. So the medical service quantity and program are almost entirely depend the supplier’s technical judgment and benefit-driven. Medical institutions and workers are in a dominant position, and the demand price is lack of elasticity. Thus, the medical market is an information asymmetric market. Medical institutions and employees are in the superior information position, and may obtain unreasonable income. But consumers are in the inferior information position, and have to pay large medical costs. According to China health statistics yearbook 2013, from 2008 to 2012, the number of outpatient visits augmented 50%, the times of hospitalization increased by 80%. Therefore, under this third-party reimbursement medical insurance model, both supply and demand sides have the impulse of expanding medical needs. In this regard, the lack of effective supervision and restraint mechanisms for government and health insurance agencies should also undertake overtreatment and excessive growth of medical expenditure.
6 Conclusions and policy suggestions
A body of literature has investigate the implementing effect of fundamental social healthcare insurances (NCMS, UEBMI and URBMI) in China. However, the research outcomes are inconsistent of these studies. Some studies find out the access to healthcare insurance increases medical spending for surveyed households, while some others hold that the households’ medical expenses are reduced than before. Given this inconsistence, this paper applied a newly developed meta-analysis to combine the heterogeneity for published literature, and examine the true effect of healthcare insurances. Through establishing conditional Dirichlet-based Bayesian semi-parametric model, heterogeneity test with a random-effects model, sensitivity analysis, publication bias test, mixed-effects model and subgroup meta-analysis, several sound conclusions are drawn as follows:
First, the introduction of conditional Dirichlet-based Bayesian semi-parametric model may develop the common used meta-analysis. This model examines the overall effect of healthcare insurances, and the results suggest the implement of the healthcare insurances have not really reduce households’ medical expense. Second, we conduct a series of tests to examine the heterogeneity and build mixed effects meta-regression analysis model to explore what factors lead to inconsistent conclusions. The random effects meta-analysis model is built, and find it indeed exists heterogeneity in true effects. Mixed effects meta-regression model implies that the age group may is the heterogeneity source other than insurance type, implement period, model section and sample size. The elderly are more likely to increase the medical spending than other groups. Finally, when using IV approach and OLS method to assess the implementation effect for the healthcare insurance, it is inclined to lead to a reduced impact on medical expense. It suggests that applying these two methods is inclined to draw an unreliable conclusions. We deduce this is because this two methods can’t solve the sample-selection bias when compared with the two-part model and difference-in-difference model.
According to the discussion and conclusions, we propose several suggestions for China’s social medical insurance. On the one hand, in view of the supply side of medical services, government should improve the medical security supervision system. Specially, it should deepen reform and supervise interactively the medical service system, the basic medical security system, pharmaceutical and medical equipment supply and marketing system, medical price management system, financial support system and health supervision management system. Aiming to the drug supervision and management departments, for years, the government emphasize on review and approval, but neglect regulation; emphasize on inspection, but neglect disposition. In order to get rid of the “drug-maintaining-medicine” system and control the excessive growth of medical costs, the drug supervision and management departments should change the traditional regulatory mode, use the concept of feed forward, concurrent, and feedback to establish and gradually improve the new mechanism. Besides, the government should invest more funds to the hospitals in county and township levels to improve the medical environment and treatment level, at the same time, increase the level of salary and welfare to encourage and appeal to more talents. On the other hand, the medical institutions should coordinate the reimbursement ratio for different kinds of social groups. Especially for the elderly, they are more likely to suffer from catastrophic illness, thus lead to more expenses than other groups. According to the Chinese Academy of Social Sciences, by 2050, the proportion the aged over 65 is projected to reach nearly a quarter (the proportion is 10% in 2014). As ageing may will drag economic growth and the future delivery of public services, the challenges of a greying population are looming large for social healthcare services. In addition, the elder should pay attention to the disease prevention, and invest more capital to prevention- healthcare and nursing.
It should be noted that this paper employs a hybrid method to examine the implementing impact of China’s social healthcare insurances based on quantitative literature. However, the sample characteristic is various for vast studies, and the meta-analysis should include more variables. In addition, there are also some studied investigating the impact of healthcare insurance on total household consumption, non-medical expenditure, inpatient (outpatient) medical expense. Therefore, we may further take into consideration more sample characteristics, and explore the impact on total household consumption, non-medical expenditure and so on, so as to provide policy references for policy makers.
References
Ariizumi H (2008) Effect of public long-term care insurance on consumption, medical care demand, and welfare. J Health Econ 27(6):1423–1435
Bairoliya N, Canning D, Miller R et al (2017) The macroeconomic and welfare implications of rural health insurance and pension reforms in China. J Econ Ageing (In press)
Begg CB, Mazumdar M (1994) Operating characteristics of a rank correlation test for publication bias. Biometrics 50(4):1088–1101
Berkey CS, Hoaglin DC, Mosteller F et al (1995) A random effects regression model for meta-analysis. Stat Med 14(4):395–411
Boland MR, Tsiachristas A, Kruis AL et al (2013) The health economic impact of disease management programs for COPD: a systematic literature review and meta-analysis. BMC Pulm Med 13:40
Burr D (2012) bspmma: an R package for Bayesian semi-parametric models for meta-analysis. J Stat Softw 50(4):1–23
Burr D, Doss H (2005) A Bayesian semi-parametric model for random-effects meta-analysis. J Am Stat Assoc 100:242–251
Campanella P, Lovato E, Marone C et al (2015) The impact of electronic health records on healthcare quality: a systematic review and meta-analysis. Eur J Public Health 26(1):60–64
Campanella P, Vukovic V, Parente P et al (2016) The impact of Public Reporting on clinical outcomes: a systematic review and meta-analysis. BMC Health Serv Res 16(1):1–14
Chen L, Yip W, Chang MC et al (2007) The effects of Taiwan’s National Health Insurance on access and health status of the elderly. Health Econ 16(3):223–242
Cheng SH, Chiang TL (1997) The effect of universal health insurance on health care utilization in Taiwan: results from a natural experiment. J Am Med Assoc 278(2):89–93
Costafont J, Hernández-Quevedo C (2015) Concentration indices of income-related self-reported health: a meta-regression analysis. Appl Econ Perspect Policy 37(4):45–63
Duan N, Manning WG, Morris CN et al (1983) Comparison of for alternative care models for the demand medical. J Bus Econ Stat 1(2):115–126
Egger M, Smith GD, Schneider M et al (1997) Bias in meta-analysis detected by a simple, graphical test. Br Med J 315(7109):629–634
Ferguson TS (1973) A Bayesian analysis of some nonparametric problems. Ann Stat 1:209–230
Ferguson TS (1974) Prior distributions on spaces of probability measures. Ann Stat 2:615–629
Galárraga O, Sosa-Rubí SG, Salinas-Rodríguez A et al (2010) Health insurance for the poor: impact on catastrophic and out-of-pocket health expenditures in Mexico. Eur J Health Econ 11(5):437–447
Gallet CA, Doucouliagos H (2017) The impact of healthcare spending on health outcomes: a meta-regression analysis. Soc Sci Med 179:9–17
Glass GV (1976) Primary, secondary, and meta-analysis of research. Educ Res 5(10):3–8
Goldman HH, Frank RG, Burnam MA et al (2006) Behavioral health insurance parity for federal employees. N Engl J Med 354(13):1378–1386
Gopalakrishnan S, Ganeshkumar P (2013) Systematic reviews and meta-analysis: understanding the best evidence in primary healthcare. J Fam Med Prim Care 2(1):9–14
Grossman M (1972) On the concept of health capital and the demand for health. J Political Econ 2:223–255
Hedges LV, Olkin I (1985) Statistical methods for meta-analysis. Academic Press, San Diego, pp 347–359
Huang F, Gan L (2012) Research on moral hazard in medical insurance: evidence from micro data. J Financial Res 5:193–206 (In Chinese)
Huang F, Gan L (2017) The impacts of China’s urban employee basic medical insurance on healthcare expenditures and health outcomes. Health Econ 26(2):149–163
Hughes SL, Ulasevich A, Weaver FM et al (1997) Impact of home care on hospital days: a meta-analysis. Health Serv Res 32(4):415–432
Kopecky KA, Koreshkova T (2010) The impact of medical and nursing home expenses and social insurance policies on savings and inequality. Federal Reserve Bank Of Atlanta working paper, no. 2010-19
Lei XY, Lin WC (2009) The new cooperative medical scheme in rural China: Does more coverage mean more service and better health? Health Econ 18(S2):S25–S46
Light RJ, Pillemer DB (1984) Summing up: the science of reviewing research. Harvard University Press, Cambridge
Liu GG, Zhao Z (2006) Urban employee health insurance reform and the impact on out-of-pocket payment in China. Int J Health Plan Manag 21(3):211–228
Liu H, Zhao Z (2014) Does health insurance matter? Evidence from China’s urban resident basic medical insurance. J Comp Econ 42(4):1007–1020
Liu D, Tsegai DW (2011) The New cooperative medical scheme (NCMS) and its implications for access to health care and medical expenditure: evidence from rural China. ZEF-Discussion papers on development, policy no, p 155
Luo J, Leng WD (2013) Theory and practice for systematic review/meta-analysis. Press of Military Medical Sciences, Beijing
Nguyen KT, Khuat OTH, Ma S et al (2012) Impact of health insurance on health care treatment and cost in Vietnam. Am J Public Health 102(8):1450–1461
Palmer MG, Nguyen TMT (2012) Mainstreaming health insurance for people with disabilities. J Asian Econ 23(5):600–613
Pashchenko S, Porapakkarm P (2013) Quantitative analysis of health insurance reform: separating regulation from redistribution. Rev Econ Dyn 16(3):383–404
Rosenberg MS, Adams DC, Gurevitch JC (1997) Metawin: statistical software for meta-analysis with resampling tests. Sinauer Associates, Sunderland
Sheu JT, Lu JF (2014) The spillover effect of National Health Insurance on household consumption patterns: evidence from a natural experiment in Taiwan. Soc Sci Med 111(6):41–49
Shor E, Roelfs D, Vang ZM (2017) The Hispanic mortality paradox’ revisited: meta-analysis and meta-regression of life-course differentials in Latin American and Caribbean immigrants’ mortality. Soc Sci Med 186:20–33
Sinclair SH, Smetters KA (2004) Health shocks and the demand for annuities. Working paper, Congressional Budget Office, Washington, DC
Sparrow R, Suryahadi A, Widyanti W (2013) Social health insurance for the poor: targeting and impact of Indonesia’s Askeskin programme. Soc Sci Med 96:264–271
Stanley T (2005) Beyond publication bias. J Econ Surv 19(3):309–345
Stanley TD, Jarrel SB (1989) Meta-regression analysis: a quantitative method of literature surveys. J Econ Surv 3(2):161–170
Sterne JAC, Egger M (2001) Funnel plots for detecting bias in meta-analysis: guidelines on choice of axis. J Clin Epidemiol 54(10):1046–1055
Su CH, LI QY, Wang DH (2013) The influence of different basic medical insurance on Chinese residents’ medical consumption: based on the CHNS data. Res Econ Manag 10:23–30 (In Chinese)
Sun X, Jackson S, Carmichael G et al (2009) Catastrophic medical payment and financial protection in rural China: evidence from the New Cooperative Medical Scheme in Shandong Province. Health Econ 18(1):103–119
Sun X, Sleigh AC, Carmichael GA et al (2010) Health payment-induced poverty under China’s New Cooperative Medical Scheme in rural Shandong. Health Policy Plan 25(5):419–426
Van Houwelingen HC, Arends LR, Stijnen T (2002) Advanced methods in meta-analysis: multivariate approach and meta-regression. Stat Med 21(4):589–624
Viechtbauer W (2010) Conducting meta-analyses in R with the metafor package. J Stat Softw 36(3):1–48
Wagstaff A (2010) Estimating health insurance impacts under unobserved heterogeneity: the case of Vietnam’s health care fund for the poor. Health Econ 19(2):189–208
Wagstaff A, Lindelow M (2008) Can insurance increase financial risk? The curious case of health insurance in China. J Health Econ 27(4):990–1005
Wagstaff A, Lindelow M, Jun G et al (2009) Extending health insurance to the rural population: an impact evaluation of China’s new cooperative medical scheme. J Health Econ 28(1):1–19
Wagstaff A, Pradhan M (2006) Health insurance impacts on health and nonmedical consumption in a developing country. World Bank Policy Research working paper, no. 3563
Wen SJ, Song SB (2013) Analysis on medical insurance impact on Chinese rural elders’ health demand. Chin Health Econ 32(7):24–26 (In Chinese)
Xue WL, Lu JH (2012) A study on effect of medical insurance status on the aged’ medical expenses. Popul J 22(1):61–67 (In Chinese)
Yip W, Hsiao W (2009) China’s health care reform: a tentative assessment. China Econ Rev 20(4):613–619
Yu B, Meng Q, Collins C et al (2010) How does the new cooperative medical scheme influence health service utilization? A study in two provinces in rural China. BMC Health Serv Res 10(1):1–9
Zhang L, Tong X (2014) Utilization of in-patient service and their influencingfactors among the elderly in rural china: an empirical analysis based on the data of CHARLS. Nanjing J Soc Sci 4:67–74 (In Chinese)
Acknowledgements
This paper is supported by the National Natural Science Foundation of China (NSFC) under grant No. 71473155; the Young Star of Science and Technology plan project of China’s Shaanxi province No. 2016KJXX-14; the China Postdoctoral Science Foundation under grant No. 2014T70130 . The authors would like to thank the anonymous referees as well as the editors.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
Each author declares that he/she has no conflict of interest. This article does not contain any studies with human participants or animals performed by any of the authors. Informed consent was obtained from all individual participants included in the study.
Additional information
Communicated by X. Li.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Chai, J., Xing, L., Zhou, Y. et al. Impact of healthcare insurance on medical expense in China: new evidence from meta-analysis. Soft Comput 22, 5201–5213 (2018). https://doi.org/10.1007/s00500-017-2928-5
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-017-2928-5