1 Introduction

It turned out that the real world is too complex and difficult to characterize by classical mathematical approach. The known models in many disciplines such as medicine, economics, sociology are insufficient and ineffective. First results connected with uncertainties and more complicated problems to which we cannot use the classical methods were obtained by Zadeh (1965). He introduced the notion of fuzzy set by using the membership function which associates with each point of a set a real number from [0, 1]. It was the extension of the indicator function of a set which can take only two values 0 or 1. Moreover, it had some resemblance to probability or density. In 1999, Molodtsov proposed a new mathematical tool for dealing uncertainties. Molodtsov (1999) introduced the idea of soft set for which he used an adequate parameterization. Molodtsov presented the fundamental results of this theory and many applications of it in game theory, operations research, probability, etc. Since the publication of his work, the theory of soft sets has been developed rapidly by many mathematicians. In 2011, Shabir and Naz introduced the notion of soft topology, soft open and soft closed sets, soft interior and soft closure, soft neighborhood, soft point (Shabir and Naz 2011). Some basic properties of soft separating axioms were also examined in their paper and were deeper investigated in Hussain and Ahmad (2011), Min (2011). Later some other properties of soft topological spaces were also examined: soft countability axioms (Rong 2012), soft continuity of soft mappings (Aras and Sonmez 2013; Aygünoğlu and Aygün 2012). The connection with Zadeh’s fuzzy sets and the topological structure of the family of such sets was also considered (Zorlutuna et al. 2012).

While solving some abstract mathematical problems (also connected with decision making), we operate very often in terms of a set and a topology introduced on it. As we can have many topologies on a given set, it is important to know which properties are independent of the choice of the topology. For instance, two homeomorphic spaces share many topological properties such as for instance compactness, connectedness, being Hausdorff, but they also may differ: there are two homeomorphic metric spaces such that one of them is complete and the other is not.

In real functions theory, the topologies which have the same family of sets with nonempty interior play very important role as they also have the same family of dense sets, of nowhere dense sets and the sets with nowhere dense boundary. We use these facts, especially in the field of topologies generated by lower or semi-lower density operators. To distinguish topologies with such properties, we call them similar. This notion was introduced in Bartoszewicz et al. (2014), and there were presented some basic properties of such topologies. It was observed that the similar topologies may differ with compactness, separating and countability axioms. The idea of similar topologies was developed in Filipczak and Terepeta (2015), where the similarity of density-type topologies was examined. In (Filipczak and Terepeta 2016), there was presented the problem of continuity of functions with similar topologies on the domain or the range. Recently, in Lindner (2015) the idea of resolvability of similar topologies was also discussed. One of the most known examples of such pair of topologies is the natural topology and the Sorgenfrey topology on reals (generated by the base consisting of intervals of the form [a; b), \(a<b\) and \(a,b\in \mathbb {R}\); this topology is also called lower limit topology).

The main aim of this paper is to introduce the concept of similarity of soft topological spaces and examine some basic properties of similar soft topologies. It will be shown that this idea is different from homeomorphism of soft topological spaces. Moreover, we will present some examples of similar soft topologies which may have different separating and countability axioms and may differ with respect to connectedness.

2 Preliminaries

In that section, we will present some basic definitions and denotations. Let X be an initial universe such that \(|X|\ge 2\), E be a set of parameters. By \({\mathcal {P}}(X)\) we denote the power set of X. For our purpose, it is more convenient to introduce the necessary notions for the same set of parameters E, but we also present similar definitions for another sets of parameters \(A, B\subset E\). Observe that in some definitions this led us to mistakes, which was pointed out in Ali et al. (2009). Most definitions are based on the paper (Shabir and Naz 2011; Ali et al. 2009).

Definition 1

Let \(F: E\rightarrow {\mathcal {P}}(X)\). A pair \((F,E)=\{ (e,F(e)): e \in E\}\) is called the soft set on the universe X. If \( e\in E\) then (e, F(e)) will be called a soft element of (F, E) and we will write \((e, F(e))\in (F,E)\).

In other words, a soft set is the family of subsets of X which is parameterized by the elements of the set E. If \(A\subset E\), then we can consider soft sets parameterized by the elements of this set: \((F,A)=\{ (e,F(e)): e \in A\}\). The class of all soft sets on X with the set of parameters A will be denoted by \(SS_A(X)\). If \(A=E\), then we will write shortly SS(X).

It is easy to observe that a soft set is not a set. Although there are some similarities of the definitions and theorems between soft topological spaces and topological spaces, there are a lot of differences. They arise especially when the cardinality |E| of the set E of parameters is greater than 1. If \(|E|=1\), then a soft set (F, E) can be treated as a set and then the behavior of soft topological space \({\mathcal {T}}_{} \) is analogous to a topological space. In this paper, both situations are considered.

Definition 2

The soft complement \((F,E)^c\) of a soft set (F, E) is a soft set \((F^c,E)\) defined by a mapping \(F^c:E\rightarrow {\mathcal {P}}(X)\) in the following way: \(F^c(e)=X{\setminus } F(e)\) for any \(e\in E\). \(F^c\) is called the soft complement function of F. Clearly \(((F,E)^c)^c=(F,E)\).

Definition 3

The soft set (F, E) is called the null soft set if \(F(e)=\emptyset \) for any \(e\in E\). The null soft set will be denoted by \(\Phi _E\). The soft set (F, E) is called an absolute soft set if \(F(e)=X\) for any \(e\in E\). The absolute set is denoted by \(X_E\).

It is evident that \(X_E^c=\Phi _E\) and \(\Phi _E^c=X_E\). Due to this definition, we will distinguish a universe X from a soft set \(X_E\). In all above definitions, we may also put another set of parameters \(A\subset E\) instead of E. Then, we obtain the restricted notions of a soft set, null soft set and absolute soft set (see Ali et al. 2009). Similarly, for any \(A,B\subset E\) we can define soft subsets.

Definition 4

Let \(A,B\subset E\). We will say that (F, A) is a soft subset of (G, B) (denoted by \((F,A)\sqsubseteq (G,B)\)) if \(A\subset B\) and \(F(e)\subseteq G(e)\) for any \(e\in A\). (F, A) is soft equal to (G, B) if \((F,A)\sqsubseteq (G,B)\) and \((G,B)\sqsubseteq (F,A)\).

In Maji et al. (2003), in analogous way there was defined a soft intersection and a soft union of two soft sets with arbitrary \(A,B\subset E\) as the sets of parameters.

Definition 5

(Maji et al. 2003) The intersection of the soft sets (F, A) and (G, B) is the soft set (H, C) if \(C=A\cap B\) and \(H(e)=F(e)\cap G(e)\) for any \(e\in C\). The intersection will be denoted by \((H,C)=(F,A)\sqcap (G,B)\)).

The union of the soft sets (F, A) and (G, B) is the soft set (H, C) if \(C=A\cup B\) and

$$\begin{aligned} H(e)=\left\{ \begin{array}{ll} F(e) &{} \text { if } e\in A{\setminus } B \\ G(e) &{} \text { if } e\in B{\setminus } A \\ F(e)\cup G(e) &{} \text { if } e\in A\cap B. \end{array}\right. \end{aligned}$$

The union will be denoted by \((H,C)=(F,A)\sqcup (G,B)\).

The above definition of soft intersection is kept repeating in many papers, although in Ali et al. (2009) there are some counterexamples showing that this definition and its consequences lead us to misunderstanding. We would like to present the reasoning of the authors of Ali et al. (2009), to emphasize the inaccuracy observed in this definition.

Example 1

Let \(X=\{ x_1, x_2, x_3\}\), \(E=\{ e_1, e_2\}\), \(A=\{ e_1\}\), \(B=\{ e_2\}\). Let \((F,A)=\{(e_1, \{ x_1\})\}\) and \((G,B)=\{(e_2, \{ x_2\})\}\). Then, \(C=A\cap B=\emptyset \) and we cannot define \((F,A)\sqcap (G,B)\) as a soft set. From this we have also the problem with De Morgan’s law: \(\left( (F,A)\sqcup (G,B)\right) ^c=(F,A)^c \sqcap (G,B)^c\) as the right side of this equality is not correctly defined.

To ensure that the introduced notions are free from the problems described in Example 1. Ali et al. presented some alternative definitions (extended and restricted). In order to avoid the problems associated with the lack of precision in Definition 5, from now on we will consider only one set E of parameters and our definitions will coincide with those presented in Ali et al. (2009).

Definition 6

The intersection of the soft sets (F, E) and (G, E) is the soft set (H, E) such that \(H(e)=F(e)\cap G(e)\) for all \(e\in E\). The union of the soft sets (F, E) and (G, E) is the soft set (H, E) such that \(H(e)=F(e) \cup G(e)\) for all \( e\in E\). The intersection and the union will be denoted by \((F,E)\sqcap (G,E)\) and \((F,E)\sqcup (G,E)\), respectively.

Let \(x\in X\). If (F, E) is a soft set such that \(F(e)=\{x\}\) for all \(e\in E\), then we will denote it by \((\{x\}, E)\) (or shortly by x) and call it a soft point. We will say that a soft point \((\{x\}, E) \) belongs to a soft set (F, E) (we will shortly write \(x\in (F,E)\)) if \(x\in F(e)\) for all \(e\in E\). From this it immediately follows that \(x\notin (F, E)\) if \(x\notin F(e)\) for some \(e\in E\). Note that if \((\{x\}, E)\sqcap (F,E)=\Phi _E\), then \(x\notin (F,E)\), but the converse is not true.

Example 2

Let \(X=\{ x_1, x_2\}\), \(E=\{ e_1, e_2\}\). Put \((F,E)=\{ (e_1, \{x_1\} ), (e_2, \{x_2\} )\). Then, \((\{x_1\}, E)\not \sqsubseteq (F,E)\) but \((\{x_1\}, E)\sqcap (F,E)=\{ (e_1, \{x_1\} ), (e_2, \emptyset )\}\ne \Phi _E\).

Example 3

Observe that the condition \(x\in (F,E)\sqcup (G,E)\) does not mean that \(x\in (F,E)\) or \(x\in (G,E)\). Indeed, let \(X=\{ x_1, x_2\}\), \(E=\{ e_1, e_2\}\) and put

$$\begin{aligned} (F,E)= & {} \{(e_1, \{ x_1\}), \{(e_2, \{ x_2\})\}, \\ (G,E)= & {} \{(e_1, \{ x_2\}), \{(e_2, \{ x_1\})\}. \end{aligned}$$

Then, \((\{ x_1\}, E)\sqsubseteq (F,E)\sqcup (G,E)=X_E\), but \((\{ x_1\}, E)\not \sqsubseteq (F,E)\) and \((\{ x_1\}, E)\not \sqsubseteq (G,E)\) (equivalently: \(x_1\in (F,E)\sqcup (G,E)\), but \(x_1\notin (F,E)\) and \(x_1\notin (G,E)\)).

Analogously to Definition 6 we may define arbitrary unions and intersections.

Definition 7

Let I be an arbitrary set of indexes and \(\{(F_i,E)\}_{i\in I}\) be a subfamily of SS(X).

  • The intersection of these soft sets is a soft set (H, E) such that \(H(e)=\bigcap \nolimits _{i\in I}F_i(e)\) for each \(e\in E\). We write

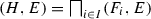
  • The union of these soft sets is a soft set (H, E) such that \(H(e)=\bigcup \nolimits _{i\in I}F_i(e)\) for each \(e\in E\). We write \((H,E)=\bigsqcup \nolimits _{i\in I} (F_i,E)\).

Example 4

Let \(X=\mathbb {R}\), \(E=\{e_1, e_2, e_3\}\). Define the family of soft sets as follows: for any \(n\in \mathbb {N}\) put \((F_n, E)=\left\{ \left( e_1, \left( -\frac{1}{n}, \frac{1}{n}\right) \right) , \left( e_2, [0, n] \right) , \left( e_3, \left( -n, n\right) \right) \right\} \). Then,

and

$$\begin{aligned} \bigsqcup \limits _{n\in {\mathbb {N}}} (F_n,E)=\left\{ (e_1, (-1,1)), (e_2, [0,\infty )), (e_3, (-\infty ,\infty ))\right\} . \end{aligned}$$

Definition 8

The difference \((F,E){\setminus }(G,E)\) of the soft sets (F, E) and (G, E) is the soft set (H, E) such that \(H(e)=F(e)\setminus G(e)\) for any \(e\in E\).

2.1 Soft topology and soft separating axioms

Many mathematicians inspired by Molodtsov introduced some other operations on soft sets and explored their properties. For details, see Hussain and Ahmad (2011), Min (2011), Shabir and Naz (2011). We will focus on the concept of soft topologies introduced by Shabir and Naz (2011). This concept is similar to the idea of topology, but there are some differences.

Definition 9

(Shabir and Naz 2011) Let \({\mathcal {T}}_{}\) be a collection of soft sets over a universe X. We will say that \({\mathcal {T}}_{}\) is a soft topology on X if

(t1):

\(\Phi _E, X_E \in {\mathcal {T}}_{}\),

(t2):

the intersection of any two sets from \({\mathcal {T}}_{}\) belongs to \({\mathcal {T}}_{}\),

(t3):

the union of any number of soft sets from \({\mathcal {T}}_{}\) belongs to \({\mathcal {T}}_{}\).

The triplet \((X,{\mathcal {T}}_{}, E)\) is called soft topological space on X. The soft sets from the family \({\mathcal {T}}_{}\) are called soft open sets, their complements—soft closed sets.

It is clear that the intersection of two soft topologies on X is also a soft topology. The union of two soft topologies may not be a topology as it is shown below.

Example 5

Let \(X=\{ x_1, x_2, x_3\}\) and \(E=\{ e_1, e_2\}\). Put \({\mathcal {T}}_{1}=\{ \Phi _E, (F_1,E), (F_2,E), (F_3,E), X_E \}\) and \({\mathcal {T}}_{2}=\{ \Phi _E, (G_1,E), (G_2,E), (G_3,E), X_E \}\), where

$$\begin{aligned} (F_1,E)= & {} \{(e_1, \{x_1\}), (e_2, \{x_1\})\}\\ (F_2,E)= & {} \{(e_1, \{x_1\}), (e_2, \{x_1, x_2\})\} \\ (F_3,E)= & {} \{(e_1, X), (e_2, \{x_1, x_3\})\} \\ (G_1,E)= & {} \{(e_1, \{x_1\}), (e_2, \{x_1\})\} \\ (G_2,E)= & {} \{(e_1, \{x_2\}), (e_2, \{x_2\})\}\\ (G_3,E)= & {} \{(e_1, \{x_1, x_2\}), (e_2, \{x_1, x_2\})\}. \end{aligned}$$

Then, \({\mathcal {T}}_{1}\) and \({\mathcal {T}}_{2}\) are soft topologies, but

$$\begin{aligned} {\mathcal {T}}_{}={\mathcal {T}}_{1}\cup {\mathcal {T}}_{2}= & {} \{\Phi _E, (F_1,E), (F_2,E), (F_3,E),\\&(G_2,E), (G_3,E), X_E \} \end{aligned}$$

is not a soft topology, because

$$\begin{aligned} (F_2,E)\sqcap (G_2,E)=\{(e_1, \emptyset ), (e_2, \{x_2\}) \} \notin {\mathcal {T}}_{}. \end{aligned}$$

A soft topology \({\mathcal {T}}_{1}\) is said to be weaker (or coarser) than a soft topology \({\mathcal {T}}_{2}\) if \({\mathcal {T}}_{1}\sqsubset {\mathcal {T}}_{2}\) (what means \({\mathcal {T}}_{1}\sqsubseteq {\mathcal {T}}_{2}\) and \({\mathcal {T}}_{1}\ne {\mathcal {T}}_{2}\)). In that case \({\mathcal {T}}_{2}\) is said to be stronger (or finer) than \({\mathcal {T}}_{1}\). If \({\mathcal {T}}_{1}\sqsubset {\mathcal {T}}_{2}\) or \({\mathcal {T}}_{2}\sqsubset {\mathcal {T}}_{1}\), then they are called to be comparable. Let \({\mathcal {T}}_{id}=\{ \Phi _E, X_E \}\) and \({\mathcal {T}}_{d}=SS(X)\). Then, \({\mathcal {T}}_{id}\) is called the indiscrete soft topology and \({\mathcal {T}}_{d}\) is called the discrete soft topology. The collection of all soft topologies on X forms a lattice, with respect to soft set inclusion, in which \({\mathcal {T}}_{id}\) and \({\mathcal {T}}_{d}\) are the smallest and the greatest elements, respectively (Aygünoğlu and Aygün 2012).

Let \({\mathcal {T}}_{}\) be a soft topology on X. Put \({\mathcal {T}}(e)=\{ F(e): (F, E)\in {\mathcal {T}}_{} \}\) for \(e\in E\). It was proved in Shabir and Naz (2011) that \({\mathcal {T}}(e)\) is a topology on X for any \(e\in E\). (It is called e-parameter topology in Shabir and Naz (2011) or crisp topology in Hazra et al. (2012).) The converse does not hold.

Example 6

Consider the family \({\mathcal {T}}_{}\) from Example 5. As it was shown earlier \({\mathcal {T}}_{}\) is not a soft topology. Simultaneously both families

$$\begin{aligned} {\mathcal {T}}(e_1)= & {} \{ \emptyset , \{x_1\}, \{x_2\},\{x_1,x_2\}, X\} \\ {\mathcal {T}}(e_2)= & {} \{ \emptyset , \{x_1\}, \{x_2\},\{x_1,x_2\},\{x_1,x_3\}, X\} \end{aligned}$$

are topologies.

From the above example, it follows that even the union of e-parameter topologies is a topology on X, the union of soft topologies may not be a soft topology on X: \({\mathcal {T}}(e_1)\cup {\mathcal {T}}(e_2)= {\mathcal {T}}(e_2)\) is a topology, while \({\mathcal {T}}_{}={\mathcal {T}}_{1}\cup {\mathcal {T}}_{2}\) is not a soft topology.

Situation changes when E is a singleton.

Theorem 1

Let \(E=\{e\}\), \({\mathcal {T}} =\{(e, H(e)): \ H(e)\in {\mathcal {R}}\}\), \({\mathcal {T}}(e)=\{ H(e): (e, H(e))\in {\mathcal {T}} \}\), where \({\mathcal {R}}\subseteq {\mathcal {P}}(X)\). Then, \({\mathcal {T}}\) is a soft topology if and only if \({\mathcal {T}}(e)\) is a topology on X.

Proof

It is sufficient to show that if \({\mathcal {T}}(e)\) is a topology on X, then \({\mathcal {T}}\) defined above is a soft topology. From the assumption, \(\emptyset , X\in {\mathcal {T}}(e)\). Hence \((e, \emptyset )\in {\mathcal {T}}\) and \((e, X)\in {\mathcal {T}}\), so \(\Phi _E, X_E\in {\mathcal {T}}\). Let \((H,E), (G,E)\in {\mathcal {T}}_{} \). Hence \((H,E)=(e, H(e))\) and \( (G,E)=(e, G(e))\) and \(H(e), G(e)\in {\mathcal {T}}(e)\). As \({\mathcal {T}}(e)\) is a topology on X, so \(H(e)\cap G(e)\in {\mathcal {T}}(e)\). Therefore, \((H,E)\sqcap (G,E)=(e, H(e))\sqcap (e, G(e))=(e, H(e)\cap G(e))\in {\mathcal {T}}\). Let \((A_{i}, E)\in {\mathcal {T}}\) for \(i\in I\). That means \((A_{i}, E)=(e, A_i(e))\) for \(i\in I\). \( {\mathcal {T}}(e)\) is a topology, so \(\bigcup \nolimits _{i\in I} A_i\in {\mathcal {T}}(e)\). Therefore, \(\bigsqcup \nolimits _{i\in I}(A_i,E)=\bigsqcup \nolimits _{i\in I}\left( e, A_i(e)\right) =\left( e, \bigcup \nolimits _{i\in I} A_i(e)\right) \in {\mathcal {T}}_{} \), what finishes the proof. \(\square \)

From above, we immediately obtain the following.

Corollary 1

Let \(E=\{e\}\), \({\mathcal {T}}_{1} =\{(e, H(e)), \ H(e)\in {\mathcal {R}}_1\}\) and \({\mathcal {T}}_{2}=\{(e, G(e)), \ G(e)\in {\mathcal {R}}_2\}\), where \({\mathcal {R}}_1, {\mathcal {R}}_2\subseteq {\mathcal {P}}(X)\). \({\mathcal {T}}_{1}\cup {\mathcal {T}}_{2}\) is a soft topology if and only if \({\mathcal {T}}_{1}(e)\cup {\mathcal {T}}_{2}(e)\) is a topology on X.

Observe, that soft topologies on a set X with E as the set of parameters are not equivalent to the general topologies on the set X. Therefore, we cannot adopt all claims concerning general topology to a soft topology. We will illustrate this fact in the following part of this paper.

It is easy to show that

Theorem 2

Let \(\Sigma \) be a topology on a set X. Put

$$\begin{aligned} (F,E)=\{(e, F(e)):F(e)\in \Sigma \wedge e\in E\}. \end{aligned}$$

The family \({\mathcal {T}}(\Sigma )\) of all soft sets described above is a soft topology on X.

The proof straightforwardly follows from Definitions 6, 7 and 9.

The soft topology \({\mathcal {T}}(\Sigma )\) will be called a soft topology onXgenerated by\(\Sigma \). If for any \(e\in E\) the same set \(U\in \Sigma \) is assigned to each parameter \(e\in E\): \(F(e)=U\), then obtained topology will be called a single set soft topology onXgenerated by\(\Sigma \) (denoted by \(\widehat{\mathcal {T}}(\Sigma )\)). Notice that for any \(e\in E\) we have \({\mathcal {T}}_{} (e)=\widehat{\mathcal {T}}(e)=\Sigma \).

Following Shabir and Naz (2011) and Zorlutuna et al. (2012), the soft interior of a soft set (F, E) is the largest soft open set (with respect to \({\mathcal {T}}_{} \)) included in (F, E) (it will be denoted by \(\text {Int}_{{\mathcal {T}}_{} }(F,E)\)), the soft closure of (F, E) (denoted \(\overline{(F,E)}\)) is the smallest soft closed set which contains (F, E). It is shown (Shabir and Naz 2011) that \((\overline{F},E)\sqsubseteq \overline{(F,E)}\), where \(\overline{F}(e)=\overline{F(e)}\) is the closure of F(e) in \({\mathcal {T}}_{}(e)\) for \(e\in E\), and the equality holds if and only if the complement of (F, E) is soft open in \({\mathcal {T}}_{}\). From this we have the following theorem.

Theorem 3

Let \(\Sigma \) be a topology on a set X. (G, E) is soft closed in \({\mathcal {T}}(\Sigma )\) if and only if

$$\begin{aligned} (G,E)=\{ (e,G(e)):(G(e))^c\in \Sigma \}. \end{aligned}$$

Proof

Observe that if (G, E) is soft closed in \({\mathcal {T}}(\Sigma )\), then \((G,E)^c\in {\mathcal {T}}(\Sigma )\), hence

$$\begin{aligned} (G,E)= \overline{(G,E)}=(\overline{G},E). \end{aligned}$$

Therefore, for any \(e\in E\) we have \(G(e)=\overline{G(e)}\), so G(e) is closed in \(\Sigma \), what finishes the first part of the proof.

Assume now that \((G,E)=\{ (e,G(e)):(G(e))^c\in \Sigma \}\). We will show that (G, E) is closed in \({\mathcal {T}}(\Sigma )\). Since

$$\begin{aligned} (G,E)^c=(G^c,E)=\{ (e, (G(e))^c):e\in E\} \end{aligned}$$

and the soft set \(\{ (e, (G(e))^c):e\in E\}\) is soft open in \({\mathcal {T}}(\Sigma )\), we obtain that \((G,E)^c\) is soft open, which completes the proof. \(\square \)

It is evident that \(\widehat{\mathcal {T}}(\Sigma )\sqsubset {\mathcal {T}}(\Sigma )\). Moreover, a single set soft topology on X generated by \(\Sigma \) inherits soft separating axioms after \(\Sigma \), unlike \({\mathcal {T}}(\Sigma )\). Remind (Shabir and Naz 2011) that \((X, {\mathcal {T}}_{} ,E)\) is

\(T_0\) :

if for any \(x, y \in X\) such that \(x\ne y\) there exist soft open sets (F, E) and (G, E) such that \(x \in (F , E)\) and \(y \notin (F , E)\)or\(y \in (G, E)\) and \(x\notin (G, E)\);

\(T_1\) :

if for any \(x, y \in X\) such that \(x\ne y\) there exist soft open sets (F, E) and (G, E) such that \(x \in (F , E)\) and \(y \notin (F , E)\)and\(y \in (G, E)\) and \(x\notin (G, E)\);

\(T_2\) :

if for any \(x, y \in X\) such that \(x\ne y\) there exist disjoint soft open sets (F, E) and (G, E) such that \(x \in (F , E)\) and \(y \in (G , E)\);

\(T_3\) :

if \((X, {\mathcal {T}}_{} ,E)\) is soft \(T_1\) and soft regular, what means that for any \(x\in X\) and a soft closed set (G, E) such that \(x\notin (G, E)\) there exist disjoint soft open sets \((F_1, E)\) and \((F_2, E)\) for which \(x \in (F_1, E)\) and \((G, E)\sqsubseteq (F_2, E)\);

\(T_4\) :

if \((X, {\mathcal {T}}_{} ,E)\) is soft \(T_1\) and soft normal, what means that for any disjoint soft closed sets \((G_1, E)\) and \((G_2,E)\) there exist disjoint soft open sets \((F_1, E)\) and \((F_2, E)\) for which \((G_1, E)\sqsubseteq (F_1, E)\) and \((G_2, E)\sqsubseteq (F_2, E)\).

Theorem 4

If \((X,\Sigma )\) is \(T_i\) space, \(i=0, \ldots , 4\), then \((X, \widehat{\mathcal {T}}(\Sigma ), E)\) is soft \(T_i\) space, \(i=0, \ldots , 4\).

Proof

We will start with the proof for \(T_2\), as the proofs for \(T_0\) and \(T_1\) are analogous. Let \(x, y\in X\), \(x\ne y\). As \((X,\Sigma )\) is \(T_2\), there are disjoint sets \(U, V\in \Sigma \) such that \(x\in U\) and \(y\in V\). Put

$$\begin{aligned} (F,E)=\{(e,U):e\in E\} \quad \text {and }\ (G,E)=\{(e,V):e\in E\}. \end{aligned}$$

Then, we obtain soft sets \((F,E), (G,E)\in \widehat{\mathcal {T}}(\Sigma )\) such that

$$\begin{aligned} (F,E)\sqcap (G,E)=\{(e,U\cap V):e\in E\}=\Phi _E, \end{aligned}$$

\(x\in (F,E)\) and \(y\in (G,E)\), so \((X, \widehat{\mathcal {T}}(\Sigma ), E)\) is soft \(T_2\).

Let \(i=3\). Take a point \(x\in X\) and a soft set (G, E) which is closed in \( \widehat{\mathcal {T}}(\Sigma ) \) and does not contain x. Let \((G,E)=\{ (e,H):H^c\in \Sigma \wedge e\in E\}\). From the definition of single set soft topology, it follows that \(\{(e, \{x\}):e\in E\}\sqcap (G,E)=\Phi _E\) and \(x\notin H\). \(\Sigma \) is \(T_3\), so there exist disjoint open sets \(U_1, U_2\in \Sigma \) such that \(x\in U_1\), \(H\subset U_2\). By putting \(( F_1, E)=\{ (e,U_1):e\in E\}\) and \( (F_2,E)=\{ (e,U_2):e\in E\} \), we obtain two soft open and disjoint sets \(( F_1, E)\) and \(( F_2, E)\) for which \(x\in ( F_1, E)\) and \((G,E)\sqsubseteq ( F_2, E)\), which completes the proof of this case.

The proof for \(i=4\) is very similar. Take two soft close (in \(\widehat{\mathcal {T}}(\Sigma )\)) and disjoint sets \((G_1, E)\) and \((G_2, E)\). Then, they are of the form

$$\begin{aligned} (G_1,E)= & {} \{ (e,H_1):H_1^c\in \Sigma \wedge e\in E\}\\ (G_2,E)= & {} \{ (e,H_2):H_2^c\in \Sigma \wedge e\in E\}. \end{aligned}$$

As \((G_1, E)\) and \((G_2, E)\) are disjoint and

$$\begin{aligned} (G_2,E)=\{(e, H_1\cap H_2):H_1^c, H_2^c\in \Sigma \wedge e\in E\}, \end{aligned}$$

we have \(H_1\cap H_2=\emptyset \). From the assumption \((X, \Sigma )\) is \(T_4\), so there are two disjoint open sets \(U_1, U_2\in \Sigma \) such that \(H_1\subset U_1\) and \(H_2\subset U_2\). Let \((F_i,E)=\{ (e,U_i):e\in E\}\), \(i=1,2\). Then, \((F_1, E), (F_2, E)\in \widehat{\mathcal {T}}(\Sigma )\) and \((G_1, E)\sqsubseteq (F_1, E)\), \((G_2, E)\sqsubseteq (F_2, E)\). Moreover, \((F_1, E)\sqcap (F_2, E)=\{(e, U_1\cap U_2):e\in E\}=\Phi _E\), what finishes the proof, that \((X, \widehat{\mathcal {T}}(\Sigma ), E)\) is soft \(T_4\). \(\square \)

Observe that contrary to ordinary topologies, \(T_4\) soft topology may not be \(T_3\).

Example 7

Assume that \(|E|\ge 2\). The soft discrete topology \({\mathcal {T}}_{d}\) is \(T_2\), \(T_4\) but not \(T_3\).

Indeed, take \(x,y\in X\), \(x\ne y\). Then, \((F_1, E)=\{ (e, \{x\}):e\in E\}\) and \((F_2, E)=\{ (e, \{y\}):e\in E\}\) are soft open, disjoint and \(x\in (F_1, E)\), \(y\in (F_2, E)\), hence \({\mathcal {T}}_{d}\) is \(T_2\). As in this topology all sets are soft clopen, it follows immediately that it is also \(T_4\). We will show now that \({\mathcal {T}}_{d}\) is not \(T_3\). Take \(e_1\in E\). Put \((G, E)=\{ (e, G(e)):G(e_1)=\{x\} \wedge G(e)=\{y\}\) for \(e\ne e_1\}\). Then, (G, E) is soft closed, \(x\notin (G,E)\) and x cannot be separated by a soft open set from (G, E). \(\square \)

The next example shows that for the soft topology generated by \(\Sigma \) the separating axioms of \(\Sigma \) may not be inherited. We will show that if \(\Sigma \) is \(T_3\), the topology \({\mathcal {T}}(\Sigma )\) may not be \(T_3\). It shows that a soft topology is not a kind of product of ordinary topologies, because the product of \(T_3\) is always \(T_3\).

Example 8

Assume that \(E=\{e_1, e_2\}\) and \(|X|=\mathbb {R}\). Denote by \(\tau _{nat}\) the natural topology on the real line. Then, \({\mathcal {T}}(\tau _{nat})\) is not \(T_3\).

Indeed, it is easy to observe that for any \(x\in \mathbb {R}\) and intervals [a, b], [c, d] such that \(x\in [a,b]\) and \(x\notin [c,d]\) we cannot separate x from the soft set

$$\begin{aligned} (G,E)=\{(e_1, [a,b]), (e_2, [c,d]\} \end{aligned}$$

which is soft closed in \({\mathcal {T}}(\tau _{nat})\).

3 Soft base

Definition 10

(Çağman et al. 2011) Let \((X, {\mathcal {T}}_{}, E)\) be a soft topological space and \({\mathcal {B}}\subset {\mathcal {T}}_{}\). If every element of \({\mathcal {T}}_{}\) is a union of elements of \({\mathcal {B}}\), then \({\mathcal {B}}\) is called a soft base for the soft topology \({\mathcal {T}}_{} \).

Example 9

Consider the topology \({\mathcal {T}}_{2}\) from Example 5. The family \({\mathcal {B}}=\{ \Phi _E, X_E, (G_1,E), (G_2,E)\}\) is a soft base for this topology.

Let \({\mathcal {T}}_{}\) be a soft topology over the universe X and \({\mathcal {B}}\) be its base. By \({\mathcal {B}}(e)\) we will denote the family \({\mathcal {B}}(e)=\{ B(e): (e, B(e))\in {\mathcal {B}} \}\) for \(e\in E\).

Theorem 5

If \({\mathcal {B}}\) is a soft base for soft topology \({\mathcal {T}}_{} \), then \({\mathcal {B}}(e)\) is a base for topology \({\mathcal {T}}_{} (e)\) for any \(e\in E\).

Proof

Let \({\mathcal {B}}=\{(B_{\lambda }, E)\}_{\lambda \in \Lambda }\) be a soft base for a soft topology \({\mathcal {T}}_{} \). Then,

$$\begin{aligned} X_E= & {} \{(e, X):e\in E\}=\bigsqcup _{\lambda \in \Lambda }\left\{ \left( e, B_{\lambda }(e)\right) :e\in E\right\} \\= & {} \left\{ \left( e, \bigcup _{\lambda \in \Lambda } B_{\lambda }(e)\right) :e\in E\right\} \end{aligned}$$

hence \(X= \bigcup _{\lambda \in \Lambda } B_{\lambda }(e)\in {\mathcal {T}}_{} (e)\) for any \(e\in E\). Analogously \(\emptyset \in {\mathcal {T}}_{} (e)\) for \(e\in E\). Take an arbitrary soft set \((F,E)\in {\mathcal {T}}_{} \). Then, there exists a subfamily \(\Lambda _0\subset \Lambda \) such that \((F,E)=\bigsqcup _{\lambda \in \Lambda _0}(B_{\lambda }, E)\) with \((B_{\lambda }, E)\in {\mathcal {B}}\). Then,

$$\begin{aligned} (F,E)= & {} \bigsqcup _{\lambda \in \Lambda _0}\left\{ \left( e, B_{\lambda }(e)\right) :e\in E\right\} \\= & {} \left\{ \left( e, \bigcup _{\lambda \in \Lambda _0} B_{\lambda }(e)\right) :e\in E\right\} \\= & {} \left\{ \left( e, F(e)\right) :F(e)=\bigcup _{\lambda \in \Lambda _0} B_{\lambda }(e), e\in E\right\} . \end{aligned}$$

From the definition of e-parameter topology, we obtain that \( F(e)=\bigcup _{\lambda \in \Lambda _0} B_{\lambda }(e)\in {\mathcal {T}}_{} (e)\) and \(\{B_{\lambda }(e)\}_{\lambda \in \Lambda }\) is a base for the topology \({\mathcal {T}}_{}(e) \). \(\square \)

The next example shows that the converse does not hold.

Example 10

Let \(X=\{ x_1, x_2\}\) and \(E=\{ e_1, e_2\}\). Put

$$\begin{aligned} {\mathcal {T}}_{}=\{ \Phi _E, (F_1,E), (F_2,E), (F_3,E), (F_4,E), X_E \}, \end{aligned}$$

where

$$\begin{aligned} (F_1,E)= & {} \{(e_1, \{x_2\}), (e_2, X)\} \\ (F_2,E)= & {} \{(e_1, \emptyset ), (e_2,\{x_2\} )\} \\ (F_3,E)= & {} \{(e_1, \{x_2\}), (e_2, \{x_1\})\} \\ (F_4,E)= & {} \{(e_1, \{x_1\}), (e_2, \{x_2\})\} . \end{aligned}$$

\({\mathcal {T}}_{}\) is a soft topology on X, hence \({\mathcal {T}}(e_1)={\mathcal {T}}(e_2)=\{ \emptyset , \{x_1\}, \{x_2\}, X\} \) are topologies in the set X.

Put \({\mathcal {B}}=\{\Phi _E, (F_3,E), (F_4,E), X_E \}.\) Then, \({\mathcal {B}}(e_1)={\mathcal {B}}(e_2)=\{\emptyset , \{x_1\}, \{x_2\}, X \}\) are bases for topologies \({\mathcal {T}}_{}(e_1)\) and \({\mathcal {T}}_{}(e_2)\), while \({\mathcal {B}}\) is not a base for soft topology \({\mathcal {T}}_{}\), because the soft set \((F_2,E)\) cannot be represented as a union of soft sets from the family \({\mathcal {B}}\).

Analogously as Theorem we can prove the following:

Theorem 6

Let \(E=\{e\}\). The family \({\mathcal {B}}\) is a soft base for soft topology \({\mathcal {T}}_{} \) if and only if \({\mathcal {B}}(e)\) is a base for topology \({\mathcal {T}}_{} (e)\).

4 Similarity

Consider the families \({\mathcal {F}}, {\mathcal {G}}\) of nonempty soft sets over the universe X and the same the set E of parameters. Let \({\mathcal {F}}^*= {\mathcal {F}}\setminus \{\Phi _E\}\)

Definition 11

We say that the family \({\mathcal {F}}\) is coinitial with \({\mathcal {G}}\) if for every soft set \((G, E)\in {\mathcal {G}}^*\) there exists a soft set \((F, E)\in {\mathcal {F}}^*\) such that \((F, E)\sqsubseteq (G, E)\).

Observe that coinitial families may not be comparable.

Example 11

Let \(X=\{ x_1, x_2, x_3\}\) and \(E=\{ e_1, e_2\}\). Put

$$\begin{aligned} {\mathcal {F}}= & {} \{(F_1, E), (F_2, E), (F_3, E)\}\\ {\mathcal {G}}= & {} \{(G_1, E), (G_2, E), (G_3, E)\}, \end{aligned}$$

where the sets \((F_i, E)\) and \((G_i,E)\) for \(i\in \{1,2,3\}\) are defined in Example 5. Then, the families \({\mathcal {F}}, {\mathcal {G}}\) are not comparable and \({\mathcal {G}}\) is coinitial with \({\mathcal {F}}\), because for any \((F_i,E)\in {\mathcal {F}}\) there is \((G_{j(i)},E)\in {\mathcal {G}}\) (namely \((G_{j(i)},E)=(G_1,E)\)) such that \((G_{j(i)},E)\sqsubseteq (F_i,E)\), \(i\in \{1,2,3\}\).

Example 12

Let \(X=\mathbb {R}\), \(E=\{e_1, e_2\}\) and

$$\begin{aligned} (F,E)= & {} \{ (e_1, F_1(e_1)), (e_2,F_2(e_2))\}\\ (G,E)= & {} \{ (e_1, \emptyset ), (e_2,G_2(e_2)), \end{aligned}$$

where \(F_1(e_1)\) is open in discrete topology, \(F_2(e_2)\) is open in natural topology and \(G_2(e_2)\) is open in Sorgenfrey topology on the real line. Put \({\mathcal {T}}_{1}=\{\Phi _E, X_E, (F,E)\}\) and \({\mathcal {T}}_{2}=\{\Phi _E, X_E, (G,E)\}\). Then, soft topology \({\mathcal {T}}_{1}\) is coinitial with \({\mathcal {T}}_{2} \) as any nonempty soft set \((G,E)=\{ (e_1, \emptyset ), (e_2,G_2(e_2))\in {\mathcal {T}}_{2}^*\) contains a nonempty soft set \((F,E)=\{ (e_1, \emptyset ), (e_2,F_2(e_2))\in {\mathcal {T}}_{1}^*\).

Note that if the family \({\mathcal {F}}\) is coinitial with \({\mathcal {G}}\), then \({\mathcal {F}}(e)\) may not be coinitial with \({\mathcal {G}}(e)\) for some \(e\in E\).

Example 13

Let \(X=\{ x_1, x_2, x_3\}\) and \(E=\{ e_1, e_2\}\). Put

$$\begin{aligned} {\mathcal {F}}= & {} \{(F_1, E), (F_2, E), (F_3, E)\}\\ {\mathcal {G}}= & {} \{(G_1, E), (G_2, E), (G_3, E)\}, \end{aligned}$$

where

$$\begin{aligned} (F_1,E)= & {} \{(e_1, \{x_1\}), (e_2, \emptyset )\} \\ (F_2,E)= & {} \{(e_1, X), (e_2,\{x_1\} )\} \\ (F_3,E)= & {} \{(e_1, \{x_1\}), (e_2, \{x_1\})\} \\ (G_1,E)= & {} \{(e_1, \{x_1\}), (e_2, \{x_2\})\}\\ (G_2,E)= & {} \{(e_1, X), (e_2, \{x_2\})\}\\ (G_3,E)= & {} \{(e_1,X), (e_2, \{x_2\})\} . \end{aligned}$$

Then, \({\mathcal {F}}\) is coinitial with \( {\mathcal {G}}\), as for any \((G_i,E)\in {\mathcal {G}}\) there is \((F_{j(i)},E)\in {\mathcal {F}}\) (namely \((F_{j(i)},E)=(F_1,E)\)) such that \((F_{j(i)},E)\sqsubseteq (G_i,E)\) for \(i\in \{1,2,3\}\). Simultaneously \({\mathcal {F}}(e_1)={\mathcal {G}}(e_1)= \{\{x_1\}, X\}\), \({\mathcal {F}}(e_2)=\{\emptyset , \{x_1\}\}\) and \({\mathcal {G}}(e_2)= \{ \{x_2\}\}\), so \({\mathcal {F}}(e_2)\) is not coinitial with \({\mathcal {G}}(e_2)\).

If a family \({\mathcal {F}}\) is coinitial with \({\mathcal {G}}\) and \({\mathcal {G}}\) is coinitial with \({\mathcal {F}}\), then we will say that the families \({\mathcal {F}}\) and \({\mathcal {G}}\) are mutually coinitial.

Let \({\mathcal {T}}_{1}\) and \({\mathcal {T}}_{2}\) be soft topologies over the same universe X with the same set of parameters E.

Definition 12

We say that the spaces \((X,{\mathcal {T}}_{1}, E)\) and \((X,{\mathcal {T}}_{2}, E)\) are similar (or shortly, that the soft topologies \({\mathcal {T}}_{1}\) and \({\mathcal {T}}_{2}\) are similar, denoted by \({\mathcal {T}}_{1} \approx {\mathcal {T}}_{2}\)), if the families \({\mathcal {T}}_{1}\) and \({\mathcal {T}}_{2}\) are mutually coinitial.

Denote by \( {\mathcal {NI}}({\mathcal {T}}_{})\) the family of soft sets with nonempty soft interior in soft topology \({\mathcal {T}}_{} \). Straightforward from the definition of soft interior we can immediately obtain:

Theorem 7

The soft topologies \({\mathcal {T}}_{1}\) and \({\mathcal {T}}_{2} \) are similar if and only if \({\mathcal {NI}}({\mathcal {T}}_{1})={\mathcal {NI}}({\mathcal {T}}_{2})\).

Theorem 8

Let \({\mathcal {B}}_1\), \({\mathcal {B}}_2\) be soft bases of soft topologies \({\mathcal {T}}_{1}, {\mathcal {T}}_{2}\), respectively. \({\mathcal {B}}_1\), \({\mathcal {B}}_2\) are mutually coinitial if and only if topologies \({\mathcal {T}}_{1}, {\mathcal {T}}_{2}\) are similar.

Proof

Put \({\mathcal {B}}_1=\{ (F_{\lambda }, E): \lambda \in \Lambda \}\), \({\mathcal {B}}_2=\{ (G_{\alpha }, E): \alpha \in A\}\). Assume that \({\mathcal {B}}_1\) is coinitial with \({\mathcal {B}}_2\). We will show that \( {\mathcal {NI}}({\mathcal {T}}_{2})\subset {\mathcal {NI}}({\mathcal {T}}_{1})\). Take an arbitrary soft set \((G,E)\in {\mathcal {T}}_{2}^*\) (what means \((G,E)\in {\mathcal {NI}}({\mathcal {T}}_{2})\)). Then, there exists a subfamily \(A_0\subset A\) such that

$$\begin{aligned} (G,E)=\bigsqcup _{\alpha \in A_0} (G_{\alpha }, E) \end{aligned}$$

where \( (G_{\alpha }, E)\in {\mathcal {B}}_2\).

As \({\mathcal {B}}_1\) is coinitial with \({\mathcal {B}}_2\), so for any \((G_{\alpha }, E)\in {\mathcal {B}}_2^*\) with \(\alpha \in A_0\) there exists \((F_{\lambda }, E)\in {\mathcal {B}}_1^*\) such that \((F_{\lambda }, E)\sqsubseteq (G_{\alpha }, E)\). Hence \((F_{\lambda }, E)\sqsubseteq (G_{\alpha }, E)\sqsubseteq (G,E)\) and

$$\begin{aligned} \Phi _E\ne (F_{\lambda }, E)= \text {Int}_{{\mathcal {T}}_{1}}(F_{\lambda },E)\sqsubseteq \text {Int}_{{\mathcal {T}}_{1} }(G,E). \end{aligned}$$

Therefore, any nonempty and soft open set in \({\mathcal {T}}_{2}\) has nonempty soft interior in \({\mathcal {T}}_{1}\). In analogous way, we prove that if \({\mathcal {B}}_2\) is coinitial with \({\mathcal {B}}_1\), then \( {\mathcal {NI}}({\mathcal {T}}_{1})\subset {\mathcal {NI}}({\mathcal {T}}_{2})\), which according to Theorem 7 finishes the proof of the first part of theorem.

Assume now that \({\mathcal {T}}_{1} \approx {\mathcal {T}}_{2}\). Then, \( {\mathcal {NI}}({\mathcal {T}}_{1}) = {\mathcal {NI}}({\mathcal {T}}_{2})\). Let \((F_{\lambda }, E)\in {\mathcal {B}}_1^*\subset {\mathcal {T}}_{1}\). From similarity, we have that it has nonempty interior in \({\mathcal {T}}_{_2}\): \(\text {Int}_{{\mathcal {T}}_{2}}(F_{\lambda }, E)\ne \Phi _E\). Hence, there exists a subfamily \(A_0\) of A such that \(\text {Int}_{{\mathcal {T}}_{2}}(F_{\lambda }, E)= \bigsqcup _{\alpha \in A_0} (G_{\alpha }, E)\) where \((G_{\alpha }, E)\in {\mathcal {B}}_2\). The set \(\text {Int}_{{\mathcal {T}}_{2}}(F_{\lambda }, E)\) is nonempty; therefore, there is \(\alpha _0\in A_0\) such that \((G_{\alpha _0},E)\) is not soft null. We obtain

$$\begin{aligned} \Phi _E\ne (G_{\alpha _0},E)\sqsubseteq \text {Int}_{{\mathcal {T}}_{2}}(F_{\lambda }, E) \sqsubseteq (F_{\lambda }, E)=\text {Int}_{{\mathcal {T}}_{1}}(F_{\lambda }, E). \end{aligned}$$

Therefore, \({\mathcal {B}}_2 \) is coinitial with \({\mathcal {B}}_1\). By taking any \((G_{\alpha }, E)\in {\mathcal {B}}_2^*\subset {\mathcal {T}}_{2}\), in the same way we show that \({\mathcal {B}}_1 \) is coinitial with \({\mathcal {B}}_2\), which completes the proof. \(\square \)

Example 14

Let \(X=\mathbb {R}\), \(E=\{e_1, e_2\}\), \(e_1, e_2\in \mathbb {R}\). For positive numbers \(\lambda _1, \lambda _2, a_1, b_1, a_2, b_2 \) put \(\lambda =\{\lambda _1, \lambda _2\}\), \(a=\{a_1,a_2\}\), \(b=\{b_1,b_2\}\) and define the sets

$$\begin{aligned}&(F, E)_{\lambda }=\left\{ \left( e_1, [e_1-\lambda _1, e_1+\lambda _1)\right) , \right. \\&\quad \left. \left( e_2, [e_2-\lambda _2, e_2+\lambda _2)\right) \right\} , \\&(G, E)_{ab}=\left\{ \left( e_1, (e_1-a_1, e_1+b_1)\right) ,\right. \\&\quad \left. \left( e_2, (e_2-a_2, e_2+b_2)\right) \right\} . \end{aligned}$$

By \({\mathcal {T}}_{1}\) and \({\mathcal {T}}_{2}\) we denote the soft topologies generated by soft bases \({\mathcal {B}}_1=\left\{ (F, E)_{\lambda }:\lambda _1, \lambda _2>0\right\} \) and \({\mathcal {B}}_2=\left\{ (G, E)_{ab}: a_1, b_1, a_2, b_2 >0\right\} \), respectively. The bases \({\mathcal {B}}_1\) and \({\mathcal {B}}_2\) are mutually coinitial, hence \({\mathcal {T}}_{1} \approx {\mathcal {T}}_{2}\).

Theorem 9

If soft topologies \({\mathcal {T}}_{1}, {\mathcal {T}}_{2}\) are similar then \({\mathcal {T}}_{1}(e), {\mathcal {T}}_{2}(e)\) are also similar for any \(e\in E\).

Proof

First we will show that if soft topology \({\mathcal {T}}_{1}\) is coinitial with \( {\mathcal {T}}_{2}\), then for any \(e\in E\) topology \({\mathcal {T}}_{1}(e)\) is coinitial with \({\mathcal {T}}_{2}(e)\). Take a nonempty set \(G(e)\in {\mathcal {T}}_{2}(e)\). Then, it corresponds with a nonempty soft set \((G,E)\in {\mathcal {T}}_{2}\). As \({\mathcal {T}}_{1}\) is coinitial with \( {\mathcal {T}}_{2}\), so there exists a nonempty soft set \( (F,E)\in {\mathcal {T}}_{1}\) such that \((F,E)\sqsubseteq (G,E)\). Hence \({\mathcal {T}}_{1}(e)\) is coinitial with \({\mathcal {T}}_{2}(e)\). The proof of the case when \({\mathcal {T}}_{2}\) is coinitial with \( {\mathcal {T}}_{1}\) is analogous. \(\square \)

Note that if \({\mathcal {T}}(e)\) and \( {\mathcal {T}}(e)\) are similar, then the soft topologies \({\mathcal {T}}_{1}, {\mathcal {T}}_{2}\) may not be similar.

Example 15

Let \(X=\mathbb {R}\), \(E=\{e_1, e_2\}\). Put

$$\begin{aligned} {\mathcal {T}}_{1}= & {} \{\Phi _E, X_E, (F_1, E), (F_2,E)\}\\ {\mathcal {T}}_{2}= & {} \{\Phi _E, X_E, (G_1, E), (G_2,E)\}, \end{aligned}$$

where soft sets \(F_j (e_i)\), \(G_j (e_i)\), \(i,j=1,2\), are of the form

$$\begin{aligned} (F_1,E)= & {} \{ (e_1, F(e_1)), (e_2,X)\}\\ (F_2,E)= & {} \{ (e_1, X), (e_2,F(e_2)\}\\ (G_1,E)= & {} \{ (e_1, G(e_1)), (e_2,\emptyset )\}\\ (G_2,E)= & {} \{ (e_1, \emptyset ), (e_2,G(e_2)\}, \end{aligned}$$

where \(F(e_i)\) is open in natural topology and \(G(e_i)\) is open in Sorgenfrey topology on the real line. Then, topologies \({\mathcal {T}}_{1}(e_i)=\{ \emptyset , X, F(e_i)\}\) and \({\mathcal {T}}_{2}(e_i)=\{ \emptyset , X, G(e_i)\}\), \(i=1,2\), are similar while soft topologies \({\mathcal {T}}_{1}\) and \({\mathcal {T}}_{2}\) are not similar because \((G_1,E)\in {\mathcal {T}}_{2}\) does not contain any nonempty soft set open in \({\mathcal {T}}_{1}\).

Let denote by \({\mathbb {T}}(X, E)\) the family of all soft topologies over the universe X with the same set of parameters E. As we mentioned earlier, \({\mathbb {T}}(X, E)\) is a lattice with respect to soft inclusion. The family \({\mathbb {T}}(X, E)\) can be also treated as a lattice with join and meet operations defined for \({\mathcal {T}}_{1}, {\mathcal {T}}_{2} \in {\mathbb {T}}(X,E)\) as follows: \({\mathcal {T}}_{1} \wedge {\mathcal {T}}_{2}={\mathcal {T}}_{1}\cap {\mathcal {T}}_{2}\) and \({\mathcal {T}}_{1} \vee {\mathcal {T}}_{2}={\mathcal {T}}_{} ({\mathcal {T}}_{1}\cup {\mathcal {T}}_{2})\), where \({\mathcal {T}}_{} (A\cup B)\) stands for the topology generated by the union of A and B. It is natural to ask whether the family \( {\mathbb {S}}(X,E)\) of all similar soft topologies forms a sublattice of \( {\mathbb {T}}(X,E)\). The answer is negative due to the following theorem.

Theorem 10

  1. (a)

    There exist topologies \({\mathcal {T}}_{1}\), \({\mathcal {T}}_{2}\) such that \({\mathcal {T}}_{1} \approx {\mathcal {T}}_{2}\) and \({\mathcal {T}}_{1} \cap {\mathcal {T}}_{2}\not \approx {\mathcal {T}}_{1}\).

  2. (b)

    There exist topologies \({\mathcal {T}}_{1}\), \({\mathcal {T}}_{2}\) such that \({\mathcal {T}}_{1} \approx {\mathcal {T}}_{2}\) and \({\mathcal {T}}({\mathcal {T}}_{1} \cup {\mathcal {T}}_{2})\not \approx {\mathcal {T}}_{1}\).

Proof

First we will show that the intersection of similar soft topologies may not be similar to any of them. Let \(X=\mathbb {R}\), \(E=\{e_1, e_2\}\). Put \({\mathcal {T}}_{1}=\{\Phi _E, X_E, (F, E)\}\) and \( {\mathcal {T}}_{2}=\{\Phi _E, X_E, (G, E)\}\), where

$$\begin{aligned} (F,E)= & {} \{(e_1,F_1(e_1)), (e_2, F_2(e_2)): F_1(e_1)\\= & {} (2n+1, \infty ), F_2(e_2)=(-\infty , -2k),\ n,k\in \mathbb {N}\}\\ (G,E)= & {} \{(e_1,G_1(e_1)), (e_2,G_2(e_2)): G_1(e_1)= (2n, \infty ), \\&G_2(e_2)=(-\infty , -2k-1),\ n,k\in \mathbb {N}\}. \end{aligned}$$

Then, \({\mathcal {T}}_{1}\), \({\mathcal {T}}_{2}\) are soft similar, but their intersection \({\mathcal {T}}_{1} \cap {\mathcal {T}}_{2}\) is not similar to any of them.

Now we will show (b). Let \(X=\mathbb {R}\), \(E=\{e_1, e_2\}\). Put

$$\begin{aligned} {\mathcal {B}}_1= & {} \{(e_1, F(e_1)), (e_2, F(e_2)): F(e_i)=[a_i,b_i),\\&a_i,b_i\in \mathbb {R},\ a_i<b_i,\ i=1,2\}\\ {\mathcal {B}}_2= & {} \{(e_1, G(e_1)), (e_2, G(e_2)): G(e_i)=(a_i,b_i],\\&a_i,b_i\in \mathbb {R},\ a_i<b_i,\ i=1,2\}. \end{aligned}$$

Let \({\mathcal {T}}_{1}\) be a soft topology for which \({\mathcal {B}}_1\) is a base, \({\mathcal {T}}_{2}\) be a soft topology for which \({\mathcal {B}}_2\) is a base. Then, \({\mathcal {T}}_{1} \approx {\mathcal {T}}_{2}\). Take \((F,E)=\{(e_1, [a_1,b_1)), (e_2, [a_2,b_2))\}\) and \((G,E)=\{(e_1, (c_1,a_1]), (e_2, (c_2,a_2])\}\), where, \(a_i, b_i,c_i\in \mathbb {R}\), \(c_i<a_i<b_i\) for \(i=1,2\). Then, the set \((H,E)=(F,E)\sqcap (G,E)=\{(e_1, \{a_1\}),(e_2, \{a_2\})\} \) is soft open in the soft topology \({\mathcal {T}}_{}={\mathcal {T}}_{}({\mathcal {T}}_{1}\cup {\mathcal {T}}_{2})\), but it does not contain any nonempty soft set from \({\mathcal {T}}_{1}\) or \({\mathcal {T}}_{2}\). Hence, \({\mathcal {T}}_{}\not \approx {\mathcal {T}}_{1} \). \(\square \)

The next examples show that similar topologies may differ with respect to connectedness and may have different countability and separating axioms.

Example 16

Let \(X=\mathbb {R}\), \(E=\{e\}\) and \({\mathcal {T}}_{1}\) be a soft topology generated by the base \({\mathcal {B}}_1\) from Theorem 10(b). Then, soft sets \((e,(-\infty ,b))\) and \((e, [b,\infty ))\) are both soft open in \({\mathcal {T}}_{1}\). Hence, \(X_E=(e,(-\infty ,b))\sqcup (e, [b,\infty ))\), so X is not soft connected. Simultaneously, \({\mathcal {T}}_{1}\) is similar to soft topology \({\mathcal {T}}_{2}={\mathcal {T}}(\tau _{nat})\) which is connected.

Moreover, topology \({\mathcal {T}}_{1}\) is soft first countable and not soft second countable while \({\mathcal {T}}_{2}\) is soft second countable (Rong 2012).

Example 17

Let \(X=\mathbb {R}\), \(|E|\ge 2\). Topologies \({\mathcal {T}}(\tau _{nat})\) and \(\widehat{\mathcal {T}}(\tau _{nat})\) are similar, and due to Theorem 4 and Example 8 they have different separating axioms. The same holds for \({\mathcal {T}}_{d}\) and \(\widehat{\mathcal {T}}(\tau _{discr})\), where \(\tau _{discr}\) stands for the discrete topology on \(\mathbb {R}\).

Now we will show that the notion of similarity of soft topological spaces is different from the homeomorpism of such spaces. Remind that the mapping \(f: (X, {\mathcal {T}}_{X}, E) \rightarrow (Y, {\mathcal {T}}_{Y}, E)\) is soft continuous if for each open set (G, E) on Y its inverse image \(f^{-1}(G,E)\) is soft open on X (Aras and Sonmez 2013). If f is a bijection, soft continuous and \(f^{-1}\) is soft continuous, then f is said to be a soft homeomorphism and X, Y are called soft homeomorphic. From Aras and Sonmez (2013), it follows that bijection f is a homeomorphism if and only if it is a soft continuous and soft closed mapping.

Theorem 11

  1. (a)

    There exist homeomorphic soft topologies which are not similar.

  2. (b)

    There exist similar soft topologies which are not soft homeomorphic.

Proof

(a) Let \(X=\{ x_1, x_2, x_3\}\), \(E=\{e_1, e_2\}\). Define two topologies on X with E as a set of parameters:

$$\begin{aligned} {\mathcal {T}}_{1}= & {} \{\Phi _E, X_E, (F_1, E), (F_2, E)\}\\ {\mathcal {T}}_{2}= & {} \{\Phi _E, X_E, (G_1, E), (G_2, E), \end{aligned}$$

where

$$\begin{aligned} (F_1,E)= & {} \{(e_1, \{x_1, x_2\}), (e_2, \{x_3\})\}\\ (F_2,E)= & {} \{(e_1, X), (e_2, \{x_3\})\} \\ (G_1,E)= & {} \{(e_1, \{x_2, x_3\}), (e_2, \{x_1\})\} \\ (G_2,E)= & {} \{(e_1, X), (e_2, \{x_1\})\}. \end{aligned}$$

Let \(f: (X, {\mathcal {T}}_{1}, E)\rightarrow (X, {\mathcal {T}}_{2}, E)\) be describe by a formula: \(f(x_1)=x_2\), \(f(x_2)=x_3\) and \(f(x_3)=x_1\). Then, f is a bijection; it is soft continues and soft open, as \(f(F_1,E)= \{(e_1, \{x_2, x_3\}), (e_2, \{x_1\})\}=(G_1,E)\) and \(f(F_2,E)= \{(e_1, X), (e_2, \{x_1\})\}=(G_2,E)\). \((X, {\mathcal {T}}_{1})\) and \((X, {\mathcal {T}}_{2})\) are soft homeomorphic, but they are not similar.

(b) Let \(X=\mathbb {R}\), \(E=\{e\}\) and \(x_1\in \mathbb {R}\). Put \({\mathcal {T}}_{1}=\{(e, F(e)): F(e)\in \tau _{nat}\}\) and \({\mathcal {T}}_{2}=\{ (e, G(e)): G(e)\in \tau _{nat} \wedge x_1\notin G(e)\}\). Then, \({\mathcal {T}}_{1} \approx {\mathcal {T}}_{2}\) and \({\mathcal {T}}_{1}\) is a soft normal space, while \({\mathcal {T}}_{2}\) is \(T_1\). Assume that there is a homeomorphism \(h: (X, {\mathcal {T}}_{1}, E)\rightarrow (X, {\mathcal {T}}_{2}, E)\). Then, it is a closed mapping, so it preserves normality of spaces. Hence, \({\mathcal {T}}_{1}\) and \({\mathcal {T}}_{2}\) should be both normal, which is a contradiction. \(\square \)