Abstract
The multiple-travelling salesman problem (MTSP) is a computationally complex combinatorial optimisation problem, with several theoretical and real-world applications. However, many state-of-the-art heuristic approaches intended to specifically solve MTSP, do not obtain satisfactory solutions when considering an optimised workload balance. In this article, we propose a method specifically addressing workload balance, whilst minimising the overall travelling salesman’s distance. More specifically, we introduce the two phase heuristic algorithm (TPHA) for MTSP, which includes an improved version of the K-means algorithm by grouping the visited cities based on their locations based on specific capacity constraints. Secondly, a route planning algorithm is designed to assess the ideal route for each above sets. This is achieved via the genetic algorithm (GA), combined with the roulette wheel method with the elitist strategy in the design of the selection process. As part of the validation process, a mobile guide system for tourists based on the Baidu electronic map is discussed. In particular, the evaluation results demonstrate that TPHA achieves a better workload balance whilst minimising of the overall travelling distance, as well as a better performance in solving MTSP compared to the route planning algorithm solely based on GA.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The salesman problem (TSP) is typically an NP problem Garey and Johnson (1979), whose objective is to determine the shortest path across a set of randomly located cities, each of them visited only once (with the exception of the starting point). From a graph theory perspective, the core task of TSP is to obtain a minimum Hamiltonian cycle. However, some real-world problems cannot be modelled via a traditional simple TSP with one single salesman, including personnel scheduling Masmoudi and Mellouli (2014), patrol planning Ghadiry et al. (2015), and goods distributing (Liu and Zhang 2014; An and Wei 2011). To address this issue, Multiple TSP (MTSP) has been specifically designed to consider a multiple-travelling salesman problem.
The aim of MTSP is to minimise the overall distance across n cities where m salesmen start and complete their journeys at the same city, and the other locations are visited only once. Clearly, TSP is a special case of MTSP for \(m=1\). Heuristic approaches can be utilised to solve MTSP Kiraly and Abonyi (2011), such as the ant colony optimisation algorithm (ACO) Singh and Mehta (2014), particle swarm optimisation algorithm (PSO) Yan et al. (2012), and the genetic algorithm (GA) Avin et al. (2012), to name but a few. However, there are a variety of aspects, which require further improvements. For example, ACO has a slow convergence speed, PSO tends to have local optimisation issues, and GA is prone to be trapped in the premature convergence and heavily depends on the initial population.
In this article, we propose a heuristic MTSP algorithm to obtain an optimised workload balance, whilst minimising the overall salesmen’s travelling distance. The main contributions of our method include:
-
1.
An extension of the current research on the balance problem associated with MTSP, which can be regarded as a multi-objective programming problem. In particular, MTSP and its objective function are initialised to consider the most appropriate conditions, which include the shortest distance and the minimised difference of the distance travelled by each salesman.
-
2.
A specific focus on the integration between the workload balance and the minimisation of the overall travelling salesmen’s distance. To achieve this, we propose the two phase heuristic algorithm (TPHA) for MTSP. In the first phase, we improve the K-means algorithm by grouping all cities into m subsets depending on their locations, based on some capacity constraints. In the second phase, the route planning algorithm based on GA is designed to obtain the ideal route for each city.
-
3.
The roulette wheel method is combined with the elitist strategy to design the GA selection operation. Not only does the operation preserve the best individuals, but it also ensures that the most appropriate fitness of the individual is identified for the next generation. Subsequently, the method of cross-operation is utilised to select the modified order crossover (MOC), which is based on the gene segment as the initial step. This operation can produce a new generation, even if the two parent chromosomes are identical. The main benefit of MOC includes an approach to address local optima and premature convergence.
-
4.
The planning of the travel route through specific scenic locations over a period spanning several days was used as testing platform. A mobile guide system for tourists was designed, which is based on the Baidu electronic map and on TPHA. Firstly, the system locates the visitors’ positions via GPS, and subsequently its utilises TPHA to provide the appropriate route plan through a balanced number of scenic locations for each day. The overall travelling distance is also minimised.
The rest of the paper is organised as follows: in Sect. 2, we discuss the current state-of-the-art methods and techniques in the field. Section 3 provides a detailed description of MTSP in detail and the mathematical model used in this context is introduced. Section 4 focuses on the properties of TPHA, and in Sect. 5 the evaluation results are discussed. Finally, Sect. 6 concludes the article by summarising its main contributions discussing future research directions.
2 Related work
There is extensive research on TSP, including TSP with time windows Falcon and Nayak (2010), TSP with minimum ratio (Ghadle and Muley 2014). Most of the existing solutions consider different constraints, whilst finding a minimum Hamiltonian cycle. Currently, the approaches to TSP are divided into exact and approximate algorithms. The former mainly includes dynamic programming Li (2013), branch and bound Mahfoudh et al. (2015), integer linear programming Pham and Huynh (2015), etc. However, if the scale of the TSP becomes too large, its overall computational time and solution space will increase exponentially.
Inspired by biological activities or natural phenomena, some well-known heuristic algorithms have been developed to solve large-scale TSPs, including ACO, PSO, and GA. There are significant research opportunities in the improvement in such heuristic algorithms and their combination. Pham and Huynh (2015) propose two new crossover operators to improve the global ergodic property of GA, which is a better solution for classical TSP, but not for complex TSP with multiple constraints. Ye et al. (2014) introduce an improved dynamic programming algorithm to deal with large-scale data, used as crossover and mutation operator in GA. Atif et al. (2012) integrate K-means algorithm Hu (2014) with the greedy algorithm and Lin Kernighan’s algorithm Helsgun (2014) to create an enhanced solution for large-scale TSP. However, this method is significantly affected by the scale of the subset partition.
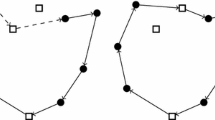
Example described in Sect. 3 a MTSP, b MTSP with balance of workload
A Multi-travelling salesman problem (MTSP) is characterised by more than one salesman and as a consequence, MTSP typically has a higher level of complexity compared to TSP. MTSP can be converted into TSP, and Gorenstein (1970) propose a basic strategy to achieve this, based on m salesmen, and \(m-1\) virtual cities. These are used to define a gap between different travelling salesmen, whilst the distance between the virtual cities is considered infinite. Yuan et al. (2013) discuss a new crossover operator called two-part chromosome crossover for the genetic algorithm in order to obtain near-optimal solutions of MTSP. However, this method is affected by the growth of the chromosome length and the overall cost of the solution. Kaliaperumal et al. (2015) present the Modified Two-Part Chromosome Crossover to address MTSP by employing a genetic algorithm for nearby optimal solutions. However, this method allocates a different number of the cities for each salesman, and therefore, it cannot successfully address MTSP with workload balance. Osaba et al. Hosseinabadi et al. (2014) propose the Real-World Dial-a-Ride problem, which is modelled as a MTSP. In particular, they propose GELS-GA, a new hybrid algorithm, which achieves optimal values even in highly complex scenarios. Finally, Alves and Lopes (2015) consider the workload balance of MTSP and develop GA to reduce both the overall distance and the difference between the distances travelled by each salesman.
3 Modelling of the MTSP
Typically, MTSP only aims to obtain the least total cost of distance or time. For example, Fig. 1 depicts a scenario defined by 3 salesmen and 9 cities, where node 0 is the starting and ending point.
As shown in Fig. 1a, there are two salesmen traversing two cities, respectively, whereas all the other ones are traversed by the third salesman. It is clear that the salesmen’s workloads are unbalanced. As discussed above, the main objective of MTSP is to minimise the overall distance travelled by all salesmen, which may cause an unbalanced workload problem. Figure 1b shows an ideal solution for MTSP with workload balance. In order to achieve a balanced allocation of workload, there are typically two different strategies. The first aims to balance the number of cities assigned to each salesman, whereas the second focuses on optimising the balance of the distances travelled by each salesman.
Formally speaking, MTSP with m salesmen and n cities is defined as a complete graph
where \(V = \{v_{1}, \ldots , v_{n}\}\) represents cities with the starting location at vertex \(v_0\), and each edge \((v_{i},v_{j})\) is associated with a weight \(d_{ij}\) (\(d_{ij} >0\), \(d_{ii} = \infty , v_{i},v_{j} \in V\)), which represents the cost of the path (in terms of distance or time) between cities i and j. We define the maximum number of cities Q for each salesman to achieve workloads balance as
As a consequence, one of the objectives of MTSP is to determine m sequences of Hamiltonian cycles over G, with the least total cost so that each salesman visit one and only one city. The objective function of MTSP is therefore
subject to
where
-
i refers to a city (\(i =1,\ldots ,n\)), so that the starting location is 0;
-
t refers to a salesman (\(t=1,\ldots ,m\)), where m is the total number of salesmen;
-
\(d_{ij}\) represents the distance between the cities i and j;
-
Q is the maximum number of cities travelled by each salesman;
-
\(r_{ijt} \in \{0,1\}\), such that \(r_{ijt}=1\) if the salesman t travels directly from city i to city j, and \(r_{ijt}=0\), otherwise;
-
\(y_{ti}\in \{0,1\}\) and \(y_{ti}=1\) if the salesman t visited the city i, and \(y_{ti}=0\), otherwise.
In particular, Eq. 4 ensures that each city must be visited by one salesman exactly once. Equations 5 and 6 indicate that all the salesmen’s itineraries must begin and end at the same city. Finally, Eq. 7 ensures that the number of cities traversed by each salesman cannot exceed a specific value.
4 Two phase heuristic algorithm for MTSP
As discussed above, TPHA consists of a clustering algorithm, which aims to assign individual cities to m sets, and subsequently, a heuristic algorithm is implemented to plan a route for each city set. K-means is a very popular algorithm for partitioning a large dataset into multiple subsets, which is based on the Euclidean distance as the fitness function. This implies that the elements within a cluster are relatively concentrated and therefore meet the MTSP requirements. In this article, we combine K-means with the maximal capacity constraint to balance the number of cities belonging to the corresponding subsets. Despite a relatively large variety of clustering algorithms, which could be potentially applied in this context, K-means currently offers the most appropriate option. In fact, our proposed method focuses on city locations measured in terms of Euclidean distance, supporting our choice. In future research, we aim to comparatively assess the accuracy and feasibility of other clustering algorithms.
GA is renowned for its global search efficiency, and good scalability. In this work, we utilise the roulette wheel method and the elitist strategy as the selection operation of GA, where MOC is set to be the gene segment associated with the initial step. This operation can produce a new generation, even if the two parent chromosomes are identical. Furthermore, MOC can address the issue of local optima and premature convergence.
4.1 City clustering based on improved K-means
In the original K-means algorithm, k cities are randomly selected as centres of the corresponding cluster, which subsequently identifies all nearby cities via the fitness function, whilst adjusting the centroid location accordingly. These steps are repeated until the convergence of algorithm is obtained. However, the original K-means algorithm cannot meet the objective of achieving a balanced number of cities.
Let \(V = \{ V_{i}: i = 1, \ldots , n\}\) be the set of n cities and assume that the initial cluster set \(s = (c_{1}, \ldots c_{k})\), \(\bar{v}_j\) has \(c_{j}\) as its centroid, where \(\bar{v}_j = v_{i_{j}}, j = 1, \ldots , k\). Also assume that the number of cities in each cluster \(q_{j}\) is set to 0.
The K-means algorithm used in this work includes the following steps:
- Step 1 :
-
Set the capacity of each cluster, where \(\displaystyle {Q = \lceil \frac{n}{m} \rceil }\) is the capacity constraint.
- Step 2 :
-
Calculate the distance of each city \(v_{i} \in V\) to the cluster centre \(\bar{v}_j \) with
$$\begin{aligned} ||v_{i} - \bar{v}_j ||= & {} \sqrt{(x_{i} - \bar{x}_j)^{2}+(y_{i} - \bar{y}_j)^{2}}, \nonumber \\&i = 1,\ldots ,n, \quad j = 1,\ldots ,k, \end{aligned}$$(8)and sort all the distance values \(||v_{i} - \bar{v}_j ||\) in ascending order.
- Step 3 :
-
If there is a city \(v_{i} \in V\) with minimum distance to the centroid \(c_{j}\), then let \(q_{j} = q_{j} +1\), and then calculate whether the current number of cities in \(c_{j}\) is satisfied with \(q_{j} \le Q\). If it is, then \(v_{i}\) is assigned to \(c_{i}\). Otherwise, let the distance value \(||v_{i} - \bar{v}_j || = \infty \) between the city \(v_{i}\) and the centroid. Repeat the steps until all cities are assigned.
- Step 4 :
-
The coordinates of the centroid is updated via
$$\begin{aligned} \left\{ \begin{array}{ccc} \bar{x}_{j} &{}=&{} \displaystyle {\frac{1}{|c_{j}|}\sum _{v_{i} \in c_{j}}x_i}\\ \bar{y}_{j} &{}=&{} \displaystyle {\frac{1}{|c_{j}|}\sum _{v_{i} \in c_{j}}y_i} \end{array} \right. \end{aligned}$$(9)where \(|c_{j}|\) is the number of cities in the cluster \(c_{j}\). If the coordinates of the centroid are not changed, then the result is assumed to convergence, and move to Step 5; otherwise, go to Step 2.
- Step 5 :
-
The clustering process is complete with the output cluster \(s = (c_{1}, \ldots , c_{k})\).
4.2 Route planning based on GA
The main GA parameters include parameter initialisation, initial population, evaluation of fitness function, the selection and the crossover operation, as well as the mutation operation. Table 1 lists some important parameters related to the algorithm.
Different GA approaches might involve different encoding, crossover and mutation operations, which may lead to a divergence of the iterative process. Therefore, it is necessary to redesign the above operations to ensure that the optimal solution is indeed attained.
4.3 Initial population encoding
In order to provide an integration of the definition of GA with the problem introduced above, it is necessary to identify a suitable encoding operator, which determines the evolution of the population. In any GA approach, a binary representation is generally applied to describe the corresponding target problems. However, according to the properties of TSP, each city can be associated with an integer, which represents a path \(1, \ldots ,n\), corresponding to a route scheme type. Therefore, solving TSP implies finding the shortest distance between any two numbers associated with two cities (Chen 2013).
4.4 Fitness function
The fitness function is used to assess individual elements in the corresponding group. The selection operation based on the fitness value is one of the main steps in GA, and, to a large extent, it determines the performance of GA. In particular, a high value of the fitness evaluation implies that an individual has a high probability of being chosen. The fitness function F(x) is defined as
where x represents an individual, and D(x) is the distance travelled by the individual x. As can be seen from Eq. 10, an individual x follwoing a shorter path will clearly have a high fitness value and will also have a high genetic probability to be selected for the next generation.
4.5 Selection strategy
The selection strategy is an important step in the evolutionary operation of GA, as it affects its efficiency. As discussed above, in this article we combine the roulette wheel method with the elitist strategy as the selection strategy of TPHA. More specifically, the former selects a chromosome in a statistical fashion based solely on its fitness value. On the other hand, the latter moves the individual with the best fitness at the current generation to the next one. Compared to the original roulette wheel method, the TPHA selection strategy allows to retain a “superior” individual. More specifically, we have the following steps:
- Step 1 :
-
Assume \(P_{size}\) is the size of population, and \(X_{i}^{k}\) is the i-th individual in \(X^{k}\). Evaluate the i-th individual’s fitness value \(F_{i}^{k}\) in descending order. Subsequently, the individual with the best fitness at the current generation is moved to the next one.
- Step 2 :
-
The probability of each individual to be selected is evaluated as
$$\begin{aligned} p_i = \frac{F_{i}^{k}}{\sum \nolimits _{i=1}^{G}F_{i}^{k}} \end{aligned}$$(11)where \(p_i\) is assigned to each individual \(X_{i}^{k}\) based on the order of calculation.
- Step 3 :
-
The next generation is selected via the roulette wheel strategy by randomly generating a uniformly distributed number \(\delta \) within (0, 1). If
$$\begin{aligned} \sum _{j=0}^{i-1}p_{j} \le \delta \le \sum _{j=0}^{i}p_{j}, \end{aligned}$$then \(X_{i}^{k}\) is selected to the next generation. Repeat the above steps until all the parent chromosomes have been selected.
As shown in Fig. 2, the greater the fitness value, the higher the probability of being selected will be.
4.6 Crossover operation
Two parent chromosomes \(P_1\) and \(P_2\) are selected according to the crossover probability \(p_c\). This generates two intersection points, which identify the corresponding segments \(\Delta p_1\) and \(\varDelta p_2\). Child 1 is then assigned to \(\Delta p_1\) as the initial gene, whilst the equivalent components of \(P_2\)’s chromosome are ignored. Finally, the remaining part is added to child 1. Child 2 is defined in a similar manner. As an example, Fig. 3, depicts the scenario with 8 cities, where the integers in [0, 7] are associated with the two parents’ chromosomes. The randomly selected parent 1’s gene segment (e.g. 5213) is used as the initial gene for child 1, and the identical parts of parent 2’s chromosome are ignored. Finally, the remaining component is added to child 1. The same procedure also applies to child 2.
4.7 Mutation operation
The mutation operation plays an important role in improving local search capability, whilst maintaining the variability of the population. It also prevents the premature GA convergence. This work utilises the swapping mutation, as follows: via the mutation probability \(p_m\) a chromosome is selected, and then two crossing points are randomly identified, whilst the selected points are exchanged. Figure 4 shows the case with 8 cities again, so that a route scheme is associated with the sequence of integers corresponding to cities (5, 2, 1, 3, 7, 4, 0, 6). Two selected swapping gene points are node 3 and node 6, which are swapped to generate the offspring.
If the scheduled termination condition is satisfied (i.e. the number of iterations is larger than G), then the iteration is halted, and the corresponding path is considered satisfactory.
4.8 Detailed workflow
The detailed workflow includes the following steps:
- Step 1 :
-
Initialisation of the parameters, including G, \(P_{\mathrm{size}}\), \(p_c\) and \(p_m\), and the generation of initial population \(X^{1}\). We assume \(x_{\mathrm{best}} = X_{1}^{1}, D_{\mathrm{best}}= D(X_{1}^{1})\), \(k=1, j = 2, m = 1\), and \(n=1\).
- Step 2 :
-
Assessment of each individual’s evaluation value for each generation, \(D_{i}^{k}= D(X_{i}^{k})\), where the fitness value \(F_{i}^{k}= D(X_{i}^{k})\), for \(i = 1, \ldots , P_{\mathrm{size}}\). For \(X_{\mathrm{min}}^{k}\), if \(\displaystyle {\min _{x \in X^{k}}{\{D(X)\}} = D(X_{\mathrm{min}}^{k})}\), then \(D_{\mathrm{min}} = D(X_{\mathrm{min}})\), and \(Y _{1} = X_{\mathrm{min}}^{k}\). Otherwise, \(D_{\mathrm{best}}\) remains unchanged.
- Step 3 :
-
Evaluation of the probability of the corresponding individual to be selected for each generation via
$$\begin{aligned} p_i = \frac{F_{i}^{k}}{\displaystyle {\sum \nolimits _{i=1}^{G}F_{i}^{k}}} \end{aligned}$$ - Step 4 :
-
if \(j > P_{\mathrm{size}}\), then move to Step 5. Otherwise, randomly generate \(\delta \in U(0,1)\). If
$$\begin{aligned} \sum _{j=0}^{i-1}p_{j} \le \delta \le \sum _{j=0}^{i}p_{j}, \end{aligned}$$then \(X_{i}^{k}\) is selected for the next generation. Let \(Y_{j} = X_{i}^{k}, j = j+1\), and repeat this step.
- Step 5 :
-
The sequence A is obtained by the random number of integers \(1,\ldots P_{\mathrm{size}}\). The individuals in population Y are subsequently rearranged according to A to obtain the population Z. Set \(X^{k} = Y\).
- Step 6 :
-
if \(m>P_{size}\) then \(m=1\), and move to Step 8. Otherwise, randomly generate a number \(r \in U(0,1)\), and move to Step 7.
- Step 7 :
-
if \(r < p_{c}\), then \([sub \, x_{1} \; sub \, x_{2}]=CS(x_{m}^{k}, x_{m+1}^{k})\), and
$$\begin{aligned} S=\left[ sub \, x_{1} \; sub \, x_{2}, X_{m}^{k}, X_{m+1}^{k}\right] . \end{aligned}$$Select two chromosomes \(x_1\) and \(x_2\) with a smaller evaluation value via
$$\begin{aligned} min_{x \in S}{\{D(x)\}} = D(x_{1}) \end{aligned}$$and
$$\begin{aligned} min_{x \in S\setminus x_{1}}{\{D(x)\}} = D(x_{2}). \end{aligned}$$Let the next generation \(X_{m}^{k+1} = x_1\) and \(X_{m+1}^{k+1} = x_2\), and move to Step 6.
- Step 8 :
-
if \(n > P_{size}\), let \(n=1\) and move to Step 10. Otherwise, randomly generate a number \(r \in U(0,1)\), and then move to Step 9.
- Step 9 :
-
if \(r < p_{m}\), then execute the mutation operation on \(X_{n}^{k}\) to obtain \(V_{n}^{k+1}\), \( X_{n}^{k+1}=V_{n}^{k+1}\). Let \(n=n+1\) and then move to Step 8.
- Step 10 :
-
Set \(k=k+1\). If \(k<G\), then move to Step 2. Otherwise, terminate the algorithm, and output \(X_{\mathrm{best}}\) and \(D_{\mathrm{best}}\).
The detailed flowchart of TPHA is shown in Fig. 5.
5 Applications and experiments
Tourism route planning is a well-known application of MTSP, where a tourist needs to traverse various scenic locations subject to minimising the travelled distance. Due to the constraint of a limited daily travel time, the number of locations need to be balanced. Suppose there are n scenic locations, therefore a tourist will spend m days visiting all of them. Another important requirement is minimising the time spent travelling between different locations. Furthermore, it is assumed that a tourist starts and completes his/her journey at the same hotel every day. In other words, we have the following constraints:
-
The tourist will not change his/her hotel accommodation during his staying in a city.
-
Each location is visited once and only once.
-
The daily travel time is fixed, which limits the number of locations visited each day.
-
The tourist will return to his/her hotel every day.
As part of the evaluation process, sixteen scenic areas in Nanjing city (China) were selected as shown on the Baidu map in Fig. 6. The hotel accommodation was set as the Phoenix Universal Hotel. Table 2 shows a detailed description of the locations, and Fig. 7 shows their corresponding latitude and longitude coordinates.
Coordinates of the locations described in Table 2
5.1 Experiments
First of all, by using TPHA, specific locations are assigned to different clusters based on their latitude and longitude coordinates, and let the number of days \(m =k =4\). The number of (daily visited) areas Q, (\({Q = \lceil \frac{n}{m}\rceil }\)) is evaluated, which determines the capacity constraints for each day. The original K-means algorithm randomly selects four locations as the initial centroid, it calculates the distance between them and the corresponding centroid, and finally it utilises the fitness function to arrange them to join the appropriate cluster, as shown in Fig. 8. However, our improved K-means algorithm includes the capacity constraints of each cluster set, allowing the number of locations in each cluster to be more balanced, as shown in Fig. 9.
In the second phase, TPHA uses the redesigned GA to plan routes for the four clusters. In order to test its performance, we downloaded the standard dataset from TSPLIB (http://comopt.ifi.uniheidelberg.de/software/TSPLIB95/).
The experimental results of the improved GA are subsequently compared with other typical algorithms. The related parameters are set via experiments as follows: \(G = 2000\), \(P_{\mathrm{size}}= 500\), \(p_{c} =0.80\), and \(p_{c} = 0.1\) The experimental results are shown in Fig. 10. Table 3 depicts the comparison of the GA experimental results with the ant colony algorithm (ACA) Liu et al. (2012) and the nearest neighbour method (NN) Wang (2014). OHC is the best known solution, and the deviation of the best found solution to the best known solution err is defined as follows:
Note that a small error rate indicates that a better solution of the method has been achieved.
As shown in Table 3, the improved GA version clearly demonstrates that better results are obtained compared to the nearest neighbour method. Although the error rate of ACA is lower than the improved GA, the time complexity of ACA is \(O(G n^{2}m)\), where G represents the total number of iterations, n is the number of cities, and m the number of ants. On the other hand, the time complexity of the improved GA is \(O(G P_{\mathrm{size}}\), which is lower (Fig. 11).
The integration of TPHA with the improved GA is utilised for the second phase of the route plan. The related parameters are set as follows: \(G =100\), \(P_{\mathrm{size}} = 100\), \(p_{c} = 0.90\), and \(p_{m} = 0.05\).
Figures 12 and 13 show that with the original GA the length of chromosome is longer, not only increasing the computation time and reducing the convergence speed, but also increasing the total distance, as shown in Table 4.
5.2 Design of the prototype
In this section, the design of a mobile guide system for tourists based on the Baidu electronic map SDK and Android 4.2 mobile platform is discussed.
As shown in Fig. 13, the mobile guide system consists of the following classes:
-
Class MainActivity describes the completion of the Baidu electronic map loading, including the verification of API key, the detection of network states and the management of map life cycle.
-
Class TPHA invokes the class MKsearchListener, which obtains the location information, whilst GA carries out the path planning.
-
Class ItemizedOverlay invokes the class GpsActivity to obtain the current location, and marks it on the map.
-
Class RouteOverlay is used to identify the route
-
GraphicsOverlay is utilised to show the path information on the Baidu electronic map.
-
Finally, getDistance() is used to obtain the associated cost.
Figures 14 and 15 show the 4-day travel path planned with TPHA and GA, respectively, demonstrating that TPHA has a better performance.
As shown in Table 5, the distance of total route planned with TPHA is 150.7 km, whilst the distance of total route planned with GA is 159.4 km.
6 Conclusions
In this article, we have discussed the significance of MTSP, both from a theoretical and real-world applications point of view. In order to address the issues raised by MTSP, we propose TPHA, which integrates improved K-means and the redesigned GA to obtain the balanced and short-distance routes. Furthermore, this work specifically focuses on the workload balance subject to minimising the overall salesmen’s travelling distance. Experimental results show that the proposed TPHA has a better performance in solving MTSP with lower system overheads, and a mobile guide system for tourists was implemented to further demonstrate this.
Future research efforts will include the investigation of the time cost, the traffic and other constraints in order to model more complex and dynamic MTSP, whilst improving the performance and function of the route planning algorithm. Furthermore, we are aiming to consider different locations by analysing the corresponding datasets whenever available. This will be also facilitated by integrating text mining techniques to extract information from social media, blogs and general websites to validate the accuracy of the identified routes.
References
Alves RMF, Lopes CR (2015) Using genetic algorithms to minimize the distance and balance the routes for the multiple traveling salesman problem. In: Proceedings Sendai, CEC, pp 1–8
An H, Wei L (2011) Synthetically improved genetic algorithm on the traveling salesman problem in material transportation. In: Proceedings Harbin, Heilongjiang, EMEIT, pp 3386–3371
Atif AK, Muhammad UK, Muneeb I (2012) Multilevel graph partitioning scheme to solve traveling salesman problem. In: Proceedings Las Vegas, NV, ITNG, pp 458–463
Avin R, Agin D, Adnan M (2012) Solving TSP using genetic algorithms—case of Kosovo, Advances in Computer Science, pp 256–260
Chen P (2013) An improved genetic algorithm for solving the traveling salesman problem. In: Proceedings Shenyang, ICNC, pp 397–401
Falcon R, Nayak A (2010) The one-commodity traveling salesman problem with selective pickup and delivery: an ant colony approach. In: Proceedings Barcelona, Spain, CEC, pp 4326–4333
Garey MR, Johnson DS (1979) Computers and intractability: a guide to the theory of NP-completeness, in computers and intractability, vol 24, New York, pp 90–91
Ghadiry W, Habibi J, Aghdam AG (2015) Generalized formulation for trajectory optimization in patrolling problems. In: Proceedings Halifax, NS, CCECE, pp 231–236
Ghadle KP, Muley YM (2014) An application of assignment problem in traveling salesman problem (TSP). J Eng Res Appl 4(1):169–172
Gorenstein S (1970) Printing press scheduling for multi-edition periodicals. Manag Sci 16(6):373–383
Helsgun K (2014) Solving the equality generalized traveling salesman problem using the Lin–Kernighan–Helsgaun algorithm. Math Program Comput 7(3):269–287
Hosseinabadi AAR, Kardgar M, Shojafar M et al (2014) GELS-GA: hybrid metaheuristic algorithm for solving multiple travelling salesman problem. In: Proceedings Okinawa, ISDA, pp 76–81
Hu CQ (2014) A K-means algorithm. J Changchun Univ Technol 35(2):139–142
Kaliaperumal R, Ramalingam A, Sripriya J (2015) A modified two part chromosome crossover for solving MTSP using genetic algorithms. In: Proceedings ICARCSET, New York, 2015, pp 1–4
Kiraly A, Abonyi J (2011) Optimization of Multiple Traveling Salesmen Problem by a Novel Representation Based Genetic Algorithm, in International Computational in Engineering. Vol. 366, pp. 241-269
Li J (2013) An improved dynamic programming algorithm for bitonic TSP. In Proceedings ISCCCA-13, Paris, France, pp 24–27
Liu M, Zhang PY (2014) New hybrid genetic algorithm for solving the multiple traveling saleman problem: an example of distribution of emergence materials. J Syst Manag 23(02):247–254
Liu Y, Shen X, Chen H (2012) An adaptive ant colony algorithm based on common information for solving the traveling salesman problem. In: Proceedings Shandong, ICSAI, pp 763–766
Mahfoudh SS, Khaznaji W, Bellalouna M (2015) A branch and bound algorithm for the porbabilistic traveling salesman problem. In: Proceedings Takamatsu, SNPD, pp 1–6
Masmoudi M, Mellouli R (2014) MILP for synchronized-mTSPTW: application to home healthCare scheduling. In: Proceedings Metz, CoDIT, pp 297–302
Pham DT, Huynh TTB (2015) New mechanism of combination crossover operators in genetic algorithm for solving the traveling salesman problem, in knowledge and systems engineering, 2nd ed., vol 326, Switzerland, pp 367–379
Singh G, Mehta R (2014) Implementation of travelling salesman problem using ant colony optimization. J Eng Res Appl 6(3):385–389
Wang Y (2014) A nearest neighbor method with a frequency graph for traveling salesman problem. In: Proceedings IHMSC. Hangzhou, pp 335–338
Ye C, Yang ZC, Yan TX (2014) An efficient and scalable algorithm for the traveling salesman problem. In: Proceedings Beijing, ICSESS, pp 335–339
Yan XS, Zhang C, Luo WJ et al (2012) Solve traveling salesman problem using particle swarm optimization algorithm. Int J Comput Sci Issues 9(6):264–271
Yuan S, Skinner B, Huang S, Liu D (2013) A new crossover approach for solving the multiple travelling salesmen problem using genetic algorithms. Eur J Oper Res 228(1):72–82
Acknowledgements
We would like to thank the reviewers in advance for their comments to help us improve the quality of this paper. This work was jointly sponsored by the National Natural Science Foundation of China under Grant 61472192 and the Scientific and Technological Support Project (Society) of Jiangsu Province under Grant BE2016776.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
All authors declare that they have no conflict of interest.
Ethical approval
This article does not contain any studies with human participants or animals performed by any of the authors.
Additional information
Communicated by V. Loia.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Xu, X., Yuan, H., Liptrott, M. et al. Two phase heuristic algorithm for the multiple-travelling salesman problem. Soft Comput 22, 6567–6581 (2018). https://doi.org/10.1007/s00500-017-2705-5
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-017-2705-5