Simulated annealing least squares twin support vector machine (SA-LSTSVM) for pattern classification

Abstract

Least squares twin support vector machine (LSTSVM) is a relatively new version of support vector machine (SVM) based on non-parallel twin hyperplanes. Although, LSTSVM is an extremely efficient and fast algorithm for binary classification, its parameters depend on the nature of the problem. Problem dependent parameters make the process of tuning the algorithm with best values for parameters very difficult, which affects the accuracy of the algorithm. Simulated annealing (SA) is a random search technique proposed to find the global minimum of a cost function. It works by emulating the process where a metal slowly cooled so that its structure finally “freezes”. This freezing point happens at a minimum energy configuration. The goal of this paper is to improve the accuracy of the LSTSVM algorithm by hybridizing it with simulated annealing. Our research to date suggests that this improvement on the LSTSVM is made for the first time in this paper. Experimental results on several benchmark datasets demonstrate that the accuracy of the proposed algorithm is very promising when compared to other classification methods in the literature. In addition, computational time analysis of the algorithm showed the practicality of the proposed algorithm where the computational time of the algorithm falls between LSTSVM and SVM.

1 Introduction

Support vector machine (SVM), first introduced by Cortes and Vapnik (1995), is a classification technique based on the structural risk minimization (SRM) algorithm. The algorithm rapidly became used in many classification tasks due to its success in recognizing handwritten characters in which it outperformed precisely trained neural networks. In addition to recognizing handwritten characters, SVMs performed successful classification in other applications such as: time series prediction (Ruan et al. 2013), pattern classification (Wu et al. 2010), and bioinformatics (Guyon et al. 2002; Sartakhti et al. 2012). A comprehensive tutorial on the SVM classifier algorithm has been published by Burges (1998).

After the introduction of SVM in 1995, different versions of this powerful classifier were advanced including the least squares twin support vector machine (LSTSVM), introduced in 2009 (Arun Kumar and Gopal 2009). LSTSVM combines the idea behind least squares SVM (LSSVM) (Suykens and Vandewalle 1999) and twin SVM (TSVM) (Khemchandani and Chandra 2007).

A crucial challenge in LSTSVM and all other versions of SVM is how to set their parameters with best values. LSTSVM has four parameters which are highly dependent on the nature of the problem. Therefore, finding best values for these parameters is almost impossible for user.Our current research suggests that this is the first study to find the best values for LSTSVM parameters. However, there are several methods for dominating this challenge in SVM. Huang and Wang (2006) proposed a genetic algorithm (GA) approach for parameter optimization. They evaluated several medicine datasets using their proposed GA-based SVM. Ren and Bai (2010) also presented two approaches for parameter optimization in SVM, GA-SVM and particle swarm optimization (PSO) SVM. A hybrid ant colony optimization (ACO) based classifier model which simultaneously optimizes SVM kernel parameters and selects the optimum feature subset has been proposed by Huang (2009). Salimi et al. proposed a method that hybridized SVM and simulated annealing (SA) (Sartakhti et al. 2012). In addition, Lin et al. (2008) develops a simulated annealing approach for parameter determination and feature selection in the SVM, termed SA-SVM.

Simulated annealing is an optimization algorithm which solves the problem of becoming fixed at local minima (or maxima) by allowing less optimum moves to be chosen sometimes by some probability. The method was described independently by Kirkpatrick et al. (1983) and by Černỳ (1985). Simulated annealing selects a solution in each iteration by first checking if the neighbor solution is better than the current solution. If it is, the new solution will be accepted unconditionally. If, however, the neighbor solution is not better, it will be accepted based on some probability depending on how much it differs from the neighbor solution and the value of the current solution. In this paper, we have integrated Simulated Annealing with LSTSVM to identify the optimal parameters which enhance LSTSVM accuracy. Our experimental results have demonstrated that the proposed method has higher accuracies compared to other well-known versions of SVM. In addition, for all evaluated data sets the proposed algorithm outperformed C4.5 which is a powerful algorithm in classification context. Furthermore, computational time analysis showed that our proposed algorithm is faster than SVM and it is completely a practical algorithm for classification tasks.

The rest of this paper is organized as follows. A brief review of basic concepts including SVM and some different versions of the algorithm is presented in Sect. 2. The proposed SA-LSTSVM algorithm is introduced in Sect. 3. Section 4 gives the experimental results, and finally in Sect. 5 conclusions are presented.

2 Basic concepts

This section presents a brief review of different versions of SVM. The versions presented are the standard SVM, TSVM, and LSTSVM.

2.1 Support vector machine

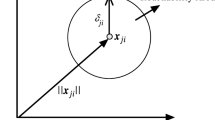
SVM is a maximum margin classifier which means that its goal is to minimize classification error and at the same time maximize the margin between two classes. For example, given a set of training points $(x_{i},y_{i})$, $i=1,\ldots ,n$ each input training data $x_{i} \in \mathbb {R}^{d}$ belongs to either of two classes with labels $y_{i} \in {-1,+1}$. SVM seeks a hyperplane with equation $w.x+b=0$ which can satisfy the following constraints

$$\begin{aligned}&y_{i}(w.x_{i}+b) \ge 1,\quad \forall i. \end{aligned}$$

(1)

where w is the weight vector and b is the bias term. Such a hyperplane could be obtained by solving Eq. 2:

$$\begin{aligned}&\mathrm{Minimize}\,\,\, f(x)=\frac{\Vert w\Vert ^{2}}{2} \nonumber \\&\mathrm{subject}\,\mathrm{to}\,\, y_{i}(w.x_{i}+b)-1\ge 0 \end{aligned}$$

(2)

The geometric interpretation of this formulation is depicted in Fig. 1 for a toy example.

Fig. 1

Geometric interpretation of SVM

An important problem with SVM is its computational time. If “l” indicates the size of training data samples, then the computational complexity of SVM is of order $O(l^{3})$, which is very expensive.

2.2 Twin support vector machine

In SVM only one hyperplane performs the task of partitioning samples into two groups of positive and negative classes. In 2007, Khemchandani and Chandra (2007) proposed TSVM to use two hyperplanes in which samples are assigned to a class according to their distance from each hyperplane. The main equations of TSVM are:

$$\begin{aligned}&x_{i}w^{(1)}+b^{(1)}=0 \nonumber \\&x_{i}w^{(2)}+b^{(2)}=0 \end{aligned}$$

(3)

where $w^{(i)}$ and $b^{(i)}$ are weight vectors and bias terms of the ith hyperplane. In TSVM each hyperplane is a representative of the samples of its class. This concept is geometrically depicted in Fig. 2 for a toy example.

Fig. 2

Geometric interpretations of twin SVM

In TSVM, the two hyperplanes are non-parallel with each being closest to the samples of its own class and farthest from the samples of the opposite class (Ding et al. 2014; Shao et al. 2011). Assuming A and B indicate data points of class $+1$ and class $-1$, respectively, the two hyperplanes are obtained by solving (4) and (5).

$$\begin{aligned}&\mathrm{Minimize} \quad \frac{1}{2}(Aw^{(1)}+e_{1}b^{(1)})^{\mathrm{T}}(Aw^{(1)}+e_{1}b^{(1)})+c_{1}e^\mathrm{T}_{2}q \nonumber \\&\mathrm{w.r.t. }\;\; w^{(1)}, b^{(1)} \nonumber \\&\mathrm{subject} \, \mathrm{to} \quad -(Bw^{(1)}+e_{2}b^{(1)})+q \ge e_{2}, \quad \; q \ge 0 \end{aligned}$$

(4)

$$\begin{aligned}&\mathrm{Minimize} \quad \frac{1}{2}(Bw^{(2)}+e_{2}b^{(2)})^{\mathrm{T}}(Bw^{(2)}+e_{2}b^{(2)})+c_{2}e^\mathrm{T}_{1}q \nonumber \\&\mathrm{w.r.t.} \;\; w^{(2)},b^{(2)} \nonumber \\&\mathrm{subject} \, \mathrm{to} \quad Aw^{(2)}+e_{1}b^{(2)}+q \ge e_{1}, \quad \; q \ge 0 \end{aligned}$$

(5)

In these equations, q is a vector contains the slack variables, $e_{i} \; (i \in \{1,2\})$ is a column vector of ones with arbitrary length, and $c_{1}$ and $c_{2}$ are penalty parameters. Once the hyperplanes are obtained, a new data point is assigned to class $+1$ or class $-1$ depending on to which hyperplane the point is closer in terms of perpendicular distance.

In TSVM, the number of constraints in the equation of each hyperplane is equal to the number of samples in the opposite class. Therefore, if there is an equal number of samples in the two classes, the number of constraints for each hyperplane in TSVM is equal to half the number of constraints in SVM. The computational complexity of TSVM is $O((l/2)^{3})$ (Tomar and Agarwal 2014). It can be shown that the TSVM increases the speed of the algorithm by a factor of 4 compared to the traditional SVM, i.e. it is four times faster when compared to the SVM.

2.3 Least squares twin support vector machine

LSTSVM (Arun Kumar and Gopal 2009; Shao et al. 2012) is a binary classifier which combines the idea of LSSVM (Suykens and Vandewalle 1999; Mitra et al. 2007) and TSVM. LSTSVM employs “least squares of errors” to modify inequality constraints in TSVM to equality constraints by solving a set of linear equations rather than two quadratic programming problems (QPPs). Experiments have shown that LSTSVM can considerably reduce the training time, while still achieving competitive classification accuracy (Suykens and Vandewalle 1999; Gao et al. 2011). Because LSTSVM is a combination of TSVM and LSSVM, it dramatically reduces the time complexity of SVM. This is because LSTSVM solves equality constraints instead of inequality constraints as in LSSVM which makes the computational speed of the algorithm faster. The number of constraints in each hyperplane in LSTSVM is half of that in SVM which again results in very low computational complexity when compared to SVM. LSTSVM also has far better accuracy compared to SVM in most classification tasks.

LSTSVM finds its hyperplanes by minimizing Eqs. (6) and (7) which are linearly solvable. By solving (6) and (7), values of w and b for each hyperplane are obtained according to (8) and (9).

$$\begin{aligned}&\mathrm{Minimize} \quad \frac{1}{2}(Aw^{(1)}+eb^{(1)})^{\mathrm{T}}(Aw^{(1)}+eb^{(1)})+ \frac{c_{1}}{2}q^{\mathrm{T}}q \nonumber \\&\mathrm{w.r.t.} \;\; w^{(1)},b^{(1)} \nonumber \\&\mathrm{subject} \, \mathrm{to} \quad (Bw^{(1)}+eb^{(1)})+q=e \end{aligned}$$

(6)

$$\begin{aligned}&\mathrm{Minimize} \quad \frac{1}{2}(Bw^{(2)}+eb^{(2)})^{\mathrm{T}}(Bw^{(2)}+eb^{(2)})+ \frac{c_{2}}{2}q^{\mathrm{T}}q \nonumber \\&\mathrm{w.r.t.} \;\; w^{(2)},b^{(2)} \nonumber \\&\mathrm{subject} \, \mathrm{to} \quad (Aw^{(2)}+eb^{(2)})+q=e \end{aligned}$$

(7)

$$\begin{aligned} \begin{bmatrix} w^{(1)} \\ b^{(1)} \end{bmatrix} =-\left( F^{T}F + \frac{1}{c_{1}} E^{T}E\right) ^{-1}F^{\mathrm{T}}e \end{aligned}$$

(8)

$$\begin{aligned} \begin{bmatrix} w^{(2)} \\ b^{(2)} \end{bmatrix} =-\left( E^{\mathrm{T}}E + \frac{1}{c_{2}} F^{\mathrm{T}}F\right) ^{-1}E^{\mathrm{T}}e \end{aligned}$$

(9)

where $E=\begin{bmatrix} A&e \end{bmatrix}$ and $F= \begin{bmatrix} B&e \end{bmatrix}$ whereas A, B, e and q are introduced in Sect. 2.2.

Fig. 3

Pseudo code of simulated annealing

3 Proposed algorithm

LSTSVM has four parameters $c_{1}$, $c_{2}$, $\mathrm{sigma}_{1}$ and $\mathrm{sigma}_{2}$ which should be set by the user where $c_{1}$ and $c_{2}$ represent the amount of error for each class and sigma$_{1}$ and sigma$_{2}$ measure the impact of error on each hyperplane. These four parameters are highly dependent on the nature of the problem which means that for different problems, they would have different optimum values. This affects the accuracy of LSTSVM and is considered as a weakness.

Genetic algorithms, analytical gradient, numerical gradient and Monte Carlo are examples of methods used to find the optimum values for the parameters. Simulated annealing (SA) is also used to find global optimum values for parameters. Although SA is time consuming, it achieves better accuracies compared to other methods. In this study the SA algorithm is used to find the best global values for LSTSVM parameters.

3.1 Simulated annealing

SA is a technique to find the best solution for an optimization problem by trying random variations of the current solution. It is a generalization of a Monte Carlo method for examining equations of state and frozen states of n-body systems. Figure 3 shows the pseudo code of the SA heuristic.

In each step, SA considers some neighboring state $s_{i}$ of the current state $s_{\mathrm{current}}$, and decides between moving to state $s_{i}$ or staying in state $s_{\mathrm{current}}$ with some probability. The new state ($s_{i}$) will be accepted if it has a better fitness compared to the current state ($s_{\mathrm{current}}$). If, however, the new state has lower fitness, it will be accepted with the probability showed in line 13 of the pseudo code. Note that the definition of “fitness” depends on the goal of the problem. These probabilistic movements ultimately lead the system to a state with almost optimum solution.

3.2 SA-LSTSVM

This section presents the proposed SA-LSTSVM algorithm in more detail. As already stated, LSTSVM has four parameters, two for each of the hyperplanes, which depend on nature of the problem. In SA a set of states is defined where each state has a set of parameters which include $c_{1}$, $c_{2}$, sigma$_{1}$ and sigma$_{2}$. The start state and its parameters are initiated by the user. For each state, SA defines a set of neighbors (which are also part of the state set). To find optimum values for LSTSVM parameters, the values of parameters for each particular state will initially differ from its neighbors. At first, there is a great difference between the parameter values of each two neighbor states, but the difference decreases as the algorithm iterates. In each iteration, a neighbor will be selected randomly. If the selected neighbor has higher accuracy than the current state, the selected neighbor will be taken and its parameters values (c and sigma) used as new parameter values. Figure 4 shows the pseudo code of the combined algorithm.

Fig. 4

Algorithm outline: SA-LSTSVM

Table 1 Characteristics of the small data sets

Table 2 Experimental results of SA-LSTSVM and other algorithms

4 Experimental results

In this section, we describe the experiments designed to evaluate the performance of the proposed algorithm using some benchmark datasets. To achieve more reliable test results, our experiments used the k-fold cross-validation technique. This technique minimizes the bias associated with the random sampling of training (Delen et al. 2005). The k-fold cross-validation technique randomly divides the whole dataset into k mutually exclusive and approximately equal size subsets. Each classification algorithm was trained and tested k times using these subsets. Each time one of the k folds is taken as a test set, the remaining $(k-1)$ folds are used as training data. Averaged results of the k-fold cross-validation are considered as the final results. In our evaluation, we used tenfold cross-validation which is a very common case in the context. Furthermore, because simulated annealing tries random variations of the current solution, one may criticize the proposed method that it will be very time consuming for large data sets. To answer this comment, we run our experiments on two types of data sets: small data sets with $<$2000 samples, and larger data sets with 3000 to 100,000 samples.

4.1 Small data sets

In this section, nine standard small data sets from the UCI repository (Bache and Lichman 2013) were evaluated. Table 1 shows some features of these data sets.

Table 2 presents the evaluation results of SA-LSTSVM and six other algorithms on these data sets. These algorithms are SVM, four different versions of SVM and a decision tree classification algorithm, C4.5 (Quinlan 1993), which has been selected because of its good performance in classification tasks. Bold text indicates best accuracies for each data set.

Fig. 5

Changes in the accuracy of SA-LSTSVM for different values of c and sigma on Australian Credit Approval data set

Fig. 6

Changes in the accuracy of SA-LSTSVM for different values of c and sigma on Liver Disorder data set

Fig. 7

Changes in the accuracy of SA-LSTSVM for different values of c and sigma on CMC data set

Fig. 8

Changes in the accuracy of SA-LSTSVM for different values of c and sigma on Statlog (Heart) data set

Fig. 9

Changes in the accuracy of SA-LSTSVM for different values of c and sigma on Hepatitis data set

Fig. 10

Changes in the accuracy of SA-LSTSVM for different values of c and sigma on Ionosphere data set

In this table the average accuracy of tenfold cross-validation together with the variance of the accuracies are shown as accuracy $\pm$ variance. For SA-LSTSVM the best values of c and sigma are shown, too. Reported accuracies for TSVM, GEPSVM (Mangasarian and Wild 2006), and PSVM (Fung and Mangasarian 2001) are all extracted from Arun Kumar and Gopal (2009).

Figures 4, 5, 6, 7, 8, 9, 10, 11 and 12 show the accuracy of the SA-LSTSVM algorithm for each of the nine data sets for different values of c and sigma. In some figures, the relation between values of the parameters and the accuracy of SA-LSTSVM is obvious, e.g. Fig. 9, however, for some others, e.g. Fig. 7 there is not an obvious relationship between the accuracy of SA-LSTSVM and values of the parameters. As it is mentioned before the optimum values for parameters are problem dependent. The SA algorithm is used to find the highest accuracy among continuous values of c and sigma.

Fig. 11

Changes in the accuracy of SA-LSTSVM for different values of c and sigma on Sonar data set

Fig. 12

Changes in the accuracy of SA-LSTSVM for different values of c and sigma on Congressional Voting Records data set

Fig. 13

Changes in the accuracy of SA-LSTSVM for different values of c and sigma on Breast Cancer Wisconsin data set

Fig. 14

Changes of c and sigma in SA-LSTSVM on Australian Credit Approval data set

Fig. 15

Changes of c and sigma in SA-LSTSVM on Liver Disorder data set

Fig. 16

Changes of c and sigma in SA-LSTSVM on CMC data set

Fig. 17

Changes of c and sigma in SA-LSTSVM on Statlog (Heart) data set

Fig. 18

Changes of c and sigma in SA-LSTSVM on Hepatitis data set

Fig. 19

Changes of c and sigma in SA-LSTSVM on Ionosphere data set

Figures 13, 14, 15, 16, 17, 18, 19, 20 and 21 show how the values of c and sigma changed during iterations of the SA algorithm for the nine data sets. In these figures, the blue shows the changes in the value of c and the red curve shows how sigma changes during the iterations. As it can be seen from the figures, the way the algorithm moves toward the optimum values for parameters depends on the data set.

Figures 22, 23, 24, 25, 26, 27, 28, 29, 30 and 31 show how the accuracy of the SA-LSTSVM algorithm changes during iterations of SA algorithm on the data sets. The figures show that as the algorithm iterates the average accuracy increases, but the accuracy variances decreased. The figures also show that using SA-LSTSVM it is possible to achieve the global best accuracy in a limited number of iterations ($<$60 iteration in most of the data sets).

Fig. 20

Changes of c and sigma in SA-LSTSVM on Sonar data set

Fig. 21

Changes of c and sigma in SA-LSTSVM on Congressional Voting Records data set

Fig. 22

Changes of c and sigma in SA-LSTSVM on Breast Cancer Wisconsin data set

Fig. 23

Changes of the accuracy of SA-LSTSVM on Australian Credit Approval data set

Fig. 24

Changes of the accuracy of SA-LSTSVM on Liver Disorder data set

Fig. 25

Changes of the accuracy of SA-LSTSVM on CMC data set

Fig. 26

Changes of the accuracy of SA-LSTSVM on Statlog (Heart) data set

Fig. 27

Changes of the accuracy of SA-LSTSVM on Hepatitis data set

Fig. 28

Changes of the accuracy of SA-LSTSVM on Ionosphere data set

Fig. 29

Changes of the accuracy of SA-LSTSVM on Sonar data set

Fig. 30

Changes of the accuracy of SA-LSTSVM on Congressional Voting Records data set

Fig. 31

Changes of the accuracy of SA-LSTSVM on Breast Cancer Wisconsin data set

4.2 Larger data sets

To evaluate the performance of SA-LSTSVM on larger data sets, we used David Musicant’s NDC Data Generator (Musicant 1998) to generate data sets with 3000, 4000, 5000, 10,000, and 100,000 samples and 32 features. Results of running each algorithm are shown in Table 3. The best accuracy for each data set is shown in boldface. As it is shown in the table, again SA-LSTSVM has the highest accuracies among all versions of SVM for all data sets. However, only in NDC-100k data set, C4.5 obtains a better accuracy compared to SA-LSTSVM.

4.3 Statistical comparison of classifiers

The above experiments showed that for all of the studied datasets, the accuracy of SA-LSTSVM is higher than other compared algorithms. However, there still a question remains which is “Are these differences statistically significant?”. In other words, it is important to show that these algorithms are statistically different. In Demšar (2006), Demsar introduced different ways of comparing algorithms over multiple data sets. Since we have seven algorithms for comparison, we choose to use Friedman test which is a non-parametric counterpart of ANOVA. Although there are some implementations of the Friedman test in some software tools like MATLAB and KEEL (Alcal-Fdez et al. 2009), we chose to implement the test by ourselves in MATLAB. The Friedman test ranks the algorithms for each dataset separately in the way that the best performing algorithm getting the rank 1, the second best ranked 2 and so on. In case of ties, e.g. in CMC, Hepatitis, Congressional Voting Records, and NDC-4k, the average ranks are assigned. Table 4 shows the ranks of the classifiers for different datasets used in this paper. Numbers inside the parenthesis are the ranks of classifiers for the corresponding dataset. The final row contains the average ranks of each classifier which is computed as $R_{j} = \frac{1}{N}\sum _{i}r_{i}^{j}$, where $r_{i}^{j}$ is the rank of the jth algorithm on the ith dataset. Note that since for NDC-100k two of the algorithms do not converged, we do not count this dataset in the evaluation.

Table 3 Experimental results of SA-LSTSVM and other algorithms on larger data sets

Table 4 Rankings of the classifiers for each dataset

The null-hypothesis is that all the algorithms are equivalent. Then the Friedman statistic is calculated and finally the critical value of the distribution of the Friedman statistic is compared with the statistic itself. The null-hypothesis will be rejected if the statistic is higher than the critical value.

The Friedman statistic is computed as follows:

$$\begin{aligned} \chi _{\mathrm{F}}^{2} = \frac{12N}{k(k+1)}\left[ \sum _{j}R_{j}^{2}-\frac{k(k+1)^{2}}{4}\right] . \end{aligned}$$

(10)

In this equation, k and N are the total number of classifiers and the total number of datasets, respectively. In our case $k = 7$ and $N = 13$. The statistic is distributed according to $\chi _{\mathrm{F}}^{2}$ with $k-1$ degrees of freedom, when N and k are big enough (as a rule of thumb, $N>10$ and $k>5$) which is our case (Demšar 2006). Iman and Davenport (1980) showed that Friedman’s $\chi _{\mathrm{F}}^{2}$ is undesirably conservative and they proposed a better statistic as bellow.

$$\begin{aligned} F_{\mathrm{F}} = \frac{(N-1)\chi _{\mathrm{F}}^{2}}{N(k-1)-\chi _{\mathrm{F}}^{2}} \end{aligned}$$

(11)

which is distributed according to the F-distribution with $k-1$ and $(k-1)(N-1)$ degrees of freedom.

The computed Friedman statistic and the corresponding $F_{\mathrm{F}}$ statistic for our experiments are:

$$\begin{aligned} \chi _{\mathrm{F}}^{2}&= \frac{12*13}{7*8}\bigg [ (1^{2}+2.923^{2}+3.538^{2}+5.576^{2}&\nonumber \\&\quad +4.038^{2}+6.153^{2}+4.769^{2})-\frac{7*8^{2}}{4}\bigg ] = 50.3 \end{aligned}$$

$$\begin{aligned}&F_{\mathrm{F}} = \frac{12*50.3}{13*6-50.3} = 21.8&\end{aligned}$$

With seven algorithms and 13 datasets, $F_{\mathrm{F}}$ is distributed according to the F distribution with $7-1=6$ and $(7-1)\times (13-1) = 72$ degrees of freedom. The critical value of F(6, 72) for $\alpha = 0.05$ is 2.23, so we reject the null-hypothesis which means that the algorithms are statistically different.

By rejecting the null-hypothesis we can proceed with a post-hoc test. Since we want to compare all other classifiers with our proposed SA-LSTSVM, we will use the Bonferroni–Dunn test (Dunn 1961). In Demšar (2006) it is explained that based on Nemenyi test (Nemenyi 1963), the performance of two classifiers is significantly different if the corresponding average ranks differ by at least the critical difference

$$\begin{aligned}&\mathrm{CD} = q_{\alpha }\sqrt{\frac{k(k+1)}{6N}}&\end{aligned}$$

where $q_{\alpha }$ is the critical value.

Table 5 Computational time analysis (in second) of SVM, LSTSVM and SA-LSTSVM

The Bonferroni–Dunn test controls the family wise error rate by diving $\alpha$ by the number of comparisons made which is $k-1$ in this case. The alternative way to compute the same test as it is introduced in Demšar (2006) is to compute the critical difference, CD, using the same equation as the Nemenyi test, but using the critical values for $\frac{\alpha }{(k-1)}$. The critical value $q_{0.05}$ for seven classifiers is 2.638 and, therefore, we have CD $= 2.638\sqrt{\frac{7*8}{6*13}}=2.235$. Using this critical difference, we can conclude that:

• SA-LSTSVM performs significantly better that LSTSVM, since $1-2.923 < 2.235$

• SA-LSTSVM performs significantly better that TSVM, since $1-3.538 < 2.235$

• SA-LSTSVM performs significantly better that GEPSVM, since $1-5.576 < 2.235$

• SA-LSTSVM performs significantly better that PSVM, since $1-4.038 < 2.235$

• SA-LSTSVM performs significantly better that SVM, since $1-6.153 < 2.235$

• SA-LSTSVM performs significantly better that C4.5, since $1-4.769 < 2.235$.

4.4 Computational time analysis

As stated in Sect. 2.3, LSTSVM is computationally faster than SVM with a computational time better than SVM by a factor of 4. SA is a probabilistic meta heuristic algorithm which takes random walks through the problem space. This may suggest that the SA-LSTSVM algorithm may be computationally very slow. However, our computational time analysis indicates otherwise.

Table 5 shows the computational times in second for the SA-LSTSVM, LSTSVM and SVM algorithm for all of the data sets. For the SA-LSTSVM algorithm the maximum number of iterations considered in the experiment was 25. This number was chosen because with this value for $k_{\mathrm{max}}$, the algorithm achieves good accuracies for each of the different data sets. Although, we did not have any claim about the running time of the proposed SA-LSTSVM, Table 5 shows that the computational time of the SA-LSTSVM algorithm falls between the computational time of LSTSVM algorithm, which is the fastest version of SVM, and the standard SVM. In the table, the $*$ sign shows that the computational time is extremely high and the algorithm does not converge to an acceptable accuracy in a reasonable time. Although, the obtained computational times for LSTSVM are better than SA-LSTSVM and SVM, the proposed SA-LSTSVM has higher accuracies when compared to both LSTSVM and SVM for all data sets.

5 Conclusion

The LSTSVM algorithm is a relatively new addition of the family of SVM classifier algorithms and being based on non-parallel twin hyperplanes has shown good classification performance. However, the algorithm has parameters which are problem dependent and finding the optimum values for these parameters is itself a challenging problem that affects the accuracy of the algorithm. In this paper we have proposed an improved LSTSVM algorithm (SA-LSTSVM) by hybridizing it with the well-known simulated annealing (SA) algorithm to determine the optimum parameter values for the LSTSVM algorithm. Experimental results on data sets with different sizes have demonstrated that the algorithm has higher accuracies compared to other well-known classification algorithms while its computational time is also reasonable.