Parametric testing statistical hypotheses for fuzzy random variables

Abstract

In this paper, a method is proposed for testing statistical hypotheses about the fuzzy parameter of the underlying parametric population. In this approach, using definition of fuzzy random variables, the concept of the power of test and p value is extended to the fuzzy power and fuzzy p value. To do this, the concepts of fuzzy p value have been defined using the $\alpha$-optimistic values of the fuzzy observations and fuzzy parameters. This paper also develop the concepts of fuzzy type-I, fuzzy type-II errors and fuzzy power for the proposed hypothesis tests. To make decision as a fuzzy test, a well-known index is employed to compare the observed fuzzy p value and a given significance value. The result provides a fuzzy test function which leads to some degrees to accept or to reject the null hypothesis. As an application of the proposed method, we focus on the normal fuzzy random variable to investigate hypotheses about the related fuzzy parameters. An applied example is provided throughout the paper clarifying the discussions made in this paper.

1 Introduction

The purpose of statistical inference is to draw conclusions about a population on the basis of data obtained from a sample of that population. Hypothesis testing is the process used to evaluate the strength of evidence from the sample and provides a framework for making decisions related to the population, i.e., it provides a method for understanding how reliably one can extrapolate observed findings in a sample under study to the larger population from which the sample was drawn. The investigator formulates a specific hypothesis, evaluates data from the sample, and uses these data to decide whether they support the specific hypothesis. The classical parametric approaches usually depend on certain basic assumptions about the underlying population such as: crisp observations, exact parameters, crisp hypotheses, and crisp possible decisions. In practical studies, however, it is frequently difficult to assume that the parameter, for which the distribution of a random variable is determined, has a precise value or the value of the random variable is recorded as a precise value or the hypotheses of interest are presented as exact relations, and so on. Therefore, to achieve suitable testing statistical methods dealing with imprecise information, we need to model the imprecise information and extend the usual approaches to imprecise environments. Since its introduction by Zadeh (1965), fuzzy set theory has been developed and applied in some statistical contexts to deal with uncertainty conditions such as above situations. Specially, the topic of testing statistical hypotheses in fuzzy environments has extensively been studied. Below is a brief review of some studies relevant to the present work. Arnold (1996, 1998) presented an approach for testing fuzzily formulated hypotheses based on crisp data, in which he proposed and considered generalized definitions of the probabilities of the errors of type-I and type-II. Viertl (2006, 2011) used the extension principle to obtain the generalized estimators for a crisp parameter based on fuzzy data. He also developed some other statistical inferences for the crisp parameter, such as generalized confidence intervals and p value, based on fuzzy data. Taheri and Behboodian (1999) formulated the problem of testing fuzzy hypotheses when the observations are crisp. They presented some definitions for the probabilities of type-I and type-II errors, and proved an extended version of the Neyman–Pearson Lemma. Their approach has been extended by Torabi et al. (2006) to the case in which the data are fuzzy, too. Taheri and Behboodian (2001) also studied the problem of testing hypotheses from a Bayesian point of view when the observations are ordinary and the hypotheses are fuzzy. Taheri and Arefi (2009) presented an approach to the problem of testing fuzzy hypotheses, based on the so-called fuzzy critical regions. Grzegorzewski (2000) suggested some fuzzy tests for crisp hypotheses concerning an unknown parameter of a population using fuzzy random variables (FRVs). Montenegro et al. (2001, 2004), using a generalized metric for fuzzy numbers, proposed a method to test hypotheses about the fuzzy mean of a FRV in one and two populations settings. Gonzalez-Rodríguez et al. (2006) extended a one-sample bootstrap method of testing about the mean of a general fuzzy random variable. Gil et al. (2006) introduced a bootstrap approach to the multiple-sample test of means for imprecisely valued sample data. Chachi and Taheri (2011) introduced a new approach to construct fuzzy confidence intervals for the fuzzy mean of a FRV. Filzmoser and Viertl (2004) and Parchami et al. (2010) presented $p$ value-based approaches to the problem of testing hypothesis, when the available data or the hypotheses of interest are fuzzy, respectively. Hryniewicz (2006b) investigated the concept of $p$ value in a possibilistic context in which the concept of $p$ value is generalized for the case of imprecisely defined statistical hypotheses and vague statistical data.

On the other hand, there have been some studies on non-parametric statistical testing hypotheses in fuzzy environment. Concerning the purposes of this paper, let us briefly review some of the literature on this topic. Kahraman et al. (2004) proposed some algorithms for fuzzy non-parametric rank-sum tests based on fuzzy random variables. Grzegorzewski (1998) introduced a method to estimate the median of a population using fuzzy random variables. He (Grzegorzewski 2004) also demonstrated a straightforward generalization of some classical non-parametric tests for fuzzy random variables based on a metric in the space of fuzzy numbers. He also (Grzegorzewski 2005, 2009) studied some non-parametric median fuzzy tests for fuzzy observations showing a degree of possibility and a degree of necessity (Dubois and Prade 1983) for evaluating the underlying hypotheses. In addition, he (Grzegorzewski 2008) proposed a modification of the classical sign test to cope with fuzzy data which was so-called bi-robust test, i.e., a test which is both distribution free and which does not depend so heavily on the shape of the membership functions used for modeling fuzzy data. Denœux et al. (2005), using a fuzzy partial ordering on closed intervals, extended the non-parametric rank-sum tests based on fuzzy data. For evaluating the hypotheses of interest at a crisp or a fuzzy significance level, they employed the concepts of fuzzy $p$ value and degree of rejection of the null hypothesis quantified by a degree of possibility and a degree of necessity. Hryniewicz (2006a) investigated the fuzzy version of the Goodman–Kruskal $\gamma$-statistic described by ordered categorical data. Lin et al. (2010) considered the problem of two-sample Kolmogorov–Smirnov test for continuous fuzzy intervals based on a crisp test statistic. Taheri and Hesamian (2011) introduced a fuzzy version of the Goodman–Kruskal $\gamma$-statistic for two-way contingency tables when the observations were crisp, but the categories were described by fuzzy sets. In this approach, a method was also developed for testing of independence in the two-way contingency tables. Taheri and Hesamian (2012) extended the Wilcoxon signed-rank test to the case where the available observations are imprecise and underlying hypotheses are crisp. Hesamian and Chachi (2013) developed the concepts of fuzzy cumulative distribution function and fuzzy empirical cumulative distribution function and investigated the large sample property of the classical empirical cumulative distribution function for fuzzy empirical cumulative distribution function. They proposed a method for developing two-sample Kolmogorov–Smirnov test for the case when the data are observations of fuzzy random variables, and the hypotheses are imprecise. For more on fuzzy statistics including testing hypotheses for imprecise data, see for example Bertoluzza et al. (2002), Buckley (2006), Kruse and Meyer (1987), Nguyen and Wu (2006), Viertl (2011).

This paper develops an approach to test hypotheses for an unknown fuzzy parameter based on fuzzy random variables. To do this, we extend the concept of fuzzy power function and fuzzy p value to investigate the hypotheses of interest. Finally, a decision rule is suggested to accept or reject the null and alternative hypotheses. We also provide a computational procedure and an example to express the proposed method to test statistical hypotheses for a normal FRV.

This paper is organized as follows: Section 2 briefly reviews the classical parametric testing hypotheses and some definitions from fuzzy numbers. In the same section, some results about $\alpha$-optimistic values of a fuzzy number are derived to recontract a so-called definition of fuzzy random variables introduced in Sect. 3. In Sect. 4, one-sided and two-sided hypotheses about a fuzzy parameter of a FRV are defined. The concept of fuzzy power and fuzzy p value for testing hypotheses about a fuzzy parameter of a continuous parametric population is also introduced. Then, the proposed method is applied for testing hypotheses about the fuzzy parameters of a normal FRV in Sect. 4.1. A numerical example is then provided in Sect. 5 to clarify the discussions made in this paper. Section 6 compares the proposed method to the other similar existing methods. Finally, a brief conclusion is provided in Sect. 7. In addition, the proofs of the main results in this paper are provided in Appendix.

2 Preliminaries

2.1 Testing statistical hypotheses: the classical approach

Let $\mathbf {X} = ({X}_1,\ldots ,{X}_n)$ be a random sample, with the observed value $\mathbf x = (x_1,\ldots ,x_n)$, from a continuous population with density function $f_{\varvec{\theta }}$ where ${\varvec{\theta }}\in \varTheta \subseteq \mathbb {R}^p$, $p\ge 1$. The decision rule to test the null hypothesis $H_0: \theta \in \varTheta _0$ versus the alternative $H_1:\theta \in \varTheta _1$ is typically denoted by

$$\begin{aligned} \varphi (\mathbf x )=\left\{ \begin{array}{ll} 1 &{}\quad \text {if}\ T(\mathbf x )\in \mathbf C _{\delta },\\ 0 &{}\quad \text {if}\ T(\mathbf x )\notin \mathbf C _{\delta }, \end{array} \right. \end{aligned}$$

where $\mathbf C _{\delta }\subseteq \mathbb {R}$ is the critical region, $\delta$ is the significance level, and $T(\mathbf {X} )$ is a test statistic. The power function of $\varphi (\mathbf {X} )$ is defined by $\pi _\varphi (\theta ) = E_{\theta }[\varphi (\mathbf {X} )] = \mathbf P _{\theta } (T(\mathbf X )\in \mathbf C _{\delta })$. Note that, if the underlying family of distribution functions has the MLR property (Monotone Likelihood Ratio property) in $T$ then $\pi _\varphi (\theta ) = E_{\theta }[\varphi (\mathbf {X} )]$ is a non-decreasing function of $\theta$ (for more see Lehmann and Romano 2005; Shao 2003). Finally, at a given significance level $\delta$, the hypothesis $H_0$ is completely rejected if and only if p value $<\delta$, where $p\hbox { value}=\inf \{\delta \in [0,1]:T(\mathbf x )\in \mathbf C _{\delta }\}$ (Shao 2003). So, to accept or reject the null hypothesis, we have a test as follows

$$\begin{aligned} \psi (\mathbf x )=\left\{ \begin{array}{ll} 1 &{}\quad \text {if } p\hbox { value} <\delta ,\\ 0 &{}\quad \text {if } p\hbox { value}\ge \delta . \end{array} \right. \end{aligned}$$

2.2 Fuzzy numbers

Let ${\mathbb {R}}$ be the set of all real numbers. A fuzzy set of ${\mathbb {R}}$ is a mapping $\mu _{\widetilde{A}}:{\mathbb {R}}\rightarrow [0,1]$, which assigns to each $x\in {\mathbb {R}}$ a degree of membership $0\le \mu _{\widetilde{A}}(x)\le 1$. For each $\alpha \in (0,1]$, the subset $\{x\in {\mathbb {R}}\mid \mu _{\widetilde{A}}(x)\ge \alpha \}$ is called the level set or $\alpha$-cut of $\widetilde{A}$ and is denoted by $\widetilde{A}[\alpha ]$. The set $\widetilde{A}[0]$ is also defined equal to the closure of $\{x\in {\mathbb {R}}\mid \mu _{\widetilde{A}}(x)>0\}$. A fuzzy set $\widetilde{A}$ of ${\mathbb {R}}$ is called a fuzzy number if it satisfies the following three conditions.

• 1. For each $\alpha \in [0,1]$, the set $\widetilde{A}[\alpha ]$ is a compact interval, which will be denoted by $[\widetilde{A}^L_{\alpha }, \widetilde{A}^U_{\alpha }]$. Here, $\widetilde{A}^L_{\alpha }=\inf \{x\in {\mathbb {R}}\mid \mu _{\widetilde{A}}(x)\ge \alpha \}$ and $\widetilde{A}^U_{\alpha }=\sup \{x\in {\mathbb {R}}\mid \mu _{\widetilde{A}}(x)\ge \alpha \}$.

• 2. For $\alpha ,\beta \in [0,1]$, with $\alpha <\beta$, $\widetilde{A}[\beta ]\subseteq \widetilde{A}[\alpha ]$.

• 3. There is a unique real number $x^*=x^*_{\widetilde{A}}\in {\mathbb {R}}$, such that $\widetilde{A}(x^*)=1$. Equivalently, the set $\widetilde{A}[1]$ is a singleton.

The set of all fuzzy numbers is denoted by ${\mathcal {F}}({\mathbb {R}})$. Moreover, we denote by $\mathcal {F}_c(\mathbb {R})$ the set of all fuzzy numbers with continuous membership function.

Lemma 1

(Lee 2005) Let $\widetilde{A}\in {\mathcal {F}}({\mathbb {R}})$. Then$,$ both the maps $\alpha \mapsto \widetilde{A}^L_{\alpha }$ and $\alpha \mapsto \widetilde{A}^U_{\alpha }$ are left continuous on $[0,1]$.

A $LR$-fuzzy number $\widetilde{A} = (a,a^l,a^r)_{LR}$ where $a^l,a^r\ge 0$, is defined as follows

$$\begin{aligned} \mu _{\widetilde{A}}(x)=\left\{ \begin{array}{ll} L(\frac{a-x}{a^l}) &{}\quad a-a^{l} \le x \le a,\\ R(\frac{x-a}{a^r}) &{}\quad a<x\le a+a^{r},\\ \end{array}\right. \end{aligned}$$

where $L$ and $R$ are continuous and strictly decreasing functions with $L(0)=R(0) = 1$ and $L(1)=R(1) = 0$ (Lee 2005). A special type of $LR$-fuzzy numbers is the so-called triangular fuzzy numbers with the shape functions $L(x)=R(x)=\max \{0,1-|x|\}$, $x\in \mathbb {R}$.

A well-known ordering of fuzzy numbers, used in the sections below for defining the hypotheses of interest is defined as follows:

Definition 1

(Wu 2005) Let $\widetilde{A},\widetilde{B}\in \mathcal {F}(\mathbb {R})$, then

• 1. $\widetilde{A}\asymp (\not =)\widetilde{B}$, if $\widetilde{A}^L_\alpha =(\not =)\widetilde{B}^L_\alpha$ and $\widetilde{A}^U_\alpha =(\not =)\widetilde{B}^U_\alpha$ for any $\alpha \in [0,1]$.

• 2. $\widetilde{A}\preceq (\prec )\widetilde{B}$, if $\widetilde{A}^L_\alpha \le (<) \widetilde{B}^L_\alpha$ and $\widetilde{A}^U_\alpha \le (<) \widetilde{B}^U_\alpha$ for any $\alpha \in [0,1]$.

• 3. $\widetilde{A}\succeq (\succ )\widetilde{B}$, if $\widetilde{A}^L_\alpha \ge (>)\widetilde{B}^L_\alpha$ and $\widetilde{A}^U_\alpha \ge (>) \widetilde{B}^U_\alpha$ for any $\alpha \in [0,1]$.

2.3 $\alpha$-Optimistic values

In this subsection, we drive some results about the $\alpha$-optimistic values of a fuzzy number. We will use these results to reconstruct a definition of fuzzy random variable that we use in the next sections.

For a given fuzzy number $\widetilde{A}$, the credibility of the event $\{\widetilde{A}\ge r\}$ is defined by Liu (2004) as follows:

$$\begin{aligned} \mathrm{Cr}\{\widetilde{A}\ge r\}:=\frac{1}{2}\left( \sup _{y\in [r,+\infty )}\mu _{\widetilde{A}}(y)\!+\!1-\!\sup _{y\in (-\infty ,r)}\mu _{\widetilde{A}}(y)\right) ,\nonumber \\ \end{aligned}$$

(1)

It is worth noting that: (1) $\mathrm{Cr}\{\widetilde{A}\ge r\} \in [0,1]$ and (2) $\mathrm{Cr}\{\widetilde{A}\ge r\}=1-\mathrm{Cr}\{\widetilde{A}< r\}$.

Here, we recall the definition of the $\alpha$-optimistic, but with a small change in the structure of the original definition. For a fuzzy number $\widetilde{A}$ and the real number $\alpha \in [0,1]$, the $\alpha$-optimistic value of $\widetilde{A}$, denoted by $\widetilde{A}_{\alpha }$, is rewritten by

$$\begin{aligned} \widetilde{A}_{\alpha }:=\sup \{x\in \widetilde{A}[0]\mid \mathrm{Cr}\{\widetilde{A}\ge x\}\ge \alpha \}. \end{aligned}$$

(2)

Remark 1

It is mentioned that, according to the Liu’s definition, the $\alpha$-optimistic value of the fuzzy number $\widetilde{A}$ is defined as follows

$$\begin{aligned} \widetilde{A}_{\alpha }:=\sup \{x\in \mathbb {R} \mid \mathrm{Cr}\{\widetilde{A}\ge x\}\ge \alpha \}. \end{aligned}$$

(3)

Therefore, we observe that $\widetilde{A}_0=\infty$ and $\widetilde{A}_{\alpha }\in [\widetilde{A}^{L}_{\alpha },\widetilde{A}^{R}_{\alpha })$ for $\alpha \in (0,1]$. While, by Eq. (2), each value of $\widetilde{A}_{\alpha }$ belongs to $\widetilde{A}[0]$ (which is a compact interval, due to the definition of a fuzzy number), for all $\alpha \in [0,1]$. Moreover, it is clear that $\widetilde{A}_{\alpha }$ is a non-increasing function of $\alpha \in [0,1]$ (see Liu 2004, for more details).

Example 1

For a given $LR$-fuzzy number $\widetilde{A} = (a,a^l,a^r)$, it is easily seen that

$$\begin{aligned} \widetilde{A}_{\alpha }=\left\{ \begin{array}{ll} a+a^rR^{-1}(2\alpha ) &{}\quad \text {for }0.0 \le \alpha \le 0.5,\\ a-a^{l}L^{-1}(2(1-\alpha ))&{}\quad \text {for }0.5 \le \alpha \le 1.0. \end{array} \right. \end{aligned}$$

Specially, if $\widetilde{A}=(a,a^l,a^r)_T$ is a triangular fuzzy number, then

$$\begin{aligned} \widetilde{A}_{\alpha }=\left\{ \begin{array}{ll} a^r-2\alpha (a^r-a)&{}\quad \text {for }0.0 \le \alpha \le 0.5,\\ 2a-a^l-2\alpha (a-a^l) &{}\quad \text {for }0.5 \le \alpha \le 1.0. \end{array} \right. \end{aligned}$$

For instance, the $\alpha$-optimistic values of $\widetilde{A}=(-2,0,1)_T$ are obtained as

$$\begin{aligned} \widetilde{A}_{\alpha }=\left\{ \begin{array}{ll} 1-2\alpha &{}\quad \text {for }0.0 \le \alpha \le 0.5,\\ 2-4\alpha &{}\quad \text {for }0.5 \le \alpha \le 1.0. \end{array} \right. \end{aligned}$$

In the rest of this section, we drive some properties of $\alpha$-optimistic values of a fuzzy number $\widetilde{A}$ and its relation to $\alpha$-cuts of $\widetilde{A}$.

Theorem 1

For $\widetilde{A}\in {\mathcal {F}}({\mathbb {R}}),$ suppose $\phi _{\widetilde{A}}:[0,1]\rightarrow {\mathbb {R}}$ is the function defined by $\phi _{\widetilde{A}}(\alpha )=\widetilde{A}_{\alpha }$. Then$,$

• (i) For each $\alpha \in [0,1],$

  $$\begin{aligned}&\phi _{\widetilde{A}}(\alpha )\\&\quad =\!\left\{ \begin{array}{ll} \widetilde{A}_{2\alpha }^U &{}\quad 0.0\!\le \! \alpha \le 0.5,\\ \sup \{x\le x^*\mid \mu _{\widetilde{A}}(x)\le 2(1\!-\!\alpha )\} &{}\quad 0.5<\alpha \le 1, \end{array}\right. \end{aligned}$$

  where $x^*=x^*_{\widetilde{A}}\in {\mathbb {R}}$ is the unique real number which satisfies $\widetilde{A}(x^*)=1$.

• (ii) $\phi _{\widetilde{A}}$ is a decreasing and left continuous function.

Proof

The proof of Theorem 1 is postponed to the Appendix.

Here, we investigate another useful property of the function $\phi _{\widetilde{A}}$. For a fuzzy number $\widetilde{A}\in {\mathcal {F}}({\mathbb {R}})$, let $\psi _{\widetilde{A}}:[0,1]\rightarrow {\mathbb {R}}$ be a function defined as follows.

$$\begin{aligned} \forall \alpha \in [0,1],\quad \psi _{\widetilde{A}}(\alpha )=\left\{ \begin{array}{ll} \widetilde{A}_{2\alpha }^U &{} \quad \alpha \in [0,0.5],\\ \widetilde{A}_{2(1-\alpha )}^L &{}\quad \alpha \in (0.5,1].\end{array}\right. \end{aligned}$$

(4)

According to Lemma 1, this function is decreasing, left continuous on $[0,0.5]$ and right continuous on $(0.5,1]$. Moreover, according to part (i) of the previous theorem, $\psi _{\widetilde{A}}(\alpha )=\phi _{\widetilde{A}}(\alpha )$, for all $\alpha \in [0,0.5]$.

Lemma 2

If $\alpha _0\in (0.5,1]$ is a point of continuity of either $\psi _{\widetilde{A}}$ or $\phi _{\widetilde{A}}$ then the values of the two functions coincide at this point.

Proof

The proof of Lemma 2 is postponed to the Appendix.

Remark 2

From Lemma 2, note that the $\alpha$-cuts of a fuzzy number $\widetilde{A}\in \mathcal {F}_c(\mathbb {R})$ can be rewritten as $\widetilde{A}[\alpha ]=[\widetilde{A}_{1-\alpha /2},$ $\widetilde{A}_{\alpha /2}]$, $\alpha \in [0,1]$. Therefore, the membership function of the fuzzy number $\widetilde{A}$ can be obtained from the representation theorem (e.g., see Lee 2005) as follows

$$\begin{aligned} \mu _{\widetilde{A}}(x)=\sup _{\alpha \in [0,1]}I(x\in [\widetilde{A}_{1-\alpha /2}, \widetilde{A}_{\alpha /2}]),\quad x\in \mathbb {R}. \end{aligned}$$

Remark 3

From Lemma 2, note that the ordering of fuzzy numbers $\widetilde{A}$ and $\widetilde{B}$ introduced in Definition 1 is equivalent to:

• 1. $\widetilde{A}\asymp (\not =)\widetilde{B}$, if $\widetilde{A}_{\alpha }=(\not =)\widetilde{B}_{\alpha }$ for any $\alpha \in [0,1]$.

• 2. $\widetilde{A}\preceq (\prec )\widetilde{B}$, if $\widetilde{A}_{\alpha }\le (<) \widetilde{B}_{\alpha }$ for any $\alpha \in [0,1]$.

• 3. $\widetilde{A}\succeq (\succ )\widetilde{B}$, if $\widetilde{A}_{\alpha }\ge (>)\widetilde{B}_{\alpha }$ for any $\alpha \in [0,1]$.

3 Fuzzy random variables

Let $(\varOmega ,\mathcal {A}, \mathbf {P})$ be a probability space, $\widetilde{X}:\varOmega \rightarrow \mathcal {F}({\mathbb {R}})$ be a fuzzy-valued function, $X$ be a random variable having distribution function $f_{\varvec{\theta }}$ with a vector of parameters $\varvec{\theta }=(\theta _1,\ldots ,\theta _p)\in \varTheta$ in which $\varTheta \subset {{\mathbb {R}}}^p$ be the parameter space, $p\ge 1$. Throughout this paper, we assume that all random variables have the same probability space $(\varOmega ,\mathcal {A}, \mathbf {P})$.

It is mentioned that Kwakernaak (1978, 1979) introduced a notion of FRVs as follows: given a probability space $(\varOmega ,\mathcal {A},\mathbf {P})$, a mapping $\widetilde{X}:\varOmega \rightarrow \mathcal {F}(\mathbb {R})$ is said to be a FRV if for all $\alpha \in [0,1]$, the two real-valued mappings $\widetilde{X}^{L}_{\alpha }:\varOmega \rightarrow \mathbb {R}$ and $\widetilde{X}^{U}_{\alpha }:\varOmega \rightarrow \mathbb {R}$ are real-valued random variables. Here, we rewrite the Kwakernaak’s definition of FRV using $\alpha$-optimistic values of a fuzzy number as follows

Definition 2

(Hesamian and Chachi 2013) The fuzzy-valued function $\widetilde{X}:\varOmega \rightarrow \mathcal {F}(\mathbb {R})$ is called a FRV if $\widetilde{X}_{\alpha }(\omega ):\varOmega \rightarrow \mathbb {R}$ is a real-valued random variable for all $\alpha \in [0 , 1]$.

Based on Theorem 1 and Remark 2, note that our definition of a FRV is just a restriction of FRVs defined by Kwakernaak. So, a FRV can be addressed by its $\alpha$-optimistic values instead of its $\alpha$-cuts which is the reason that we use credibility index in this paper.

Definition 3

FRVs $\widetilde{X}$ and $\widetilde{Y}$ are called identically distributed if $\widetilde{X}_{\alpha }$ and $\widetilde{Y}_{\alpha }$ are identically distributed, for all $\alpha \in [0,1]$. In addition, they are called independent if each random variable $\widetilde{X}_{\alpha }$ is independent of each random variable $\widetilde{Y}_{\alpha }$, for all $\alpha \in [0,1]$. Similarly, we say that $\widetilde{\mathbf{X }}=(\widetilde{X}_1,\ldots ,\widetilde{X}_n)$ is a random sample of size $n$ if $\widetilde{X}_i$ are independent and identically distributed FRVs. The observed fuzzy random sample is denoted by $\widetilde{\mathbf{x }}=(\widetilde{x}_1,\ldots ,\widetilde{x}_n)$.

Here, consider a special case of FRVs as the member of a family of a classical parametric population which is introduced by Wu (2005) (see also Chachi and Taheri 2011).

Definition 4

A FRV $\widetilde{X}$ is said to have a (classical) parametric continuous density function with fuzzy parameter $\widetilde{\varvec{\theta }}:\varTheta \rightarrow (\mathcal {F}(\mathbb {R}))^p$, denoted by $\big \{f_{\widetilde{\varvec{\theta }}}:\widetilde{\varvec{\theta }} \in (\mathcal {F}(\mathbb {R}))^p \big \}$, if for all $\alpha \in [0,1]$, $\widetilde{X}_{\alpha }\sim f_{(\widetilde{\varvec{\theta })}_{\alpha }}$, where $(\widetilde{\varvec{\theta }})_{\alpha }=((\widetilde{\theta }_1)_{\alpha },\ldots ,(\widetilde{\theta }_p)_{\alpha })$.

Remark 4

It is mentioned that a necessary and sufficient condition to say $\widetilde{X}\sim f_{\widetilde{\varvec{\theta }}}$, $\widetilde{\varvec{\theta }} \in (\mathcal {F}(\mathbb {R}))^p$ is that $\widetilde{X}_{\alpha _1}$ is “stochastically greater than $\widetilde{X}_{\alpha _2}$ for any $\alpha _1<\alpha _2$, i.e., $F_{\widetilde{X}_{\alpha _2}}(x)\ge F_{\widetilde{X}_{\alpha _1}}(x)$ for all $x\in \mathbb {R}$. For instance, let $\widetilde{X}_{\alpha }\sim N(\widetilde{\mu }_{1-\alpha },\widetilde{\sigma ^2}_{1-\alpha })$, where $\widetilde{\mu }\in \mathcal {F}(\mathbb {R})$ and $\widetilde{\sigma ^2}\in \mathcal {F}((0,\infty ))$. Then, it is easy to verify that $F_{\widetilde{X}_{\alpha _2}}(x)\ge F_{\widetilde{X}_{\alpha _1}}(x)$ for all $x\in \mathbb {R}$ and for every $\alpha _1<\alpha _2$. So, $\widetilde{X}$ is said to be normally distributed with fuzzy parameters $\widetilde{\mu }$ and $\widetilde{\sigma ^2}$ if $\widetilde{X}_{\alpha }\sim N(\widetilde{\mu }_{1-\alpha },\widetilde{\sigma ^2}_{1-\alpha })$. As another example, assume that $\widetilde{X}_{\alpha }\sim exp(\widetilde{\lambda }_{1-\alpha })$ where $\widetilde{\lambda }\in \mathcal {F}(0,\infty )$. Then, one can observe that $F_{\widetilde{X}_{\alpha _2}}(x)\ge F_{\widetilde{X}_{\alpha _1}}(x)$ for all $x\in \mathbb {R}$ and for every $\alpha _1<\alpha _2$ where $F_{\lambda }(x)=1-e^{-\lambda x}$, $x>0$. So, $\widetilde{X}\sim exp(\widetilde{\lambda })$ if $\widetilde{X}_{\alpha }\sim exp(\widetilde{\lambda }_{1-\alpha })$ for all $\alpha \in [0,1]$.

Remark 5

Based on definition of a normal fuzzy random variable introduced by Wu (2005), a fuzzy random variable $\widetilde{X}$ is called normally distributed with fuzzy parameters $\widetilde{\mu }$ and $\widetilde{\sigma ^2}$ if and only if $\widetilde{X}^L_{\alpha }\sim N(\widetilde{\mu }^L_{\alpha },(\widetilde{\sigma ^2})^L_{\alpha })$ and $\widetilde{X}^U_{\alpha }\sim N(\widetilde{\mu }^U_{\alpha },(\widetilde{\sigma ^2})^U_{\alpha })$. However, it is easy to verify that “$\widetilde{X}^U_{\alpha }$ is not stochastically greater than $\widetilde{X}^L_{\alpha }$” for any $\alpha \in [0,1]$. But, as it noted in Remark 4, we modified the definition of a normal fuzzy random variable using the concepts of $\alpha$-optimistic values.

Now, based on a fuzzy random sample $\widetilde{\mathbf{X }}=(\widetilde{X}_1,\ldots ,\widetilde{X}_n)$, we are going to generalize the classical parametric tests for FRVs.

4 Testing hypotheses for FRVs

In this section, based on fuzzy random sample, we develop a procedure for testing statistical hypothesis. In fact, we wish to test the following hypotheses:

Definition 5

Let $\widetilde{X}$ be a FRV from a continuous parametric population with fuzzy parameter $\tilde{{\tau }}$. Then:

• 1. Any hypothesis of the form

  $$\begin{aligned} \widetilde{H}: \tilde{\tau }\asymp \tilde{\tau }_0 \equiv \widetilde{H} : (\tilde{\tau })_{\alpha }=(\tilde{\tau }_0)_{\alpha } \quad \text {for all}\ \alpha \in [0,1], \end{aligned}$$

  is called a simple hypothesis.

• 2. Any hypothesis of the form

  $$\begin{aligned} \widetilde{H} : \tilde{\tau }\succ \tilde{\tau }_0 \equiv \widetilde{H}: (\tilde{\tau })_{\alpha }>(\tilde{\tau }_0)_{\alpha } \quad \text {for all}\ \alpha \in [0,1], \end{aligned}$$

  is called a right one-sided hypothesis.

• 3. Any hypothesis of the form

  $$\begin{aligned} \widetilde{H}: \tilde{\tau }\prec \tilde{\tau }_0 \equiv \widetilde{H} : (\tilde{\tau })_{\alpha }<(\tilde{\tau }_0)_{\alpha } \quad \text {for all}\ \alpha \in [0,1], \end{aligned}$$

  is called a left one-sided hypothesis.

• 4. Any hypothesis of the form

  $$\begin{aligned} \widetilde{H} : \tilde{\tau }\ne \tilde{\tau }_0 \equiv \widetilde{H}: (\tilde{\tau })_{\alpha }\ne (\tilde{\tau }_0)_{\alpha } \quad \text {for all}\ \alpha \in [0,1], \end{aligned}$$

  is called to be a two-sided hypothesis.

In the following, by introducing some definitions and lemmas, we propose a procedure to investigate a hypothesis about the fuzzy parameters of the population. To do this, we will develop the concepts of fuzzy type-I and fuzzy type-II errors, fuzzy power and fuzzy p value for FRVs.

Definition 6

Let $\varphi$ be the classical test function for testing $H_0:\tau =\tau _0$ against one-sided $H_1:\tau >(<)\tau _0$ (or two-sided $H_1:\tau \ne \tau _0$) alternative hypothesis. For testing $\widetilde{H}_0 : \tilde{\tau }\asymp \tilde{\tau }_0$ against the alternative hypothesis introduced in Definition 5, the test statistic, based on a random sample $\widetilde{\mathbf{X }}$, is defined to be the fuzzy set $\widetilde{\varphi }(\widetilde{\mathbf{X }})$ with $\alpha$-cuts $\left[ (\widetilde{\varphi })^{L}_{\alpha }(\widetilde{\mathbf{X }}),(\widetilde{\varphi })^{U}_{\alpha }(\widetilde{\mathbf{X }})\right]$, where

$$\begin{aligned}&(\widetilde{\varphi })^{L}_{\alpha }(\widetilde{\mathbf{X }}) = \inf _{\beta \ge \alpha }(\varphi (\widetilde{\mathbf{X }}_{\beta })),\quad (\widetilde{\varphi })^{L}_{\alpha }(\widetilde{\mathbf{X }})= \sup _{\beta \ge \alpha }(\varphi (\widetilde{\mathbf{X }}_{\beta })), \end{aligned}$$

(5)

in which $\widetilde{\mathbf{X }}_{\beta }=((\widetilde{X}_1)_{\beta },(\widetilde{X}_2)_{\beta },\ldots ,(\widetilde{X}_n)_{\beta })$.

Definition 7

Let $\widetilde{\varphi }(\widetilde{\mathbf{X }})$ be the fuzzy test function for testing $\widetilde{H}_0 : \tilde{\tau }\asymp \tilde{\tau }_0$ against the alternative hypothesis introduced in Definition 5. The power of $\widetilde{\varphi }$ in $\widetilde{\tau }^{*}$ is defined to be the fuzzy set $\widetilde{\pi }_{\widetilde{\varphi }}(\widetilde{\tau }^{*})$ with $\alpha$-cuts $\left[ (\widetilde{\pi }_{\widetilde{\varphi }}(\widetilde{\tau }^{*})^{L}_{\alpha },(\widetilde{\pi }_{\widetilde{\varphi }}(\widetilde{\tau }^{*}))^{U}_{\alpha }\right]$, where

$$\begin{aligned} (\widetilde{\pi }_{\widetilde{\varphi }}(\widetilde{\tau }^{*}))^{L}_{\alpha }&= \inf _{\beta \ge \alpha }E_{H^{\beta }:\widetilde{\tau }_{\beta } =(\widetilde{\tau }^{*})_{\beta }}[\varphi (\widetilde{\mathbf{X }}_{\beta })], ~(\widetilde{\pi }_{\widetilde{\varphi }}(\widetilde{\tau }^{*}))^{U}_{\alpha } \nonumber \\&= \sup _{\beta \ge \alpha }E_{H^{\beta }:\widetilde{\tau }_{\beta } =(\widetilde{\tau }^{*})_{\beta }}[\varphi (\widetilde{\mathbf{X }}_{\beta })], \end{aligned}$$

and $\widetilde{\mathbf{X }}_{\beta }=((\widetilde{X}_1)_{\beta },(\widetilde{X}_2)_{\beta },\ldots ,(\widetilde{X}_n)_{\beta })$, $E_H[T]$ denotes the expectation of $T$ given $H$.

Lemma 3

Assume that $\widetilde{\mathbf{X }}=(\widetilde{X}_1,\ldots ,\widetilde{X}_n)$ is a fuzzy random sample from a continuous family of population $\{f_{\widetilde{\tau }}(x);x\in \mathbb {R}, \widetilde{\tau }\in \widetilde{\varTheta }\}$. If the family of density functions $\{f_{\tau }(x);x\in \mathbb {R}, \tau \in \varTheta \}$ has the MLR property in $T$ and $\varphi$ is a non-increasing function of $T,$ then $\widetilde{\pi }_{\widetilde{\varphi }}$ is a non-increasing function of $\widetilde{\tau },$ i.e.$,$ for every $\widetilde{\tau }_1,\widetilde{\tau }_2\in \widetilde{\varTheta }$ where $\widetilde{\tau }_1\prec \widetilde{\tau }_2,$ we have $\widetilde{\pi }_{\widetilde{\varphi }}(\widetilde{\tau }_1)\preceq \widetilde{\pi }_{\widetilde{\varphi }}(\widetilde{\tau }_2)$.

Proof

The proof is postponed to the Appendix.

Definition 8

Consider testing hypothesis

$$\begin{aligned} \widetilde{H}_0:\tilde{\tau }= \tilde{\tau }_0 \quad \hbox {versus}\quad \widetilde{H}_1:\tilde{\tau }= \tilde{\tau }_1, \end{aligned}$$

(6)

in which, it is assumed that $\tilde{\tau }_0\prec \tilde{\tau }_1$ or $\tilde{\tau }_0\succ \tilde{\tau }_1$. Then, $\widetilde{\pi }_{\widetilde{\varphi }}(\tilde{\tau }_0)$ and $1-\widetilde{\pi }_{\widetilde{\varphi }}(\tilde{\tau }_1)$ are called fuzzy type-I and fuzzy type-II errors denoted by $\widetilde{\alpha }_{\widetilde{\varphi }}$ and $\widetilde{\beta }_{\widetilde{\varphi }}$, respectively.

Here, similar to the approaches introduced in Hesamian and Taheri (2013), Hesamian and Chachi (2013), the fuzzy p value for testing hypotheses presented in Definition 5 is given as follows.

Definition 9

Consider testing the null hypothesis $\widetilde{H}_0 : \tilde{\tau }\asymp \tilde{\tau }_0$ versus the alternative one-sided hypothesis $\widetilde{H}_1: \tilde{\tau }(\succ )\prec \tilde{\tau }_0$ or two-sided hypothesis $\widetilde{H}_1: \tilde{\tau }\ne \tilde{\tau }_0$. The fuzzy p value is defined to be the fuzzy set $\widetilde{p}$ with $\alpha$-cuts $\left[ \widetilde{p}^{L}_{\alpha },\widetilde{p}^{U}_{\alpha }\right]$, where

$$\begin{aligned} \widetilde{p}^{L}_{\alpha }=\inf _{\beta \ge \alpha }\inf \{\delta \in [0,1] :T(\widetilde{\mathbf{x }}_{\beta })\in \mathbf C ^{\beta }_{\delta }\}, \end{aligned}$$

and

$$\begin{aligned} \widetilde{p}^{U}_{\alpha }=\sup _{\beta \ge \alpha }\inf \{\delta \in [0,1] :T(\widetilde{\mathbf{x }}_{\beta })\in \mathbf C ^{\beta }_{\delta }\}, \end{aligned}$$

where $T$ denotes the classical test statistic and $\mathbf C ^{\beta }_{\delta }$ is the related critical region to test the null hypothesis $H^{\beta }_0 : \widetilde{\tau }_{\beta }=(\widetilde{\tau }_0)_{\beta }$ versus the alternative one-sided hypothesis $H^{\beta }_1: \widetilde{\tau }_{\beta }>(<)(\widetilde{\tau }_0)_{\beta }$ (or two-sided hypothesis $H^{\beta }_1: \widetilde{\tau }_{\beta }\ne (\widetilde{\tau }_0)_{\beta }$) based on the random sample $\widetilde{\mathbf{X }}_{\beta }$.

Finally, in the problem of testing a hypothesis based on the fuzzy random sample $\widetilde{\mathbf{X }}=(\widetilde{X}_1,\ldots ,\widetilde{X}_n)$, we propose the following definition of a fuzzy test function:

Definition 10

The fuzzy-valued function $\widetilde{\varphi }:\mathcal{F}^n({\mathbb {R}})\rightarrow \mathcal{F}(\{0,1\})$ is called a fuzzy test whenever $\widetilde{\psi }(\widetilde{\mathbf{X }})$, as a fuzzy set on $\{0,1\}$, shows the degrees of rejection and acceptance of the hypothesis $H_0$ for any $\widetilde{\mathbf{X }}$. Here, “0” and “1” stand for acceptance and rejection of the null hypothesis, respectively, and $\mathcal{F}(\{0,1\})$ is the class of all fuzzy sets on $\{0,1\}$.

Definition 11

For the problem of testing hypotheses $\widetilde{H}_0:\widetilde{\tau }\asymp \widetilde{\tau }_0$ where $\widetilde{\tau }_0 \in \mathcal {F}(\varTheta )$, based on the fuzzy random sample $\widetilde{\mathbf{X }}=(\widetilde{X}_1,\ldots ,\widetilde{X}_n)$ and at a given significance level $\delta \in (0,1]$, the fuzzy test is defined to be the following fuzzy set

$$\begin{aligned} \widetilde{\psi }(\widetilde{\mathbf{X }})=\left\{ \frac{\mathrm{Cr}(\widetilde{p}\ge \delta )}{0},\frac{\mathrm{Cr}(\widetilde{p}< \delta ) }{1}\right\} . \end{aligned}$$

(7)

This test accepts the null hypothesis with the credibility degree of $\mathrm{Cr}(\widetilde{p}\ge \delta )$ (degree of acceptance), and rejects it with the credibility degree of $\mathrm{Cr}(\widetilde{p}< \delta )=1-\mathrm{Cr}(\widetilde{p}\ge \delta )$ (degree of rejection).

4.1 Testing hypotheses about the fuzzy parameters of a normal FRV

A particular class of parametric statistical testing hypotheses is the testing hypotheses about the parameters of a normal population. Here, we are going to apply the proposed method in the previous section for a normal FRV, i.e., assume that $\widetilde{\mathbf{X }}=(\widetilde{X}_1,\ldots ,\widetilde{X}_n)$ be a random sample from a normal population and $\widetilde{\varTheta }=\mathcal{F}(\varTheta )$ be the class of all fuzzy numbers on the parameter space $\varTheta =\{(\theta ,\sigma ^2):\theta \in \mathbb {R},\sigma$ $\in (0,\infty )\}$.

Remark 6

Consider testing $\widetilde{H}_0: \tilde{\theta }\asymp \tilde{\theta }_0$ for a normal FRV where $\widetilde{\sigma }^2$ is known. Therefore, the $\alpha$-cuts of the fuzzy p value defined in Definition 9 are reduced as follows

• 1. for testing alternative hypothesis $\widetilde{H}_1: \tilde{\theta }\succ \tilde{\theta }_0$,

  $$\begin{aligned}&\widetilde{p}^{L}_{\alpha }=\inf _{\beta \ge \alpha }\left[ 1-\varPhi \left( \frac{\sqrt{n}(\overline{\widetilde{x}}_{\beta } -(\widetilde{\theta }_{0})_{1-\beta })}{\sqrt{\widetilde{\sigma }^{2}_{1-\beta }}}\right) \right] ,\\&\widetilde{p}^{U}_{\alpha }=\sup _{\beta \ge \alpha }\left[ 1- \varPhi \left( \frac{\sqrt{n}(\overline{\widetilde{x}}_{\beta } -(\widetilde{\theta }_{0})_{1-\beta })}{\sqrt{\widetilde{\sigma }^{2}_{1-\beta }}}\right) \right] . \end{aligned}$$

• 2. for testing alternative hypothesis $\widetilde{H}_1: \tilde{\theta }\prec \tilde{\theta }_0$,

  $$\begin{aligned}&\widetilde{p}^{L}_{\alpha } = \inf _{\beta \ge \alpha }\varPhi \left( \frac{\sqrt{n}(\overline{\widetilde{x}}_{\beta } -(\widetilde{\theta }_{0})_{1-\beta })}{\sqrt{\widetilde{\sigma }^{2}_{1-\beta }}}\right) ,\\&\widetilde{p}^{U}_{\alpha } = \sup _{\beta \ge \alpha }\varPhi \left( \frac{\sqrt{n}(\overline{\widetilde{x}}_{1-\beta } -(\widetilde{\theta }_{0})_{1-\beta })}{\sqrt{\widetilde{\sigma }^{2}_{1-\beta }}}\right) . \end{aligned}$$

• 3. for testing alternative hypothesis $\widetilde{H}_1: \tilde{\theta }\ne \tilde{\theta }_0$,

  $$\begin{aligned}&\widetilde{p}^{L}_{\alpha }=2\inf _{\beta \ge \alpha }\varPhi \left( -\sqrt{n}|\frac{\overline{\widetilde{x}}_{\beta } -(\widetilde{\theta }_{0})_{1-\beta }}{\sqrt{\widetilde{\sigma }^{2}_{1-\beta }}}|\right) ,\\&\widetilde{p}^{U}_{\alpha }=2\sup _{\beta \ge \alpha } \varPhi \left( -\sqrt{n}|\frac{\overline{\widetilde{x}}_{\beta } -(\widetilde{\theta }_{0})_{1-\beta }}{\sqrt{\widetilde{\sigma }^{2}_{1-\beta }}}|\right) , \end{aligned}$$

  where $\varPhi$ denotes the standard normal cumulative distribution function and $\overline{\widetilde{x}}_{\beta }=1/n\sum ^{n}_{i=1}{(\widetilde{x}_i)_{\beta }}$.

Now assume that $\widetilde{\sigma }^2$ is unknown. In this case, the $\alpha$-cuts of the fuzzy p value are given as follows

• 1. for testing alternative hypothesis $\widetilde{H}_1: \tilde{\theta }\succ \tilde{\theta }_0$,

  $$\begin{aligned}&\widetilde{p}^{L}_{\alpha }= \inf _{\beta \ge \alpha }\mathbf P \left( \mathbf t _{n-1}\ge \frac{\sqrt{n}(\overline{\widetilde{x}}_{\beta } -(\widetilde{\theta }_{0})_{1-\beta })}{\sqrt{\widetilde{s}^{2}_{1-\beta }}}\right) ,\\&\widetilde{p}^{U}_{\alpha }= \sup _{\beta \ge \alpha }\mathbf P \left( \mathbf t _{n-1}\ge \frac{\sqrt{n}(\overline{\widetilde{x}}_{\beta } -(\widetilde{\theta }_{0})_{1-\beta })}{\sqrt{\widetilde{s}^{2}_{1-\beta }}}\right) . \end{aligned}$$

• 2. for testing alternative hypothesis $\widetilde{H}_1: \tilde{\theta }\prec \tilde{\theta }_0$,

  $$\begin{aligned}&\widetilde{p}^{L}_{\alpha }= \inf _{\beta \ge \alpha }\mathbf P \left( \mathbf t _{n-1}\le \frac{\sqrt{n}(\overline{\widetilde{x}}_{\beta } -(\widetilde{\theta }_{0})_{1-\beta })}{\sqrt{\widetilde{s}^{2}_{1-\beta }}}\right) ,\\&\widetilde{p}^{U}_{\alpha } = \sup _{\beta \ge \alpha }\mathbf P \left( \mathbf t _{n-1}\le \frac{\sqrt{n}(\overline{\widetilde{x}}_{\beta } -(\widetilde{\theta }_{0})_{1-\beta })}{\sqrt{\widetilde{s}^{2}_{1-\beta }}}\right) . \end{aligned}$$

• 3. for testing alternative hypothesis $\widetilde{H}_1: \tilde{\theta }\ne \tilde{\theta }_0$ ,

  $$\begin{aligned}&\widetilde{p}^{L}_{\alpha } = 2\inf _{\beta \ge \alpha }\mathbf P \left( \mathbf t _{n-1}\le -\sqrt{n}|\frac{\overline{\widetilde{x}}_{\beta } -(\widetilde{\theta }_{0})_{1-\beta }}{\sqrt{\widetilde{s}^{2}_{1-\beta }}}|\right) ,\\&\widetilde{p}^{U}_{\alpha } = 2\sup _{\beta \ge \alpha }\mathbf P \left( \mathbf t _{n-1}\le -\sqrt{n}|\frac{\overline{\widetilde{x}}_{\beta } -(\widetilde{\theta }_{0})_{1-\beta }}{\sqrt{\widetilde{s}^{2}_{1-\beta }}}|\right) , \end{aligned}$$

  where $\mathbf t _{n-1}$ denotes the $\mathbf t$-student distribution with degree of freedom $n-1$ and $\widetilde{s}^2_{\beta }=\frac{1}{n-1}\sum ^{n}_{i=1}{((\widetilde{x}_i)_{\beta } - \overline{\widetilde{x}}_{\beta })^2}$.

Remark 7

Here, we describe calculating the fuzzy power to test about $\widetilde{\mu }$ for a normal FRV. We explain the method for the case of testing $\widetilde{H}_0:\tilde{\theta }= \tilde{\theta }_0$ versus $\widetilde{H}_1:\tilde{\theta }\succ \tilde{\theta }_0$ (the other cases can be obtained similarly). First, assume that $\widetilde{\sigma }^2$ is known. From Definition 7, it is easy to verify that the $\alpha$-cuts of the fuzzy power at $\widetilde{\theta }^{*}(\succ \tilde{\theta }_0)$ are obtain as follows

$$\begin{aligned}&(\widetilde{\pi }_{\widetilde{\varphi }}(\widetilde{\theta }^{*}))^{L}_{\alpha }=\inf _{\beta \ge \alpha }\left[ 1-\varPhi \left( \sqrt{n}\frac{(c_{\beta } -(\widetilde{\theta }^{*})_{1-\beta })}{\sqrt{\widetilde{\sigma }^2_{1-\beta }}}\right) \right] ,\\&(\widetilde{\pi }_{\widetilde{\varphi }}(\widetilde{\theta }^{*}))^{U}_{\alpha } =\sup _{\beta \ge \alpha }\left[ 1-\varPhi \left( \sqrt{n}\frac{(c_{\beta } -(\widetilde{\theta }^{*})_{1-\beta })}{\sqrt{\widetilde{\sigma }^2_{1-\beta }}}\right) \right] , \end{aligned}$$

where $c_{\beta }=(\widetilde{\theta }_0)_{1-\beta }+z_{1-\frac{\delta }{2}} \frac{\sqrt{\widetilde{\sigma }^2_{1-\beta }}}{\sqrt{n}}$.

Now if $\widetilde{\sigma }^2$ is unknown then, for testing $\widetilde{H}_0:\tilde{\theta }= \tilde{\theta }_0$ versus $\widetilde{H}_1:\tilde{\theta }\succ \tilde{\theta }_0$, the $\alpha$-cuts of $\widetilde{\pi }_{\widetilde{\varphi }}$ at $\widetilde{\theta }^{*}(\succ \tilde{\theta }_0)$ are given by

$$\begin{aligned}&(\widetilde{\pi }_{\widetilde{\varphi }}(\widetilde{\theta }^{*}))^{L}_{\alpha } =\inf _{\beta \ge \alpha }\left[ 1-\mathbf P \left( \mathbf t _{n-1}\le \sqrt{n}\frac{(c_{\beta } -(\widetilde{\theta }^{*})_{1-\beta })}{\sqrt{\widetilde{s}^{2}_{1-\beta }}}\right) \right] ,\\&(\widetilde{\pi }_{\varphi }(\widetilde{\theta }^{*}))^{U}_{\alpha }= \sup _{\beta \ge \alpha }\left[ 1-\mathbf P \left( \mathbf t _{n-1}\le \sqrt{n}\frac{(c_{\beta }-(\widetilde{\theta }^{*})_{1-\beta })}{\sqrt{\widetilde{s}^{2}_{1-\beta }}}\right) \right] , \end{aligned}$$

where $c_{\beta }=(\widetilde{\theta }_0)_{1-\beta }+\mathbf t _{n-1,\frac{\delta }{2}}\frac{\sqrt{\widetilde{s}^{2}_{1-\beta }}}{\sqrt{n}}$.

Remark 8

Now, consider testing the null hypothesis $\widetilde{H}_0: \tilde{\sigma }^2\asymp \tilde{\sigma }^2_0$. From Definition 9, the $\alpha$-cuts of the fuzzy p value are given by $\left[ \widetilde{p}^{L}_{\alpha },\widetilde{p}^{U}_{\alpha }\right]$, where

• 1. for testing alternative hypothesis $\widetilde{H}_1 :\tilde{\sigma }^2\succ \tilde{\sigma }^{2}_0$,

  $$\begin{aligned} \widetilde{p}^{L}_{\alpha }&= \inf _{\beta \ge \alpha }\mathbf P _{H^{\beta }_0: \widetilde{\sigma }^{2}_{\beta } = (\widetilde{\sigma }^{2}_{0})_{\beta }} \left( \widetilde{S}^{2}_{\beta }\ge \widetilde{s}^{2}_{\beta }\right) \\&= \inf _{\beta \ge \alpha }\mathbf P \left( \mathcal {\chi }^{2}_{n-1}\ge \frac{(n-1)\widetilde{s}^{2}_{\beta }}{(\widetilde{\sigma }^{2}_{0})_{1-\beta }}\right) ,\\ \widetilde{p}^{U}_{\alpha }&= \sup _{\beta \ge \alpha }\mathbf P _{H^{\beta }_0:\widetilde{\sigma }^{2}_{\beta }= (\widetilde{\sigma }^{2}_{0})_{\beta }}\left( \widetilde{S}^{2}_{\beta }\ge \widetilde{s}^{2}_{\beta }\right) ,\\&= \sup _{\beta \ge \alpha }\mathbf P \left( \mathcal {\chi }^{2}_{n-1}\ge \frac{(n-1)\widetilde{s}^{2}_{\beta }}{(\widetilde{\sigma }^{2}_{0})_{1-\beta }}\right) . \end{aligned}$$

• 2. for testing alternative hypothesis $\widetilde{H}_1 :\tilde{\sigma }^2\prec \tilde{\sigma }^{2}_0$,

  $$\begin{aligned} \widetilde{p}^{L}_{\alpha }&= \inf _{\beta \ge \alpha }\mathbf P _{H^{\beta }_0:\widetilde{\sigma }^{2}_{\beta }= (\widetilde{\sigma }^{2}_{0})_{\beta }}\left( \widetilde{S}^{2}_{\beta }\le \widetilde{s}^{2}_{\beta }\right) ,\\&= \inf _{\beta \ge \alpha }\mathbf P \left( \mathcal {\chi }^{2}_{n-1}\le \frac{(n-1)\widetilde{s}^{2}_{\beta }}{(\widetilde{\sigma }^{2}_{0})_{1-\beta }}\right) ,\\ \widetilde{p}^{U}_{\alpha }&= \sup _{\beta \ge \alpha }\mathbf P _{H^{\beta }_0:\widetilde{\sigma }^{2}_{\beta } = (\widetilde{\sigma }^{2}_{0})_{\beta }}\left( \widetilde{S}^{2}_{\beta }\le \widetilde{s}^{2}_{\beta }\right) ,\\&= \sup _{\beta \ge \alpha }\mathbf P \left( \mathcal {\chi }^{2}_{n-1}\le \frac{(n-1)\widetilde{s}^{2}_{\beta }}{(\widetilde{\sigma }^{2}_{0})_{1-\beta }}\right) . \end{aligned}$$

• 3. for testing alternative hypothesis $\widetilde{H}_1 :\tilde{\sigma }^2\ne \tilde{\sigma }^{2}_0$,

  $$\begin{aligned} \widetilde{p}^{L}_{\alpha }&= 2\inf _{\beta \ge \alpha }\min \left\{ \mathbf{P }_{H^{\beta }_0:\widetilde{\sigma }^{2}_{\beta } =(\widetilde{\sigma }^{2}_{0})_{\beta }}(\widetilde{S}^{2}_{\beta }\le \widetilde{s}^{2}_{\beta }),\right. \\&\quad \left. \mathbf{P }_{H^{\beta }_0:\widetilde{\sigma }^{2}_{\beta } = (\widetilde{\sigma }^{2}_{0})_{\beta }}(\widetilde{S}^{2}_{\beta }\ge \widetilde{s}^{2}_{\beta })\right\} ,\\&= 2\inf _{\beta \ge \alpha }\min \left\{ \mathbf{P } \left( \mathcal {\chi }^{2}_{n-1}\le \frac{(n-1)\widetilde{s}^{2}_{\beta }}{(\widetilde{\sigma }^{2}_{0})_{1-\beta }}\right) ,\right. \\&\quad \left. \mathbf{P } \left( \mathcal {\chi }^{2}_{n-1}\ge \frac{(n-1)\widetilde{s}^{2}_{\beta }}{(\widetilde{\sigma }^{2}_{0})_{1-\beta }}\right) \right\} ,\\ \widetilde{p}^{U}_{\alpha }&= 2\sup _{\beta \ge \alpha }\min \left\{ \mathbf{P }_{H^{\beta }_0:\widetilde{\sigma }^{2}_{\beta } =(\widetilde{\sigma }^{2}_{0})_{\beta }}(\widetilde{S}^{2}_{\beta }\le \widetilde{s}^{2}_{\beta }),\right. \\&\quad \left. \mathbf{P }_{H^{\beta }_0:\widetilde{\sigma }^{2}_{\beta } = (\widetilde{\sigma }^{2}_{0})_{\beta }}(\widetilde{S}^{2}_{\beta }\ge \widetilde{s}^{2}_{\beta }) \right\} ,\\&= 2\sup _{\beta \ge \alpha }\min \left\{ \mathbf{P } \left( \mathcal {\chi }^{2}_{n-1}\le \frac{(n-1)\widetilde{s}^{2}_{\beta }}{(\widetilde{\sigma }^{2}_{0})_{1-\beta }}\right) ,\right. \\&\quad \left. \mathbf{P } \left( \mathcal {\chi }^{2}_{n-1}\ge \frac{(n-1)\widetilde{s}^{2}_{\beta }}{(\widetilde{\sigma }^{2}_{0})_{1-\beta }}\right) \right\} , \end{aligned}$$

  where $\mathcal {\chi }^{2}_{n-1}$ denotes the Chi-square distribution with degree of freedom $n-1$.

By a similar manner described by Remarks 6–8, we can obtain the fuzzy power and fuzzy p value for testing about $\widetilde{\sigma ^2}$ for a normal FRV.

Remark 9

It should be mentioned that, based on Remark 5, all definitions of hypotheses given in this paper are just a rewritten version of Wu’s ones (Wu 2005).

5 Numerical example

In this section, we provide a numerical example to clarify the discussions in this paper and give the possible application of the proposed method for normal FRVs.

Example 2

(Elsherif et al. 2009) Based on a random sample of the received signal from a target, assume we have fuzzy observations $\widetilde{\mathbf{x }}=(\widetilde{x}_1,\widetilde{x}_2,\ldots ,\widetilde{x}_{25})$ (as shown in Table 1) measured in nanowatt which is approximately normally distributed $N(\widetilde{\theta },\widetilde{\sigma }^2)$. We wish to test the following hypothesis:

$$\begin{aligned} \left\{ \begin{array}{ll} \widetilde{H}_0 : &{} \tilde{\theta }\asymp \tilde{\theta }_0\asymp (1.35, 1.50, 1.80)_T , \\ \widetilde{H}_1 : &{} \tilde{\theta }\prec \widetilde{\theta }_0. \end{array} \right. \end{aligned}$$

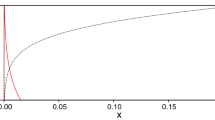
Applying the procedure proposed in Sect. 4.1, using Remark 6, the fuzzy p value is derived point by point and its membership function is shown in Fig. 1. This membership function can be interpreted as “about $0.075$”. Therefore, at level of $\delta =0.05$, the fuzzy test for testing $\widetilde{H}_0 : \tilde{\theta }\asymp (1.35, 1.50, 1.80)_T$ is obtained as $\widetilde{\psi }(\widetilde{\mathbf{X }}) = \left\{ \frac{ 0.905 }{0},\frac{ 0.095 }{1} \right\}$. So, with respect to the observed fuzzy observations and at significance level of $\delta =0.05$, the null hypothesis $\widetilde{H}_0:\tilde{\theta }\asymp (1.35, 1.50, 1.80)_T$ is accepted with a degree of $0.905$ and it is rejected with a degree of $0.095$. Such a result may be interpreted as “we absolutely tend to accept $\widetilde{H}_0$”. In addition, based on Remark 7, the membership of the fuzzy power at $\tilde{\theta }^{*} \asymp (0.50, 0.70, 0.80)_T$ is shown in Fig. 2 which is interpreted as “about $0.999$”.

Now, suppose that we want to test the following hypotheses about $\widetilde{\sigma ^{2}}$:

$$\begin{aligned} \left\{ \begin{array}{ll} \widetilde{H}_0 : &{} \widetilde{\sigma }^2\asymp \widetilde{\sigma }^{2}_{0}\asymp (0.30, 0.50 ,0.70)_T , \\ \widetilde{H}_1 : &{} \widetilde{\sigma }^2\succ \widetilde{\sigma }^{2}_{0}. \end{array} \right. \end{aligned}$$

From Remark 6, the membership function of the fuzzy p value is obtained as “about $0.83$” whose membership function is shown in Fig. 3. Therefore, the fuzzy test to test $\widetilde{H}_0 : \widetilde{\sigma }^2\asymp (0.30, 0.50 ,0.70)_T$ versus $\widetilde{H}_1 : \widetilde{\sigma }^2\succ \widetilde{\sigma }^{2}_{0}$, at significance level of $\delta =0.05$, is obtained as $\widetilde{\psi }(\widetilde{\mathbf{X }}) = \left\{ \frac{0.991}{0},\frac{0.009}{1} \right\}$. In such a case, therefore, we are strongly convinced to accept $\widetilde{H}_0 : \widetilde{\sigma }^2\asymp (0.30, 0.50 ,0.70)_T$, at significance level of $\delta =0.05$.

Fig. 1

The membership function of the fuzzy p value and the significance level in Example 2 for testing $\widetilde{H}_0:\ \tilde{\theta }\asymp (1.35, 1.50, 1.80)_T$ against $\widetilde{H}_1:\ \tilde{\theta }\prec (1.35, 1.50, 1.80)_T$

Fig. 2

The membership function of the fuzzy power at $\tilde{\theta }^{*} \asymp (0.50, 0.70, 0.80)_T$ in Example 2

Fig. 3

The membership function of the fuzzy p value and the significance level in Example 2 for testing $\widetilde{H}_0 : \widetilde{\sigma }^2 \asymp (0.30, 0.50 ,0.70)_T$ against $\widetilde{H}_1 : \widetilde{\sigma }^2\succ (0.30, 0.50 ,0.70)_T$

Table 1 The observed fuzzy random sample in Example 2

6 A comparison study

It should be mentioned that Akbari and Rezaei (2009, 2010) extended the classical approach for testing statistical hypotheses about the (crisp) mean or variance of a normal distribution by introducing some fuzzy numbers to interpret the sentences “larger than”, “smaller than” or “not equal” for population’s parameters based on imprecise observations. Parchami et al. (2010) defined an extension of fuzzy p value for a crisp random sample of a normal distribution to test imprecisely hypothesis test about the mean. Arefi and Taheri (2011) extended the classical critical region for testing fuzzy hypothesis about the parameters of the classical normal distribution based on fuzzy data. Wu (2005) considered the problem of hypotheses test with fuzzy data. Based on a concept of fuzzy random variable, first he defined the fuzzy mean of the normal distribution. Then, based on a proposed ranking method, he defined the hypotheses about the population’s fuzzy mean. He considered two cases: (1) the variance of the population is known, (2) the variance of the population is unknown. Finally, he introduced a fuzzy test based on the classical critical region. However, for both cases, he assigned a crisp number into the structure of testing hypothesis’s method: for the case (1) the variance of the population is considered as a crisp number and for the case (2) the variance of the fuzzy sample is calculated based on core of the fuzzy data as a crisp number. As we observe, in all above methods, the variance of the normal population is considered as a crisp number. However, for testing fuzzy hypothesis about mean of a normal population, it is reasonable that the variance of the population is also considered as a imprecise value. So, it may be an advantage of our method with respect to above-mentioned methods. Geyer and Meeden considered the problem of the classical optimal hypothesis tests for the binomial distribution (in general for discrete data with crisp parameter) using an interval estimation of a binomial proportion (Geyer and Meeden 2005). They introduced the notion of fuzzy confidence intervals by inverting families of randomized tests. Then, they introduce a notion of fuzzy p value in which it is only a function of the parameters of the model. Finally, they provided a unified description of fuzzy confidence interval, fuzzy p values and fuzzy decision. However, their proposed method is not a fuzzy method in general, since this approach does not consider the imprecise information about the model such as imprecise observations or imprecise hypotheses and it does not lead to a fuzzy decision. Viertl (2011) and Filzmoser and Viertl (2004) also extend a concept of fuzzy p value when the observations are fuzzy and hypotheses are crisp. Arnold (1996, 1998) proposed a method for testing fuzzy hypotheses about the population parameter with crisp data. He provided some definitions for the probability of type-I and type-II errors and presented the best test for the one-parameter exponential family.

As it is observed, in all above-proposed methods for testing statistical hypothesis, at least one of the essential population’s information such as data, hypothesis or population’s parameters play a crisp role in the structure of testing procedure. While, by restructuring the concept of fuzzy random variable, we involved the population’s information including: fuzzy data and fuzzy parameters into the hypothesis test, type-I error (or type-II error) and power of test. Finally, we obtained a fuzzy test to make decision for accepting or rejecting the fuzzy hypothesis of interest about the fuzzy parameters.

7 Conclusions

This paper proposes a method for testing hypotheses about the fuzzy parameters of a fuzzy random variable. In this approach, we reconstruct a well-known concept of a fuzzy random variable using the concept of $\alpha$-optimistic values. Then, we extended the concepts of the fuzzy power test and fuzzy p value. Finally, based on the credibility index, to compare the observed fuzzy p value and the crisp significance level, the fuzzy hypothesis of interest can be accepted or rejected with degrees of conviction between $0$ and $1$.

Although we focused on testing hypotheses about the parameters of a normal fuzzy random variable, the proposed method is general and it can be applied for other kinds of fuzzy random variables as well. Moreover, it can be applied for other kind of testing hypothesis such as comparing two independent fuzzy random variables of two populations, the one-way or two-way analysis of variance and non-parametric approaches including testing hypothesis. However, the proposed method can be applied only for fuzzy numbers involved in a problem of statistical hypothesis testing. Moreover, the topic of testing hypothesis for fuzzy parameters of a fuzzy random variable can be extended to the case where the level of significance is given by a fuzzy number, too. To do this, one can easily apply the credibility index for comparing two fuzzy numbers into the decision making.

Appendix: Proof of the main results

This appendix provides the mathematical proofs of the theoretical results in our paper.

Proof of Theorem 1

• (i) Let $g_{\widetilde{A}}:{\mathbb {R}}\rightarrow [0,1]$ be given by $g_{\widetilde{A}}(x)=\mathrm{Cr}(\widetilde{A}\ge x)$. Then

  $$\begin{aligned} \widetilde{A}_{\alpha }=\sup \{x\in \widetilde{A}[0]\mid g_{\widetilde{A}}(x)\ge \alpha \}. \end{aligned}$$

  First, let $\alpha \in [0,0.5)$. Since

  $$\begin{aligned} g_{\widetilde{A}}\big (\widetilde{A}_{2\alpha }^U\big )&= \frac{1}{2}\left( \sup _{y\in [\widetilde{A}_{2\alpha }^U,+\infty )}\mu _{\widetilde{A}}(y)+1\sup _{(-\infty , \widetilde{A}_{2\alpha }^U)}\mu _{\widetilde{A}}(y)\right) \\&= \frac{1}{2}(2\alpha )=\alpha , \end{aligned}$$

  we have $\widetilde{A}_{\alpha }\ge \widetilde{A}_{2\alpha }^U$. On the other hand, for each $z>\widetilde{A}_{2\alpha }^U$, $\sup _{y\in [z,+\infty )}\mu _{\widetilde{A}}(y)=\widetilde{A}(z)$ and $\sup _{y\in (-\infty ,z)}\mu _{\widetilde{A}}(y)=1$. Therefore,

  $$\begin{aligned} g_{\widetilde{A}}(z)&= \mathrm{Cr}(\widetilde{A}\ge z)\\&= \frac{1}{2}\left( \sup _{y\in [z,+\infty )}\mu _{\widetilde{A}}(y)+1 -\sup _{y\in (-\infty ,z)}\mu _{\widetilde{A}}(y)\right) \\&= \frac{1}{2}\widetilde{A}(z)<\alpha . \end{aligned}$$

  Hence, $\{x\in {\mathbb {R}}\mid g_{\widetilde{A}}(x)\ge \alpha \}\cap (\widetilde{A}_{2\alpha }^U,+\infty )=\emptyset$, which by the previous part implies that $\widetilde{A}_{\alpha }=\widetilde{A}_{2\alpha }^U$. Now suppose $\alpha \in [0.5,1]$ and let $x_0:=\sup \{x\le x^*\mid \mu _{\widetilde{A}}(x)\le 2(1-\alpha )\}$. Then, $\mu _{\widetilde{A}}(x)\le 2(1-\alpha )$, for all $x<x_0$. Hence,

  $$\begin{aligned} \sup _{y\in [x_0,+\infty )}\mu _{\widetilde{A}}(y)\!=\!1\quad \text{ and }\quad \sup _{y\in (-\infty ,x_0)}\mu _{\widetilde{A}}(y)\!\le \! 2(1\!-\!\alpha ). \end{aligned}$$

  Therefore, $g_{\widetilde{A}}(x_0)\ge \alpha$ which implies that $\phi _{\widetilde{A}}(\alpha )\ge x_0$. On the other hand, for $x>x_0$, since $\mu _{\widetilde{A}}(x)>2(1-\alpha )$, we have

  $$\begin{aligned} g_{\widetilde{A}}(x)&= \frac{1}{2}\left( \sup _{y\in [x,+\infty )}\mu _{\widetilde{A}}(y)+1-\sup _{y\in (-\infty ,x)}\mu _{\widetilde{A}}(y)\right) \\&\ge \frac{1}{2}\big (1+1-\mu _{\widetilde{A}}(x)\big )<\alpha . \end{aligned}$$

  Hence, $\phi _{\widetilde{A}}(\alpha )=x_0$. Note that, according to what has been proved, $\phi _{\widetilde{A}}(0.5)=\sup \{x\le x^*\mid \mu _{\widetilde{A}}(x)\le 1\}=x^*=\widetilde{A}_{2(0.5)}^U$. Thus, the law of $\phi _{\widetilde{A}}$ can be written in the following form.

  $$\begin{aligned}&\forall \alpha \in [0,1],\quad \phi _{\widetilde{A}}(\alpha )\nonumber \\&\quad =\left\{ \begin{array}{ll} \widetilde{A}_{2\alpha }^U &{}\quad 0\le \alpha \le 0.5, \\ \sup \{x\le x^*\mid \mu _{\widetilde{A}}(x)\le 2(1\!-\!\alpha )\} &{}\quad 0.5\!\le \!\alpha \le 1. \end{array}\right. \nonumber \\ \end{aligned}$$

  (8)

• (ii) It is clear that $\phi _{\widetilde{A}}$ is decreasing on $[0,1]$. By the previous part, since for each $\alpha \in [0,0.5]$, $\phi _{\widetilde{A}}(\alpha )=\widetilde{A}_{2\alpha }^U$, using Lemma 1, $\phi _{\widetilde{A}}$ is left continuous on $[0,0.5]$.

For $\alpha \in (0.5,1]$, suppose $\{\alpha _n\}_{n\in \mathbb N}$ is an increasing sequence in $(0.5,1]$ with $\alpha _n\rightarrow \alpha$. First, suppose that $\phi _{\widetilde{A}}(\alpha )=x^*$. Then, for each $x<x^*$, $\mu _{\widetilde{A}}(x)\le 2(1-\alpha )\le 2(1-\alpha _n)$. Hence $\phi _{\widetilde{A}}(\alpha _n)\ge x^*$, for all $n\in \mathbb N$. On the other hand, since $\alpha _n>0.5$, we have $\phi _{\widetilde{A}}(\alpha _n)\le x^*$. Combining the two arguments, we obtain $\phi _{\widetilde{A}}(\alpha _n)=x^*$, for all $n\in \mathbb N$. Hence, in this case $\phi _{\widetilde{A}}(\alpha _n)=x^*\rightarrow \phi _{\widetilde{A}}(\alpha )=x^*$. Now suppose $\phi _{\widetilde{A}}\alpha )<x^*$. Then, for each $y\in {\mathbb {R}}$ with $\phi _{\widetilde{A}}(\alpha )<y<x^*$, $\mu _{\widetilde{A}}(y)>2(1-\alpha )$. Therefore, $\mu _{\widetilde{A}}(y)>2(1-\alpha _n)$, for large values of $n\in \mathbb N$. This implies that $\phi _{\widetilde{A}}(\alpha _n)\le y$. Hence $\phi _{\widetilde{A}}(\alpha _n)\rightarrow \phi _{\widetilde{A}}(\alpha )$. This completes the proof of the left continuity of $\phi _{\widetilde{A}}$ on $(0.5,1]$.

Proof of Lemma 2

First suppose $\alpha _0\in (0.5,1]$ is a point of continuity of $\psi _{\widetilde{A}}$. Let $x_0:=\phi _{\widetilde{A}}(\alpha _0)$. Then $\widetilde{A}_{2(1-\alpha _0)}^L\le x_0$. If $\widetilde{A}_{2(1-\alpha _0)}^L< x_0$ then $\mu _{\widetilde{A}}(x)=2(1-\alpha _0)$, for all $x\in [\widetilde{A}_{2(1-\alpha _0)}^L, x_0)$. In this case for each $\alpha <\alpha _0$, since $2(1-\alpha )>2(1-\alpha _0)$, we have $\widetilde{A}_{2(1-\alpha )}^L\ge x_0$ which contradicts the assumption of continuity of $\psi _{\widetilde{A}}$ at $\alpha _0$. Hence

$$\begin{aligned} \psi _{\widetilde{A}}(\alpha _0)=\widetilde{A}_{2(1-\alpha _0)}^L=x_0=\phi _{\widetilde{A}}(\alpha _0). \end{aligned}$$

Suppose, on the contrary, that $\alpha _0$ is a point of discontinuity of $\psi _{\widetilde{A}}$. Then, there $\epsilon _0>0$ such that for each $n\in \mathbb N$, one can find $\alpha _n\in (\alpha _0-\frac{1}{n},\alpha )$ with $\psi _{\widetilde{A}}(\alpha _n)>\psi _{\widetilde{A}}(\alpha _0)+\epsilon _0$. With out loss of generality, we may assume that $\{\alpha _n\}_{n\in \mathbb N}$ is an increasing sequence. Since $\psi _{\widetilde{A}}$ is a monotonic function, there exists an increasing sequence $\{\alpha '_n\}_{n\in \mathbb N}$ converging to $\alpha _0$ such that $\alpha '_n\le \alpha _n$, for each $n\in \mathbb N$, and $\psi _{\widetilde{A}}$ is continuous on the set $\{\alpha '_n\mid n\in \mathbb N\}$. Let also $\{\beta _n\}_{n\in \mathbb N}$ be a decreasing sequence converging to $\alpha _0$ which consist of continuity points of $\psi _{\widetilde{A}}$. Then

$$\begin{aligned} \phi _{\widetilde{A}}(\alpha '_n)&= \psi _{\widetilde{A}}(\alpha '_n)\ge \psi _{\widetilde{A}}(\alpha _n)\ge \psi _{\widetilde{A}}(\alpha _0)+\epsilon _0>\psi _{\widetilde{A}}(\alpha _0)\\&\ge \psi _{\widetilde{A}}(\beta _n)=\phi _{\widetilde{A}}(\beta _n), \end{aligned}$$

for each $n\in \mathbb N$. Hence

$$\begin{aligned} \forall n\in \mathbb N,\quad \phi _{\widetilde{A}}(\alpha '_n)-\phi _{\widetilde{A}}(\beta _n)>\epsilon _0, \end{aligned}$$

which implies that $\phi _{\widetilde{A}}$ is also discontinuous at this point.

Proof of Lemma 3

Assume $\widetilde{\tau }_1\prec \widetilde{\tau }_2$. Note that, from Definition 3, $\widetilde{\pi }_{\widetilde{\varphi }}(\widetilde{\tau }_1)\preceq \widetilde{\pi }_{\widetilde{\varphi }}(\widetilde{\tau }_2)$ if and only if $(\widetilde{\pi }_{\widetilde{\varphi }}(\widetilde{\tau }_1))^{L}_{\alpha }\le (\widetilde{\pi }_{\widetilde{\varphi }}(\widetilde{\tau }_2))^{L}_{\alpha }$ and $(\widetilde{\pi }_{\widetilde{\varphi }}(\widetilde{\tau }_1))^{U}_{\alpha }\le (\widetilde{\pi }_{\widetilde{\varphi }}(\widetilde{\tau }_2))^{U}_{\alpha }$ for all $\alpha \in [0,1]$. Now, since $\widetilde{\tau }_1\prec \widetilde{\tau }_2$, we have $(\tilde{\tau }_1)_{\alpha }<(\tilde{\tau }_1)_{\alpha }$ for all $\alpha \in [0,1]$. On the other hand, due to the assumption and MLR property of the underlying family of density function, we know that $E_{(\widetilde{\tau }^{*})_{\beta }}[\varphi (\widetilde{\mathbf{X }}_{\beta })]$ is a non-decreasing function of $\widetilde{\tau }_{\beta }$ for every $\beta \in [0,1]$. So for every $\alpha \in [0,1]$, we have

$$\begin{aligned} (\widetilde{\pi }_{\widetilde{\varphi }}(\widetilde{\tau }_1))^{L}_{\alpha }&= \inf _{\beta \ge \alpha }E_{H^{\beta }:\widetilde{\tau }_{\beta }=(\widetilde{\tau }_1)_{\beta }}(\varphi (\widetilde{\mathbf{X }}_{\beta }))\\&\le \inf _{\beta \ge \alpha }E_{H^{\beta }:\widetilde{\tau }_{\beta }=(\widetilde{\tau }_2)_{\beta }}(\varphi (\widetilde{\mathbf{X }}_{\beta }))\\&= (\widetilde{\pi }_{\widetilde{\varphi }}(\widetilde{\tau }_2))^{L}_{\alpha }, \end{aligned}$$

and

$$\begin{aligned} (\widetilde{\pi }_{\widetilde{\varphi }}(\widetilde{\tau }_1))^{U}_{\alpha }&= \sup _{\beta \ge \alpha }E_{H^{\beta }:\widetilde{\tau }_{\beta }=(\widetilde{\tau }_1)_{\beta }}(\varphi (\widetilde{\mathbf{X }}_{\beta }))\\&\le \sup _{\beta \ge \alpha }E_{H^{\beta }:\widetilde{\tau }_{\beta }=(\widetilde{\tau }_2)_{\beta }}(\varphi (\widetilde{\mathbf{X }}_{\beta }))\\&= (\widetilde{\pi }_{\widetilde{\varphi }}(\widetilde{\tau }_2))^{U}_{\alpha }, \end{aligned}$$

which is the desired result.