1 Introduction

Fuzzy initial value problem (FIVP) has been studied by many researchers. Buckley and Feuring (2000, 2001) presented two methods to consider this problem. In the first method, they solved two crisp problems by taking initial value as the right and left end-points of the given fuzzy initial value. Then they hoped for each time \(t\), the values of solutions were right and left end-points of a fuzzy number. However, they showed by some examples that this does not take place in general. In the another method, they deduced the solution by using Zadeh’s extension principle. According to this principle, they first solved the associated crisp problem. Then the crisp initial value was replaced by fuzzy initial value to get a fuzzy function. Then the authors checked if this function satisfies the differential equation and fuzzy initial conditions. Although this method works for linear equations, it will not work for nonlinear equations and even linear equation systems (Buckley et al. 2002).

Perfilieva et al. (2008) used an approach similar to the Buckley and Feuring’s first method. Different from Buckley and Feuring, as well as the other researchers, they thought that the dependence of the solution on argument is fuzzy and in order to find dependence’s membership degree, they used fuzzy transforms and Lukasiewicz implication.

Hüllermeier (1997) showed that differential equations can be transformed into crisp differential inclusions.

Gasilov et al. (2011a, b), Barros et al. (2013) and Gomes and Barros (2012) considered the solution as a fuzzy set of real functions. To find the solution Barros et al. (2013) and Gomes and Barros (2012) proposed concepts of fuzzy calculus, analogically to classical calculus, and studied fuzzy differential equations in terms of this calculus. Under certain conditions, they established the existence of a solution for the first-order fuzzy initial value problem and suggested a solution method. Gasilov et al. (2011a, b) benefitted from properties of linear transformations and proposed a method to find fuzzy bunch of solution functions for linear equation. The method is applicable both to high-order linear differential equations and to system of linear differential equations.

Most of researchers assumes the derivative in the differential equation as a derivative of a fuzzy function in some sense. In earlier researches the derivative was considered as Hukuhara derivative. Studies in this direction was made by Kaleva (1987, 1990, 2006). When Hukuhara derivative is used, then uncertainty of the solution may increase infinitely with time. Furthermore, Bede and Gal (2005) showed that a simple fuzzy function, generated by multiplication of differentiable crisp function and a fuzzy number, may not have Hukuhara derivative. In order to overcome this difficulty Bede and Gal (2005) developed the generalized derivative concept and after that the studies about this subject were accelerated (Bede 2006; Bede et al. 2007; Khastan and Nieto 2010; Khastan et al. 2011; Chalco-Cano and Román-Flores 2008, 2009; Chalco-Cano et al. 2007, 2008). Calculation of the generalized derivatives up to \(n\)th order is divided to \(2^{n}\) cases and this made difficult to implement these derivatives to high-order equations and equations system (Khastan et al. 2009). Moreover, a simple fuzzy function may not have generalized derivative. The other difficulty is about interpreting the obtained \(2^{n}\) solutions correctly and how this model of derivative reflects the nature of the considered problem.

In this paper we consider the fuzzy initial value problem as a set of crisp problems. Using properties of linear transformations, we propose a new method to solve FIVP. For clarity we explain the proposed method for second order fuzzy linear differential equations, but the results are true for high-order equations too. We show the fuzzy solution by our method coincides with extension principle’s results.

Paper consists of 6 sections including Introduction. In Second section the necessary preliminary information is given. In Third section, FIVP is defined. The solution method is described in Fourth section. In Fifth section, this method is applied to examples and compared with the method, which uses generalized Hukuhara derivative. In Sixth section, results are interpreted.

2 Preliminaries

2.1 A matrix representation of the solution in the crisp case

In this section, we consider crisp initial value problem (IVP) for second order homogeneous linear differential equation (not necessary with constant coefficients):

$$\begin{aligned} \left\{ \begin{array}{l} x^{\prime \prime }+a_{1}(t)x^{\prime }+a_{2}(t)x=0, \\ x(0)=a, \\ x^{\prime }(0)=b, \end{array} \right. \end{aligned}$$
(1)

where \(a,b\!\in \! \mathbb{R }\). Let \(x_{1}(t)\) and \(x_{2}(t)\) be linear independent solutions of the differential equation and \(\mathbf{s }(t)=\left( x_{1}(t),\ x_{2}(t)\right) \). Then the solution of (1) can be represented as

$$\begin{aligned} x(t)=w_{1}(t)\ a+w_{2}(t)\ b \end{aligned}$$
(2)

or, in vector form (using dot product) as

$$\begin{aligned} x(t)=\mathbf{w }(t)\cdot \mathbf{u } \end{aligned}$$
(3)

where

$$\begin{aligned} \mathbf{w }(t)=\mathbf{s }(t)\ M^{-1}. \end{aligned}$$
(4)

and \(M{=}\left[ \begin{array}{cc} x_{1}(0) &{} x_{2}(0) \\ x_{1}^{\prime }(0) &{} x_{2}^{\prime }(0) \end{array} \right] \!, \mathbf{u }=(a,\ b), \mathbf{w }(t)\!=\!(w_{1}(t),\ w_{2}(t))\).

One can see, that \(w_{1}(t)\) and \(w_{2}(t)\) are the solutions of (1) corresponding to the initial values \((x(0),\ x^{\prime }(0))=(1,\ 0)\) and \( (x(0),\ x^{\prime }(0))=(0,\ 1)\), respectively. We note that \(M\) is the Wronski matrix at \(t=0\), and if \(a_{1}(t)\) and \(a_{2}(t)\) are continuous functions, it is invertible.

2.2 Preliminaries of the fuzzy sets theory

Below, we use the notation \(\widetilde{u}=(u_{L}(r),u_{R}(r))\), \( 0\le r\le 1\) to indicate a fuzzy number in parametric form. We denote \( \underline{u}=u_{L}(0)\) and \(\overline{u}=u_{R}(0)\) to indicate the left and the right end-points of \(\widetilde{u}\), respectively. An \(\alpha \)-cut of \( \widetilde{u}\) is an interval \([u_{L}(\alpha ),\ u_{R}(\alpha )]\), which we denote as \(u_{\alpha }=[\underline{u_{\alpha }},\ \overline{u_{\alpha }}]\).

We represent a triangular fuzzy number as \(\widetilde{u}=(a,c,b)\) for which \( u_{L}(r)=a+r(c-a), u_{R}(r)=b+r(c-b)\) and \(\underline{u}=a\), \(\overline{u} =b\). In geometric interpretations, we refer to the point \(c\) as a vertex.

Let us consider a triangular fuzzy number \(\widetilde{u}=(p,\ 0,\ q)\) the vertex of which is \(0\) (Note that \(p<0\) and \(q>0\) in this case). Then \( u_{L}(\alpha )=(1-\alpha )\ p\) and \(u_{R}(\alpha )=(1-\alpha )\ q\) and consequently, \(\alpha \)-cuts are intervals \([(1-\alpha )\ p,\ (1-\alpha )\ q]=(1-\alpha )\ [p,\ q]\). From the last representation one can see that an \( \alpha \)-cut is similar to the interval \([p,\ q]\) (i.e. to the \(0\)-cut) with similarity coefficient \((1-\alpha )\).

We often express a fuzzy number \(\widetilde{u}\) as \(\widetilde{u}=u_{cr}+ \widetilde{u}_{un}\) (crisp part + uncertainty). Here \(u_{cr}\) is a number with membership degree \(1\) and represents the crisp part (the vertex) of \( \widetilde{u}\); while \(\widetilde{u}_{un}\) represents the uncertain part with vertex at the origin. For a triangular fuzzy number \(\widetilde{u} =(a,c,b)\) we have \(u_{cr}=c\) and \(\widetilde{u}_{un}=(a-c,0,b-c)\). If fuzzy number \(\widetilde{u}\) is in parametric form, then \(u_{cr}\), in general, is not unique. In this case, we can choose \(u_{cr}\) arbitrarily to the extent that \(u_{L}(1)\le u_{cr}\le u_{R}(1)\). For instance, we can put \( u_{cr}=0.5(u_{L}(1)+u_{R}(1))\).

Let \(\widetilde{u}\) and \(\widetilde{v}\) be fuzzy numbers. A fuzzy set \( \widetilde{K}\) on \(R^{2}\) with membership function \(\mu _{\widetilde{K} }(x,y)=\min \left\{ \mu _{\widetilde{u}}(x),\mu _{\widetilde{v}}(y)\right\} \) we call a fuzzy number vector and denote as \(\widetilde{K}=(\widetilde{u},\ \widetilde{v})\). In the \(xy\)-coordinate plane, the vector \(\widetilde{K}=( \widetilde{u},\ \widetilde{v})\) forms a fuzzy region in the form of rectangle. Furthermore, the \(\alpha \)-cuts of the region are rectangles nested within one another.

3 A fuzzy initial value problem (FIVP)

In this section, we describe a fuzzy initial value problem (FIVP) and concept of solution which we propose. We investigate a fuzzy initial value problem with crisp linear differential equation and fuzzy initial values. Such a FIVP can arise in modelling of a process the dynamics of which is crisp but there are uncertainties in initial values. Consider the second order fuzzy initial value problem:

$$\begin{aligned} \left\{ \begin{array}{l} x^{\prime \prime }+a_{1}(t)x^{\prime }+a_{2}(t)x=f(t), \\ x(0)=\widetilde{A}, \\ x^{\prime }(0)=\widetilde{B}, \end{array} \right. \end{aligned}$$
(5)

where \(\widetilde{A},\ \widetilde{B}\) are fuzzy numbers and \(a_{1}(t),\ a_{2}(t)\) and \(f(t)\) are continuous crisp functions. Let us represent the initial values as \(\widetilde{A}=a_{cr}+\widetilde{a}\) and \(\widetilde{B} =b_{cr}+\widetilde{b}\), where \(a_{cr}\) and \(b_{cr}\) are crisp numbers while \( \widetilde{a}\) and \(\widetilde{b}\) are fuzzy numbers. We split the FIVP (5) to the following problems:

  1. (1)

    Associated crisp problem (which is non-homogeneous)

    $$\begin{aligned} \left\{ \begin{array}{l} x^{\prime \prime }+a_{1}(t)x^{\prime }+a_{2}(t)x=f(t), \\ x(0)=a_{cr}, \\ x^{\prime }(0)=b_{cr}. \end{array} \right. \end{aligned}$$
    (6)
  2. (2)

    Homogeneous problem with fuzzy initial values

    $$\begin{aligned} \left\{ \begin{array}{l} x^{\prime \prime }+a_{1}(t)x^{\prime }+a_{2}(t)x=0, \\ x(0)=\widetilde{a}, \\ x^{\prime }(0)=\widetilde{b}. \end{array} \right. \end{aligned}$$
    (7)

It is easy to see if \(x_{cr}(t)\) and \(\widetilde{x}_{un}(t)\) are solutions of (6) and (7) respectively, then \(\widetilde{x} (t)=x_{cr}(t)+\widetilde{x}_{un}(t)\) is a solution of the given problem (). Hence, (5) is reduced to solving a homogeneous equation with fuzzy initial conditions (7). Therefore, we will investigate how to solve (7).

Depending on different definitions for derivative of fuzzy function or different definitions for solution of differential equation, the problem (7) can be interpreted by different ways. Here we interpret the problem (7) as a set of crisp problems (1). Each problem is obtained by taking the initial values \(a\) from \(\left[ \underline{a},\ \overline{a}\right] \) and \(b\) from \(\left[ \underline{b},\ \overline{b} \right] \). We denote by \(x_{ab}(t)\) the solution of the crisp problem (). Let \(\mu _{ab}=\min \left\{ \mu _{\widetilde{a}}(a),\mu _{ \widetilde{b}}(b)\right\} \) (where \(\mu _{\widetilde{a}}(a)\) denotes the membership degree of \(a\) in \(\widetilde{a}\)). We assume the function \( x_{ab}(t)\) be an element of fuzzy solution set with membership degree \(\mu _{ab}\). Then the fuzzy solution can be defined as follows:

$$\begin{aligned} \widetilde{X}&= \left\{ x_{ab}(\cdot )\mid x^{\prime \prime }+a_{1}(t)x^{\prime }+a_{2}(t)x=0;\right. \nonumber \\&\quad \left. x(0)=a;\ x^{\prime }(0)=b;\ a\in \widetilde{a};\ b\in \widetilde{b}\right\} \end{aligned}$$
(8)

where

$$\begin{aligned} \mu _{\widetilde{X}}(x_{ab}(\cdot ))=\min \left\{ \mu _{\widetilde{a} }(a),\mu _{\widetilde{b}}(b)\right\} \end{aligned}$$
(9)

and by \(a\in \widetilde{u}\) we mean \(a\in \left[ \underline{u},\ \overline{u} \right] .\)

The solution, defined above, of FIVP can be classified as united solution set (USS) (Kearfott 1996; Muzzioli and Reynaerts 2006).

4 The solution method

Let linear independent solutions of the crisp equation (7),\(\ x_{1}(t)\) and \(x_{2}(t),\) be known. Then we can constitute the vector-function \( \mathbf{w }(t)\) (see, formula 4). According (2) and (8) we have:

$$\begin{aligned} \widetilde{X}=\left\{ x_{ab}=\mathbf{w }\cdot \mathbf{u }\mid \mathbf{u }=(a, b) ;\ a\in \widetilde{a};\ b\in \widetilde{b}\right\} \!. \end{aligned}$$
(10)

Let us fix time \(t\) and put \(\mathbf{v }=\mathbf{w }(t)\). Then from (10 ) we have:

$$\begin{aligned} \widetilde{X}(t)=\left\{ x=\mathbf{v }\cdot \mathbf{u }\mid \mathbf{u }=(a, b);\ a\in \widetilde{a};\ b\in \widetilde{b}\right\} \end{aligned}$$
(11)

with membership function

$$\begin{aligned} \mu _{\widetilde{X}(t)}(x)=\min \left\{ \mu _{\widetilde{a}}(a),\mu _{ \widetilde{b}}(b)\right\} \!. \end{aligned}$$
(12)

To determine how is the set \(\widetilde{X}(t)\) we consider the transformation \(T(\mathbf{u })=\mathbf{v }\cdot \mathbf{u }\) (here \(\mathbf{v }\) is a fixed vector). One can see, that \(T:\mathbb{R }^{2}\rightarrow \mathbb{R }^{1}\) is a linear transformation. Therefore, \(\widetilde{X}(t)\) is the image of the set \(\widetilde{K}=\left\{ \mathbf{u }=(a, b)\mid a\in \widetilde{a};\ b\in \widetilde{b}\right\} =(\widetilde{a},\ \widetilde{b})\) under the linear transformation \(T(\mathbf{u })\).

We shall make use of the following facts about linear transformations (Anton and Rorres 2005):

  1. 1.

    A linear transformation maps the origin (zero vector) to the origin (zero vector).

  2. 2.

    Under a linear transformation the images of a pair of similar figures (bodies) are also similar.

  3. 3.

    Under a linear transformation the images of nested figures (bodies) are also nested. In addition, we shall reference a property of fuzzy number vectors.

  4. 4.

    The fuzzy set \(\widetilde{K}=(\widetilde{a},\ \widetilde{b})\) forms a fuzzy region in the \(ab\)-coordinate plane, its vertex is located at the origin and its boundary is a rectangle. Furthermore, the \(\alpha \)-cuts of the region are rectangles nested within one another.

The facts 1–4 allow us to make the following conclusion. The vector \( \widetilde{K}=(\widetilde{a},\ \widetilde{b})\) forms a fuzzy rectangle in the \(ab\)-coordinate plane. The linear transformation \(T:\mathbb{R } ^{2}\rightarrow \mathbb{R }^{1}\) maps this fuzzy rectangle to a fuzzy interval. The \(\alpha \)-cuts of this fuzzy interval are nested within one another. Therefore, the solution at any time forms a fuzzy number. Note that the left and right end-points of this fuzzy number are the images of two corners of the rectangle \(\widetilde{K}=(\widetilde{a},\ \widetilde{b})\). Therefore according to (11) to find the lower and upper boundaries of the solution it is sufficient to analyze the behavior of 4 corner points.

4.1 Particular case when initial values are triangular fuzzy numbers

In particular, if \(\widetilde{a}\) and \(\widetilde{b}\) are triangular fuzzy numbers, the \(\alpha \)-cuts of the region \(\widetilde{K}=(\widetilde{a},\ \widetilde{b})\) are nested rectangles, furthermore, they are similar. According to the discussion above, their images are intervals that also are nested and similar, consequently, form a triangular fuzzy number \(\widetilde{ X}(t)\). Therefore, \(\widetilde{X}(t)\) can be represented in the form \( \widetilde{X}(t)=(\underline{x}(t),0,\overline{x}(t))\). Now we investigate how to calculate \(\underline{x}(t)\) and \(\overline{x}(t)\).

Let \(\widetilde{a}=(\underline{a},0,\overline{a})\), \(\widetilde{b}\!=\!( \underline{b},0,\overline{b})\) and \(\mathbf{w }(t)\!=\!(w_{1}(t),w_{2}(t))\). Since \(\overline{x}(t)\) and \(\underline{x}(t)\) are respectively the maximum and minimum values among all products \(\mathbf{w }(t)\cdot \mathbf{u }= aw_{1}(t)+bw_{2}(t)\), then we have:

$$\begin{aligned} \overline{x}(t)&= \max \left\{ \underline{a}w_{1}(t),\ \overline{a} w_{1}(t)\right\} \ +\ \max \left\{ \underline{b}w_{2}(t),\ \overline{b} w_{2}(t)\right\} \end{aligned}$$
(13)
$$\begin{aligned} \underline{x}(t)&= \min \left\{ \underline{a}w_{1}(t),\ \overline{a} w_{1}(t)\right\} \ +\ \min \left\{ \underline{b}w_{2}(t),\ \overline{b} w_{2}(t)\right\} \nonumber \\ \end{aligned}$$
(14)

Note that an \(\alpha \)-cut of \(\widetilde{X}(t)\) can be determined by similarity:

$$\begin{aligned} X_{\alpha }(t)=\left[ \underline{x_{\alpha }}(t),\overline{x_{\alpha }}(t) \right] =(1-\alpha )\left[ \underline{x}(t),\overline{x}(t)\right] . \end{aligned}$$
(15)

Formulas (13–14) for \(\underline{x}(t)\) and \(\overline{x} (t)\) allow us to represent the solution in a new way:

$$\begin{aligned} \widetilde{X}(t)=w_{1}(t)\ \widetilde{a}+w_{2}(t)\ \widetilde{b}, \end{aligned}$$
(16)

where the operations are assumed to be multiplication of real number with fuzzy one, and addition of fuzzy numbers.

4.2 General case when initial values are parametric fuzzy numbers

In the general case, when \(\widetilde{a}\) and \(\widetilde{b}\) are arbitrary fuzzy numbers, the solution can be obtained by using \(\alpha \)-cuts. Let \( a_{\alpha }=\left[ \underline{a_{\alpha }},\overline{a_{\alpha }}\right] \) and \(b_{\alpha }=\left[ \underline{b_{\alpha }},\overline{b_{\alpha }}\right] \). Then \(K_{\alpha }=\left[ \underline{a_{\alpha }},\overline{a_{\alpha }} \right] \times \left[ \underline{b_{\alpha }},\overline{b_{\alpha }}\right] \) . By similar argumentation to the preceding case, for the \(\alpha \)-cut of the solution we obtain the following formulas:

$$\begin{aligned} X_{\alpha }(t)&= \left[ \underline{x_{\alpha }}(t),\overline{x_{\alpha }}(t) \right] \!,\\ \overline{x_{\alpha }}(t)&= \max \left\{ \underline{a_{\alpha }}w_{1}(t), \overline{a_{\alpha }}w_{1}(t)\right\} \\&\quad +\max \left\{ \underline{b_{\alpha }} w_{2}(t),\overline{b_{\alpha }}w_{2}(t)\right\} \\ \underline{x_{\alpha }}(t)&= \min \left\{ \underline{a_{\alpha }}w_{1}(t), \overline{a_{\alpha }}w_{1}(t)\right\} \\&\quad +\min \left\{ \underline{b_{\alpha }} w_{2}(t),\overline{b_{\alpha }}w_{2}(t)\right\} \!. \end{aligned}$$

On the base of these formulas we can conclude that the solution’s representation

$$\begin{aligned} \widetilde{X}(t)=w_{1}(t)\ \widetilde{a}+w_{2}(t)\ \widetilde{b} \end{aligned}$$
(17)

is valid in general. Thus, the solution by our approach coincides with the solution obtained from (2) by application of the extension principle.

4.3 Solution algorithm

Based on the arguments above, we propose the following algorithm to solve FIVP (5):

  1. 1.

    Represent the initial values as \(\widetilde{A}=a_{cr}+\widetilde{a}\) and \(\widetilde{B}=b_{cr}+\widetilde{b}\).

  2. 2.

    Find linear independent solutions \(x_{1}(t)\) and \(x_{2}(t)\) of the crisp differential equation \(x^{\prime \prime }+a_{1}(t)x^{\prime }+a_{2}(t)x=0\). Constitute the vector-function \(\mathbf{s }(t)=\left( x_{1}(t),\ x_{2}(t)\right) \), the matrix \(M\) and calculate the vector-function \(\mathbf{ w }(t)=\left( w_{1}(t),\ w_{2}(t)\right) \) by formula (4).

  3. 3.

    Find the solution \(x_{cr}(t)\) of the non-homogeneous crisp problem (6).

  4. 4.

    The solution of the given problem (5) is

    $$\begin{aligned} \widetilde{x}(t)=x_{cr}(t)+w_{1}(t)\ \widetilde{a}+w_{2}(t)\ \widetilde{b}. \end{aligned}$$
    (18)

Remark The approach is valid also for the general case, when \(n\)th order initial value problem is considered.

5 Examples

In this section, to demonstrate how the proposed method works, we solve 2 examples.

Example 1 Let us consider the second order fuzzy initial value problem:

$$\begin{aligned} \left\{ \begin{array}{l} x^{\prime \prime }-3x^{\prime }+2x=0, \\ x(0)=(-0.5,\ 0,\ 1), \\ x^{\prime }(0)=(\ -1,\ 0,\ 1). \end{array} \right. \end{aligned}$$
(19)

We note that the problem is homogeneous and the initial values are fuzzy numbers with vertices at 0. Therefore, the solution can be calculated by the formula (17).

\(x_{1}(t)=e^{t}\) and \(x_{2}(t)=e^{2t}\) are linear independent solutions for the differential equation \(x^{\prime \prime }-3x^{\prime }+2x=0\). Hence, \( \mathbf{s }=\left( e^{t}\!,\ \ e^{2t}\right) \!,\ M=\left[ \begin{array}{cc} 1 &{} 1 \\ 1 &{} 2 \end{array} \right] \ \) and \(\ \mathbf{w }=\mathbf{s }(t)\ M^{-1}=\left( 2e^{t}-e^{2t},\ \ e^{2t}-e^{t}\right) \). Then the formula (17) gives the solution of the given problem:

$$\begin{aligned} \widetilde{x}(t)=(2e^{t}-e^{2t})\ (-0.5,\ 0,\ 1)+(e^{2t}-e^{t})\ (-1,\ 0,\ 1),\nonumber \\ \end{aligned}$$
(20)

where the arithmetical operations are considered to be fuzzy operations.

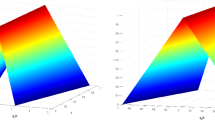
The fuzzy solution \(\widetilde{x}(t)\) forms a band in the \(tx\)-coordinate space (Fig. 1).

Fig. 1
figure 1

The fuzzy solution, obtained by the proposed method, for Example 1

Full size image

Since the initial values are triangular fuzzy numbers, an \(\alpha \)-cut of the solution can be determined by similarity with coefficient \((1-\alpha )\) , i.e.

$$\begin{aligned} x_{\alpha }(t)=(1-\alpha )\left[ \underline{x}(t),\ \overline{x}(t)\right] . \end{aligned}$$
(21)

Example 2 Consider the FIVP:

$$\begin{aligned} \left\{ \begin{array}{l} x^{\prime \prime }-3x^{\prime }+2x=4t-6, \\ x(0)=(1.5,\ 2,\ 3), \\ x^{\prime }(0)=(\ \ 2,\ \ 3,\ 4). \end{array} \right. \end{aligned}$$
(22)

We represent the initial values as \(\widetilde{A}=(1.5,\ 2,\ 3)=2+(-0.5,\ 0,\ 1), \widetilde{B}=(2,\ \ 3,\ 4)=3+(-1,\ 0,\ 1).\) We solve crisp non-homogeneous problem

$$\begin{aligned} \left\{ \begin{array}{l} x^{\prime \prime }-3x^{\prime }+2x=4t-6, \\ x(0)=2, \\ x^{\prime }(0)=3 \end{array} \right. \end{aligned}$$

and find the crisp solution

\(x_{cr}(t)=2t+\left[ 2(2e^{t}-e^{2t})+(e^{2t}-e^{t})\right] =2t+3e^{t}-e^{2t}\) (the dashed line in the middle of Fig. 2).

Fig. 2
figure 2

The fuzzy solution, obtained by the proposed method, for Example 2. Dashed line represents the crisp solution

Full size image

Fuzzy homogeneous problem to find the uncertainty of the solution is as follows:

$$\begin{aligned} \left\{ \begin{array}{l} x^{\prime \prime }-3x^{\prime }+2x=0, \\ x(0)=(-0.5,\ 0,\ 1), \\ x^{\prime }(0)=(-1,\ 0,\ 1). \end{array} \right. \end{aligned}$$

This problem is the same as Example 1. Hence, the solution is

$$\begin{aligned} \widetilde{x}_{un}(t)=(2e^{t}-e^{2t})\ (-0.5,\ 0,\ 1)+(e^{2t}-e^{t})\ (-1,\ 0,\ 1).\nonumber \\ \end{aligned}$$
(23)

We add this uncertainty to the crisp solution and get the fuzzy solution of the given FIVP (22):

$$\begin{aligned} \widetilde{x}(t)&= x_{cr}(t)+\widetilde{x}_{un}(t)\nonumber \\&= 2t+(2e^{t}-e^{2t})\ (1.5,\ 2,\ 3)+(e^{2t}-e^{t})\ (0,\ 1,\ 2). \nonumber \\ \end{aligned}$$
(24)

The fuzzy solution \(\widetilde{x}(t)\) forms a band in the \(tx\)-coordinate space (Fig. 2).

We can express the solution \(\widetilde{x}(t)\) also via \(\alpha \)-cuts, which are intervals \(x_{\alpha }(t)=\left[ \underline{x_{_{\alpha }}}(t),\ \overline{x_{_{\alpha }}}(t)\right] \) at any time \(t\). Since the initial values are triangular fuzzy numbers, \(\widetilde{x}_{un}(t)\) also is a triangular fuzzy number, say \(\widetilde{x}_{un}(t)=(\underline{x_{un}}(t),\ 0,\ \overline{x_{un}}(t))\) (One can use the formulas (13–14) to calculate \(\underline{x_{un}}(t)\) and \(\overline{x_{un}}(t)\)). Consequently, an \(\alpha \)-cut of \(\widetilde{x}_{un}(t)\) can be determined by similarity with coefficient \((1-\alpha )\), i.e.

$$\begin{aligned} x_{un,\ \alpha }(t)=(1-\alpha )\left[ \underline{x_{un}}(t),\ \overline{ x_{un}}(t)\right] . \end{aligned}$$
(25)

Adding the crisp solution gives the \(\alpha \)-cut of the solution \( \widetilde{x}(t)\):

$$\begin{aligned} \left[ \underline{x_{_{\alpha }}}(t),\ \overline{x_{_{\alpha }}}(t)\right] =x_{cr}(t)+(1-\alpha )\left[ \underline{x_{un}}(t),\ \overline{x_{un}}(t) \right] . \end{aligned}$$
(26)

In Fig. 3 we show the fuzzy solution via its \(\alpha \)-cuts: \(1\) -cut or crisp solution (dashed line), 0.7-cut (dotted lines), 0.3-cut (dashed-dotted lines), 0-cut (continues lines) of the solution.

Fig. 3
figure 3

The fuzzy solution, obtained by the proposed method, for Example 2 and its \(\alpha \)-cuts

Full size image

In the next example, we compare our solution with the solution which uses generalized Hukuhara derivative (Khastan and Nieto 2010). To see the differences better we consider an easy case, when differential equation is homogeneous. Furthermore, we consider initial values with vertex at 0.

Example 3 Let us consider FIVP:

$$\begin{aligned} \left\{ \begin{array}{l} x^{\prime \prime }=-4x, \\ x(0)=(\ -1,\ 0,\ 0.5), \\ x^{\prime }(0)=(-0.5,\ 0,\ 0.5). \end{array} \right. \end{aligned}$$
(27)

\(x_{1}(t)=\cos 2t\) and \(x_{2}(t)=\sin 2t\) are linear independent solutions for the differential equation \(x^{\prime \prime }+4x=0\) (Note that for our approach the equations \(x^{\prime \prime }+4x=0\) and \(x^{\prime \prime }=-4x\) are equivalent). Then

$$\begin{aligned} \mathbf{s }&= \left( \cos 2t,\ \ \sin 2t\right) , \ M=\left[ \begin{array}{cc} 1 &{} 0 \\ 0 &{} 2 \end{array} \right] \ \hbox {and} \\ \mathbf{w }&= \mathbf{s }(t)\ M^{-1}=\left( \cos 2t,\ \ \ \frac{1}{2}\sin 2t\right) . \end{aligned}$$

By formula (17), our method gives the following solution:

$$\begin{aligned} \widetilde{x}(t)=\cos 2t\ (-1,\ 0,\ 0.5)+\frac{1}{2}\sin 2t\ (-0.5,\ 0,\ 0.5).\qquad \end{aligned}$$
(28)

The fuzzy solution \(\widetilde{x}(t)\) forms a band in the \(tx\)-coordinate space (Fig. 4). The solution is periodic (with period of \(\pi \)), as in the crisp case. The uncertainty does not increase essentially or does not vanish as time goes. It changes periodically. This fact also corresponds to the expectations from the crisp case.

Fig. 4
figure 4

The fuzzy solution, obtained by the proposed method, for Example 3

Full size image

Below we solve the FIVP (27) by the method, which uses generalized Hukuhara derivative (Khastan and Nieto 2010). We have to analyze four systems, depending on different kinds of derivative.

  1. (1)

    (1, 1) system is as follows:

    $$\begin{aligned} \left\{ \begin{array}{l} \underline{x}^{\prime \prime }(t;\alpha )=-4\overline{x}(t;\alpha ), \\ \overline{x}^{\prime \prime }(t;\alpha )=-4\underline{x}(t;\alpha ), \\ \underline{x}(0;\alpha )=\underline{A_{\alpha }};\ \ \ \ \ \overline{x} (0;\alpha )=\overline{A_{\alpha }}, \\ \underline{x}^{\prime }(0;\alpha )=\underline{B_{\alpha }};\ \ \ \ \ \overline{x}^{\prime }(0;\alpha )=\overline{B_{\alpha }}. \end{array} \right. \end{aligned}$$

We solve the system with respect to \(\overline{x}(t;\alpha )\) and get \( \overline{x}(t;\alpha )=c_{1}e^{-2t}+c_{2}e^{2t}+c_{3}\cos 2t+c_{4}\sin 2t\). Using initial values we have:

$$\begin{aligned} c_{1}&= \frac{2(\overline{A_{\alpha }}-\underline{A_{\alpha }})-(\overline{ B_{\alpha }}-\underline{B_{\alpha }})}{8}; \\ c_{2}&= \frac{2(\overline{ A_{\alpha }}-\underline{A_{\alpha }})+(\overline{B_{\alpha }}-\underline{ B_{\alpha }})}{8}; \\ c_{3}&= \frac{\overline{A_{\alpha }}+\underline{A_{\alpha }}}{2}; c_{4}=\frac{\overline{B_{\alpha }}+\underline{B_{\alpha }}}{4}. \end{aligned}$$

Formula for \(\underline{x}(t;\alpha )\) can be obtained using the relation \( \underline{x}(t;\alpha )=-\frac{1}{4}\overline{x}^{\prime \prime }(t;\alpha ) \).

Summarizing we have:

$$\begin{aligned} \underline{x}(t;\alpha )&= -c_{1}e^{-2t}-c_{2}e^{2t}+c_{3}\cos 2t+c_{4}\sin 2t, \\ \overline{x}(t;\alpha )&= \ \ \ c_{1}e^{-2t}+c_{2}e^{2t}+c_{3}\cos 2t+c_{4}\sin 2t. \end{aligned}$$

We present graphics of \(\underline{x}(t;\alpha )\) (down line) and \(\overline{ x}(t;\alpha )\) (upper line) in Fig. 5.

Fig. 5
figure 5

The fuzzy solution for Example 3, obtained using generalized (1,1)-derivative

Full size image

We see the solution under Hukuhara derivative is not periodic as it is expected from the crisp case. Also the initial uncertainty increases infinitely as times goes. Therefore, in the case of (1, 1)-derivative we do not have an appropriate fuzzy solution.

  1. (2)

    (2, 2) system is as follows:

    $$\begin{aligned} \left\{ \begin{array}{l} \underline{x}^{\prime \prime }(t;\alpha )=-4\overline{x}(t;\alpha ), \\ \overline{x}^{\prime \prime }(t;\alpha )=-4\underline{x}(t;\alpha ), \\ \underline{x}(0;\alpha )=\underline{A_{\alpha }};\ \ \ \ \ \overline{x} (0;\alpha )=\overline{A_{\alpha }}, \\ \underline{x}^{\prime }(0;\alpha )=\overline{B_{\alpha }};\ \ \ \ \ \overline{x}^{\prime }(0;\alpha )=\underline{B_{\alpha }}. \end{array} \right. \end{aligned}$$

We note that this system is similar to the system in the preceding case: only the last 2 initial values are different. The solution is represented in Fig. 6. Since the solution function is assumed to have (2, 2)-derivative, we see this solution is not (2, 2)-solution (the support of such a solution must become narrow with time) (Khastan and Nieto 2010). Consequently, we have not a fuzzy solution, which is valid on all the interval \(\left[ 0,+\infty \right) \).

  1. (3)

    (1, 2) system is as follows:

    $$\begin{aligned} \left\{ \begin{array}{l} \underline{x}^{\prime \prime }(t;\alpha )=-4\underline{x}(t;\alpha ), \\ \overline{x}^{\prime \prime }(t;\alpha )=-4\overline{x}(t;\alpha ), \\ \underline{x}(0;\alpha )=\underline{A_{\alpha }};\ \ \ \ \ \overline{x} (0;\alpha )=\overline{A_{\alpha }}, \\ \underline{x}^{\prime }(0;\alpha )=\underline{B_{\alpha }};\ \ \ \ \ \overline{x}^{\prime }(0;\alpha )=\overline{B_{\alpha }}. \end{array} \right. \end{aligned}$$
Fig. 6
figure 6

The fuzzy solution for Example 3, obtained using generalized (2,2)-derivative

Full size image

Equation and initial values for \(\underline{x}(t;\alpha )\) are independent from \(\overline{x}(t;\alpha )\) and vice versa. Consequently, \(\underline{x} (t;\alpha )\) and \(\overline{x}(t;\alpha )\) can be calculated separately. Graphics of \(\underline{x}(t;\alpha )\) and \(\overline{x}(t;\alpha )\) (Fig. 7) are the same as dashed-dotted lines in Fig. 4. Since the solution function is assumed to be a (1, 2)-differentiable fuzzy function, as in the preceding case we see from Fig. 7 that it is not a valid fuzzy function on \(\left[ 0,\infty \right) \). Consequently, we have not a fuzzy solution on all the interval \(\left[ 0,+\infty \right) \).

  1. (4)

    (2, 1) system is as follows:

    $$\begin{aligned} \left\{ \begin{array}{l} \underline{x}^{\prime \prime }(t;\alpha )=-4\underline{x}(t;\alpha ), \\ \overline{x}^{\prime \prime }(t;\alpha )=-4\overline{x}(t;\alpha ), \\ \underline{x}(0;\alpha )=\underline{A_{\alpha }};\ \ \ \ \ \overline{x} (0;\alpha )=\overline{A_{\alpha }}, \\ \underline{x}^{\prime }(0;\alpha )=\overline{B_{\alpha }};\ \ \ \ \ \overline{x}^{\prime }(0;\alpha )=\underline{B_{\alpha }}. \end{array} \right. \end{aligned}$$

This system is solved similarly to the preceding one. Graphics of \( \underline{x}(t;\alpha )\) and \(\overline{x}(t;\alpha )\) (Fig. 8) are the same as dotted lines in Fig. 4. In this case the solution also is not a valid (2, 1)-differentiable fuzzy function on \(\left[ 0,\infty \right) \).

Fig. 7
figure 7

The fuzzy solution for Example 3, obtained using generalized (1,2)-derivative

Full size image
Fig. 8
figure 8

The fuzzy solution for Example 3, obtained using generalized (2,1)-derivative

Full size image

It is worth noting in this paper, generalized differentiable solutions are understood in the sense that the solutions considered have no switching points. Obviously, if we consider switching points and the two types of differentiability alternately, then we obtain more solutions (see Bede and Stefanini 2012). On the other hand, following the results of Bede and Stefanini (2012), it is easy to check that when the initial values are symmetric numbers, the solution (18) obtained by the proposed method is gH-differentiable on \(\left[ 0,+\infty \right) \) and satisfies Eq. (5) exactly. This circumstance can be considered as an advantage of the proposed method.

Now, let us discuss relation between the proposed method and the one by Barros et al. (2013), Gomes and Barros (2012). Barros et al. (2013), Gomes and Barros (2012) also consider the solution as a fuzzy set of real functions. Based on Zadeh’s extension principle, they define the concepts of derivative and integral operators for fuzzy set of functions. Some properties that occur with the classical operators are checked for fuzzy operators, such as Fundamental Theorem of Calculus. The authors study fuzzy differential equations in terms of the new fuzzy derivative. Under certain conditions, they prove the existence of a solution for the first-order fuzzy initial value problem, and propose a solution method.

Further development of the proposed approach for high-order equations requires that other operations (for example, the summation) are also defined for fuzzy sets of functions in an effective manner similar to derivative and integral. But it is not easy task. To see, let us consider formula (4) from Gomes and Barros (2012):

where \(X\) is a fuzzy set of functions. The authors interpreted the sum as

$$\begin{aligned}&\left\{ x_{0}+\int _{0}^{t}f(s,x(s))\,ds\!\mid \right. \\&\left. \qquad x_0=x(0)\in \left[ X_{0}\right] ^{\alpha },f(\cdot ,x(\cdot ))\in \left[ F(\cdot ,X(\cdot ))\right] ^{\alpha }\right\} . \end{aligned}$$

One can see that this sum is not a Minkowski sum, it is a “dependent” sum: if a function takes participation in the first operand it takes participation in the second one simultaneously. Such a sum may be useful, but obtaining considerable results by using this sum is not easy.

To explain the main difference of our method from the method mentioned above, let us consider FIVP (5). Actually, we represent the differential equation as \(\widehat{L}\,X=f\), where \(\widehat{L}\) is Zadeh’s extension of \(L=D^{2}+a_{1}D+a_{2}\), i.e. we consider at once the extension of whole \(L\), not its separate parts.

Summarizing, besides of that we greet the fuzzy calculus proposed by Barros et al. (2013), Gomes and Barros (2012), it seems that to obtain new results, in addition to derivative and integral, other operations also must be developed.

6 Conclusion

In this paper we have investigated the fuzzy initial value problem as a set of crisp problems. We have proposed a solution method based on the properties of linear transformations. For clarity we have explained the proposed method for second order linear differential equation. We have shown that the fuzzy solution by our method coincides with result of extension principle. As an example we have shown that the deduced solution has no difficulties of Hukuhara differentiable solutions and generalized differentiable solutions.