1 Introduction

Neuro-fuzzy systems proved to be efficient in many fields of data mining. They combine the ability to handle imprecise data and to modify the parameters of elaborated models to better fit the data. The more complicated a model is, the more suitable it is to use fuzzy approach (Zadeh et al. 1973). The fuzzy approach can provide better models, even for non-fuzzy data, than non-fuzzy systems.

The crucial part of the fuzzy system is the fuzzy rule base composed of fuzzy rules (implications). Creation of the fuzzy rule base is a difficult task. This procedure has enormous influence on the quality of results elaborated by the system. The rules can implement the knowledge of experts or can be created automatically from the presented data. The rules of the fuzzy model split the input domain into regions. This procedure can be reversed in order to obtain the rules from presented data. The domain is split into regions and the regions are transformed into premises of the rules. This approach is commonly used. There are three main ways of domain partition grid split (Jang 1993; Setnes and Babuška 2001), scatter split (clustering) and hierarchical split (Hoffmann and Nelles 2001; Jakubek et al. 2006; Nelles and Isermann 1996; Nelles et al. 2000; Simiński 2008, 2009, 2010). The most common method is scatter split (clustering) (Abonyi et al. 2002; Bauman et al. 1990; Chen et al. 1998; Czogała et al. 2000; Wang et al. 1994). Clustering avoids the curse of dimensionality, which is the main problem of grid partition. The main disadvantage of many clustering algorithms is their inability to discover the number of clusters. Is such cases the number of clusters is passed to the algorithm as a parameter.

In high dimensional data sets not always all dimensions (attributes) are relevant. Some of them can be treated as noise and have minor importance. The reduction of dimensionality may be done for a whole data set (global dimensionality reduction) or individually for each cluster. The global feature transformation (e.g. PCA or SVD) causes problems with interpretability of elaborated models. Dimension reduction without feature transformation can be achieved by feature selection. The global approach selects the same subset of attributes for all clusters whereas each cluster may need its own subspace. This is the idea of subspace clustering (Friedman and Meulman 2004; Gan et al. 2006; Kriegel et al. 2009; Müller et al. 2009; Parsons et al. 2004; Sim et al. 2012) where each cluster may be extracted in its own subspace. There are two kinds of subspace clustering: bottom-up and top-down (Parsons et al. 2004). The former approach splits the clustering space with a grid and analyses the density of data examples in each grid cell extracting the relevant dimensions [e.g. CLIQUE (Agrawal et al. 1998), ENCLUS (Cheng et al. 1999), MAFIA (Goil et al. 1999)]. The latter (top–down) approach starts with full dimensional clusters and tries to throw away the dimensions of minor importance [e.g. PROCLUS (Aggarwal et al. 1999), ORCLUS (Aggarwal et al. 2000), δ-Clusters (Yang et al. 2002), FSC (Gan and Wu 2008; Gan et al. 2006)]. In algorithms mentioned above the attribute is valid or invalid in a certain cluster, the weight of the attribute in each cluster is either 0 or 1. In our solution the clustering algorithm assigns values from the interval [0, 1]. The attributes have partial importance in the subspace. This approach creates fuzzy rules in individual weighted subspaces.

The contribution of the paper is the neuro-fuzzy system with weighted attributes.

In the paper we follow the general rule for symbols: the blackboard bold uppercase characters \({(\mathbb{A})}\) are used to denote the sets, uppercase italics (A)—the cardinality of sets, uppercase bolds \((\mathbf{A})\)—matrices, lowercase bolds \((\mathbf{a})\)—vectors, lowercase italics (a)—scalars and set elements. Table 1 lists the symbols used in the paper.

Table 1 Symbols used in the papers
Full size table
Table 2 Number of tuples and attributes in the real life data sets
Full size table

The paper is organised as follows: Sect. 2 introduces the new neuro-fuzzy system with parameterized consequences and weighted attributes (architecture—Sect. 2.1, creation of a fuzzy model—Sect. 2.2). Section 3 describes the data sets (Sect. 3.1) and experiments with results (Sect. 3.2). Finally Sect. 4 summarises the paper.

2 Fuzzy inference system with parameterized consequences and attributes’ weights

Fuzzy inference system with parameterized consequences and weights attributes is an extension of the neuro-fuzzy system with parameterized consequences ANNBFIS (Czogała et al. 2000; Łęski and Czogała 1999) which is the combination of the Mamdani and Assilan (1975), Takagi and Sugeno (1985) and Sugeno and Kang (1988) approach. The fuzzy sets in consequences are isosceles triangles (as in the Mamdami–Assilan system), but are not fixed—their location is calculated as a linear combination of attribute values as in the Takagi–Sugeno–Kang system. The important feature is the logical interpretation of fuzzy implication (cf. Eq. 11). The idea of the system with parameterized consequences is presented in Fig. 1. The figure is taken from (Czogała et al. 2000) with modifications.

Fig. 1
figure 1

The scheme of the neuro-fuzzy system with parameterized consequences. The input has two attributes and the rule base is composed of two fuzzy rules. The premises of the rules are responsible for determining the firing strength of the rules. The firing strength is the left operand of the fuzzy implication. The right hand operand is the \({\mathbb{B}}\) fuzzy triangle set, the location of which is determined by formula 7. The result of the rth fuzzy implication is a fuzzy set \({\mathbb{B}^{\prime}_l}\). The fuzzy results of the implications are then aggregated. The non-informative part (the gray rectangular in the picture) is thrown away in aggregation. The informative part (the white mountain-like part of \({\mathbb{B}^{\prime}}\) set) is then defuzzyfied with the centre of gravity method. The defuzzyfied answer of the system is number y 0

Full size image

2.1 Architecture of the system

The system with parameterized consequences is the MISO system. The rule base \({\mathbb{L}}\) contains fuzzy rules l in form of fuzzy implications

$$ l : {\mathbf{x}} \;\; \mathrm{is}\, {\mathfrak{a}}\; \rightsquigarrow\;y \,\mathrm{is}\, {\mathfrak{b}}, $$
(1)

where \(\mathbf{x} = [x_1, x_2, \ldots, x_N]^\mathrm{T}\) and y are linguistic variables, \({\mathfrak{a}}\) and \({\mathfrak{b}}\) are fuzzy linguistic terms (values). Data tuples are represented by vectors \(\left[\mathbf{x}, y\right]^\mathrm{T}\), where \(\mathbf{x}\) is a vector of descriptors and y is the decision attribute of the tuples. Both the descriptors and decision are real numbers.

In the following text we will describe the situation only for one rule, but we will omit the index of the rule in the following formulae as not to complicate the notation.

The linguistic variable \({\mathfrak{a}}\) (in the rule’s premise) is represented in the system as a fuzzy set \({\mathbb{A}}\) in N-dimensional space. Each fuzzy rule has its own premise and consequence. For each dimension n the set \({\mathbb{A}_n}\) is described with the Gaussian membership function:

$$ u_{{\mathbb{A}}_n} \left(x_n\right) = \exp \left( - \frac{\left(x_n - v_n\right)^2}{2s_n^2} \right), $$
(2)

where v n is the core location for nth attribute and s n is this attribute Gaussian bell deviation (fuzziness).

The membership of a tuple \(\mathbf{x}\) to the premise \({\mathbb{A}}\) of the rule is the T-norm of memberships to all dimensions in the rule’s premise. Because each dimension i has its own weight z i , we use the weighted T-norm (Rutkowski and Cpałka 2003) to determine the membership of the data example to the fuzzy set \({\mathbb{A}}\) in rule’s premise:

$$ \begin{aligned} u_{\mathbb{A}} & = T\left(u_{{\mathbb{A}}_1}, \ldots, u_{{\mathbb{A}}_N}; z_1, \dots, z_N \right) \nonumber \\ &= T\left(1 - z_1 \left(1-u_{{\mathbb{A}}_1}\right), \ldots, 1 - z_N \left(1-u_{{\mathbb{A}}_N}\right) \right). \end{aligned} $$
(3)

In the system the product T-norm is used so the above Eq. (3) is expressed as:

$$ u_{\mathbb{A}} = T\left(u_{{\mathbb{A}}_1}, \ldots, u_{{\mathbb{A}}_N}; z_1, \dots, z_N \right) = \prod ^N_{n=1} \left( 1 - z_n \left(1-u_{{\mathbb{A}}_n} \right)\right). $$
(4)

Membership of a data tuple to the fuzzy set in lth rule’s premise is the firing strength of the rule for the tuple (from now on we use the rule’s index l)

$$ F_l \left({\mathbf{x}}\right) = u_{l{\mathbb{A}}} \left({\mathbf{x}}\right) \in [0, 1]. $$
(5)

To avoid misunderstandings please keep in mind the meanings of the symbols: \({u_{\mathbb{A}_n}}\) stands for membership of the nth descriptor to the fuzzy set \({\mathbb{A}_n}\) in the premise for nth attribute of a certain rule (the index of which we omit here) as in formulae 2, 3, 4, \({u_{l \mathbb{A}}}\) stands for membership of the whole data tuple to the premise of the lth rule—it is lth rule’s firing strength (as in formula 5).

Combining 2 and 4 we get firing strength F of lth rule for data vector (tuple) \(\mathbf{x}\):

$$ F_l ({\mathbf{x}}) = \prod ^N_{n=1} \left( 1 - z_{ln}^f \left\{ 1 - \exp \left[ -\frac{\left(x_{n} - v_{ln}\right)^2}{2 s_{ln}^2} \right] \right\} \right). $$
(6)

The term \({\mathfrak{b}}\) (in formula (1)) describing the lth rule’s consequence is represented by an isosceles triangle fuzzy set \({\mathbb{B}_l}\) with the base width w l , the altitude of the triangle equals 1. The localisation y l of the core of the triangle fuzzy set is determined by linear combination of input attribute values with attribute weights taken into account:

$$ \begin{aligned} y_l &= {\mathbf{p}}^{\mathrm{T}}_l \cdot \mathit{diag}\left(\left[1, {\mathbf{z}}^{\mathrm{T}}_l \right]\right) \cdot \left[1, {\mathbf{x}}^{\mathrm{T}} \right]^{\mathrm{T}} \nonumber\\ &= \left[p_{l 0}, p_{l 1}, \ldots, p_{l N} \right] \cdot \left[ \begin{array}{llll} 1 & 0 & \cdots & 0 \\ 0 & z_{l 1} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 &\cdots & z_{lN} \end{array} \right] \cdot \left[ \begin{array}{l} 1 \\ x_{1}\\ \vdots\\ x_N \end{array} \right]. \end{aligned} $$
(7)

The above formula 7 can also be written as

$$ y_l = \sum_{n = 1}^N p_{ln} z_{ln} x_n + p_{l 0} = \sum_{n = 0}^N p_{ln} z_{ln} x_n, $$
(8)

where z l0 = 1 and x 0 = 1.

The output of the lth rule is the fuzzy value of the fuzzy implication:

$$ u_{l{\mathbb{B}}^{\prime}} \left({\mathbf{x}}\right) = u_{l{\mathbb{A}}} \left({\mathbf{x}}\right) \,\rightsquigarrow\, u_{l{\mathbb{B}}}\left({\mathbf{x}}\right), $$
(9)

where squiggle arrow \((\rightsquigarrow)\) stands for fuzzy implication. The shape of the fuzzy set \({\mathbb{B}^{\prime}}\) depends on the used fuzzy implication (Czogała et al. 2000). In our system we use Reichenbach implication (Reichenbach et al. 1935)

$$ p\, \rightsquigarrow\,q = 1 - p + pq. $$
(10)

The answers \({u_{l\mathbb{B}^{\prime}}}\) of all L rules are then aggregated into one fuzzy answer of the system:

$$ u_{{\mathbb{B}}^{\prime}} \left({\mathbf{x}}\right) = \mathop{\bigoplus}\limits^L_{l = 1} u_{l{\mathbb{B}}^{\prime}} \left({\mathbf{x}}\right), $$
(11)

where \(\bigoplus\) stands for the aggregation operator. In order to get the non-fuzzy answer y 0 the fuzzy set \({\mathbb{B}^{\prime}}\) is defuzzified with MICOG method (Czogała et al. 2000). This approach removes the non-informative parts of the aggregated fuzzy sets and takes into account only the informative parts (cf. description of Fig. 1). The aggregation and defuzzyfication may be quite expensive, but it has been proved (Czogała et al. 2000) that the defuzzyfied system output can be expressed as:

$$ y_0 = \frac{\sum^L_{l=1} g_l\left({\mathbf{x}}\right) y_l({\mathbf{x}})} {\sum^L_{l=1} g_l\left({\mathbf{x}}\right)}. $$
(12)

The function g depends on the fuzzy implication, in the system the Reichenbach one is used, so for the lth rule function g is

$$ g_l \left({\mathbf{x}}\right) = \frac{w_l}{2} F_l\left({\mathbf{x}}\right). $$
(13)

The forms of g function for various implications can be found in the original work introducing the ANNBFIS system (Czogała et al. 2000). Some inaccuracies are discussed in Nowicki (2006) and Łęski (2008).

2.2 Creation of the fuzzy model

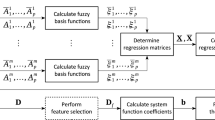
Creation of the fuzzy model (fuzzy rule base) is done in three steps: partition of the input domain (Sect. 2.2.1), extraction of rules’ premises (Sect. 2.2.2) and tuning of the rules (this step is also responsible for creation of rules consequences)—Sect. 2.2.3.

2.2.1 Partition of the input domain

For domain partition we use modification (Simiński 2012) of the FCM clustering algorithm (Dunn 1973) where the weights are the values from the interval [0, 1]. Thus each cluster is fuzzy in two ways:

  1. 1.

    Data tuples have fuzzy membership to clusters. The sum of membership of one data tuple to all clusters is 1 (cf. Eq. 16). This is common in the fuzzy clustering paradigm.

  2. 2.

    The cluster itself has fuzzy possession of attributes. This means that the cluster spreads in a fuzzy way upon the dimensions. The sum of dimensions weight of one cluster is 1 (cf. Eq. 16).

Our clustering method is based on minimising the criterion function J

$$ J = \sum^C_{c=1} \sum^X_{i=1} u_{c i}^m {\sum^N_{n=1} z_{cn}^f \left(x_{in} - v_{cn}\right)^2}. $$
(14)

where m and f ≠ 1 (the case of f = 1 is discussed on Eq. 20) are parameters, u ci stands for membership of ith data example \(\left(\mathbf{x}_i\right)\) to cth cluster, z cn stands for weight of nth attribute (descriptor) in cth cluster, x in is nth descritor of ith data tuple, v cn is nth attibute of centre of cth cluster.

The centre of cth cluster is defined as

$$ {\mathbf{v}}_{c} = \frac{\sum^X_{i=1} u_{c i} {\mathbf{x}}_i}{\sum^X_{i=1} u_{c i}}. $$
(15)

Two constraints are put on dimension weights and partition matrix:

  1. 1.

    The sum of membership values to all clusters for each data tuple is one:

    $$ \forall {i \in [1,X]} : \; \sum^C_{c = 1} u_{c i} = 1. $$
    (16)
  2. 2.

    The sum of dimension weights z for all dimensions N in each cluster c equals one:

    $$ \forall {i \in [1, C]} : \; \sum^N_{n = 1} z_{in} = 1. $$
    (17)

Applying of Langrange multipliers leads to the following formulae:

$$ u_{c i} = \frac{ \left(\sum^N_{n=1} z_{cn}^f \left(x_{in} - v_{cn}\right)^2 \right)^{\frac{1}{1-m}}} {\sum^C_{j=1} \left(\sum^N_{n=1} z_{jn}^f \left( x_{in} - v_{jn}\right) ^2 \right)^{\frac{1}{1-m}} }, $$
(18)
$$ z_{c i} = \frac{ \left( {\sum_{k=1}^X u^m_{c k}\, \left( x_{k i} - v_{c i}\right)^2}\right)^{\frac{1}{1-f}} } { \sum_{n=1}^N \left( {\sum_{k=1}^X u^m_{c k}\, \left( x_{kn} - v_{c n} \right) ^2}\right)^{\frac{1}{1-f}} }. $$
(19)

The data are clustered by alternating application of formulae 15, 18 and 19.

The procedure described above cannot be used if f = 1. The objective function (14) becomes

$$ J = \sum^C_{l=1} \sum^X_{i=1} u_{l i}^m {\sum^N_{n=1} z_{ln} \left(x_{in} - v_{ln}\right)^2}. $$
(20)

In such a case the attribute n of the lth rule for which the sum

$$ \sum^X_{i=1} u_{l i}^m { z_{ln} \left(x_{in} - v_{ln}\right)^2} $$
(21)

is minimal gets the weight z ln  = 1 and other attributes of this rule get zero weights (because of the constraint expressed by formula 17).

2.2.2 Extraction of rules

The clustering procedure elaborates memberships and weights gathered in matrices \(\mathbf{U} = \{u_{ij}\}\) and \(\mathbf{Z} = \{z_{ij}\}\) respectively which are then converted into premises’ parameters v, s and z. The number of rules is equal to the number of clusters: L = C.

The cores v of rules’ premises are calculated with formula 15. The fuzzification parameter s is calculated with formula (Czogała et al. 2000)

$$ {\mathbf{s}}_i = \sqrt{ \frac{\sum^X_{j=1} u^m_{ij} \left({\mathbf{v}}_i - {\mathbf{x}}_j \right)^2}{\sum^X_{j=1} u^m_{ij}}} . $$
(22)

The extraction of the weights of attributes is slightly more complicated. The constraint expressed by formula 17 makes the sum of all weights in a rule equal one. If two attributes have weights greater than zero, their values have to be lower than one. If all N attributes have the same weights, their weight is z = 1/N (cf. Eq. 17) and if firing strengths of all attributes are the same and equal F n , the firing strength of the whole rule is (cf. Eq. 6)

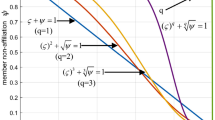
$$ \begin{aligned} F (N, F_n) = \prod_{n = 1}^N \left[ 1 - z^f \left(1-F_n \right) \right] = \left[ 1 - \frac{1}{N^f} \left(1-F_n \right) \right]^N. \end{aligned} $$
(23)

If all attributes are minimally fired (zero firing strengths) the total firing strength of the whole rule tends to one (with increase in the number of attributes), so there is no difference if the attributes are fired or not. This is highly unsatisfactory. The Fig. 2 presents this phenomenon.

Fig. 2
figure 2

Firing strength F for the whole rule (Eq. 6) when all attributes have the equal firing strength F n in function of number of attributes (N) and attribute’s weight exponent f = 2 without augmentation. If the weights of the attributes are not augmented the firing strength of the whole rule tends to one independently whether the attributes are fired of not. The figure comprises 11 draws for values from F n  = 0.0 to 1.0 with 0.1 step. The gray lines are only to join the firing strengths for the same F n values. They have no physical meaning, because the number of attributes N has only discrete values

Full size image

This can be easily avoided by augmenting of the weights of the attributes in a rule. The attribute weights for one rule are divided by the maximal values of them. This maximal values is always greater than zero. In this procedure all weights in this rule are scaled and the maximum weights become one:

$$ \forall l \in {\mathbb{L}} : z_{ln} \leftarrow \frac{z_{ln}}{\max_{i \in [1 .. N]} z_{l i}} . $$
(24)

2.2.3 Tuning of rule parameters

In neuro-fuzzy systems the parameters of the model are tuned to better fit the data. In this system the parameters of the premises (v and s in Eq. 2, z in Eq. 4) and the values of the supports w of the sets in consequences are tuned with the gradient method. The linear coefficients p (Eq. 7) for the calculation of the localisation of the consequence sets are calculated with the pseudoinverse matrix. For tuning parameters of the model the square error is used

$$ E = \frac{(y - y_0)^2}{2}, $$
(25)

where y is the original value and y 0 is the value elaborated by the system (cf. Eq. 12). For q parameter in jth rule the differential has the following form:

$$ \frac{\partial E}{\partial q_j} = \frac{\partial E}{\partial y_0} \cdot \frac{\partial y}{\partial g} \cdot \frac{\partial g}{\partial F} \cdot \frac{\partial F}{\partial q_j}. $$
(26)

Formula (26) is valid for v,  s and z parameters. For width w of the isosceles triangle in the rule’s consequence the following formula is used:

$$ \frac{\partial E}{\partial w_i} = \frac{\partial E}{\partial y} \cdot \frac{\partial y}{\partial g} \cdot \frac{\partial g}{\partial w_i}. $$
(27)

The differentials in Eq. 26 are:

$$ \frac{\partial E}{\partial y_0} = -(y - y_0) $$
(28)

and

$$ \frac{\partial y_0}{\partial g} = \frac{y_j - y_0} {\sum^L_{i=1} g\left(F_i ({\mathbf{x}}), w_i \right)}. $$
(29)

The differentials \(\frac{\partial g}{\partial F}\) and \(\frac{\partial g}{\partial w}\) depend on the used implication (cf. Eq. 13). For Reichenbach implication we have:

$$ \frac{\partial g}{\partial F} = \frac{w}{2} $$
(30)

and

$$ \frac{\partial g}{\partial w} = \frac{F}{2}. $$
(31)

For q j being v jm parameter (the core of the mth attribute in jth rule) we get (cf. Eq. 6)

$$ \begin{aligned} \frac{\partial F}{\partial v_{jm}} & = \prod ^N_{\substack{n=1\\ n\neq m}} \left( 1 - z_{in}^f \left\{ 1 - \exp \left[ -\frac{ \left(x_{n} - v_{in} \right)^2}{2 s_{in}^d} \right] \right\} \right) \cdots \nonumber \\ &\cdots z^f_{jm}\exp \left[ -\frac{ \left( x_{n} - v_{jm} \right) ^2}{2 s_{jm}^2} \right] \cdot \left[ 2 \frac{ \left( x_{m} - v_{jm} \right)}{2 s_{jm}^2}\right]. \end{aligned} $$
(32)

For q j being s jm parameter (the fuzzification of the mth attribute in jth rule) in Eq. 26 we get:

$$ \begin{aligned} \frac{\partial F}{\partial s_{jm}} = & \prod ^N_{\substack{n=1\\ n\neq j}} \left( 1 - z_{in}^f \left\{ 1 - \exp \left[ -\frac{ \left( x_{n} - v_{in} \right) ^2}{2 s_{in}^2} \right] \right\} \right) \cdots\nonumber\\ & \cdots z^f_{jm}\exp \left[ -\frac{ \left( x_{n} - v_{jm} \right)^2}{2 s_{jm}^2} \right] \cdot \left[ 2\frac{\left( x_{n} - v_{jm} \right)^2}{2 s_{jm}^3} \right] . \end{aligned} $$
(33)

And finally for q j being z jm (the weight of the mth attribute in jth rule) parameter in Eq. 26 we get:

$$ \begin{aligned} \frac{\partial F}{\partial z_{jm}} = & \prod ^N_{\substack{n=1\\ n\neq j}} \left( 1 - z_{in}^f \left\{ 1 - \exp \left[ -\frac{ \left(x_{n} - v_{in} \right) ^2}{2 s_{in}^d} \right] \right\} \right) \cdots \nonumber \\ & \cdots \left\{-1+ \exp \left[ -\frac{f \left(x_{n} - v_{jm} \right)^2}{2 s_{jm}^2} \right] \right\}. \end{aligned} $$
(34)

The linear parameters for localisation of the cores of triangle fuzzy sets in consequences are calculated as a solution to the linear equation expressed by Eq. 7. To avoid numerical problems the pseudoreverse matrix is calculated. In the calculation the weights are also taken into account.

For f = 0 (which switches off the attributes’ weights) the proposed system is identical with ANNBFIS system described in (Czogała et al. 2000).

3 Experiments

The experiments were conducted on real-life data sets depicting methane concentration, death rate, breast cancer recurrence time, concrete compressive strength and ozone concentration. All real life data sets are normalised (to mean 0 and standard deviation 1). Some parameters of data sets are gathered in Table 2.

3.1 Data set description

The ‘Methane’ data set contains the real life measurements of air parameters in a coal mine in Upper Silesia (Poland). The parameters (measured in 10 s intervals) are: AN31—the flow of air in the shaft, AN32—the flow of air in the adjacent shaft, MM32—concentration of methane (CH4), production of coal, the day of week. The 10-min sums of measurements of AN31, AN32, MM32 are added to the tuples as dynamic attributes (Sikora et al. 2005). The task is to predict the concentration of the methane in 10 min. The data is divided into a train set (499 tuples) and test set (523 tuples).

The ‘Death’ data represent the tuples containing information on various factors, the task is to estimate the death rate (Späth 1992). The first attribute (the index) is excluded from the dataset. The precise description of the attributes is available with the data set, the names of the attributes are listed in Table 7, so the description is omitted here. The data can be downloaded from a public repository. Footnote 1

The ‘Breast cancer’ data set represents the data for the breast cancer case (Asuncion and Newman 2007). Each data tuple contains 32 continuous attributes and one predictive attribute (the time to recur). Here again we will omit the description of attributes, their names are listed in Table 6. The symbol ‘se’ in the attribute’s name stands for ‘standard error’ and the adjective ‘worst’ means the ‘largest’. The data can be downloaded Footnote 2 from a public repository (Frank et al. 2010).

The ‘Concrete’ set is a real life data set describing the parameters of the concrete sample and its strength (Yeh 1998). The attributes are: cement ratio, amount of blast furnace slag, fly ash, water, superplasticizer, coarse aggregate, fine aggregate, age; the decision attribute is the concrete compressive strength. The original data set can be downloaded Footnote 3 from public repository (Frank et al. 2010).

The ‘Ozone’ set—a real life data set—describes the level of ozone in the air (Zhang and Fan 2008). The data set includes 2536 tuples with 73 attributes. The original data set can be downloaded Footnote 4 from a public repository (Frank et al. 2010). The data set has 687 tuples with missing values, these were deleted from the data set and 1847 full tuples were left. The first attribute (date) was deleted from the tuples. The tuples were numbered starting with 1. The tuples with odd numbers are used as a train set (924 tuples), the even numbered tuples constitute the test data set (923 tuples). All attributes are real numbers. The task is to predict the level of ozone (high 1 or low 0).

3.2 Results of experiments

The fuzzy models were created with train sets. The number of rules is always the same as the number of clusters and was assumed a priori as L = 5 (for the ‘Ozone’ dataset L = 3). Finding the optimal number of clusters in clustering is a difficult task. Our aim here is not to discuss this problem, but to compare the precision of our system with the one already existing. This is why we assume the a priori number of rules.

The experiments were conducted in two paradigms. In the first one—data approximation (DA)—the models are created and tested with the same train data sets. In the other—knowledge generalisation (KG)—the models are created with train data sets and tested with unseen tuples of test data sets.

Root mean square error (RMSE) measure is used to evaluate the elaborated results:

$$ RMSE = \sqrt{\frac{1}{X} \sum_{i = 0}^X \left(y \left( {\mathbf{x}}_i \right) - y_0 \left( {\mathbf{x}}_i \right) \right)^2}, $$
(35)

where \(y \left( \mathbf{x}_i \right)\) stands for original (expected) value for ith tuple and \(y_0 \left( \mathbf{x}_i \right)\) is the value elaborated by the system; X is the number of tuples.

Two main features were tested: (1) the precision of created models and (2) the weights assigned to dimensions (attributes).

3.3 Precision of models

Table 3 presents the RMSE results elaborated for various values of f parameter. For f = 0 the system elaborates the same results as ANNBFIS system. The results gathered in Table 3 are also presented as graphs in Fig. 3a–d.

Table 3 Root mean square error elaborated by our system
Full size table
Fig. 3
figure 3

Root mean square errors for the real life data sets. The results for data approximation (DA) are denoted with times signs, for knowledge generalisation (KG)—black squares. The symbols are accompanied by auxiliary lines for higher readability

Full size image

The experiments reveal that for \(f \in [1.5, 2]\) the RMSE, elaborated by the systems for various data sets, achieves its most advantageous values both for DA and KG. For f > 2 the KG error starts to grow, whereas the DA error is kept on more or less the same level. The optimal interval of f parameter seems independent from the data sets.

The Figs. 4, 5, 6 and 7 present the comparison of results elaborated by ANNBFIS (the gray lines) and our system (the black lines) with f = 2. The squares denote the expected values. The Figs. 8 and 9 present in a more detailed way the result for tuples 50–150 and 250–400 respectively. Similarly, the Fig. 10 presents the details of the Fig. 5 for tuples 400–500.

Fig. 4
figure 4

The values elaborated for the ‘Death’ data set (KG). The original values are marked with the black squares, the values elaborated by ANNBFIS by the gray line, elaborated by NFS with weighted attributes by the black line. Number of rules L = 5, f = 2

Full size image
Fig. 5
figure 5

The values elaborated for the ‘Methane’ data set (KG). The original values are marked with the black squares, the values elaborated by ANNBFIS by the gray line, elaborated by NFS with weighted attributes by the black line. Number of rules L = 5, f = 2

Full size image
Fig. 6
figure 6

The values elaborated for the ‘Breast cancer’ data set (KG). The original values are marked with the black squares, the values elaborated by ANNBFIS by the gray line, elaborated by NFS with weighted attributes by the black line. Number of rules L = 5, f = 2

Full size image
Fig. 7
figure 7

The values elaborated for the ‘Concrete’ data set (KG). The original values are marked with the black squares, the values elaborated by ANNBFIS by the gray line, elaborated by NFS with weighted attributes by the black line. Number of rules L = 5, f = 2

Full size image
Fig. 8
figure 8

The values elaborated for the ‘Concrete’ data set (KG). The original values are marked with the black squares, the values elaborated by ANNBFIS by the gray line, elaborated by NFS with weighted attributes by the black line. Number of rules L = 5, f = 2. The figure presents in a more detailed way the part of Fig. 7

Full size image
Fig. 9
figure 9

The values elaborated for the ‘Concrete’ data set (KG). The original values are marked with the black squares, the values elaborated by ANNBFIS by the gray line, elaborated by NFS with weighted attributes by the black line. Number of rules L = 5, f = 2. The figure presents in a more detailed way the part of Fig. 7

Full size image
Fig. 10
figure 10

The values elaborated for the ‘Methane’ data set (KG). The original values are marked with the black squares, the values elaborated by ANNBFIS by the gray line, elaborated by NFS with weighted attributes by the black line. Number of rules L = 5, f = 2. The figure presents in a more detailed way the part of Fig. 5

Full size image

The figures show that applying attribute weights in the fuzzy rule base results in a more precise prediction. The better prediction can be observed in Fig. 8, where the expected values are better elaborated by our systems (the black line) than by the original ANNBFIS system that does not use attribute weights in rules (the gray line).

3.3.1 Weights of attributes

Another feature tested in experiments are the weights assigned to attributes (dimensions). The Tables 4, 5, 6, 7 and Figs. 11, 12, 13 and 14 present the weights of attributes in models elaborated for real life data sets.

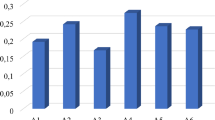
Table 4 Weights of attributes elaborated for the ‘Methane’ data set (cf. Fig. 11)
Full size table
Table 5 Weights of attributes elaborated for the ‘Concrete’ data set (cf. Fig. 12)
Full size table
Table 6 Weights of attributes elaborated for the ‘Breast cancer’ data set (cf. Fig. 13)
Full size table
Table 7 Weights of attributes elaborated for the ‘Death’ data set (cf. Fig. 14)
Full size table
Fig. 11
figure 11

Weights of attributes elaborated for the ‘Methane’ data set (cf. Table 4)

Full size image
Fig. 12
figure 12

Weights of attributes elaborated for the ‘Concrete’ data set (cf. Fig. 12)

Full size image
Fig. 13
figure 13

Weights of attributes elaborated for the ‘Breast cancer’ data set (cf. Table 6)

Full size image
Fig. 14
figure 14

Weights of attributes elaborated for the ‘Death’ data set (cf. Table 7)

Full size image

The attributes’ weights for the ‘Methane’ data set (prediction of methane concentration in a coal mine shaft) gathered in Table 4 and presented in Fig. 11 show a very interesting fact: the actual concentration of methane (the third attribute) turned out to be of minor importance in all the rules, although the task was the 10-min prediction of the concentration of the methane in the shaft. The most important attributes are the flow of air in the mine shaft (the first attribute) and the production of coal (the fourth attribute). It can be explained by the fact that excavation of coal causes tensions and splits in the rock that may release the methane gas. In two rules the most important attribute is the first one, the flow of the air in the shaft in question. In the fifth rule an interesting phenomenon can be observed. The most important attribute is the fifth one, the 10-min sum of the first attribute (flow of the air), whereas the first attribute itself has lower weight. The similar situation occurs in the case of the second attribute (flow of the air in the adjacent shaft), where the sum of air flow measurements in the adjacent shaft (the sixth attribute) is more important than the summed air flow itself (the second attribute).

The weights of attributes elaborated for the ‘Concrete’ data set are presented in Table 5 and Fig. 12. The most important attributes (all others have low weights) are: blast furnace slag (the second attribute), ratio of fly ash (the third attribute), fine aggregate (the seventh attribute) and age of concrete (the eighth attribute). In one rule the weights are more varied: the most important attribute is age, but concentration of blast furnace slag and fly ash have also quite high weights.

The weights of attributes elaborated for the ‘Breast cancer’ data set are presented in Table 6 and Fig. 6. In rule I the most important attribute is the first one (lymph nodes), which is in concordance with medical diagnose procedures. In all the rules the importance of three attributes: radius mean (the second attribute), perimeter mean (the fourth attribute) and area mean (the fifth attribute) are correlated. In rule III there are two triples of attributes of higher importance. The triple of high importance comprises: area worst (the 25th attribute), perimeter worst (the 24th attribute) and radius worst (the 22nd attribute). This triple is accompanied be the triple of slightly lower importance: area mean (the fifth attribute), perimeter mean (the fourth attribute) and radium mean (the second attribute). In one rule the weights are more varied. The important attributes are fractal dimension worst (the 31st attribute), fractal dimension standard deviation (the 21st attribute) and fractal dimension mean (the 11th attribute), smoothness standard deviation (the 16th attribute) and compactness worst (the 27th attribute).

The weights of attributes elaborated for the ‘Death’ data set are presented in Table 7 and Fig. 14. In rules I, III and V the most important attributes are the hydrocarbon pollution index (the 12th attribute) and the nitric oxide pollution index (the 13th attribute). It is interesting that the pollution index for sulphur dioxide has low weight in all rules. In the second rule the most important attribute describes scholarisation of persons over 22 (the sixth attribute).

The experiments were also executed on the ‘Ozone’ data set. This real life data set comprises 72 attributes describing the meteorological measurements (the original data set has 73 attributes, but the first one—the date—has been deleted as mentioned in the data set’s description above). The attributes are not listed here, their short description is available at the data repository, from which the data set can be downloaded. The tuples are labelled 0 or 1. The task is to classify the unseen data examples. Our system was trained with 0 or 1 labels, but it elaborates the real value answer. The answers lower than 0.5 were labelled with zero, otherwise with one. The experiments were conducted with ANNBFIS and our subspace neuro-fuzzy systems. The ANNBFIS system assigned the major class to all the answers. The subspace approach elaborated more precise results (precision: 0.926). The weights of attributes are presented in Fig. 15. In the next experiment only the attributes with weights higher than 0.7 in at least two rules were selected. This led to the selection of attributes 27 to 53. All these attributes describe the results of temperature measurements. The results were a bit poorer (precision: 0.921) than in the case when all attributes were used.

Fig. 15
figure 15

Weights of attributes elaborated for the ‘Ozone’ data set

Full size image

4 Summary

The paper describes the novel neuro-fuzzy system with weighted attributes. In this approach the attributes in a fuzzy rule have weights. The weights of attributes are numbers from the interval [0, 1]. The weights of the attributes are not assigned globally, but each fuzzy rule has its own weights of attributes. Each rule exists in its own subspace. An attribute can be important in a certain rule, but unimportant in another. This approach is inspired by subspace clustering, but in our system the attribute can have partial weight, which is uncommon in subspace clustering where attributes have full (1) or none (0) weights in a subspace.

There are two main advantages of the approach proposed in the paper:

  1. 1.

    The experiments show that fuzzy models with weighted attributes can elaborate more precise results, both for data approximation and knowledge generalisation for real life data sets in comparison with a neuro-fuzzy system that does not assign weights to attributes.

  2. 2.

    Assigning weights to attributes discovers knowledge on importance of attributes in a problem. Individual weights of attributes in each rule discover the relation between attributes. This may explain why the weights of the same attribute are low in one rule and high in another one.

The experiments show that assigned weights of the attributes are in concordance with experts’ knowledge on the physical or medical mechanisms described by the data sets.