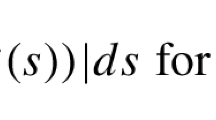Operator-valued multiplier theorems for causal translation-invariant operators with applications to control theoretic input-output stability

Abstract

We prove an operator-valued Laplace multiplier theorem for causal translation-invariant linear operators which provides a characterization of continuity from $H^\alpha ({\mathbb {R}},U)$ to $H^\beta ({\mathbb {R}},U)$ (fractional U-valued Sobolev spaces, U a complex Hilbert space) in terms of a certain boundedness property of the transfer function (or symbol), an operator-valued holomorphic function on the right-half of the complex plane. We identify sufficient conditions under which this boundedness property is equivalent to a similar property of the boundary function of the transfer function. Under the assumption that U is separable, the Laplace multiplier theorem is used to derive a Fourier multiplier theorem. We provide an application to mathematical control theory, by developing a novel input-output stability framework for a large class of causal translation-invariant linear operators which refines existing input-output stability theories. Furthermore, we show how our work is linked to the theory of well-posed linear systems and to results on polynomial stability of operator semigroups. Several examples are discussed in some detail.

1 Introduction

It is well-known (see [36, Theorem 10.3.5], [38, Theorem 9.1 ] or [41]) that a linear operator $G:L^2({\mathbb {R}},U)\rightarrow L^2({\mathbb {R}},U)$ is causal, translation-invariant and continuous if, and only if, there exists a bounded ${{\mathcal {B}}}(U)$-valued holomorphic function $\textbf{G}$ on the open right-half complex plane such that

$$\begin{aligned} Gu={{\mathcal {L}}}^{-1}(\textbf{G}{{\mathcal {L}}}u)\quad \hbox {for all~} u\in L^2({\mathbb {R}},U) \hbox {with support in~} [0,\infty ), \end{aligned}$$

(1.1)

in which case,

$$\begin{aligned} \big \Vert G\big \Vert _{{{\mathcal {B}}}(L^2({\mathbb {R}},U))}=\sup _{\textrm{Re}\,s>0}\Vert \textbf{G}(s)\Vert . \end{aligned}$$

Here, U is a complex Hilbert space, ${{\mathcal {B}}}(U)$ denotes the space of bounded linear operators $U\rightarrow U$, ${{\mathcal {L}}}$ is the Laplace transform, and causality of G means that if u and v coincide on an interval of the form $(-\infty ,\tau )$, then so do Gu and Gv.

We remark that representations of causal translation-invariant (or right-shift invariant) operators by holomorphic functions play an important role in mathematical systems and control theory in general (see [28]) and in the theory of well-posed linear systems in particular (see [36]). In a control-theoretic context, the holomorphic function $\textbf{G}$ representing the operator G — the so-called symbol of G — is referred to as the transfer function of G. The multiplier theorem [36, Theorem 10.3.5] (or [38, Theorem 9.1]) mentioned above (see representation formula (1.1)) rests on the Paley-Wiener theorem (see, for example, [4, Theorem 1.8.3] or [36, Theorem 10.3.4]), and the Hilbert space structure of $L^2({\mathbb {R}},U)$ is crucial. Indeed, it is well-known that not all causal translation-invariant operators on Banach spaces admit such a multiplier representation [29, 41].

In Sect. 3 of this paper, we prove the following generalization of the above result.

Laplace multiplier theorem. Let $\alpha ,\beta \in {\mathbb {R}}$. A linear operator $G:H^\alpha ({\mathbb {R}},U)\rightarrow H^\beta ({\mathbb {R}},U)$ is bounded, translation-invariant and causal if, and only if, there exists a ${{\mathcal {B}}}(U)$-valued holomorphic function $\textbf{G}$ on the open right-half complex plane such that

$$\begin{aligned} Gu={{\mathcal {L}}}^{-1}(\textbf{G}{{\mathcal {L}}}u)\quad \text{ for } \text{ all }~u\in H^\alpha ({\mathbb {R}},U)\,\hbox { with support bounded on the left} \end{aligned}$$

and

$$\begin{aligned} \gamma :=\sup _{\textrm{Re}\,s>0}\Vert (1+s)^{\beta -\alpha }\textbf{G}(s)\Vert <\infty , \end{aligned}$$

(1.2)

where $H^\alpha ({\mathbb {R}},U)$ is the fractional Sobolev space of U-valued tempered distributions (sometimes also referred to as a Bessel potential space). Furthermore, $\Vert G\Vert _{{{\mathcal {B}}}(H^\alpha ,H^\beta )}=\gamma$.

The above multiplier theorem appears as Theorem 3.1 in the paper. Its proof is based on the representation result for operators $L^2({\mathbb {R}},U)\rightarrow L^2({\mathbb {R}},U)$ and a natural scale of causal translation-invariant isometric isomorphisms $L^2({\mathbb {R}},U) \rightarrow H^\alpha ({\mathbb {R}},U)$. We use the Laplace multiplier theorem to derive the following corollary.

Fourier multiplier corollary. Assume that U is separable and let $\alpha ,\beta \in {\mathbb {R}}$. A linear operator $G:H^\alpha ({\mathbb {R}},U)\rightarrow H^\beta ({\mathbb {R}},U)$ is bounded, translation-invariant and causal if, and only if, there exists a ${{\mathcal {B}}}(U)$-valued holomorphic function $\textbf{G}$ on the open right-half complex plane such that

$$\begin{aligned} Gu={{\mathcal {F}}}^{-1}(\textbf{G}_0{{\mathcal {F}}}u)\quad \hbox { for all~}\ u\in H^\alpha ({\mathbb {R}},U)\quad \text{ and }\quad \gamma <\infty , \end{aligned}$$

(1.3)

in which case

$$\begin{aligned} \Vert G\Vert _{{{\mathcal {B}}}(H^\alpha ,H^\beta )}=\gamma =\mathrm{ess\,sup}_{y\in {\mathbb {R}}}\Vert (1+iy)^{\beta -\alpha }\textbf{G}_0(y)\Vert <\infty , \end{aligned}$$

where ${{\mathcal {F}}}$ denotes the Fourier transform and $\textbf{G}_0(y):=\lim _{x\downarrow 0}\textbf{G}(x+iy)$ for almost every  $y\in {\mathbb {R}}$.

We remark that the separability of U is crucial for the existence of the pointwise boundary limit $\textbf{G}_0$. The above Fourier multiplier corollary generalizes the $L^2$-result in [38, Theorems 5.2 and 6.5].

Whilst a non-causal translation-invariant bounded linear operator G on $L^2({\mathbb {R}},U)$ also admits a multiplier representation of the form (1.3) (see [5, Theorems 71–73] and [38, Theorem 5.2]), there does not exist a bounded holomorphic function $\textbf{G}$ on the open right-half plane such that $\textbf{G}_0$ is the boundary function of $\textbf{G}$. In a more general setting (where, for example, the functions in the domain and codomain of the operator may depend on several variables), the relationship between causality and holomorphicity has been explored in [17]. We remark that Fourier multiplier theorems play an important role in the abstract theory of linear and quasilinear parabolic systems [2, 3] and in the stability theory of operator semigroups (see, for example, [32, 33]). We emphasize that our work focuses on causal operators and note that causality does not play a role in much of the Fourier multiplier literature.

Returning to the above Laplace multiplier theorem, given a holomorphic ${{\mathcal {B}}}(U)$-valued function $\textbf{G}$ on the open right-half plane, it may be difficult to check directly if the quantity $\gamma$ defined in (1.2) is finite. Usually, if the boundary function $\textbf{G}_0$ exists, the imaginary axis condition

$$\begin{aligned} \gamma _0:=\mathrm{ess\,sup}_{y\in {\mathbb {R}}}\Vert (1+iy)^{\beta -\alpha }\textbf{G}_0(y)\Vert <\infty \end{aligned}$$

is easier to deal with. If $\gamma <\infty$, then $\gamma =\gamma _0$; however, if $\gamma _0<\infty$, then it does in general not follow that $\gamma =\gamma _0<\infty$. For applications of the above theorems (in a control theoretic context, for example), it is important, therefore, to identify conditions which ensure that the finiteness of $\gamma _0$ implies that of $\gamma$, in which case $\gamma =\gamma _0$. In Sect. 4 of this paper, inspired by certain results on distributional boundary values of holomorphic functions from [8,9,10, 26], we derive several such conditions. In particular, it is shown that if $\textbf{G}$ is polynomially bounded and $\gamma _0<\infty$, then $\gamma =\gamma _0$. We remark that the relevant theorems in [8,9,10, 26] are not in a suitable form to be directly applicable in the current context and, hence, we develop and prove bespoke versions of these results.

There is a rich history of analysing control systems from a functional analytic perspective, see, for instance, [13, 27, 28, 36, 43]. In the so-called input-output approach to systems and control, a system is considered as an operator, usually referred to as the input-output operator, mapping inputs (control functions) to outputs (observation functions), both of which are defined on ${\mathbb {R}}$ or $[0,\infty )$ (interpreted as the bi-lateral or uni-lateral time axis, respectively) and take values in a Hilbert space U. As causality is a key feature of physical control systems, input-output operators are assumed to be causal. Certain continuity or boundedness properties of the input-output operator are referred to as input-output stability, a theory which dates back to the 1960s (see [15]), with $L^2$-stability (finite-energy-input finite-energy-output) and $L^\infty$-stability (bounded-input bounded-output) being the most prominent examples.¹ For various classes of systems, input-output stability properties have been (i) characterized in terms of transfer functions and (ii) linked to stability concepts in the sense of Lyapunov, see, for example, [34, Chapter 12], [36, Chapter 8], [39, Section 3.7] and [42].

In Sect. 5, we apply the above Laplace multiplier theorem and the results of Sect. 4 to develop a novel control-theoretic input-output stability framework, referred to as Sobolev stability, for a large class of causal translation-invariant operators (equivalently, causal convolution operators with ${{\mathcal {B}}}(U)$-valued distributional kernels). Our new concept of Sobolev $(\alpha ,\beta )$-stability relates to the boundedness of a causal translation-invariant input-output operator G as a map from $\textrm{dom}\,G\subset H^\alpha ({\mathbb {R}},U)$ to $H^\beta ({\mathbb {R}},U)$, where $\alpha ,\beta \in {\mathbb {R}}$. It is particularly relevant in the analysis of systems which are not $L^2$-stable, but exhibit certain weaker stability properties and, as we demonstrate, can be viewed as considerable refinement of the concept of P-stability [23, 30]. In Theorem 5.4, we provide several characterizations of Sobolev $(\alpha ,\beta )$-stability of G in terms of its transfer function $\textbf{G}$, and use these to link Sobolev stability to results on polynomial decay of operator semigroups [1, 6, 30] in Proposition 5.9. We also make contact with the theory of well-posed linear systems [36] by providing, in Corollary 5.7, criteria for Sobolev $(\alpha ,\beta )$-stability of the input-output operators of well-posed linear systems.

In Sect. 6, we discuss several examples in detail, including a neutral functional differential equation and a heat equation on a square with boundary control along the top edge. Using the results on Sobolev stability from Sect. 5, we determine for which values of $\alpha$ and $\beta$ the systems under consideration are Sobolev $(\alpha ,\beta )$-stable. Finally, in Sect. 7, we derive a half-line version of the above Laplace multiplier theorem which provides a characterization of right-shift invariant bounded linear operators defined on the subspace of all $u\in H^\alpha ({\mathbb {R}},U)$ with support in $[0,\infty )$.

Apart from Sect. 3, 4, 5, 6 and 7 which we have described in some detail, the paper contains Section 2 and an Appendix (Section 8). The former is devoted to notation, terminology, background material and preliminaries, whilst the latter contains remarks on the convolution of vector-valued distributions (Appendix 1), the proofs of two results from Sect. 2 (Appendix 2) and the proof of Theorem 4.1 (Appendix 3).

Finally, throughout the paper, to simplify the presentation, we consider the scenario of causal translation-invariant linear operators, the domains and codomains of which consist of vector-valued distributions with values in the same Hilbert space U. The case of operators mapping a space of U-valued distributions to a space of Y-valued distributions (Y another Hilbert space) can be reduced to said scenario by an augmentation trick: if G is a causal translation-invariant linear operator mapping U-valued to Y-valued distributions with a ${{\mathcal {B}}}(U,Y)$-valued transfer function $\textbf{G}$, then, setting ${\tilde{U}}:=U\times Y$,

$$\begin{aligned} {\tilde{G}}:=\begin{pmatrix}0 &{}\quad 0 \\ G &{}\quad 0\end{pmatrix}\quad \text{ and }\quad {\tilde{\textbf{G}}} : = \begin{pmatrix}0 &{}\quad 0 \\ \textbf{G}&{}\quad 0\end{pmatrix}, \end{aligned}$$

the operator ${\tilde{G}}$ is causal, linear and translation invariant, maps ${\tilde{U}}$-valued distributions to ${\tilde{U}}$-valued distributions, and ${\tilde{\textbf{G}}}$, the transfer function of ${\tilde{G}}$, has values in ${{\mathcal {B}}}({\tilde{U}})={{\mathcal {B}}}({\tilde{U}},{\tilde{U}})$. The results of the paper facilitate the analysis of ${\tilde{G}}$ and ${\tilde{\textbf{G}}}$, and any conclusions can be used to draw corresponding conclusions relating to G and $\textbf{G}$, the original operator and its transfer function, respectively.

2 Preliminaries

Most mathematical notation used is standard. As usual, let ${\mathbb {N}}$, ${\mathbb {Z}}$, ${\mathbb {R}}$ and ${\mathbb {C}}$ denote the positive integers (natural numbers), integers, real numbers and complex numbers, respectively. Furthermore, we set

$$\begin{aligned} {\mathbb {N}}_0 := {\mathbb {N}}\cup \{0\}, \quad {\mathbb {R}}_+ := [0, \infty ) \quad \text {and} \quad {\mathbb {C}}_\mu := \big \{ s \in {\mathbb {C}}\, : \, \textrm{Re}\,(s) > \mu \} \quad \forall \, \mu \in {\mathbb {R}}\,. \end{aligned}$$

Let X and Z be complex Banach spaces. The space of all linear bounded operators $X\rightarrow Z$ is denoted by ${{\mathcal {B}}}(X,Z)$. Endowed with the usual induced operator norm, ${{\mathcal {B}}}(X,Z)$ becomes a Banach space. We set ${{\mathcal {B}}}(X):={{\mathcal {B}}}(X,X)$. The space of continuous functions from ${\mathbb {R}}\rightarrow X$ is denoted by $C({\mathbb {R}},X)$, and $C^\infty ({\mathbb {R}},X)$ and $C^\infty _\textrm{c}({\mathbb {R}},X)$ denote the subspaces of smooth functions and smooth functions with compact support, respectively.

For more details on the following material on spaces of vector-valued functions and distributions, we refer to

$\bullet$:

[13, Appendix A.5] and [22, Chapter III] for vector-valued measurability and integration;

$\bullet$:

[31, Chapter 4] and [38] for operator-valued ${{\mathcal {H}}}^\infty$-functions;

$\bullet$:

[2, Chapter III: Sections 4.1 and 4.2], [3, Chapter VII], [14, Chapter XVI: Section 2], [16, Chapter 8] and [43, Chapters 3, 5 and 6] for vector-valued distributions.

Let $L^p({\mathbb {R}},X)$ denote the usual Bochner-Lebesgue space of functions ${\mathbb {R}}\rightarrow X$, where $1\le p\le \infty$. As usual, $L^p_\textrm{loc}({\mathbb {R}},X)$ stands for the localized version of $L^p({\mathbb {R}},X)$. The subspace of functions in $L^p({\mathbb {R}},X)$ with support bounded on the left is denoted by $L^p_\ell ({\mathbb {R}},X)$, and we set

$$\begin{aligned} L^p_+({\mathbb {R}},X):=\{u\in L^p_\ell ({\mathbb {R}},X):\textrm{supp}\,u\subset [0,\infty )\}\subset L^p_\ell ({\mathbb {R}},X). \end{aligned}$$

Let ${{\mathcal {S}}}$ be the Schwartz space of rapidly decreasing smooth functions ${\mathbb {R}}\rightarrow {\mathbb {C}}$ and let ${{\mathcal {D}}}\subset {{\mathcal {S}}}$ be the space of compactly supported smooth test functions ${\mathbb {R}}\rightarrow {\mathbb {C}}$, endowed with their usual topologies. The spaces of all continuous linear maps ${{\mathcal {D}}}\rightarrow X$ and ${{\mathcal {S}}}\rightarrow X$ are denoted by ${{\mathcal {D}}}'(X)$ and ${{\mathcal {S}}}'(X)$, respectively. We have that ${{\mathcal {S}}}'(X)\subset {{\mathcal {D}}}'(X)$ and the elements in ${{\mathcal {D}}}'(X)$ are called X-valued distributions. A distribution in ${{\mathcal {S}}}'(X)$ is said to be tempered (or, slowly growing). The subspace of distributions in ${{\mathcal {D}}}'(X)$ with support bounded on the left is denoted by ${{\mathcal {D}}}'_{\ell }(X)$, and similarly, ${{\mathcal {S}}}'_{\ell }(X)$ stands for the space of tempered distributions having support bounded on the left.

Let $f\in L^1_\textrm{loc}({\mathbb {R}},X)$. The map ${{\mathcal {D}}}\rightarrow X,\,{\varphi }\mapsto \int _{-\infty }^{\infty }{\varphi }(t)f(t)\,\textrm{d}t$ is well defined and continuous, and we denote the corresponding regular distribution by [f]. If $f\in L^p({\mathbb {R}},X)$, $1\le p\le \infty$, or if there exists $r>0$ such that the function $t\mapsto \Vert f(t)\Vert$ is polynomially bounded on the set ${\mathbb {R}}\backslash [-r,r]$, then [f] extends to ${{\mathcal {S}}}$ and $[f]\in {{\mathcal {S}}}'(X)$.

Moreover, set

$$\begin{aligned}{} & {} {{\mathcal {O}}}_\textrm{M}:=\{\eta \in C^\infty ({\mathbb {R}},{\mathbb {C}}): \eta ^{(k)} \hbox {is polynomially bounded for every~} k\in {\mathbb {N}}_0\}, \\{} & {} {{\mathcal {O}}}_\textrm{M}^+:=\{\eta \in C^\infty ({\mathbb {R}},{\mathbb {C}}):\eta ^{(k)}\, \text{ is } \text{ polynomially } \text{ bounded } \text{ on }~[0,\infty ) \text{ for } \text{ every } k\in {\mathbb {N}}_0\} \end{aligned}$$

and, for $\tau \in {\mathbb {R}}$,

$$\begin{aligned} {{\mathcal {U}}}_\tau := \{\eta \in C^\infty ({\mathbb {R}},{\mathbb {C}}):\exists \,t_1<t_0<\tau \text{ s.t. }~\eta (t)= & {} 1\,\,\,{\forall }\,t \in (t_0,\infty )\, \text{ and }~\eta (t)\\ {}= & {} 0\,\,\,{\forall }\,t\in (-\infty ,t_1)\}. \end{aligned}$$

We note that if $\psi \in {{\mathcal {O}}}_\textrm{M}^+$, then, for every $\tau \in {\mathbb {R}}$, $\psi$ and its derivatives are polynomially bounded on $[\tau ,\infty )$. Conversely, if $\psi \in C^\infty ({\mathbb {R}},{\mathbb {C}})$ is such that $\psi$ and its derivatives are polynomially bounded on $[\tau ,\infty )$ for some $\tau \in {\mathbb {R}}$, then $\psi \in {{\mathcal {O}}}_\textrm{M}^+$. For our purposes, the most important functions $\psi \in {{\mathcal {O}}}_\textrm{M}^+$ which are not polynomially bounded on the whole real line are of the form $\psi (t)=e^{-ct}$, where $c>0$. If $\psi \in {{\mathcal {O}}}_\textrm{M}$, then $\psi {\varphi }\in {{\mathcal {S}}}$ for all ${\varphi }\in {{\mathcal {S}}}$. Consequently, the product $\psi u$, where $\psi \in {{\mathcal {O}}}_\textrm{M}$ and $u\in {{\mathcal {S}}}'(X)$, defined by

$$\begin{aligned} (\psi u)({\varphi }):=u(\psi {\varphi })\quad \forall \,{\varphi }\in {{\mathcal {S}}}, \end{aligned}$$

is a tempered X-valued distribution. For $u\in {{\mathcal {S}}}'(X)\subset {{\mathcal {D}}}'(X)$ and $\psi \in C^\infty ({\mathbb {R}},{\mathbb {C}})$, the product $\psi u$ is in ${{\mathcal {D}}}'(X)$, but in general not in ${{\mathcal {S}}}'(X)$. However, if $\psi \in {{\mathcal {O}}}_\textrm{M}^+$ and $u\in {{\mathcal {S}}}'(X)$ with $\textrm{supp}\,u\subset [\tau ,\infty )$ for some $\tau \in {\mathbb {R}}$, then it is straightforward to show that the product $\psi u$ defined by

$$\begin{aligned} (\psi u)({\varphi }):=u(\eta \psi {\varphi })\quad \forall \,{\varphi }\in {{\mathcal {S}}},\quad \text{ where }~\eta \in {{\mathcal {U}}}_\tau \hbox {is arbitrary}, \end{aligned}$$

does not depend on $\eta \in {{\mathcal {U}}}_\tau$, and $\psi u\in {{\mathcal {S}}}'(X)$.

For a function $f\in L^1({\mathbb {R}},X)$, we define the Fourier transform by

$$\begin{aligned} ({{\mathcal {F}}}f)(y):=\int _{-\infty }^\infty e^{-iy t}f(t)\,\textrm{d}t\quad \forall \,y\in {\mathbb {R}}. \end{aligned}$$

As ${{\mathcal {F}}}$ is an automorphism on ${{\mathcal {S}}}$, the definition of the Fourier transform extends to ${{\mathcal {S}}}'(X)$ via

$$\begin{aligned} ({{\mathcal {F}}}u)({\varphi }):=u({{\mathcal {F}}}{\varphi })\quad \forall \,{\varphi }\in {{\mathcal {S}}},\quad \hbox { where~}\ u\in {{\mathcal {S}}}'(X). \end{aligned}$$

It is well-known that the Fourier transform ${{\mathcal {F}}}$ is an automorphism on ${{\mathcal {S}}}'(X)$ with ${{\mathcal {F}}}$ and ${{\mathcal {F}}}^{-1}$ being sequentially continuous. If $f\in L^1({\mathbb {R}},X)$, then ${{\mathcal {F}}}[f]=[{{\mathcal {F}}}f]$. If $X=U$ is a complex Hilbert space, then the restriction of ${{\mathcal {F}}}$ to $L^1({\mathbb {R}},U)\cap L^2({\mathbb {R}},U)$ extends to an automorphism on $L^2({\mathbb {R}},U)$, in fact, $(1/\sqrt{2\pi }){{\mathcal {F}}}$ is a unitary operator on $L^2({\mathbb {R}},U)$, and so $\Vert {{\mathcal {F}}}u\Vert _{L^2({\mathbb {R}})}=\sqrt{2\pi }\Vert u\Vert _{L^2({\mathbb {R}})}$ for every $u\in L^2({\mathbb {R}},U)$.

For $\theta \in {\mathbb {R}}$ and U a complex Hilbert space, we define the Sobolev space (sometimes also called Bessel potential space)

$$\begin{aligned} H^\theta ({\mathbb {R}},U):=\big \{u\in {{\mathcal {S}}}'(U): \big (y\mapsto (1+y^2)^{\theta /2}({{\mathcal {F}}}u)(y)\big )\in L^2({\mathbb {R}},U)\big \}, \end{aligned}$$

with inner product and associated norm given by

$$\begin{aligned} \langle u,v\rangle :=\frac{1}{2\pi }\int _{-\infty }^\infty (1+y^2)^\theta \langle ({{\mathcal {F}}}u)(y),({{\mathcal {F}}}v)(y)\rangle \,\textrm{d}y,\quad \forall \, u,v\in H^\theta ({\mathbb {R}},U), \end{aligned}$$

and

$$\begin{aligned} \Vert u\Vert _{H^\theta }:=\left( \frac{1}{2\pi }\int _{-\infty }^\infty (1+y^2)^\theta \Vert ({{\mathcal {F}}}u)(y)\Vert ^2\textrm{d}y\right) ^{1/2},\quad \forall \, u\in H^\theta ({\mathbb {R}},U), \end{aligned}$$

respectively. The space $H^\theta ({\mathbb {R}},U)$ is complete and hence a Hilbert space. We note that $H^0({\mathbb {R}},U)=L^2({\mathbb {R}},U)$ and $\Vert u\Vert _{H^0}=\Vert u\Vert _{L^2}$ for all $u\in L^2({\mathbb {R}},U)$. If $\theta \ge 0$, then $H^\theta ({\mathbb {R}},U)\subset L^2({\mathbb {R}},U)$, whilst $H^\theta ({\mathbb {R}},U)$ contains non-regular distributions when $\theta <0$. We also note that if $u\in H^\theta ({\mathbb {R}},U)$, then ${{\mathcal {F}}}u\in L^2_\textrm{loc}({\mathbb {R}},U)$ whatever the value of $\theta$. We will also make use of the space $H^\theta _\ell ({\mathbb {R}},U):=H^\theta ({\mathbb {R}},U)\cap {{\mathcal {S}}}'_\ell ({\mathbb {R}},U)$ and the half-line Sobolev space

$$\begin{aligned} H^\theta _+({\mathbb {R}},U):=\{u\in H^\theta ({\mathbb {R}},U): \textrm{supp}\,u\subset [0,\infty )\}\subset H^\theta _\ell ({\mathbb {R}},U). \end{aligned}$$

The following lemma is well-known for scalar-valued $H^\theta$-spaces. As we could not find a suitable reference for the vector-valued case, a proof is included in Appendix 2.

Lemma 2.1

Let U be a complex Hilbert space and $\theta \in {\mathbb {R}}$. The following statements hold.

• (1) $C^\infty _\textrm{c}({\mathbb {R}},U)$ is dense in $H^\theta ({\mathbb {R}},U)$.

• (2) The space $\{u\in C^\infty _\textrm{c}({\mathbb {R}},U):\textrm{supp}\,u\subset (0,\infty )\}$ is dense in $H^\theta _+({\mathbb {R}},U)$.

For the rest of this section, let X be a complex Banach space. The Laplace transform ${{\mathcal {L}}}u$ of a distribution $u\in {{\mathcal {D}}}'(X)$ such that $\textrm{supp}\,u\subset [\tau ,\infty )$ and $e^{-\mu \,\cdot \,}u\in {{\mathcal {S}}}'(X)$ for some $\tau ,\mu \in {\mathbb {R}}$ is defined by

$$\begin{aligned} ({{\mathcal {L}}}u)(s):=\big (e^{-\mu \,\cdot \,}u\big )(\eta e^{-(s-\mu )\,\cdot \,})\quad \forall \,s\in {\mathbb {C}}_\mu , \end{aligned}$$

where $\eta \in {{\mathcal {U}}}_\tau$ is arbitrary. It is straightforward to show that the definition does not depend on $\eta$. The classical Laplace transform is a special case in the sense that if $f:{\mathbb {R}}\rightarrow X$ is such that $f(t)=0$ for a.e. $t\in (-\infty ,\tau )$ and $e^{-\mu \,\cdot \,}f\in L^1({\mathbb {R}},X)$ for some $\tau ,\mu \in {\mathbb {R}}$, then $({{\mathcal {L}}}[f])(s)=({{\mathcal {L}}}f)(s)$ for all $s\in {\mathbb {C}}_\mu$. For $u\in {{\mathcal {D}}}'(X)$ with $\textrm{supp}\,u$ bounded on the left, we define the abscissa of convergence $\sigma (u)$ as the infimum of all $\mu \in {\mathbb {R}}$ such that $e^{-\mu \,\cdot \,}u\in {{\mathcal {S}}}'(X)$. If no such $\mu$ exists, then we set $\sigma (u)=\infty$. If $\sigma (u)<\infty$, then the Laplace transform of u exists and is holomorphic on ${\mathbb {C}}_{\sigma (u)}$, and u is said to be Laplace transformable.

For later purposes, we state the following lemma on the vector-valued Laplace transform, the proof of which can be found in Appendix 2.

Lemma 2.2

Let $\textbf{h}:{\mathbb {C}}_\mu \rightarrow X$ be holomorphic, where $\mu \in {\mathbb {R}}$. If

$$\begin{aligned} \sup _{s\in {\mathbb {C}}_\mu }\Vert s^2\textbf{h}(s)\Vert <\infty , \end{aligned}$$

then there exists $h\in C({\mathbb {R}},X)$ such that $h(t)=0$ for all $t\le 0$, $\sup _{t>0}\Vert e^{-\nu t}t^{-1}h(t)\Vert <\infty$ and $e^{-\nu \,\cdot \,}h\in L^1({\mathbb {R}},X)$ for every $\nu >\mu$ and $({{\mathcal {L}}}h)(s)=\textbf{h}(s)$ for all $s\in {\mathbb {C}}_\mu$.

For each $\tau \in {\mathbb {R}}$, the shift or translation operator $S_\tau :L^1_\textrm{loc}({\mathbb {R}},X)\rightarrow L^1_\textrm{loc}({\mathbb {R}},X)$ is defined by $(S_\tau f)(t):=f(t-\tau )$. Letting $u\in {{\mathcal {D}}}'(X)$, the definition

$$\begin{aligned} (S_\tau u)({\varphi }):=u(S_{-\tau }{\varphi })\quad \forall \,{\varphi }\in {{\mathcal {D}}}\end{aligned}$$

extends the translation operator to ${{\mathcal {D}}}'(X)$. A linear map $T:\textrm{dom}\,T\subset {{\mathcal {D}}}'(X)\rightarrow {{\mathcal {D}}}'(X)$ is said to be translation invariant if $S_\tau u\in \textrm{dom}\,T$ and $S_\tau Tu= T S_\tau u$ for all $u\in \textrm{dom}\,T$ and all $\tau \in {\mathbb {R}}$. Furthermore, we say that T is causal if, for all $\tau \in {\mathbb {R}}$ and all $u\in \textrm{dom}\,T$, we have

$$\begin{aligned} \textrm{supp}\,u\subset [\tau ,\infty )\quad \Rightarrow \quad \textrm{supp}(Tu)\subset [\tau ,\infty ). \end{aligned}$$

It is a routine exercise to show that if T is translation invariant, then T is causal if, for all $u\in \textrm{dom}\,T$,

$$\begin{aligned} \textrm{supp}\,u\subset [0,\infty )\quad \Rightarrow \quad \textrm{supp}(Tu)\subset [0,\infty ). \end{aligned}$$

For $\mu \in {\mathbb {R}}$, we let ${{\mathcal {H}}}^\infty _\mu (X)$ denote the Hardy space of all bounded holomorphic functions ${\mathbb {C}}_\mu \rightarrow {{\mathcal {B}}}(X)$. Equipped with the norm

$$\begin{aligned} \Vert \textbf{H}\Vert _{{{\mathcal {H}}}^\infty _\mu }:=\sup _{s\in {\mathbb {C}}_\mu }\Vert \textbf{H}(s)\Vert , \end{aligned}$$

${{\mathcal {H}}}^\infty _\mu (X)$ is a Banach space. We set ${{\mathcal {H}}}^\infty (X):={{\mathcal {H}}}^\infty _0(X)$.

The following result on ${{\mathcal {H}}}^\infty ({{\mathcal {B}}}(U))$ (known as Fatou’s theorem), U a separable complex Hilbert space, will be frequently used in this paper. For the proof we refer to [31, Theorem B, Section 4.6] and [31, Theorem C, Section 4.8] or [38, Theorem 6.4].

Theorem 2.3

Let U be a separable complex Hilbert space and let $\textbf{H}\in {{\mathcal {H}}}^\infty ({{\mathcal {B}}}(U))$. Then $\textbf{H}$ has a non-tangential limit $\textbf{H}_0(y)=\lim _{s\rightarrow iy}\textbf{H}(s)$ in the strong operator topology for almost all $y\in {\mathbb {R}}$ and

$$\begin{aligned} \mathrm{ess\,sup}_{y\in {\mathbb {R}}}\Vert \textbf{H}_0(y)\Vert =\Vert \textbf{H}\Vert _{{{\mathcal {H}}}^\infty }. \end{aligned}$$

Furthermore, $\Vert \textbf{H}_0(y)\Vert =\lim _{s\rightarrow iy}\Vert \textbf{H}(s)\Vert$ non-tangentially for almost all $y\in {\mathbb {R}}$.

For notational simplicity, in the scalar-valued case (that is, when $X={\mathbb {C}}$ or $U={\mathbb {C}}$), we shall drop X or U from the notation of function and distribution spaces: for example, $C({\mathbb {R}})$, ${{\mathcal {D}}}'$, ${{\mathcal {S}}}'$, $H^\theta ({\mathbb {R}})$ and ${{\mathcal {H}}}_\mu$ stand for $C({\mathbb {R}},{\mathbb {C}})$, ${{\mathcal {D}}}'({\mathbb {C}})$, ${{\mathcal {S}}}'({\mathbb {C}})$, $H^\theta ({\mathbb {R}},{\mathbb {C}})$ and ${{\mathcal {H}}}_\mu ({\mathbb {C}})$, respectively.

3 Operator-valued multiplier theorems

The main objective of the current section is to prove the following Laplace multiplier theorem for a class of causal and translation-invariant operators. Throughout this section, let U be a complex Hilbert space.

Theorem 3.1

Let $\alpha , \beta \in {\mathbb {R}}$.

• (1) If $G\in {{\mathcal {B}}}\big (H^{\alpha }({\mathbb {R}},U), H^{\beta }({\mathbb {R}},U)\big )$ is causal and translation invariant, then there exists a unique holomorphic function $\textbf{G}:{\mathbb {C}}_0 \rightarrow {{\mathcal {B}}}(U)$ such that

  $$\begin{aligned} Gu=({{\mathcal {L}}}^{-1}\circ {{\mathcal {M}}}_\textbf{G}\circ {{\mathcal {L}}})(u)\quad \forall \,u\in H^{\alpha }_\ell ({\mathbb {R}},U) \end{aligned}$$

  (3.1)

  and

  $$\begin{aligned} \sup _{s\in {\mathbb {C}}_0}\Vert (1+s)^{\beta -\alpha }\textbf{G}(s)\Vert =\Vert G\Vert _{{{\mathcal {B}}}(H^{\alpha },H^{\beta })}, \end{aligned}$$

  (3.2)

  where ${{\mathcal {M}}}_\textbf{G}$ denotes multiplication by $\textbf{G}$.

• (2) If $\textbf{G}:{\mathbb {C}}_0 \rightarrow {{\mathcal {B}}}(U)$ is holomorphic and such that

  $$\begin{aligned} \sup _{s\in {\mathbb {C}}_0}\Vert (1+s)^{\beta -\alpha }\textbf{G}(s)\Vert <\infty , \end{aligned}$$

  (3.3)

  then there exists a unique causal translation-invariant operator $G\in {{\mathcal {B}}}\big (H^{\alpha }({\mathbb {R}},U), H^{\beta }({\mathbb {R}},U)\big )$ such that (3.1) and (3.2) hold.

Condition (3.3) means that the function $s\mapsto (1+s)^{\beta -\alpha }\textbf{G}(s)$ is in the Hardy space ${{\mathcal {H}}}^\infty ({{\mathcal {B}}}(U))$. The norm on the right-hand side of (3.2) is the operator norm induced by the norms of $H^{\alpha }({\mathbb {R}},U)$ and $H^{\beta }({\mathbb {R}},U)$.

As for the expression $(1+s)^{\beta -\alpha }$ appearing in (3.2) and (3.3), the following convention applies throughout the paper: We identify the complex power function with exponent $\theta \in {\mathbb {R}}$ with its principal branch on the domain ${\mathbb {C}}\backslash (-\infty ,0]$, and thus, $(1+s)^{\beta -\alpha }\in (0,\infty )$ if $s\in (-1,\infty )$.

Theorem 3.1 is a generalization of the following well-known result, see [36, Theorem 10.3.5], [38] or [41].

Theorem 3.2

A linear operator $G:L^2({\mathbb {R}},U) \rightarrow L^2({\mathbb {R}},U)$ is bounded, translation-invariant and causal if, and only if, there exists $\textbf{G}\in {{\mathcal {H}}}^\infty ({{\mathcal {B}}}(U))$ such that G is of the form (3.1) (with $H^\alpha _\ell ({\mathbb {R}},U)$ replaced by $L^2_+({\mathbb {R}},U)$). Moreover, G and $\textbf{G}$ determine each other uniquely, and

$$\begin{aligned} \big \Vert G\big \Vert _{{{\mathcal {B}}}(L^2({\mathbb {R}},U))}=\Vert \textbf{G}\Vert _{{{\mathcal {H}}}^\infty }. \end{aligned}$$

The proof of Theorem 3.1 is based on Theorem 3.2 and a scale of causal translation-invariant isometric isomorphisms $L^2({\mathbb {R}},U) \rightarrow H^\theta ({\mathbb {R}},U)$, $\theta \in {\mathbb {R}}$, which we shall now introduce. For which purpose, let $\theta \in {\mathbb {R}}$, set

$$\begin{aligned} \textbf{r}_\theta (s):=(1+s)^{-\theta }\quad \,\forall \,s\in {\mathbb {C}}_{-1}\quad \text{ and }\quad \rho _\theta (y):=\textbf{r}_\theta (iy)\quad \,\forall \,y\in {\mathbb {R}}, \end{aligned}$$

(3.4)

and define a linear map $R_\theta : {{\mathcal {S}}}'(U)\rightarrow {{\mathcal {S}}}'(U)$ by $R_\theta :={{\mathcal {F}}}^{-1}\circ {{\mathcal {M}}}_{\rho _\theta }\circ {{\mathcal {F}}}$. Note that

$$\begin{aligned} R_\theta u:={{\mathcal {F}}}^{-1}(\rho _\theta {{\mathcal {F}}}u)=({{\mathcal {F}}}^{-1}\rho _\theta )\star u \quad \forall \,u\in {{\mathcal {S}}}'(U). \end{aligned}$$

(3.5)

Here we have used that $\rho _\theta \in {{\mathcal {O}}}_\textrm{M}$ (equivalently, ${{\mathcal {F}}}^{-1}\rho _\theta$ is a distribution of rapid decay) from which it follows that, for every $u\in {{\mathcal {S}}}'(U)$, the products $\rho _\theta {{\mathcal {F}}}u$ and $({{\mathcal {F}}}^{-1}\rho _\theta )\star u$ are well-defined tempered distributions, so that the convolution theorem (exchange formula) can be invoked to obtain the second equality in (3.5), see Appendix 1.

The next result gathers properties of the scale of operators $R_\theta$.

Proposition 3.3

For every $\theta \in {\mathbb {R}}$, the operator $R_\theta$ defined by (3.5) has the following properties.

• (1) $R_\theta :{{\mathcal {S}}}'(U)\rightarrow {{\mathcal {S}}}'(U)$ is a sequentially continuous isomorphism and $R_\theta ^{-1}=R_{-\theta }$.

• (2) $R_\theta$ is translation invariant.

• (3) $R_\theta$ is causal.

• (4) For every $\alpha \in {\mathbb {R}}$, $R_\theta (H^\alpha ({\mathbb {R}},U))=H^{\alpha +\theta }({\mathbb {R}},U)$ and $\Vert R_\theta u\Vert _{H^{\alpha +\theta }}=\Vert u\Vert _{H^\alpha }$, that is, the restriction of $R_\theta$ to $H^\alpha ({\mathbb {R}},U)$ is an isometric isomorphism $H^\alpha ({\mathbb {R}},U)\rightarrow H^{\alpha +\theta }({\mathbb {R}},U)$.

Proposition 3.3 has some overlap with [40, Proposition 31.8] in the sense that, for the scalar-valued case, it is shown that there exists an isometric isomorphism mapping $H^\alpha ({\mathbb {R}})$ onto $H^\beta ({\mathbb {R}})$. However, the isometric isomorphism is not causal, and therefore [40, Proposition 31.8] is not suitable as a tool in the proof of Theorem 3.1.

Before we provide a proof of Proposition 3.3, it is convenient to state and prove the following technical lemma.

Lemma 3.4

Let $\theta \in {\mathbb {R}}$ and let $\textbf{r}_\theta$ and $\rho _\theta$ be defined as in (3.4). Then $\textrm{supp}({{\mathcal {F}}}^{-1}\rho _\theta )\subset [0,\infty )$, $e^{-\nu \,\cdot \,}{{\mathcal {F}}}^{-1}\rho _\theta \in {{\mathcal {S}}}'$ for all $\nu \in (-1,0)$ and $\big ({{\mathcal {L}}}({{\mathcal {F}}}^{-1}\rho _\theta )\big )(s)=\textbf{r}_\theta (s)$ for all $s\in {\mathbb {C}}_{-1}$.

Proof

Let $\theta \in {\mathbb {R}}$, $\nu \in (-1,0)$ and $k\in {\mathbb {N}}_0$ such that $k\ge 2-\theta$. Setting $\textbf{h}_\theta (s):=(1+s)^{-k}\textbf{r}_\theta (s)=(1+s)^{-(k+\theta )}$ for all $s\in {\mathbb {C}}_{-1}$, we have that $s^2\textbf{h}_\theta (s)$ is bounded on ${\mathbb {C}}_{\mu }$ for fixed but arbitrary $\mu \in (-1,\nu )$. It follows from Lemma 2.2 that there exists a function $h_\theta \in C({\mathbb {R}})$ such that $h_\theta (t)=0$ for all $t\le 0$, $e^{-\nu \,\cdot \,}h_\theta \in L^1({\mathbb {R}})$ and $({{\mathcal {L}}}h_\theta )(s)=\textbf{h}_\theta (s)$ for all $s\in {\mathbb {C}}_\mu$. In particular,

$$\begin{aligned} ({{\mathcal {F}}}h_\theta )(y)=({{\mathcal {L}}}h_\theta )(iy)=\textbf{h}_\theta (iy)\quad \forall \,y\in {\mathbb {R}}. \end{aligned}$$

Defining $r_\theta :=(1+D)^kh_\theta \in {{\mathcal {S}}}'$, where D denotes differentiation (in the distributional sense), it follows that $\textrm{supp}\,r_\theta \subset [0,\infty )$, $e^{-\nu \,\cdot \,}r_\theta \in {{\mathcal {S}}}'$, $({{\mathcal {L}}}r_\theta )(s)=\textbf{r}_\theta (s)$ for all $s\in {\mathbb {C}}_\mu$ and ${{\mathcal {F}}}r_\theta =\rho _\theta$. Consequently, $r_\theta ={{\mathcal {F}}}^{-1}\rho _\theta$ and $\big ({{\mathcal {L}}}({{\mathcal {F}}}^{-1}\rho _\theta )\big )(s)=\textbf{r}_\theta (s)$ for all $s\in {\mathbb {C}}_\mu$. The latter identity holds for every $\mu \in (-1,\nu )$, and hence it holds for all $s\in {\mathbb {C}}_{-1}$, completing the proof. $\Box$

It follows from (3.5), Lemma 3.4 and the convolution theorem for Laplace transforms (see Appendix 1) that, for every $\theta \in {\mathbb {R}}$,

$$\begin{aligned} {{\mathcal {L}}}(R_\theta u)=\textbf{r}_\theta {{\mathcal {L}}}u\quad \forall \,u\in {{\mathcal {S}}}'_\ell (U), \end{aligned}$$

and, consequently,

$$\begin{aligned} R_\theta u=\big ({{\mathcal {L}}}^{-1}\circ {{\mathcal {M}}}_{\textbf{r}_\theta }\circ {{\mathcal {L}}}\big )(u)\quad \forall \,u\in {{\mathcal {S}}}'_\ell (U). \end{aligned}$$

(3.6)

We proceed to prove Proposition 3.3.

Proof of Proposition 3.3

(1) It is immediate that $R_\theta R_{-\theta }= R_{-\theta }R_\theta =I$. Hence, $R_\theta$ is an isomorphism and $R_\theta ^{-1}=R_{-\theta }$. Moreover, as ${{\mathcal {F}}}$, ${{\mathcal {F}}}^{-1}$ and multiplication by $\rho _\theta$ are sequentially continuous on ${{\mathcal {S}}}'(U)$, it follows that $R_\theta$ is sequentially continuous.

(2) Let $\tau \in {\mathbb {R}}$ and $u\in {{\mathcal {S}}}'(U)$. Then $R_\theta S_\tau u={{\mathcal {F}}}^{-1}(\rho _\theta e^{-i\tau \,\cdot \,}{{\mathcal {F}}}u)$, and thus,

$$\begin{aligned} {{\mathcal {F}}}R_\theta S_\tau u=\rho _\theta e^{-i\tau \,\cdot \,}{{\mathcal {F}}}u=e^{-i\tau \,\cdot \,}(\rho _\theta {{\mathcal {F}}}u)= {{\mathcal {F}}}\big (S_\tau {{\mathcal {F}}}^{-1}(\rho _\theta {{\mathcal {F}}}u)\big )={{\mathcal {F}}}(S_\tau R_\theta u). \end{aligned}$$

Consequently, $R_\theta S_\tau u=S_\tau R_\theta u$, establishing the translation invariance of $R_\theta$.

(3) By Lemma 3.4, $\textrm{supp}({{\mathcal {F}}}^{-1}\rho _\theta )\subset [0,\infty )$. Using that $R_\theta u=({{\mathcal {F}}}^{-1}\rho _\theta )\star u$ for all $u\in {{\mathcal {S}}}'(U)$, causality follows from [43, Theorem 5.11-1].

(4) For $u\in H^\alpha ({\mathbb {R}},U)$, we compute

$$\begin{aligned} 2\pi \Vert R_\theta u\Vert ^2_{H^{\alpha +\theta }}= & {} \int _{-\infty }^\infty (1+y^2)^{\alpha +\theta } |\rho _\theta (y)|^2\Vert ({{\mathcal {F}}}u)(y)\Vert ^2\textrm{d}y\\ {}= & {} \int _{-\infty }^\infty (1+y^2)^{\alpha }\Vert ({{\mathcal {F}}}u)(y)\Vert ^2\textrm{d}y=2\pi \Vert u\Vert ^2_{H^\alpha }, \end{aligned}$$

where we have used that $|\rho _\theta (y)|^2=|1+iy|^{-2\theta }=(1+y^2)^{-\theta }$, showing that $R_\theta$ restricted to $H^\alpha ({\mathbb {R}},U)$ maps isometrically into $H^{\alpha +\theta }({\mathbb {R}},U)$. For $v\in H^{\alpha +\theta }({\mathbb {R}},U)$, we have that $R_{-\theta }v\in H^\alpha ({\mathbb {R}},U)$, and, by statement (1), $R_\theta (R_{-\theta }v)=v$, showing that $R_\theta$ restricted to $H^\alpha ({\mathbb {R}},U)$ maps onto $H^{\alpha +\theta }({\mathbb {R}},U)$. Hence, the restriction of $R_\theta$ to $H^\alpha ({\mathbb {R}},U)$ is an isometric isomorphism $H^\alpha ({\mathbb {R}},U)\rightarrow H^{\alpha +\theta }({\mathbb {R}},U)$. $\Box$

We are now in a position to prove Theorem 3.1.

Proof of Theorem 3.1

(1) Assume that  $G\in {{\mathcal {B}}}\big (H^{\alpha }({\mathbb {R}},U), H^{\beta }({\mathbb {R}},U)\big )$ is causal and translation invariant. An application of Proposition 3.3 yields that

$$\begin{aligned} R_{-\beta }GR_{\alpha } : L^2({\mathbb {R}},U)\rightarrow L^2({\mathbb {R}},U) \end{aligned}$$

is a causal translation-invariant bounded linear operator. Therefore, invoking Theorem 3.2, there exists a function $\textbf{H}\in {{\mathcal {H}}}^\infty ({{\mathcal {B}}}(U))$ such that

$$\begin{aligned} R_{-\beta }G R_{\alpha }v={{\mathcal {L}}}^{-1}(\textbf{H}{{\mathcal {L}}}v)\quad \forall \,v\in L^2_+({\mathbb {R}},U). \end{aligned}$$

Appealing to (3.6) and Proposition 3.3, we conclude that

$$\begin{aligned} Gu=R_\beta {{\mathcal {L}}}^{-1}\big (\textbf{H}{{\mathcal {L}}}(R_{-\alpha }u)\big )={{\mathcal {L}}}^{-1}(\textbf{G}{{\mathcal {L}}}u)=({{\mathcal {L}}}^{-1}\circ {{\mathcal {M}}}_\textbf{G}\circ {{\mathcal {L}}})(u) \quad \forall \,u\in H^\alpha _+({\mathbb {R}},U), \end{aligned}$$

where $\textbf{G}(s):=(1+s)^{\alpha -\beta }\textbf{H}(s)$. As G and ${{\mathcal {L}}}^{-1}\circ {{\mathcal {M}}}_\textbf{G}\circ {{\mathcal {L}}}$ are translation invariant, it follows that (3.1) holds. To establish uniqueness of $\textbf{G}$, let ${\tilde{\textbf{G}}}:{\mathbb {C}}_0\rightarrow {{\mathcal {B}}}(U)$ be holomorphic and assume that $Gu=({{\mathcal {L}}}^{-1}\circ {{\mathcal {M}}}_{{\tilde{\textbf{G}}}}\circ {{\mathcal {L}}})(u)$ for all $u\in H^\alpha _\ell ({\mathbb {R}},U)$. Then, for fixed ${\varphi }\in {{\mathcal {D}}}$, ${\varphi }(t)\not \equiv 0$, it follows from (3.1) that $\textbf{G}{{\mathcal {L}}}({\varphi }\otimes v)={\tilde{\textbf{G}}}{{\mathcal {L}}}({\varphi }\otimes v)$ for all $v\in U$, where $({\varphi }\otimes v)(t):={\varphi }(t)v$ for all $t\in {\mathbb {R}}$. Consequently, $({{\mathcal {L}}}{\varphi })(s)\textbf{G}(s)v=({{\mathcal {L}}}{\varphi })(s){\tilde{\textbf{G}}}(s)v$ for all $s\in {\mathbb {C}}_0$ and all $v\in U$, showing that ${\tilde{\textbf{G}}}=\textbf{G}$.

To establish the equality of norms (3.2), we invoke Theorem 3.2 again to obtain

$$\begin{aligned} \Vert R_{-\beta } G R_\alpha \Vert _{{{\mathcal {B}}}(L^2_+({\mathbb {R}},U))}=\Vert \textbf{H}\Vert _{{{\mathcal {H}}}^\infty } =\sup _{s\in {\mathbb {C}}_0}\Vert (1+s)^{\beta -\alpha }\textbf{G}(s)\Vert . \end{aligned}$$

(3.7)

Using Proposition 3.3 once again, the restriction of $R_{-\beta }$ to $H^\beta ({\mathbb {R}},U)$ is an isometric isomorphism $H^\beta ({\mathbb {R}},U)\rightarrow L^2({\mathbb {R}},U)$, and so

$$\begin{aligned} \Vert R_{-\beta }G R_\alpha u\Vert _{L^2}=\Vert GR_\alpha u\Vert _{H^\beta }\quad \forall \,u\in L^2_+({\mathbb {R}},U). \end{aligned}$$

Furthermore, $R_\alpha$ maps $L^2_+({\mathbb {R}},U)$ isometrically onto $H^\alpha _+({\mathbb {R}},U)$, and so,

$$\begin{aligned} \sup _{\Vert u\Vert _{L^2}=1,\,u\in L^2_+({\mathbb {R}},U)}\Vert GR_\alpha u\Vert _{H^\beta }=\sup _{\Vert v\Vert _{H^\alpha }=1,\,v\in H^\alpha _+({\mathbb {R}},U)}\Vert Gv\Vert _{H^\beta }. \end{aligned}$$

Therefore,

$$\begin{aligned} \Vert R_{-\beta }G R_\alpha \Vert _{{{\mathcal {B}}}(L^2_+({\mathbb {R}},U))}= \sup _{\Vert u\Vert _{L^2}=1,\,u\in L^2_+({\mathbb {R}},U)}\Vert R_{-\beta }G R_\alpha u\Vert _{L^2}=\sup _{\Vert v\Vert _{H^\alpha }=1,\,v\in H^\alpha _+({\mathbb {R}},U)}\Vert Gv\Vert _{H^\beta }. \end{aligned}$$

Hence, $\Vert G\Vert _{{{\mathcal {B}}}(H^\alpha _+,H^\beta _+)}=\Vert R_{-\beta }G R_\alpha \Vert _{{{\mathcal {B}}}(L^2_+({\mathbb {R}},U))}$, and so, by (3.7),

$$\begin{aligned} \Vert G\Vert _{{{\mathcal {B}}}(H^\alpha _+,H^\beta _+)}=\sup _{s\in {\mathbb {C}}_0}\Vert (1+s)^{\beta -\alpha }\textbf{G}(s)\Vert . \end{aligned}$$

(3.8)

Finally, let $u\in H^\alpha ({\mathbb {R}},U)$, $u\not =0$. By Lemma 2.1, there exist $u_j\in C^\infty _\textrm{c}({\mathbb {R}},U)$, $j\in {\mathbb {N}}$, such that $u_j\rightarrow u$ in $H^\alpha ({\mathbb {R}},U)$ as $j\rightarrow \infty$. Choosing $\tau _j\in {\mathbb {R}}$ such that $\textrm{supp} (S_{\tau _j}u_j)\subset [0,\infty )$, we have that $S_{\tau _j}u_j\in H^\alpha _+({\mathbb {R}},U)$ for all $j\in {\mathbb {N}}$ and, by translation invariance and (3.8),

$$\begin{aligned} \frac{\Vert Gu_j\Vert _{H^\beta }}{\Vert u_j\Vert _{H^\alpha }}=\frac{\Vert S_{\tau _j}Gu_j\Vert _{H^\beta }}{\Vert S_{\tau _j}u_j\Vert _{H^\alpha }}= \frac{\Vert G(S_{\tau _j}u_j)\Vert _{H^\beta }}{\Vert S_{\tau _j}u_j\Vert _{H^\alpha }}\le \sup _{s\in {\mathbb {C}}_0}\Vert (1+s)^{\beta -\alpha }\textbf{G}(s)\Vert . \end{aligned}$$

Consequently,

$$\begin{aligned} \frac{\Vert Gu\Vert _{H^\beta }}{\Vert u\Vert _{H^\alpha }}=\lim _{j\rightarrow \infty }\frac{\Vert Gu_j\Vert _{H^\beta }}{\Vert u_j\Vert _{H^\alpha }} \le \sup _{s\in {\mathbb {C}}_0}\Vert (1+s)^{\beta -\alpha }\textbf{G}(s)\Vert , \end{aligned}$$

which, together with (3.8) shows that (3.2) holds.

(2) Conversely, let $\textbf{G}:{\mathbb {C}}_0\rightarrow {{\mathcal {B}}}(U)$ be holomorphic and assume that (3.3) holds. Obviously, $\textbf{H}$ defined by $\textbf{H}(s):=(1+s)^{\beta -\alpha }\textbf{G}=\textbf{r}_{\alpha -\beta }(s)\textbf{G}(s)$ is in ${{\mathcal {H}}}^\infty ({{\mathcal {B}}}(U))$, and so, by Theorem 3.2 there exists a causal and translation-invariant operator $H\in {{\mathcal {B}}}(L^2({\mathbb {R}},U))$ such that $Hu=({{\mathcal {L}}}^{-1}\circ {{\mathcal {M}}}_\textbf{H}\circ {{\mathcal {L}}})(u)$ for all $u\in L^2_+({\mathbb {R}},U)$. As H and ${{\mathcal {L}}}^{-1}\circ {{\mathcal {M}}}_\textbf{H}\circ {{\mathcal {L}}}$ are translation invariant, it follows that

$$\begin{aligned} Hu=({{\mathcal {L}}}^{-1}\circ {{\mathcal {M}}}_\textbf{H}\circ {{\mathcal {L}}})(u)\quad \forall \,u\in L^2_\ell ({\mathbb {R}},U). \end{aligned}$$

(3.9)

Using Proposition 3.3, it is clear that the linear operator

$$\begin{aligned} G:=R_\beta \circ H\circ R_{-\alpha }: H^\alpha ({\mathbb {R}},U)\rightarrow H^\beta ({\mathbb {R}},U) \end{aligned}$$

is causal, translation-invariant and bounded. Furthermore, by (3.6) and (3.9),

$$\begin{aligned}{} & {} G={{\mathcal {L}}}^{-1}\circ {{\mathcal {M}}}_{\textbf{r}_\beta }\circ {{\mathcal {M}}}_\textbf{H}\circ {{\mathcal {M}}}_{\textbf{r}_{-\alpha }}\circ {{\mathcal {L}}}= {{\mathcal {L}}}^{-1}\circ {{\mathcal {M}}}_{\textbf{r}_{\beta -\alpha }\textbf{H}}\circ {{\mathcal {L}}}\\{} & {} \quad ={{\mathcal {L}}}^{-1}\circ {{\mathcal {M}}}_\textbf{G}\circ {{\mathcal {L}}}\quad \text{ on }\,\,\,\,H^\alpha _\ell ({\mathbb {R}},U), \end{aligned}$$

showing that (3.1) holds. Finally, as $H^\alpha _\ell ({\mathbb {R}},U)$ is dense in $H^\alpha ({\mathbb {R}},U)$, it is clear that G is the unique operator in ${{\mathcal {B}}}\big (H^\alpha ({\mathbb {R}},U), H^\beta ({\mathbb {R}},U)\big )$ satisfying (3.1). $\Box$

The following corollary is an immediate consequence of Theorem 3.1.

Corollary 3.5

If $G\in {{\mathcal {B}}}(L^2({\mathbb {R}},U))$ is causal and translation-invariant, then, for all $\alpha >0$ ($\alpha <0$), G restricts (extends) to a causal translation-invariant bounded linear operator $H^\alpha ({\mathbb {R}},U)\rightarrow H^\alpha ({\mathbb {R}},U)$.

Next we want to apply Theorem 3.1 to derive a Fourier multiplier theorem. To facilitate such an application of Theorem 3.1, it is convenient to state and prove an auxiliary result first.

Let ${{\mathcal {H}}}^2(U)$ be the Hardy space of all holomorphic functions ${\mathbb {C}}_0\rightarrow U$ such that

$$\begin{aligned} \Vert f\Vert _{{{\mathcal {H}}}^2}:=\sup _{x>0}\left( \int _{-\infty }^\infty \Vert f(x+iy)\Vert ^2\textrm{d}y\right) ^{1/2}<\infty . \end{aligned}$$

By the Paley-Wiener theorem (see [4, Theorem 1.8.3], [31, Section 4.8] or [36, Theorem 10.3.4]), the Laplace transform maps $L^2_+({\mathbb {R}},U)$ isomorphically onto ${{\mathcal {H}}}^2(U)$, and

$$\begin{aligned} \Vert {{\mathcal {L}}}u\Vert _{{{\mathcal {H}}}^2}=\sqrt{2\pi }\Vert u\Vert _{L^2}\quad \forall \,u\in L^2_+({\mathbb {R}},U). \end{aligned}$$

For each $f\in {{\mathcal {H}}}^2(U)$, the boundary limit $f_0(y):=\lim _{x\downarrow 0}f(x+iy)$ exists for almost every $y\in {\mathbb {R}}$, the boundary function $f_0$ is in $L^2({\mathbb {R}},U)$, the map

$$\begin{aligned} B:{{\mathcal {H}}}^2(U)\rightarrow L^2({\mathbb {R}},U),\,\,\,f\mapsto f_0 \end{aligned}$$

(3.10)

is an isometry,

$$\begin{aligned} (B\circ {{\mathcal {L}}})(u)={{\mathcal {F}}}u\quad \forall \,u\in L^2_+({\mathbb {R}},U), \end{aligned}$$

(3.11)

and $B({{\mathcal {H}}}^2(U))={{\mathcal {F}}}(L^2_+({\mathbb {R}},U))=\{g\in L^2({\mathbb {R}},U): \textrm{supp}({{\mathcal {F}}}^{-1}g)\subset [0,\infty )\}$, see [4, Theorem 1.8.3], [31, Section 4.8] or [36, Section 10.3] for details.

The following lemma relates certain Fourier multipliers to the corresponding Laplace multipliers.

Lemma 3.6

Assume that U is separable. Let $\textbf{G}:{\mathbb {C}}_0\rightarrow {{\mathcal {B}}}(U)$ be holomorphic and such that $\sup _{s\in {\mathbb {C}}_0}\Vert (1+s)^{-k}\textbf{G}(s)\Vert <\infty$ for some $k\in {\mathbb {N}}_0$. Then the limit $\textbf{G}_0(y):=\lim _{x\downarrow 0}\textbf{G}(x+iy)$ exists in the strong operator topology for almost every $y\in {\mathbb {R}}$ and

$$\begin{aligned} ({{\mathcal {F}}}^{-1}\circ {{\mathcal {M}}}_{\textbf{G}_0}\circ {{\mathcal {F}}})(u)=({{\mathcal {L}}}^{-1}\circ {{\mathcal {M}}}_{\textbf{G}}\circ {{\mathcal {L}}})(u)\quad \forall \, u\in L^2_\ell ({\mathbb {R}},U). \end{aligned}$$

Proof. Since ${{\mathcal {F}}}^{-1}\circ {{\mathcal {M}}}_{\textbf{G}_0}\circ {{\mathcal {F}}}$ and ${{\mathcal {L}}}^{-1}\circ {{\mathcal {M}}}_{\textbf{G}}\circ {{\mathcal {L}}}$ are translation-invariant, it is sufficient to show that

$$\begin{aligned} ({{\mathcal {F}}}^{-1}\circ {{\mathcal {M}}}_{\textbf{G}_0}\circ {{\mathcal {F}}})(u)=({{\mathcal {L}}}^{-1}\circ {{\mathcal {M}}}_{\textbf{G}}\circ {{\mathcal {L}}})(u)\quad \forall \, u\in L^2_+({\mathbb {R}},U). \end{aligned}$$

(3.12)

Set $\textbf{H}(s):=(1+s)^{-k}\textbf{G}(s)$ for all $s\in {\mathbb {C}}_0$. Then, $\textbf{H}\in {{\mathcal {H}}}^\infty ({{\mathcal {B}}}(U))$ and, by Theorem 2.3, there exists a boundary function $\textbf{H}_0$ such that $\textbf{H}(x+iy)$ converges to $\textbf{H}_0(y)$ in the strong operator topology for almost every $y\in {\mathbb {R}}$ as $x\downarrow 0$ and $\mathrm{ess\,sup}_{y\in {\mathbb {R}}}\Vert \textbf{H}_0(y)\Vert =\Vert \textbf{H}\Vert _{{{\mathcal {H}}}^\infty }$. Let $u\in L^2_+({\mathbb {R}},U)$ and set $H:={{\mathcal {L}}}^{-1}\circ {{\mathcal {M}}}_{\textbf{H}}\circ {{\mathcal {L}}}$. As H is causal, $Hu\in L^2_+({\mathbb {R}},U)$, and, invoking (3.11), we have that

$$\begin{aligned} {{\mathcal {F}}}(Hu)=(B\circ {{\mathcal {L}}})(Hu)={{\mathcal {M}}}_{\textbf{H}_0}B({{\mathcal {L}}}u)={{\mathcal {M}}}_{\textbf{H}_0}({{\mathcal {F}}}u)=({{\mathcal {M}}}_{\textbf{H}_0}\circ {{\mathcal {F}}})(u). \end{aligned}$$

Consequently, $Hu=({{\mathcal {F}}}^{-1}\circ {{\mathcal {M}}}_{\textbf{G}_0}\circ {{\mathcal {F}}})(u)$, and thus,

$$\begin{aligned} ({{\mathcal {F}}}^{-1}\circ {{\mathcal {M}}}_{\textbf{H}_0}\circ {{\mathcal {F}}})(u)=({{\mathcal {L}}}^{-1}\circ {{\mathcal {M}}}_{\textbf{H}}\circ {{\mathcal {L}}})(u)\quad \forall \, u\in L^2_+({\mathbb {R}},U). \end{aligned}$$

An application of $(I+D)^k$ (recall that D denotes differentiation in the distributional sense) to both sides of the above equation leads to

$$\begin{aligned} (I+D)^k({{\mathcal {F}}}^{-1}\circ {{\mathcal {M}}}_{\textbf{H}_0}\circ {{\mathcal {F}}})(u)=(I+D)^k({{\mathcal {L}}}^{-1}\circ {{\mathcal {M}}}_{\textbf{H}}\circ {{\mathcal {L}}})(u)\quad \forall \, u\in L^2_+({\mathbb {R}},U). \end{aligned}$$

Using standard properties of the Fourier and Laplace transforms, it follows that

$$\begin{aligned} ({{\mathcal {F}}}^{-1}\circ {{\mathcal {M}}}_{\rho _{-k}\textbf{H}_0}\circ {{\mathcal {F}}})(u)=({{\mathcal {L}}}^{-1}\circ {{\mathcal {M}}}_{\textbf{r}_{-k}\textbf{H}}\circ {{\mathcal {L}}})(u)\quad \forall \, u\in L^2_+({\mathbb {R}},U), \end{aligned}$$

where $\textbf{r}_{-k}$ and $\rho _{-k}$ are given by (3.4). As $\textbf{r}_{-k}\textbf{H}=\textbf{G}$ and $\rho _{-k}\textbf{H}_0= \textbf{G}_0$, equation (3.12) follows from the above identity. $\Box$

We are now in the position to prove the following Fourier multiplier result.

Corollary 3.7

Assume that U is separable and let $\alpha , \beta \in {\mathbb {R}}$.

• (1) If $G:H^{\alpha }({\mathbb {R}},U) \rightarrow H^{\beta }({\mathbb {R}},U)$ is a bounded linear causal translation-invariant operator, then there exists a unique holomorphic function $\textbf{G}:{\mathbb {C}}_0 \rightarrow {{\mathcal {B}}}(U)$ such that

  $$\begin{aligned} Gu=({{\mathcal {F}}}^{-1}\circ {{\mathcal {M}}}_{\textbf{G}_0}\circ {{\mathcal {F}}})(u)\quad \forall \,u\in H^{\alpha }({\mathbb {R}},U) \end{aligned}$$

  (3.13)

  and

  $$\begin{aligned} \sup _{s\in {\mathbb {C}}_0}\Vert (1+s)^{\beta -\alpha }\textbf{G}(s)\Vert =\Vert G\Vert _{{{\mathcal {B}}}(H^{\alpha },H^{\beta })}=\mathrm{ess\,sup}_{y\in {\mathbb {R}}}\Vert (1+iy)^{\beta -\alpha }\textbf{G}_0(y)\Vert , \nonumber \\ \end{aligned}$$

  (3.14)

  where $\textbf{G}_0(y):=\lim _{x\downarrow 0}\textbf{G}(x+iy)$, with the limit existing in the strong operator topology for almost every $y\in {\mathbb {R}}$, and ${{\mathcal {M}}}_{\textbf{G}_0}$ denotes the operator of multiplication by $\textbf{G}_0$.

• (2) Conversely, if $\textbf{G}:{\mathbb {C}}_0 \rightarrow {{\mathcal {B}}}(U)$ is holomorphic and such that

  $$\begin{aligned} \sup _{s\in {\mathbb {C}}_0}\Vert (1+s)^{\beta -\alpha }\textbf{G}(s)\Vert <\infty , \end{aligned}$$

  (3.15)

  then $\textbf{G}_0(y):=\lim _{x\downarrow 0}\textbf{G}(x+iy)$ exists in the strong operator topology for almost every $y\in {\mathbb {R}}$, G given by (3.13) is a bounded linear causal translation-invariant operator $H^{\alpha }({\mathbb {R}},U) \rightarrow H^{\beta }({\mathbb {R}},U)$ and (3.14) holds.

Proof

(1) Assume that  $G\in {{\mathcal {B}}}\big (H^{\alpha }({\mathbb {R}},U), H^{\beta }({\mathbb {R}},U)\big )$ is causal and translation invariant. By statement (1) of Theorem 3.1 there exists a unique holomorphic function $\textbf{G}:{\mathbb {C}}_0 \rightarrow {{\mathcal {B}}}(U)$ such that $Gu=({{\mathcal {L}}}^{-1}\circ {{\mathcal {M}}}_\textbf{G}\circ {{\mathcal {L}}})(u)$ for all $u\in H^\alpha _\ell ({\mathbb {R}},U)$ and the first equality in (3.14) holds. Hence, the function $\textbf{r}_{\alpha -\beta }\textbf{G}$ is in ${{\mathcal {H}}}^\infty ({{\mathcal {B}}}(U))$, and so, Theorem 2.3 yields that the boundary limit $\textbf{G}_0(y):=\lim _{x\downarrow 0}\textbf{G}(x+iy)$ exists in the strong operator topology for almost every $y\in {\mathbb {R}}$ (here separability of U is used) and

$$\begin{aligned} \mathrm{ess\,sup}_{y\in {\mathbb {R}}}\Vert \rho _{\alpha -\beta }\textbf{G}_0(y)\Vert =\Vert \textbf{r}_{\alpha -\beta }\textbf{G}\Vert _{{{\mathcal {H}}}^\infty }. \end{aligned}$$

(3.16)

Consequently, the second equality in (3.14) also holds. Furthermore, it follows from Lemma 3.6 that

$$\begin{aligned} ({{\mathcal {F}}}^{-1}\circ {{\mathcal {M}}}_{\textbf{G}_0}\circ {{\mathcal {F}}})(u)=({{\mathcal {L}}}^{-1}\circ {{\mathcal {M}}}_\textbf{G}\circ {{\mathcal {L}}})(u)\quad \forall \,u\in C^{\infty }_\textrm{c}({\mathbb {R}},U). \end{aligned}$$

Therefore,

$$\begin{aligned} Gu=({{\mathcal {F}}}^{-1}\circ {{\mathcal {M}}}_{\textbf{G}_0}\circ {{\mathcal {F}}})(u)\quad \forall \,u\in C^\infty _\textrm{c}({\mathbb {R}},U). \end{aligned}$$

(3.17)

Next, we note that

$$\begin{aligned} {{\mathcal {F}}}^{-1}\circ {{\mathcal {M}}}_{\textbf{G}_0}\circ {{\mathcal {F}}}=R_\beta \circ {{\mathcal {F}}}^{-1}\circ {{\mathcal {M}}}_{\rho _{\alpha -\beta }\textbf{G}_0}\circ {{\mathcal {F}}}\circ R_{-\alpha }. \end{aligned}$$

(3.18)

By (3.16), the function $y\mapsto \Vert \rho _{\alpha -\beta }(y)\textbf{G}_0(y)\Vert$ is essentially bounded. Combining this with Proposition 3.3, it follows that the right-hand side of (3.18) is a bounded operator from $H^\alpha ({\mathbb {R}},U)$ to $H^\beta ({\mathbb {R}},U)$, and thus, ${{\mathcal {F}}}^{-1}\circ {{\mathcal {M}}}_{\textbf{G}_0}\circ {{\mathcal {F}}}\in {{\mathcal {B}}}\big (H^{\alpha }({\mathbb {R}},U),H^{\beta }({\mathbb {R}},U)\big )$. Therefore, since $C^\infty _\textrm{c}({\mathbb {R}},U)$ is dense in $H^\alpha ({\mathbb {R}},U)$ by Lemma 2.1, equation (3.17) yields that $Gu=({{\mathcal {F}}}^{-1}\circ {{\mathcal {M}}}_{\textbf{G}_0}\circ {{\mathcal {F}}})(u)$ for all $u\in H^\alpha ({\mathbb {R}},U)$, establishing (3.13).

(2) Conversely, let $\textbf{G}:{\mathbb {C}}_0\rightarrow {{\mathcal {B}}}(U)$ be holomorphic and assume that (3.15) holds. By Theorem 3.1, there exists a unique causal translation-invariant operator $G\in {{\mathcal {B}}}\big (H^{\alpha }({\mathbb {R}},U), H^{\beta }({\mathbb {R}},U)\big )$ such that

$$\begin{aligned} Gu=({{\mathcal {L}}}^{-1}\circ {{\mathcal {M}}}_\textbf{G}\circ {{\mathcal {L}}})(u)\quad \forall \,u\in H^{\alpha }_\ell ({\mathbb {R}},U) \end{aligned}$$

and (3.14) holds. By (3.15), $\textbf{G}$ is polynomially bounded, and thus it follows from Lemma 3.6 that $\textbf{G}_0(y):=\lim _{x\downarrow 0}\textbf{G}(x+iy)$ exists in the strong operator topology for almost every $y\in {\mathbb {R}}$ (here separability of U is used) and

$$\begin{aligned} Gu={{\mathcal {L}}}^{-1}\circ {{\mathcal {M}}}_\textbf{G}\circ {{\mathcal {L}}}={{\mathcal {F}}}^{-1}\circ {{\mathcal {M}}}_{\textbf{G}_0}\circ {{\mathcal {F}}}\quad \forall \,u\in C^\infty _\textrm{c}({\mathbb {R}},U). \end{aligned}$$

Moreover, since $\textbf{r}_{\alpha -\beta }\textbf{G}\in {{\mathcal {H}}}^\infty ({{\mathcal {B}}}(U))$, it follows that (3.16) holds. Therefore, as in the proof of statement (1), we have that ${{\mathcal {F}}}^{-1}\circ {{\mathcal {M}}}_{\textbf{G}_0}\circ {{\mathcal {F}}}\in {{\mathcal {B}}}\big (H^{\alpha }({\mathbb {R}},U),H^{\beta }({\mathbb {R}},U)\big )$, and, invoking the denseness of $C^\infty _\textrm{c}({\mathbb {R}},U)$ in $H^{\alpha }({\mathbb {R}},U)$ (see Lemma 2.1), the above identity yields that $Gu=({{\mathcal {F}}}^{-1}\circ {{\mathcal {M}}}_{\textbf{G}_0}\circ {{\mathcal {F}}})(u)$ for all $u\in H^\alpha ({\mathbb {R}},U)$, completing the proof. $\Box$

We close this section by showing how Proposition 3.3 can be used to derive a generalization of the Paley-Wiener theorem which provides a natural isomorphism between $H^\theta _+({\mathbb {R}},U)$ and a suitably weighted ${{\mathcal {H}}}^2$-space. To this end, we introduce the space

$$\begin{aligned} {{\mathcal {H}}}^{2,\theta }(U):=\textbf{r}_\theta {{\mathcal {H}}}^2(U)=\{\textbf{u}:{\mathbb {C}}_0\rightarrow U:\textbf{u}\, \text{ holomorphic } \text{ and } \,\textbf{r}_{-\theta }\textbf{u}\in {{\mathcal {H}}}^2(U)\},\quad \theta \in {\mathbb {R}}\end{aligned}$$

of holomorphic functions, where $\textbf{r}_\theta$ is defined in (3.4). Endowed with the norm $\Vert \textbf{u}\Vert _{{{\mathcal {H}}}^{2,\theta }}:=\Vert \textbf{r}_{-\theta }\textbf{u}\Vert _{{{\mathcal {H}}}^2}$, the space ${{\mathcal {H}}}^{2,\theta }(U)$ is complete.

The following result contains the classical Paley-Wiener theorem as a special case.

Proposition 3.8

Let $\theta \in {\mathbb {R}}$. The Laplace transform maps $H^\theta _+({\mathbb {R}},U)$ isomorphically onto ${{\mathcal {H}}}^{2,\theta }(U)$ and

$$\begin{aligned} \Vert {{\mathcal {L}}}u\Vert _{{{\mathcal {H}}}^{2,\theta }}=\sqrt{2\pi }\Vert u\Vert _{H^\theta }\quad \forall \, u\in H^{\theta }_+({\mathbb {R}},U). \end{aligned}$$

(3.19)

Proof

Let $\theta \in {\mathbb {R}}$ and $u\in {{\mathcal {S}}}'(U)$. It follows from (3.5) and Lemma 3.4 that

$$\begin{aligned} {{\mathcal {L}}}(R_\alpha u)=\textbf{r}_\alpha {{\mathcal {L}}}u\quad \forall \,u\in {{\mathcal {S}}}'_\ell (U),\,\,\forall \,\alpha \in {\mathbb {R}}. \end{aligned}$$

(3.20)

Let $u\in H^\theta _+({\mathbb {R}},U)$. Proposition 3.3 ensures that $R_{-\theta } u\in L_+^2({\mathbb {R}},U)$ and $\Vert u\Vert _{H^\theta }=\Vert R_{-\theta } u\Vert _{L^2}$, and thus,

$$\begin{aligned} \sqrt{2\pi }\Vert u\Vert _{H^\theta }=\sqrt{2\pi }\Vert R_{-\theta } u\Vert _{L^2}=\Vert {{\mathcal {L}}}(R_{-\theta } u)\Vert _{{{\mathcal {H}}}^2}, \end{aligned}$$

(3.21)

where, in the last equality, we have used the classical Paley-Wiener theorem. Appealing to (3.20), we see that ${{\mathcal {L}}}(R_{-\theta } u)=\textbf{r}_{-\theta }{{\mathcal {L}}}u$, which combined with (3.21) gives

$$\begin{aligned} \sqrt{2\pi }\Vert u\Vert _{H^\theta }=\Vert \textbf{r}_{-\theta }{{\mathcal {L}}}u\Vert _{{{\mathcal {H}}}^2}=\Vert {{\mathcal {L}}}u\Vert _{{{\mathcal {H}}}^{2,\theta }}, \end{aligned}$$

showing that ${{\mathcal {L}}}$ maps $H^\theta _+({\mathbb {R}},U)$ isomorphically into ${{\mathcal {H}}}^{2,\theta }(U)$ and (3.19) holds.

To show surjectivity, let $\textbf{v}\in {{\mathcal {H}}}^{2,\theta }(U)$. By the classical Paley-Wiener theorem there exists $u\in L_+^2({\mathbb {R}},U)$ such that $\textbf{v}=\textbf{r}_{\theta }{{\mathcal {L}}}u$. Setting $v:= R_\theta u$, we have that $v\in H^\theta _+({\mathbb {R}},U)$ by Proposition 3.3. By (3.20), ${{\mathcal {L}}}v={{\mathcal {L}}}(R_\theta u)=\textbf{r}_\theta {{\mathcal {L}}}u=\textbf{v}$, showing that ${{\mathcal {L}}}$ maps $H^\theta _+({\mathbb {R}},U)$ onto ${{\mathcal {H}}}^{2,\theta }(U)$. $\Box$

4 Boundary values of vector-valued holomorphic functions defined on the right-half plane

In this section, we explore the key hypothesis (3.3) on the holomorphic function $\textbf{G}$ in Theorem 3.1 in greater detail: In particular, under the assumption that the limit $\textbf{G}_0(y)=\lim _{x\downarrow 0}\textbf{G}(x+iy)$ exists in the strong operator topology for almost every $y\in {\mathbb {R}}$, we shall consider the imaginary axis condition

$$\begin{aligned} \mathrm{ess\,sup}_{y\in {\mathbb {R}}}\Vert (1+iy)^{\beta -\alpha }\textbf{G}_0(y)\Vert <\infty . \end{aligned}$$

(4.1)

The motivation for our interest in (4.1) is that the verification of the imaginary axis condition (4.1) is usually considerably easier than establishing the uniform boundedness of $(1+s)^{\beta -\alpha }\textbf{G}(s)$ on the open right-half plane. We shall identify conditions under which the existence of the strong limit $\textbf{G}_0(y)=\lim _{x\downarrow 0}\textbf{G}(x+iy)$ together with the imaginary axis condition (4.1) is sufficient for the function $s\mapsto (1+s)^{\beta -\alpha } \textbf{G}(s)$ to be in ${{\mathcal {H}}}^\infty ({{\mathcal {B}}}(U))$. This will involve the consideration of the boundary behaviour of $\textbf{G}(x+iy)$ in the sense of distributions as $x\downarrow 0$.

For a holomorphic function $\textbf{G}:{\mathbb {C}}_0\rightarrow X$, X a complex Banach space, set

$$\begin{aligned} \textbf{G}_x(y):=\textbf{G}(x+iy)\quad \forall \,y\in {\mathbb {R}},\quad \hbox { where~}\ x>0. \end{aligned}$$

The following result addresses the existence and properties of boundary distributions for X-valued holomorphic functions defined on ${\mathbb {C}}_0$.

Theorem 4.1

Let X be a complex Banach space, $\textbf{G}:{\mathbb {C}}_0\rightarrow X$ be holomorphic, and assume that there exist $M\ge 0$ and $m,k\in {\mathbb {N}}_0$ such that

$$\begin{aligned} \Vert \textbf{G}(s)\Vert \le M \big (1+|s|\big )^m\big (1+(\textrm{Re}\,s)^{-k}\big )\quad \forall \,s\in {\mathbb {C}}_0. \end{aligned}$$

(4.2)

Then there exists a tempered distribution $\Gamma \in {{\mathcal {S}}}'(X)$ (the so-called boundary distribution of $\textbf{G}$) such that $[\textbf{G}_x]\rightarrow \Gamma$ in ${{\mathcal {S}}}'(X)$ as $x\downarrow 0$, $\textrm{supp}({{\mathcal {F}}}^{-1}\Gamma )\subset [0,\infty )$ and ${{\mathcal {L}}}({{\mathcal {F}}}^{-1}\Gamma )=\textbf{G}$.

An alternative to the growth bound (4.2) is given by

$$\begin{aligned} \Vert \textbf{G}(s)\Vert \le N \big (1+|s|\big )^n\big (\textrm{Re}\,s\big )^{-k}\quad \forall \,s\in {\mathbb {C}}_0, \end{aligned}$$

(4.3)

where $N>0$ and $n\in {\mathbb {N}}_0$, see, for example, [8, equation (6.60)] and [10, equation (4.7)]. Trivially, if (4.3) holds, then so does (4.2) with $M=N$ and $m=n$. Conversely, if (4.2) is satisfied, then it is straightforward to show that (4.3) holds with $N=2M$ and $n=m+k$. Consequently, Theorem 4.1 remains valid when (4.2) is replaced by (4.3).

In the scalar-valued case, Theorem 4.1 is a special case of [8, Theorem 4.7.4]. For vector-valued functions, the existence of tempered boundary distributions is stated, without proof, in [9, Theorem 4.1]. We refer the reader to Appendix 3 for a proof of Theorem 4.1.

Next, we investigate under what conditions boundary distributions and pointwise boundary limits coincide. In this paper, our focus will be on the situation wherein $X={{\mathcal {B}}}(U)$, where U is a complex Hilbert space. It is well-known that if U is separable, then pointwise boundary limits of functions in ${{\mathcal {H}}}^\infty ({{\mathcal {B}}}(U))$ exist in the strong operator topology, but not necessarily in the norm topology of ${{\mathcal {B}}}(U)$, and the strong limit need not be Bochner measurable (as a ${{\mathcal {B}}}(U)$-valued function), but will be weakly measurable. Therefore, it would be too restrictive to assume that the pointwise boundary limit of a holomorphic function $\textbf{G}:{\mathbb {C}}_0\rightarrow {{\mathcal {B}}}(U)$ is in $L^1_\textrm{loc}({\mathbb {R}},{{\mathcal {B}}}(U))$ (locally Bochner integrable).

Therefore, it is useful to consider the weak integral (also called Pettis integral) for ${{\mathcal {B}}}(U)$-valued functions, where U is a complex Hilbert space. Let $\Omega \subset {\mathbb {R}}$ be a set of positive Lebesgue measure. A function $F:\Omega \rightarrow {{\mathcal {B}}}(U)$ is said to be weakly measurable if the scalar-valued function $\Omega \rightarrow {\mathbb {C}},\,t\mapsto \langle F(t)u,v\rangle$ is Lebesgue measurable for all $u,v\in U$. Furthermore, if F is weakly measurable, then the function $\Omega \rightarrow {\mathbb {C}},\,t\mapsto \Vert F(t)\Vert$ is Lebesgue measurable (see, for example, [22, Proof of Theorem 3.5.5]). For $1\le p\le \infty$, let $L^p_\textrm{w}(\Omega ,{{\mathcal {B}}}(U))$ denote the space of functions $F:\Omega \rightarrow {{\mathcal {B}}}(U)$ such that F is weakly measurable and

$$\begin{aligned} \Vert F\Vert _{L^p_\textrm{w}}:= & {} \left( \int _{\Omega }\Vert F(t)\Vert ^p\textrm{d}t\right) ^{1/p}<\infty \,\,\,\, \hbox { if~}\ p<\infty \quad \text{ and }\\ \Vert F\Vert _{L^\infty _\textrm{w}}:= & {} \textrm{ess}\,\textrm{supp}\Vert F(t)\Vert <\infty \,\,\,\,\hbox { if~}\ p=\infty . \end{aligned}$$

It is well-known that $L^p_\textrm{w}(\Omega ,{{\mathcal {B}}}(U))$ is complete, and, for $F\in L^1_\textrm{w}(\Omega ,{{\mathcal {B}}}(U))$, there exists a unique integral $\int _\Omega F(t)\,\textrm{d}t\in {{\mathcal {B}}}(U)$ such that

$$\begin{aligned} \left\langle \left( \int _\Omega F(t)\,\textrm{d}t\right) u,v\right\rangle =\int _\Omega \langle F(t)u,v\rangle \,\textrm{d}t\quad \forall \,u,v\in U, \end{aligned}$$

and

$$\begin{aligned} \left\| \int _\Omega F(t)\,\textrm{d}t\right\| \le \int _{\Omega }\Vert F(t)\Vert \,\textrm{d}t=\Vert F\Vert _{L^1_\textrm{w}}, \end{aligned}$$

see, for example, [13, Appendix A.5]. Under the assumption that U is separable, weak measurability of $F:\Omega \rightarrow {{\mathcal {B}}}(U)$ implies that F is also strongly measurable, that is, the function $\Omega \rightarrow U,\,t\mapsto F(t)u$ is Bochner measurable for every $u\in U$, see [22, Theorem 3.5.5]. Therefore, if U is separable, then the function $t\mapsto F(t)u$ is Bochner integrable for every $F\in L^p_\textrm{w}(\Omega ,{{\mathcal {B}}}(U))$ and every $u\in U$, and a routine argument shows that

$$\begin{aligned} \left( \int _\Omega F(t)\,\textrm{d}t\right) u=\int _{\Omega }F(t)u\,\textrm{d}t\quad \forall \,u\in U, \end{aligned}$$

where the integral on the left-hand side is the weak ${{\mathcal {B}}}(U)$-valued integral of F, whilst the integral on the right-hand side is the U-valued Bochner integral of Fu. Consequently, when U is separable, the weak ${{\mathcal {B}}}(U)$-valued integral can also be considered as a strong ${{\mathcal {B}}}(U)$-valued integral.

Finally, we introduce the space $L^p_\textrm{w,loc}({\mathbb {R}},{{\mathcal {B}}}(U))$ of all functions $F:{\mathbb {R}}\rightarrow {{\mathcal {B}}}(U)$ such that $F|_\Omega \in L^p_\textrm{w}(\Omega ,{{\mathcal {B}}}(U))$ for every bounded measurable set $\Omega \subset {\mathbb {R}}$. It follows from the properties listed above that, for every $F\in L^1_\textrm{w,loc}({\mathbb {R}},{{\mathcal {B}}}(U))$, the functional [F] given by

$$\begin{aligned}{}[F]({\varphi }):=\int _{-\infty }^\infty {\varphi }(t)F(t)\,\textrm{d}t\quad \forall \,{\varphi }\in {{\mathcal {D}}}\end{aligned}$$

(4.4)

is well-defined and continuous on ${{\mathcal {D}}}$, whence $[F]\in {{\mathcal {D}}}'({{\mathcal {B}}}(U))$. Similarly, if $F\in L^1_\textrm{w, loc}({\mathbb {R}},{{\mathcal {B}}}(U))$ is such that $\Vert F(t)\Vert$ is polynomially bounded on a set of the form $\{t\in {\mathbb {R}}:|t|\ge \tau \}$ for some $\tau >0$, then the right-hand side of (4.4) is well-defined for all ${\varphi }\in {{\mathcal {S}}}$, and $[F]\in {{\mathcal {S}}}'({{\mathcal {B}}}(U))$.

Throughout the rest of this section, let U be a complex Hilbert space. The next result provides a sufficient condition which guarantees that the boundary distribution of a holomorphic function is equal to the regular distribution induced by the pointwise boundary limit.

Lemma 4.2

Let $\textbf{G}:{\mathbb {C}}_0\rightarrow {{\mathcal {B}}}(U)$ be holomorphic. Assume that there exists $\Gamma \in {{\mathcal {S}}}'({{\mathcal {B}}}(U))$ such that $[\textbf{G}_x]\rightarrow \Gamma$ in ${{\mathcal {S}}}'({{\mathcal {B}}}(U))$ as $x\downarrow 0$, the limit $\textbf{G}_0(y):= \lim _{x\downarrow 0}\textbf{G}_x(y)$ exists in the strong operator topology for almost every $y\in {\mathbb {R}}$, and there exists $x_0>0$ such that, for each $a>0$, there exists $g_a\in L^1(-a,a)$ satisfying

$$\begin{aligned} \Vert \textbf{G}(x+iy)\Vert =\Vert \textbf{G}_x(y)\Vert \le g_a(y)\quad \forall \,(x,y)\in (0,x_0)\times [-a, a]. \end{aligned}$$

(4.5)

Under these conditions, $\textbf{G}_0\in L^1_\textrm{w,loc}({\mathbb {R}},{{\mathcal {B}}}(U))$ and $\Gamma ({\varphi })=[\textbf{G}_0]({\varphi })$ for all ${\varphi }\in {{\mathcal {D}}}$.

We remark that condition (4.5) is equivalent to the existence of $x_0>0$ and $g\in L^1_\textrm{loc}({\mathbb {R}})$ such that

$$\begin{aligned} \Vert \textbf{G}(x+iy)\Vert =\Vert \textbf{G}_x(y)\Vert \le g(y)\quad \forall \,(x,y)\in (0,x_0)\times {\mathbb {R}}. \end{aligned}$$

Note that if condition (4.5) is satisfied for some $x_0>0$, then it holds for all $x_0>0$. Furthermore, if $\textbf{G}$ is bounded on every bounded strip of the form $\{x+iy:x\in (0, x_0),\, |y|\le a\}$, $a > 0$, then (4.5) is satisfied.

We illustrate Lemma 4.2 with a class of examples, and demonstrate that, in the absence of condition (4.5), the conclusions of Lemma 4.2 may fail to hold.

Example 4.3

(1) Let $y_j\in {\mathbb {R}}$, $j=1,\ldots ,n$, be such that $y_j\not = y_k$ if $j\not =k$, and let $\textbf{H}:{\mathbb {C}}_0\rightarrow {{\mathcal {B}}}(U)$ be holomorphic and polynomially bounded, where U is assumed to separable. Consider the holomorphic function $\textbf{G}:{\mathbb {C}}_0\rightarrow {{\mathcal {B}}}(U)$ given by

$$\begin{aligned} \textbf{G}(s):=\bigg (\prod _{j=1}^n(s-iy_j)^{-\theta _j}\bigg )\textbf{H}(s)\quad \forall \,s\in {\mathbb {C}}_0,\quad \hbox {where \,\,} \theta _j\in (0,1) \hbox {,} j=1,\ldots ,n. \end{aligned}$$

It follows from Theorem 4.1 that there exists $\Gamma \in {{\mathcal {S}}}'({{\mathcal {B}}}(U))$ such that $[\textbf{G}_x]\rightarrow \Gamma$ in ${{\mathcal {S}}}'({{\mathcal {B}}}(U))$ as $x\downarrow 0$. As $\textbf{H}$ is polynomially bounded there exists $m\in {\mathbb {N}}$ such that $(1+s)^{-m}\textbf{H}(s)$ is bounded on ${\mathbb {C}}_0$ and it follows from Theorem 2.3 that there exists a boundary function $\textbf{H}_0\in L^\infty _\textrm{w,loc}({\mathbb {R}},{{\mathcal {B}}}(U))$ such that $\textbf{H}(x+iy)$ converges to $\textbf{H}_0(y)$ in the strong operator topology for almost every $y\in {\mathbb {R}}$ as $x\downarrow 0$. Consequently, $\textbf{G}(x+iy)$ converges to $\textbf{G}_0(y):=\prod _{j=1}^n\big (i(y-y_j)\big )^{-\theta _j}\textbf{H}_0(y)$ in the strong operator topology for almost every $y\in {\mathbb {R}}$ as $x\downarrow 0$. Furthermore, $\textbf{G}$ satisfies (4.5), and therefore Lemma 4.2 ensures that $\Gamma ({\varphi })=[\textbf{G}_0]({\varphi })$ for all ${\varphi }\in {{\mathcal {D}}}$.

(2) For $\theta \in (0,1)$, the scalar function $\textbf{G}(s)=s^{-\theta }$ is an instance of the above example. Let us now consider the case wherein $\theta =1$, that is, $\textbf{G}(s)=1/s$. It is clear that condition (4.5) is not satisfied. The existence of a distribution $\Gamma \in {{\mathcal {S}}}'$ such that $[\textbf{G}_x]\rightarrow \Gamma$ in ${{\mathcal {S}}}'$ as $x\downarrow 0$ follows from Theorem 4.1. Whilst the pointwise boundary limit $\textbf{G}_0(y)=1/(iy)$ exists for every $y\not =0$, it is not in $L^1_\textrm{loc}({\mathbb {R}},{\mathbb {C}})$, and hence does not induce a regular distribution, showing that the conclusions of Lemma 4.2 do not hold. Finally, using calculations similar to those in [18, p. 19/20], it is not difficult to show that $\Gamma =\textrm{pv}\,\textbf{G}_0+\pi \delta$, where

$$\begin{aligned} (\textrm{pv}\,\textbf{G}_0)({\varphi }):=\lim _{\varepsilon \downarrow 0}\left( \int _{-\infty }^{-\varepsilon }\textbf{G}_0(y){\varphi }(y)\textrm{d}y+\int _{\varepsilon }^\infty \textbf{G}_0(y){\varphi }(y)\textrm{d}y\right) \quad \forall \,{\varphi }\in {{\mathcal {S}}}, \end{aligned}$$

the principal-value distribution induced by $\textbf{G}_0$. $\Diamond$

For $T\in {{\mathcal {D}}}'({{\mathcal {B}}}(U))$ and $u,v\in U$, it is convenient to define a scalar-valued distribution $T^{u,v}\in {{\mathcal {D}}}'$ by $T^{u,v}({\varphi }):=\langle T({\varphi })u,v\rangle$ for all ${\varphi }\in {{\mathcal {D}}}$. We note that if $F\in L^1_\textrm{w,loc}({\mathbb {R}},{{\mathcal {B}}}(U))$, then $[F]^{u,v}=[f]$, where $f(t):=\langle F(t)u,v\rangle$ for all $t\in {\mathbb {R}}$.

Proof of Lemma 4.2

Trivially, $\textbf{G}_x$ is weakly measurable for every $x>0$, and thus $\textbf{G}_0$ is also weakly measurable. Moreover, we have that $\Vert \textbf{G}_x\Vert \in L^1_\textrm{loc}({\mathbb {R}})$ for every $x >0$, and so, for arbitrary $a > 0$, the restriction of $\Vert \textbf{G}_x\Vert$ to $[-a, a]$ is in $L^1(-a, a)$. By hypothesis, $\textbf{G}_x(y)$ converges to $\textbf{G}_0(y)$ in the strong operator topology for almost every $y\in {\mathbb {R}}$ as $x\downarrow 0$, that is, there exists a null set $N\subset {\mathbb {R}}$ such that $\lim _{x\downarrow 0}\textbf{G}_x(y)u= \textbf{G}_0(y)u$ for all $u\in \ U$ and all $y\in {\mathbb {R}}\backslash N$. Let $y\in {\mathbb {R}}\backslash N$ and $\varepsilon >0$. There exists $u\in U$ such that $\Vert u\Vert =1$ and $\Vert \textbf{G}_0(y)\Vert \le \Vert \textbf{G}_0(y)u\Vert +\varepsilon$. Hence,

$$\begin{aligned} \Vert \textbf{G}_0(y)\Vert \le \liminf _{x\downarrow 0}\Vert \textbf{G}_x(y)u\Vert +\varepsilon \le \liminf _{x\downarrow 0}\Vert \textbf{G}_x(y)\Vert +\varepsilon . \end{aligned}$$

This holds for every $y\in {\mathbb {R}}\backslash N$ and $\varepsilon >0$, and thus, we obtain that, for every $a>0$,

$$\begin{aligned} \Vert \textbf{G}_0(y)\Vert \le \liminf _{x\downarrow 0}\Vert \textbf{G}_x(y)\Vert \le g_a(y)\quad \hbox { for a.e. }\ y\in [-a,a]. \end{aligned}$$

Consequently, $\textbf{G}_0\in L^1_\textrm{w, loc}({\mathbb {R}},{{\mathcal {B}}}(U))$, and therefore, $\textbf{G}_0$ induces a regular distribution $[\textbf{G}_0]\in {{\mathcal {D}}}'({{\mathcal {B}}}(U))$.

Let ${\varphi }\in {{\mathcal {D}}}$, let $a>0$ be such that $\textrm{supp}\,{\varphi }\subset [-a, a]$ and let $u,v\in U$. It is clear that the function $y\mapsto \langle \textbf{G}_x(y)u,v\rangle {\varphi }(y)$ is in $L^1({\mathbb {R}})$ for every $x>0$ and $\langle \textbf{G}_x(y)u,v\rangle {\varphi }(y)\rightarrow \langle \textbf{G}_0(y)u,v\rangle {\varphi }(y)$ for almost every $y\in {\mathbb {R}}$ as $x\downarrow 0$. Furthermore, there exists $g_a \in L^1(-a, a)$ such that (4.5) holds, and so

$$\begin{aligned} |\langle \textbf{G}_x(y)u,v\rangle {\varphi }(y)|\le {\tilde{g}}_a(y)|{\varphi }(y)|\quad \forall \,(x,y)\in (0,x_0)\times {\mathbb {R}}, \end{aligned}$$

where ${\tilde{g}}_a(y):=\Vert u\Vert \Vert v\Vert g_a(y)$ for $y \in [-a, a]$ and ${\tilde{g}}_a(y) := 0$ for $|y|>a$. Trivially, the function ${\tilde{g}}_a|{\varphi }|$ is in $L^1({\mathbb {R}})$, and an application of Lebesgue’s dominated convergence theorem shows that $\langle \textbf{G}_x u,v\rangle {\varphi }\rightarrow \langle \textbf{G}_0 u,v\rangle {\varphi }$ in $L^1({\mathbb {R}})$ as $x\downarrow 0$, and so,

$$\begin{aligned}{}[\textbf{G}_x]^{u,v}({\varphi })&=\int _{-\infty }^{\infty }{\varphi }(y)\langle \textbf{G}_x(y)u,v\rangle \,\textrm{d}y\\&\rightarrow \int _{-\infty }^{\infty }{\varphi }(y)\langle \textbf{G}_0(y)u,v\rangle \,\textrm{d}y=[\textbf{G}_0]^{u,v}({\varphi })\quad \text{ as } x\downarrow 0. \end{aligned}$$

On the other hand, $[\textbf{G}_x]^{u,v}({\varphi })\rightarrow \Gamma ^{u,v}({\varphi })$ as $x\downarrow 0$, and thus, $\langle [\textbf{G}_0]({\varphi })u,v\rangle =\langle \Gamma ({\varphi })u,v\rangle$. This holds for all $u,v\in U$, showing that $[\textbf{G}_0]({\varphi })=\Gamma ({\varphi })$. The claim now follows as ${\varphi }\in {{\mathcal {D}}}$ was arbitrary. $\Box$

Corollary 4.4

Assume that U is separable and let $\textbf{G}:{\mathbb {C}}_0\rightarrow {{\mathcal {B}}}(U)$ be holomorphic and polynomially bounded on ${\mathbb {C}}_0$. Then the limit $\textbf{G}_0(y):=\lim _{x\downarrow 0}\textbf{G}_x(y)$ exists in the strong operator topology for almost every $y\in {\mathbb {R}}$, $\textbf{G}_0$ is weakly measurable, $\textbf{G}_0$ is polynomially bounded, $[\textbf{G}_0]\in {{\mathcal {S}}}'({{\mathcal {B}}}(U))$ and $[\textbf{G}_x]\rightarrow [\textbf{G}_0]$ in ${{\mathcal {S}}}'({{\mathcal {B}}}(U))$ as $x\downarrow 0$.

Proof

The function $\textbf{G}$ is polynomially bounded on ${\mathbb {C}}_0$, and so, there exist $M>0$ and $m\in {\mathbb {N}}_0$ such that

$$\begin{aligned} \Vert \textbf{G}(s)\Vert \le M|1+s|^m\le M(1+|s|)^m\quad \forall \,s\in {\mathbb {C}}_0. \end{aligned}$$

(4.6)

The function $\textbf{H}(s):=(1+s)^{-m}\textbf{G}(s)$ is in ${{\mathcal {H}}}^\infty ({{\mathcal {B}}}(U))$ and it follows from Theorem 2.3 that there exists a boundary function $\textbf{H}_0\in L^\infty _\textrm{w}({\mathbb {R}},{{\mathcal {B}}}(U))$ such that $\textbf{H}(x+iy)$ converges to $\textbf{H}_0(y)$ in the strong operator topology for almost every $y\in {\mathbb {R}}$ as $x\downarrow 0$. Consequently, $\textbf{G}_x(y)\rightarrow (1+iy)^m\textbf{H}_0(y)=:\textbf{G}_0(y)$ in the strong operator topology for almost every $y\in {\mathbb {R}}$ as $x\downarrow 0$. The weak measurability of $\textbf{G}_0$ follows from that of $\textbf{H}_0$, and, furthermore, $\textbf{G}_0$ is polynomially bounded as $\textbf{H}_0\in L^\infty _\textrm{w}({\mathbb {R}},{{\mathcal {B}}}(U))$. Consequently, $[\textbf{G}_0]\in {{\mathcal {S}}}'({{\mathcal {B}}}(U))$.

It remains to show that $[\textbf{G}_x]\rightarrow [\textbf{G}_0]$ in ${{\mathcal {S}}}'({{\mathcal {B}}}(U))$ as $x\downarrow 0$. To this end, we note that (4.2) holds with $k=0$ as follows from (4.6). Moreover, for arbitrary $x_0>0$, $\textbf{G}$ is bounded on the bounded strip $\{x+iy:x\in (0, x_0),\, |y|\le a\}$ for every $a > 0$, and so (4.5) is satisfied. Invoking Theorem 4.1 and Lemma 4.2, we see that there exists $\Gamma \in {{\mathcal {S}}}'({{\mathcal {B}}}(U))$ such that $[\textbf{G}_x]\rightarrow \Gamma$ in ${{\mathcal {S}}}'({{\mathcal {B}}}(U))$ as $x\downarrow 0$ and $\Gamma ({\varphi })=[\textbf{G}_0]({\varphi })$ for all ${\varphi }\in {{\mathcal {D}}}$. But ${{\mathcal {D}}}$ is dense in ${{\mathcal {S}}}$ and so $\Gamma ({\varphi })=[\textbf{G}_0]({\varphi })$ for all ${\varphi }\in {{\mathcal {S}}}$. Consequently, $[\textbf{G}_0]=\Gamma$ and $[\textbf{G}_x]\rightarrow [\textbf{G}_0]$ in ${{\mathcal {S}}}'({{\mathcal {B}}}(U))$ as $x\downarrow 0$. $\Box$

The following theorem shows that if a holomorphic function $\textbf{G}:{\mathbb {C}}_0\rightarrow {{\mathcal {B}}}(U)$ satisfies condition (4.2) and the boundary distribution of $\textbf{G}$ is in $L^\infty _\textrm{w}({\mathbb {R}},{{\mathcal {B}}}(U))$, then $\textbf{G}$ is bounded on ${\mathbb {C}}_0$.

Theorem 4.5

Let $\textbf{G}:{\mathbb {C}}_0\rightarrow {{\mathcal {B}}}(U)$ be holomorphic. Assume that there exist $M>0$ and $m,k\in {\mathbb {N}}_0$ such that (4.2) holds and the boundary distribution $\Gamma \in {{\mathcal {S}}}'({{\mathcal {B}}}(U))$ of $\textbf{G}$ (which exists by Theorem 4.1) is such that $\Gamma =[F]$, where $F\in L^\infty _\textrm{w}({\mathbb {R}},{{\mathcal {B}}}(U))$. Then the following statements hold.

• (1)  $\textbf{G}\in {{\mathcal {H}}}^\infty ({{\mathcal {B}}}(U))$ and $\Vert \textbf{G}\Vert _{{{\mathcal {H}}}^\infty }\le \Vert F\Vert _{L^\infty _\textrm{w}}$.

• (2) Under the additional assumption that U is separable, $\textbf{G}_x(y)\rightarrow F(y)$ in the strong operator topology for almost every $y\in {\mathbb {R}}$ as $x\downarrow 0$, and $\Vert \textbf{G}\Vert _{{{\mathcal {H}}}^\infty }=\Vert F\Vert _{L^\infty _\textrm{w}}$.

Proof

(1) Let $u,v\in U$. It is clear that the scalar holomorphic function $\textbf{G}^{u,v}$ defined by $\textbf{G}^{u,v}(s):=\langle \textbf{G}(s)u,v\rangle$ satisfies (4.2) (with M replaced by $\Vert u\Vert \Vert v\Vert M$) and $\textbf{G}^{u,v}$ has $\Gamma ^{u,v}\in {{\mathcal {S}}}'$ as its boundary distribution, that is,

$$\begin{aligned}{}[\textbf{G}^{u,v}_x]\rightarrow \Gamma ^{u,v}=[F]^{u,v}=[F^{u,v}]\quad \hbox {in~} {{\mathcal {S}}}' \hbox {}\quad \text{ as } x\downarrow 0, \end{aligned}$$

(4.7)

where $\textbf{G}^{u,v}_x(y):=\langle \textbf{G}_x(y)u,v\rangle$ for all $y\in {\mathbb {R}}$ and $F^{u,v}$ is the scalar-valued function in $L^\infty ({\mathbb {R}})$ given by $F^{u,v}(y):=\langle F(y)u,v\rangle$ for all $y\in {\mathbb {R}}$. An application of [8, Theorem 6.5.1 and commentary below (6.60)] or [10, Theorem 5.2] shows that $\textbf{G}^{u,v}\in {{\mathcal {H}}}^\infty$. Consequently, $\textbf{G}^{u,v}$ has a boundary function $g_{u,v}\in L^\infty ({\mathbb {R}})$ such that $\textbf{G}^{u,v}_x(y)\rightarrow g_{u,v}(y)$ almost everywhere as $x\downarrow 0$ and

$$\begin{aligned} \Vert \textbf{G}^{u,v}\Vert _{{{\mathcal {H}}}^\infty }=\Vert g_{u,v}\Vert _{L^\infty }. \end{aligned}$$

(4.8)

Moreover, by [19, Theorem 3.1 (Chapter I) and Corollary 3.2 (Chapter II)], $\textbf{G}^{u,v}_x$ converges to $g_{u,v}$ in the weak$^*$-topology as $x\downarrow 0$, and so, a fortiori, $[\textbf{G}^{u,v}_x]\rightarrow [g_{u,v}]$ in ${{\mathcal {S}}}'$ as $x\downarrow 0$. Invoking (4.7), we obtain that there exists a null set $N_{u,v}\subset {\mathbb {R}}$ depending on u and v such that

$$\begin{aligned} F^{u,v}(y)=g_{u,v}(y)\quad \forall \,y\in {\mathbb {R}}\backslash N_{u,v}, \end{aligned}$$

(4.9)

which, together with (4.8), gives

$$\begin{aligned} |\langle \textbf{G}(s)u,v\rangle |\le \Vert \textbf{G}^{u,v}\Vert _{{{\mathcal {H}}}^\infty }=\Vert F^{u,v}\Vert _{L^\infty }\le \Vert F\Vert _{L^\infty _\textrm{w}}\Vert u\Vert \Vert v\Vert \quad \forall \,u,v\in U,\,\forall \,s\in {\mathbb {C}}_0. \end{aligned}$$

Now $\sup _{\Vert v\Vert =1}|\langle \textbf{G}(s)u,v\rangle |=\Vert \textbf{G}(s)u\Vert$ for all $s\in {\mathbb {C}}_0$ and $u\in U$, and thus,

$$\begin{aligned} \Vert \textbf{G}(s)u\Vert \le \Vert F\Vert _{L^\infty _\textrm{w}}\Vert u\Vert \quad \forall \,u\in U,\,\forall \,s\in {\mathbb {C}}_0, \end{aligned}$$

showing that $\Vert \textbf{G}\Vert _{{{\mathcal {H}}}^\infty }\le \Vert F\Vert _{L^\infty _\textrm{w}}$ and $\textbf{G}\in {{\mathcal {H}}}^\infty ({{\mathcal {B}}}(U))$.

(2) Now assume that U is separable. By statement (1), $\textbf{G}\in {{\mathcal {H}}}^\infty ({{\mathcal {B}}}(U))$, and consequently, it follows from Theorem 2.3 that there exists a boundary function $\textbf{G}_0\in L^\infty _\textrm{w}({\mathbb {R}},{{\mathcal {B}}}(U))$ such that $\textbf{G}_x(y)$ converges to $\textbf{G}_0(y)$ in the strong operator topology for almost every $y\in {\mathbb {R}}$ as $x\downarrow 0$ and $\Vert \textbf{G}\Vert _{{{\mathcal {H}}}^\infty }=\Vert \textbf{G}_0\Vert _{L^\infty _\textrm{w}}$. It remains to show that

$$\begin{aligned} F(y)=\textbf{G}_0(y)\quad \hbox { for a.e.\ }\ y\in {\mathbb {R}}. \end{aligned}$$

(4.10)

Let the function $g_{u,v}$ and the set $N_{u,v}$ be defined as in the proof of statement (1). We note that there exist null sets ${\tilde{N}}_{u,v}\subset {\mathbb {R}}$, depending on u and v, such that

$$\begin{aligned} \langle \textbf{G}_0(y)u,v\rangle =g_{u,v}(y)\quad \forall \,y\in {\mathbb {R}}\backslash {\tilde{N}}_{u,v}. \end{aligned}$$

(4.11)

Let $V\subset U$ be a countable dense subset and let N be the union of all sets $N_{u,v}$ and ${\tilde{N}}_{u,v}$ with $u,v\in V$. Then, as a countable union of null sets, N is a null set and it follows from (4.9) and (4.11) that

$$\begin{aligned} \langle F(y)u,v\rangle =\langle \textbf{G}_0(y)u,v\rangle \quad \forall \,u,v\in V,\,\forall \,y\in {\mathbb {R}}\backslash N. \end{aligned}$$

As V is dense in U, we conclude that

$$\begin{aligned} \langle F(y)u,v\rangle =\langle \textbf{G}_0(y)u,v\rangle \quad \forall \,u,v\in U,\,\forall \,y\in {\mathbb {R}}\backslash N, \end{aligned}$$

which in turn implies that (4.10) holds. $\Box$

The next result is of particular importance for our purposes.

Proposition 4.6

Let $\textbf{G}:{\mathbb {C}}_0\rightarrow {{\mathcal {B}}}(U)$ be holomorphic and assume that there exist

• (i) $M>0$ and $m,k\in {\mathbb {N}}_0$ such that (4.2) is satisfied;

• (ii) $x_0>0$ such that, for every $a>0$, (4.5) holds for some $g_a\in L^1(-a,a)$.

For $\theta \in {\mathbb {R}}$, let $\textbf{r}_\theta$ and $\rho _\theta$ be as in (3.4). If the limit $\textbf{G}_0(y)=\lim _{x\downarrow 0}\textbf{G}_x(y)$ exists in the strong operator topology for almost every $y\in {\mathbb {R}}$ and $\rho _\theta \textbf{G}_0\in L^\infty _\textrm{w}({\mathbb {R}},{{\mathcal {B}}}(U))$, then $\textbf{r}_\theta \textbf{G}\in {{\mathcal {H}}}^\infty ({{\mathcal {B}}}(U))$ and $\Vert \textbf{r}_\theta \textbf{G}\Vert _{{{\mathcal {H}}}^\infty }\le \Vert \rho _\theta \textbf{G}_0\Vert _{L^\infty _\textrm{w}}$, with equality holding when U is separable.

Note that if U is separable and $\textbf{G}$ is of so-called bounded type (that is, $\textbf{G}$ is in the Nevanlinna class) [31, Section 4.2], or equivalently, $\textbf{G}$ is of the form $\textbf{G}=\textbf{N}/\textbf{d}$, where $\textbf{N}\in {{\mathcal {H}}}^\infty ({{\mathcal {B}}}(U))$ and $\textbf{d}$ is a scalar-valued ${{\mathcal {H}}}^\infty$-function such that $\textbf{d}(s)\not =0$ for all $s\in {\mathbb {C}}_0$, then $\lim _{x\downarrow 0}\textbf{G}_x(y)$ exists in the strong operator topology for almost every $y\in {\mathbb {R}}$, see [31, Sections 4.3 and 4.6].

Proof of Proposition 4.6

By Theorem 4.1, there exists $\Gamma \in {{\mathcal {S}}}'({{\mathcal {B}}}(U))$ such that $[\textbf{G}_x]\downarrow \Gamma$ in ${{\mathcal {S}}}'({{\mathcal {B}}}(U))$ as $x\downarrow 0$. Assuming that the limit $\textbf{G}_0(y)=\lim _{x\downarrow 0}\textbf{G}_x(y)$ exists in the strong operator topology for almost every $y\in {\mathbb {R}}$, Lemma 4.2 guarantees that $\Gamma ({\varphi })=[\textbf{G}_0]({\varphi })$ for all ${\varphi }\in {{\mathcal {D}}}$. By hypothesis $\rho _\theta \textbf{G}_0\in L^\infty _\textrm{w}({\mathbb {R}},{{\mathcal {B}}}(U))$, hence $[\textbf{G}_0]\in {{\mathcal {S}}}'({{\mathcal {B}}}(U))$, and therefore, $\Gamma ({\varphi })=[\textbf{G}_0]({\varphi })$ for all ${\varphi }\in {{\mathcal {S}}}$. Setting $\textbf{H}:=\textbf{r}_\theta \textbf{G}$, we have that

$$\begin{aligned} \Vert \textbf{H}(s)\Vert \le M\big (1+|s|\big )^n(1+\big (\textrm{Re}\,s)^{-k}\big )\quad \forall \,s\in {\mathbb {C}}_0, \end{aligned}$$

where n is the smallest non-negative integer such that $n\ge m-\min \{0,\theta \}$, showing that $\textbf{H}$ satisfies the growth condition (4.2). It is clear that $\textbf{H}(x+iy)\rightarrow \rho _\theta (y)\textbf{G}_0(y)$ in the strong operator topology for almost every $y\in {\mathbb {R}}$ as $x\downarrow 0$, and $\rho _\theta \Gamma =\rho _\theta [\textbf{G}_0]=[\rho _\theta \textbf{G}_0]\in {{\mathcal {S}}}'({{\mathcal {B}}}(U))$ is the boundary distribution of $\textbf{H}$. As $\rho _\theta \textbf{G}_0\in L^\infty _\textrm{w}({\mathbb {R}},{{\mathcal {B}}}(U))$, an application of Theorem 4.5 to $\textbf{H}$ shows that $\textbf{r}_\theta \textbf{G}=\textbf{H}\in {{\mathcal {H}}}^\infty ({{\mathcal {B}}}(U))$ and $\Vert \textbf{r}_\theta \textbf{G}\Vert _{{{\mathcal {H}}}^\infty }=\Vert \textbf{H}\Vert _{{{\mathcal {H}}}^\infty }\le \Vert \rho _\theta \textbf{G}_0\Vert _{L^\infty _\textrm{w}}$, with equality holding under the additional assumption of separability of U. $\Box$

The following corollary is an immediate consequence of Corollary 4.4 and Proposition 4.6.

Corollary 4.7

Assume that U is separable. For $\theta \in {\mathbb {R}}$, let $\textbf{r}_\theta$ and $\rho _\theta$ be as in (3.4). Let $\textbf{G}:{\mathbb {C}}_0\rightarrow {{\mathcal {B}}}(U)$ be holomorphic and polynomially bounded on ${\mathbb {C}}_0$. Under these conditions, the limit $\textbf{G}_0(y)=\lim _{x\downarrow 0}\textbf{G}_x(y)$ exists in the strong operator topology for almost every $y\in {\mathbb {R}}$, $\textbf{G}_0$ is weakly measurable, and, furthermore, if $\rho _\theta \textbf{G}_0\in L^\infty _\textrm{w}({\mathbb {R}},{{\mathcal {B}}}(U))$, then $\textbf{r}_\theta \textbf{G}\in {{\mathcal {H}}}^\infty ({{\mathcal {B}}}(U))$ and $\Vert \textbf{r}_\theta \textbf{G}\Vert _{{{\mathcal {H}}}^\infty }=\Vert \rho _\theta \textbf{G}_0\Vert _{L^\infty _\textrm{w}}$.

5 Sobolev stability

In this section, we develop a new input-output stability framework for a large class of causal translation-invariant linear operators defined on spaces of vector-valued distributions. Using Theorem 3.1, the results of Sect. 4 and well-known theorems on the representation of translation-invariant operators by convolution kernels (impulse responses), we provide characterizations of boundedness properties of such operators (as maps from $H^\alpha ({\mathbb {R}},U)$ to $H^\beta ({\mathbb {R}},U)$) in terms of the Laplace transforms of their kernels (transfer functions). Throughout this section, let U be a complex Hilbert space.

Before addressing the main topic of this section, it is convenient to state and prove the following lemma.

Lemma 5.1

Let $\alpha \in {\mathbb {R}}$ and $u_k\in H^\alpha ({\mathbb {R}},U)$, $k\in {\mathbb {N}}$. If $u_k\rightarrow u$ in $H^\alpha ({\mathbb {R}},U)$ as $k\rightarrow \infty$, then $u_k\rightarrow u$ in ${{\mathcal {S}}}'(U)$ as $k\rightarrow \infty$.

Proof

Let $(u_k)_{k\in {\mathbb {N}}}$ be a convergent sequence in $H^\alpha ({\mathbb {R}},U)$ with limit u. If $\alpha \ge 0$, then $u_k\rightarrow u$ in $L^2({\mathbb {R}},U)$, and so, $u_k\rightarrow u$ in ${{\mathcal {S}}}'(U)$ as $k\rightarrow \infty$. Let us now assume that $\alpha <0$. By Proposition 3.3, $R_{-\alpha }u_k\rightarrow R_{-\alpha }u$ in $L^2({\mathbb {R}},U)$ as $k\rightarrow \infty$. Consequently, $R_{-\alpha }u_k\rightarrow R_{-\alpha }u$ in ${{\mathcal {S}}}'(U)$ as $k\rightarrow \infty$. Invoking Proposition 3.3 once more, we have that $R_{-\alpha }^{-1}=R_{\alpha }$ is a sequentially continuous operator from ${{\mathcal {S}}}'(U)$ into itself, and thus, $u_k\rightarrow u$ in ${{\mathcal {S}}}'(U)$ as $k\rightarrow \infty$. $\Box$

Recall that ${{\mathcal {D}}}'_{\ell }(X)$ denotes the subspace of all distributions in ${{\mathcal {D}}}'(X)$ with support bounded on the left, where $X=U$ or ${{\mathcal {B}}}(U)$. If $K\in {{\mathcal {D}}}'_{\ell }({{\mathcal {B}}}(U))$, then the convolution product $K\star u$ is a well-defined distribution in ${{\mathcal {D}}}'_{\ell }(U)$ for all $u\in {{\mathcal {D}}}'_{\ell }(U)$, see Appendix 1. It is useful to recall the close relationship between causal translation-invariant operators on ${{\mathcal {D}}}'(U)$ and convolution operators with kernels in ${{\mathcal {D}}}'({{\mathcal {B}}}(U))$ supported on $[0,\infty )$. In the following, when considering linear operators $G:\textrm{dom}\,G\subset {{\mathcal {D}}}'(U)\rightarrow {{\mathcal {D}}}'(U)$, it is always understood that $\textrm{dom}\,G$ is endowed with the relative topology induced by ${{\mathcal {D}}}'(U)$.

Proposition 5.2

Let $G:\textrm{dom}\,G\subset {{\mathcal {D}}}'(U)\rightarrow {{\mathcal {D}}}'(U)$ be a linear operator such that $C^\infty _\textrm{c}({\mathbb {R}},U)\subset \textrm{dom}\,G$. The following statements hold.

• (1) If G is continuous, causal and translation invariant, then there exists a unique $K\in {{\mathcal {D}}}'({{\mathcal {B}}}(U))$ such that $\mathrm{supp\,}K\subset [0,\infty )$ and $Gu=K\star u$ for all $u\in {{\mathcal {D}}}'_{\ell }(U)\cap \textrm{dom}\,G$.

• (2) If there exists $K\in {{\mathcal {D}}}'({{\mathcal {B}}}(U))$ such that $\mathrm{supp\,}K\subset [0,\infty )$ and $Gu=K\star u$ for all $u\in C^\infty _\textrm{c}({\mathbb {R}},U)$, then G is continuous, causal and translation invariant.

• (3) Let $\alpha ,\beta \in {\mathbb {R}}$. If $\textrm{dom}\,G=H^\alpha ({\mathbb {R}},U)$, $G\in {{\mathcal {B}}}(H^\alpha ({\mathbb {R}},U), H^\beta ({\mathbb {R}},U))$, and G is causal and translation invariant, then there exists $K\in {{\mathcal {D}}}'({{\mathcal {B}}}(U))$ such that $\mathrm{supp\,}K\subset [0,\infty )$ and $Gu=K\star u$ for all $u\in H^\alpha _\ell ({\mathbb {R}},U)$.

Proof

(1) Denote the restriction of G to $C^\infty _\textrm{c}({\mathbb {R}},U)$ by $G_\textrm{c}$. As G is assumed to be continuous, it is clear that $G_\textrm{c}$ is continuous as an operator from $C^\infty _\textrm{c}({\mathbb {R}},U)$ to ${{\mathcal {D}}}'(U)$. Consequently, it follows from [43, Theorems 3.5-1 and 5.10-1] that there exists a unique $K\in {{\mathcal {D}}}'({{\mathcal {B}}}(U))$ such that

$$\begin{aligned} Gu=G_\textrm{c}u=K\star u\quad \forall \,u\in C^\infty _\textrm{c}({\mathbb {R}},U). \end{aligned}$$

(5.1)

The identity $Gu=K\star u$ extends to all $u\in {{\mathcal {D}}}'_{\ell }(U)\cap \textrm{dom}\,G$ by the denseness of $C^\infty _\textrm{c}({\mathbb {R}},U)$ in ${{\mathcal {D}}}'(U)$, the continuity assumption on G, and the continuity properties of the convolution product (see Appendix 1). Invoking [43, Theorem 5.11-1], the causality of G, and (5.1), we conclude that $\mathrm{supp\,}K\subset [0,\infty )$.

(2) This statement is a consequence of results in [43, Chapter 5].

(3) As $G\in {{\mathcal {B}}}(H^\alpha ({\mathbb {R}},U), H^\beta ({\mathbb {R}},U))$, the restriction $G_\textrm{c}$ of G to $C^\infty _\textrm{c}({\mathbb {R}},U)$ is a continuous operator from $C^\infty _\textrm{c}({\mathbb {R}},U)$ to $H^\beta ({\mathbb {R}},U)$. Consequently, appealing to Lemma 5.1, $G_\textrm{c}$ is continuous as an operator from $C^\infty _\textrm{c}({\mathbb {R}},U)$ to ${{\mathcal {D}}}'(U)$. The claim now follows by arguments identical to those used in the proof of statement (1). $\Box$

The distribution K appearing in Proposition 5.2 is called the kernel or impulse response of the operator G. If $\sigma (K)<\infty$ (finite abscissa of convergence), then $\textbf{G}(s):=({{\mathcal {L}}}K)(s)$ exists for all $s\in {\mathbb {C}}_{\sigma (K)}$ and the function $\textbf{G}$, a ${{\mathcal {B}}}(U)$-valued holomorphic function defined on ${\mathbb {C}}_{\sigma (K)}$, is referred to as the transfer function of G. If $u\in {{\mathcal {D}}}'_{\ell }(U)$ is such that $\sigma (u)<\infty$, then $K\star u$ is Laplace transformable and

$$\begin{aligned} ({{\mathcal {L}}}Gu)(s)=\textbf{G}(s)({{\mathcal {L}}}u)(s)\quad \forall \,s\in {\mathbb {C}}_\mu , \end{aligned}$$

(5.2)

where $\mu :=\max \big (\sigma (K),\sigma (u)\big )$, see Appendix 1. Observe that $\textbf{G}$ is the unique function which satisfies (5.2). Therefore, in control theoretic applications, where Gu is the output generated by the input u, the transfer function $\textbf{G}$ is often determined by computing the (necessarily unique) function which satisfies (5.2) (such as by computing the quotient $({{\mathcal {L}}}(Gu))(s)/({{\mathcal {L}}}u)(s)$ when these quantities are scalar valued).

Definition 5.3

Let $\alpha ,\beta \in {\mathbb {R}}$. A linear operator $G:\textrm{dom}\,G\subset {{\mathcal {D}}}'(U)\rightarrow {{\mathcal {D}}}'(U)$ is said to be Sobolev $(\alpha ,\beta )$ -stable if $C^\infty _\textrm{c}({\mathbb {R}},U)\subset \textrm{dom}\,G$, $G(C^\infty _\textrm{c}({\mathbb {R}},U))\subset H^\beta ({\mathbb {R}},U)$, and there exists $\gamma >0$ such that

$$\begin{aligned} \Vert Gu\Vert _{H^\beta }\le \gamma \Vert u\Vert _{H^\alpha }\quad \forall \,u\in C^\infty _\textrm{c}({\mathbb {R}},U). \end{aligned}$$

(5.3)

The next theorem, the main result of this section, provides several characterizations of Sobolev $(\alpha ,\beta )$-stability in terms of transfer functions.

Theorem 5.4

Let $G:\textrm{dom}\,G\subset {{\mathcal {D}}}'(U)\rightarrow {{\mathcal {D}}}'(U)$ be a causal translation-invariant continuous linear operator such that $C^\infty _\textrm{c}({\mathbb {R}},U)\subset \textrm{dom}\,G$, and let $K\in {{\mathcal {D}}}'({{\mathcal {B}}}(U))$ be the kernel of G. For arbitrary $\alpha ,\beta \in {\mathbb {R}}$, the following statements are equivalent.

• (1) G is Sobolev $(\alpha ,\beta )$-stable.

• (2) There exists a unique causal and translation-invariant operator $G^\textrm{e}\in {{\mathcal {B}}}(H^\alpha ({\mathbb {R}},U), H^\beta ({\mathbb {R}},U))$ such that $G^\textrm{e}u=Gu$ for all $u\in H^\alpha ({\mathbb {R}},U)\cap \textrm{dom}\,G$.

• (3) K is Laplace transformable, $\sigma (K)\le 0$ and the transfer function $\textbf{G}$ of G satisfies

  $$\begin{aligned} \sup _{s\in {\mathbb {C}}_0}\Vert (1+s)^{\beta -\alpha }\textbf{G}(s)\Vert <\infty . \end{aligned}$$

  (5.4)

• (4) K is Laplace transformable and there exist $\mu >\max (0,\sigma (K))$ and a holomorphic function  $\textbf{G}^\textrm{e}:{\mathbb {C}}_0\rightarrow {{\mathcal {B}}}(U)$ such that $\textbf{G}^\textrm{e}$ and the transfer function $\textbf{G}$ of G coincide on ${\mathbb {C}}_\mu$ and

  $$\begin{aligned} \sup _{0<\mathrm{Re\,}s<\mu }\Vert (1+s)^{\beta -\alpha }\textbf{G}^\textrm{e}(s)\Vert <\infty . \end{aligned}$$

  (5.5)

• (5) K is Laplace transformable and there exists a holomorphic function  $\textbf{G}^\textrm{e}:{\mathbb {C}}_0\rightarrow {{\mathcal {B}}}(U)$ such that $\textbf{G}^\textrm{e}$ and the transfer function $\textbf{G}$ of G coincide on ${\mathbb {C}}_\nu$, where $\nu :={\max (0,\sigma (K))}$, and

  $$\begin{aligned} \sup _{s\in {\mathbb {C}}_0}\Vert (1+s)^{\beta -\alpha }\textbf{G}^\textrm{e}(s)\Vert <\infty . \end{aligned}$$

  (5.6)

Note that if, in statements (4) and (5), $\sigma (K)>0$, then $\textbf{G}^\textrm{e}$ is a holomorphic extension of $\textbf{G}$.

Before we prove Theorem 5.4, we state two immediate consequences in the form of a corollary.

Corollary 5.5

Let $G:\textrm{dom}\,G\subset {{\mathcal {D}}}'(U)\rightarrow {{\mathcal {D}}}'(U)$ be a causal translation-invariant continuous linear operator such that $C^\infty _\textrm{c}({\mathbb {R}},U)\subset \textrm{dom}\,G$, and let $\alpha ,\beta \in {\mathbb {R}}$.

• (1) If G is Sobolev $(\alpha ,\beta )$-stable, then $G\big (H^\alpha ({\mathbb {R}},U)\cap \textrm{dom}\,G\big )\subset H^\beta ({\mathbb {R}},U)$ and $\Vert Gu\Vert _{H^\beta }\le \gamma \Vert u\Vert _{H^\alpha }$ for all $u\in H^\alpha ({\mathbb {R}},U)\cap \textrm{dom}\,G$, where $\gamma >0$ is the constant appearing in (5.3).

• (2) If G is Sobolev $(\alpha ,\beta )$-stable, then G is Sobolev $(\alpha +\theta ,\beta +\theta )$-stable for all $\theta \in {\mathbb {R}}$.

Proof of Theorem 5.4

(1) $\Rightarrow$ (2). Assume that statement (1) holds. As $C^\infty _\textrm{c}({\mathbb {R}},U)$ is dense in $H^\alpha ({\mathbb {R}},U)$ (by Lemma 2.1), it follows from (5.3) that there exists a unique operator $G^\textrm{e}\in {{\mathcal {B}}}(H^\alpha ({\mathbb {R}},U),H^\beta ({\mathbb {R}},U))$ such that $G^\textrm{e}u=Gu$ for all $u\in C^\infty _\textrm{c}({\mathbb {R}},U)$. We proceed to show that $G^\textrm{e}$ and G coincide on $H^\alpha ({\mathbb {R}},U)\cap \textrm{dom}\,G$. To this end, let $u\in H^\alpha ({\mathbb {R}},U)\cap \textrm{dom}\,G$. Lemma 2.1 guarantees the existence of a sequence $(u_k)_{k\in {\mathbb {N}}}$ in $C^\infty _\textrm{c}({\mathbb {R}},U)$ such that $u_k\rightarrow u$ in $H^\alpha ({\mathbb {R}},U)$ as $k\rightarrow \infty$. Since $G^\textrm{e}\in {{\mathcal {B}}}(H^\alpha ({\mathbb {R}},U),H^\beta ({\mathbb {R}},U))$, we have that $G^\textrm{e}u_k\rightarrow G^\textrm{e}u$ in $H^\beta ({\mathbb {R}},U)$ as $k\rightarrow \infty$. Invoking Lemma 5.1, we conclude that

$$\begin{aligned} u_k\rightarrow u\quad \hbox { in \,\,}\ {{\mathcal {S}}}'(U)\quad \text{ and }\quad G^\textrm{e}u_k\rightarrow G^\textrm{e}u \quad \hbox {in \,\,} {{\mathcal {S}}}'(U) \hbox {}\qquad \text{ as } k\rightarrow \infty . \end{aligned}$$

(5.7)

As $G^\textrm{e}u_k=Gu_k$ for all $k\in {\mathbb {N}}$, the second convergence gives

$$\begin{aligned} Gu_k\rightarrow G^\textrm{e}u\quad \hbox {in \,\,} {{\mathcal {S}}}'(U) \hbox {\qquad as~} k\rightarrow \infty . \end{aligned}$$

(5.8)

The first convergence in (5.7) implies that $u_k\rightarrow u$ in ${{\mathcal {D}}}'(U)$ as $k\rightarrow \infty$, whence $Gu_k\rightarrow Gu$ in ${{\mathcal {D}}}'(U)$ as $k\rightarrow \infty$ as G is continuous. Appealing to (5.8) shows that $Gu=G^\textrm{e}u$ in ${{\mathcal {D}}}'(U)$. In particular, the distribution Gu extends continuously to ${{\mathcal {S}}}$, and hence is tempered and coincides with $G^\textrm{e}u$. As $u\in H^\alpha ({\mathbb {R}},U)\cap \textrm{dom}\,G$ was arbitrary, it follows that G and $G^\textrm{e}$ coincide on $H^\alpha ({\mathbb {R}},U)\cap \textrm{dom}\,G$. It is a routine exercise to show that $G^\textrm{e}$ inherits the properties of translation-invariance and causality from G.

(2) $\Rightarrow$ (3). Invoking Theorem 3.1, we conclude that there exists a holomorphic function $\textbf{G}^\textrm{e}:{\mathbb {C}}_0\rightarrow {{\mathcal {B}}}(U)$ such that

$$\begin{aligned} \sup _{s\in {\mathbb {C}}_0}\Vert (1+s)^{\beta -\alpha }\textbf{G}^\textrm{e}(s)\Vert <\infty , \end{aligned}$$

(5.9)

and $G^\textrm{e}u=\big ({{\mathcal {L}}}^{-1}\circ {{\mathcal {M}}}_{\textbf{G}^\textrm{e}_0}\circ {{\mathcal {L}}}\big )\big (u\big )$ for all $u\in H^\alpha _\ell ({\mathbb {R}},U)$. By [43, Theorem 6.5-1] there exists a Laplace transformable $K^\textrm{e}\in {{\mathcal {D}}}'({{\mathcal {B}}}(U))$ with $\textrm{supp}\,K^\textrm{e}\subset [0,\infty )$, $\sigma (K^\textrm{e})\le 0$ and $({{\mathcal {L}}}K^\textrm{e})(s)=\textbf{G}^\textrm{e}(s)$ for all $s\in {\mathbb {C}}_0$. Invoking the convolution theorem (exchange formula) for the Laplace transform (see Appendix 1), we obtain

$$\begin{aligned} G^\textrm{e}u=({{\mathcal {L}}}^{-1}\circ {{\mathcal {M}}}_{\textbf{G}^\textrm{e}}\circ {{\mathcal {L}}})u=({{\mathcal {L}}}^{-1}\circ {{\mathcal {M}}}_{{{\mathcal {L}}}K^\textrm{e}}\circ {{\mathcal {L}}})u =K^\textrm{e}\star u\quad \forall \,u\in C^\infty _\textrm{c}({\mathbb {R}},U). \end{aligned}$$

Therefore,

$$\begin{aligned} K\star u=Gu=G^\textrm{e}u=K^\textrm{e}\star u\quad \forall \,u\in C^\infty _\textrm{c}({\mathbb {R}},U). \end{aligned}$$

(5.10)

To establish that statement (3) holds, it is sufficient to prove that $K=K^\textrm{e}$. Indeed, in this case it follows from (5.9) that inequality (5.4) is satisfied. To show that $K=K^\textrm{e}$, let ${\varphi }\in {{\mathcal {D}}}$ and $v\in U$, and set $\psi :={\check{{\varphi }}}\in {{\mathcal {D}}}$, where the superscript “  $\check{}$  ” denotes reflection, that is, ${\check{{\varphi }}}(t):={\varphi }(-t)$ for all $t\in {\mathbb {R}}$. Then $K\star \psi \in C^\infty ({\mathbb {R}},{{\mathcal {B}}}(U))$, $K\star (\psi \otimes v)\in C^\infty ({\mathbb {R}},U)$ and

$$\begin{aligned} K({\varphi })v=K({\check{\psi }})v=(K\star \psi )(0)v=(K\star (\psi \otimes v))(0). \end{aligned}$$

Similarly, $K^\textrm{e}({\varphi })v=(K^\textrm{e}\star (\psi \otimes v))(0)$. Together with an application of (5.10) with $u=\psi \otimes v$ this shows that $K({\varphi })v=K^\textrm{e}({\varphi })v$. This holds for all ${\varphi }\in {{\mathcal {D}}}$ and all $v\in U$, and thus $K=K^\textrm{e}$.

(3) $\Rightarrow$ (4). This implication is trivially true.

(4) $\Rightarrow$ (5). Since K is Laplace transformable, $\textrm{supp}\,K\subset [0,\infty )$ (by Proposition 5.2) and $\mu >\sigma (K)$, it follows that the function $\textbf{G}$ is polynomially bounded on ${\mathbb {C}}_\mu$ (see, for example, [43, Theorem 6.5-1]). Now $\textbf{G}^\textrm{e}|_{{\mathbb {C}}_\mu }=\textbf{G}|_{{\mathbb {C}}_\mu }$, and so, it follows from (5.5) that $\textbf{G}^\textrm{e}$ is polynomially bounded on ${\mathbb {C}}_0$. An application of Corollary 4.7 to $\textbf{G}^\textrm{e}$ shows that (5.6) is satisfied.

(5) $\Rightarrow$ (1). Assume that statement (5) holds, that is, there exists a holomorphic function $\textbf{G}^\textrm{e}:{\mathbb {C}}_0\rightarrow {{\mathcal {B}}}(U)$ of $\textbf{G}$ such that $\textbf{G}^\textrm{e}(s)=\textbf{G}(s)$ for all $s\in {\mathbb {C}}_\nu$ and (5.6) is satisfied. To show that G is Sobolev $(\alpha ,\beta )$-stable, we note that, by Theorem 3.1, there exists a translation-invariant and causal operator $G^\textrm{e}\in {{\mathcal {B}}}(H^\alpha ({\mathbb {R}},U),H^\beta ({\mathbb {R}},U))$ such that

$$\begin{aligned} G^\textrm{e}u=\big ({{\mathcal {L}}}^{-1}\circ {{\mathcal {M}}}_{\textbf{G}^\textrm{e}}\circ {{\mathcal {L}}}\big (u)\quad \forall \,u\in H^\alpha _\ell ({\mathbb {R}},U). \end{aligned}$$

Consequently,

$$\begin{aligned} \big ({{\mathcal {L}}}(Gu)\big )(s)=\textbf{G}(s)({{\mathcal {L}}}u)(s)=\textbf{G}^\textrm{e}(s)({{\mathcal {L}}}u)(s) =\big ({{\mathcal {L}}}(G^\textrm{e}u)\big )(s)\quad \forall \,u\in C^\infty _\textrm{c}({\mathbb {R}},U),\,\,\forall \,s\in {\mathbb {C}}_\nu , \end{aligned}$$

showing that $Gu=G^\textrm{e}u$ for all $u\in C^\infty _\textrm{c}({\mathbb {R}},U)$, and thereby completing the proof. $\Box$

The following corollary shows that, under suitable assumptions, Sobolev $(\alpha ,\beta )$-stability follows if the transfer function satisfies a natural boundedness condition on the imaginary axis.

Corollary 5.6

Let $G:\textrm{dom}\,G\subset {{\mathcal {D}}}'(U)\rightarrow {{\mathcal {D}}}'(U)$ be a causal translation-invariant continuous linear operator such that $C^\infty _\textrm{c}({\mathbb {R}},U)\subset \textrm{dom}\,G$ and let $K\in {{\mathcal {D}}}'({{\mathcal {B}}}(U))$ be the kernel of G. Assume that K is Laplace transformable and there exists a holomorphic function  $\textbf{G}^\textrm{e}:{\mathbb {C}}_0\rightarrow {{\mathcal {B}}}(U)$ such that $\textbf{G}^\textrm{e}(s)=\textbf{G}(s)$ for all $s\in {\mathbb {C}}_\nu$, where $\textbf{G}$ is the transfer function of G and $\nu :=\max \big (0,\sigma (K)\big )$. Then, for $\alpha ,\beta \in {\mathbb {R}}$, the following statements hold.

• (1) Under the assumption that the following three conditions are satisfied:

  • (i) there exist $M>0$, $m,k\in {\mathbb {N}}_0$ and $\mu >\nu$ such that

    $$\begin{aligned} \Vert \textbf{G}^\textrm{e}(s)\Vert \le M\big (1+|s|^m\big )\big (1+(\textrm{Re}\,s\big )^{-k})\quad \hbox {for all~} s\in {\mathbb {C}}\hbox {such that~} 0<\textrm{Re}\,s<\mu , \end{aligned}$$

  • (ii) there exist $x_0>0$ such that, for every $a>0$, there exists $g_a\in L^1(-a,a)$ satisfying

    $$\begin{aligned} \Vert \textbf{G}^\textrm{e}(x+iy)\Vert \le g_a(y)\quad \forall \,(x,y)\in (0,x_0)\times [-a,a], \end{aligned}$$

  • (iii) the limit $\textbf{G}^\textrm{e}_0(y)=\lim _{x\downarrow 0}\textbf{G}^\textrm{e}_x(y)$ exists in the strong operator topology for almost every $y\in {\mathbb {R}}$,

  the operator G is Sobolev $(\alpha ,\beta )$-stable, provided that

  $$\begin{aligned} \mathrm{ess\,sup}_{y\in {\mathbb {R}}}\Vert (1+iy)^{\beta -\alpha }\textbf{G}^\textrm{e}_0(y)\Vert <\infty . \end{aligned}$$

  (5.11)

• (2) Assume that U is separable and $\textbf{G}^\textrm{e}$ is polynomially bounded on the strip $0<\textrm{Re}\,s<\mu$ for some $\mu >\nu$. Under these conditions, the limit $\textbf{G}^\textrm{e}_0(y)=\lim _{x\downarrow 0}\textbf{G}^\textrm{e}_x(y)$ exists in the strong operator topology for almost every $y\in {\mathbb {R}}$, and, if (5.11) holds, then  G is Sobolev $(\alpha ,\beta )$-stable.

Proof

(1) By Proposition 5.2, $\textrm{supp}\,K\subset [0,\infty )$, and so, the function $\textbf{G}={{\mathcal {L}}}K$ is polynomially bounded on ${\mathbb {C}}_\mu$ as follows from [43, Theorem 6.5-1]. Thus, by condition (i), there exist $N\ge M$ and an integer $n\ge m$ such that

$$\begin{aligned} \Vert \textbf{G}^\textrm{e}(s)\Vert \le N\big (1+|s|^n\big )\big (1+(\textrm{Re}\,s)^{-k}\big )\quad \forall \,s\in {\mathbb {C}}_0. \end{aligned}$$

Hence, $\textbf{G}^\textrm{e}$ satisfies the hypotheses of Proposition 4.6 (with $\theta =\alpha -\beta$). Consequently, if $\mathrm{ess\,sup}_{y\in {\mathbb {R}}}\Vert (1+iy)^{\beta -\alpha }\textbf{G}^\textrm{e}_0(y)\Vert <\infty$, then Proposition 4.6 guarantees that $\sup _{s\in {\mathbb {C}}_0}\Vert (1+s)^{\beta -\alpha }\textbf{G}^\textrm{e}(s)\Vert <\infty$. Sobolev $(\alpha ,\beta )$-stability of G now follows from Theorem 5.4.

(2) Assume that U is separable and the function $\textbf{G}^\textrm{e}$ is polynomially bounded on the strip $0<\textrm{Re}\,s<\mu$ for some $\mu >\nu$. As in the proof of statement (1), we have that $\textbf{G}$ is polynomially bounded on ${\mathbb {C}}_\mu$, and thus, $\textbf{G}^\textrm{e}$ is polynomially bounded on ${\mathbb {C}}_0$. It follows that conditions (i) and (ii) of statement (1) hold. Moreover, there exists $k\in {\mathbb {N}}_0$ such that $\textbf{H}(s):=(1+s)^{-k}\textbf{G}^\textrm{e}(s)$ is bounded on ${\mathbb {C}}_0$ and therefore, as U is assumed to be separable, the limit $\textbf{H}_0(y)=\lim _{x\downarrow 0}\textbf{H}(x+iy)$ exists in the strong operator topology for almost every $y\in {\mathbb {R}}$, implying that condition (iii) of statement (1) is also satisfied. As a consequence, the claim now follows from statement (1). $\Box$

Next, we make contact with the theory of well-posed linear state-space systems, see, for example, the monograph [36]. Each of these systems has a translation-invariant and causal input-output operator $G\in {{\mathcal {B}}}(L^2_\mu ({\mathbb {R}},U))$ for some $\mu \in {\mathbb {R}}$, where the Hilbert space $L^2_\mu ({\mathbb {R}},U)$ is defined by

$$\begin{aligned} L^2_\mu ({\mathbb {R}},U):=\{u\in L^2_\textrm{loc}({\mathbb {R}},U):e^{-\mu \,\cdot \,}u\in L^2({\mathbb {R}},U)\}\quad \text{ and }\quad \langle u,v\rangle _{L^2_\mu }:=\langle e^{-\mu \,\cdot \,}u,e^{-\mu \,\cdot \,}v\rangle _{L^2}. \end{aligned}$$

Conversely, for every translation-invariant and causal operator G belonging to ${{\mathcal {B}}}(L^2_\mu ({\mathbb {R}},U))$ for some $\mu \in {\mathbb {R}}$, there exists a well-posed state-space system which has G as its input-output operator. If $G\in {{\mathcal {B}}}(L^2_\mu ({\mathbb {R}},U))$ is translation invariant and causal, then, invoking Proposition 5.2, there exists a kernel $K\in {{\mathcal {D}}}'({{\mathcal {B}}}(U))$ such that $\textrm{supp}\,K\subset [0,\infty )$ and $Gu=K\star u$ for all $u\in L^2_{\mu ,\,\ell }({\mathbb {R}},U)$, where $L^2_{\mu ,\ell }({\mathbb {R}},U)$ denotes the subspace of $L^2_\mu ({\mathbb {R}},U)$ all functions with support bounded on the left. Furthermore, the causal translation-invariant operator $G_\mu \in {{\mathcal {B}}}(L^2({\mathbb {R}},U))$ given by

$$\begin{aligned} G_\mu u=e^{-\mu \,\cdot \,}G\big (e^{\mu \,\cdot \,}u\big )\quad \forall \,u\in L^2({\mathbb {R}},U) \end{aligned}$$

has kernel $K_\mu :=e^{-\mu \,\cdot \,}K\in {{\mathcal {D}}}'({{\mathcal {B}}}(U))$, and an application of Theorem 5.4 to $G_\mu$ with $\alpha =\beta =0$ shows that $\sigma (K_\mu )\le 0$ and $\sup _{s\in {\mathbb {C}}_0}\Vert ({{\mathcal {L}}}K_\mu )(s)\Vert <\infty$. Consequently, $\sigma (K)\le \mu$ and the transfer function $\textbf{G}={{\mathcal {L}}}K$ of G satisfies that $\sup _{s\in {\mathbb {C}}_\mu }\Vert \textbf{G}(s)\Vert <\infty$, that is, $\textbf{G}\in {{\mathcal {H}}}^\infty _\mu ({{\mathcal {B}}}(U))$.

The above discussion shows that Theorem 5.4 is applicable to the input-output operators of well-posed linear systems. The following corollary is an immediate consequence of Theorem 5.4 and Corollary 5.6.

Corollary 5.7

Let $\mu \ge 0$, $\alpha ,\beta \in {\mathbb {R}}$ and let $G\in {{\mathcal {B}}}(L^2_\mu ({\mathbb {R}},U))$ be causal and translation-invariant with transfer function $\textbf{G}\in {{\mathcal {H}}}^\infty _\mu ({{\mathcal {B}}}(U))$. The following statements hold.

• (1) The operator G is Sobolev $(\alpha ,\beta )$-stable if, and only if, there exists a holomorphic extension $\textbf{G}^\textrm{e}:{\mathbb {C}}_0\rightarrow {{\mathcal {B}}}(U)$ of $\textbf{G}$ such that $\sup _{0<\mathrm{Re\,}s<\mu }\Vert (1+s)^{\beta -\alpha }\textbf{G}^\textrm{e}(s)\Vert <\infty$.

• (2) Assume that there exists a holomorphic extension $\textbf{G}^\textrm{e}:{\mathbb {C}}_0\rightarrow {{\mathcal {B}}}(U)$ of $\textbf{G}$ satisfying the conditions (i)-(iii) of statement (1) of Corollary 5.6. If $\mathrm{ess\,sup}_{y\in {\mathbb {R}}}\Vert (1+iy)^{\beta -\alpha }\textbf{G}^\textrm{e}_0(y)\Vert <\infty$, then G is Sobolev $(\alpha ,\beta )$-stable.

• (3) Assume that U is separable and there exists a holomorphic extension $\textbf{G}^\textrm{e}:{\mathbb {C}}_0\rightarrow {{\mathcal {B}}}(U)$ of $\textbf{G}$ such that $\textbf{G}^\textrm{e}$ is polynomially bounded on the strip $0<\textrm{Re}\,s<\mu$. If $\mathrm{ess\,sup}_{y\in {\mathbb {R}}}\Vert (1+iy)^{\beta -\alpha }\textbf{G}^\textrm{e}_0(y)\Vert <\infty$, then G is Sobolev $(\alpha ,\beta )$-stable.

Statements (1) and (2) can be understood as a substantial generalization of [30, Theorem 6]. To explain this, we recall the concept of P-stability [23, 30]: a holomorphic function $\textbf{H}:\Omega \rightarrow {{\mathcal {B}}}(U)$, where $\Omega \subset {\mathbb {C}}$ is open and such that ${\overline{{\mathbb {C}}}}_0\subset \Omega$, is said to be P-stable of order $\alpha \ge 0$ if the following two conditions are satisfied:

(i) $\sup _{s\in {\mathbb {C}}_\mu }\Vert \textbf{H}(s)\Vert <\infty$ for all $\mu >0$;

(ii) there exists $M>0$ such that $\Vert \textbf{H}(iy)\Vert \le M(1+|y|^\alpha )$ for all $y\in {\mathbb {R}}$.

Let $\mu \in {\mathbb {R}}$ and let $G\in {{\mathcal {B}}}(L^2_\mu ({\mathbb {R}},U))$ be causal and translation-invariant. The growth bound $\omega (G)$ of G is defined by

$$\begin{aligned} \omega (G):=\inf \{\nu \le \mu : G\in {{\mathcal {B}}}(L^2_{\nu ,\ell }({\mathbb {R}},U))\}. \end{aligned}$$

We note that the definition is meaningful because $L^2_{\nu ,\ell }({\mathbb {R}},U)\subset L^2_{\mu ,\ell }({\mathbb {R}},U)\subset L^2_\mu ({\mathbb {R}},U)$ for all $\nu \le \mu$. Furthermore, we say that G is regular if its transfer function $\textbf{G}$ has the property that $\textbf{G}(x)$ converges in ${{\mathcal {B}}}(U)$ with respect to the strong operator topology as $x\rightarrow \infty$, where $x\in (0,\infty )$.

Whilst [30, Theorem 6] is formulated in a state-space setting with time-domain $[0,\infty )$, an inspection of the proofs of [30, Theorem 6 and Lemma 7] shows that [30, Theorem 6] can be rephrased in our double-time axis input-output framework as follows.²

Proposition 5.8

Let $\mu \ge 0$ and let $G\in {{\mathcal {B}}}(L^2_\mu ({\mathbb {R}},U))$ be causal, translation-invariant and regular with transfer function $\textbf{G}\in {{\mathcal {H}}}^\infty _\mu ({{\mathcal {B}}}(U))$. Assume that $\textbf{G}$ has a holomorphic extension $\textbf{G}^\textrm{e}:\Omega \rightarrow {{\mathcal {B}}}(U)$, where $\Omega \subset {\mathbb {C}}$ is open and such that ${\overline{{\mathbb {C}}}}_0\subset \Omega$. For $\alpha \ge 0$, the following statements hold.

• (1) If $\textbf{G}^\textrm{e}$ is P-stable of order $\alpha$ and there exist $M>0$ and $k\in {\mathbb {N}}_0$ such that

  $$\begin{aligned} \Vert \textbf{G}^\textrm{e}(s)\Vert \le M (\textrm{Re}\,s)^{-k}\quad \hbox {for all~} s\in {\mathbb {C}}\hbox {such that~} 0<\textrm{Re}\,s<1, \end{aligned}$$

  then G is Sobolev $(\alpha ,0)$-stable.

• (2) If $\omega (G)=0$ and G is Sobolev $(\alpha ,0)$-stable, then $\textbf{G}^\textrm{e}$ is P-stable of order $\alpha$.

Proof

The hypotheses of statement (1) imply that $\textbf{G}^\textrm{e}$ satisfies the conditions (i)-(iii) of statement (1) of Corollary 5.6, and thus, statement (1) is a special case of statement (2) of Corollary 5.7. Statement (2) is an immediate consequence of Theorem 5.4. $\Box$

As for statement (2), it is clear that, in the absence of the condition $\omega (G)=0$, Sobolev stability does not necessarily imply P-stability (see Examples 6.1,  6.2 and 6.4 below).

We close this section, by linking Sobolev stability to certain results on polynomial decay of strongly continuous semigroups [1, 6, 30].

Proposition 5.9

Let T(t) be a strongly continuous semigroup on U, denote its generator by A, and let $\alpha >0$. Assume that $\sup _{t\ge 0}\Vert T(t)\Vert <\infty$ and the intersection of the spectrum of A with $i{\mathbb {R}}$ is empty. The following statements are equivalent.

• (1) $\sup _{t\ge 0}\Vert t^{1/\alpha }T(t)A^{-1}\Vert <\infty$.

• (2) $\sup _{y\in {\mathbb {R}}}\Vert (1+iy)^{-\alpha } (iyI-A)^{-1}\Vert <\infty$.

• (3) $\sup _{s\in {\mathbb {C}}_0}\Vert (1+s)^{-\alpha } (sI-A)^{-1}\Vert <\infty$.

• (4) The convolution operator $L^2_{\ell }({\mathbb {R}},U)\rightarrow L^2_\textrm{loc}({\mathbb {R}},U),\,\,u\mapsto \int _{-\infty }^{\,\cdot }T(\,\cdot \,-\tau )u(\tau )\,\textrm{d}\tau$ is Sobolev $(\alpha ,0)$-stable.

Proof

The equivalence (1) $\Leftrightarrow$  (2) follows from [6, Theorem 2.4]. The implication (3) $\Rightarrow$ (2) holds trivially, whilst the implication (2) $\Rightarrow$  (3) follows from the fact that, by the Hille-Yosida theorem, there exists $M>0$ such that

$$\begin{aligned} \Vert (sI-A)^{-1}\Vert \le M(\textrm{Re}\,s)^{-1}\quad \forall \,s\in {\mathbb {C}}_0 \end{aligned}$$

combined with an application of Proposition 4.6 with $\textbf{G}(s)=(sI-A)^{-1}$. Finally, the transfer function of the convolution operator in statement (4) is $(sI-A)^{-1}$, and thus, the equivalence (3) $\Leftrightarrow$ (4) is a consequence of Theorem 5.4. $\Box$

6 Examples

To illustrate the results in the previous sections, we discuss five examples.

Example 6.1

(Rational functions) Let U be a complex Hilbert space. Following [31], a ${{\mathcal {B}}}(U)$-valued function $\textbf{G}$ is called rational if it is meromorphic on ${\mathbb {C}}\cup \{\infty \}$. The Laurent expansion of $\textbf{G}$ at $\infty$ is of the form

$$\begin{aligned} \textbf{G}(s)=\sum _{j=d}^\infty G_js^{-j},\quad G_j\in {{\mathcal {B}}}(U),\,\,d\in {\mathbb {Z}},\,\,G_d\not =0 \end{aligned}$$

(6.1)

and converges in a neighbourhood of $\infty$. The integer d is said to be the relative degree of $\textbf{G}$. It is not difficult to see that $\textbf{G}$ is rational if, and only if, $\textbf{G}=\textbf{P}/\textbf{q}$, where $\textbf{P}$ is a ${{\mathcal {B}}}(U)$-valued polynomial and $\textbf{q}$ is a scalar-valued polynomial. For the relative degree d of $\textbf{G}$ we have that $d=\deg \textbf{q}-\deg \textbf{P}$. Furthermore, a ${{\mathcal {B}}}(U)$-valued function $\textbf{G}$ is rational if, and only if, it is the Laplace transform of a distribution $K=\Phi +\Delta$, where $\Phi$ and $\Delta$ are of the form

$$\begin{aligned} \Phi (t):=\left\{ \begin{aligned}&\sum _{j=0}^nt^{l_j}e^{\lambda _j t}F_j,&t\ge 0\\&0,&t<0 \end{aligned}\right. , \quad \Delta :=\sum _{j=0}^m \delta ^{(j)}D_j,\quad F_j,D_j\in {{\mathcal {B}}}(U),\,\,n,m,l_j\in {\mathbb {N}}_0,\,\, \lambda _j\in {\mathbb {C}}. \end{aligned}$$

Let $\textbf{G}$ be a ${{\mathcal {B}}}(U)$-valued rational function with relative degree d, set $K:={{\mathcal {L}}}^{-1}\textbf{G}$, let $\mu \in {\mathbb {R}}$ be such that $\textbf{G}$ is holomorphic on ${\overline{{\mathbb {C}}}}_\mu$ and let $G_\mu$ be the convolution operator with kernel $e^{-\mu \,\cdot \,}K$. Note that the transfer function $\textbf{G}_\mu$ of $G_\mu$ is given by $\textbf{G}_\mu (s)=\textbf{G}(s+\mu )$. It follows from Theorem 5.4 that $G_\mu$ is Sobolev $(0,\beta )$-stable for every $\beta \le d$. Moreover, the relative degree of $\textbf{G}$ can be characterized in terms of Sobolev stability of $G_\mu$ as follows:

$$\begin{aligned} d=\max \{\beta \in {\mathbb {R}}:G_\mu \,\text{ is } \text{ Sobolev } (0,\beta )-\text{ stable }\}. \end{aligned}$$

(6.2)

The above identity is an immediate consequence of Theorem 5.4 and the fact that the relative degrees of the functions $\textbf{G}$ and $\textbf{G}_\mu$ coincide.

The concept of relative degree and the identity (6.2) extend to ${{\mathcal {B}}}(U)$-valued functions which are meromorphic at  $\infty$, that is, functions $\textbf{G}$ which can be represented by a Laurent series of the form (6.1) on some neighbourhood of $\infty$. The resolvents of bounded linear operators provide a class of examples of ${{\mathcal {B}}}(U)$-valued functions which are meromorphic at $\infty$.

We close this example by remarking that the notion of relative degree plays an important role in classical and adaptive control of finite-dimensional systems. Whilst attempts (see, for example, [12]) have been made to extend it to systems with irrational transfer functions, a fully adequate generalization is still missing. We feel that the concept of Sobolev stability (or some localized version of it) might be a suitable tool to facilitate such a generalization, and we are planning to pursue this in future research.

$\Diamond$

Example 6.2

(Series connection of a rational transfer function and a delay line) Let $\textbf{G}$ be a ${{\mathcal {B}}}(U)$-valued rational function, where U is a complex Hilbert space, assume that $\textbf{G}$ is holomorphic on ${\overline{{\mathbb {C}}}}_0$, and let G be the convolution operator on ${{\mathcal {D}}}'_\ell (U)$ with kernel ${{\mathcal {L}}}^{-1}\textbf{G}$. Define the operator H by $Hu:=\delta _\tau \star (Gu)$ for all $u\in {{\mathcal {D}}}'(U)$, where $\delta _\tau$ is the Dirac distribution supported at $\tau >0$. Then the transfer function $\textbf{H}$ of H is given by $\textbf{H}(s)=e^{-\tau s}\textbf{G}(s)$. It follows from Theorem 5.4 and Example 6.1 that

$$\begin{aligned} \max \{\beta \in {\mathbb {R}}:\hbox {} H \hbox {is Sobolev~} (0,\beta )\hbox {-stable}\}=\text{ relative } \text{ degree } \text{ of } \textbf{G}. \end{aligned}$$

This is not surprising since convolution with $\delta _\tau$ leaves any regularity properties unchanged. $\Diamond$

Example 6.3

(A neutral functional differential equation) Consider the controlled and observed neutral functional differential equation

$$\begin{aligned} \dot{w}(t)- \dot{w}(t-r) =-aw(t)+u(t), \quad z(t)=w(t), \end{aligned}$$

(6.3)

where $a,\tau >0$ are positive parameters, u is the control function or input and z is the observation or output. We assume that u has support bounded on the left. Taking Laplace transforms (under zero initial conditions) of (6.3) and computing $({{\mathcal {L}}}z)(s) /({{\mathcal {L}}}u)(s)$ shows that the transfer function of (6.3) is given by

$$\begin{aligned} \textbf{G}(s)=\frac{1}{s(1-e^{-\tau s})+a}\,, \end{aligned}$$

see equation (5.2) and the subsequent commentary. It follows from [24] that the function $\textbf{G}$ has the following properties:

(i) $\sup _{s\in {\mathbb {C}}_\mu }|\textbf{G}(s)|<\infty$ for every $\mu >0$;

(ii) there exists an open set $\Omega$ containing ${\overline{{\mathbb {C}}}}_0$ such that $\textbf{G}$ is holomorphic on $\Omega$;

(iii) there exist poles $s_j$ ($j\in {\mathbb {N}}$) of $\textbf{G}$ such that $\mathrm{Re\,}s_j<0$, $\mathrm{Re\,}s_j\rightarrow 0$ and $|s_j|\rightarrow \infty$ as $j\rightarrow \infty$;

(iv) $\textbf{G}$ is not bounded on ${\mathbb {C}}_0$, that is, $\textbf{G}\not \in {{\mathcal {H}}}^\infty$;

(v) $\textbf{G}(s)/(1+s)$ is bounded on ${\mathbb {C}}_0$.

In particular, it follows that the causal and translation-invariant input-output operator G of (6.3) (that is, the map $u\mapsto z$ under zero initial conditions) maps $L^2_{\mu ,\ell }({\mathbb {R}})$ boundedly into itself for every $\mu >0$. An application of Theorem 5.4 guarantees that G is Sobolev (1, 0)-stable. $\Diamond$

Example 6.4

(A 1-dimensional heat equation) Consider the following heat equation on the unit interval with Dirichlet control and Neumann observation at the right end point:

$$\begin{aligned} \left. \begin{aligned} \frac{\partial w}{\partial t}(\xi ,t)&=\frac{\partial ^2 w}{\partial \xi ^2}(\xi ,t),\quad \frac{\partial w}{\partial \xi }(0,t)=0,\quad w(1,t)=u(t),\quad \xi \in (0,1), \\ z(t)&=\frac{\partial w}{\partial \xi }(1,t). \end{aligned}\right\} \end{aligned}$$

(6.4)

As in Example 6.3, u is the input and z is output, both of which take values in $U={\mathbb {C}}$. We assume that u has support bounded on the left. Calculating $({{\mathcal {L}}}z)(s)/({{\mathcal {L}}}u)(s)$ (under zero initial conditions) is routine and shows that the transfer function $\textbf{G}$ is given by

$$\begin{aligned} \textbf{G}(s) = \sqrt{s} \tanh (\sqrt{s}) \quad \forall \, s \in {\mathbb {C}}_0\,, \end{aligned}$$

see equation (5.2) and the subsequent commentary. The function $\textbf{G}$ is not bounded on any right-half complex plane (and thus is not the transfer function of a well-posed state-space system [36]), but evidently satisfies

$$\begin{aligned} \sup _{s\in {\mathbb {C}}_0} \big |(1+s)^{-\frac{1}{2}} \textbf{G}(s) \big |<\infty . \end{aligned}$$

(6.5)

Therefore, the input-output operator G of (6.4) (that is, the convolution operator with kernel ${{\mathcal {L}}}^{-1}\textbf{G}$) is (1/2, 0)-Sobolev stable by Theorem 5.4. Corollary 5.5 yields that G is $(1/2 + \theta ,\theta )$-Sobolev stable for all $\theta \in {\mathbb {R}}$. $\Diamond$

Example 6.5

(A 2-dimensional heat equation) Consider the following controlled and observed heat equation on the unit square $\Omega :=(0,1)\times (0,1)$:

$$\begin{aligned} \left. \begin{aligned}&\frac{\partial w}{\partial t}(\xi _1,\xi _2,t)=\frac{\partial ^2 w}{\partial \xi _1^2}(\xi _1,\xi _2,t) +\frac{\partial ^2 w}{\partial \xi _2^2}(\xi _1,\xi _2,t),\\&w(0,\xi _2,t)=0,\quad w(1,\xi _2,t)=0,\\&\frac{\partial w}{\partial \xi _2}(\xi _1,0,t)=0,\quad \frac{\partial w}{\partial \xi _2}(\xi _1,1,t)={\tilde{u}}(\xi _1,t),\\&{\tilde{z}}(\xi _1,t)=w(\xi _1,\kappa ,t)\,, \end{aligned}\right\} \quad (\xi _1,\xi _2) \in \Omega \,, \end{aligned}$$

(6.6)

where $\kappa \in [0,1)$ is a parameter which specifies the $\xi _2$-position at which the observation is taken. We choose as input and output space $U=L^2(0,1)$, and the U-valued input and output functions u and z are given by $u(t):={\tilde{u}}(\,\cdot \,,t)$ and $z(t):={\tilde{z}}(\,\cdot \,,t)$. The control function u acts via a Neumann boundary condition along the top edge of the square, and is assumed to have support bounded to the left. For each $t\ge 0$, the output z(t) corresponds to the observation of the profile $w(\,\cdot \,,\kappa ,t)$. As may be shown by arguments analogous to those used in [7], the mapping $L^2_{\ell }({\mathbb {R}},U)\rightarrow L^2_{\ell }({\mathbb {R}},U)~$, $u \mapsto z$ determined by (6.6) under zero initial conditions is well-defined and continuous. The present example is based on [20, Section 4, Example (7)], which in turn is inspired by [21, Example 7.14], and we refer the reader to [7] for more details of controlled and observed heat equations on bounded domains in ${\mathbb {R}}^n$.

The transfer function $\textbf{G}$ is given by

$$\begin{aligned} \textbf{G}(s)v=\sqrt{2}\sum _{n=1}^\infty h_n(s;\kappa ) \zeta _n(v) \sin (n\pi \,\cdot ) \quad \forall \, v \in L^2(0,1)\,, \end{aligned}$$

where $\zeta _n$ are the Fourier sine coefficients of v, namely,

$$\begin{aligned} \zeta _n(v)=\sqrt{2}\langle v , \sin (n\pi \,\cdot ) \rangle _{L^2(0,1)}=\sqrt{2}\int _0^1v(\eta ) \sin (n\pi \eta )\, \textrm{d}\eta \quad \forall \, n \in {\mathbb {N}}\,, \end{aligned}$$

and

$$\begin{aligned} h_n(s; \kappa ):=\frac{\cosh (\kappa \sqrt{s+n^2\pi ^2})}{\sqrt{s+n^2\pi ^2}\,\sinh (\sqrt{s+n^2\pi ^2})} \quad \forall \, s \in {\mathbb {C}}_{-\pi ^2},\; \forall \, n \in {\mathbb {N}}\,. \end{aligned}$$

The function $\textbf{G}$ belongs to ${{\mathcal {H}}}^\infty ({{\mathcal {B}}}(U))$ and so, by Theorem 3.1, the input-output operator of (6.6) extends to a causal translation-invariant operator $G\in {{\mathcal {B}}}(L^2({\mathbb {R}},U))$.

We claim that $s \mapsto (1+s)^\theta \textbf{G}(s)$ is bounded on ${\mathbb {C}}_0$ for all $\theta \in {\mathbb {R}}$, so that G is $(\alpha ,\beta )$-Sobolev stable for all $(\alpha ,\beta ) \in {\mathbb {R}}^2$ by Theorem 5.4. Since $\textbf{G}$ is bounded on ${\mathbb {C}}_0$, the claim for non-positive $\theta$ is trivial, and so we focus on the case that $\theta >0$. By statement (2) of Corollary 5.6 it suffices to show that $y \mapsto (1+ iy)^\theta \textbf{G}_0(y) = (1+ iy)^\theta \textbf{G}(iy)$ is bounded on ${\mathbb {R}}$.

For which purpose, let $y\in {\mathbb {R}}$, set $s_n=s_n(y):=\sqrt{iy +n^2\pi ^2} \ne 0$ for all $n \in {\mathbb {N}}$, and note that

$$\begin{aligned} s_n = (y^2 + n^4 \pi ^4)^{\frac{1}{4}} e^{i \arg (s_n)} \quad \text {and} \quad \textrm{Re}\,s_n = (y^2 + n^4 \pi ^4)^{\frac{1}{4}} \cos (\arg (s_n))\,.\end{aligned}$$

Standard hyperbolic identities give that

$$\begin{aligned} \cosh (\kappa s_n)&= \cosh (\kappa \,\textrm{Re}\,s_n)\cos (\kappa \,\textrm{Im}\,s_n) + i \sinh (\kappa \,\textrm{Re}\,s_n)\sin (\kappa \,\textrm{Im}\,s_n) \\ \text {and} \quad |\cosh (\kappa s_n) |^2&= \cosh ^2(\kappa \,\textrm{Re}\,s_n) - \sin ^2(\kappa \,\textrm{Im}\,s_n) \le \cosh ^2(\kappa \,\textrm{Re}\,s_n) \,. \end{aligned}$$

Similarly,

$$\begin{aligned} \sinh (s_n)&= \sinh (\textrm{Re}\,s_n)\cos (\textrm{Im}\,s_n) + i \cosh (\textrm{Re}\,s_n)\sin (\textrm{Im}\,s_n) \\ \text {and} \quad |\sinh (s_n) |^2&= \sinh ^2(\textrm{Re}\,s_n) + \sin ^2(\textrm{Im}\,s_n) \ge \sinh ^2(\textrm{Re}\,s_n) \,. \end{aligned}$$

Consequently, there exists a constant $k>0$ such that

$$\begin{aligned} \left|\frac{\cosh (\kappa s_n)}{\sinh (s_n) }\right|&\le \frac{\cosh (\kappa \,\textrm{Re}\,s_n)}{\sinh ( \textrm{Re}\,s_n)}\le k\exp \big ((\kappa -1)(y^2 + n^4 \pi ^4)^{\frac{1}{4}} \cos (\arg (s_n))\big ) \nonumber \\&\le k\exp \big ((1/\sqrt{2})(\kappa -1)(y^2 + n^4 \pi ^4)^{\frac{1}{4}} \big ) \quad \forall \, y \in {\mathbb {R}}, \quad \forall \, n \in {\mathbb {N}}, \end{aligned}$$

where we have used that $\kappa - 1 <0$ and $\arg (s_n) \in (-\pi /4, \pi /4)$. Therefore,

$$\begin{aligned} |h_n(i y ; \kappa ) \vert \le \frac{k}{n \pi } \exp \big ((1/\sqrt{2})(\kappa -1)(y^2 + n^4 \pi ^4)^{\frac{1}{4}} \big )\quad \forall \, y \in {\mathbb {R}}, \; \forall \, n \in {\mathbb {N}}.\end{aligned}$$

It is straightforward to show that, for each fixed $\theta >0$, there exist $y^*>0$ and $y^*_n \in [0,y^*]$ for every $n \in {\mathbb {N}}$ such that

$$\begin{aligned} \max _{y >0} |(1+i y)^\theta h_n(i y ; \kappa ) |= |(1+i y_n^*)^\theta h_n(i y^*_n ; \kappa ) |\,. \end{aligned}$$

In particular, there exist constants $l, \lambda >0$ such that

$$\begin{aligned} \max _{y >0} |(1+i y)^\theta h_n(i y ; \kappa ) |\le l e^{-\lambda n} \quad \forall \, n \in {\mathbb {N}}\,.\end{aligned}$$

Since

$$\begin{aligned} \Vert (1+i y)^\theta \textbf{G}(i y)v \Vert _{L^2(0,1)} \le \Big (\sum _{n=1}^\infty |(1+i y)^\theta h_n(i y ; \kappa ) \vert \Big ) \Vert v \Vert _{L^2(0,1)} \quad \forall \, v \in L^2(0,1), \; \forall \, y \in {\mathbb {R}}\,,\end{aligned}$$

the claim is proven.$\Diamond$

7 Remarks on right-shift invariant operators on the half-line

In this section, we indicate how the results in Sections 3-5 can be used to obtain corresponding results for right-shift invariant operators acting on functions defined on the half-line. Recall the half-line space $H^\alpha _+({\mathbb {R}},U)$, $\alpha \in {\mathbb {R}}$, defined in Section 2. By Lemma 2.1, $H^\alpha _+({\mathbb {R}},U)$ is the closure of the subspace $\{u\in C^\infty ({\mathbb {R}},U):\textrm{supp}\,u\subset (0,\infty )\}$ with respect to the norm topology of $H^\alpha ({\mathbb {R}},U)$. Throughout this section, U denotes a complex Hilbert space.

An operator $G\in {{\mathcal {B}}}(H^\alpha _+({\mathbb {R}},U),H^\beta _+({\mathbb {R}},U))$ is said to be right-shift invariant if $S_\tau G=G S_\tau$ for all $\tau \ge 0$. It is straightforward to show that right-shift invariance of G implies causality, in the sense that, for all $\tau \ge 0$ and all $u\in H^\alpha _+({\mathbb {R}},U)$,

$$\begin{aligned} \textrm{supp}\,u\subset [\tau ,\infty )\quad \Rightarrow \quad \textrm{supp}(Gu)\subset [\tau ,\infty ). \end{aligned}$$

The following lemma shows that a right-shift invariant operator in ${{\mathcal {B}}}(H^\alpha _+({\mathbb {R}},U),H^\beta _+({\mathbb {R}},U))$ has a unique causal and translation-invariant bilateral extension belonging to ${{\mathcal {B}}}(H^\alpha ({\mathbb {R}},U),H^\beta ({\mathbb {R}},U))$.

Lemma 7.1

Let $\alpha , \beta \in {\mathbb {R}}$.

• (1) If $G\in {{\mathcal {B}}}(H^\alpha _+({\mathbb {R}},U),H^\beta _+({\mathbb {R}},U))$ is right-shift invariant, then there exists a unique causal and translation-invariant operator $G^\textrm{b}\in {{\mathcal {B}}}(H^\alpha ({\mathbb {R}},U),H^\beta ({\mathbb {R}},U))$ such that

  $$\begin{aligned} G^\textrm{b}|_{H^\alpha _+({\mathbb {R}},U)}=G \quad \text {and} \quad \Vert G^\textrm{b}\Vert _{{{\mathcal {B}}}(H^\alpha ,H^\beta )}=\Vert G\Vert _{{{\mathcal {B}}}(H^\alpha _+,H^\beta _+)}\,.\end{aligned}$$

• (2) If G is a causal and translation-invariant operator in ${{\mathcal {B}}}(H^\alpha ({\mathbb {R}},U),H^\beta ({\mathbb {R}},U))$, then the restriction $G_+:=G|_{H^\alpha _+({\mathbb {R}},U)}$ is a right-shift invariant operator in ${{\mathcal {B}}}(H^\alpha _+({\mathbb {R}},U),H^\beta _+({\mathbb {R}},U))$ and, furthermore,  $\Vert G_+\Vert _{{{\mathcal {B}}}(H^\alpha _+,H^\beta _+)}=\Vert G\Vert _{{{\mathcal {B}}}(H^\alpha ,H^\beta )}$.

The above lemma is a generalization of [38, Theorem 6.2] which addresses the $L^2$-case ($\alpha =\beta =0)$. The arguments used in [38] extend to the case of arbitrary $\alpha$ and $\beta$, and therefore, we do not include a proof of Lemma 7.1.

The following corollary, a right-half line version of Theorem 3.1, provides a characterization of right-shift invariant bounded operators $G:H^{\alpha }_+({\mathbb {R}},U)\rightarrow H^{\beta }_+({\mathbb {R}},U)$. It is an immediate consequence of Theorem 3.1 and Lemma 7.1.

Corollary 7.2

Let $\alpha , \beta \in {\mathbb {R}}$.

• (1) If $G:H^{\alpha }_+({\mathbb {R}},U) \rightarrow H^{\beta }_+({\mathbb {R}},U)$ is a bounded linear right-shift invariant operator, then there exists a unique holomorphic function $\textbf{G}:{\mathbb {C}}_0 \rightarrow {{\mathcal {B}}}(U)$ such that

  $$\begin{aligned}{} & {} \sup _{s\in {\mathbb {C}}_0}\Vert (1+s)^{\beta -\alpha }\textbf{G}(s)\Vert = \Vert G\Vert _{{{\mathcal {B}}}(H^\alpha _+,H^\beta _+)}\quad \,\,\text{ and }\quad \\{} & {} Gu=({{\mathcal {L}}}^{-1}\circ {{\mathcal {M}}}_{\textbf{G}}\circ {{\mathcal {L}}})(u)\,\,\,\forall \,u\in H^{\alpha }_+({\mathbb {R}},U). \end{aligned}$$

• (2) Conversely, if $\textbf{G}:{\mathbb {C}}_0 \rightarrow {{\mathcal {B}}}(U)$ is holomorphic and such that $\sup _{s\in {\mathbb {C}}_0}\Vert (1+s)^{\beta -\alpha }\textbf{G}(s)\Vert <\infty$, then $G:={{\mathcal {L}}}^{-1}\circ {{\mathcal {M}}}_{\textbf{G}}\circ {{\mathcal {L}}}$ is a right-shift invariant bounded operator $H^{\alpha }_+({\mathbb {R}},U) \rightarrow H^{\beta }_+({\mathbb {R}},U)$ and $\Vert G\Vert _{{{\mathcal {B}}}(H^\alpha _+,H^\beta _+)}=\sup _{s\in {\mathbb {C}}_0}\Vert (1+s)^{\beta -\alpha }\textbf{G}(s)\Vert$.

The above corollary is a generalization of a well-known result for the $L^2$-case ($\alpha =\beta =0$), see, for example, [41]. For the special case wherein $\alpha =\beta =1$ and $U={\mathbb {C}}$, statement (1) can also be found in [29]. Whilst Corollary 7.2 is essentially identical to [20, Theorem 3.1], we mention that it has been derived here by somewhat different means.

The half-line space $H^{\alpha }_+({\mathbb {R}},U)$ is a so-called zero-trace space because, for $\alpha >1/2$, it can be shown that if $u\in H^{\alpha }_+({\mathbb {R}},U)$, then $u^{(j)}(0)=0$ for all $j\in {\mathbb {N}}_0$ such that $j<\alpha -1/2$ (see, for example, [3, Chapter VIII, Theorem 1.6.8]). Another half-line version of $H^{\alpha }({\mathbb {R}},U)$ (when $\alpha \ge 0$) is the space of restrictions $\{u|_{[0,\infty )}:u\in H^{\alpha }({\mathbb {R}},U)\}$ equipped with the norm $\Vert u\Vert :=\inf \{\Vert v\Vert _{H^\alpha }:v|_{[0,\infty )}=u\}$. This is a bigger space than $H^{\alpha }_+({\mathbb {R}},U)$ and a characterization of right-shift invariant bounded linear operators on this space is more difficult and is addressed in [20].

Finally, by an argument very similar to that leading to Corollary 7.2, a right-half line version of the Fourier multiplier result in Corollary 3.7 can derived. Furthermore, Lemma 7.1 and Corollary 7.2 together with the results in Sects. 4 and 5 can be used to develop a theory of Sobolev stability for right-shift invariant operators defined on half-line spaces.

Appendix

The purpose of the appendix is twofold: to present some background material on the convolution of vector-valued distributions (Appendix 1) and to provide proofs of Lemmas 2.1 and 2.2 (Appendix 2) and Theorem 4.1 (Appendix 3).

1.1 Appendix 1: Remarks on the convolution of vector-valued distributions

Let X be a complex Banach space and let $Z=X$ or $Z={{\mathcal {B}}}(X)$. The subspace of all distributions in ${{\mathcal {D}}}'(Z)$ with support bounded on the left is denoted by ${{\mathcal {D}}}'_\ell (Z)$. As usual, we set ${{\mathcal {D}}}'_\ell :={{\mathcal {D}}}'_\ell ({\mathbb {C}})$. In the following, when using the term “convolution product”, we mean a bilinear mapping which is continuous in each argument. It is well-known that there exists a unique convolution product

$$\begin{aligned} {{\mathcal {D}}}'_\ell ({{\mathcal {B}}}(X))\times {{\mathcal {D}}}'_\ell (X)\rightarrow {{\mathcal {D}}}'_\ell (X),\,\,(K,u)\mapsto K\star u \end{aligned}$$

(8.1)

satisfying

$$\begin{aligned} (k\otimes T)\star (f\otimes x)=(k\star f)\otimes (Tx)\quad \forall \,k,f\in {{\mathcal {D}}}'_\ell ,\,\,\forall \,T\in {{\mathcal {B}}}(X), \,\,\forall \,x\in X, \end{aligned}$$

where $k\star f$ is the standard convolution product of the scalar-valued distributions k and f, see [3, p. 432/433], [14, Chapter XVI: Section 2], [16, Chapter 8] or [43, Chapter 5].

If K and u are Laplace transformable, then the convolution theorem (exchange formula) for Laplace transforms holds:

$$\begin{aligned} \big ({{\mathcal {L}}}(K\star u)\big )(s)=({{\mathcal {L}}}K)(s)({{\mathcal {L}}}u)(s)\quad \text{ for } \text{ all } s\in {\mathbb {C}}\, \text{ such } \text{ that } \,\textrm{Re}\,s> \max \{\sigma (K),\sigma (u)\}, \end{aligned}$$

see [14, Chapter XVI: Section 2], [16, Chapter 8] or [43, Chapter 6].

If K and u have supports which are bilaterally unbounded, then it is still possible to define a convolution product of K and u, provided certain assumptions are satisfied. For the current purposes, it is sufficient to consider the case wherein K is of the form $K=k\otimes I$, where k is a scalar-valued distribution. We set ${{\mathcal {O}}}'_\textrm{C}:={{\mathcal {F}}}^{-1}{{\mathcal {O}}}_\textrm{M}\subset {{\mathcal {S}}}'$ (distributions of rapid decay) and recall that there exists a well-defined scalar convolution product

$$\begin{aligned} {{\mathcal {O}}}'_\textrm{C}\times {{\mathcal {S}}}'\rightarrow {{\mathcal {S}}}',\,\,(k,f)\mapsto k\star f, \end{aligned}$$

see [35, Théorème XI (Chapitre VII)] or [40, Definition 30.2]. By [35, Théorème XV (Chapitre VII)] or [40, Theorem 30.4], the convolution theorem (exchange formula) for Fourier transforms holds:

$$\begin{aligned} {{\mathcal {F}}}(k\star f)=({{\mathcal {F}}}k)({{\mathcal {F}}}f)\quad \forall \,k\in {{\mathcal {O}}}'_\textrm{C},\,\,\forall \,f\in {{\mathcal {S}}}'. \end{aligned}$$

(8.2)

Note that the multiplication on the right-hand side of (8.2) is well-defined because ${{\mathcal {F}}}k\in {{\mathcal {O}}}_\textrm{M}$ and ${{\mathcal {F}}}f\in {{\mathcal {S}}}'$. An application of [3, Appendix: Theorem 1.5.3] together with arguments similar to those used in the proof of [3, Appendix: Theorem 1.9.1] shows that there exists a unique convolution product

$$\begin{aligned} {{\mathcal {O}}}'_\textrm{C}\times {{\mathcal {S}}}'(X)\rightarrow {{\mathcal {S}}}'(X),\,\,(k,u)\mapsto k\star u \end{aligned}$$

(8.3)

satisfying

$$\begin{aligned} k\star (f\otimes x)=(k\star f)\otimes x\quad \forall \,k\in {{\mathcal {O}}}'_\textrm{C},\,\,\forall \,f\in {{\mathcal {S}}}',\,\,\forall \,x\in X. \end{aligned}$$

(8.4)

It is a routine exercise to show that if the supports of $k\in {{\mathcal {O}}}'_\textrm{C}$ and $u\in {{\mathcal {S}}}'(X)$ are bounded on the left, then $k\star u$ in the sense of (8.3) coincides with $(k\otimes I)\star u$ in the sense of (8.1).

The identity (8.4), together with (8.2), the denseness of ${{\mathcal {S}}}'\otimes X$ in ${{\mathcal {S}}}'(X)$ [3, Appendix: Theorem 1.3.6] and continuity properties of the Fourier transform and the convolution product (8.3), shows that convolution theorem for Fourier transforms (8.2) carries over to the vector-valued case, that is,

$$\begin{aligned} {{\mathcal {F}}}(k\star u)=({{\mathcal {F}}}k)({{\mathcal {F}}}u)\quad \forall \,k\in {{\mathcal {O}}}'_\textrm{C},\,\,\forall \,u\in {{\mathcal {S}}}'(X). \end{aligned}$$

(8.5)

1.2 Appendix 2: Proofs of Lemmas 2.1 and 2.2

Proof of Lemma 2.1

In the following, let $V=U$ or $V={\mathbb {C}}$. By statements (3) and (4) of Proposition 3.3, the restriction of the operator $R_\theta$ to $L^2({\mathbb {R}},V)$ is a causal isomorphism from $L^2({\mathbb {R}},V)$ onto $H^\theta ({\mathbb {R}},V)$ (for every $\theta \in {\mathbb {R}}$). To avoid awkward notation, we use the same symbol $R_\theta$ to denote the scalar- and vector-valued versions of the operator. As usual, the tensor product $F({\mathbb {R}},{\mathbb {C}})\otimes U\subset F({\mathbb {R}},U)$, where $F=L^2$, $F=C^\infty _\textrm{c}$ or $F=H^\theta$, is defined as the vector space spanned by all finite linear combinations $\sum _{j=1}^n f_j\otimes u_j$, where $f_j\in F({\mathbb {R}},{\mathbb {C}})$, $u_j\in U$ and $(f_j\otimes u_j)(\,\cdot \,):= f_j(\,\cdot \,)u_j$.

(1) As $R_\theta (L^2({\mathbb {R}},V))=H^\theta ({\mathbb {R}},V)$ for $V=U,{\mathbb {C}}$, $L^2({\mathbb {R}},{\mathbb {C}})\otimes U$ is dense in $L^2({\mathbb {R}},U)$ and

$$\begin{aligned} R_\theta (L^2({\mathbb {R}},{\mathbb {C}})\otimes U)=R_\theta (L^2({\mathbb {R}},{\mathbb {C}}))\otimes U=H^\theta ({\mathbb {R}},{\mathbb {C}})\otimes U, \end{aligned}$$

it follows that $H^\theta ({\mathbb {R}},{\mathbb {C}})\otimes U$ is dense in $H^\theta ({\mathbb {R}},U)$. Now $C^\infty _\textrm{c}({\mathbb {R}},{\mathbb {C}})$ is dense in $H^\theta ({\mathbb {R}},{\mathbb {C}})$ (see, for example, [37, Lemma 15.10]), implying that $C^\infty _\textrm{c}({\mathbb {R}},{\mathbb {C}})\otimes U$ is dense $H^\theta ({\mathbb {R}},U)\otimes U$, and thus, $C^\infty _\textrm{c}({\mathbb {R}},U)$ is dense in $H^\theta ({\mathbb {R}},U)$.

(2) Invoking the causality of $R_\theta$ and $R^{-1}_\theta =R_{-\theta }$, it follows that $R_\theta (L^2_+({\mathbb {R}},V))=H^\theta _+({\mathbb {R}},V)$ for $V=U,{\mathbb {C}}$. By an argument similar to that used in the proof of statement (1), we obtain that $H^\theta _+({\mathbb {R}},{\mathbb {C}})\otimes U$ is dense in $H^\theta _+({\mathbb {R}},U)$. Consequently, as $H^\theta _+({\mathbb {R}},{\mathbb {C}})$ is the closure of the subspace $\{u\in C^\infty ({\mathbb {R}},{\mathbb {C}}):\textrm{supp}\,u\subset (0,\infty )\}$ with respect to the norm topology of $H^\theta ({\mathbb {R}},U)$ (see [25, Theorem 3.29]), the space $\{u\in C^\infty _\textrm{c}({\mathbb {R}},U):\textrm{supp}\,u\subset (0,\infty )\}$ is dense in $H^\theta _+({\mathbb {R}},U)$. $\Box$

Proof of Lemma 2.2

We proceed in two steps.

Step 1: $\mu \ge 0$. In this case, it follows from an application of [4, Theorem 2.5.1] (with, in the notation of [4], $\omega =\mu$, $q(s)=s\textbf{h}(s)$ and $b=1$) that there exists $h\in C({\mathbb {R}},X)$ such that $h(t)=0$ for all $t\le 0$, $\sup _{t>0}\Vert e^{-\nu t}t^{-1}h(t)\Vert <\infty$ for every $\nu >\mu$ and $({{\mathcal {L}}}h)(s)=\textbf{h}(s)$ for all $s\in {\mathbb {C}}_\mu$. Furthermore, letting $\nu >\mu$, and choosing $0<\varepsilon <\nu -\mu$, we have that

$$\begin{aligned} M:=\sup _{t>0}\Vert e^{-(\nu -\varepsilon ) t}t^{-1}h(t)\Vert <\infty . \end{aligned}$$

Consequently, $\Vert e^{-\nu t}h(t)\Vert \le Mte^{-\varepsilon t}$ for all $t\ge 0$, showing that $e^{-\nu \,\cdot \,}h\in L^1({\mathbb {R}},X)$ and completing the proof of the claim when $\mu \ge 0$.

Step 2: $\mu <0$. Set $\textbf{g}(s):=\textbf{h}(s+\mu )$ for all $s\in {\mathbb {C}}_0$. Then $\textbf{g}$ is a holomorphic X-valued function on ${\mathbb {C}}_0$ such that $\sup _{s\in {\mathbb {C}}_0}\Vert s^2\textbf{g}(s)\Vert <\infty$. By Step 1, there exists $g\in C({\mathbb {R}},X)$ such that $g(t)=0$ for all $t\le 0$, $\sup _{t>0}\Vert e^{-\omega t}t^{-1}g(t)\Vert <\infty$ and $e^{-\omega \,\cdot \,}g\in L^1({\mathbb {R}},X)$ for every $\omega >0$ and $({{\mathcal {L}}}g)=\textbf{g}(s)$ for all $s\in {\mathbb {C}}_0$. Routine arguments show that the function $h:{\mathbb {R}}\rightarrow X,\,\,t\mapsto e^{\mu t}g(t)$ has all the required properties. $\Box$

1.3 Appendix 3: Proof of Theorem 4.1

Before we prove Theorem 4.1, we develop some auxiliary material which will play a key role in the proof.

For $n\in {\mathbb {N}}_0$, we define $h_n:{\mathbb {C}}\backslash (i{\mathbb {R}})\rightarrow {\mathbb {R}}_+$ by

$$\begin{aligned} h_n(s):=\left\{ \begin{aligned}&(1+|s|^2)^n (\textrm{Re}\,s)^{-n},&0<|\textrm{Re}\,s|&\,\le 1\\&(1+|s|^2)^n,&|\textrm{Re}\,s|&\,>1. \end{aligned}\right. \end{aligned}$$

Throughout this appendix, let X be a complex Banach space. The following result is a special case of [26, Lemma 2] (translated from the upper/lower- to the right/left-half plane setting).

Lemma 8.1

Let $\textbf{F}:{\mathbb {C}}\backslash (i{\mathbb {R}})\rightarrow X$ be holomorphic, and, for $x\in {\mathbb {R}}$, $x\not =0$, set $\textbf{F}_x(y):=\textbf{F}(x+iy)$ for all $y\in {\mathbb {R}}$. If there exist $n\in {\mathbb {N}}_0$ and $L>0$ such that

$$\begin{aligned} \Vert \textbf{F}(s)\Vert \le Lh_n(s)\quad \forall \,s\in {\mathbb {C}}\backslash (i{\mathbb {R}}), \end{aligned}$$

(8.6)

then there exists $\Phi \in {{\mathcal {S}}}'(X)$ such that $\big ([\textbf{F}_x]-[\textbf{F}_{-x}]\big )\rightarrow \Phi$ in ${{\mathcal {S}}}'(X)$ as $x\downarrow 0$.

Next we relate the growth conditions (8.6) and (4.2). In view of the condition (4.2), we set

$$\begin{aligned} g_{m,k}(s):=(1+|s|)^m(1+(\textrm{Re}\,s)^{-k})\quad \forall \,s\in {\mathbb {C}}_0, \end{aligned}$$

where $k,m\in {\mathbb {N}}_0$.

Lemma 8.2

Let $k,m\in {\mathbb {N}}_0$. The exists $C>0$ such that, for all $s\in {\mathbb {C}}_0$,

$$\begin{aligned} g_{m,k}(s)\le C\left\{ \begin{aligned}&h_k(s),\quad&\hbox { if~}\ k\ge m\\&h_m(s), \quad&\hbox { if~}\ k<m.\end{aligned}\right. \end{aligned}$$

Proof

Let $s\in {\mathbb {C}}_0$ and write $s=x+iy$, where $x>0$ and $y\in {\mathbb {R}}$.

Case 1: $k\ge m$. If $x>1$, then $|s|>1$, and so,

$$\begin{aligned} g_{m,k}(s)\le 2(1+|s|)^m\le 2(1+|s|)^k\le 2(1+|s|^2)^k. \end{aligned}$$

If $0<x\le 1$, then

$$\begin{aligned} g_{m,k}(s)\le 2(1+|s|)^m x^{-k}\le 2(1+|s|)^k x^{-k}\le 2\gamma ^k(1+|s|^2)^kx^{-k}, \end{aligned}$$

where $\gamma :=\max _{a\ge 0}(1+a)(1+a^2)^{-1}=1/\big (2(\sqrt{2}-1)\big )$. We conclude that in this case

$$\begin{aligned} g_{m,k}(s)\le 2\gamma ^k h_k(s)\quad \forall \,s\in {\mathbb {C}}_0. \end{aligned}$$

Case 2: $k<m$. If $x>1$, then $|s|>1$, and so,

$$\begin{aligned} g_{m,k}(s)\le 2(1+|s|)^m\le 2(1+|s|^2)^m. \end{aligned}$$

Furthermore, if $0<x<1$, then

$$\begin{aligned} g_{m,k}(s)\le 2(1+|s|)^m x^{-k}\le 2(1+|s|)^m x^{-m}\le 2\gamma ^m(1+|s|^2)^m x^{-m}. \end{aligned}$$

Consequently, we have that

$$\begin{aligned} g_{m,k}(s)\le 2\gamma ^m h_m(s)\quad \forall \,s\in {\mathbb {C}}_0. \end{aligned}$$

The claim now follows with $C=2\gamma ^{\max (k,m)}$. $\Box$

We are now in the position to prove Theorem 4.1.

Proof of Theorem 4.1

We proceed in three steps.

Step 1: Existence of the boundary distribution  $\Gamma$.

To use Lemma 8.1, we define a holomorphic function $\textbf{F}:{\mathbb {C}}\backslash (i{\mathbb {R}})\rightarrow X$ by setting $\textbf{F}(s):=\textbf{G}(s)$ when $\textrm{Re}\,s>0$ and $\textbf{F}(s):=0$ when $\textrm{Re}\,s<0$. As $\textbf{G}$ satisfies the growth bound (4.2), it follows from Lemma 8.2 that (8.6) holds for $\textbf{F}$ with $n=\max (k,m)$ and $L=MC$. The existence of $\Gamma \in {{\mathcal {S}}}'(X)$ such that $[\textbf{G}_x]\rightarrow \Gamma$ in ${{\mathcal {S}}}'(X)$ as $x\downarrow 0$ is now guaranteed by Lemma 8.1.

Step 2: $\textrm{supp}\,{{\mathcal {F}}}^{-1}\Gamma \subset [0,\infty )$.

We note that, for every $\mu >0$, there exists a constant $M_\mu >0$ such that

$$\begin{aligned} \frac{\Vert \textbf{G}(s)\Vert }{|s|^{m+2}}\le \frac{M_\mu }{|s|^2}\quad \forall \,s\in {\mathbb {C}}_\mu , \end{aligned}$$

as follows from (4.2). Defining the holomorphic X-valued function $\textbf{H}$ by

$$\begin{aligned} \textbf{H}(s):=\frac{1}{s^{m+2}}\textbf{G}(s)\quad \forall \,s\in {\mathbb {C}}_0, \end{aligned}$$

we see that $\sup _{s\in {\mathbb {C}}_\mu }\Vert s^2\textbf{H}(s)\Vert \le M_\mu$ for every $\mu >0$. Invoking Lemma 2.2 shows that there exists $H\in C({\mathbb {R}},X)$ such that $H(t)=0$ for all $t\le 0$, $e^{-\mu \,\cdot \,}H\in L^1({\mathbb {R}},X)$ for every $\mu >0$ and

$$\begin{aligned} \textbf{H}(s)=\int _{-\infty }^\infty e^{-st}H(t)\,\textrm{d}t\quad \forall \,s\in {\mathbb {C}}_0. \end{aligned}$$

Therefore,

$$\begin{aligned} \textbf{H}(x+iy)=\int _{-\infty }^\infty e^{-iyt}\big (e^{-xt}H(t)\big )\,\textrm{d}t=\big ({{\mathcal {F}}}(e^{-x\,\cdot \,}H)\big )(y) \quad \forall \,x>0,\,\,\forall \,y\in {\mathbb {R}}. \end{aligned}$$

Let now $x>0$ be fixed, but arbitrary. Setting $\textbf{H}_x(y):=\textbf{H}(x+iy)$ for all $y\in {\mathbb {R}}$, the above can be expressed as

$$\begin{aligned} \textbf{H}_x={{\mathcal {F}}}(e^{-x\,\cdot \,}H). \end{aligned}$$

Obviously, $(x+iy)^{m+2}\textbf{H}_x(y)=\textbf{G}_x(y)$ for all $y\in {\mathbb {R}}$. Defining $b(y):=(x+iy)^{m+2}$ for all $y\in {\mathbb {R}}$, this can be written as $b\textbf{H}_x=\textbf{G}_x$. Noting that $b[\textbf{H}_x]=[b\textbf{H}_x]$, we obtain

$$\begin{aligned} {{\mathcal {F}}}\big ((xI+D)^{m+2}[e^{-x\,\cdot \,}H]\big )=b{{\mathcal {F}}}[e^{-x\,\cdot \,}H]= b[{{\mathcal {F}}}(e^{-x\,\cdot \,}H)]=b[\textbf{H}_x]=[b\textbf{H}_x]=[\textbf{G}_x], \nonumber \\ \end{aligned}$$

(8.7)

where D denotes distributional differentiation. Since $H(t)=0$ for all $t<0$, it follows that $\textrm{supp}\big ((xI+D)^{m+2}[e^{-x\,\cdot \,}H]\big )\subset [0,\infty )$, and so,

$$\begin{aligned} \textrm{supp}\big ({{\mathcal {F}}}^{-1}[\textbf{G}_x]\big )\subset [0,\infty ). \end{aligned}$$

This holds for all $x>0$, and, since $[\textbf{G}_x]\rightarrow \Gamma$ in ${{\mathcal {S}}}'(X)$ as $x\downarrow 0$, the continuity of ${{\mathcal {F}}}^{-1}$ then guarantees that $\textrm{supp}\,{{\mathcal {F}}}^{-1}\Gamma \subset [0,\infty )$.

Step 3: ${{\mathcal {L}}}({{\mathcal {F}}}^{-1}\Gamma )=\textbf{G}$.

Note that, by (8.7),

$$\begin{aligned} (xI+D)^{m+2}[e^{-x\,\cdot \,}H]={{\mathcal {F}}}^{-1}[\textbf{G}_x]. \end{aligned}$$

(8.8)

Next, we let x go to 0. As we do not know that $[H]\in {{\mathcal {S}}}'(X)$, it cannot be concluded that the left-hand side of (8.8) converges to $D^{m+2}[H]$ in ${{\mathcal {S}}}'(X)$ as $x\downarrow 0$. However, $[H]\in {{\mathcal {D}}}'(X)$, and so it is clear that

$$\begin{aligned} (xI+D)^{m+2}[e^{-x\,\cdot \,}H]\rightarrow D^{m+2}[H]\,\,\,\, \hbox {in~} {{\mathcal {D}}}'(X) \hbox {}\quad \text{ as } x\downarrow 0. \end{aligned}$$

Together with (8.8) and the convergence of $[\textbf{G}_x]$ to $\Gamma$ in ${{\mathcal {S}}}'(X)$ as $x\downarrow 0$, this implies

$$\begin{aligned} (D^{m+2}[H])({\varphi })=({{\mathcal {F}}}^{-1}\Gamma )({\varphi })\quad \forall \,{\varphi }\in {{\mathcal {D}}}. \end{aligned}$$

Hence, for $c>0$,

$$\begin{aligned} \big (e^{-c\,\cdot \,}D^{m+2}[H]\big )({\varphi }) =\big (e^{-c\,\cdot \,}({{\mathcal {F}}}^{-1}\Gamma )\big )({\varphi })\quad \forall \,{\varphi }\in {{\mathcal {D}}}. \end{aligned}$$

(8.9)

Obviously, as the distribution ${{\mathcal {F}}}^{-1}\Gamma$ is tempered and has support in $[0,\infty )$, it is Laplace transformable. Since $e^{-c\,\cdot \,}\in {{\mathcal {O}}}_\textrm{M}^+$, the distribution $e^{-c\,\cdot \,}({{\mathcal {F}}}^{-1}\Gamma )$ is also tempered, and hence Laplace transformable. It is sufficient to prove that

$$\begin{aligned} \big ({{\mathcal {L}}}(e^{-c\,\cdot \,}({{\mathcal {F}}}^{-1}\Gamma ))\big )(s)=\textbf{G}(s+c)\quad \forall \,s\in {\mathbb {C}}_0. \end{aligned}$$

(8.10)

Indeed, as $c>0$ is arbitrary, it then follows that $\big ({{\mathcal {L}}}({{\mathcal {F}}}^{-1}\Gamma )\big )(s)= \textbf{G}(s)$ for all $s\in {\mathbb {C}}_0$.

We proceed to establish (8.10). Using an induction argument, it can be shown that

$$\begin{aligned} \big (e^{-c\,\cdot \,}D^n[H]\big )({\varphi })= \sum _{k=0}^n\left( {\begin{array}{c}n\\ k\end{array}}\right) c^k\big (D^{n-k}(e^{-c\,\cdot \,}[H])\big )({\varphi }) \quad \forall \,n\in {\mathbb {N}}_0,\,\,\forall \,{\varphi }\in {{\mathcal {D}}}. \qquad \end{aligned}$$

(8.11)

We postpone the derivation of (8.11) to the end of the proof.

As $e^{-c\,\cdot \,}[H]=[e^{-c\,\cdot \,}H]$ and $e^{-c\,\cdot \,}H\in L^1({\mathbb {R}},X)$, we have that $e^{-c\,\cdot \,}[H]\in {{\mathcal {S}}}'(X)$. Consequently, $D^j(e^{-c\,\cdot \,}[H])$ is in ${{\mathcal {S}}}'(X)$ for every $j\in {\mathbb {N}}_0$, and it follows from (8.9), (8.11) and the denseness of ${{\mathcal {D}}}$ in ${{\mathcal {S}}}$ that

$$\begin{aligned} \big (e^{-c\,\cdot \,}({{\mathcal {F}}}^{-1}\Gamma )\big )\big ({\varphi })=\sum _{k=0}^{m+2}\left( {\begin{array}{c}m+2\\ k\end{array}}\right) c^k \big (D^{m+2-k}(e^{-c\,\cdot \,} [H])\big )({\varphi })\quad \forall \,{\varphi }\in {{\mathcal {S}}}. \end{aligned}$$

Taking Laplace transforms on both sides of the above identity yields

$$\begin{aligned} \big ({{\mathcal {L}}}(e^{-c\,\cdot \,}({{\mathcal {F}}}^{-1}\Gamma ))\big )(s)= & {} \left( \sum _{k=0}^{m+2} \left( {\begin{array}{c}m+2\\ k\end{array}}\right) c^ks^{m+2-k}\right) \textbf{H}(s+c)\\ {}= & {} (s+c)^{m+2}\textbf{H}(s+c)\quad \forall \,s\in {\mathbb {C}}_0, \end{aligned}$$

whence

$$\begin{aligned} \big ({{\mathcal {L}}}(e^{-c\,\cdot \,}({{\mathcal {F}}}^{-1}\Gamma ))\big )(s)=\textbf{G}(s+c)\quad \forall \,s\in {\mathbb {C}}_0, \end{aligned}$$

which is (8.10).

It remains to derive (8.11). Trivially, (8.11) is valid for $n=0$. Assume now that (8.11) holds for some $n\in {\mathbb {N}}_0$. Setting $\psi :=e^{-c\,\cdot \,}$ and $T^{(k)}:=D^k T$ for $T\in {{\mathcal {S}}}'(X)$ and $k\in {\mathbb {N}}_0$, the induction hypothesis takes the form

$$\begin{aligned} \psi [H]^{(n)}=\sum _{k=0}^n\left( {\begin{array}{c}n\\ k\end{array}}\right) c^k(\psi [H])^{(n-k)}\qquad \hbox { on~}\ {{\mathcal {D}}}. \end{aligned}$$

As $\psi [H]^{(n+1)}=(\psi [H]^{(n)})'+c\psi [H]^{(n)}$ (on ${{\mathcal {D}}}$), it follows from the induction hypothesis and a straightforward calculation that

$$\begin{aligned} \psi [H]^{(n+1)}=\sum _{k=0}^n\left( {\begin{array}{c}n\\ k\end{array}}\right) c^k(\psi [H])^{(n+1-k)}+\sum _{k=1}^{n+1}\left( {\begin{array}{c}n\\ k-1\end{array}}\right) c^k(\psi [H])^{(n+1-k)}\qquad \hbox { on~}\ {{\mathcal {D}}}. \end{aligned}$$

As

$$\begin{aligned} \left( {\begin{array}{c}n\\ 0\end{array}}\right)= & {} 1=\left( {\begin{array}{c}n+1\\ 0\end{array}}\right) ,\quad \left( {\begin{array}{c}n\\ n\end{array}}\right) =1=\left( {\begin{array}{c}n+1\\ n+1\end{array}}\right) \quad \text{ and }\\{} & {} \left( {\begin{array}{c}n\\ k-1\end{array}}\right) +\left( {\begin{array}{c}n\\ k\end{array}}\right) =\left( {\begin{array}{c}n+1\\ k\end{array}}\right) \,\,\,\forall \,k\in \{1,\ldots ,n\}, \end{aligned}$$

we conclude that

$$\begin{aligned} \psi [H]^{(n+1)}=\sum _{k=0}^{n+1}\left( {\begin{array}{c}n+1\\ k\end{array}}\right) c^k(\psi [H])^{(n+1-k)}\qquad \hbox { on~}\ {{\mathcal {D}}}, \end{aligned}$$

completing the induction argument. $\Box$