A survey on compressed sensing approach to systems and control

Abstract

In this survey paper, we review recent advances of compressed sensing applied to systems and control. Compressed sensing has been actively researched in the field of signal processing and machine learning. More recently, the method has been applied to systems and control problems, such as sparse feedback gain design, reduced-order control, and maximum hands-off control. This paper introduces these important applications of compressed sensing to systems and control. MATLAB programs for the numerical examples shown in this survey paper are available as supplementary materials.

1 Preface

It is our great pleasure to be able to contribute this article on the occasion of Eduardo Sontag’s 70th birthday.

Eduardo and the second author (hereafter I and me) both studied for Ph. D. under the guidance of the late Professor Rudolf E. Kalman. We belonged to the Center for Mathematical System Theory that Professor Kalman established in the University of Florida. I became a member of the Center in the fall of 1974, and when I came in, Eduardo was already there; he was two years ahead of me.

We both belonged to the Mathematics department as students to satisfy course requirements for Ph. D. As he was two years ahead, his main duty was to finish his Ph. D. thesis then.

His mathematical capability was simply enormous—sharp, precise, and knowledgeable, especially in algebra. He has already written several papers on systems over rings when I first met him, and I was very impressed.

In the Center where we worked for Ph. D., we shared the same habit of working late at night. We would very often come to the office around 8 or 9 pm and stayed there until 2 or 3 am in the morning.

During this time, we talked about, and discussed many things: mathematics, control theory, politics, and so on. I do not remember much of the details, but I can still recall two episodes.

At one point, our (and also Center’s) main issue was concerned with how one can grasp the notion of uniqueness of canonical realizations. At that time, we were both working on realization theory. He on algebraic systems, and myself on infinite-dimensional systems.

At least from a philosophical point of view, this is a very crucial issue—critical for modeling. If we have two essentially different models based on the same data, how can we safely draw a sound conclusion based on these different models? Such a nonuniqueness could shake the ground for the validity of a modeling process. Uniqueness of canonical realizations can save such a nuisance.

The trouble is that beyond the category of finite-dimensional linear systems, naive notions of canonical realizations do not work. One needs to be more careful for arriving at a desired uniqueness result.

Eduardo and I had some discussions, and we agreed upon the observation that the notion of canonical realizations should be taken in a categorical sense. Further, observability is the key to this. If one works with an algebraic category, the observability should be understood in an algebraic sense; if you work with a topological context, then the observability should be topological.

These observations later led to further developments for me, and they flourished into more concrete and useful realizations. I can still recall the vivid image of the night we had this discussion together. We were young, were enthusiastic, and had plenty of time to discuss. Those were golden days. I feel very fortunate to have him as a friend and an esteemed colleague.

I would like to conclude this preface by giving the second episode related to his skills in using chopsticks.

At one point—I do not remember when—I gave him a pair of chopsticks. I should remind the reader that the Japanese cuisine and chopsticks were not very popular in the USA then in the 1970s. (For example, there were no sushi shops in Gainesville.) The Japanese food was slowly gaining popularity, and so were chopsticks. Eduardo was curious and also interested in getting skillful at them. I probably gave him some basics in using chopsticks, and he would occasionally practice them when he wanted to relax from research and study. He soon (perhaps half a year later) became very good at using them, and he should be rightly proud of it. Again, to repeat, using chopsticks was not popular then. I am also proud of giving him a first motivation for becoming skillful at them.

Almost 50 years have passed since then. We chose different research directions, so we have had only one joint paper [1] together. However, I cherish wonderful mutual relationships and am grateful for his long-term friendship. Little did we dream then of a day that both of us would still remain in the academia and keep the same friendship as the old days in Florida.

I would also like to mention yet one more thing. The first author, Masaaki Nagahara, was a star student of mine, and is now my esteemed colleague. Hence, in light of our relationship, he can be regarded as your (Eduardo’s) academic nephew. In this way, our academic lineage continues, and that all dates back to our good old days.

So, Eduardo, enjoy this volume, which is a wonderful tribute to your great achievements, and I wish you many happy returns of the day, year and the occasion. My heartiest congratulations!

2 Introduction

In 1997, Eduardo Sontag and his colleagues have studied sparse approximation [2] to approximate a function in a functional space by a small number of basis functions. This idea has been extended to a very rich research area called compressed sensing, on which a number of recent studies have focused in the field of signal processing, machine learning, and statistics [3,4,5,6,7]. The core idea, which is very similar to [2], of compressed sensing is to consider sparsity in the signal analysis. A sparse signal (e.g., a sparse vector or a sparse matrix) is a signal that contains very few nonzero elements. To measure the sparsity of a signal, we use the $\ell ^0$ norm, the number of nonzero elements in the signal, and if the $\ell ^0$ norm is much smaller than the size (or the length) of the signal, then the signal is said to be sparse. We can find sparse signals around us. For example, audio signals are sparse in the frequency domain, since they have frequency components only in the low frequencies. In particular, the human voice can be assumed to be in the frequency range of 30  –  3400  Hz, called the telephone bandwidth, by which the voice can be coded at the sampling rate 8000  Hz [8]. Also, a pulse signal is sparse in the time domain, since it is active (i.e., nonzero) only in a short duration of time. This property has been applied, for example, to the reflection seismic survey in geophysics [9,10,11].

More recently, compressed sensing has been applied to the design of control systems, where the property of sparsity is used for reducing the number of parameters that determine the control. A motivation of sparse control design is for networked control, where observation data and control signals are exchanged between the controlled plant and the controller through a rate-limited wireless network. In networked control, the technique of compressed sensing plays an important role to realize resource-aware control that aims at reducing the communication and computational burden. For this purpose, sparse optimization to minimize the $\ell ^0$ norm of a control packet sent through a rate-limited network has been proposed in [12,13,14,15,16,17]. Resource-aware control is also achieved by the minimum actuator placement [18,19,20,21,22,23], which minimizes the number of actuators, or control inputs, that achieve a given control objective, such as controllability.

In networked control, it is also preferred for implementation to represent a controller in a compact size. For this, the design of a sparse feedback control gain has been proposed in [24,25,26,27,28,29]. In general, there should be a tradeoff between the closed-loop performance and the sparsity of the gain, for which see the review paper [30] for detailed discussions. In addition, reduced-order control [31] is also a good strategy to obtain a compact representation of a controller, which is related to compressed sensing of matrices [32,33,34,35,36].

The compressed sensing approach has also been proposed in the context of optimal control. In particular, the papers [37, 38] have introduced a new type of optimal control called the maximum hands-off control, which minimizes the $L^0$ norm of a continuous-time control signal under control constraints. Namely, maximum hands-off control is the sparsest control that has the minimum length of time duration on which the control is active (i.e., nonzero) to achieve a control objective with constraints. We note that hands-off control has a long time duration over which the control is exactly zero, which is actually used in practical control systems, sometimes called gliding or coasting. An example of hands-off control is a stop-start system [39, 40] in automobiles where the engine is automatically shut down when the automobile is stationary. Also in a hybrid vehicle, the internal combustion engine is stopped when the vehicle is at a stop or at a low speed while the electric motor is alternatively active [41,42,43]. In these systems, fuel consumption and CO or CO$_2$ emissions can be effectively reduced. Railway vehicles [44, 45] and free-flying robots [46] also take advantage of hands-off control. By these properties, hands-off control is also called green control [47].

Recent studies have also explored mathematical properties of maximum hands-off control. Maximum hands-off control is mathematically described as an $L^0$ optimal control, which is very hard to solve. Borrowing the idea of $\ell ^1$ relaxation in compressed sensing, $L^1$ optimal control has been proposed in [38] to solve the $L^0$ optimal control. Since the $L^1$ optimal control, also known as minimum fuel control, has been extensively studied in the 1960’s (see, e.g., [48]), the problem is easy to solve. In [38], the equivalence between $L^0$ and $L^1$ optimal controls is established under some mild assumptions. Fundamental properties of maximum hands-off control, such as the value function [49] and necessary conditions [50] have been investigated. Efficient numerical algorithms for maximum hands-off control have been proposed in recent papers [51,52,53]. Finally, practical applications of maximum hands-off control have been reported for electrically tunable lens [54], spacecraft maneuvering [55], and thermally activated building systems [56].

This survey paper provides an overview of recent advances of compressed sensing approaches to systems and control. The paper is organized as follows: Sect. 3 introduces the design of sparse feedback gains. In Sect. 4, reduced-order control as an application of compressed sensing is discussed. In Sect. 5, the maximum hands-off control is introduced and its mathematical properties are shown. Finally, Sect. 6 provides concluding remarks.

2.1 Notation

Let x be a vector. The $\ell ^p$ norm $\Vert x\Vert _p$ with $p\in (0,\infty )$ is defined by

$$\begin{aligned} \Vert x\Vert _p \triangleq \bigg (\sum _i \vert x_i\vert ^p\bigg )^{1/p}, \end{aligned}$$

(1)

where $x_i$ is the ith element of x. Also, the $\ell ^0$ norm $\Vert x\Vert _0$ is defined by

$$\begin{aligned} \Vert x\Vert _0 \triangleq \#\bigl (\textrm{supp}(x)\bigr ), \end{aligned}$$

(2)

where $\textrm{supp}(x)$ is the support set of x, that is,

$$\begin{aligned} \textrm{supp}(x) \triangleq \bigl \{i: x_i\ne 0\bigr \}, \end{aligned}$$

(3)

and $\#\bigl (\textrm{supp}(x)\bigr )$ is the number of elements in the finite set $\textrm{supp}(x)$.

Let A be a matrix. The transpose of A is denoted by $A^\top$, the trace by $\textrm{tr}(A)$, and the rank by $\textrm{rank}(A)$. The ith largest singular value of A is denoted by $\sigma _i(A)$, and the maximum singular value by $\sigma _{\max }(A)$. For matrix A, we denote by $\Vert A\Vert$ the Frobenius norm:

$$\begin{aligned} \Vert A\Vert \triangleq \sqrt{\textrm{tr}(A^\top A)} = \sqrt{\sum _{i=1}^n \sigma _i^2(A)}, \end{aligned}$$

(4)

and by $\Vert A\Vert _*$ the nuclear norm:

$$\begin{aligned} \Vert A\Vert _*\triangleq {\textrm{tr}}\bigl (\sqrt{A^\top A}\bigr ) = \sum _{i=1}^n \sigma _i(A), \end{aligned}$$

(5)

where $\sqrt{A^\top A}$ is a positive semidefinite matrix that satisfies $\bigl (\sqrt{A^\top A}\bigr )^2=A^\top A$. Also, the $\ell ^0$ and $\ell ^1$ norms of matrix A are, respectively, defined by

$$\begin{aligned} \Vert A\Vert _0 \triangleq \#\bigl (\textrm{supp}(A)\bigr ),\quad \Vert A\Vert _1 \triangleq \sum _{i,j} \vert a_{ij}\vert , \end{aligned}$$

(6)

where $a_{ij}$ is the (i, j)th element of A. By ${\mathcal {S}}_n$, we denote the set of $n\times n$ real symmetric matrices. For $A\in {\mathcal {S}}_n$, matrix inequalities $A\succ 0$, $A\succeq 0$, $A\prec 0$, and $A\preceq 0$, respectively, mean A is positive definite, positive semidefinite, negative definite, and negative semidefinite. For $A\in {\mathbb {R}}^{n\times m}$ with $r=\textrm{rank}(A)<n$, $A^\perp$ is a matrix that satisfies

$$\begin{aligned} A^\perp \in {\mathbb {R}}^{(n-r)\times n},\quad A^\perp A = 0,\quad A^\perp A^{\perp \top } \succ 0. \end{aligned}$$

(7)

We note that $A^\perp$ is not uniquely determined for a given A. In fact, if $A^\perp$ satisfies (7), then for any nonsingular $T\in {\mathbb {R}}^{(n-r)\times (n-r)}$, $TA^\perp$ also satisfies (7). The results using $A^\perp$ shown in this paper are valid for any matrix satisfying (7). For a closed subset $\Omega$ of a normed space ${\mathcal {S}}$ with norm $\Vert \cdot \Vert$, the projection of $X\in {\mathcal {S}}$ onto $\Omega$ is denoted by $\Pi _{\Omega }(X)$, that is,

$$\begin{aligned} \Pi _{\Omega }(X) \in \mathop {\text {arg}\,\text {min}}\limits _{Z\in \Omega } \Vert Z-X\Vert . \end{aligned}$$

(8)

3 Sparse feedback gain design

In this section, we will introduce a compressed sensing approach to the design of sparse feedback gains. As mentioned in the previous section, a sparse feedback gain is preferable in networked control systems as resource-aware control.

3.1 Problem formulation

Let us consider the following linear time-invariant system:

$$\begin{aligned} {\dot{x}}(t) = Ax(t) + Bu(t),\quad t\ge 0, \end{aligned}$$

(9)

where $x(t)\in {\mathbb {R}}^n$, $u(t)\in {\mathbb {R}}^m$, $A\in {\mathbb {R}}^{n\times n}$, and $B\in {\mathbb {R}}^{n\times m}$. We assume (A, B) is stabilizable (or asymptotically controllable [57]). Then, there exists a state feedback gain $K\in {\mathbb {R}}^{m\times n}$ such that the control

$$\begin{aligned} u(t) = Kx(t), \end{aligned}$$

(10)

asymptotically stabilizes system (9). In other words, the matrix $A+BK$ is Hurwitz [57, Proposition 5.5.6], which is equivalent to the existence of $Q \succ 0$ such that the following matrix inequality holds [58, Corollary 3.5.1]:

$$\begin{aligned} (A+BK)^\top Q + Q(A+BK) \prec 0. \end{aligned}$$

(11)

In this inequality, K and Q are both unknown variables, and hence, it is not linear. To make the inequality linear, we introduce new variables $P\triangleq Q^{-1}$ and $Y\triangleq KP$. Then, from inequality (11), we have the following inequalities:

$$\begin{aligned} P \succ 0,\quad AP + PA^\top + BY + Y^\top B^\top \prec 0. \end{aligned}$$

(12)

These are called linear matrix inequalities (LMIs), which play an important role in linear control systems design [58].

Now, the problem of sparse feedback gain design is formulated as follows:

Problem 1

(Sparse feedback gain) Find Y that has the minimum $\ell ^0$ norm among matrices satisfying the LMIs in (12).

Suppose $Y\in {\mathbb {R}}^{m\times n}$ is sparse, or $\Vert Y\Vert _0\ll mn$, where $\Vert Y\Vert _0$ is the $\ell ^0$ norm of Y defined in (6). Then, choosing the output as $y=P^{-1}x$, one can implement a sparse output feedback gain $u=Yy$.

3.2 Solution by sparse optimization

Let us consider how to obtain such a sparse solution. First, we slightly change the LMIs in (12) as follows:

$$\begin{aligned} P \succeq \epsilon I,~~ AP + PA^\top + BY + Y^\top B^\top \preceq -\epsilon I, \end{aligned}$$

(13)

with a small number $\epsilon >0$. Then the set

$$\begin{aligned} \Lambda \triangleq \{Y \in {\mathbb {R}}^{m\times n}: \exists P \succeq \epsilon I, AP + PA^\top + BY + Y^\top B^\top \preceq -\epsilon I\}, \end{aligned}$$

(14)

becomes a closed subset of ${\mathbb {R}}^{m\times n}$. We note that if $Y\in \Lambda$, then this Y satisfies (12).

Now, Problem 1 is described as an optimization problem of

$$\begin{aligned} \mathop {\textrm{minimize}}\limits _{Y} \Vert Y\Vert _0 \text { subject to } Y \in \Lambda . \end{aligned}$$

(15)

We note that this is a combinatorial optimization and hard to directly solve as in compressed sensing. Therefore, we approximate the $\ell ^0$ norm of the matrix Y by the $\ell ^1$ norm $\Vert Y\Vert _1$, the sum of absolute values of the elements in Y as defined in (6). In fact, the $\ell ^1$ norm is the convex envelope [32, 59] or the convex relaxation [7, Sect. 3.2], or the $\ell ^0$ norm. By using the $\ell ^1$ norm, the $\ell ^0$ optimization in (15) is reduced to the following convex optimization problem:

$$\begin{aligned} \mathop {\textrm{minimize}}\limits _{Y} \Vert Y\Vert _1 \text { subject to } Y \in \Lambda , \end{aligned}$$

(16)

where $\Vert Y\Vert _1$ is the $\ell ^1$ norm defined in (6). The $\ell ^1$ norm heuristic approach for sparse feedback gains has been proposed in [25, 26].

To numerically solve the convex optimization problem (16), one can adapt the Douglas–Rachford splitting algorithm [60, 61]:

$$\begin{aligned} \begin{aligned} Y[k+1]&= S_{\gamma }(Z[k]),\\ Z[k+1]&= Z[k] + \Pi _{\Lambda }(2Y[k+1]-Z[k])-Y[k+1],\quad k=0,1,2,\ldots . \end{aligned} \end{aligned}$$

(17)

In this algorithm, $S_{\gamma }$ is the soft-thresholding function defined by

$$\begin{aligned}{}[S_{\gamma }(V)]_{ij} \triangleq {\left\{ \begin{array}{ll} V_{ij}-\gamma , &{} \text {if } V_{ij}\ge \gamma ,\\ 0, &{} \text {if } -\gamma<V_{ij}<\gamma ,\\ V_{ij}+\gamma , &{} \text {if } V_{ij}\le -\gamma , \end{array}\right. } \end{aligned}$$

(18)

where $[S_{\gamma }(V)]_{ij}$ is the (i, j)th entry of $S_{\gamma }(V)\in {{\mathbb {R}}}^{m\times n}$, and $\Pi _{\Lambda }$ is the projection onto the set $\Lambda$. The projection $\Pi _\Lambda$ onto the closed and convex subset $\Lambda$ can be obtained by solving another LMI optimization [62, Section 2.1] (see also [29]):

Lemma 1

For matrix $Y\in {\mathbb {R}}^{m\times n}$, the projection $\Pi _\Lambda (Y)$ is the solution of the following optimization problem:

$$\begin{aligned} \mathop {\textrm{minimize}}\limits _{S,Z} ~~ \text {tr}(S)~~ \text {subject to} ~~ \begin{bmatrix}S &{} (Z-Y)^\top \\ (Z-Y) &{} I\end{bmatrix} \succ 0, \quad Z \in \Lambda . \end{aligned}$$

(19)

Other formulations of sparse feedback gain design have also been proposed. First, the iterative greedy LMI [29] is an alternating projection method to find an s-sparse matrix Y that satisfies $\Vert Y\Vert _0\le s$ in the LMI subset $\Lambda$ for given $s\in {\mathbb {N}}$. The projection of matrix Y onto the subset of s-sparse matrices is given by

$$\begin{aligned} \mathop {\text {arg}\,\text {min}}\limits _{Z} \Vert Z-Y\Vert \text { subject to } \Vert Z\Vert _0\le s. \end{aligned}$$

(20)

This projection is known to be the s-sparse operator ${\mathcal {H}}_s(Y)$, which sets all but the s largest (in magnitude) elements of Y to 0 [61, 63]. We note that the optimization in (20) may have multiple solutions in general, and the projection is not uniquely determined. In this case, we choose one matrix randomly. Applying the projection $\Pi _\Lambda$ computed by (19) and the s-sparse operator ${\mathcal {H}}_s$ alternatively as

$$\begin{aligned} Y[k+1] = {\mathcal {H}}_s \circ \Pi _\Lambda (Y[k]),\quad k=0,1,2,\ldots , \end{aligned}$$

(21)

with an initial guess Y[0], we can find an s-sparse matrix in $\Lambda$.

Next, the paper [26] has proposed to design a row sparse feedback gain, which can reduce the number of control channels in a multiple-input system. A row sparse gain is obtained by minimizing the row norm:

$$\begin{aligned} \Vert Y\Vert _{r1} \triangleq \sum _{i=1}^m \max _{1\le j\le n} \vert Y_{ij}\vert , \end{aligned}$$

(22)

instead of the $\ell ^1$ norm in (16). Finally, [25] has proposed sparse feedback gain design for $H^2$ control by using the $\ell ^1$ norm heuristic approach with LMIs.

3.3 Numerical example

Here, we design a sparse feedback gain for the linear plant (9) with

$$\begin{aligned} A = \begin{bmatrix} 0&{}\qquad 0&{}\qquad 1.1320&{}\qquad 0&{}\qquad -1.0000\\ 0&{}\qquad -0.0538&{}\qquad -0.1712&{} \qquad 0&{}\qquad 0.0705\\ 0&{}\qquad 0&{}\qquad 0&{}\qquad 1.0000&{}\qquad 0\\ 0&{}\qquad 0.0485&{}\qquad 0&{} \qquad -0.8556&{}\qquad -1.0130\\ 0&{}\qquad -0.2909&{} \qquad 0&{}\qquad 1.0532&{}\qquad -0.6859 \end{bmatrix},\quad B = \begin{bmatrix} 0&{}\quad 0&{}\quad 0\\ -0.1200&{}\quad 1.0000&{}\quad 0\\ 0&{} \quad 0&{}\quad 0\\ 4.4190&{}\quad 0&{}\quad -1.6650\\ 1.5750&{}\quad 0&{}\quad -0.0732 \end{bmatrix}. \nonumber \\ \end{aligned}$$

(23)

This model, named AC2, is taken from the benchmark problem set in COMPL$_e$ib library [64].

First, we solve the $\ell ^1$ norm optimization in (16). We take $\epsilon = 10^{-6}$ for (14). Using YALMIP [65] and SeDuMi [66] on MATLAB, we obtain the following solution:

$$\begin{aligned} Y_{\ell ^1} = \begin{bmatrix} 0&{}\qquad 0&{}\qquad 0&{}\qquad 0&{}\qquad 0\\ -0.4800&{}\qquad -0.4800&{}\qquad -0.4800&{}\qquad -0.4800&{}\qquad 0.4800\\ 0&{}0&{}0&{}0&{}0\\ \end{bmatrix} \times 10^{-6}.\nonumber \\ \end{aligned}$$

(24)

This is a sparse matrix, and we obtain a sparse feedback gain.

Next, we solve the $\ell ^0$ optimization (15) by alternating projection [29] given in (21) with sparsity $s=1$. The solution is obtained as

$$\begin{aligned} Y_{\textrm{alt}} = \begin{bmatrix} 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{} -1.367&{} 0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0\\ \end{bmatrix} \times 10^{-6}. \end{aligned}$$

(25)

We confirm that $\Vert Y_{\textrm{alt}}\Vert _0 = 1$ and it is sparser than $Y_{\ell ^1}$, while the alternating projection method needs more iterations than the $\ell ^1$ optimization. You can check the numerical computation by yourself using the MATLAB program available at [67].

4 Reduced-order control design

The problem of reduced-order control is to find a low-order controller, which has a much less order than the controlled plant. This problem is known to be NP-hard [68] due to the rank condition introduced below. Then, we can adapt the idea of compressed sensing to solve this problem.

4.1 Problem formulation

Let us consider the following linear time-invariant system:

$$\begin{aligned} {\dot{x}}(t) = Ax(t) + Bu(t),\quad y(t) = Cx(t),\quad t\ge 0, \end{aligned}$$

(26)

where $x(t)\in {\mathbb {R}}^n$, $u(t)\in {\mathbb {R}}^m$, $y(t)\in {\mathbb {R}}^p$, $A\in {\mathbb {R}}^{n\times n}$, $B\in {\mathbb {R}}^{n\times m}$, and $C\in {\mathbb {R}}^{p\times n}$.

For this system, we consider an output-feedback controller $u=Ky$ of order $n_c$, which is strictly less than n. Such a controller is called a reduced-order controller. Then, the reduced-order controller design is described as the following feasibility problem [69]:

Problem 2

(Reduced-order controller) Find symmetric matrices $X, Y\in {\mathcal {S}}_n$ such that the rank condition

$$\begin{aligned} \textrm{rank} \begin{bmatrix}X &{}\quad I\\ I &{} Y \end{bmatrix} \le n + n_c, \end{aligned}$$

(27)

and the LMIs

$$\begin{aligned} \begin{bmatrix}X &{}\quad I\\ I &{}\quad Y \end{bmatrix} \succeq 0,~~ B^\perp (AX+XA^\top )B^{\perp \top } \preceq -\epsilon I,~~ C^{\top \perp }(YA + A^\top Y)C^{\top \perp \top } \preceq -\epsilon I, \end{aligned}$$

(28)

hold for some $\epsilon >0$.

4.2 Solution by alternating projection

To solve this problem, we introduce an algorithm using nuclear norm minimization [35, 59] to approximately solve the rank-constrained LMIs in Problem 2. The idea is to approximate the matrix rank by the nuclear norm defined in (5), the sum of the singular values of the matrix, which is known to be the convex relaxation of the matrix rank [32, 59].

Using the nuclear norm, Problem 2 is reduced to the following problem:

$$\begin{aligned} \mathop {\textrm{minimize}}\limits _{(X,Y) \in {\mathcal {S}}_n^2}~ \left\| \begin{bmatrix}X &{}\quad I\\ I &{}\quad Y \end{bmatrix} \right\| _* \text { subject to } F(X,Y)\preceq 0, \end{aligned}$$

(29)

where F(X, Y) is defined such that the inequality $F(X,Y)\preceq 0$ is equivalent to the LMIs in (28). This is a convex optimization problem and is easily solved.

Another approach to Problem 2 is alternating projection. Let us consider the following two subsets of ${\mathcal {S}}_n^2$:

$$\begin{aligned} \Omega _r&\triangleq \left\{ (X,Y)\in {\mathcal {S}}_n^2: \textrm{rank} \begin{bmatrix}X &{}\quad I\\ I &{} Y \end{bmatrix} \le r\right\} , \end{aligned}$$

(30)

$$\begin{aligned} \Lambda&\quad \triangleq \{(X,Y) \in {\mathcal {S}}_n^2: F(X,Y)\preceq 0\}, \end{aligned}$$

(31)

where $r=n+n_c$. The alternating projection alternatively applies two projections $\Pi _{\Omega _r}$ and $\Pi _{\Lambda }$ onto $\Omega _r$ and $\Lambda$, respectively. That is, we iteratively compute

$$\begin{aligned} (X[k+1], Y[k+1]) = \Pi _{\Lambda }\circ \Pi _{\Omega _r}(X[k],Y[k]),\quad k=0,1,2,\ldots , \end{aligned}$$

(32)

with initial guess $(X[0],Y[0])\in {\mathcal {S}}_n^2$. The projection $\Pi _{\Omega _r}(X,Y)$ for given $(X,Y) \in {\mathcal {S}}_n^2$ is easily computed by the alternating direction method of multipliers (ADMM), for which see Sect. 4.3 for details. The projection $\Pi _{\Lambda }$ can also be easily computed using Lemma 1.

It is reported in [70] that the alternating projection method can solve some reduced-order control problems that the nuclear norm heuristic approach cannot solve (see Example 4.4). We also note that many control problems, such as $H^2$ and $H^\infty$ control problems, are described as LMIs with the rank condition, which can also be solved by the method introduced in this section.

4.3 ADMM algorithm for projection $\Pi _{\Omega _r}$

Here, we show the ADMM algorithm for the projection $\Pi _{\Omega _r}$ defined in (30). For given $(X,Y)\in {\mathcal {S}}_n^2$, the projection $\Pi _{\Omega _r}(X,Y)$ can be written by definition as

$$\begin{aligned} \Pi _{\Omega _r}(X,Y) \in \mathop {\text {arg}\,\text {min}}\limits _{(V,W)\in \Omega _r} \Vert V-X\Vert ^2 + \Vert W-Y\Vert ^2. \end{aligned}$$

(33)

We note that the subset $\Omega _r$ is closed but non-convex, and hence, there may exist multiple minimizers for the right-hand side of (33). To solve the minimization problem in (33), we consider the indicator function ${\mathcal {I}}_r$ defined by

$$\begin{aligned} {\mathcal {I}}_r(Z) \triangleq {\left\{ \begin{array}{ll} 0,&{}\text {if } \textrm{rank}(Z)\le r,\\ +\infty , &{}\text {otherwise.}\end{array}\right. } \end{aligned}$$

(34)

Then, the projection $\Pi _{{\mathcal {C}}_r}(Z)$ onto the set of rank-r matrices

$$\begin{aligned} {\mathcal {C}}_r \triangleq \{Z\in {\mathbb {R}}^{2n\times 2n}: \textrm{rank}(Z)\le r\}. \end{aligned}$$

(35)

is easily computed via the singular value decomposition $Z=U\Sigma V^\top$. Let $\Sigma _r$ be a truncated matrix of $\Sigma$ by setting all but r largest in magnitude diagonal entries of $\Sigma$ to 0. Then, $\Pi _{{\mathcal {C}}_r}(Z)$ is given by

$$\begin{aligned} \Pi _{{\mathcal {C}}_r}(Z) = U\Sigma _r V^\top . \end{aligned}$$

(36)

Then, the minimization problem in (33) is equivalently described as

$$\begin{aligned} \begin{aligned} \mathop {\textrm{minimize}}\limits _{(V,W)\in {\mathcal {S}}_n^2, {\tilde{Z}}\in {\mathcal {S}}_{2n}} \quad&\Vert V-X\Vert ^2 + \Vert W-Y\Vert ^2 + {\mathcal {I}}_r({\tilde{Z}})\\ \text {subject to} \quad&{\tilde{Z}} = \begin{bmatrix}V&{}I\\ I&{}W\end{bmatrix}. \end{aligned} \end{aligned}$$

(37)

This optimization problem can be efficiently solved by the ADMM algorithm [71]. The iterative algorithm is given by

$$\begin{aligned} V[k+1]&= \left( 1+\frac{\rho }{2}\right) ^{-1}\left( X + \frac{\rho }{2}M_{11}[k]\right) , \end{aligned}$$

(38)

$$\begin{aligned} W[k+1]&= \left( 1+\frac{\rho }{2}\right) ^{-1}\left( Y + \frac{\rho }{2}M_{22}[k]\right) , \end{aligned}$$

(39)

$$\begin{aligned} {\tilde{Z}}[k+1]&= \Pi _{{\mathcal {C}}_r}\left( \begin{bmatrix}V[k+1]&{}I\\ I&{}W[k+1]\end{bmatrix} - Z[k]\right) , \end{aligned}$$

(40)

$$\begin{aligned} Z[k+1]&= Z[k] + {\tilde{Z}}[k+1] - \begin{bmatrix}V[k+1]&{}I\\ I&{}W[k+1]\end{bmatrix}, \\ k&= 0,1,2,\ldots , \nonumber \end{aligned}$$

(41)

where $\rho >0$ is the step size, and $M_{11}[k],M_{22}[k]\in {\mathbb {R}}^{n\times n}$ are defined as

$$\begin{aligned} \begin{bmatrix} M_{11}[k]&{}\qquad M_{12}[k]\\ M_{21}[k]&{}\qquad M_{22}[k]\end{bmatrix} \triangleq {\tilde{Z}}[k] + Z[k]. \end{aligned}$$

(42)

A detailed explanation of this algorithm is found in [70].

4.4 Numerical example

We first consider the linear plant (26) with A and B given in (23) and

$$\begin{aligned} C = \begin{bmatrix} 1&{}\qquad 0&{}\qquad 0&{}\qquad 0&{}\qquad 0\\ 0&{}\qquad 1&{} \qquad 0&{}\qquad 0&{}\qquad 0\\ 0&{}\qquad 0&{}\qquad 1&{}\qquad 0&{}\qquad 0\\ \end{bmatrix}. \end{aligned}$$

(43)

This is model AC2 from the COMPL$_e$ib library [64]. For this system, we compute a static controller with $n_c=0$ that stabilizes the plant. We use YALMIP [65] and SeDuMi [66] on MATLAB to solve the nuclear norm minimization (29). The obtained static controller is

$$\begin{aligned} K = \begin{bmatrix} 0.8666&{}\quad 0.1591&{}\quad 0.5204\\ 0.0898&{} -0.8733&{} 0.2193\\ 2.293&{} 0.4493&{} 2.308\\ \end{bmatrix}, \end{aligned}$$

(44)

with which the poles of the closed-loop system (i.e., the eigenvalues of $A+BKC$) are

$$\begin{aligned} -0.4639 \pm 1.5368\mathrm j, -0.3076 \pm 1.0758\mathrm j, -0.9446, \end{aligned}$$

(45)

and hence this K certainly stabilizes the plant. We note that the alternating projection (32) with zero matrices as the initial guess also gives almost the same K as (44).

Next, let us consider another linear time-invariant plant with

$$\begin{aligned} A = \begin{bmatrix} 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 1&{} 0&{} 0&{} 0&{} 0&{} -1\\ 0&{} 1&{} 0&{} 0&{} 0&{} 0\\ 0&{} 0&{} 0&{} 0&{} 0&{} 0\\ 0&{} 0&{} 0&{} 1&{} 0&{} 0\\ 0&{} 0&{} -1&{} 0&{} 1&{} 0\\ \end{bmatrix},\quad B = \begin{bmatrix} -1&{}\quad -3\\ 0&{} 0\\ 0&{} 1\\ 0&{} -1\\ 0&{} -1\\ 0&{} 0\\ \end{bmatrix},\quad C = \begin{bmatrix} 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{} 0&{} 0&{} 0&{} 0&{} 1\\ \end{bmatrix}.\nonumber \\ \end{aligned}$$

(46)

This model is NN12 from the COMPL$_e$ib library [64].

First, the nuclear norm minimization failed to find a stabilizing static controller. On the other hand, the alternating projection (32) successfully outputs the following static controller

$$\begin{aligned} K = \begin{bmatrix} 42.18&{}\quad -49.24\\ -9.623&{} 11.29\\ \end{bmatrix}. \end{aligned}$$

(47)

With this static controller, the closed-loop poles become

$$\begin{aligned} -6.7037, -2.1107, -0.0638 \pm 1.0266\mathrm j, -0.3406 \pm 0.1843\mathrm j, \end{aligned}$$

and hence K stabilizes the plant. The MATLAB program to run the numerical examples above is available at [67].

5 Maximum hands-off control

In this section, we introduce a compressed sensing approach to continuous-time optimal control. For this, we first define the $L^0$ norm for a Lebesgue measurable function u: $[0,T]\rightarrow {\mathbb {R}}$ with fixed $T>0$:

$$\begin{aligned} \Vert u\Vert _{L^0} \triangleq \mu _L\bigl (\textrm{supp}(u)\bigr ), \end{aligned}$$

(48)

where $\mu _L$ is the Lebesgue measure, and $\textrm{supp}(u)$ is the support set of function u, that is,

$$\begin{aligned} \textrm{supp}(u) \triangleq \bigl \{t\in [0,T]: u(t)\ne 0\bigr \}. \end{aligned}$$

(49)

We note that the definition of $L^0$ norm in (48) is consistent with that of $\ell ^0$ norm defined in (2). The $L^0$ norm can be understood as the time length over which the signal takes nonzero values. Then, if a continuous-time signal $\{u(t): t\in [0,T]\}$ has the $L^0$ norm $\Vert u\Vert _{L^0}$ much smaller than the horizon length T, then u is said to be sparse.

Such sparse control is important in practical applications for which energy consumption should be considered. When control is sparse, the actuator can stop when the signal value is zero, and the energy consumption can be dramatically reduced. To maximally enhance energy conservation by sparse control, we adopt maximum hands-off control described below.

5.1 Maximum hands-off control problem

Let us consider the following single-input linear time-invariant system:

$$\begin{aligned} {\dot{x}}(t) = Ax(t) + bu(t),\quad t\ge 0,\quad x(0) = \xi , \end{aligned}$$

(50)

where $x(t)\in {\mathbb {R}}^n$ is the state, $u(t)\in {\mathbb {R}}$ is the control, and $A\in {\mathbb {R}}^{n\times n}$ and $b\in {\mathbb {R}}^{n\times 1}$ are state-space matrices. For this linear system, we consider the problem of maximum hands-off control described as follows.

Problem 3

(Maximum hands-off control) Fix terminal time $T>0$. Find a control $\{u(t): t\in [0,T]\}$ that minimizes $\Vert u\Vert _{L^0}$ such that it satisfies the control magnitude constraint¹

$$\begin{aligned} \Vert u\Vert _{L^\infty } \triangleq \mathop {\mathrm {ess\,sup}}\limits _{t\in [0,T]} \vert u(t)\vert \le 1, \end{aligned}$$

(51)

and steers the state x(t) in (50) from $x(0)=\xi$ to $x(T) = 0$.

5.2 Existence

First, we consider the existence of maximum hands-off control. For this, we define the T-controllable set [72]:

Definition 1

(T-controllable set) Let $T>0$. The set of initial states of (50) that can be transferred to the origin by some control $\{u(t): t\in [0,T], \Vert u\Vert _{L^\infty }\le 1\}$ is called the T-controllable set. We denoted the T-controllable set by ${\mathcal {R}}(T)$.

The T-controllable set ${\mathcal {R}}(T)$ is represented as

$$\begin{aligned} {\mathcal {R}}(T) = \biggl \{-\int _0^T e^{-At}bu(t)dt: \Vert u\Vert _{L^\infty }\le 1\biggr \}. \end{aligned}$$

(52)

From the definition of ${\mathcal {R}}(T)$, if $\xi \in {\mathcal {R}}(T)$, then there exists a control $\{u(t): t\in [0,T], \Vert u\Vert _{L^\infty }\le 1\}$ that transfers x(t) from $\xi$ to the origin in time T. We call this control a feasible control, and denote by ${\mathcal {U}}(T,\xi )$ the set of all feasible controls. The feasible set is also represented as

$$\begin{aligned} {\mathcal {U}}(T,\xi ) = \biggl \{ u: \Vert u\Vert _{L^\infty }\le 1, ~\xi = - \int _0^T e^{-At}bu(t)dt\biggr \}. \end{aligned}$$

(53)

It is easily shown that $\xi \in {\mathcal {R}}(T)$ if and only if there exists $u\in {\mathcal {U}}(T,\xi )$. In other words, if $\xi \not \in {\mathcal {R}}(T)$, then there is no feasible control, and ${\mathcal {U}}(T,\xi )$ is empty. In this case, if we take sufficiently large ${\tilde{T}}>T$, then ${\mathcal {U}}({\tilde{T}},\xi )$ may be non-empty. Then, we consider the minimum time among all T such that ${\mathcal {U}}(T,\xi )$ is non-empty, which is defined by

$$\begin{aligned} T^*(\xi ) \triangleq \inf \{T\ge 0: \exists u, u\in {\mathcal {U}}(T,\xi )\}. \end{aligned}$$

(54)

For the minimum time, the following theorem holds [48, Section 6-8][73, Section III.19]:

Theorem 1

Suppose that $T^*(\xi )<\infty$. Then, there exists a minimum-time control $u^*\in {\mathcal {U}}(T^*(\xi ),\xi )$. Moreover, for any $T>T^*(\xi )$, the set ${\mathcal {U}}(T,\xi )$ is non-empty.

From this theorem, we can show the existence of maximum hands-off control [74]:

Theorem 2

Suppose that the initial state $\xi$ satisfies $T^*(\xi )<\infty$, and the terminal time T is strictly greater than $T^*(\xi )$. Then, there exists at least one maximum hands-off control (i.e., an optimal solution of Problem 3).

5.3 Equivalence theorem

The maximum hands-off control problem (Problem 3) is hard to solve. Hence, we borrow the idea of the $\ell ^1$-norm heuristic approach introduced in compressed sensing. Namely, we consider to minimize the $L^1$ norm of u:

$$\begin{aligned} \Vert u\Vert _{L^1} \triangleq \int _0^T \vert u(t) \vert dt. \end{aligned}$$

(55)

Minimizing the $L^1$ norm instead of the $L^0$ norm in Problem 3 is known as the minimum fuel control [48]:

Problem 4

(Minimum fuel control) Fix terminal time $T>0$. Find a control $\{u(t): t\in [0,T]\}$ that minimizes $\Vert u\Vert _{L^1}$ in (55) such that it satisfies the control magnitude constraint (51), and steers the state x(t) in (50) from $x(0)=\xi$ to $x(T) = 0$.

The minimum fuel control is a classical and well-studied control problem. This problem can be easily solved by, e.g., time discretization [74], by which the problem is reduced to a standard convex optimization problem with the $\ell ^1$ norm.

A question is when these two optimal control problems are equivalent. An equivalent theorem has been obtained in [38, 74]:

Theorem 3

Suppose that T and $\xi$ are chosen such that $T^*(\xi )<\infty$ and $T>T^*(\xi )$. Suppose also that there exists an $L^1$ optimal control $u^*_1(t)$ (i.e., a solution of Problem 4) that takes $\pm 1$ or 0 for almost all $t\in [0,T]$. Then, $u^*_1(t)$ is also $L^0$ optimal (i.e., a solution of Problem 3).

A control that takes $\pm 1$ or 0 for almost all t is called a bang-off-bang control. Theorem 3 suggests to first solve Problem 4, and see the solution. If it is bang-off-bang, then it is also maximum hands-off control. The following theorem gives a sufficient condition for the $L^1$ optimal control to be bang-off-bang:

Theorem 4

Suppose that T and $\xi$ are chosen such that $T^*(\xi )<\infty$ and $T>T^*(\xi )$. Suppose also that A is non-singular and (A, b) is controllable. Then, the $L^1$ optimal control is bang-off-bang, and hence, it is also $L^0$ optimal.

The equivalence is easily checked before solving Problem 4.

Fig. 1

$L^1$ optimal control that is bang-off-bang

Fig. 2

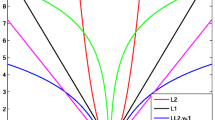
State variables $x_i(t)$, $i=1,2,3,4$ by the $L^1$ optimal control in Fig. 1

5.4 Numerical example

Let us consider the linear time-invariant system (50) with

$$\begin{aligned} A = \begin{bmatrix} 0&{}\quad -1&{}\quad 0&{}\quad 0\\ 1&{} 0&{} 0&{} 0\\ 0&{} 1&{} 0&{} 0\\ 0&{} 0&{} 1&{} 0\\ \end{bmatrix},\quad b = \begin{bmatrix} 2\\ 0\\ 0\\ 0\\ \end{bmatrix}. \end{aligned}$$

(56)

We take $\xi = [1,1,1,1]^\top$ and $T=10$. For this system, we compute the maximum hands-off control. Since A is singular, we cannot use Theorem 4. Therefore, we first solve Problem 4, and check whether the solution is bang-off-bang. By using time discretization and the alternating direction method of multipliers (ADMM) [61, Chapter 9], we obtain the $L^1$ optimal control shown in Fig. 1.

We can see that the $L^1$ optimal control takes only $\pm \,1$ and 0, and hence, it is bang-off-bang. From Theorem 3, this is also maximum hands-off control, a solution of Problem 3. By this control, the state $x(t)=[x_1(t),x_2(t),x_3(t),x_4(t)]^\top$ is transferred to the origin, as shown in Fig. 2.

6 Conclusion

In this survey paper, we have introduced compressed sensing approaches to three control problems, namely sparse feedback gain design, reduced-order control, and maximum hands-off control. Not limited to these control problems, compressed sensing has also been applied to important control problems such as minimum actuator placement [18,19,20], discrete-valued control [75, 76], and system identification [77, 78]. We hope the readers develop further new approaches of compressed sensing to systems and control.