Input-to-state stability of Lur’e systems

Abstract

An input-to-state stability theory, which subsumes results of circle criterion type, is developed in the context of continuous-time Lur’e systems. The approach developed is inspired by the complexified Aizerman conjecture.

1 Introduction

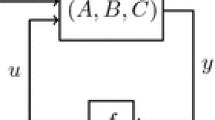
We will be concerned with controlled Lur’e systems of the form

$$\begin{aligned} \dot{x}= Ax + Bf(Cx) + B_\mathrm{e}v, \end{aligned}$$

(1.1)

where A, B, $B_\mathrm{e}$ and C are matrices of appropriate formats, f is a locally Lipschitz nonlinearity and v denotes the input or forcing. Obviously, system (1.1) can be thought of as a feedback system, namely the linear controlled and observed system

$$\begin{aligned} \dot{x}= Ax+ Bu+ B_\mathrm{e}v,\quad y=Cx \end{aligned}$$

with nonlinear output feedback $u=f(y)$.

Lur’e systems are a common and important class of nonlinear systems and there is a large body of work on the absolute stability theory of these systems: see, for example [6, 7, 16, 19, 27, 28]. Traditionally, Lyapunov approaches to the stability theory of systems of the form (1.1) consider unforced Lur’e systems (i.e., $v=0$ in (1.1)), whilst Lur’e systems with forcing (usually acting through B, that is, $B_\mathrm{e}=B$) have been studied using the input–output framework initiated by Sandberg and Zames in the 1960s, see, for example [27]. More recently, forced Lur’e systems have been analysed in the context of input-to-state stability (ISS) theory, see [1, 2, 12, 13] (and [22] for discrete-time systems). In [1], an ISS result is obtained for Lur’e systems (1.1) under the assumptions that $B_\mathrm{e} = B$, the underlying linear system has the positive real property and the nonlinearity (which may have superlinear growth) satisfies a suitable cone condition. Partial extensions of the classical Popov and circle criteria to an ISS setting can be found in [2] and [12, 13], respectively. The concept of ISS (for a general controlled nonlinear system) appears first in [23] published in 1989. The theory of ISS which has been subsequently developed, provides a natural stability framework for nonlinear systems with inputs, merging, in a sense, Lyapunov and input–output approaches to stability (the latter initiated by Sandberg and Zames in the 1960s). We refer the reader to [3, 25] for overviews of ISS theory.

In this paper, we derive an ISS result which is reminiscent of the complexified Aizerman conjecture [9, 10] (see [7, 17, 18, 27] for details on the original real Aizerman conjecture). More precisely, let K be a matrix of appropriate format and assume that every complex matrix in the ball $\{F:\Vert F-K\Vert <r\}$, where $r>0$, is a stabilizing output feedback gain for the linear system (A, B, C). The main result of the paper (Theorem 3.2) guarantees that, under this hypothesis, the nonlinear system (1.1) is ISS for every locally Lipschitz nonlinearity f for which there exists a $\mathcal {K}_\infty$ function $\alpha$ such that

$$\begin{aligned} \Vert f(\xi )-K\xi \Vert \le r\Vert \xi \Vert -\alpha (\Vert \xi \Vert )\quad \text{ for } \text{ all }\quad \xi . \end{aligned}$$

(1.2)

As a corollary (see Corollary 3.10), we derive a clear-cut ISS version of the circle criterion: it is shown that, under conditions very similar to those of the circle criterion, the Lur’e system (1.1) is ISS. In particular, Corollary 3.10 contains earlier ISS versions [12, 13] of the circle criterion as special cases. Moreover, a further corollary (Corollary 3.11) shows that the conditions of the usual textbook version of the circle criterion for global asymptotic stability (see [7, 16, 27]) are actually sufficient for ISS.

Finally, we mention that if A is not Hurwitz and f is bounded (for example, if f is of “saturation” type), then the nonlinearity is not “powerful” enough to counteract large (but bounded) inputs (at least if $\mathrm{im}\,B\subset \mathrm{im}\,B_\mathrm{e}$) and the Lur’e system (1.1) is not ISS (see [20] and Proposition 3.4 in the current paper). Correspondingly, it is not difficult to show that if A is not Hurwitz, f is bounded and every complex output feedback gain in the ball $\{F:\Vert F-K\Vert <r\}$ is stabilizing, then there does not exist $\alpha \in \mathcal {K}_\infty$ such that (1.2) holds (see Proposition 3.4).

1.1 Notation and terminology

As usual, $\mathbb {R}$ and $\mathbb {C}$ denote the fields of real and complex numbers, respectively. We set $\mathbb {R}_+:=[0,\infty )$.

In the following, let $\mathbb {F}=\mathbb {R}$ or $\mathbb {F}=\mathbb {C}$. For $K\in \mathbb {C}^{m\times p}$ and $r>0$, we define the open ball in $\mathbb {F}^{m\times p}$ with centre K and radius r:

$$\begin{aligned} \mathbb {B}_{\mathbb {F}}(K,r):=\{M\in \mathbb {F}^{m\times p}:\Vert M-K\Vert <r\}. \end{aligned}$$

For $M\in \mathbb {C}^{n\times m}$, let $M^*$ denote the Hermitian transposition of M (transposition if M is real). The open right-half of the complex plane $\mathbb {C}$ is denoted by $\mathbb {C}_+$. The Hardy space of all bounded holomorphic functions $\mathbb {C}_+\rightarrow \mathbb {C}^{p\times m}$ is denoted by $H^\infty (\mathbb {C}^{p\times m})$. The norm of a function $H\in H^\infty (\mathbb {C}^{p\times m})$ is given by

$$\begin{aligned} \Vert H\Vert _{H^\infty }=\sup _{s\in \mathbb {C}_+}\Vert H(s)\Vert , \end{aligned}$$

where $\Vert \cdot \Vert$ is the operator norm on $\mathbb {C}^{p\times m}$ induced by the 2-norms on $\mathbb {C}^m$ and $\mathbb {C}^p$.

Let $A\in \mathbb {C}^{n\times n}$ be Hurwitz (that is, all eigenvalues of A have negative real parts), let $B\in \mathbb {C}^{n\times m}$ and $C\in \mathbb {C}^{p\times n}$. The structured stability radius of A with respect to the perturbation structure given by B and C is defined by

$$\begin{aligned} r_{\mathbb {F}}(A; B, C):= \inf \{\left\| \Delta \right\| :\Delta \in \mathbb {F}^{m \times p}\quad \text{ and }\quad A+B\Delta C\quad \mathrm{is~not~Hurwitz}\}. \end{aligned}$$

The number $r_{\mathbb {C}}(A; B, C)$ is said to be the complex stability radius, whilst $r_{\mathbb {R}}(A; B, C)$ is called the real stability radius, see [8, 10]. Note that, even if A, B and C are real, the perturbation $\Delta$ in the definition of $r_{\mathbb {C}}(A; B, C)$ is in $\mathbb {C}^{m \times p}$.

Finally, we recall the definitions of certain classes of comparison functions. Let $\mathcal {K}$ denote the set of all continuous functions $\varphi :\mathbb {R}_+\rightarrow \mathbb {R_+}$ such that $\varphi (0)=0$ and $\varphi$ is strictly increasing. Moreover,

$$\begin{aligned} \mathcal {K}_\infty := \{\varphi \in \mathcal {K}: \varphi (s)\rightarrow \infty \quad \text{ as }\quad s\rightarrow \infty \}. \end{aligned}$$

We denote by $\mathcal {KL}$ the set of functions $\psi :\mathbb {R}_+\times \mathbb {R}_+ \rightarrow \mathbb {R}_+$ with the following properties: $\psi (\cdot \,, t)\in \mathcal {K}$ for every $t\ge 0$, and $\psi (s,\cdot \,)$ is non-increasing with $\lim _{t\rightarrow \infty }\psi (s, t) = 0$ for every $s\ge 0$. Note that, following [24–26], continuity is not imposed in the above definition of a $\mathcal {KL}$-function. It is known that a discontinuous $\mathcal {KL}$-function can be bounded from above by a continuous $\mathcal {KL}$-function, see [24, Proposition 7]. For more details on comparison functions, we refer the reader to [15].

2 Preliminaries

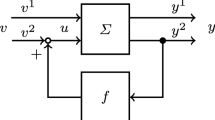
Set $\Sigma :=\mathbb {R}^{n\times n}\times \mathbb {R}^{n\times m}\times \mathbb {R}^{p\times n}$. With a triple $(A,B,C)\in \Sigma$, we associate the following controlled and observed linear system

$$\begin{aligned} \dot{x}=Ax+Bu,\quad y=Cx. \end{aligned}$$

(2.1)

The transfer function (matrix) G of (2.1) (or of the triple (A, B, C)) is given by

$$\begin{aligned} G(s)=C(sI-A)^{-1}B. \end{aligned}$$

The closed-loop system obtained by application of linear feedback of the form $u=Ky+v$ to (2.1), where $K\in \mathbb {R}^{m \times p}$ and $v\in L^{\infty }_{ loc }(\mathbb {R}_+,\mathbb {R}^m)$, is described by the triple $(A+BKC,B,C)\in \Sigma$. The associated transfer function is

$$\begin{aligned} G^K(s):=C(sI-A-BKC)^{-1}B=G(s)(I-KG(s))^{-1}. \end{aligned}$$

We denote the set of stabilizing output feedback matrices for (A, B, C) by $\mathbb {S}_{\mathbb {F}}(A,B,C)$, that is,

$$\begin{aligned} \mathbb {S}_{\mathbb {F}}(A,B,C):=\{K\in \mathbb {F}^{m \times p}: A+BKC\, \text{ is } \text{ Hurwitz }\}, \end{aligned}$$

where $\mathbb {F}=\mathbb {R}$ or $\mathbb {F}=\mathbb {C}$, and we will be speaking of real or complex stabilizing output feedback matrices, respectively. Moreover, defining

$$\begin{aligned} \mathbb {S}_{\mathbb {F}}(G):=\{K\in \mathbb {F}^{m \times p}: G^K \in H^{\infty }(\mathbb {C}^{p \times m})\}, \end{aligned}$$

we have that

$$\begin{aligned} \mathbb {S}_{\mathbb {F}}(A,B,C)\subseteq \mathbb {S}_{\mathbb {F}}(G). \end{aligned}$$

(2.2)

If $\mathbb {S}_{\mathbb {F}}(A,B,C)\not =\emptyset$, then (A, B, C) is stabilizable and detectable and equality holds in (2.2).

The following lemma provides some simple properties of linear output feedback.

Lemma 2.1

Let $(A, B, C)\in \Sigma$ with transfer function G, let $K\in \mathbb {C}^{m \times p}$ and let $r>0$.

• (a) $\mathbb {S}_{\mathbb {C}} \left( G\right) -K = \mathbb {S}_{\mathbb {C}} \left( G^K\right)$.

• (b) $\mathbb {B}_{\mathbb {C}}(K,r) \subseteq \mathbb {S}_{\mathbb {C}} \left( G\right)$ if, and only if, $\mathbb {B}_{\mathbb {C}}(0, r) \subseteq \mathbb {S}_{\mathbb {C}} \left( G^K\right)$.

• (c) $(G^K)^L= G^{K+L}$ for all $L\in \mathbb {C}^{m \times p}$.

• (d) $\mathbb {B}_{\mathbb {C}}(K, r) \subseteq \mathbb {S}_{\mathbb {C}} \left( G\right)$ if, and only if, $\left\| G^K\right\| _{H^{\infty }} \le 1/r$.

Assume that, in Lemma 2.1, the matrix K is real, that is, $K\in \mathbb {R}^{m \times p}$. Then statements (a) and (b) and the sufficiency part of statement (d) remain valid if $\mathbb {B}_\mathbb {C}$ and $\mathbb {S}_\mathbb {C}$ are replaced by $\mathbb {B}_\mathbb {R}$ and $\mathbb {S}_\mathbb {R}$, respectively. However, the condition $\mathbb {B}_\mathbb {R}(K,r)\subseteq \mathbb {S}_\mathbb {R}(G)$ does not imply that $\left\| G^K\right\| _{H^{\infty }} \le 1/r$.

Proof of Lemma 2.1

The proofs of statements (a)–(c) are straightforward and are therefore omitted.

We proceed to prove statement (d). Assuming that $\left\| G^K\right\| _{H^{\infty }} \le 1/r$, it is clear that $\mathbb {B}_{\mathbb {C}}(0,r) \subseteq \mathbb {S}_{\mathbb {C}} \left( G^K\right)$ (by the “small-gain theorem”). Hence, by statement (b), $\mathbb {B}_{\mathbb {C}}(K,r) \subseteq \mathbb {S}_{\mathbb {C}} \left( G\right)$.

We prove the reverse implication by contraposition. To this end, assume $\left\| G^K\right\| _{H^{\infty }}>1/r$. We have to show that there exists $L\in \mathbb {B}_{\mathbb {C}}(K,r)$ such that $L\not \in \mathbb {S}_{\mathbb {C}} \left( G\right)$. By assumption, $\left\| G^K(z)\right\| > 1/r$ for some $z\in \mathbb {C}_+$. As is well known from matrix theory, there exists $M\in \mathbb {C}^{m \times p}$ with $\left\| M\right\| = 1/{\left\| G^K(z)\right\| }< r$ and $\det (I - MG^K(z)) = 0$. Now

$$\begin{aligned} M(G^K)^M=MG(I-MG^K)^{-1}=(I-MG^K)^{-1}-I, \end{aligned}$$

and we conclude that $M(G^K)^M$ has a pole at z. Setting $L:=K+M$ and using statement (c), we see that $G^L=G^{K+M}=(G^K)^M$ has a pole at z, showing that $L\not \in \mathbb {S}_{\mathbb {C}} \left( G\right)$. Obviously, $L\in \mathbb {B}_{\mathbb {C}}(K,r)$, completing the proof of statement (d). $\Box$

Next we state a version of the well-known bounded real lemma which is convenient for our purposes.

Lemma 2.2

Let $(A, B, C)\in \Sigma$. Assume that A is Hurwitz and that the transfer function G of (A, B, C) satisfies $\left\| G\right\| _{H^{\infty }} \le 1$. Then there exist a positive semi-definite matrix $P = P^* \in \mathbb {R}^{n \times n}$ and a matrix $L\in \mathbb {R}^{m\times n}$ such that

$$\begin{aligned} A^*P + PA = - C^*C - L^*L \quad \text{ and }\quad PB = - L^*. \end{aligned}$$

Proof

By elementary stability radius theory, $r_{\mathbb {C}}(A;B,C)=1/\left\| G\right\| _{H^{\infty }}\ge 1$, see [8, 10]. Hence, by [8, Theorem 3.3], there exists a matrix $Q = Q^* \in \mathbb {R}^{n \times n}$ which solves the algebraic Riccati equation

$$\begin{aligned} A^*Q + QA - C^*C - QBB^*Q = 0. \end{aligned}$$

Setting $P := - Q$ and $L := -B^*P$, it follows that P solves the Lyapunov matrix equation

$$\begin{aligned} A^*P + PA = -C^*C - L^*L. \end{aligned}$$

(2.3)

Since A is Hurwitz, (2.3) has a unique solution which is given by

$$\begin{aligned} P = \int _0^{\infty } e^{A^*t}(C^*C + L^*L)e^{At} \mathrm{d}t, \end{aligned}$$

see, for example [10, Corollary 3.3.46]. Obviously, the matrix $C^*C + L^*L$ is positive semi-definite and it follows that P is positive semi-definite, completing the proof. $\square$

In the following, we will consider linear systems of the form

$$\begin{aligned} \dot{x}= Ax+ Bu+B_\mathrm{e}v,\quad y=Cx \end{aligned}$$

(2.4)

where

$$\begin{aligned} (A,B,B_\mathrm{e},C)\in \Sigma _\mathrm{e}:=\mathbb {R}^{n\times n}\times \mathbb {R}^{n\times m}\times \mathbb {R}^{n\times m_\mathrm{e}} \times \mathbb {R}^{p\times n} \end{aligned}$$

It is convenient to define the behaviour $\mathcal {B}(A, B, B_\mathrm{e}, C)$ of (2.4) (or of the quadruple $(A,B,B_\mathrm{e}, C)$) by

$$\begin{aligned} \mathcal {B}(A, B,B_\mathrm{e}, C):=\{(v,u,x,y) \in \mathcal {T}:(v,u,x,y)\, \text{ satisfies }\,(2.4)\}, \end{aligned}$$

where

$$\begin{aligned} \mathcal {T:=}\,L^{\infty }_{ loc }(\mathbb {R}_+,\mathbb {R}^{m_\mathrm{e}}) \times L^{\infty }_{ loc }(\mathbb {R}_+,\mathbb {R}^m) \times W^{1,1}_{ loc }(\mathbb {R}_+,\mathbb {R}^n) \times C(\mathbb {R}_+,\mathbb {R}^p). \end{aligned}$$

Obviously, in the above definition of $\mathcal {B}(A, B, B_\mathrm{e}, C)$, the solution x of the differential equation in (2.4) has to be understood in the sense of Carathéodory. A triple (v, u, x, y) is in $\mathcal {B}(A, B, B_\mathrm{e}, C)$ if, and only if,

$$\begin{aligned} x(t) = e^{At}x(0) + \int _0^t e^{A(t-s)}\big (B u(s)+B_\mathrm{e}v(s)\big ) d s\quad \forall \,t\ge 0 \end{aligned}$$

and $y=Cx$.

We now use the bounded real lemma to obtain a quadratic form useful in stability analysis.

Proposition 2.3

Let $(A, B, B_\mathrm{e}, C)\in \Sigma _\mathrm{e}$ and assume that $\mathbb {B}_{\mathbb {C}}(K, r) \subseteq \mathbb {S}_{\mathbb {C}} \left( A,B,C\right)$, where $K \in \mathbb {R}^{m \times p}$ and $r > 0$. Then there exists positive semi-definite $P = P^* \in \mathbb {R}^{n \times n}$ with the following property: for every $\alpha \in \mathcal {K}_\infty$, there exists $\beta \in \mathcal {K}_\infty$, such that, for every $(v,u,x,y)\in \mathcal {B}(A, B, B_\mathrm{e}, C)$, the function $V :\mathbb {R}^n \rightarrow \mathbb {R}_+$ defined by $V(\zeta ):= \left\langle P\zeta , \zeta \right\rangle$ satisfies

$$\begin{aligned} \frac{ d }{ d t}V(x(t)) \le - r^2\left\| y(t)\right\| ^2+\left\| u(t)-Ky(t)\right\| ^2+\Vert x(t)\Vert \alpha (\Vert x(t)\Vert )+\beta (\Vert v(t)\Vert ) \end{aligned}$$

for almost every $t\ge 0$.

For the proof of this result, the following simple lemma will be useful.

Lemma 2.4

If $\alpha \in \mathcal {K}_{\infty }$, then there exists $\beta \in \mathcal {K}_{\infty }$ such that

$$\begin{aligned} s_1s_2 \le s_1 \alpha (s_1) + \beta (s_2)\quad \forall \,s_1, s_2 \ge 0. \end{aligned}$$

Proof

If $s_2 \le \alpha (s_1)$, then $s_1s_2 \le s_1 \alpha (s_1)$; and if $s_2 > \alpha (s_1)$, then $s_1 < \alpha ^{-1}(s_2)$, so that $s_1s_2 < s_2 \alpha ^{-1}(s_2)$. Hence $\beta (s_2) := s_2 \alpha ^{-1}(s_2)$ satisfies all the requirements. $\square$

Proof of Proposition 2.3

Set $A_K:=A+BKC$, and consider the system $(A_K, rB, C)$, the transfer function of which is $rG^K$, where $G(s)=C(sI-A)^{-1}B$. By hypothesis,

$$\begin{aligned} \mathbb {B}_{\mathbb {C}}(K, r) \subseteq \mathbb {S}_{\mathbb {C}} \left( A,B,C\right) =\mathbb {S}_{\mathbb {C}} \left( G\right) . \end{aligned}$$

Hence, $A_K$ is Hurwitz and, furthermore, it follows from statement (d) of Lemma 2.1 that, $r\left\| G^K\right\| _{H^\infty }\le 1$. An application of Lemma 2.2 to the system $(A_K, rB, C)$ shows that there exist a positive semi-definite matrix $Q=Q^* \in \mathbb {R}^{n \times n}$ and a matrix $L\in \mathbb {R}^{m\times n}$ such that

$$\begin{aligned} A_K^*Q + QA_K = - C^*C - L^*L\quad \text{ and }\quad rQB = - L^*. \end{aligned}$$

(2.5)

Define the quadratic form U by $U(\zeta ) := \left\langle Q\zeta , \zeta \right\rangle$ for all $\zeta \in \mathbb {R}^n$. Let $(v,u, x, y) \in \mathcal {B}(A, B, B_\mathrm{e}, C)$ be arbitrary. Writing $w:=u-Ky$, then, trivially, the quadruple $(v, w, x, y)\in \mathcal {B}(A_K, B, B_\mathrm{e}, C)$ and we obtain that, for almost every $t\ge 0$,

$$\begin{aligned} \frac{ d }{ d t}U(x(t))&= 2\left\langle Qx(t), A_Kx(t) + Bw(t)+B_\mathrm{e}v(t) \right\rangle \\&= \left\langle (A_K^*Q + QA_K)x(t), x(t) \right\rangle +2\left\langle x(t), QBw(t) \right\rangle \\&\quad +2\left\langle Qx(t), B_\mathrm{e}v(t) \right\rangle . \end{aligned}$$

Setting $c:=2\Vert Q\Vert \Vert B_\mathrm{e}\Vert$ and invoking (2.5), it follows that, for almost every $t\ge 0$,

$$\begin{aligned} \frac{ d }{ d t}U(x(t)) \le&- \left\| Cx(t)\right\| ^2 - \left\| Lx(t)\right\| ^2 - \frac{2}{r}\left\langle Lx(t), w(t) \right\rangle +c\Vert x(t)\Vert \Vert v(t)\Vert \\ =&- \left\| y(t)\right\| ^2 - \left\| Lx(t) + \frac{1}{r} w(t)\right\| ^2 + \frac{1}{r^2}\left\| w(t)\right\| ^2 +c\Vert x(t)\Vert \Vert v(t)\Vert . \end{aligned}$$

By Lemma 2.4, for a given $\alpha \in \mathcal {K}_{\infty }$, there exists $\beta \in \mathcal {K}_{\infty }$ such that

$$\begin{aligned} r^2 cs_1s_2\le s_1 \alpha (s_1) + \beta (s_2) \qquad \forall \,s_1, s_2 \ge 0. \end{aligned}$$

Consequently, for almost every $t\ge 0$,

$$\begin{aligned} \frac{ d }{ d t}U(x(t))\le - \left\| y(t)\right\| ^2+\frac{1}{r^2}\left( \left\| u(t)-Ky(t)\right\| ^2+\Vert x(t)\Vert \alpha (\Vert x(t)\Vert ) +\beta (\Vert v(t)\Vert )\right) . \end{aligned}$$

The claim now follows with $P:=r^2Q$. $\square$

The next proposition (inspired by [1]) gurantees the existence of another quadratic form which will be useful in the ISS analysis of Lur’e systems

Proposition 2.5

Let $(A, B,B_\mathrm{e}, C)\in \Sigma _\mathrm{e}$ and assume that the pair (A, C) is detectable. Then there exists a positive-definite matrix $P= P^* \in \mathbb {R}^{n \times n}$ and $\delta >0$ such that, for every $(v,u, x, y) \in \mathcal {B}(A, B, B_\mathrm{e}, C)$, the function $V: \mathbb {R}^n \rightarrow \mathbb {R}_+$ defined by $V(\zeta ):= \left\langle P\zeta , \zeta \right\rangle$ satisfies

$$\begin{aligned} \frac{ d }{ d t}V(x(t)) \le -\delta \left\| x(t)\right\| ^2 + \left\| y(t)\right\| ^2 + \left\| u(t)\right\| ^2+\left\| v(t)\right\| ^2 \quad \text{ for } \text{ a.e. }\quad t\ge 0. \end{aligned}$$

Proof

By detectability of (A, C), there exists $H \in \mathbb {R}^{n \times p}$ such that $A+HC$ is Hurwitz. Consequently, there exists a (unique) positive-definite solution $Q = Q^*$ of the Lyapunov equation

$$\begin{aligned} (A+HC)^*Q + Q(A+HC) = -I, \end{aligned}$$

(2.6)

see, for example [10, Corollary 3.3.46]. Define the quadratic form U by $U(\zeta ) := \left\langle Q\zeta , \zeta \right\rangle$ and let $(v,u, x, y)\in \mathcal {B}(A, B, B_\mathrm{e}, C)$. Then

$$\begin{aligned} \frac{ d }{ d t}U(x(t)) = 2\left\langle Qx(t), \dot{x}(t) \right\rangle \quad \text{ for } \text{ a.e. }\quad t\ge 0. \end{aligned}$$

Setting $w:=Bu+B_\mathrm{e}v$ and invoking (2.6), we conclude that, for almost every $t\ge 0$,

$$\begin{aligned} \frac{ d }{ d t}U (x(t))&= \left\langle Qx(t), (A+HC)x(t) \right\rangle - \left\langle Qx(t), HCx(t) \right\rangle + \left\langle Qx(t), w(t) \right\rangle \\&\quad +\left\langle (A+HC)x(t), Qx(t) \right\rangle - \left\langle HCx(t), Qx(t) \right\rangle + \left\langle w(t), Qx(t) \right\rangle \\&= -\left\| x(t)\right\| ^2 - 2\left\langle Qx(t), Hy(t) \right\rangle + 2\left\langle Qx(t), w(t) \right\rangle . \end{aligned}$$

An application of the Cauchy–Schwarz inequality and subsequent use of the elementary inequality $ab\le a^2/c^2 + c^2b^2$ (which is valid for all real a, b and c, $c\not =0$) show that there exist positive constants $c_1, c_2, c_3$ and $c_4$ such that, for all $(v, u, x, y)\in \mathcal {B}(A, B, B_\mathrm{e}, C)$,

$$\begin{aligned} \frac{ d }{ d t}U (x(t)) \le -c_1\left\| x(t)\right\| ^2 + c_2 \left\| y(t)\right\| ^2 + c_3 \left\| u(t)\right\| ^2&+c_4 \left\| v(t)\right\| ^2\\&\quad \text{ for } \text{ a.e. }\quad t\ge 0. \end{aligned}$$

Setting $c_5:=1/\max \{c_2,c_3,c_4\}$, the claim follows with $P=c_5Q$ and $\delta :=c_1c_5$. $\square$

3 ISS of Lur’e systems

In this section, we will apply the results provided in Sect. 2 to prove ISS properties for Lur’e systems of the form

$$\begin{aligned} \dot{x}(t) = Ax + Bf(Cx) + B_\mathrm{e}v, \end{aligned}$$

(3.1)

where $(A,B,B_\mathrm{_e}, C)\in \Sigma _\mathrm{e}$, $f:\mathbb {R}^p\rightarrow \mathbb {R}^m$ is locally Lipschitz and $v\in L^\infty _\mathrm{loc}(\mathbb {R}_+,\mathbb {R}^{m_\mathrm{e}})$ is the control (forcing, input) function. Obviously, (3.1) can (and should) be thought of as the feedback system given by

$$\begin{aligned} \dot{x}= Ax+Bu+B_\mathrm{e}v,\quad y=Cx;\quad u=f(y). \end{aligned}$$

Frequently, we shall refer to (3.1) as the Lur’e system $(A,B,B_\mathrm{e}, C,f)$.

It is convenient to define the behaviour $\mathcal {B}(A, B, B_\mathrm{e}, C,f)$ of (3.1) (or of the Lure’e system $(A,B,B_\mathrm{e}, C,f)$) by

$$\begin{aligned} \mathcal {B}(A, B, B_\mathrm{e}, C,f):= & {} \Big \{(v, x) \in L^{\infty }_{ loc }(\mathbb {R}_+, \mathbb {R}^{m_\mathrm{e}}) \times W^{1,1}_\mathrm{loc}(\mathbb {R}_+,\mathbb {R}^n):\\&\qquad (v,x)\,\text{ satisfies }\, (3.1)\,\text{ a.e. } \text{ on }\,\mathbb {R}_+\Big \}. \end{aligned}$$

This definition may seem restrictive, since only trajectories defined on the whole half-line $\mathbb {R}_+$ are included in the behaviour. However, in the following, we will impose an assumption on f which implies that f is linearly bounded, and hence, for every initial condition $x(0)=x^0$ and every $v\in L^{\infty }_{ loc }(\mathbb {R}_+,\mathbb {R}^{m_\mathrm{e}})$, there exists a unique absolutely continuous solution of (3.1) which is defined on $\mathbb {R}_+$.

The following lemma is obvious and does not require a proof.

Lemma 3.1

Let $(A, B, B_\mathrm{e}, C)\in \Sigma _\mathrm{e}$, let $f:\mathbb {R}^p\rightarrow \mathbb {R}^m$ be locally Lipschitz and let $(v,x)\in L^{\infty }_\mathrm{loc}(\mathbb {R}_+,\mathbb {R}^{m_\mathrm{e}}) \times W^{1,1}_\mathrm{loc}(\mathbb {R}_+,\mathbb {R}^n)$. Then $(v, x) \in \mathcal {B}(A, B, B_\mathrm{e}, C,f)$ if, and only if, $(v,f \circ Cx, x, Cx) \in \mathcal {B}(A, B, B_\mathrm{e}, C)$.

The Lur’e system (3.1) (or the quintuple $(A,B, B_\mathrm{e}, C,f)$) is said to be input-to-state stable (ISS) if there exist $\psi \in \mathcal {KL}$ and $\varphi \in \mathcal {K}$ such that, for all $(v, x) \in \mathcal {B}(A, B, B_\mathrm{e}, C, f)$,

$$\begin{aligned} \left\| x(t)\right\| \le \psi (\left\| x(0)\right\| , t) + \varphi (\left\| v\right\| _{L^\infty (0,t)}) \quad \forall \,t\ge 0. \end{aligned}$$

(3.2)

The concept of ISS (for a general controlled nonlinear system) appeared first in [23]. For overviews of ISS theory, we refer the reader to [3, 25].

We say that two functions $V_1,V_2:\mathbb {R}^n \rightarrow \mathbb {R}_+$ are $\mathcal {K}_{\infty }$-equivalent if there exist $\alpha _1,\alpha _2\in \mathcal {K}_{\infty }$ such that $\alpha _1(V_1(\zeta )) \le V_2(\zeta ) \le \alpha _2(V_1(\zeta ))$ for all $\zeta \in \mathbb {R}^n$. A continuously differentiable function $V:\mathbb {R}^n \rightarrow \mathbb {R}_+$ is said to be an ISS-Lyapunov function for (3.1) (or for $(A, B, B_\mathrm{e}, C,f)$) if V and $\left\| \cdot \right\| _{\mathbb {R}^n}$ are $\mathcal {K}_{\infty }$-equivalent and there exist $\beta ,\gamma \in \mathcal {K}_{\infty }$ such that, for all $(v, x) \in \mathcal {B}(A,B, B_\mathrm{e},C,f)$,

$$\begin{aligned} \frac{ d }{ d t}V(x(t)) \le -\beta (\left\| x(t)\right\| ) + \gamma (\left\| v(t)\right\| ) \quad \text{ for } \text{ a.e. }\quad t\ge 0 \end{aligned}$$

It is a well-known result in ISS theory (see, for example [25]) that the existence of an ISS-Lyapunov function guarantees ISS.

We are now ready to state and prove the main result of this paper.

Theorem 3.2

Let $(A, B, B_\mathrm{e}, C)\in \Sigma _\mathrm{e}$, $f:\mathbb {R}^p\rightarrow \mathbb {R}^m$ be locally Lipschitz, $r > 0$ and $K \in \mathbb {R}^{m \times p}$. If $\mathbb {B}_{\mathbb {C}}(K, r) \subseteq \mathbb {S}_{\mathbb {C}} \left( A,B,C\right)$ and there exists $\alpha \in \mathcal {K}_{\infty }$ such that

$$\begin{aligned} \left\| f(\xi ) - K\xi \right\| \le r \left\| \xi \right\| - \alpha (\left\| \xi \right\| ) \quad \forall \,\xi \in \mathbb {R}^p, \end{aligned}$$

(3.3)

then the Lur’e system $(A, B, B_\mathrm{e}, C,f)$ is ISS.

In particular, if A is Hurwitz, then the Lur’e system $(A, B, B_\mathrm{e}, C,f)$ is ISS, provided that there exists $\alpha \in \mathcal {K}_{\infty }$ such that $\left\| f(\xi )\right\| \le r\left\| \xi \right\| - \alpha (\left\| \xi \right\| )$ for all $\xi \in \mathbb {R}^p$, where $r=r_{\mathbb {C}}(A;B,C)$. This shows that the complex stability radius $r_{\mathbb {C}}(A;B,C)$ provides a measure of the robustness of ISS of the linear system $\dot{x}=Ax+B_\mathrm{e}v$ with respect to additive nonlinear perturbations F of the form $F(x)=Bf(Cx)$.

Proof of Theorem 3.2

It is sufficient to show that there exists an ISS-Lyapunov function for $(A, B, B_\mathrm{e}, C, f)$. This will be done by constructing two functions V and W and then showing that $V+W$ is an ISS-Lyapunov function.

Since $\mathbb {B}_{\mathbb {C}}(K, r)\subseteq \mathbb {S}_{\mathbb {C}} \left( A,B,C\right)$, it is clear that the system (A, B, C) is stabilizable and detectable. Proposition 2.5 guarantees the existence of a positive definite $Q = Q^* \in \mathbb {R}^{n \times n}$ and a positive $\delta >0$ such that, for every $(v,u,x,y)\in \mathcal {B}(A, B, B_\mathrm{e}, C)$, the function $U_0: \mathbb {R}^n \rightarrow \mathbb {R}_+$ defined by $U_0(\zeta ):= \left\langle Q\zeta , \zeta \right\rangle$ satisfies

$$\begin{aligned} \frac{ d }{ d t}U_0(x(t)) \le - \delta \left\| x(t)\right\| ^2 + \left\| y(t)\right\| ^2 + \left\| u(t)\right\| ^2+\left\| v(t)\right\| ^2 \quad \text{ for } \text{ a.e. }\quad t\ge 0. \end{aligned}$$

Let $(v,x) \in \mathcal {B}(A, B, B_\mathrm{e}, C, f)$. Then, by Lemma 3.1, $(v, f\circ Cx, x, Cx) \in \mathcal {B}(A, B, B_\mathrm{e}, C, f)$, and thus

$$\begin{aligned} \frac{ d }{ d t}U_0(x(t)) \le - \delta \left\| x(t)\right\| ^2 + \left\| Cx(t)\right\| ^2 + \left\| f(Cx(t))\right\| ^2+\left\| v(t)\right\| ^2 \quad \text{ for } \text{ a.e. }\quad t\ge 0. \end{aligned}$$

(3.4)

By (3.3),

$$\begin{aligned} \Vert f(\xi )\Vert ^2\le c_0\Vert \xi \Vert ^2\quad \forall \,\xi \in \mathbb {R}^p, \end{aligned}$$

where $c_0:=2(\Vert K\Vert ^2+r^2)$. Setting

$$\begin{aligned} U:=\frac{1}{1+c_0}U_0 \quad \text{ and }\quad \varepsilon :=\frac{\delta }{1+c_0}, \end{aligned}$$

it then follows from (3.4) that, for every $(v,x) \in \mathcal {B}(A, B, B_\mathrm{e}, C, f)$,

$$\begin{aligned} \frac{ d }{ d t}U(x(t))\le - \varepsilon \left\| x(t)\right\| ^2 + \left\| Cx(t)\right\| ^2 + \left\| v(t)\right\| ^2 \quad \text{ for } \text{ a.e. }\quad t\ge 0. \end{aligned}$$

(3.5)

It is convenient to define constants

$$\begin{aligned} c_1:=r\sqrt{\varepsilon /2},\quad c_2:=\sqrt{\varepsilon /2},\quad c_3:=\Vert C\Vert ^2 \end{aligned}$$

and to choose positive constants $c_4$ and $c_5$ such that

$$\begin{aligned} c_4\Vert \zeta \Vert \le \sqrt{U(\zeta )}\le c_5\Vert \zeta \Vert \quad \forall \,\zeta \in \mathbb {R}^n, \end{aligned}$$

(3.6)

with

$$\begin{aligned} c_4=\frac{1}{\sqrt{(1+c_0)\Vert Q^{-1}\Vert }}\quad \text{ and }\quad c_5=\sqrt{\frac{\Vert Q\Vert }{1+c_0}} \end{aligned}$$

being a possible choice.

Furthermore, we define $\mu :\mathbb {R}_+\rightarrow \mathbb {R}_+$ by

$$\begin{aligned} \mu (s):=\frac{\varepsilon }{4}\min \left\{ c_4^2s^3,\frac{c_1c_4\alpha (c_2c_4s/c_5)}{c_3c_5}\right\} \quad \forall \,s\ge 0, \end{aligned}$$

where $\alpha$ is the $\mathcal {K}_{\infty }$-function from (3.3), the existence of which is part of the hypothesis. It is obvious that $\mu \in \mathcal {K}_{\infty }$. By Proposition 2.3, there exist positive semi-definite $P = P^* \in \mathbb {R}^{n \times n}$ and $\beta \in \mathcal {K}_{\infty }$ such that, for every $(v,u,x,y)\in \mathcal {B}(A, B, B_\mathrm{e}, C)$, the function $V :\mathbb {R}^n\rightarrow \mathbb {R}_+$ defined by $V(\zeta ): = \left\langle P\zeta , \zeta \right\rangle$ satisfies

$$\begin{aligned} \frac{ d }{ d t}V(x(t))&\le - r^2\left\| y(t)\right\| ^2 +\left\| u(t)-Ky(t)\right\| ^2+\Vert x(t)\Vert \mu (\Vert x(t)\Vert )\\&\quad +\beta (\Vert v(t)\Vert )\quad \text{ for } \text{ a.e. }\quad t\ge 0 \end{aligned}$$

Let $(v,x)\in \mathcal {B}(A, B, B_\mathrm{e}, C,f)$. Then, by Lemma 3.1, $(v,f\circ Cx,x,Cx)\in \mathcal {B}(A, B, B_\mathrm{e}, C)$, and thus,

$$\begin{aligned} \frac{ d }{ d t}V(x(t))&\le - r^2\left\| Cx(t)\right\| ^2 + \left\| f(Cx(t))-KCx(t)\right\| ^2 +\Vert x(t)\Vert \mu (\Vert x(t)\Vert )\nonumber \\&\quad +\beta (\Vert v(t)\Vert )\quad \text{ for } \text{ a.e. }\quad t\ge 0. \end{aligned}$$

(3.7)

Invoking (3.3), we have

$$\begin{aligned} \left\| f(\xi ) - K\xi \right\| ^2 - r^2\left\| \xi \right\| ^2 \le -2\alpha (\left\| \xi \right\| )r\left\| \xi \right\| + \alpha ^2(\left\| \xi \right\| ) \quad \forall \,\xi \in \mathbb {R}^p. \end{aligned}$$

Inequality (3.3) implies in particular that $\alpha (s)\le rs$ for all $s\ge 0$, and so

$$\begin{aligned} \left\| f(\xi ) - K\xi \right\| ^2 - r^2\left\| \xi \right\| ^2\le -r\left\| \xi \right\| \alpha (\left\| \xi \right\| ) \quad \forall \,\xi \in \mathbb {R}^p. \end{aligned}$$

Using this estimate in (3.7), we obtain

$$\begin{aligned} \frac{ d }{ d t}V(x(t))&\le - r\left\| Cx(t)\right\| {}\alpha (\left\| Cx(t)\right\| ) +\Vert x(t)\Vert \mu (\Vert x(t)\Vert )\nonumber \\&\,\quad +\beta (\Vert v(t)\Vert )\quad \text{ for } \text{ a.e. }\quad t\ge 0. \end{aligned}$$

(3.8)

We will now “adjust” U by composing it with a suitable function h, that is, we will be considering

$$\begin{aligned} W:=h\circ U. \end{aligned}$$

The function $h:\mathbb {R}_+\rightarrow \mathbb {R}_+$ is given by

$$\begin{aligned} h(s)=\int _0^sk(\sigma ) d \sigma \quad \forall \,s\ge 0, \end{aligned}$$

where $k:\mathbb {R}_+\rightarrow \mathbb {R}_+$ is defined as follows:

$$\begin{aligned} k(0):=0\quad \text{ and }\quad k(s):=\min \left\{ s, \frac{c_1c_4\alpha (c_2\sqrt{s}/c_5)}{c_3\sqrt{s}}\right\} \quad \forall \,s>0. \end{aligned}$$

Obviously, h is continuously differentiable and

$$\begin{aligned} 0\le h'(s)=k(s)\le \frac{rc_1c_2c_4}{c_3c_5}=:c_6\quad \forall \,s\ge 0, \end{aligned}$$

(3.9)

where we have used again that $\alpha (s)\le rs$ for all $s\ge 0$.

We claim that

$$\begin{aligned} h'(U(\zeta ))\big (-\varepsilon \Vert \zeta \Vert ^2+\Vert C\zeta \Vert ^2\big )\le -2\Vert \zeta \Vert \mu (\Vert \zeta \Vert )+ r\Vert C\zeta \Vert \alpha (\Vert C\zeta \Vert )\quad \forall \,\zeta \in \mathbb {R}^n. \end{aligned}$$

(3.10)

To avoid breaking the flow of the argument, we relegate the verification of (3.10) to the end of the proof.

Invoking (3.5), it follows that, for every $(v,x) \in \mathcal {B}(A, B, B_\mathrm{e}, C, f)$,

$$\begin{aligned} \frac{ d }{ d t}W(x(t))&= \frac{ d }{ d t}h\big (U(x(t))\big )\le h'\big (U(x(t))\big )\big [- \varepsilon \left\| x(t)\right\| ^2 +\left\| Cx(t)\right\| ^2\\&\quad + \left\| v(t)\right\| ^2\big ] \quad \text{ for } \text{ a.e. }\quad t\ge 0. \end{aligned}$$

Combining this with (3.10) shows that, for every $(v,x) \in \mathcal {B}(A, B, B_\mathrm{e}, C, f)$,

$$\begin{aligned} \frac{ d }{ d t}W(x(t))&\le -2\Vert x(t)\Vert \mu (\Vert x(t)\Vert )+r\Vert Cx(t)\Vert \alpha (\Vert Cx(t)\Vert ) +c_6\left\| v(t)\right\| ^2\nonumber \\&\quad \quad \text{ for } \text{ a.e. }\quad t\ge 0, \end{aligned}$$

(3.11)

where we have used (3.9). Defining $\gamma \in \mathcal {K}_{\infty }$ by $\gamma (s): =\beta (s)+c_6s^2$ for all $s\ge 0$, it follows from (3.8) and (3.11) that, for every $(v,x) \in \mathcal {B}(A, B, B_\mathrm{e}, C, f)$,

$$\begin{aligned} \frac{ d }{ d t}(V+W)(x(t))\le -\Vert x(t)\Vert \mu (\Vert x(t)\Vert )+\gamma (\Vert v(t)\Vert )\quad \text{ for } \text{ a.e. }\quad t\ge 0. \end{aligned}$$

(3.12)

Consequently, if $V+W$ and $\left\| \cdot \right\| _{\mathbb {R}^n}$ are $\mathcal {K}_{\infty }$-equivalent, then $V+W$ is an ISS-Lyapunov function for $(A, B, B_\mathrm{e}, C, f)$. To show that $V+W$ and $\left\| \cdot \right\| _{\mathbb {R}^n}$ are $\mathcal {K}_{\infty }$-equivalent, note that

$$\begin{aligned} (V+W)(\zeta )\le c_7\Vert \zeta \Vert ^2=\eta _1(\Vert \zeta \Vert )\quad \forall \,\zeta \in \mathbb {R}^n, \end{aligned}$$

(3.13)

where $c_7:=\Vert P\Vert +c_5^2c_6$ and $\eta _1\in \mathcal {K}_{\infty }$ is defined by $\eta _1(s):=c_7s^2$ for all $s\ge 0$. Moreover, noting that $h\in \mathcal {K}_{\infty }$, it is clear that $\eta _2$, defined by $\eta _2(s):=h(c_4^2s^2)$ for all $s\ge 0$, is also in $\mathcal {K}_{\infty }$, and it follows that

$$\begin{aligned} (V+W)(\zeta )\ge h(U(\zeta ))\ge h(c_4^2\Vert \zeta \Vert ^2)=\eta _2(\Vert \zeta \Vert )\quad \forall \, \zeta \in \mathbb {R}^n. \end{aligned}$$

(3.14)

Inequalities (3.13) and (3.14) show that $V+W$ and $\left\| \cdot \right\| _{\mathbb {R}^n}$ are $\mathcal {K}_{\infty }$-equivalent. We have now established that $V+W$ is an ISS-Lyapunov function for $(A, B, B_\mathrm{e}, C, f)$.

It only remains to prove that (3.10) holds. To this end, using (3.6), we estimate,

$$\begin{aligned} h'(U(\zeta ))=k(U(\zeta ))\le \frac{c_1\alpha (c_2\left\| \zeta \right\| )}{c_3\Vert \zeta \Vert } \quad \forall \,\zeta \in \mathbb {R}^n,\quad \zeta \not =0. \end{aligned}$$

Consequently,

$$\begin{aligned} c_3\Vert \zeta \Vert ^2h'(U(\zeta ))\le c_1\Vert \zeta \Vert \alpha (c_2\left\| \zeta \right\| )\quad \forall \,\zeta \in \mathbb {R}^n. \end{aligned}$$

(3.15)

We consider two cases.

Case a. If $\Vert C\zeta \Vert ^2>\varepsilon \Vert \zeta \Vert ^2/2$, then it follows from (3.15) and the definition of $c_1$, $c_2$ and $c_3$ that

$$\begin{aligned} \Vert C\zeta \Vert ^2h'(U(\zeta ))\le r\Vert C\zeta \Vert \alpha (c_2\left\| \zeta \right\| ) \le r\Vert C\zeta \Vert \alpha (\left\| C\zeta \right\| ). \end{aligned}$$

Case b. If $\Vert C\zeta \Vert ^2\le \varepsilon \Vert \zeta \Vert ^2/2$, then trivially,

$$\begin{aligned} \Vert C\zeta \Vert ^2h'(U(\zeta ))\le \frac{\varepsilon }{2}\Vert \zeta \Vert ^2h'(U(\zeta )). \end{aligned}$$

Therefore, we conclude

$$\begin{aligned} \Vert C\zeta \Vert ^2h'(U(\zeta ))\le \max \left\{ \frac{\varepsilon }{2}\Vert \zeta \Vert ^2h'(U(\zeta )), r\Vert C\zeta \Vert \alpha (\left\| C\zeta \right\| )\right\} \quad \forall \,\zeta \in \mathbb {R}^n. \end{aligned}$$

(3.16)

Furthermore, using again (3.6), we obtain

$$\begin{aligned} h'(U(\zeta ))=k(U(\zeta ))\ge \min \left\{ c_4^2\Vert \zeta \Vert ^2, \frac{c_1c_4\alpha (c_2c_4\Vert \zeta \Vert /c_5)}{c_3c_5\Vert \zeta \Vert }\right\} \quad \forall \,\zeta \in \mathbb {R}^n,\quad \zeta \not =0, \end{aligned}$$

implying that

$$\begin{aligned} 2\Vert \zeta \Vert \mu (\Vert \zeta \Vert )\le \frac{\varepsilon }{2}\Vert \zeta \Vert ^2h'(U(\zeta ))\quad \forall \,\zeta \in \mathbb {R}^n. \end{aligned}$$

(3.17)

Combination of (3.16) and (3.17) yields

$$\begin{aligned} h'(U(\zeta ))\Vert C\zeta \Vert ^2+ 2\Vert \zeta \Vert \mu (\Vert \zeta \Vert )\le \varepsilon \Vert \zeta \Vert ^2h'(U(\zeta )) +r\Vert C\zeta \Vert \alpha (\Vert C\zeta \Vert )\quad \forall \,\zeta \in \mathbb {R}^n, \end{aligned}$$

which is equivalent to (3.10), completing the proof. $\square$

The ISS property of the Lur’e system $(A,B,B_\mathrm{e},C,f)$, guaranteed by Theorem 3.2, means that there exist $\psi \in \mathcal {KL}$ and $\varphi \in \mathcal {K}$ such that the ISS estimate (3.2) holds for all $(v, x)\in \mathcal {B}(A, B, B_\mathrm{e}, C, f)$. As follows from ISS theory, the comparison functions $\psi$ and $\varphi$ depend only on the $\mathcal {K}_{\infty }$-functions $\mu$, $\gamma$, $\eta _1$ and $\eta _2$, see (3.12)–(3.14). These functions in turn depend only on A, B, $B_\mathrm{e}$, C, K, r and $\alpha$, but not on f. This means that, in the context of Theorem 3.2, there exist comparison functions $\psi \in \mathcal {KL}$ and $\varphi \in \mathcal {K}$ such that, for every f satisfying (3.3), the ISS estimate (3.2) holds. Furthermore, it can be shown that if $\alpha$ is linear, then we can choose $\psi$ and $\varphi$ as follows: $\psi (s,t)=Me^{-at}s$ and $\varphi (s)=bs$ for suitable constants $M\ge 1$ and $a,b>0$.

As the following example shows, Theorem 3.2 does not remain true if the condition on $\alpha$ is relaxed to $\alpha \in \mathcal {K}$.

Example 3.3

Define $\alpha \in \mathcal {K}{\setminus } \mathcal {K}_{\infty }$ by $\alpha (s) := 1 - e^{-s}$ and $f :\mathbb {R} \rightarrow \mathbb {R}$ by $f(\xi ) := \xi -$sgn$(\xi )\alpha (|\xi |)$. Consider the one-dimensional forced Lur’e system

$$\begin{aligned} \dot{x}(t) = -x(t) + f(x(t)) + v(t). \end{aligned}$$

Obviously, $-1 + k$ is Hurwitz for all $k\in \mathbb {C}$ with $|k| < 1$ and

$$\begin{aligned} |f(\xi )|=|\xi |-\alpha (|\xi |)\quad \forall \,\xi \in \mathbb {R}. \end{aligned}$$

Consequently, with the exception of the condition $\alpha (s)\rightarrow \infty$ as $s\rightarrow \infty$, the hypotheses of Theorem 3.2 are satisfied. Choosing $v(t) = 1 + \varepsilon$ for some positive $\varepsilon$, we have $\dot{x}(t) \ge \varepsilon$ for all $t \ge 0$ and hence the Lur’e system is not ISS. $\square$

We note that, in the unforced case ($v = 0$), the equilibrium 0 in Example 3.3 is globally asymptotically stable. In fact, it can be shown that if $\mathbb {B}_{\mathbb {C}}(K, r) \subseteq \mathbb {S}_{\mathbb {C}} \left( A, B, C\right)$, then, for any locally Lipschitz $f :\mathbb {R}^p \rightarrow \mathbb {R}^m$, satisfying $\left\| f(\xi ) - K\xi \right\| < r \left\| \xi \right\|$ for all $\xi \in \mathbb {R}^p{\setminus }\{0\}$, the equilibrium 0 of the unforced Lur’e system

$$\begin{aligned} \dot{x} = Ax + Bf(Cx) \end{aligned}$$

is globally asymptotically stable.

The following result identifies a class of Lur’e systems for which condition (3.3) does not hold and hence Theorem 3.2 does not apply. The result also shows that, under a mild additional assumption, these Lur’e systems are not ISS.

Proposition 3.4

Let $(A, B, B_\mathrm{e}, C)\in \Sigma _\mathrm{e}$, $f:\mathbb {R}^p\rightarrow \mathbb {R}^m$ be locally Lipschitz, $r > 0$ and $K \in \mathbb {R}^{m \times p}$. Assume that A is not Hurwitz, f is bounded and $\mathbb {B}_{\mathbb {C}}(K, r)\subseteq \mathbb {S}_{\mathbb {C}} \left( A,B,C\right)$. Then the following statements hold.

(a) There does not exist $\alpha \in \mathcal {K}_{\infty }$ such that $\Vert f(\xi )-K\xi \Vert \le r\Vert \xi \Vert -\alpha (\Vert \xi \Vert )$ for all $\xi \in \mathbb {R}^p$ (that is, condition (3.3) does not hold).

(b) Under the additional assumption that $\mathrm{im}\,B\subset \mathrm{im}\,B_\mathrm{e}$, the Lur’e system $(A, B, B_\mathrm{e}, C,f)$ is not ISS.

Proof

(a) Since A is not Hurwitz, it is clear that $r\le \Vert K\Vert$. Moreover,

$$\begin{aligned} r\Vert \xi \Vert -\Vert f(\xi )-K\xi \Vert \le r\Vert \xi \Vert -\Vert K\xi \Vert +\Vert f(\xi )\Vert \quad \forall \,\xi \in \mathbb {R}^p. \end{aligned}$$

Let $\xi _0\in \mathbb {R}^p$ be such that $\Vert \xi _0\Vert =1$ and $\Vert K\xi _0\Vert =\Vert K\Vert$. Then, for all $a\ge 0$, we have

$$\begin{aligned} r\Vert a\xi _0\Vert -\Vert f(a\xi _0)-K(a\xi _0)\Vert \le a(r-\Vert K\Vert )+\Vert f(a\xi _0)\Vert \le \sup _{\xi \in \mathbb {R}^p}\Vert f(\xi )\Vert <\infty , \end{aligned}$$

yielding the claim.

(b) We first prove the claim under the assumption that (A, B) is controllable. Let $z(\cdot \,;w)$ denote the solution of the initial value problem

$$\begin{aligned} \dot{z}=Az+Bw,\quad z(0)=0. \end{aligned}$$

Then there exists $w\in L^\infty (\mathbb {R}_+,\mathbb {R}^m)$ such that $x:=z(\cdot \,;w)$ is unbounded (because otherwise the linear system (A, B, I) would be bounded-input–bounded-output stable, and therefore, by controllability and observability of (A, B, I), A would be Hurwitz, which is not possible). By boundedness of f, we have that $w-f(Cx)\in L^\infty (\mathbb {R}_+,\mathbb {R}^m)$, and, since $\text{ im }\,B\subset \text{ im }\,B_\mathrm{e}$, there exists $v\in L^\infty (\mathbb {R}_+,\mathbb {R}^{m_\mathrm{e}})$ such that $B_\mathrm{e}v=B(w-f(Cx))$. Thus,

$$\begin{aligned} \dot{x}=Ax+Bw=Ax+Bf(Cx)+B_\mathrm{e}v. \end{aligned}$$

Since v is bounded and x is unbounded, it follows that the Lur’e system is not ISS.

If (A, B) is not controllable, then combining an argument similar to that used above with Kalman’s controllability decomposition yields the claim. $\square$

Results which are (vaguely) related to Proposition 3.4 can be found in [20], where it is shown that, under suitable assumptions, a “small” signal ISS property holds for Lur’e systems with nonlinearities of “saturation” type.

We now illustrate Theorem 3.2 by two examples.

Example 3.5

We consider a system modelling a sequence of linked chemical reactions inspired by [21]:

$$\begin{aligned} \left. \begin{aligned} \dot{z}_1&= g(z_3) - a_1z_1 + d_1, \\ \dot{z}_2&= z_1 - a_2z_2 + d_2, \\ \dot{z}_3&= z_2 - a_3z_3 + d_3, \end{aligned}\right\} \end{aligned}$$

(3.18)

where $z_1, z_2$ and $z_3$ represent the concentrations of reagents, $a_1$, $a_2$ and $a_3$ are positive constants, $d_1, d_2$ and $d_3$ represent external disturbances and the locally Lipschitz nonlinearity $g:\mathbb {R}_+\rightarrow \mathbb {R}_+$ represents inhibition of creation of reagent $z_1$ depending on the concentration of reagent $z_3$. The latter means that g is a decreasing function and hence g has negative derivative (provided that g is differentiable). The feedback loop corresponding to g, sometimes referred to as negative feedback, is common in metabolic control mechanisms, see Section 7.2 from [21]. Setting

$$\begin{aligned} A:= \begin{pmatrix} -a_1 &{}\quad 0 &{}\quad 0 \\ 1 &{}\quad -a_2 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad -a_3 \end{pmatrix},\quad B:= \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix},\quad C := \begin{pmatrix} 0&0&1 \end{pmatrix}, \end{aligned}$$

the system (3.18) can be written in the form

$$\begin{aligned} \dot{z}=Az+Bg(Cz)+d, \end{aligned}$$

(3.19)

where $z:=(z_1,z_2,z_3)^*$ and $d:=(d_1,d_2,d_3)^*$.

Note that $z_1, z_2$ and $z_3$ are naturally non-negative. Since A is a Metzler matrix (all off-diagonal entries are non-negative), B and C have non-negative entries and g maps $\mathbb {R}_+$ into $\mathbb {R}_+$, it is well known that, for non-negative initial conditions and for non-negative disturbances, the corresponding trajectories of (3.19) are non-negative (here vectors are referred to as non-negative if each component is non-negative).

The matrix A is Hurwitz and thus, the transfer function G of the single-input single-output system (A, B, C), given by $G(s)=C(sI-A)^{-1}B$, is bounded and holomorphic on $\mathbb {C}_+$. From a routine argument, it follows that

$$\begin{aligned} \Vert G\Vert _{H^\infty }=G(0)=\frac{1}{a_1a_2a_3}. \end{aligned}$$

Consequently, setting $r:=a_1a_2a_3>0$, we have

$$\begin{aligned} \mathbb {B}_{\mathbb {C}}(0, r)\subseteq \mathbb {S}_{\mathbb {C}} \left( A,B,C\right) . \end{aligned}$$

(3.20)

Since $g:\mathbb {R_+}\rightarrow \mathbb {R_+}$ is decreasing (and excluding the trivial case $g(\xi )\equiv 0$), it is clear that there exists a unique number $\xi ^\dagger >0$ such that $g(\xi ^\dagger )=r\xi ^\dagger$. A straightforward calculation shows that the vector

$$\begin{aligned} z^\dagger :=-A^{-1}br\xi ^\dagger =(a_2a_3\xi ^\dagger , a_3\xi ^\dagger ,\xi ^\dagger )^*\not =0 \end{aligned}$$

is the unique equilibrium of (3.19) with $d(t)\equiv 0$.

Before we can apply Theorem 3.2, we need to transform (3.19) in such a way that the equilibrium $z^\dagger$ is moved to the origin. To this end, define $f:\mathbb {R}\rightarrow \mathbb {R}$ by

$$\begin{aligned} f(\xi )=\left\{ \begin{array}{l l} g(\xi +\xi ^\dagger )-g(\xi ^\dagger )&{}\quad \text {for}\quad \xi \ge -\xi ^\dagger \\ g(0)-g(\xi ^\dagger )&{} \quad \text {for}\quad \xi <-\xi ^\dagger . \end{array}\right. \end{aligned}$$

Let z(0) and d be non-negative and let z be the corresponding (non-negative) solution z of (3.19). Defining the function x by $x(t)=z(t)-z^\dagger$, it follows that

$$\begin{aligned} \dot{x}=Ax+Bf(Cx)+d. \end{aligned}$$

(3.21)

We note that 0 is an equilibrium of (3.21) with $d(t)\equiv 0$. Furthermore, if (3.21) is ISS (with respect to the equilibrium 0), then (3.19) is ISS (with respect to the equilibrium $z^\dagger$) for non-negative disturbances d, that is, there exist $\psi \in \mathcal {KL}$ and $\varphi \in \mathcal {K}_{\infty }$ such that, for all $z(0)\in \mathbb {R}^3_+$ and non-negative $d\in L^\infty _\mathrm{loc}(\mathbb {R}_+, \mathbb {R}^3_+)$,

$$\begin{aligned} \left\| z(t) - z^\dagger \right\| \le \psi \left( \left\| z(0) - z^\dagger \right\| , t\right) + \varphi \left( \left\| d\right\| _{L^{\infty }(0, t)} \right) \quad \forall \, t \ge 0. \end{aligned}$$

(3.22)

Therefore, appealing to (3.20) and invoking Theorem 3.2, we may conclude that (3.19) is ISS, provided that there exists $\alpha \in \mathcal {K}_\infty$ such that

$$\begin{aligned} |g(\xi +\xi ^\dagger )-g(\xi ^\dagger )|\le r|\xi |-\alpha (|\xi |)\quad \forall \,\xi \ge -\xi ^\dagger . \end{aligned}$$

(3.23)

Let us consider a typical negative feedback nonlinearity g:

$$\begin{aligned} g(\xi ) := \frac{1}{1 + \xi }\quad \forall \,\xi \ge 0. \end{aligned}$$

(3.24)

It is easy to verify that, in this case,

$$\begin{aligned} |g(\xi +\xi ^\dagger )-g(\xi ^\dagger )|\le \frac{|\xi |}{1+\xi ^\dagger }\quad \forall \,\xi \ge -\xi ^\dagger . \end{aligned}$$

(3.25)

If $r>1/2$, then a routine calculation shows that $\xi ^\dagger <1$ and so,

$$\begin{aligned} \frac{1}{1+\xi ^\dagger }=g(\xi ^\dagger )=r\xi ^\dagger <r, \end{aligned}$$

showing that (3.23) holds with $\alpha$ given by $\alpha (s) =r(1-\xi ^\dagger )s$. Consequently, if g is given by (3.24), then (3.19) is ISS, provided that $r=a_1a_2a_3>1/2$. We mention that this conclusion can also be obtained by writing (3.21) in component form

$$\begin{aligned} \left. \begin{aligned} \dot{x}_1&= f(x_3) - a_1x_1 + d_1, \\ \dot{x}_2&= x_1 - a_2x_2 + d_2, \\ \dot{x}_3&= x_2 - a_3x_3 + d_3 \end{aligned}\right\} \end{aligned}$$

(3.26)

and applying a suitable nonlinear small-gain ISS theorem for feedback interconnections of several subsystems, see [4, Theorem 11] or [5, Corollary 5.6].¹ We will make more systematic contact with small-gain ideas further below (see Corollary 3.8 and the paragraph after the proof of Corollary 3.8).

To consider a specific numerical example, let g is given by (3.24) and choose $a_1=a_2=1$ and $a_3=3/5$. Then $r=a_1a_2a_3=3/5>1/2$ and hence (3.19) is ISS. Note that in this case $\xi ^{\dagger } =(\sqrt{69} - 3)/6$ and consequently $z^{\dagger } =\big ((\sqrt{69} - 3)/10, (\sqrt{69} - 3)/10, (\sqrt{69} - 3)/6\big )^*$. Simulations with initial state $z(0) = (1/2,1/2,1/2)^*$ and a range of disturbances are shown in Fig. 1.

Fig. 1

$\left\| z(t) - z^\dagger \right\| _2$ for different disturbances: $d^0(t) = 0$, $d^1(t) = (|\sin (t)|, |\sin (\sqrt{2}t)|, |\sin (\pi t)|)^*$, $d^2(t) = \frac{1}{2} d^1(t)$, $d^3(t) = \frac{1}{4} d^1(t)$, $d^4(t) = \frac{1}{8} d^1(t)$

Finally, to conclude the example, we mention that the above arguments establishing ISS also show that, if (3.22) holds, then, for all $z(0)\in \mathbb {R}_+^3$ and all disturbances $d\in L^\infty (\mathbb {R}_+,\mathbb {R}^3)$, possibly negative-valued, such that

$$\begin{aligned} \psi (\Vert z(0)-z^\dagger \Vert ,0)+\varphi (\Vert d\Vert&_{L^\infty (0,\infty )}) \le \min \{z^\dagger _j:j=1,2,3\}=:\mu ,\\&\text{ where }\,z^\dagger _j\,\text{ is } \text{ the }\, j\text{-th } \text{ component } \text{ of }\,z^\dagger , \end{aligned}$$

the solution z of (3.19) remains in the non-negative orthant for all times (or, equivalently, does not “escape” from the non-negative orthant in finite time). For example, if $\psi (\Vert z(0)-z^\dagger \Vert ,0)\le \mu /2$, then the solution z of (3.19) stays in $\mathbb {R}_+^3$ for all times in the presence of componentwise negative disturbances d satisfying $\varphi (\Vert d\Vert _{L^\infty (0,\infty )})\le \mu /2$.

$\square$

Example 3.5 is a single-input single-output system in the sense that $m=p=1$. In the following example, we consider a system with $m=2$ and $p=4$.

Example 3.6

Consider $(A, B, B_\mathrm{e}, C) \in \Sigma _\mathrm{e}$, where

$$\begin{aligned} A&= \begin{pmatrix} 0 &{}\quad 1&{}\quad 0 &{}\quad 0 \\ 3 &{}\quad 0 &{}\quad 0 &{}\quad 2 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \\ 0 &{}\quad -2 &{}\quad 0 &{}\quad 0 \end{pmatrix},\quad B = \begin{pmatrix} 0 &{}\quad 0 \\ 1 &{}\quad 0 \\ 0 &{}\quad 0 \\ 0 &{}\quad 1 \end{pmatrix},\quad C = \begin{pmatrix} 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \end{pmatrix} \end{aligned}$$

and $B_\mathrm{e} \in \mathbb {R}^{4 \times m_e}$, $B_\mathrm{e}\not =0$, is arbitrary. It is obvious that A is not Hurwitz and thus, the transfer function G of the minimal triple (A, B, C) is not in $H^{\infty }(\mathbb {C}^{4\times 2})$. A MATLAB calculation reveals that,

$$\begin{aligned} K := \begin{pmatrix} 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 15 &{}\quad -20/3 &{}\quad 4/3 &{}\quad 6\end{pmatrix}, \end{aligned}$$

is a stabilizing output feedback matrix and we have $\left\| G^K\right\| _{H^{\infty }} = 3.8383$. Therefore, by Lemma 2.1, there exists $r>1/4$ (for example, $r=10/39$) such that $\mathbb {B}_{\mathbb {C}}(K,r) \subseteq \mathbb {S}_{\mathbb {C}} \left( G\right) = \mathbb {S}_{\mathbb {C}} \left( A, B, C\right)$. Invoking Theorem 3.2, we conclude that the Lur’e system $(A, B, B_\mathrm{e}, C, f)$ is ISS for every locally Lipschitz $f:\mathbb {R}^4\rightarrow \mathbb {R}^2$ such that

$$\begin{aligned} \left\| f(\xi ) - K\xi \right\| \le \frac{1}{4} \left\| \xi \right\| \quad \forall \, \xi \in \mathbb {R}^4. \end{aligned}$$

(3.27)

To provide a specific example satisfying (3.27), consider the function $f:\mathbb {R}^4\rightarrow \mathbb {R}^2$ given by

$$\begin{aligned} f(\xi )=K\xi +\begin{pmatrix}\sin (\Vert \xi \Vert )/5\\ 3g(\xi )/20\end{pmatrix} \quad \forall \,\xi \in \mathbb {R}^4, \end{aligned}$$

where $g:\mathbb {R}^4\rightarrow \mathbb {R}$ is locally Lipschitz and such that $|g(\xi )|\le \Vert \xi \Vert$ for all $\xi \in \mathbb {R}^4$. Then

$$\begin{aligned} \Vert f(\xi )-K\xi \Vert =\sqrt{\frac{1}{25}\sin ^2(\Vert \xi \Vert )+\frac{9}{400} g^2(\xi )}<\frac{1}{4} \Vert \xi \Vert \quad \forall \,\xi \in \mathbb {R}^4,\quad \xi \not =0, \end{aligned}$$

implying that the Lur’e system $(A, B, B_\mathrm{e}, C, f)$ is ISS. $\square$

Theorem 3.2 says, roughly speaking, that linear stability (namely, $\mathbb {B}_{\mathbb {C}}(K, r) \subseteq \mathbb {S}_{\mathbb {C}} \left( A,B,C\right)$) implies ISS for all nonlinearities $f:\mathbb {R}^p\rightarrow \mathbb {R}^m$ satisfying (3.3). In this sense, Theorem 3.2 is reminiscent of the Aizerman conjecture, see, for example [9, 10, 17, 27]. We emphasize though that stability of the linear feedback system $\dot{x}=(A+BFC)x$ has to hold for all complex output feedback matrices F satisfying $\Vert F-K\Vert <r$. It is easy to see that the ISS conclusion in Theorem 3.2 remains true for all complex nonlinearities $f:\mathbb {C}^p\rightarrow \mathbb {C}^m$ satisfying (3.3) for all $\xi \in \mathbb {C}^p$. We will now identify a special case wherein the complex condition $\mathbb {B}_{\mathbb {C}}(K, r) \subseteq \mathbb {S}_{\mathbb {C}} \left( A,B,C\right)$ can be replaced by its real counterpart $\mathbb {B}_{\mathbb {R}}(K,r)\subseteq \mathbb {S}_{\mathbb {R}}(A,B,C)$.

Recall that a square matrix $M\in \mathbb {R}^{n\times n}$ is said to be Metzler (or essentially non-negative or quasi positive) if all its off-diagonal entries are non-negative. It is well known (and straightforward to prove) that $M\in \mathbb {R}^{n\times n}$ is Metzler if, and only if, $e^{Mt}\zeta \in \mathbb {R}^n_+$ for all $\zeta \in \mathbb {R}^n_+$ and all $t\ge 0$. We say that a matrix with real entries is non-negative if all its entries are non-negative.

Corollary 3.7

Let $(A, B, B_\mathrm{e}, C)\in \Sigma _\mathrm{e}$, $f:\mathbb {R}^p\rightarrow \mathbb {R}^m$ be locally Lipschitz, $r > 0$ and $K \in \mathbb {R}^{m \times p}$. Assume that B and C are non-negative and $A+BKC$ is Metzler. If $\mathbb {B}_{\mathbb {R}}(K, r)\subseteq \mathbb {S}_{\mathbb {R}}(A,B,C)$ and there exists $\alpha \in \mathcal {K}_{\infty }$ such that

$$\begin{aligned} \left\| f(\xi ) - K\xi \right\| \le r \left\| \xi \right\| - \alpha (\left\| \xi \right\| ) \quad \forall \,\xi \in \mathbb {R}^p, \end{aligned}$$

(3.28)

then the Lur’e system $(A, B, B_\mathrm{e}, C,f)$ is ISS.

Proof

By hypothesis, B and C are non-negative and $A_K:=A+BKC$ is Metzler. Since $\mathbb {B}_{\mathbb {R}}(K, r)\subseteq \mathbb {S}_{\mathbb {R}}(A,B,C)$, we have $\mathbb {B}_{\mathbb {R}}(0, r)\subseteq \mathbb {S}_{\mathbb {R}}(A_K,B,C)$, and thus, $r\le r_{\mathbb {R}}(A_K;B,C)$. By a stability radius result for non-negative systems proved in [11], $r_{\mathbb {R}}(A_K;B,C)=r_{\mathbb {C}}(A_K;B,C)$, and hence, $\mathbb {B}_{\mathbb {C}}(0, r)\subseteq \mathbb {S}_{\mathbb {C}}(A_K,B,C)$, or, equivalently, $\mathbb {B}_{\mathbb {C}}(K, r)\subseteq \mathbb {S}_{\mathbb {C}}(A,B,C)$. The claim now follows from Theorem 3.2. $\square$

The corollary below provides a “small-gain” interpretation of Theorem 3.2.

Corollary 3.8

Let $(A, B, B_\mathrm{e}, C)\in \Sigma _\mathrm{e}$, $K\in \mathbb {S}_\mathbb {R}(A,B.C)$, let $f:\mathbb {R}^p\rightarrow \mathbb {R}^m$ be locally Lipschitz and let G denote the transfer function of (A, B, C). If there exists $\alpha \in \mathcal {K}_{\infty }$ such that

$$\begin{aligned} \Vert G^K\Vert _{H^\infty }\frac{\Vert f(\xi )-K\xi \Vert }{\Vert \xi \Vert }\le 1- \frac{\alpha (\Vert \xi \Vert )}{\Vert \xi \Vert } \quad \forall \,\xi \in \mathbb {R}^p,\quad \xi \not =0, \end{aligned}$$

then the Lur’e system $(A, B, B_\mathrm{e}, C, f)$ is ISS.

Proof

Setting $r:=1/\Vert G^K\Vert _{H^\infty }$, it follows that $\mathbb {B}_{\mathbb {C}}(K, r)\subseteq \mathbb {S}_{\mathbb {C}}(A,B,C)$ and an application of Theorem 3.2 yields the claim. $\square$

We note that Corollary 3.8 is not a special case of general nonlinear small-gain ISS results as can be found, for example, in [14, 26]. The reason for this is that, in general, the $H^\infty$-gain $\Vert G^K\Vert _{H^\infty }$ and the ISS gain of the linear system $(A+BKC,B,C)$ do not coincide: the former is always less or equal to the latter and the difference between these two gains can be large.

Next we derive a version of Theorem 3.2 which is reminiscent of the well-known circle criterion (see [6, 7, 16, 27]). To this end, let $\mathbb {R}(s)$ denote the field of real rational functions, and recall that $H\in \mathbb {R}(s)^{m\times m}$ is said to be positive real if for every $s\in \mathbb {C}_+$ which is not a pole of H, the matrix $H^*(s)+ H(s)$ is positive semi-definite.

For convenience, we state the following well-known lemma.

Lemma 3.9

Let $H\in \mathbb {R}(s)^{m\times m}$. If H is positive real, then H does not have any poles in $\mathbb {C}_+$, $-1$ is not an eigenvalue of H(s) for every $s\in \mathbb {C}_+$ and

$$\begin{aligned} \left\| (I - H)(I + H)^{-1}\right\| _{H^{\infty }} \le 1. \end{aligned}$$

We are now in the position to state and prove a corollary of Theorem 3.2 which shows that, under conditions very similar to those of the circle criterion, the Lur’e system $(A, B, B_\mathrm{e}, C, f)$ is ISS.

Corollary 3.10

Let $(A, B, B_\mathrm{e}, C)\in \Sigma _\mathrm{e}$, $f:\mathbb {R}^p\rightarrow \mathbb {R}^m$ be locally Lipschitz, $K_1, K_2 \in \mathbb {R}^{m \times p}$ and let G denote the transfer function of (A, B, C). Assume that (A, B, C) is stabilizable and detectable and that $(I - K_2G)(I - K_1G)^{-1}$ is positive real. If there exists $\alpha \in \mathcal {K}_{\infty }$ such that

$$\begin{aligned} \left\langle f(\xi ) - K_1 \xi , f(\xi ) - K_2\xi \right\rangle \le -\alpha (\left\| \xi \right\| )\left\| \xi \right\| \quad \forall \,\xi \in \mathbb {R}^p, \end{aligned}$$

(3.29)

then the Lur’e system $(A, B, B_\mathrm{e}, C, f)$ is ISS.

Proof

Setting

$$\begin{aligned} K:=\frac{1}{2}(K_1+K_2)\quad \text{ and }\quad L:=\frac{1}{2}(K_1-K_2), \end{aligned}$$

we rewrite the left-hand side of the sector condition (3.29) in terms of K and L:

$$\begin{aligned} \left\langle f(\xi ) - K_1\xi , f(\xi ) - K_2\xi \right\rangle =&\left\langle f(\xi ) - (K+L)\xi , f(\xi ) - (K-L)\xi \right\rangle \nonumber \\ =&\left\| f(\xi ) - K\xi \right\| ^2 - \left\| L\xi \right\| ^2 \quad \forall \,\xi \in \mathbb {R}^p. \end{aligned}$$

(3.30)

Note that in conjunction with (3.29) this implies $\ker L = \{0\}$. Thus $L^*L$ is invertible and $L^{\sharp } := (L^*L)^{-1}L^* \in \mathbb {R}^{p \times m}$ is a left inverse of L. Furthermore,

$$\begin{aligned} (I - K_2G)(I - K_1G)^{-1}= (I - K_1G + 2LG)(I - K_1G)^{-1} = I + 2LG^{K_1}, \end{aligned}$$

showing that $I + 2LG^{K_1}$ is positive real. Thus, by Lemma 3.9,

$$\begin{aligned} \left\| LG^{K_1}(I + LG^{K_1})^{-1}\right\| _{H^{\infty }} \le 1. \end{aligned}$$

Trivially,

$$\begin{aligned} LG^{K_1}(I + LG^{K_1})^{-1}= LG^{K_1}(I -(-LL^\sharp )LG^{K_1})^{-1}=(LG^{K_1})^{-LL^{\sharp }}, \end{aligned}$$

and so, appealing to statement (d) of Lemma 2.1,

$$\begin{aligned} \mathbb {B}_{\mathbb {C}}(-LL^{\sharp }, 1) \subseteq \mathbb {S}_{\mathbb {C}} \left( LG^{K_1}\right) . \end{aligned}$$

(3.31)

By stabilizability and detectability of (A, B, C) and left invertibility of L, it follows that $(A_{K_1}, B, LC)$ is stabilizable and detectable, where $A_{K_1}:=A+BK_1C$. The transfer function of $(A_{K_1}, B, LC)$ is equal to $LG^{K_1}$ and so (3.31) implies

$$\begin{aligned} \mathbb {B}_{\mathbb {C}}(-LL^{\sharp }, 1) \subseteq \mathbb {S}_{\mathbb {C}} \left( A_{K_1}, B, LC\right) . \end{aligned}$$

(3.32)

Defining $g:\mathbb {R}^m\rightarrow \mathbb {R}^m$ by $g(\xi ):=f(L^{\sharp }\xi ) - K_1L^{\sharp }\xi$ for all $\xi \in \mathbb {R}^m$, it is straightforward to show that

$$\begin{aligned} \mathcal {B}(A, B, B_\mathrm{e}, C, f)=\mathcal {B}(A_{K_1}, B, B_\mathrm{e}, LC, g). \end{aligned}$$

(3.33)

We claim that it is sufficient to prove that there exists $\beta \in \mathcal {K}_{\infty }$ such that

$$\begin{aligned} \Vert g(\xi )+LL^\sharp \xi \Vert \le \Vert \xi \Vert -\beta (\Vert \xi \Vert )\quad \forall \, \xi \in \mathbb {R}^m. \end{aligned}$$

(3.34)

Indeed, if (3.34) holds, then it follows from (3.32) and an application of Theorem 3.2 that $(A_{K_1}, B, B_\mathrm{e}, LC, g)$ is ISS, and consequently, by (3.33), the Lur’e system $(A,B,B_\mathrm{e}, C,f)$ is also ISS.

We proceed to establish the existence of a function $\beta \in \mathcal {K}_{\infty }$ such that (3.34) holds. To this end, note that

$$\begin{aligned} \Vert g(\xi ) + LL^{\sharp }\xi \Vert ^2 = \Vert f(L^{\sharp }\xi )- K_1L^{\sharp }\xi + LL^{\sharp }\xi \Vert ^2 = \Vert f(L^{\sharp }\xi ) - KL^{\sharp }\xi \Vert ^2\quad \forall \,\xi \in \mathbb {R}^m. \end{aligned}$$

In conjunction with (3.29) and (3.30) this leads to

$$\begin{aligned} \Vert g(\xi ) + LL^{\sharp }\xi \Vert ^2\le \Vert LL^{\sharp }\xi \Vert ^2 -\Vert L^{\sharp }\xi \Vert \alpha (\Vert L^{\sharp } \xi \Vert ) \quad \forall \,\xi \in \mathbb {R}^m. \end{aligned}$$

Let $\xi \in \mathbb {R}^m$ and decompose $\xi =\xi _1+\xi _2$, where

$$\begin{aligned} \xi _1\in \mathrm {im}\,L=(\ker L^*)^\perp =(\ker L^\sharp )^\perp \quad \text{ and }\quad \xi _2\in (\mathrm {im}\,L)^\perp =\ker L^*=\ker L^\sharp . \end{aligned}$$

Then $\Vert LL^\sharp \xi \Vert =\Vert LL^\sharp \xi _1\Vert =\Vert \xi _1\Vert$. Moreover, there exists $c>0$ such that

$$\begin{aligned} \Vert L^\sharp \xi \Vert \ge c\Vert \xi \Vert \quad \forall \,\xi \in (\ker L^\sharp )^\perp . \end{aligned}$$

It follows that

$$\begin{aligned} \Vert g(\xi )+LL^\sharp \xi \Vert ^2&\le \Vert \xi _1\Vert ^2-c\Vert \xi _1\Vert \alpha (c\Vert \xi _1\Vert )\nonumber \\&=\Vert \xi \Vert ^2-\big (c\Vert \xi _1\Vert \alpha (c\Vert \xi _1\Vert )+\Vert \xi _2\Vert ^2\big )\quad \forall \, \xi \in \mathbb {R}^m. \end{aligned}$$

(3.35)

Defining $\beta \in \mathcal {K}_{\infty }$ by

$$\begin{aligned} \beta (s):=\frac{1}{4}\min \{c\,\alpha (c s/2),s/2\}\quad \forall \,s\ge 0, \end{aligned}$$

we have that

$$\begin{aligned} 4s\beta (2s)=\min \{c s\,\alpha (cs),s^2\}\quad \forall \,s\ge 0. \end{aligned}$$

(3.36)

Now

$$\begin{aligned} \sqrt{s_1^2+s_2^2}\,\beta \left( \sqrt{s_1^2+s_2^2}\right)&\le (s_1+s_2)\beta (s_1+s_2)\\&\le 2s_1\beta (2s_1)+2s_2\beta (2s_2)\quad \forall \,s_1,s_2\ge 0, \end{aligned}$$

and thus, by (3.36),

$$\begin{aligned} 2\sqrt{s_1^2+s_2^2}\,\beta \left( \sqrt{s_1^2+s_2^2}\right) \le cs_1\,\alpha (c s_1)+s_2^2 \quad \forall \,s_1,s_2\ge 0. \end{aligned}$$

This, in combination with (3.35), yields

$$\begin{aligned} \Vert g(\xi )+LL^\sharp \xi \Vert ^2\le \Vert \xi \Vert ^2-2\Vert \xi \Vert \beta (\Vert \xi \Vert ) \le \big (\Vert \xi \Vert -\beta (\Vert \xi \Vert )\big )^2\quad \forall \,\xi \in \mathbb {R}^m, \end{aligned}$$

showing that (3.34) holds and completing the proof. $\square$

We recall that $H\in \mathbb {R}(s)^{m\times m}$ is said to be strictly positive real if there exists $\varepsilon >0$ such that the rational matrix function $s\mapsto H(s-\varepsilon )$ is positive real.

Corollary 3.11

Let $(A, B, B_\mathrm{e}, C)\in \Sigma _\mathrm{e}$, $f:\mathbb {R}^p\rightarrow \mathbb {R}^m$ be locally Lipschitz, let G denote the transfer function of (A, B, C), and let $K_1, K_2 \in \mathbb {R}^{m \times p}$ be such that $\ker (K_1-K_2)=\{0\}$. If (A, B, C) is stabilizable and detectable, $(I - K_2G)(I - K_1G)^{-1}$ is strictly positive real and

$$\begin{aligned} \left\langle f(\xi ) - K_1 \xi , f(\xi ) - K_2\xi \right\rangle \le 0\quad \forall \,\xi \in \mathbb {R}^p, \end{aligned}$$

(3.37)

then the Lur’e system $(A, B, B_\mathrm{e}, C, f)$ is ISS.

Note that the assumptions in Corollary 3.11 are identical to those imposed in the “classical” circle criterion which guarantees global asymptotic stability, see, for example, [6, Theorem 5.1], [7, Corollary 5.8] and [16, Theorem 7.1].² Interestingly, Corollary 3.11 shows that the conditions of the circle criterion are actually sufficient for ISS. Also note that if $\ker (K_1-K_2)$ is non-trivial, then, in general, Corollary 3.11 does not hold: indeed, if $F\in \mathbb {R}^{m \times p}$ is such that $G(I - FG)^{-1}\not \in H^\infty (\mathbb {C}^{p\times m})$ (that is, the feedback gain F is not stabilizing), $f(\xi )=F\xi$ and $K_1=K_2=F$, then $(I - K_2G)(I - K_1G)^{-1}=I$ is trivially strictly positive real and (3.37) is satisfied, but 0 is not an asymptotically stable equilibrium of the (uncontrolled) Lur’e system.

The following lemma will be useful in the proof of Corollary 3.11.

Lemma 3.12

Let $H\in \mathbb {R}(s)^{m\times m}$ be proper and assume that $H(\infty )+ H^*(\infty )$ is positive definite. Then H is strictly positive real if, and only if, $H\in H^\infty (\mathbb {C}^{m\times m})$ and $H(i\omega )+H^*(i\omega )$ is positive definite for all $\omega \in \mathbb {R}$.

The above lemma is an immediate consequence of a standard characterization of the strict positive real property, see, for example [7, Theorem 5.17] or [16, Lemma 6.1].

Proof of Corollary 3.11

Set $M:=K_2-K_1$, let $\rho \ge 0$ and define

$$\begin{aligned} H_\rho :=\big (I - (K_2+\rho M)G\big )\left( I -(K_1-\rho M)G\right) ^{-1}. \end{aligned}$$

By hypothesis, $H_0$ is strictly positive real. We claim that that there exists $\hat{\rho }>0$ such that $H_\rho$ is strictly positive real for all $\rho \in [0,\hat{\rho }]$. To this end, note that

$$\begin{aligned} H_\rho =I-(1+2\rho )MG\big (I -(K_1-\rho M)G\big )^{-1}. \end{aligned}$$

(3.38)

Since $H_0$ is strictly positive real, Lemma 3.12 yields that $H_0\in H^\infty (\mathbb {C}^{m\times m})$ and, furthermore, there exists $\delta >0$ such that

$$\begin{aligned} H_0(i\omega )+H_0^*(i\omega )\ge \delta I\quad \forall \,\omega \in \mathbb {R}. \end{aligned}$$

(3.39)

Since $\ker M=\{0\}$, the matrix M is left invertible, and it follows from (3.38) (with $\rho =0$) that $G(I - K_1G)^{-1}\in H^\infty (\mathbb {C}^{p\times m})$. Consequently, there exists $\tilde{\rho }>0$ such that $G\big (I - (K_1-\rho M)G\big )^{-1} \in H^\infty (\mathbb {C}^{p\times m})$ for all $\rho \in [0,\tilde{\rho }]$ and the map

$$\begin{aligned}{}[0,\tilde{\rho }]\rightarrow H^\infty (\mathbb {C}^{m\times m}),\quad \rho \mapsto H_\rho \end{aligned}$$

is continuous. Invoking (3.39), we conclude that there exists $\hat{\rho }\in (0,\tilde{\rho }]$ such that, for each $\rho \in [0,\hat{\rho }]$, $H_\rho (i\omega )+H_\rho ^*(i\omega )\ge (\delta /2)I$ for all $\omega \in \mathbb {R}$. An application of Lemma 3.12 shows that, for all $\rho \in [0,\hat{\rho }]$, $H_\rho$ is strictly positive real and, a fortiori, positive real.

The claim will follow from Corollary 3.10, provided we can show that, for $\rho \in (0,\hat{\rho }]$, there exists $\alpha \in \mathcal {K}_{\infty }$ such that

$$\begin{aligned} \left\langle f(\xi ) - (K_1-\rho M) \xi , f(\xi ) - (K_2+\rho M)\xi \right\rangle \le -\alpha (\Vert \xi \Vert )\Vert \xi \Vert \quad \forall \,\xi \in \mathbb {R}^p.\nonumber \\ \end{aligned}$$

(3.40)

Invoking (3.37), a straightforward calculation shows that

$$\begin{aligned} \left\langle f(\xi ) - (K_1-\rho M) \xi , f(\xi ) - (K_2+\rho M)\xi \right\rangle \le -\rho (\rho +1) \Vert M\xi \Vert ^2\quad \forall \, \,\xi \in \mathbb {R}^p. \end{aligned}$$

By left invertibility of M, there exists $\mu >0$ such that $\Vert M\xi \Vert \ge \mu \Vert \xi \Vert$ for all $\xi \in \mathbb {R}^p$, and so,

$$\begin{aligned} \left\langle f(\xi ) - (K_1-\rho M) \xi , f(\xi ) - (K_2+\rho M)\xi \right\rangle \le -\mu \rho (\rho +1)\Vert \xi \Vert ^2\quad \forall \, \,\xi \in \mathbb {R}^p, \end{aligned}$$

showing that (3.40) holds with $\alpha (s)=\mu \rho (\rho +1)s$. $\square$

We now reformulate the sector condition (3.29) in the special case wherein (A, B, C) is a single-input single-output system (that is, $m=p=1$). In the single-input single-output setting, this reformulation seems more natural than (3.29).

Corollary 3.13

Let $(A, B, B_\mathrm{e}, C)\in \Sigma _\mathrm{e}$, where (A, B, C) is a single-input single-output system (that is, $m=p=1$). Let $f:\mathbb {R}\rightarrow \mathbb {R}$ be locally Lipschitz, let $k_1<k_2$ and let G denote the transfer function of (A, B, C). Assume that (A, B, C) is stabilizable and detectable and that $(1-k_2G)/(I - k_1G)$ is positive real. If there exists $\alpha \in \mathcal {K}_{\infty }$ such that

$$\begin{aligned} k_1\xi ^2+\alpha (|\xi |)|\xi |\le f(\xi )\xi \le k_2\xi ^2-\alpha (|\xi |)|\xi | \quad \forall \,\xi \in \mathbb {R}, \end{aligned}$$

(3.41)

then the Lur’e system $(A, B, B_\mathrm{e}, C, f)$ is ISS.

Note that there exists $\alpha \in \mathcal {K}_{\infty }$ such that (3.41) holds if, and only if,

$$\begin{aligned} k_1\xi ^2<f(\xi )\xi <k_2\xi ^2\quad \forall \,\xi \in \mathbb {R},\quad \xi \not =0 \end{aligned}$$

and

$$\begin{aligned} |f(\xi )-k_i\xi |\rightarrow \infty \quad \text{ as }\quad |\xi |\rightarrow \infty ,\quad i=1,2. \end{aligned}$$

Proof of Corollary 3.13

The result will follow from Corollary 3.10, provided we show that there exists $\beta \in \mathcal {K}_{\infty }$ such that

$$\begin{aligned} (f(\xi ) - k_1\xi )(f(\xi ) -k_2\xi )\le -\beta (|\xi |)|\xi | \quad \forall \,\xi \in \mathbb {R}. \end{aligned}$$

(3.42)

To this end, set

$$\begin{aligned} k:=\frac{k_1+k_2}{2}\quad \text{ and }\quad r:=\frac{k_2-k_1}{2}>0, \end{aligned}$$

and note that, by (3.41),

$$\begin{aligned} -r\xi ^2+\alpha (|\xi |)|\xi |\le f(\xi )\xi -k\xi ^2\le r\xi ^2-\alpha (|\xi |)|\xi | \quad \forall \,\xi \in \mathbb {R}, \end{aligned}$$

or, equivalently,

$$\begin{aligned} |f(\xi )-k\xi |\le r|\xi |-\alpha (|\xi |)\quad \forall \,\xi \in \mathbb {R}. \end{aligned}$$

(3.43)

Hence,

$$\begin{aligned} (f(\xi )-k\xi )^2-r^2\xi ^2\le -2r|\xi |\alpha (|\xi |)+\alpha ^2(|\xi |) \quad \forall \,\xi \in \mathbb {R}. \end{aligned}$$

Since

$$\begin{aligned} (f(\xi )-k\xi )^2=(f(\xi )-k_1\xi )(f(\xi ) -k_2\xi )+k^2\xi ^2-k_1k_2\xi ^2 \quad \forall \,\xi \in \mathbb {R} \end{aligned}$$

and $k^2-r^2=k_1k_2$, it follows that

$$\begin{aligned} (f(\xi )-k_1\xi )(f(\xi ) -k_2\xi )\le -2r|\xi |\alpha (|\xi |)+\alpha ^2(|\xi |) \quad \forall \,\xi \in \mathbb {R}. \end{aligned}$$

Finally, by (3.43), $\alpha (s)\le rs$ for all $s\ge 0$, implying that

$$\begin{aligned} (f(\xi )-k_1\xi )(f(\xi ) -k_2\xi )\le -2r|\xi |\alpha (|\xi |)+r|\xi |\alpha (|\xi |) =-r|\xi |\alpha (|\xi |) \quad \forall \,\xi \in \mathbb {R}. \end{aligned}$$

Consequently, (3.42) holds with $\beta :=r\alpha$. $\square$

Example 3.14

Consider the one-dimensional linear system $\dot{x}=u+v$ with feedback $u=f(x)$, resulting in the Lur’e system

$$\begin{aligned} \dot{x}(t) = f(x(t))+ v(t). \end{aligned}$$

(3.44)

Here we have $(A,B,B_\mathrm{e},C)=(0,1,1,1)$ and $G(s)=1/s$. Let $k_1<0$ and $k_2=0$. Note that, for every $k_1<0$,

$$\begin{aligned} \frac{1-k_2G(s)}{1-k_1G(s)}=\frac{s}{s-k_1} \end{aligned}$$

is positive real (but not strictly positive real). Let f be given by

$$\begin{aligned} f(\xi )=\left\{ \begin{array}{l l} -\xi ^3 &{}\quad \text {for}\quad |\xi |\le 1\\ -\mathrm{sgn}(\xi )\big (\ln (|\xi |)+1\big ) &{}\quad \text {for}\quad |\xi |>1. \end{array}\right. \end{aligned}$$

(3.45)

It is clear that, for any $k_1<-1$, $k_1\xi ^2<f(\xi )\xi <0$ for all $\xi \not =0$, and, as $|\xi |\rightarrow \infty$, we have that $|f(\xi )-k_1\xi |\rightarrow \infty$ and $|f(\xi )|\rightarrow \infty$. Consequently, there exists $\alpha \in \mathcal {K}_{\infty }$ such that

$$\begin{aligned} k_1\xi ^2+\alpha (|\xi |)|\xi |\le f(\xi )\xi \le -\alpha (|\xi |)|\xi | \quad \forall \,\xi \in \mathbb {R}. \end{aligned}$$

It follows now from Corollary 3.13 that the Lur’e system (3.44) is ISS. Note that the equilibrium 0 of the uncontrolled ($v=0$) system (3.44) is not exponentially stable. Also note that if f is replaced by a saturating nonlinearity g, for example,

$$\begin{aligned} g(\xi )=\left\{ \begin{array}{l l} -\xi ^3 &{}\quad \text {for}\quad |\xi |\le 1\\ -\mathrm{sgn}(\xi ) &{}\quad \text {for}\quad |\xi |>1, \end{array}\right. \end{aligned}$$

then, by Proposition 3.4, the resulting Lur’e system is not ISS. $\square$

4 Conclusions

We have developed an ISS theory for a class of Lur’e systems. The main result of this paper (Theorem 3.2) is an ISS result which is reminiscent of the complexified Aizerman conjecture in the following sense: if every linear feedback gain F in the complex ball $\mathbb {B}_{\mathbb {C}}(K,r)$ stabilizes the system (A, B, C), then the Lur’s system $\dot{x}=Ax+Bf(Cx)+B_\mathrm{e}v$ is ISS for every locally Lipschitz nonlinearity f for which there exists $\alpha \in \mathcal {K}_{\infty }$ such that $\Vert f(\xi )-K\xi \Vert \le r\Vert \xi \Vert - \alpha (\Vert \xi \Vert )$ for all $\xi$. As corollaries we have obtained a new nonlinear small-gain condition for ISS of Lur’e systems (Corollary 3.8) and several ISS versions of the classical circle criterion (Corollaries 3.10, 3.11 and 3.13).