Further stabilization and exact observability results for voltage-actuated piezoelectric beams with magnetic effects

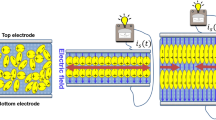
Abstract

It is well known that magnetic energy of the piezoelectric beam is relatively small, and it does not change the overall dynamics. Therefore, the models, relying on electrostatic or quasi-static approaches, completely ignore the magnetic energy stored/produced in the beam. A single piezoelectric beam model without the magnetic effects is known to be exactly observable and exponentially stabilizable in the energy space. However, the model with the magnetic effects is proved to be not exactly observable/exponentially stabilizable in the energy space for almost all choices of material parameters. Moreover, even strong stability is not achievable for many values of the material parameters. In this paper, it is shown that the uncontrolled system is exactly observable in a space larger than the energy space. Then, by using a $B^*$-type feedback controller, explicit polynomial decay estimates are obtained for more regular initial data. Unlike the classical counterparts, this choice of feedback corresponds to the current flowing through the electrodes, and it matches better with the physics of the model. The results obtained in this manuscript have direct implications on the controllability/stabilizability of smart structures such as elastic beams/plates with piezoelectric patches and the active constrained layer (ACL) damped beams/plates.

Appendix: Some results in number theory

In this section, we briefly mention some fundamental results of Diophantine’s approximation. The theorem of Khintchine (Theorem 8) plays an important role to determine the Lebesgue measure of sets investigated in this paper.

Let $f:\mathbb {N}\rightarrow \mathbb {R}^+$ be called an approximation function if

$$\begin{aligned} \mathop {\lim }\limits _{\tilde{q} \rightarrow \infty } f(\tilde{q})=0. \end{aligned}$$

A real number $\zeta$ is $f$-approximable if $\zeta$ satisfies

$$\begin{aligned} \left| ~\zeta -\frac{\tilde{p}}{\tilde{q}}~\right| <f(\tilde{q}) \end{aligned}$$

(63)

for infinitely many rational numbers $\frac{\tilde{p}}{\tilde{q}}.$ Let $P(f)$ be the set of all $f$-approximable numbers. We recall the following theorem to find the measure of sets of type $P(f).$

Theorem 8

(Khintchine’s theorem) [13, Page4] Let $\mu$ be the Lebesgue measure. Then

$$\begin{aligned} \mu (P(f))=\left\{ \begin{array}{l@{\quad }l} 0, \quad &{} \mathrm{{if}} \quad \sum \limits _{\tilde{q}\in \mathbb {N}} {\tilde{q} f(\tilde{q})}<\infty , \\ \mathrm{{full}}, \quad &{} \mathrm{if} \quad \tilde{q} f(\tilde{q}) \quad \mathrm{{is\, nonincreasing\, and}} ~ \sum \limits _{\tilde{q}\in \mathbb {N}} {\tilde{q} f(\tilde{q})}=\infty . \end{array} \right. \end{aligned}$$

(64)

Dirichlet’s theorem [14] states that every irrational number can be approximated to the order 2. The following theorem from [35] is a special case of Dirichlet’s theorem:

Theorem 9

Let $\zeta \in \mathbb {R}-\mathbb {Q}.$ Then there exists a constant $C\ge 1,$ and increasing sequences of coprime odd integers $\{\tilde{p}_j\},\{\tilde{q}_j\}$ satisfying the asymptotic relation

$$\begin{aligned} \left| ~\zeta - \frac{\tilde{p}_j}{\tilde{q}_j}~\right| \le \frac{C}{{\tilde{q}_j}^{2}},\quad j\rightarrow \infty . \end{aligned}$$

(65)

It obvious by Theorem 8 that the set $\mathbb {R}-\mathbb {Q}$ is uncountable and it has a full Lebesgue measure.

Definition 5

A real number $\zeta$ is a Liouville’s number if for every $m\in \mathbb {N}$ there exists $\frac{\tilde{p}_m}{\tilde{q}_m}$ with $p_m, q_m \in \mathbb {Z}$ such that

$$\begin{aligned} \left| ~\zeta -\frac{\tilde{p}_m}{\tilde{q}_m}~\right| <\frac{1}{\tilde{q}_m^m}. \end{aligned}$$

It is proved that any Liouville’s number is transcendental. Theorem 8 implies that the set of Liouville’s numbers is of Lebesgue measure zero.

Definition 6

A real number $\zeta$ is an algebraic number if it is a root of a polynomial equation

$$\begin{aligned} a_n x^n+ a_{n-1}x^{n-1}+ \cdots + a_1 x + a_0=0 \end{aligned}$$

with each $a_i \in \mathbb {Z},$ and at least one of $a_i$ is non-zero. A number which is not algebraic is called transcendental.

Now we give the following results of Diophantine’s approximations:

Theorem 10

There exists a set $\tilde{\mathbb {Q}}$ such that if $\zeta \in \mathbb {R}-\tilde{\mathbb {Q}},$ then for every $\varepsilon >0$ there are infinitely many $\frac{\tilde{p}}{\tilde{q}}\in \mathbb {Q}$ and a constant $C_\zeta >0$ such that

$$\begin{aligned} \left| ~\zeta -\frac{\tilde{p}}{\tilde{q}}~\right| \ge \frac{C_\zeta }{\tilde{q}^{2+\varepsilon }}. \end{aligned}$$

(66)

Moroever, $\mu (\tilde{\mathbb {Q}})=0.$

Proof

We know that the irrational algebraic numbers belong to $\tilde{\mathbb {Q}}$ by Roth’s theorem (Page 103, [14]). Therefore $\tilde{\mathbb {Q}}$ is not empty. We proceed to the second part of the lemma. The first part of the theorem implies that if $\zeta \in \tilde{\mathbb Q}$ then for all $C_\zeta >0,$ the inequality $\left| ~\zeta -\frac{\tilde{p}}{\tilde{q}}~\right| < \frac{C_\zeta }{\tilde{q}^{2+\varepsilon }}$ holds for some $\frac{\tilde{p}}{\tilde{q}}\in \mathbb {Q}.$ Now define the set

$$\begin{aligned} \tilde{\mathbb Q}_{\varepsilon }=\left\{ \zeta \in \mathbb {R}~:~ \left| ~~\zeta -\frac{\tilde{p}}{\tilde{q}}~\right| < \frac{C_\zeta }{\tilde{q}^{2+\varepsilon }} ~ {\text {for infinitely many}} \frac{\tilde{p}}{\tilde{q}}\in \mathbb {Q} \right\} . \end{aligned}$$

By the notation of Theorem 8, choose $f(\tilde{q})=\frac{C_\zeta }{\tilde{q}^{2+\varepsilon }}$ so that $\tilde{q} f(\tilde{q})$ is nonincreasing and $\sum \nolimits _{\tilde{q}\in \mathbb {N}}\frac{C_\zeta }{\tilde{q}^{1+\varepsilon }}<\infty .$ By Theorem 8, $\mu (\tilde{\mathbb Q}_{\varepsilon })=0.$ Now we prove $\tilde{\mathbb {Q}}\subset \tilde{\mathbb Q}_{\varepsilon }$ by contradiction. Assume that $\zeta \notin \tilde{\mathbb Q}_{\varepsilon }$, i.e., there are finitely many rationals $\left\{ \frac{p_i}{q_i}\right\} _{i=1,\ldots , N}$ such that

$$\begin{aligned} \left| ~\zeta -\frac{p_i}{q_i}~\right| < \frac{C_\zeta }{q_i^{2+\varepsilon }} ~~\mathrm{{for}}~~ i=1,\ldots , N, ~~\mathrm{{and}}~~\left| ~\zeta -\frac{\tilde{p}}{\tilde{q}}\right| \ge \frac{C_\zeta }{q^{2+\varepsilon }} ~~ \mathrm{{for}} ~~ \frac{\tilde{p}}{\tilde{q}}\notin \bigcup \limits _{i = 1}^N {\left\{ \frac{\tilde{p}_i}{\tilde{q}_i}\right\} }. \end{aligned}$$

The last inequality implies that $\zeta \in \mathbb {R}-\mathbb {Q}.$ This implies that the set $\mathbb {R}-\tilde{\mathbb {Q}}$ has a full Lebesgue measure. $\square$

Now define the set $\tilde{\tilde{\mathbb {Q}}}$ by

$$\begin{aligned} \tilde{\tilde{\mathbb {Q}}}=\left\{ \zeta \in \mathbb {R}~:~ \exists C>0, ~~ \left| ~\zeta -\frac{\tilde{p}}{\tilde{q}}~\right| \ge \frac{C}{\tilde{q}^{2}} {\text { for infinitely many}} ~\frac{\tilde{p}}{\tilde{q}}\in \mathbb {Q} \right\} . \end{aligned}$$

(67)

If we consider numbers $\zeta \in \mathbb {R}$ whose the partial quotients satisfy $|a_k|<C(\zeta )$ for all $k\in \mathbb {N}$ in its continued fraction expansion

$$\begin{aligned} \zeta =[a_0; a_1, a_2, \ldots ]=a_0+\frac{1}{a_1+\frac{1}{a_2+ \ddots }}, \end{aligned}$$

then $\zeta \in \tilde{\tilde{\mathbb {Q}}}.$ By Liouville’s theorem (Page 128, [26]), $\tilde{\tilde{\mathbb {Q}}}$ also contains all quadratic irrational numbers (the roots of an algebraic polynomial of degree $2$). Therefore the set is uncountable.

Lemma 6

The set $\tilde{\tilde{\mathbb {Q}}}$ has a Lebesgue measure zero.

Proof

Define the set $F_m$ by

$$\begin{aligned} F_m=\left\{ \zeta \in \mathbb {R}~:~ \left| ~\zeta -\frac{\tilde{p}}{\tilde{q}}~\right| < \frac{C}{m\tilde{q}^{2}} ~ {\text { for infinitely many}}~\frac{\tilde{p}}{\tilde{q}}\in \mathbb {Q} \right\} . \end{aligned}$$

Then $F_m$ has a full Lebesgue measure by Theorem 8, i.e., $f(\tilde{q})=\frac{C}{m\tilde{q}^2},$ and $\sum \nolimits _{\tilde{q}\in \mathbb {N}} {\tilde{q} f(\tilde{q})}=\infty .$ Now consider the set $\bigcap \nolimits _{m\in \mathbb {N}} F_m.$ This set is the countable intersection of sets $F_m,$ and each $F_m$ has full Lebesgue measure. Therefore $\mu \left( \bigcap \nolimits _{m\in \mathbb {N}} F_m\right)$ has full Lebesgue measure. Since $\tilde{\tilde{\mathbb {Q}}}=\mathbb {R}-\bigcap \nolimits _{m\in \mathbb {N}} F_m,$ then $\mu (\tilde{\tilde{\mathbb {Q}}})=0$. $\square$