A Characterization of Edge-Ordered Graphs with Almost Linear Extremal Functions

Abstract

The systematic study of Turán-type extremal problems for edge-ordered graphs was initiated by Gerbner et al. (Turán problems for Edge-ordered graphs, 2021). They conjectured that the extremal functions of edge-ordered forests of order chromatic number 2 are $n^{1+o(1)}$. Here we resolve this conjecture proving the stronger upper bound of $n2^{O(\sqrt{\log n})}$. This represents a gap in the family of possible extremal functions as other forbidden edge-ordered graphs have extremal functions $\Omega (n^c)$ for some $c>1$. However, our result is probably not the last word: here we conjecture that the even stronger upper bound of $n\log ^{O(1)}n$ also holds for the same set of extremal functions.

1 Introduction

Turán-type extremal graph theory asks how many edges an n-vertex simple graph can have if it does not contain a subgraph isomorphic to a forbidden graph. We introduce the relevant notation here.

Definition 1.1

We say that a simple graph G avoids another simple graph H, if no subgraph of G is isomorphic to H. The Turán number ${\textrm{ex}}(n,H)$ of a forbidden finite simple graph H (having at least one edge) is the maximum number of edges in an n-vertex simple graph avoiding H.

This theory has proved to be useful and applicable in combinatorics, as well as in combinatorial geometry, number theory and other parts of mathematics and theoretical computer science.

Turán-type extremal graph theory was later extended in several directions, including hypergraphs, geometric graphs, vertex-ordered graphs, convex geometric graphs, etc. Here we work with edge-ordered graphs as introduced by Gerbner et al. [5]. Let us recall the basic definitions.

Definition 1.2

An edge-ordered graph is a finite simple graph G together with a linear order on its edge set E. We often give the edge-order with an injective labeling $L: E\rightarrow {\mathbb {R}}$. We denote the edge-ordered graph obtained this way by $G^L$, in which an edge e precedes another edge f in the edge-order if $L(e)<L(f)$. We call $G^L$ the labeling or edge-ordering of G and call G the simple graph underlying $G^L$.

An isomorphism between edge-ordered graphs must respect the edge-order. A subgraph of an edge-ordered graph inherits the edge-order and so it is also an edge-ordered graph. We say that the edge-ordered graph G contains another edge-ordered graph H, if H is isomorphic to a subgraph of G otherwise we say that G avoids H.

For a positive integer n and an edge-ordered graph H with at least one edge, let the Turán number ${\textrm{ex}}_<(n,H)$ be the maximal number of edges in an edge-ordered graph on n vertices that avoids H. Fixing the forbidden edge-ordered graph H, ${\textrm{ex}}_<(n, H)$ is a function of n and we call it the extremal function of H.

A simple but important dichotomy in classical extremal graph theory is the following:

Observation 1

If F is a forest, then we have ${\textrm{ex}}(n,F)=O(n)$. Otherwise, if G is a simple graph that is not a forest, we have ${\textrm{ex}}(n,G)=\Omega (n^c)$ for some $c=c(G)>1$.

Let F be a forest on k vertices. The well-known Erdős–Sós conjecture claims that ${\textrm{ex}}(n,F)\le (k-2)n/2$, see [1]. Many special cases of this conjecture have been established, but it remains open in its full generality. However, it is easy to prove that if the minimum degree of a graph is at least $k-1$, then it contains F and this implies ${\textrm{ex}}(n,F)\le (k-2)n=O(n)$ as any graph on n vertices with more than $(k-2)n$ edges contains a subgraph of minimum degree $k-1$. To see the other direction of the observation above, consider a graph G that is not a forest. It contains a cycle $C_k$ and thus ${\textrm{ex}}(n,G)\ge {\textrm{ex}}(n,C_k)=\Omega (n^{1+1/k})$, where the bound on the extremal function of the cycle is proved by a standard application of the probabilistic method. For even values of k, see stronger lower bounds on ${\textrm{ex}}(n,C_k)$ in [8]. For odd values of k, we trivially have ${\textrm{ex}}(n,C_k)\ge \lfloor n^2/4\rfloor$ as the complete balanced bipartite graph does not contain $C_k$.

This observation gives a simple characterization of graphs with linear extremal functions and also claims the existence of a large gap in the extremal functions. Such a gap does not exist for edge-ordered graphs as there are several edge-ordered graphs (among them several distinct edge-orderings of the 4-edge path) whose extremal functions are $\Theta (n\log n)$, see [5]. Therefore one has two ways to find an analogue of Observation 1 about edge-ordered graphs. First, one can try to characterize edge-ordered graphs with strictly linear extremal functions, or one can try to characterize edge-ordered graphs with almost linear extremal function, that is, with extremal functions in the class $n^{1+o(1)}$. The former problem eluded a solution so far. We have partial results, namely characterization of connected edge-ordered graphs with linear extremal functions in the upcoming paper [7]. In this paper we address the latter problem, namely we prove the following conjecture of [5]:

Conjecture 1

The extremal function of an edge-ordered graph G is almost linear if and only if G is an edge-ordered forest of order chromatic number 2.

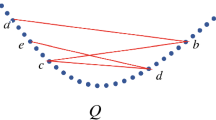
Here we use the term “edge-ordered forest” to denote an edge-ordered graph with a forest as its underlying simple graph. We use the terms “edge-ordered path” or “edge-ordered tree” similarly. The notion of order chromatic number is defined in [5]. Instead of recalling the definition we recall a simple characterization of edge-ordered forests of order-chromatic number 2, also from [5] that the reader can treat as a definition for the purposes of this paper. See Fig. 1 for an illustration.

Definition 1.3

We call a vertex v of an edge-ordered graph close if the edges incident to v are consecutive in the edge-ordering, that is, they form an interval in the edge-order.

Lemma 1.4

([5]) Let H be an edge-ordered forest with at least one edge. The order chromatic number of H is 2 if and only if H has a proper 2-coloring such that all vertices in one of the two color classes are close.

Fig. 1

Close vertices are colored in red and the non-close in blue. The tree on the left has order chromatic number higher than 2, while the one on the right has order chromatic number 2. (Colour figure online)

The most general result of Turán-type extremal graph theory is the Erdős–Stone–Simonovits theorem [2, 3]. It states that the extremal function of any non-bipartite forbidden simple graph is $\Theta (n^2)$ and gives the exact asymptotics in terms of the chromatic number of the forbidden graph. An analogous result for edge-ordered graphs appeared in [5]. It states that if the forbidden edge-ordered graph has order chromatic number larger than 2, then its extremal function is $\Theta (n^2)$ and gives the exact asymptotics in terms of its order chromatic number. A notable difference between the chromatic number of simple graphs and the order chromatic number of edge-ordered graphs is that the latter is not necessarily finite: the order chromatic number of a finite edge-ordered graph is either a positive integer or infinity.

In light of the above, the “only if” direction of Conjecture 1 is self-evident. Indeed, if the order chromatic number of an edge-ordered graph is not 2, then its extremal function is quadratic (note that the order chromatic number is 1 only for edge-ordered graphs with no edges, and extremal functions are not defined for those). And if the underlying simple graph $G_0$ of the edge-ordered graph G is not a forest, then we simply have

$$\begin{aligned} {\textrm{ex}}_<(n,G)\ge {\textrm{ex}}(n,G_0)=\Omega (n^c) \end{aligned}$$

for some $c=c(G)>1$. Here the first inequality trivially holds for the extremal functions of every edge-ordered graph and its underlying simple graph, while the equality is a special case of Observation 1 and can be simply verified for $c=k/(k-1)$ if $G_0$ contains a k-cycle.

Our main result here is proving the missing “if” direction of Conjecture 1 in a stronger form:

Theorem 1.5

If H is an edge-ordered forest with order chromatic number 2, then

$$\begin{aligned} {\textrm{ex}}_<(n,H)=n\cdot 2^{O(\sqrt{\log n})}. \end{aligned}$$

This result establishes a gap in the extremal functions of edge-ordered graphs, although this gap is smaller than the one we saw for simple graphs: if an extremal function is not of the form $n2^{O(\sqrt{\log n})}$, then it must be of the form $\Omega (n^c)$ for some $c>1$.

The vertex-ordered variant of Conjecture 1 has a longer history. Vertex-ordered graphs and their extremal functions can be defined analogously to edge-ordered graphs. Pach and the second author [9], proved the vertex-ordered version of the Erdős–Stone–Simonovits theorem in which the interval chromatic number plays the role played by the chromatic number in the classical result. They conjectured that the extremal functions of vertex-ordered forests of interval chromatic number 2 are $O(n\log ^{O(1)}n)$ or (in a weaker form of the conjecture) $n^{1+o(1)}$. Both forms of the conjecture are still open in general, but [9] proves the stronger form for vertex-ordered forests of up to 6 vertices and in a more recent paper Korándi et al. [6] prove the weaker conjecture for a large class of vertex-ordered forests.

The history of the vertex-ordered version of the conjecture goes back even more. Füredi and Hajnal [4], introduced the extremal function of 0–1 matrices in 1992 and formulated a conjecture that turns out to be equivalent to stating that an $O(n\log n)$ bound holds for the extremal function of any vertex-ordered forest of interval chromatic number 2. This proved to be too strong as Pettie [10] found a counterexample.

The rest of the paper is organized as follows. In Sect. 2 we state and prove Theorem 2.1 which serves as a single step in our density increment argument proving Theorem 1.5. This argument is presented in Sect. 3. We finish the paper with some concluding remarks in Sect. 4.

2 The Density Increment Step

As we have mentioned in the Introduction, we will use a density increment argument in the next section to prove Theorem 1.5. We use “density” informally here as we do not introduce a single parameter we would call the density of an (edge-ordered) graph, but rather we concentrate on two parameters: the average degree and the number of edges. A graph with n vertices and m edges has average degree $d=2m/n$. Note that in this setting the smaller the number of edges is (for a given average degree) the denser we consider the graph. The following theorem represents a density increment step as passing from a graph to its subgraph we only lose a constant factor in the average degree, but decrease the size (number of edges) more significantly.

Theorem 2.1

Let H be an edge-ordered forest on $\ell$ vertices with a proper 2-coloring such that one side consists of $k\ge 2$ vertices, all of which are close. If the edge-ordered graph G with m edges and average degree $d>0$ avoids H,  then G has a subgraph with at most f edges and average degree at least $d/(4k-4),$ where $f=\lfloor (134k\ell ^2/d)^{1/(k-1)}m\rfloor$.

We prove this theorem through a series of lemmas. We start by fixing the edge-ordered forest H together with k and $\ell$ as in the theorem. That is, H has $\ell$ vertices in total, out of which one side of a proper 2-coloring contains $k\ge 2$ vertices, all of which are close. For easier reference, we call these k vertices the left vertices and the remaining $\ell -k$ vertices the right vertices. Since the left vertices of H are close, we can enumerate them as $w_1,\dots ,w_k$ such that all the edges incident to $w_i$ precede any edge incident to $w_j$, whenever $i<j$.

We also fix the edge-ordered graph G with m edges and average degree $d>0$ that avoids H. G has $n=2m/d$ vertices. Let $G_0$ be its underlying simple graph and let us fix the labeling $G=G_0^L$ such that L uses the integer labels from 1 through m. We call a sequence of integer thresholds $t=(t_0,\dots ,t_k)$ satisfying $0=t_0<t_1<\cdots <t_k=m$ a grid. Using such a grid t we classify the edges of $G_0$ into k classes: we say that an edge e of G belongs to class j ($1\le j\le k$) if $t_{j-1}<L(e)\le t_j$. Let $G'$ be an arbitrary subgraph of G. For a class j and a vertex v of $G'$, we write $d_j(v)$ for the j-degree of v in $G'$, that is, for the number of class j edges incident to v in $G'$ (the dependence on the subgraph $G'$ and the grid t is omitted from the notation). Let us define the weight of a vertex v in $G'$ as $W_{G',t}(v)=\min _{1\le j\le k}d_j(v)$. See Fig. 2 for an illustration. We say that v is heavy in $G'$ if $W_{G',t}(v)\ge \ell$. The weight of the subgraph $G'$ is defined as $W_t(G')=\sum _{v\in V(G')}W_{G',t}(v)$.

Fig. 2

The figure depicts the neighborhood of a vertex v in a subgraph $G'$ of G. In this example we have $k=3$, $m=30$. Choosing the grid t consisting of the thresholds $0<10<20<30$ makes $d_1(v)=1$, $d_2(v)=3$, $d_3(v)=2$, and $W_{G',t}(v)=1$

Let $H'$ be a subgraph of H and $G'$ be a subgraph of G and let t be a grid. We call a map f a nice embedding of $H'$ in $G'$ if f maps the vertices of $H'$ to the vertices of $G'$, it induces an isomorphism between $H'$ and a subgraph of $G'$ (that is, it is injective, it maps edges to edges and it preserves the edge-order) and in addition it satisfies:

• (i) the image f(y) of any right vertex y is a heavy vertex in $G'$ and

• (ii) for any edge $w_iy$ in $H'$, $f(w_i)f(y)$ is a class i edge of $G'$.

Note that condition (ii) implies that f preserves the edge-order between edges incident to distinct left vertices. This makes it much simpler to check if a function f preserves the edge-order: beyond checking condition (ii) it is enough to compare the images of edges sharing a left vertex. This is the reason behind introducing nice embeddings, and also behind considering grids in general.

Lemma 2.2

If a subgraph $G'$ of G and a grid t satisfy $W_t(G')\ge 2\ell (u+1)n$ for some integer $u\ge 0,$ then any u-edge subgraph $H'$ of H has a nice embedding in $G'$.

Proof

We prove the lemma by induction on u. In the base case of $u=0$, $H'$ has no edges, so a nice embedding of $H'$ in $G'$ in this case is simply an injective mapping of the vertices of $H'$ to the vertices of $G'$ that maps right vertices to heavy vertices. The weight of any vertex v of $G'$ satisfies $W_{G',t}(v)\le n$, but their sum, $W_t(G')$ is at least $2\ell n$, so at least $\ell$ vertices are heavy in $G'$. Therefore we can choose a nice embedding of $H'$ in $G'$ and moreover we can even ensure that it maps all vertices of $H'$ to heavy vertices in $G'$.

Let $u\ge 1$ and assume that the statement of the lemma holds for subgraphs $H'$ of H with $u-1$ edges. Let us fix a subgraph $H'$ of H with u edges, a grid t and a subgraph $G'$ of G satisfying $W_t(G')\ge 2\ell (u+1)n$. We need to show that there is a nice embedding of $H'$ in $G'$. We distinguish two cases.

First we assume that there is a left leaf vertex in $H'$, say $w_i$. Let $H''$ be the subgraph obtained from $H'$ by removing $w_i$. It has $u-1$ edges, so we can apply the inductive hypothesis to $H''$ and find a nice embedding f of $H''$ in $G'$. Let y be the (only) neighbor of $w_i$ in $H'$. To extend f into a nice embedding of $H'$ in $G'$ all we need to do is find an image for $w_i$, a vertex x outside the image of $H''$ that is connected to f(y) by a class i edge. Indeed, conditions (i) and (ii) will be satisfied and the extended embedding still preserves the edge-order because the edge xf(y) is the only class i edge in the image of $H'$ and this determines its order among the other edges in the image $f(H')$. Clearly, y is a right vertex, so by condition (i), its image f(y) is heavy in $G'$, so there are at least $\ell$ other vertices connected to f(y) by a class i edge of $G'$. We can choose one of them outside the image of $H''$ which gives us a nice embedding of $H'$ in $G'$.

Assume now that $H'$ has no left leaf. In this case we find a right leaf y of $H'$ such that its (only) neighbor $w_i$ satisfies the condition that the edge $yw_i$ is either the smallest or the largest among the edges incident to $w_i$ in $H'$. Let us first see why such a leaf y exists. Start a path in $H'$ at an arbitrary non-isolated vertex and continue always on the lowest or the highest edge incident to the current vertex. Choose among these two options to avoid backtracking. As $H'$ is a forest, one eventually hits a leaf, say y which must be a right vertex (since by assumption there are no left leaves) and must satisfy the condition stated above.

Let us obtain $H''$ by removing y from $H'$. We will use the inductive hypothesis for $H''$ not with respect to $G'$ but with respect to a subgraph of $G'$. We call an edge xz of $G'$ eligible for z if it is a class i edge and x is heavy in $G'$. If $yw_i$ is the smallest edge at $w_i$ in $H'$, then we obtain the subgraph $G''$ by removing the $\ell$ smallest eligible edges from $G'$ for every vertex z of $G'$. Similarly, if $yw_i$ is the largest edge at $w_i$ in $H'$, then we obtain the subgraph $G''$ by removing the $\ell$ largest eligible edges from $G'$ for every vertex z of $G'$. In both cases, if there are fewer than $\ell$ eligible edges for a vertex we remove them all. This way we remove at most $\ell n$ edges in total. Note that as $G''$ is a subgraph of $G'$, therefore heavy vertices in $G''$ are also heavy in $G'$.

Let us consider how a single edge deletion changes the weights of the vertices. Clearly, only the weights of the two vertices connected by the deleted edge can change, and they decrease by at most 1. Thus, removing at most $\ell n$ edges from $G'$ decreases its weight by at most $2\ell n$, so we have

$$\begin{aligned} W_t(G'')\ge W_t(G')-2\ell n\ge 2\ell (u+1)n-2\ell n=2\ell un. \end{aligned}$$

This makes the induction hypothesis applicable, so there is a nice embedding f of $H''$ in $G''$. We want to extend f with a well chosen image x for y to obtain a nice embedding of $H'$ in $G'$. We must choose a heavy vertex x in $G'$ [to satisfy condition (i)] that is connected to $f(w_i)$ with a class i edge [to satisfy condition (ii)]. In other words, the edge $xf(w_i)$ must be eligible for $f(w_i)$. Furthermore, this vertex x must be outside the image of $H''$ and (to preserve the edge-order) the edge $xf(w_i)$ must be in the correct place in the edge-order compared to the images of the edges of $H''$.

Let us consider the case when $yw_i$ is the smallest edge of $H'$ incident to $w_i$, the other case can be handled similarly. Note that $w_i$ is not a leaf as $H'$ has no left leaves. Let $y'w_i$ be the second smallest edge of $H'$ at $w_i$. Clearly, $f(y')f(w_i)$ is a class i edge in $G''$ by condition (ii) and $f(y')$ is heavy in $G''$ by condition (i). Therefore $f(y')$ is also heavy in $G'$, so the edge $f(y')f(w_i)$ is eligible for $f(w_i)$. This is an edge in $G''$ and by the construction of $G''$ we know that $\ell$ smaller eligible edges for $f(w_i)$ were removed from $G'$. We choose x such that $xf(w_i)$ is one of these removed smaller eligible edges and x is outside the image of $H''$. This choice leads to a nice embedding of $H'$ in $G'$ because conditions (i) and (ii) are satisfied and $xf(w_i)$ (being smaller than the edge $f(y')f(w_i)$) must be the smallest class i edge in the image of $H'$. This finishes the proof of the inductive step and with that, the proof of the lemma. $\square$

We needed the subgraphs $H'$ of H and $G'$ of G for the induction to work, but we will only use the following corollary based on the special case $H'=H$, $G'=G$:

Corollary 2.3

We have $W_t(G)<2\ell ^2n$ for any grid t.

Proof

If $W_t(G)\ge 2\ell ^2n$, then H has a nice embedding in G by Lemma 2.2. This contradicts our assumption that G avoids H. $\square$

So far we considered a fixed grid. But from now on, we consider a uniform random grid, that is, we choose a grid t consisting of integer thresholds $0=t_0<t_1<t_2<\cdots <t_k=m$ uniformly from all the $\left( {\begin{array}{c}m-1\\ k-1\end{array}}\right)$ possible grids. We will use $E_t[\cdot ]$ to denote the expectation with respect to a random grid. In order for this to make sense we assume $m\ge k$. We do not lose generality with this assumption as if $m<k$, then $f\ge m$ and therefore the statement of Theorem 2.1 is satisfied with choosing G itself as the “dense” subgraph.

Let us denote the degree of a vertex v in G by $d_v$. We call this vertex v a tame vertex if one can cover the labels of at least $0.9d_v$ of the edges incident to v by $k-1$ (well chosen) intervals, each of length f. Otherwise, we call v a wild vertex. Recall that f is given in Theorem 2.1 in terms of k, $\ell$, m and d.

Lemma 2.4

Any wild vertex v of G satisfies

$$\begin{aligned} E_t[W_{G,t}(v)]\ge \frac{d_v(f+1)^{k-1}}{10k\left( {\begin{array}{c}m-1\\ k-1\end{array}}\right) }. \end{aligned}$$

Proof

Let . Consider the set S of labels of the $d_v$ edges incident to v, let $a_1$ be the cth smallest element in S and set $I_1$ to be the interval $[a_1,a_1+f]$. Note that there are exactly $c-1$ elements of S below $I_1$. For $i>1$, we consider the elements in S above $I_{i-1}$, take $a_i$ to be the cth smallest among them (if it exists) and set $I_i=[a_i,a_i+f]$. As before, we have exactly $c-1$ elements of S between $I_{i-1}$ and $I_i$. This process ends with the interval $I_{i^*}$ if there are fewer than c elements of S above $I_{i^*}$. See Fig. 3.

Fig. 3

An illustration for the proof of Lemma 2.4. The values marked are the labels of the edges incident to some wild vertex v. If we have $f=7$ and $c=3$, then the intervals $I_i$ are as shown and we have $i^*=3$ such intervals

Consider first the case $i^*<k$. The elements of S not covered by the intervals $I_1,\dots ,I_{i^*}$ are either below $I_1$, above $I_{i^*}$ or between $I_i$ and $I_{i+1}$ for some $1\le i<i^*$. We saw that we have at most $c-1$ elements of S in each of these $i^*+1$ categories, so we have at most $(i^*+1)(c-1)<d_v/10$ elements of S not covered. As $i^*\le k-1$ this means that v is tame, contrary to our assumption.

So we must have $i^*\ge k$. Consider the grids $t=(t_0,\ldots ,t_k)$ where $t_0=0$, $t_k=m$ and $t_i$ is an integer from $I_i$ for $1\le i<k$. We can choose these intermediate values $t_i$ in exactly $f+1$ ways, so we have $(f+1)^{k-1}$ such grids. For each such grid t, the edges with labels up to and including $a_1$ are class 1 edges. As $a_1$ is the cth smallest value in S, we have at least c such edges incident to v making the 1-degree of v at least c. Similarly, for $1<i\le k$, all the edges with labels above $I_{i-1}$ but at most $a_i$ are necessarily class i edges. As $a_i$ is the cth smallest element of S above $I_{i-1}$ we have at least c class i edges adjacent to v. This makes $W_{G,t}(v)\ge c$ for each of the grids considered. So by Markov’s inequality we get $E_t[W_{G,t}(v)]\ge \frac{(f+1)^{k-1}}{\left( {\begin{array}{c}m-1\\ k-1\end{array}}\right) }c\ge \frac{d_v(f+1)^{k-1}}{10k\left( {\begin{array}{c}m-1\\ k-1\end{array}}\right) }$ as needed. $\square$

Let us now fix a suitable set of intervals for every tame vertex of G. So we have $k-1$ intervals of length f associated to each tame vertex, and they collectively cover the labels of at least 0.9 fraction of the incident edges. We define a subgraph $G^*$ of G as follows. The vertices of $G^*$ are the tame vertices of G, the edges of $G^*$ are the edges uv of G such that both u and v are tame and the label L(uv) is covered by an interval associated to u and also by a (possibly different) interval associated to v. Note that our construction ensures that the labels of each star subgraph in $G^*$ are covered by the intervals associated to the center vertex.

Lemma 2.5

$G^*$ has at least m/2 edges.

Proof

Instead of counting edges in $G^*$, we count edges of G outside $G^*$. For each such edge e we blame one of the vertices connected by e: either a wild vertex or a tame vertex with none of the intervals associated to it covering L(e).

If v is tame, the associated intervals cover the labels of $0.9d_v$ edges, so we blame v for the exclusion of at most $0.1d_v$ edges. All together, tame vertices are blamed for the exclusion of at most $\sum _{v\mathrm {\ tame}}0.1d_v\le 0.1\sum _vd_v=0.2m$ edges.

By Corollary 2.3 we have $W_t(G)<2\ell ^2n$ for any grid t. So this holds for the expected weight too, giving the first inequality below:

$$\begin{aligned} 2\ell ^2n> & {} E_t[W_t(G)]\\= & {} \sum _vE_t[W_{G,t}(v)]\\\ge & {} \sum _{v\mathrm {\ wild}}E_t[W_{G,t}(v)]\\\ge & {} \sum _{v\mathrm {\ wild}}\frac{d_vf^{k-1}}{10k\left( {\begin{array}{c}m-1\\ k-1\end{array}}\right) }\\= & {} \frac{f^{k-1}}{10k\left( {\begin{array}{c}m-1\\ k-1\end{array}}\right) }\sum _{v\mathrm {\ wild}}d_v, \end{aligned}$$

where the equation in the second line is the linearity of expectation, and the inequality in the fourth line comes from Lemma 2.4.

If v is wild, it is blamed for the exclusion of all $d_v$ incident edges. Thus, wild vertices are blamed for the exclusion of at most

$$\begin{aligned} \sum _{t\mathrm {\ wild}}d_v\le \frac{20k\ell ^2n\left( {\begin{array}{c}m-1\\ k-1\end{array}}\right) }{f^{k-1}}<0.3m \end{aligned}$$

edges, where the first inequality comes from the calculation in the previous paragraph, while the second inequality is guaranteed by the coarse bound $\left( {\begin{array}{c}m-1\\ k-1\end{array}}\right) <m^{k-1}$ and the choice of f in the statement of Theorem 2.1.

As the exclusion of at most 0.2m edges from $G^*$ is blamed on tame vertices and the exclusion of at most 0.3m edges is blamed on wild vertices we must have at least m/2 edges not excluded. $\square$

All we need to finish the proof of Theorem 2.1 is Lemma 2.5.

Proof

(Proof of Theorem 2.1) Let us summarize what we proved so far. We fixed H and G as in the theorem and further fixed a labeling L giving the labels $1,\dots ,m$ to the m edges of the underlying simple graph $G_0$ of G making $G=G_0^L$. We identified a subgraph $G^*$ of G where the labels of the edges in each star subgraph can be covered by $k-1$ intervals of length f each. Finally, we proved Lemma 2.5 stating that $G^*$ has at least m/2 edges.

We partition $G^*$ into subgraphs as follows: For , we define $G^*_j$ to be the subgraph of $G^*$ consisting of the edges e with $(j-1)f<L(e)\le jf$. A vertex v of $G^*$ is a vertex of $G^*_j$ if at least one of the edges incident to v is in $G^*_j$. Note that the edges with labels from an interval of length f can show up in at most two different subgraphs $G^*_j$, therefore any vertex of $G^*$ shows up in at most $2k-2$ subgraphs $G^*_j$.

Clearly, $G^*_j$ is a subgraph of G with at most f edges. To finish the proof of the theorem we only need to establish that one of them has high enough average degree. For this, consider the disjoint union Z of all the graphs $G^*_j$. Each edge of $G^*$ appears exactly once in Z, so we have $|E(Z)|=|E(G^*)|\ge m/2$. Each of the vertices of $G^*$ has at most $2k-2$ copies in Z, so we have $|V(Z)|\le (2k-2)|V(G^*)|\le (2k-2)n$. This makes the average degree of Z at least $m/((2k-2)n)=d/(4k-4)$. At least one of the constituent graphs $G^*_j$ has average degree at least as high as their disjoint union Z, finishing our proof. $\square$

3 Proof of Theorem 1.5

To prove Theorem 1.5 we will use Theorem 2.1 recursively. This is a standard calculation, but we write it down in full details to be self-contained. We make no effort to optimize the constants.

Let H be an edge-ordered forest of order chromatic number 2. By Lemma 1.4 it satisfies the conditions of Theorem 2.1 for the appropriate values of the parameters k and $\ell$ unless the number of vertices on one side of the bipartition is $k=1$. However, if $k=1$, then H is an edge-ordered star (with a few isolated vertices possibly added) and therefore it has a single edge-ordering up to isomorphism. In this case its extremal function agrees with the extremal function of its underlying simple graph, which is linear. Therefore we can assume $k>1$ and then Theorem 2.1 does apply to H.

Let $G_0$ be an arbitrary edge-ordered graph avoiding H. If $G_0$ has $n_0$ vertices and $m_0\ge 1$ edges, then it has average degree $d_0=2m_0/n_0$. To simplify our calculation we will introduce various constants $c_i$ depending on H and not depending on $G_0$. By Theorem 2.1, $G_0$ contains a subgraph $G_1$ with $m_1\le c_1m_0/d_0^{c_2}$ edges and average degree $d_1\ge d_0/c_3$, where $c_1=(134k\ell ^2)^{1/(k-1)}>1$, $c_2=1/(k-1)>0$ and $c_3=4k-4>1$. Any subgraph of $G_0$ must also avoid H, so we can apply Theorem 2.1 recursively: for $t\ge 0$ let $G_{t+1}$ be a subgraph of $G_t$ as specified in the theorem. If we write $d_t$ for the average degree of $G_t$ and $m_t$ for the number of edges in $G_t$, we have

$$\begin{aligned} d_{t+1}\ge d_t/c_3\quad m_{t+1}\le c_1m_t/d_t^{c_2} \end{aligned}$$

for every $t\ge 0$. This recursion solves to

$$\begin{aligned} d_t\ge \frac{d_0}{c_3^t}\quad m_t\le \frac{c_1^tc_3^{c_2\left( {\begin{array}{c}t\\ 2\end{array}}\right) }}{d_0^{c_2t}}m_0. \end{aligned}$$

The average degree cannot exceed the number of edges, so $m_t\ge d_t$ holds for all t. This inequality can be rearranged to obtain

$$\begin{aligned} d_0^{c_2t}\le \frac{m_0}{d_0}\cdot (c_1c_3)^t\cdot c_3^{c_2\left( {\begin{array}{c}t\\ 2\end{array}}\right) }. \end{aligned}$$

This implies that at least one of the following three inequalities must hold for every t:

$$\begin{aligned} d_0^{c_2t/3}\le & {} \frac{m_0}{d_0},\end{aligned}$$

(1)

$$\begin{aligned} d_0^{c_2t/3}\le & {} (c_1c_3)^t, \end{aligned}$$

(2)

$$\begin{aligned} d_0^{c_2t/3}\le & {} c_3^{c_2\left( {\begin{array}{c}t\\ 2\end{array}}\right) }. \end{aligned}$$

(3)

We choose . Here and further in this calculation we use $\log$ to denote the binary logarithm. We need $t\ge 1$ for our calculations, so here we assume $d_0>1$. Our choice ensures that (3) does not hold. If (2) holds, we have $d_0\le (c_1c_3)^{3/c_2}$ and therefore

$$\begin{aligned} m_0=n_0d_0/2\le c_4n_0, \end{aligned}$$

(4)

with $c_4=(c_1c_3)^{3/c_2}/2$. Note that as $c_4>1/2$, this bound holds also in the case $d_0\le 1$ that we earlier excluded. If (1) holds, inserting the value of t we obtain

$$\begin{aligned} \frac{n_0}{2}=\frac{m_0}{d_0}\ge 2^{\frac{2c_2\log ^2d_0}{9\log c_3}}. \end{aligned}$$

Rearrangement gives

$$\begin{aligned} \log d_0\le c_5\sqrt{\log n_0}, \end{aligned}$$

for $c_5=\sqrt{\frac{9\log c_3}{2c_2}}$. This yields

$$\begin{aligned} m_0=n_0d_0/2\le n_02^{c_5\sqrt{\log n_0}}. \end{aligned}$$

(5)

As either (4) or (5) must hold for any edge-ordered graph $G_0$ having $n_0$ vertices and $m_0$ edges, we have

$$\begin{aligned} {\textrm{ex}}_<(n,H)\le \max (c_4n,n2^{c_5\sqrt{\log n}})=n2^{O(\sqrt{\log n})} \end{aligned}$$

as needed.

4 Concluding Remarks

The main open problem related to this paper is whether our Theorem 1.5 can be improved. We believe it can be improved and so we formulate the following conjecture that is the edge-ordered analogue of a similar conjecture on vertex-ordered graphs from [9].

Conjecture 2

${\textrm{ex}}_<(n,H)=n\log ^{O(1)}n$ holds for all edge-ordered forests H of order chromatic number 2.

Such strong upper bounds were proved for several small edge-ordered paths in [5], including all 4-edge edge-ordered paths. In particular, an upper bound $O(n\log n)$ was proved for the extremal function of all edge-ordered 4-edge paths of order chromatic number 2 but for the equivalent exceptional cases of the path $P_5^{1342}$ and $P_5^{4213}$. (The upper index should be interpreted as the list of labels along the path.) For the extremal function of these exceptional edge-ordered paths an $O(n\log ^2n)$ bound was proved. In an upcoming paper [7] we extend this study to most edge-ordered 5-edge paths of order chromatic number 2, proving an upper bound of either O(n), $O(n\log n)$ or $O(n\log ^2 n)$ for their extremal functions, but (up to equivalence) four exceptional edge-ordered 5-edge paths: $P_6^{14523}$, $P_6^{15423}$, $P_6^{31254}$ and $P_6^{14532}$ eluded our efforts and for their extremal functions only the weaker upper bounds from this paper apply.

From the other direction, we know many edge-ordered forests of order chromatic number 2 (including several edge-ordered 4-edge paths) whose extremal function is $\Omega (n\log n)$ (see [5]) but we do not have a single example with a extremal function higher than that. Learning from Pettie’s refutation [10] of a conjecture of Füredi and Hajnal [4] (see the context in the Introduction), we refrain from making too strong a conjecture here, instead we ask whether an edge-ordered version of Pettie’s example can be found, that is an edge-ordered tree of order chromatic number 2 with extremal function $\Omega (n\log n\log \log n)$ (or higher)?