Leray Numbers of Tolerance Complexes

Abstract

Let K be a simplicial complex on vertex set V. K is called d-Leray if the homology groups of any induced subcomplex of K are trivial in dimensions d and higher. K is called d-collapsible if it can be reduced to the void complex by sequentially removing a simplex of size at most d that is contained in a unique maximal face. Motivated by results of Eckhoff and of Montejano and Oliveros on “tolerant” versions of Helly’s theorem, we define the t-tolerance complex of K, ${\mathcal {T}}_{t}(K)$, as the simplicial complex on vertex set V whose simplices are formed as the union of a simplex in K and a set of size at most t. We prove that for any d and t there exists a positive integer h(t, d) such that, for every d-collapsible complex K, the t-tolerance complex ${\mathcal {T}}_t(K)$ is h(t, d)-Leray. As an application, we present some new tolerant versions of the colorful Helly theorem.

1 Introduction

Let ${\mathcal {F}}$ be a finite family of non-empty sets. The nerve of ${\mathcal {F}}$ is the simplicial complex

$$\begin{aligned} N({\mathcal {F}}) = \left\{ {\mathcal {F}}' \subset {\mathcal {F}}: \bigcap _{A\in {\mathcal {F}}'} A \ne \varnothing \right\} . \end{aligned}$$

A simplicial complex K is called d-representable if it is isomorphic to the nerve of a family of convex sets in ${\mathbb {R}}^d$.

Two closely related notions are the d-collapsibility and d-Lerayness of a complex, which were introduced by Wegner in [23] as generalizations of d-representability. Let V be a finite set, and let K be a simplicial complex on vertex set V. A face $\sigma$ in K is said to be free if there exists exactly one maximal face of K that contains $\sigma$. Given a free face $\sigma$ of cardinality at most d, we call the operation of removing from K all faces containing $\sigma$ an elementary d-collapse. The complex K is called d-collapsible if all of its faces can be removed by performing a sequence of elementary d-collapses. The collapsibility number of K, denoted by C(K), is the minimum integer d such that K is d-collapsible.

Let ${{\mathbb {F}}}$ be a field. For an integer $i\ge -1$, let ${\tilde{H}}_{i}\left( K\right)$ be the reduced i-dimensional homology group of K with coefficients in ${\mathbb {F}}$. For $U\subset V$, the subcomplex of K induced by U is the complex $K[U]=\{\sigma \in K:\, \sigma \subset U\}.$ The complex K is called d-Leray (over ${{\mathbb {F}}}$) if all its induced subcomplexes have trivial reduced homology groups in dimensions d and higher; that is, if ${\tilde{H}}_{i}\left( K[U]\right) = 0$ for all $i \ge d$ and $U\subset V$. The Leray number of K (over ${{\mathbb {F}}}$), denoted by L(K), is the minimum integer d such that K is d-Leray.

It was shown in [23] that every d-representable complex is d-collapsible, and that every d-collapsible complex is d-Leray. See the survey paper by Tancer [21] for an overview of d-representability, d-collapsibility and d-Lerayness.

Helly’s theorem [8] is a fundamental result in combinatorial geometry that asserts the following: for every finite family of convex sets in ${\mathbb {R}}^d$, if every subfamily of size at most $d+1$ has a point in common, then the whole family has a point in common. See, for example, [1] for an overview of results and open problems related to Helly’s theorem.

Let K be a complex on vertex set V. A missing face of K is a set $\tau \subset V$ such that $\tau \notin K$ but $\sigma \in K$ for any $\sigma \subsetneq \tau$. The Helly dimension of K, denoted by h(K), is the maximum dimension of a missing face of K. Helly’s theorem is equivalent to the fact that, if K is d-representable, then $h(K)\le d$.

Since the boundary of a k-dimensional simplex has non-trivial homology in dimension $k-1$, then every d-Leray complex K does not contain the boundary of a k-dimensional simplex as an induced subcomplex, for any $k> d$. This shows that the bound $h(K) \le d$ also holds when K is d-Leray (and therefore the same holds when K is d-collapsible).

Let ${\mathcal {H}}$ be an r-uniform hypergraph on vertex set V. The covering number of ${\mathcal {H}}$, denoted by $\tau ({\mathcal {H}})$, is the minimum size of a set $U\subset V$ such that U intersects all the edges of ${\mathcal {H}}$. The hypergraph ${\mathcal {H}}$ is called t-critical if $\tau ({\mathcal {H}})=t$ and $\tau ({\mathcal {H}}')<t$ for every hypergraph ${\mathcal {H}}'$ that is obtained from ${\mathcal {H}}$ be removing an edge. The Erdős-Gallai number $\eta (r,t)$ is the maximum number of vertices in an r-uniform t-critical hypergraph. Equivalently, $\eta (r,t)$ is the minimum positive integer n such that for every r-uniform hypergraph ${\mathcal {H}}$ with $\tau ({\mathcal {H}}) \ge t$ there exists an ${\mathcal {H}}' \subset {\mathcal {H}}$ with $|V({\mathcal {H}}')| \le n$ such that $\tau ({\mathcal {H}}') \ge t$. Erdős and Gallai showed in [7] that $\eta (2,t)=2t$ and $\eta (r,2)=\left\lfloor \left( \frac{r+2}{2}\right) ^2\right\rfloor$. For general r and t, Tuza proved in [22] the bound

$$\begin{aligned} \eta (r,t)< \left( {\begin{array}{c}r+t-1\\ r-1\end{array}}\right) +\left( {\begin{array}{c}r+t-2\\ r-1\end{array}}\right) , \end{aligned}$$

which is tight up to a constant factor. Recently, an improved bound $\eta (3,t)\le \left( {\begin{array}{c}t+2\\ 2\end{array}}\right) +O(t^{5/3})$ was proved by Kézdy and Lehel in [13]. In particular, we have $\eta (r,t)=O(t^{r-1})$ for r fixed and $t\rightarrow \infty$, and $\eta (r,t)=O(r^t)$ for t fixed and $r\rightarrow \infty$.

Let ${\mathcal {F}}$ be a finite family of sets. We say that ${\mathcal {F}}$ has a point in common with tolerance t if there is a subfamily ${\mathcal {F}}'\subset {\mathcal {F}}$ such that $|{\mathcal {F}}'|\ge |{\mathcal {F}}|-t$ and $\cap _{A\in {\mathcal {F}}'} A \ne \varnothing$. In other words, ${\mathcal {F}}$ has a point in common with tolerance t if there exists a point in ${{\mathbb {R}}}^d$ intersecting all but at most t of the sets in ${\mathcal {F}}$.

The following “tolerant version” of Helly’s theorem was observed by Eckhoff in [6], and independently by Montejano and Oliveros in [18].

Theorem 1.1

(Eckhoff [6, Section 6], Montejano and Oliveros  [18, Theorem 3.1]) Let ${\mathcal {F}}$ be a finite family of convex sets in ${{\mathbb {R}}}^d$, and let $t\ge 0$ be an integer. If every subfamily ${\mathcal {F}}'\subset {\mathcal {F}}$ of size at most $\eta (d+1,t+1)$ has a point in common with tolerance t, then ${\mathcal {F}}$ has a point in common with tolerance t.

In fact, it was shown in [18] (and implicitly in [6]) that any family of sets satisfying a “Helly property” satisfies also a corresponding “tolerant Helly property”. In terms of simplicial complexes, this may be stated as follows:

Let K be a simplicial complex on vertex set V. For any integer $t\ge 0$, we define the simplicial complex

$$\begin{aligned} {\mathcal {T}}_{t}(K)&= \{\eta \cup \tau :\, \eta \in K, \, \tau \subset V,\, |\tau |\le t\} \\&= \{\sigma \subset V: \exists \eta \subset \sigma , |\sigma \setminus \eta |\le t, \, \eta \in K\}. \end{aligned}$$

We call ${\mathcal {T}}_{t}(K)$ the t-tolerance complex of K. Note that ${\mathcal {T}}_{0}(K)=K$ for every complex K.

Theorem 1.2

(Montejano-Oliveros [18, Theorem 1.1]) Let K be a simplicial complex with $h(K)\le d$, and let $t\ge 0$ be an integer. Then, $h({\mathcal {T}}_{t}(K))\le \eta (d+1,t+1)-1$.

It is natural to ask whether we can achieve a stronger conclusion by strengthening the assumptions on K. By replacing the Helly dimension with the collapsibility or Leray number, the following conjectures arise:

Conjecture 1.3

Let K be a d-Leray simplicial complex. Then, ${\mathcal {T}}_{t}(K)$ is $(\eta (d+1,t+1)-1)$-Leray.

Conjecture 1.4

Let K be a d-collapsible simplicial complex. Then, ${\mathcal {T}}_{t}(K)$ is $(\eta (d+1,t+1)-1)$-collapsible.

Let $t\ge 1$, and let A and B be two disjoint sets of size $t+1$ each. Let K be the simplicial complex on vertex set $A\cup B$ whose maximal faces are the sets A and B. It is easy to check that K is 1-collapsible, and therefore 1-Leray (in fact, it is easy to show that it is even 1-representable). On the other hand, the complex ${\mathcal {T}}_{t}(K)$ is the boundary of the simplex $A\cup B$. That is, ${\mathcal {T}}_{t}(K)$ is a 2t-dimensional sphere. In particular, it is not 2t-Leray. Therefore, for $d=1$, the bound $\eta (2,t+1)-1= 2t+1$ in Conjectures 1.3 and 1.4 cannot be improved.

For $t=1$, it was shown in [19] and independently in [18, Theorem 3.2] that there exists a d-representable complex K such that ${\mathcal {T}}_{1}(K)$ is the boundary of a $\left( \left\lfloor \left( \frac{d+3}{2}\right) ^2\right\rfloor -1\right)$-dimensional simplex. In particular, ${\mathcal {T}}_{1}(K)$ is not $\left( \left\lfloor \left( \frac{d+3}{2}\right) ^2\right\rfloor -2\right)$-Leray. Therefore, for $t=1$, the bound $\eta (d+1,2)-1=\left\lfloor \left( \frac{d+3}{2}\right) ^2\right\rfloor -1$ in Conjectures 1.3 and 1.4 cannot be improved.

On the other hand, it was recently shown in [9] that for $d=2$ and $t=3$ the bound in Theorem 1.1 is not tight. This suggests that the bounds in Conjectures 1.4 and 1.3 may also not be sharp in general.

Our main result is the following:

Theorem 1.5

Let K be a d-collapsible complex, and let $t\ge 0$ be an integer. Then, ${\mathcal {T}}_{t}(K)$ is h(t, d)-Leray, where $h(0,d)=d$ for all $d\ge 0$, and for $t>0$,

$$\begin{aligned} h(t,d)= \left( \sum _{s=1}^{\min \{t,d\}} \left( {\begin{array}{c}d\\ s\end{array}}\right) (h(t-s,d)+1)\right) + d. \end{aligned}$$

Note that we require the stronger property (collapsibility) for K, and obtain only the weaker property (Leray) for the tolerance complex. For $d=1$, we obtain the tight bound $h(t,1)=2t+1=\eta (2,t+1)-1$. For $d>1$, h(t, d) is larger than the conjectural bound $\eta (d+1,t+1)-1$. However, when t is fixed, we have $h(t,d)=O(d^{t+1})$, which is of the same order of magnitude as that of $\eta (d+1,t+1)-1$.

In the special case $d=2, t=1$, we can prove the following stronger bound:

Theorem 1.6

Let K be a 2-collapsible complex. Then, ${\mathcal {T}}_{1}(K)$ is 5-Leray.

Note that, since $5=\eta (3,2)-1$, the bound in Theorem 1.6 is tight.

In [11, 12], Kalai and Meshulam studied the effects of different operations on the Leray numbers of simplicial complexes. They showed that unions and intersections of simplicial complexes [11], and certain projections of complexes [12], preserve the boundedness of Leray numbers. By Theorems 1.5 and 1.6, the t-tolerance construction ${\mathcal {T}}_t(\cdot )$ is another example of such a “Leray preserving” operation (although under the stronger assumption of bounded collapsibility of the original complex). It would be interesting to find other such operations.

1.1 Organization

The paper is organized as follows. In Sect. 2 we present some basic facts about simplicial complexes, homology and collapsibility. In Sect. 3 we prove some auxiliary topological results that we will use later. In Sect. 4 we prove our main result, Theorem 1.5. In Sect. 5 we prove Theorem 1.6 about the Leray number of the 1-tolerance complex of a 2-collapsible complex. In Sect. 6 we present some applications to tolerant versions of the colorful Helly theorem.

2 Background

In this section we recall some basic definitions and results about simplicial complexes, homology and collapsibility.

2.1 Simplicial Complexes

Let V be a finite set and let $K\subset 2^V$ be a family of sets. K is called a simplicial complex if $\sigma \in K$ for all $\tau \in K$ and $\sigma \subset \tau$. The set V is called the vertex set of K. A set $\sigma \in K$ is called a simplex or a face of K. The dimension of a simplex $\sigma \in K$ is $\dim (\sigma )=|\sigma |-1$. For short, we call a k-dimensional simplex a k-simplex. Let K(k) be the set of all k-simplices.

The dimension of the complex K, denoted by $\dim (K)$, is the maximal dimension of a simplex in K.

$K'$ is a subcomplex of K if it is a simplicial complex, and each simplex of $K'$ is also a simplex of K.

Let $U\subset V$. The subcomplex of K induced by U is the complex

$$\begin{aligned} K[U]=\{\sigma \in K:\, \sigma \subset U\}. \end{aligned}$$

Let $\sigma \in K$. We define the link of $\sigma$ in K to be the subcomplex

$$\begin{aligned} {{\,\textrm{lk}\,}}(K,\sigma )= \{\tau \in K: \, \sigma \cap \tau =\varnothing ,\, \sigma \cup \tau \in K\}, \end{aligned}$$

the star of $\sigma$ in K to be the subcomplex

$$\begin{aligned} {{\,\textrm{st}\,}}(X,\sigma )= \{\tau \in K:\, \sigma \cup \tau \in K\} \end{aligned}$$

and the costar of $\sigma$ in K to be the subcomplex

$$\begin{aligned} {{\,\textrm{cost}\,}}(K,\sigma ) = \{\tau \in K:\, \sigma \not \subset \tau \}. \end{aligned}$$

If $\sigma =\{v\}$, we write ${{\,\textrm{lk}\,}}(K,v)={{\,\textrm{lk}\,}}(K,\{v\})$, ${{\,\textrm{st}\,}}(K,v)={{\,\textrm{st}\,}}(K,\{v\})$ and $K{\setminus } v= {{\,\textrm{cost}\,}}(K,\{v\})=K[V{\setminus } \{v\}]$.

Let X, Y be simplicial complexes on disjoint vertex sets. We define the join of X and Y to be the simplicial complex

$$\begin{aligned} X *Y= \{ \sigma \cup \tau :\, \sigma \in X, \tau \in Y\}. \end{aligned}$$

Let $v\in V$. If $v\in \tau$ for every maximal face $\tau \in K$ we say that K is a cone over v.

For $U\subset V$, we denote by $2^U=\{\sigma :\, \sigma \subset U\}$ the complete complex on vertex set U.

2.2 Simplicial Homology

Let K be a simplicial complex, and let ${{\mathbb {F}}}$ be a field. Let ${\tilde{H}}_{k}\left( K\right)$ be the k-th reduced homology group of K with coefficients in ${{\mathbb {F}}}$. We say that K is acyclic if ${\tilde{H}}_{k}\left( K\right) =0$ for all $k\ge -1$.

A useful tool for computing homology is the Mayer-Vietoris long exact sequence:

Theorem 1.7

(Mayer–Vietoris) Let X, Y be simplicial complexes. Then, there is an exact sequence

$$\begin{aligned} \cdots \rightarrow {\tilde{H}}_{k}\left( X\cap Y \right) \rightarrow {\tilde{H}}_{k}\left( X \right) \bigoplus {\tilde{H}}_{k}\left( Y \right) \rightarrow {\tilde{H}}_{k}\left( X\cup Y \right) \rightarrow {\tilde{H}}_{k-1}\left( X\cap Y \right) \rightarrow \cdots \end{aligned}$$

The following special case will be of use later:

Theorem 1.8

Let K be a simplicial complex on vertex set V, and let $v\in V$. Then, there is an exact sequence

$$\begin{aligned} \cdots \rightarrow {\tilde{H}}_{k}\left( {{\,\textrm{lk}\,}}(K,v) \right) \rightarrow {\tilde{H}}_{k}\left( K\setminus v \right) \rightarrow {\tilde{H}}_{k}\left( K \right) \rightarrow {\tilde{H}}_{k-1}\left( {{\,\textrm{lk}\,}}(K,v) \right) \rightarrow \cdots \end{aligned}$$

Proof

Let $A=K{\setminus } v$ and $B={{\,\textrm{st}\,}}(K,v)$. By Theorem 2.1, we have a long exact sequence

$$\begin{aligned} \cdots \rightarrow {\tilde{H}}_{k}\left( A\cap B \right) \rightarrow {\tilde{H}}_{k}\left( A \right) \bigoplus {\tilde{H}}_{k}\left( B \right) \rightarrow {\tilde{H}}_{k}\left( A\cup B \right) \rightarrow {\tilde{H}}_{k-1}\left( A\cap B \right) \rightarrow \cdots \end{aligned}$$

Note that B is a cone over v, and therefore ${\tilde{H}}_{k}\left( B \right) =0$ for all k. Moreover, $A\cup B=K$ and $A\cap B={{\,\textrm{lk}\,}}(K,v)$. So, we obtain a long exact sequence

$$\begin{aligned} \cdots \rightarrow {\tilde{H}}_{k}\left( {{\,\textrm{lk}\,}}(K,v) \right) \rightarrow {\tilde{H}}_{k}\left( K\setminus v \right) \rightarrow {\tilde{H}}_{k}\left( K \right) \rightarrow {\tilde{H}}_{k-1}\left( {{\,\textrm{lk}\,}}(K,v) \right) \rightarrow \cdots \end{aligned}$$

$\square$

Another useful way of computing homology is by the application of nerve theorems. Let $X_1,\ldots ,X_m$ be simplicial complexes. The nerve of the family $\{X_1,\ldots ,X_m\}$ is the simplicial complex

$$\begin{aligned} N(\{X_1,\ldots ,X_m\})= \left\{ I\subset [m]:\, \bigcap _{i\in I} X_i\ne \{\varnothing \}\right\} , \end{aligned}$$

where $[m]:=\{1,2,\ldots ,m\}$. Roughly speaking, given a family of simplicial complexes, a nerve theorem describes how much the topology of the nerve of the family reflects the topology of the union of the complexes, when every non-empty intersection of the complexes satisfies certain topological restrictions (see e.g. [3, Theorem 6] or [17, Theorem 2.1]). Here, we will use the following simple version of the nerve theorem:

Theorem 1.9

(Leray’s Nerve Theorem) Let $X_1,\ldots ,X_m$ be simplicial complexes, and let $X=\bigcup _{i=1}^m X_i$. If, for every $I\subset [m]$, $\bigcap _{i\in I} X_i$ is either empty or acyclic, then

$$\begin{aligned} {\tilde{H}}_{k}\left( X\right) \cong {\tilde{H}}_{k}\left( N(\{X_1,\ldots ,X_m\})\right) \end{aligned}$$

for all $k\ge -1$.

For the union of simplicial complexes, the Leray number can be bounded by the following result by Kalai and Meshulam.

Theorem 1.10

(Kalai and Meshulam [11]) Let $X = \bigcup _{i=1}^{r} X_i$. Then,

$$\begin{aligned} L(X) \le \sum _{i=1}^{r}(L(X_i)+1)-1. \end{aligned}$$

2.2.1 Relative Homology

Let ${{\mathbb {F}}}$ be a field. Let X be a simplicial complex and let Y be a subcomplex of X. Let $C_k(X,Y)$ be the ${{\mathbb {F}}}$-vector space generated by the ordered k-simplices in $X\setminus Y$, under the relations

$$\begin{aligned}{}[v_0,\ldots ,v_k]=\text {sgn}(\pi ) [v_{\pi (0)},\ldots ,v_{\pi (k)}], \end{aligned}$$

for every k-simplex $\{v_0,\ldots ,v_k\}\in X\setminus Y$ and permutation $\pi :\{0,\ldots ,k\}\rightarrow \{0,\ldots ,k\}$. We define a linear map $\partial _k: C_k(X,Y)\rightarrow C_{k-1}(X,Y)$ that acts on the spanning set by

$$\begin{aligned} \partial _k[v_0,\ldots ,v_k]= \sum _{\begin{array}{c} i\in \{0,\ldots ,k\}:\\ \{v_0,\ldots ,v_{i-1},v_{i+1},\ldots ,v_k\}\notin Y \end{array}} (-1)^i [v_0,\ldots ,v_{i-1},v_{i+1},\ldots ,v_k]. \end{aligned}$$

We define the group of k-cycles as $Z_k(X,Y)=\text {Ker}(\partial _k)$ and the group of k-boundaries as $B_k(X,Y)=\text {Im}(\partial _{k+1})$. For any k, we have $B_k(X,Y)\subset Z_k(X,Y)$, so we can define the quotient

$$\begin{aligned} H_{k}\left( X,Y\right) =Z_k(X,Y)/B_k(X,Y). \end{aligned}$$

We call $H_{k}\left( X,Y\right)$ the k-th relative homology group of the pair $Y \subset X$. The relative homology of the pair $Y\subset X$ is related to the homology of the two complexes via the following result:

Theorem 1.11

(Long exact sequence of a pair) Let $Y\subset X$ be simplicial complexes. Then, there is an exact sequence

$$\begin{aligned} \cdots \rightarrow {\tilde{H}}_{k}\left( Y\right) \rightarrow {\tilde{H}}_{k}\left( X\right) \rightarrow H_{k}\left( X,Y\right) \rightarrow {\tilde{H}}_{k-1}\left( Y\right) \rightarrow \cdots \end{aligned}$$

2.3 Collapsibility

We will need the following properties, showing that d-collapsibility is “hereditary”:

Lemma 1.12

(Wegner [23]) Let K be a d-collapsible complex on vertex set V, and let $U\subset V$. Then, K[U] is also d-collapsible.

Lemma 1.13

(Khmelnitsky [14], see also [15, Prop 3.7]) Let K be a d-collapsible complex, and let $\sigma \in K$. Then, ${{\,\textrm{lk}\,}}(K,\sigma )$ is also d-collapsible.

It will be convenient to use the following equivalent definition of d-collapsibility:

Lemma 1.14

(Tancer [20, Lemma 5.2]) Let K be a simplicial complex. Then, K is d-collapsible if and only if one of the following holds:

• $\dim (K)<d$, or

• There exists some $\sigma \in K$ such that $|\sigma |=d$, $\sigma$ is contained in a unique maximal face $\tau \ne \sigma$ of K, and ${{\,\textrm{cost}\,}}(K,\sigma )$ is d-collapsible.

3 Some Topological Preliminaries

In this section we prove some auxiliary results on the homology groups of simplicial complexes that we will later need.

Using the Mayer-Vietoris exact sequence (Theorem 2.1) and Leray’s Nerve Theorem (Theorem 2.3), we can prove the following.

Lemma 1.15

Let $X_1,\ldots , X_m$ be simplicial complexes, and let $X=\bigcup _{i=1}^m X_i$. If for all $I\subset [m]$ of size at least 2, the complex $\cap _{i\in I} X_i$ is non-empty and acyclic, then

$$\begin{aligned} {\tilde{H}}_{k}\left( X\right) \cong \bigoplus _{i=1}^m {\tilde{H}}_{k}\left( X_i\right) . \end{aligned}$$

for all $k\ge -1$.

Proof

We argue by induction on m. For $m=1$ the claim is trivial. Assume $m>1$. Since $\bigcap _{i\in I} X_i$ is non-empty and acyclic for every $I\subset [m-1]$, we obtain, by the induction hypothesis,

$$\begin{aligned} {\tilde{H}}_{k}\left( \bigcup _{i=1}^{m-1} X_i\right) \cong \bigoplus _{i=1}^{m-1}{\tilde{H}}_{k}\left( X_i\right) \end{aligned}$$

for all $k\ge -1$.

Since $X=\left( \bigcup _{i=1}^{m-1} X_i\right) \cup X_m$, we have by Theorem 2.1 a long exact sequence

$$\begin{aligned} \cdots \rightarrow {\tilde{H}}_{k}\left( \bigcup _{i=1}^{m-1} (X_i\cap X_m)\right) \rightarrow \bigoplus _{i=1}^m {\tilde{H}}_{k}\left( X_i\right) \rightarrow {\tilde{H}}_{k}\left( X\right) \rightarrow {\tilde{H}}_{k-1}\left( \bigcup _{i=1}^{m-1} (X_i\cap X_m)\right) \rightarrow \cdots \end{aligned}$$

Hence, it is enough to show that

$$\begin{aligned} {\tilde{H}}_{k}\left( \bigcup _{i=1}^{m-1} (X_i\cap X_m)\right) =0 \end{aligned}$$

for all $k\ge -1$.

By the assumptions of this lemma, the nerve $N=N(\{X_i\cap X_m\}_{i=1}^{m-1})$ is the complete complex on vertex set $[m-1]$. Moreover, for all $I\subset [m-1]$, the complex

$$\begin{aligned} \bigcap _{i\in I} (X_i\cap X_m) = \bigcap _{i\in I\cup \{m\}} X_i \end{aligned}$$

is acyclic. Therefore, by Theorem 2.3, we obtain

$$\begin{aligned} {\tilde{H}}_{k}\left( \bigcup _{i=1}^{m-1} (X_i\cap X_m)\right) \cong {\tilde{H}}_{k}\left( N\right) =0 \end{aligned}$$

for all $k\ge -1$. Thus,

$$\begin{aligned} {\tilde{H}}_{k}\left( X\right) \cong \bigoplus _{i=1}^m {\tilde{H}}_{k}\left( X_i\right) \end{aligned}$$

for all $k\ge -1$. $\square$

We can think of Lemma 3.1 as a variant of the Nerve Theorem, and indeed our proof is similar to proofs of other versions of the Nerve theorem using the Mayer-Vietoris exact sequence, see e.g. [4, 5].

We will also need the following simple result about relative homology:

Lemma 1.16

Let X be a simplicial complex on vertex set V, and let $Y\subset X$ be a subcomplex. Assume that there is some $\sigma \in X$ and subcomplexes $W\subset Z\subset X[V\setminus \sigma ]$ such that

$$\begin{aligned} X\setminus Y = \{ \eta \cup \sigma : \eta \in Z\setminus W\}. \end{aligned}$$

Then,

$$\begin{aligned} H_{k+|\sigma |}\left( X,Y\right) \cong H_{k}\left( Z,W\right) \end{aligned}$$

for all k.

Proof

Let $\sigma =\{v_1,\ldots ,v_{|\sigma |}\}$. For all k, let $\phi _k: C_{k+|\sigma |}(X,Y )\rightarrow C_{k}(Z,W )$ be defined by

$$\begin{aligned} \phi _k([u_0,\ldots ,u_{k},v_1,\ldots ,v_{|\sigma |}])= [u_0,\ldots ,u_{k}] \end{aligned}$$

for any $\{u_0,\ldots ,u_{k}\}\in Z\setminus W$, and extended linearly. Note that the maps $\phi _k$ are linear isomorphisms. Denote by $\partial _k$ the boundary operator of $C_k(X,Y )$ and by $\partial '_k$ the boundary operator of $C_k(Z,W)$. We are left to show that $\phi$ is a chain map. That is, for any $\eta =\{u_0,\ldots ,u_{k}\}\in Z\setminus W$, we need to show that

$$\begin{aligned} \phi _{k-1}(\partial _{k+|\sigma |}([u_0,\ldots ,u_{k},v_1,\ldots ,v_{|\sigma |}]))= \partial '_k( \phi _{k}([u_0,\ldots ,u_{k},v_1,\ldots ,v_{|\sigma |}])). \end{aligned}$$

We have

$$\begin{aligned}{} & {} \partial _{k+|\sigma |}([u_0,\ldots ,u_{k},v_1,\ldots ,v_{|\sigma |}])\nonumber \\{} & {} \quad = \sum _{\begin{array}{c} i\in \{0,\ldots ,k\}:\\ \eta \cup \sigma \setminus \{u_i\}\notin Y \end{array}} (-1)^i [u_0,\ldots ,u_{i-1},u_{i+1},\ldots ,u_{k},v_1,\ldots ,v_{|\sigma |}] \\{} & {} \qquad + \sum _{\begin{array}{c} j\in \{1,\ldots ,|\sigma |\}:\\ \eta \cup \sigma \setminus \{v_j\}\notin Y \end{array}} (-1)^{k+j} [u_0,\ldots ,u_{k},v_1,\ldots ,v_{j-1},v_{j+1},\ldots ,v_{|\sigma |}]. \end{aligned}$$

Note that, since $X{\setminus } Y = \{ \tau \cup \sigma : \tau \in Z{\setminus } W\}$, $\eta \cup \sigma {\setminus }\{u_i\}\in Y$ if and only if $\eta \setminus \{u_i\}\in W$, and $\eta \cup \sigma {\setminus } \{v_j\}\in Y$ for all $1\le j\le |\sigma |$. Therefore, we have

$$\begin{aligned}{} & {} \partial _{k+|\sigma |}([u_0,\ldots ,u_{k},v_1,\ldots ,v_{|\sigma |}]) \\{} & {} \quad = \sum _{\begin{array}{c} i\in \{0,\ldots ,k\}:\\ \eta \setminus \{u_i\}\notin W \end{array}} (-1)^i [u_0,\ldots ,u_{i-1},u_{i+1},\ldots ,u_{k},v_1,\ldots ,v_{|\sigma |}]. \end{aligned}$$

Hence,

$$\begin{aligned}{} & {} \phi _{k-1}(\partial _{k+|\sigma |}([u_0,\ldots ,u_{k},v_1,\ldots ,v_{|\sigma |}]))\nonumber \\{} & {} \quad = \sum _{\begin{array}{c} i\in \{0,\ldots ,k\}:\\ \eta \setminus \{u_i\}\notin W \end{array}} (-1)^i [u_0,\ldots ,u_{i-1},u_{i+1},\ldots ,u_{k}]\nonumber \\{} & {} \quad =\partial '_k([u_0,\ldots ,u_k])= \partial '_k(\phi _k([u_0,\ldots ,u_{k},v_1,\ldots ,v_{|\sigma |}])). \end{aligned}$$

So $C_{k+|\sigma |}(X,Y )$ and $C_{k}(Z,W )$ are isomorphic as chain complexes, and in particular have isomorphic homology groups. $\square$

4 Proof of Theorem 1.5

In this section, we present the proof of Theorem 1.5. Note that the construction of the tolerance complexes depends on the vertex set of the original complex. For the construction of tolerance complexes, we will consider the vertex set of K[U] to be the set U, the vertex set of ${{\,\textrm{cost}\,}}(K,\sigma )$ to be V, and the vertex set of ${{\,\textrm{lk}\,}}(K,\sigma )$ to be $V\setminus \sigma$.

The main ingredient in the proof of Theorem 1.5 is the following result.

Proposition 1.17

Let K be a simplicial complex, and $\sigma \in K$ such that $\sigma$ is contained in a unique maximal simplex $\sigma \cup U \in K$, where $U\ne \varnothing$. Then, for all k,

$$\begin{aligned}&H_{k}\left( {\mathcal {T}}_{t}(K),{\mathcal {T}}_{t}({{\,\textrm{cost}\,}}(K,\sigma ))\right) \\&\quad \cong \bigoplus _{\begin{array}{c} W\subset V\setminus (\sigma \cup U):\\ |W|=t \end{array}} {\tilde{H}}_{k-|\sigma |-1}\left( \bigcup _{\begin{array}{c} \sigma '\subset \sigma :\\ 1\le |\sigma '|\le t \end{array}} {\mathcal {T}}_{t-|\sigma '|}({{\,\textrm{lk}\,}}(K,\sigma \setminus \sigma ')[U\cup W])\right) . \end{aligned}$$

We postpone the proof of Proposition 4.1 to the end of this section.

Recall that h(t, d) is defined as follows: $h(0,d)=d$ for all $d\ge 0$, and for $t>0$,

$$\begin{aligned} h(t,d)= \left( \sum _{s=1}^{\min \{t,d\}} \left( {\begin{array}{c}d\\ s\end{array}}\right) (h(t-s,d)+1)\right) + d. \end{aligned}$$

Theorem 1.5

Let K be a d-collapsible complex, and let $t\ge 0$ be an integer. Then, ${\mathcal {T}}_{t}(K)$ is h(t, d)-Leray.

Proof

Let V be the vertex set of K. We will show that ${\tilde{H}}_{k}\left( {\mathcal {T}}_{t}(K)\right) =0$ for $k\ge h(t,d)$. This is sufficient to prove the statement of the theorem, since ${\mathcal {T}}_{t}(K)[W]={\mathcal {T}}_{t}(K[W])$ and, by Lemma 2.6, K[W] is d-collapsible for every $W\subset V$.

We argue by induction on t. If $t=0$ the statement obviously holds, since every d-collapsible complex is d-Leray.

Let $t\ge 1$. We argue by induction on the size of K, that is, the number of simplices in K. If $\dim (K)<d$, then $\dim ({\mathcal {T}}_{t}(K))<d+t< h(t,d)$, so the statement holds. Otherwise, by Lemma 2.8, there is some $\sigma \in K$ such that $|\sigma |=d$, $\sigma$ is contained in a unique maximal face $\tau \ne \sigma$ of K, and ${{\,\textrm{cost}\,}}(K,\sigma )$ is d-collapsible.

Let $U=\tau \setminus \sigma \ne \varnothing$. By applying Theorem 2.5 to the pair ${\mathcal {T}}_{t}({{\,\textrm{cost}\,}}(K,\sigma )) \subset {\mathcal {T}}_{t}(K)$, we obtain the following long exact sequence:

$$\begin{aligned} \cdots \rightarrow {\tilde{H}}_{k}\left( {\mathcal {T}}_{t}({{\,\textrm{cost}\,}}(K,\sigma ))\right) \rightarrow {\tilde{H}}_{k}\left( ({\mathcal {T}}_{t}(K))\right) \rightarrow H_{k}\left( {\mathcal {T}}_{t}(K),{\mathcal {T}}_{t}({{\,\textrm{cost}\,}}(K,\sigma ))\right) \rightarrow \cdots \end{aligned}$$

By the induction hypothesis, ${\tilde{H}}_{k}\left( {\mathcal {T}}_{t}({{\,\textrm{cost}\,}}(K,\sigma ))\right) =0$ for $k\ge h(t,d)$. Therefore, it is sufficient to show that $H_{k}\left( {\mathcal {T}}_{t}(K),{\mathcal {T}}_{t}({{\,\textrm{cost}\,}}(K,\sigma ))\right) =0$ for $k\ge h(t,d)$.

By Proposition 4.1, it is sufficient to show that, for every $W\subset V\setminus (\sigma \cup U)$ of size t, the homology group

$$\begin{aligned} {\tilde{H}}_{k}\left( \bigcup _{\begin{array}{c} \sigma '\subset \sigma :\\ 1\le |\sigma '|\le t \end{array}} {\mathcal {T}}_{t-|\sigma '|}({{\,\textrm{lk}\,}}(K,\sigma \setminus \sigma ')[U\cup W])\right) \end{aligned}$$

is trivial for $k\ge h(t,d)-|\sigma |-1=h(t,d)-d-1$. Note that, for any $\sigma '\subset \sigma$, by Lemma 2.6 and Lemma 2.7, the complex ${{\,\textrm{lk}\,}}(K,\sigma \setminus \sigma ')[U\cup W]$ is d-collapsible. Hence, by the induction hypothesis, for any $\sigma '\subset \sigma$ of size $1\le |\sigma '|\le t$, the complex ${\mathcal {T}}_{t-|\sigma '|}({{\,\textrm{lk}\,}}(K,\sigma \setminus \sigma ')[U\cup W])$ is $h(t-|\sigma '|,d)$-Leray. So, by Theorem 2.4,

$$\begin{aligned} L\left( \bigcup _{\begin{array}{c} \sigma '\subset \sigma :\\ 1\le |\sigma '|\le t \end{array}} {\mathcal {T}}_{t-|\sigma '|}({{\,\textrm{lk}\,}}(K,\sigma \setminus \sigma ')[U\cup W])\right)&\le \left( \sum _{\begin{array}{c} \sigma '\subset \sigma :\\ 1 \le |\sigma '|\le t \end{array}} h(t-|\sigma '|,d)+1\right) -1 \\&= \left( \sum _{s=1}^{\min \{t,d\}}\left( {\begin{array}{c}d\\ s\end{array}}\right) (h(t-s,d)+1)\right) -1\\&= h(t,d)-d-1. \end{aligned}$$

In particular,

$$\begin{aligned} {\tilde{H}}_{k}\left( \bigcup _{\begin{array}{c} \sigma '\subset \sigma :\\ 1\le |\sigma '|\le t \end{array}} {\mathcal {T}}_{t-|\sigma '|}({{\,\textrm{lk}\,}}(K,\sigma \setminus \sigma ')[U\cup W])\right) =0 \end{aligned}$$

for $k\ge h(t,d)-d-1$, as wanted. $\square$

As mentioned in the introduction, we can give explicit formulas for h(t, d) in some special cases, and understand its asymptotic behaviour for fixed t as d tends to infinity.

Lemma 1.18

• $h(t,1)=2t+1$,

• $h(1,d)=d^2+2d$,

• For fixed t, $h(t,d)=O(d^{t+1})$.

Proof

First, we show that $h(t,1)=2t+1$. We argue by induction on t. For $t=0$ we have $h(0,1)=1=2t+1$. Now, assume $t>0$. Then, by the definition of h(t, d) and the induction hypothesis, we obtain

$$\begin{aligned} h(t,1)= h(t-1,1)+1+1= 2(t-1)+3= 2t+1. \end{aligned}$$

Next, we show that $h(1,d)=d^2+2d$. Indeed, this follows immediately from the definition of h(t, d):

$$\begin{aligned} h(1,d)= d(h(0,d)+1)+d = d^2+2d. \end{aligned}$$

Finally, we show that, for fixed t, $h(t,d)=O(d^{t+1})$. We argue by induction on t. For $t=0$ we have $h(0,d)=d=O(d)$. Let $t>1$. We will show that there is some constant $C_t$ such that, for large enough d, $h(t,d)\le C_t d^{t+1}$. By the definition of h(t, d) and the induction hypothesis, we have,

$$\begin{aligned} h(t,d)&= \left( \sum _{s=1}^{t} \left( {\begin{array}{c}d\\ s\end{array}}\right) (h(t-s,d)+1)\right) + d\\&\le \left( \sum _{s=1}^t \frac{d^s}{s!} (C_{t-s} d^{t-s+1} +1)\right) +d\\&= \left( \sum _{s=1}^t\frac{C_{t-s}}{s!}\right) d^{t+1} + \left( \sum _{s=1}^t \frac{d^s}{s!} +d \right) \\&\le C_t d^{t+1} \end{aligned}$$

for $C_t >\sum _{s=1}^t\frac{C_{t-s}}{s!}$ and large enough d. So, for fixed t, we have $h(t,d)=O(d^{t+1})$. $\square$

Finally, we prove Proposition 4.1. We will need the following auxiliary results.

Lemma 1.19

Let K be a simplicial complex on vertex set V, and let $\sigma \in K$. Then,

$$\begin{aligned} {\mathcal {T}}_{t}(K)\setminus&{\mathcal {T}}_{t}({{\,\textrm{cost}\,}}(K,\sigma )) \\=&\left\{ \sigma \cup \eta :\, \eta \in {\mathcal {T}}_{t}({{\,\textrm{lk}\,}}(K,\sigma ))\setminus \left( \bigcup _{\begin{array}{c} \sigma '\subset \sigma :\\ 1\le |\sigma '|\le t \end{array}} {\mathcal {T}}_{t-|\sigma '|}({{\,\textrm{lk}\,}}(K[V\setminus \sigma '],\sigma \setminus \sigma ')) \right) \right\} . \end{aligned}$$

Proof

Suppose $\tau \in {\mathcal {T}}_{t}(K)\setminus {\mathcal {T}}_{t}({{\,\textrm{cost}\,}}(K,\sigma ))$. Since $\tau \in {\mathcal {T}}_{t}(K)$, we can write $\tau =\tau '\cup \tau ''$, where $\tau '\in K$ and $|\tau ''|\le t$. Moreover, we must have $\tau ' \supset \sigma$. Otherwise, $\tau '\in {{\,\textrm{cost}\,}}(K,\sigma )$, a contradiction to $\tau \notin {\mathcal {T}}_{t}({{\,\textrm{cost}\,}}(K,\sigma ))$.

Let $\eta =\tau \setminus \sigma$. Then, we can write $\eta = (\tau '{\setminus } \sigma )\cup \tau ''$. Since $\tau '{\setminus }\sigma \in {{\,\textrm{lk}\,}}(K,\sigma )$, we obtain $\eta \in {\mathcal {T}}_{t}({{\,\textrm{lk}\,}}(K,\sigma ))$. We claim that

$$\begin{aligned} \eta \notin \bigcup _{\begin{array}{c} \sigma '\subset \sigma :\\ 1\le |\sigma '|\le t \end{array}} {\mathcal {T}}_{t-|\sigma '|}({{\,\textrm{lk}\,}}(K[V\setminus \sigma '],\sigma \setminus \sigma ')). \end{aligned}$$

Assume for contradiction that $\eta \in {\mathcal {T}}_{t-|\sigma '|}({{\,\textrm{lk}\,}}(K[V{\setminus } \sigma '],\sigma {\setminus } \sigma '))$ for some $\sigma '\subset \sigma$, $1\le |\sigma '|\le t$. Then, we can write

$$\begin{aligned} \eta =\eta _1\cup \eta _2, \end{aligned}$$

where $\eta _1\cap \sigma =\varnothing$, $\eta _1\cup (\sigma {\setminus } \sigma ')\in K$ and $|\eta _2|\le t-|\sigma '|$. Hence, we obtain

$$\begin{aligned} \tau =\sigma \cup \eta = (\eta _1\cup (\sigma \setminus \sigma ')) \cup (\sigma '\cup \eta _2). \end{aligned}$$

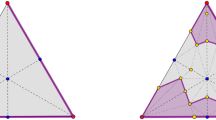
Since $\sigma \not \subset \eta _1\cup (\sigma \setminus \sigma ')$ and $|\sigma ' \cup \eta _2| \le t$, we have $\tau \in {\mathcal {T}}_{t}({{\,\textrm{cost}\,}}(K,\sigma ))$, which is a contradiction to the assumption $\tau \in {\mathcal {T}}_{t}(K)\setminus {\mathcal {T}}_{t}({{\,\textrm{cost}\,}}(K,\sigma ))$ (see Fig. 1).

For the opposite direction, suppose $\tau =\sigma \cup \eta$, where

$$\begin{aligned} \eta \in {\mathcal {T}}_{t}({{\,\textrm{lk}\,}}(K,\sigma ))\setminus \left( \bigcup _{\begin{array}{c} \sigma '\subset \sigma :\\ 1\le |\sigma '|\le t \end{array}} {\mathcal {T}}_{t-|\sigma '|}({{\,\textrm{lk}\,}}(K[V\setminus \sigma '],\sigma \setminus \sigma '))\right) . \end{aligned}$$

We claim that $\tau \in {\mathcal {T}}_{t}(K){\setminus }{\mathcal {T}}_{t}({{\,\textrm{cost}\,}}(K,\sigma ))$. Since $\eta \in {\mathcal {T}}_{t}({{\,\textrm{lk}\,}}(K,\sigma ))$, we can write $\eta =\eta _1\cup \eta _2$, where $\eta _1\cap \sigma =\varnothing$, $\eta _1\cup \sigma \in K$ and $|\eta _2|\le t$. Therefore, $\tau =(\eta _1\cup \sigma )\cup \eta _2\in {\mathcal {T}}_{t}(K)$. We are left to show that $\tau \notin {\mathcal {T}}_{t}({{\,\textrm{cost}\,}}(K,\sigma ))$. Assume for contradiction that $\tau \in {\mathcal {T}}_{t}({{\,\textrm{cost}\,}}(K,\sigma ))$. Then, we can write $\tau =\tau _1\cup \tau _2$, where $\tau _1\in K$, $\sigma \not \subset \tau _1$ and $|\tau _2|\le t$. Let $\sigma '=\tau _2\cap \sigma$. Since $\sigma \not \subset \tau _1$ and $\sigma \subset \tau$, we must have $\sigma '\ne \varnothing$. In particular, $1 \le |\sigma '| \le t$. We can write $\eta$ as follows:

$$\begin{aligned} \eta = \tau \setminus \sigma = (\tau _1\setminus (\sigma \setminus \sigma '))\cup (\tau _2\setminus \sigma '). \end{aligned}$$

Note that $\tau _1{\setminus } (\sigma {\setminus } \sigma ')\in {{\,\textrm{lk}\,}}(K[V{\setminus } \sigma '],\sigma {\setminus } \sigma ')$ and $|\tau _2\setminus \sigma '|\le t-|\sigma '|$. Thus, $\eta \in {\mathcal {T}}_{t-|\sigma '|}({{\,\textrm{lk}\,}}(K[V{\setminus } \sigma '],\sigma {\setminus } \sigma '))$, which is a contradiction to the assumption on $\eta$. This completes the proof. $\square$

Fig. 1

Illustration of the first direction in the proof of Lemma 4.3: Let $\tau \in {\mathcal {T}}_{t}(K){\setminus }{\mathcal {T}}_{t}({{\,\textrm{cost}\,}}(K,\sigma ))$. Then $\tau =\tau '\cup \tau ''$, where $\sigma \subset \tau '\in K$, and $|\tau ''|\le t$. Therefore, setting $\eta =(\tau '\setminus \sigma )\cup \tau ''$, we obtain $\tau =\sigma \cup \eta$, where $\eta \in {\mathcal {T}}_{t}({{\,\textrm{lk}\,}}(K,\sigma ))$ (a). Moreover, $\eta \notin {\mathcal {T}}_{t-|\sigma '|}({{\,\textrm{lk}\,}}(K[V\setminus \sigma '],\sigma \setminus \sigma '))$ for any $\sigma '\subset \sigma$, $1\le |\sigma '|\le t$. Otherwise, $\eta =\eta _1\cup \eta _2$, where $\eta _1\cup (\sigma \setminus \sigma ')\in K$ (and therefore, since $\sigma \not \subset \eta _1\cup (\sigma \setminus \sigma ')$, $\eta _1\cup (\sigma \setminus \sigma ')\in {{\,\textrm{cost}\,}}(K,\sigma )$), and $|\eta _2|\le t-|\sigma '|$. But then, since $\tau =(\eta _1\cup (\sigma \setminus \sigma '))\cup (\sigma '\cup \eta _2)$, we obtain $\tau \in {\mathcal {T}}_{t}({{\,\textrm{cost}\,}}(K,\sigma ))$, a contradiction (b)

By Lemmas 3.2 and 4.3, we obtain:

Corollary 1.20

Let K be a simplicial complex, and let $\sigma \in K$. Then, for all k, we have

$$\begin{aligned}{} & {} H_{k}\left( {\mathcal {T}}_{t}(K), {\mathcal {T}}_{t}({{\,\textrm{cost}\,}}(K,\sigma ))\right) \\{} & {} \quad \cong H_{k-|\sigma |}\left( {\mathcal {T}}_{t}({{\,\textrm{lk}\,}}(K,\sigma )),{\mathcal {T}}_{t}({{\,\textrm{lk}\,}}(K,\sigma ))\cap \left( \bigcup _{\begin{array}{c} \sigma '\subset \sigma :\\ 1\le |\sigma '|\le t \end{array}} {\mathcal {T}}_{t-|\sigma '|}({{\,\textrm{lk}\,}}(K[V\setminus \sigma '],\sigma \setminus \sigma ')) \right) \right) . \end{aligned}$$

Proof of Proposition 4.1

Let

$$\begin{aligned} Y=\bigcup _{\begin{array}{c} \sigma '\subset \sigma :\\ 1\le |\sigma '|\le t \end{array}} {\mathcal {T}}_{t-|\sigma '|}({{\,\textrm{lk}\,}}(K[V\setminus \sigma '],\sigma \setminus \sigma ')). \end{aligned}$$

By Corollary 4.4, we have

$$\begin{aligned} H_{k}\left( {\mathcal {T}}_{t}(K),{\mathcal {T}}_{t}({{\,\textrm{cost}\,}}(K,\sigma ))\right) \cong H_{k-|\sigma |}\left( {\mathcal {T}}_{t}({{\,\textrm{lk}\,}}(K,\sigma )),{\mathcal {T}}_{t}({{\,\textrm{lk}\,}}(K,\sigma ))\cap Y\right) . \end{aligned}$$

By applying Theorem 2.5 to the pair ${\mathcal {T}}_{t}({{\,\textrm{lk}\,}}(K,\sigma ))\cap Y \subset {\mathcal {T}}_{t}({{\,\textrm{lk}\,}}(K,\sigma ))$, we obtain a long exact sequence

$$\begin{aligned} \cdots \rightarrow {\tilde{H}}_{k-|\sigma |}\left( {\mathcal {T}}_{t}({{\,\textrm{lk}\,}}(K,\sigma ))\right) \rightarrow H_{k-|\sigma |}\left( {\mathcal {T}}_{t}({{\,\textrm{lk}\,}}(K,\sigma )),{\mathcal {T}}_{t}({{\,\textrm{lk}\,}}(K,\sigma ))\cap Y\right) \rightarrow \\ \rightarrow {\tilde{H}}_{k-|\sigma |-1}\left( {\mathcal {T}}_{t}({{\,\textrm{lk}\,}}(K,\sigma ))\cap Y\right) \rightarrow {\tilde{H}}_{k-|\sigma |-1}\left( {\mathcal {T}}_{t}({{\,\textrm{lk}\,}}(K,\sigma ))\right) \rightarrow \cdots \end{aligned}$$

Note that ${{\,\textrm{lk}\,}}(K,\sigma )=2^U$; therefore,

$$\begin{aligned} {\mathcal {T}}_{t}({{\,\textrm{lk}\,}}(K,\sigma ))=2^U*\{\tau \subset V\setminus (U\cup \sigma ):\, |\tau |\le t\}. \end{aligned}$$

In particular, since $U\ne \varnothing$, ${\mathcal {T}}_{t}({{\,\textrm{lk}\,}}(K,\sigma ))$ is contractible. Hence,

$$\begin{aligned} H_{k-|\sigma |}\left( {\mathcal {T}}_{t}({{\,\textrm{lk}\,}}(K,\sigma )),{\mathcal {T}}_{t}({{\,\textrm{lk}\,}}(K,\sigma ))\cap Y\right) \cong {\tilde{H}}_{k-|\sigma |-1}\left( {\mathcal {T}}_{t}({{\,\textrm{lk}\,}}(K,\sigma ))\cap Y\right) . \end{aligned}$$

We can write

$$\begin{aligned} {\mathcal {T}}_{t}({{\,\textrm{lk}\,}}(K,\sigma ))\cap Y = \bigcup _{\begin{array}{c} W\subset V\setminus (\sigma \cup U):\\ |W|=t \end{array}} 2^{U\cup W} \cap Y = \bigcup _{\begin{array}{c} W\subset V\setminus (\sigma \cup U):\\ |W|=t \end{array}} Y_W, \end{aligned}$$

(4.1)

where

$$\begin{aligned} Y_W= Y[U\cup W] =\bigcup _{\begin{array}{c} \sigma '\subset \sigma :\\ 1\le |\sigma '|\le t \end{array}} {\mathcal {T}}_{t-|\sigma '|}({{\,\textrm{lk}\,}}(K,\sigma \setminus \sigma ')[U\cup W]). \end{aligned}$$

Let $m>1$, and let $W_1,\ldots ,W_m\subset V\setminus (\sigma \cup U)$ be distinct sets, such that $|W_i|=t$ for all $i\in [m]$. Then,

$$\begin{aligned} \bigcap _{i=1}^m Y_{W_i} = \bigcup _{\begin{array}{c} \sigma '\subset \sigma :\\ 1\le |\sigma '|\le t \end{array}} {\mathcal {T}}_{t-|\sigma '|}({{\,\textrm{lk}\,}}(K,\sigma \setminus \sigma ')[U\cup (\cap _{i=1}^m W_i)]). \end{aligned}$$

Since $|\cap _{i=1}^m W_i|\le t-1$, we have, for any $v\in \sigma$,

$$\begin{aligned} U\cup (\cap _{i=1}^m W_i) \in {\mathcal {T}}_{t-1}({{\,\textrm{lk}\,}}(K,\sigma \setminus \{v\})[U\cup (\cap _{i=1}^m W_i)]). \end{aligned}$$

In particular, it implies

$$\begin{aligned} U\cup (\cap _{i=1}^m W_i) \in \bigcap _{i=1}^m Y_{W_i}, \end{aligned}$$

and hence, we conclude

$$\begin{aligned} \bigcap _{i=1}^m Y_{W_i}= 2^{U\cup (\cap _{i=1}^m W_i)}. \end{aligned}$$

Since $U\ne \varnothing$, the intersection $\bigcap _{i=1}^m Y_{W_i}$ is non-empty and acyclic. Therefore, by applying Lemma 3.1 to (4.1), we obtain

$$\begin{aligned}{} & {} {\tilde{H}}_{k-|\sigma |-1}\left( {\mathcal {T}}_{t}({{\,\textrm{lk}\,}}(K,\sigma ))\cap Y\right) \cong \bigoplus _{\begin{array}{c} W\subset V\setminus (\sigma \cup U):\\ |W|=t \end{array}} {\tilde{H}}_{k-|\sigma |-1}\left( Y_W\right) \\{} & {} \quad \cong \bigoplus _{\begin{array}{c} W\subset V\setminus (\sigma \cup U):\\ |W|=t \end{array}}{\tilde{H}}_{k-|\sigma |-1}\left( \bigcup _{\begin{array}{c} \sigma '\subset \sigma :\\ 1\le |\sigma '|\le t \end{array}} {\mathcal {T}}_{t-|\sigma '|}({{\,\textrm{lk}\,}}(K,\sigma \setminus \sigma ')[U\cup W])\right) , \end{aligned}$$

as wanted. $\square$

5 Improved Bound for $d=2, t=1$

By Theorem 1.5 and Lemma 4.2, it follows that the 1-tolerance complex ${\mathcal {T}}_{1}(K)$ is $(d^2+2d)$-Leray for every d-collapsible complex K. This is of the same order of magnitude, but larger than the conjectural bound $\eta (d+1,2)-1= \left\lfloor \left( \frac{d+3}{2}\right) ^2\right\rfloor -1$ for $d > 1$. In this section, we prove Theorem 1.6, which gives a tight bound for the Leray number of ${\mathcal {T}}_{1}(K)$, in the special case that K is 2-collapsible.

For the proof we will need the following Lemma:

Lemma 1.21

Let K be a 2-collapsible complex on vertex set V. Let $\sigma =\{u,v\}\in K$ such that $\sigma$ is contained in a unique maximal face $\sigma \cup U$, where $U\ne \varnothing$. Let $w\in V{\setminus }(U\cup \sigma )$. Then,

$$\begin{aligned} {\tilde{H}}_{k}\left( {{\,\textrm{lk}\,}}(K,v)[U\cup \{w\}] \cup {{\,\textrm{lk}\,}}(K,u)[U\cup \{w\}]\right) =0 \end{aligned}$$

for $k\ge 2$.

Proof

Let $A={{\,\textrm{lk}\,}}(K,v)[U\cup \{w\}]$ and $B={{\,\textrm{lk}\,}}(K,u)[U\cup \{w\}]$. By Mayer–Vietoris (Theorem 2.1), we have a long exact sequence

$$\begin{aligned} \cdots \rightarrow {\tilde{H}}_{k}\left( A\right) \bigoplus {\tilde{H}}_{k}\left( B\right) \rightarrow {\tilde{H}}_{k}\left( A\cup B\right) \rightarrow {\tilde{H}}_{k-1}\left( A\cap B\right) \rightarrow \cdots \end{aligned}$$

Since K is 2-collapsible, then, by Lemmas 2.6 and 2.7, A and B are also 2-collapsible. In particular, ${\tilde{H}}_{k}\left( A\right) ={\tilde{H}}_{k}\left( B\right) =0$ for $k\ge 2$. Therefore, it is enough to show that

$$\begin{aligned} {\tilde{H}}_k(A\cap B)=0 \end{aligned}$$

for $k\ge 1$. If $w\notin A\cap B$, then

$$\begin{aligned} A\cap B=2^U, \end{aligned}$$

and the claim holds. Otherwise, assume $w\in A\cap B$. By Theorem 2.2, we have a long exact sequence

$$\begin{aligned} \cdots \rightarrow {\tilde{H}}_{k}\left( (A\cap B)\setminus w \right) \rightarrow {\tilde{H}}_{k}\left( A\cap B \right) \rightarrow {\tilde{H}}_{k-1}\left( {{\,\textrm{lk}\,}}(A\cap B,w) \right) \rightarrow \cdots \end{aligned}$$

Note that $(A\cap B)\setminus w = 2^U$; hence, ${\tilde{H}}_{k}\left( (A\cap B){\setminus } w\right) =0$ for all k. Thus, it is enough to show that

$$\begin{aligned} {\tilde{H}}_{k}\left( {{\,\textrm{lk}\,}}(A\cap B,w)\right) = {\tilde{H}}_{k}\left( {{\,\textrm{lk}\,}}(K,\{v,w\})[U] \cap {{\,\textrm{lk}\,}}(K,\{u,w\})[U]\right) =0 \end{aligned}$$

for $k\ge 0$. Let

$$\begin{aligned} Z={{\,\textrm{lk}\,}}(K,\{v,w\})[U] \cap {{\,\textrm{lk}\,}}(K,\{u,w\})[U]. \end{aligned}$$

We will show that Z is in fact a complete complex.

Note that a set $\tau \subset U$ is a missing face of Z if and only if it is a missing face of ${{\,\textrm{lk}\,}}(K,\{v,w\})[U]$ or a missing face of ${{\,\textrm{lk}\,}}(K,\{u,w\})[U]$. Moreover, $\tau \subset U$ is a missing face of ${{\,\textrm{lk}\,}}(K,\{v,w\})[U]$ if and only if there is some $\eta \subset \{v,w\}$ such that $\tau \cup \eta$ is a missing face of K. Similarly, $\tau$ is a missing face of ${{\,\textrm{lk}\,}}(K,\{u,w\})$ if and only if there is some $\eta \subset \{u,w\}$ such that $\tau \cup \eta$ is a missing face of K.

Assume for contradiction that Z contains a missing face $\tau \subset U$ of size at least two. Recall that, since K is 2-collapsible, all the missing faces of K are of size at most 3. Then, since $U\in {{\,\textrm{lk}\,}}(K,\{u,v\})$, $\tau$ must be of the form $\tau = \{x,y\}$, where $\{x,y,w\}$ is a missing face of K.

Now, we look at the induced subcomplex $L=K[\{u,v,w,x,y\}]$. By Lemma 2.6, L is 2-collapsible. It is easy to check that the missing faces of L are exactly the two sets $\{u,v,w\}$ and $\{x,y,w\}$. Then, we observe that ${{\,\textrm{lk}\,}}(L, w)$ is a 1-dimensional sphere, and that $L\setminus w= 2^{\{u,v,x,y\}}$ is contractible. Therefore, by applying Theorem 2.2, we obtain ${\tilde{H}}_2(L)\ne 0$. This implies that L is not 2-Leray, which is a contradiction to L being 2-collapsible. Hence, Z is a complete complex, and therefore ${\tilde{H}}_{k}\left( Z\right) =0$ for all $k\ge 0$. $\square$

Theorem 1.6

Let K be a 2-collapsible complex. Then, ${\mathcal {T}}_{1}(K)$ is 5-Leray.

Proof

The proof is exactly the same as the $t=1$ case of the proof of Theorem 1.5, except that we replace the use of the Kalai-Meshulam bound (Theorem 2.4) by Lemma 5.1. $\square$

6 Tolerance in Colorful Helly Theorems

The colorful Helly theorem is one of the most important generalizations of Helly’s theorem. It was observed by Lovász, and first appeared in Bárány’s paper [2]. It asserts the following.

Theorem 1.22

(Lovász, Bárány [2]) Let ${\mathcal {F}}$ be a finite family of convex sets in ${{\mathbb {R}}}^d$, and let ${\mathcal {F}}_1,{\mathcal {F}}_2,\ldots ,{\mathcal {F}}_{d+1}\subset {\mathcal {F}}$. If for every $A_1\in {\mathcal {F}}_1, \ldots , A_{d+1}\in {\mathcal {F}}_{d+1}$, the family $\{A_1,\ldots ,A_{d+1}\}$ has a point in common, then there is some $i\in [d+1]$ such that ${\mathcal {F}}_i$ has a point in common.

Note that the colorful Helly theorem implies Helly’s theorem, by assuming all ${\mathcal {F}}_i$’s are identical. In [18, Theorem 4.4], a tolerant version of the colorful Helly theorem in the plane was proved. It was stated in the special case $d=2$, $t=1$, but their argument holds in general:

Theorem 1.23

(Montejano and Oliveros [18, Theorem 4.4]) Let ${\mathcal {F}}$ be a finite family of convex sets in ${{\mathbb {R}}}^d$, and let ${\mathcal {F}}_1,{\mathcal {F}}_2,\ldots ,{\mathcal {F}}_{d+1}\subset {\mathcal {F}}$. Suppose that every subfamily ${\mathcal {F}}'$ of ${\mathcal {F}}$ of size $\eta (d+1,t+1)$ has a subfamily ${\mathcal {F}}''\subset {\mathcal {F}}'$ of size $|{\mathcal {F}}''|\ge |{\mathcal {F}}'|-t$ such that for any $A_1\in {\mathcal {F}}_i\cap {\mathcal {F}}'',\ldots , A_{d+1}\in {\mathcal {F}}_{d+1}\cap {\mathcal {F}}''$, $\{A_1,\ldots ,A_{d+1}\}$ has a point in common.

Then, there is some $i\in [d+1]$ such that ${\mathcal {F}}_i$ has a point in common with tolerance t.

For completeness, we present a proof, closely following the argument presented in [18] for the special case $d=2, t=1$.

Proof of Theorem 6.2

Consider the hypergraph ${\mathcal {H}}$ whose vertex set is ${\mathcal {F}}$ and whose edges are the subfamilies $\{A_1,\ldots ,A_{d+1}\}$, such that $A_i\in {\mathcal {F}}_i$ for all $i\in [d+1]$, and $\cap _{i=1}^{d+1} A_i=\emptyset$.

By the assumption of the theorem, every subhypergraph of ${\mathcal {H}}$ consisting of $\eta (d+1,t+1)$ vertices has covering number at most t. Therefore, by the definition of $\eta (d+1,t+1)$, ${\mathcal {H}}$ has covering number at most t. That is, there is a subfamily ${\mathcal {F}}'$ of ${\mathcal {F}}$ of size $|{\mathcal {F}}'|\ge |{\mathcal {F}}|-t$ such that every $\{A_1,\ldots ,A_{d+1}\}\subset {\mathcal {F}}'$, where $A_i\in {\mathcal {F}}_i$ for all $i\in [d+1]$, has a point in common. Therefore, by Theorem 6.1 (applied to the family ${\mathcal {F}}'$), there is some i such that ${\mathcal {F}}_i\cap {\mathcal {F}}'$ has a point in common. Since $|{\mathcal {F}}_i \cap {\mathcal {F}}'|\ge |{\mathcal {F}}_i|-t$, ${\mathcal {F}}_i$ has a point in common with tolerance t. $\square$

Similarly as above, we observe that Theorem 6.2 implies Theorem 1.1, by assuming all ${\mathcal {F}}_i$’s are identical.

As an application of our main results, we obtain new tolerant variants of the colorful Helly theorem.

A family M of subsets of a non-empty set V is a matroid if it satisfies

• (i) $\varnothing \in M$,

• (ii) for all $A' \subset A \subset V$, if $A \in M$ then $A' \in M$, and

• (iii) if $A, B \in M$ and $|A| < |B|$, then there exists $x \in B \setminus A$ such that $A \cup \{x\} \in M$.

The rank function of a matroid M on V is a function $\rho : 2^V \rightarrow {\mathbb {N}}$ such that for every $W \subset V$, $\rho (W)$ equals to the maximal size of $W' \subset W$ with $W' \in M$. Note that the conditions (i) and (ii) allow us to regard a matroid M as a simplicial complex. The colorful Helly theorem can be generalized topologically as follows.

Theorem 1.24

(Kalai and Meshulam, [10, Theorem 1.6]) Let K be a d-Leray complex on V and let M be a matroid on V with rank function $\rho$. If $M \subset K$, then there exists $\sigma \in K$ such that $\rho (V \setminus \sigma ) \le d$.

Taking K to be the nerve of the family ${\mathcal {F}}$ and M to be the matroid whose members are the subfamilies of ${\mathcal {F}}$ containing at most one member from each ${\mathcal {F}}_i$, we can recover Theorem 6.1 from Theorem 6.3.

By combining Theorem 6.3 with Theorems 1.5 and 1.6, we obtain the following results.

Theorem 1.25

Let ${\mathcal {F}}$ be a finite family of convex sets in ${{\mathbb {R}}}^d$, and let ${\mathcal {F}}_1,{\mathcal {F}}_2,\ldots ,{\mathcal {F}}_{h(t,d)+1}\subset {\mathcal {F}}$. A subfamily ${\mathcal {F}}'\subset {\mathcal {F}}$ is called colorful if there exists a surjective map $\varphi :[h(t,d)+1]\rightarrow {\mathcal {F}}'$ such that $\varphi (i)\in {\mathcal {F}}_i$ for all $i\in [h(t,d)+1]$.

If every colorful subfamily of ${\mathcal {F}}$ has a point in common with tolerance t, then there is some $i\in [h(t,d)+1]$ such that ${\mathcal {F}}_i$ has a point in common with tolerance t.

Theorem 1.26

Let ${\mathcal {F}}$ be a finite family of convex sets in ${{\mathbb {R}}}^2$, and let ${\mathcal {F}}_1,{\mathcal {F}}_2,\ldots ,{\mathcal {F}}_6\subset {\mathcal {F}}$. A subfamily ${\mathcal {F}}'\subset {\mathcal {F}}$ is called colorful if there exists a surjective map $\varphi :[6]\rightarrow {\mathcal {F}}'$ such that $\varphi (i)\in {\mathcal {F}}_i$ for all $i\in [6]$.

If every colorful subfamily of ${\mathcal {F}}$ has a point in common with tolerance 1, then there is some $i\in [6]$ such that ${\mathcal {F}}_i$ has a point in common with tolerance 1.

Theorems 6.4 and 6.5 follow from Theorem 6.3 by a standard “duplicating vertices" argument. For completeness, we include the proof of Theorem 6.5 (the proof of Theorem  6.4 is essentially identical).

Proof of Theorem 6.5

Let $V=\{ (A,i):\, i\in [6],\, A\in {\mathcal {F}}_i\}$. Let $\pi : V\rightarrow {\mathcal {F}}$ be the projection $\pi (A,i)=A$. Let X be the simplicial complex on vertex set V whose simplices are the sets $\sigma \subset V$ such that $\pi (\sigma )\in {\mathcal {T}}_{1}(N({\mathcal {F}}))$. By Theorem 1.6, since $N({\mathcal {F}})$ is 2-collapsible, ${\mathcal {T}}_1(N({\mathcal {F}}))$ is 5-Leray.

We will show that X is also 5-Leray. Indeed, let $U\subset V$. Let ${\mathcal {F}}'=\pi (U)\subset {\mathcal {F}}$. Then

$$\begin{aligned} X[U]=\{ \sigma \subset U:\, \pi (\sigma )\in {\mathcal {T}}_1(N({\mathcal {F}}'))\}. \end{aligned}$$

By [16, Lemma 2.14], X[U] is homotopy equivalent to ${\mathcal {T}}_1(N({\mathcal {F}}'))$, and in particular

$$\begin{aligned} {\tilde{H}}_k(X[U])\cong {\tilde{H}}_k( {\mathcal {T}}_1(N({\mathcal {F}}')))=0 \end{aligned}$$

for all $k\ge 5$. Therefore, X is 5-Leray.

For $i\in [6]$, let $V_i=\{(A,i):\, A\in {\mathcal {F}}_i\}$. The sets $V_1,\ldots , V_6$ form a partition of V. We define the partition matroid

$$\begin{aligned} M= \{ \sigma \subset V:\, |\sigma \cap V_i|\le 1 \text { for all } i\in [6]\}. \end{aligned}$$

It is well known and easy to check that M is indeed a matroid, and the rank of a set $U\subset V$ is $|\{i\in [6]:\, U\cap V_i\ne \emptyset \}|$.

Note that for any maximal face $\sigma$ of M, $\pi (\sigma )$ is a colorful subfamily of ${\mathcal {F}}$, and therefore $\pi (\sigma )\in {\mathcal {T}}_1(N({\mathcal {F}}))$. So, $\sigma \in X$. That is, we have $M\subset X$. By Theorem 6.3, there exists $\sigma \in X$ such that the rank of its complement is at most 5. That is, there is some $i\in [6]$ such that $V_i\subset \sigma$. In particular, $V_i\in X$. This means that ${\mathcal {F}}_i=\pi (V_i)\in {\mathcal {T}}_1(N({\mathcal {F}}))$. In other words, ${\mathcal {F}}_i$ has a point in common with tolerance 1. $\square$

As a special case, we obtain the following colorful versions of a theorem of Nadler [19].

Let ${\mathcal {H}}$ be a family of half-spaces in ${{\mathbb {R}}}^d$. We say that ${\mathcal {H}}$ is a k-fold cover of ${{\mathbb {R}}}^d$ if every point in ${{\mathbb {R}}}^d$ belongs to at least k half-spaces in ${\mathcal {H}}$. We say that ${\mathcal {H}}$ is a minimal k-fold cover if any proper subfamily ${\mathcal {H}}'\subset {\mathcal {H}}$ is not a k-fold cover.

Theorem 1.27

(Nadler [19]) Let N(k, d) be the maximum size of a minimal k-fold cover of ${{\mathbb {R}}}^d$ by open half-spaces. Then N(k, d) is finite, and in particular $N(k,1)=2k$ and $N(2,d)=\lfloor ((d+3)/2)^2\rfloor$.

Note that a family of half-spaces $H_1,\ldots ,H_m$ is a k-fold cover of ${{\mathbb {R}}}^d$ if and only if their complements $H_1^c,\ldots ,H_m^c$ do not have a point in common with tolerance $k-1$. Therefore, it follows immediately from Theorem 1.1 that $N(k,d)\le \eta (d+1,k)$. Similarly, we obtain from Theorems 6.4 and 6.5:

Corollary 1.28

Let ${\mathcal {H}}$ be a family of half-spaces in ${{\mathbb {R}}}^d$, and let ${\mathcal {H}}_1,\ldots ,{\mathcal {H}}_{h(k-1,d)+1}\subset {\mathcal {H}}$ such that ${\mathcal {H}}_i$ is a k-fold cover of ${{\mathbb {R}}}^d$ for all $i\in [h(k-1,d)+1]$. Then, there exists $\phi :[h(k-1,d)+1]\rightarrow {\mathcal {H}}$ such that $\phi (i)\in {\mathcal {H}}_i$ for all $i\in [h(k-1,d)+1]$ and the image of $\phi$ is a k-fold cover of ${{\mathbb {R}}}^d$.

Corollary 1.29

Let ${\mathcal {H}}$ be a family of half-planes in ${{\mathbb {R}}}^2$, and let ${\mathcal {H}}_1,\ldots ,{\mathcal {H}}_{6}\subset {\mathcal {H}}$ such that ${\mathcal {H}}_i$ is a 2-fold cover of ${{\mathbb {R}}}^2$ for all $i\in [6]$. Then, there exists $\phi :[6]\rightarrow {\mathcal {H}}$ such that $\phi (i)\in {\mathcal {H}}_i$ for all $i\in [6]$ and the image of $\phi$ is a 2-fold cover of ${{\mathbb {R}}}^2$.

It may be interesting to try to find a direct combinatorial or geometric proof of Theorems 6.4 and 6.5.