The Universality of the Resonance Arrangement and Its Betti Numbers

Abstract

The resonance arrangement $\mathcal {A}_n$ is the arrangement of hyperplanes which has all non-zero 0/1-vectors in $\mathbb {R}^n$ as normal vectors. It is the adjoint of the Braid arrangement and is also called the all-subsets arrangement. The first result of this article shows that any rational hyperplane arrangement is the minor of some large enough resonance arrangement. Its chambers appear as regions of polynomiality in algebraic geometry, as generalized retarded functions in mathematical physics and as maximal unbalanced families that have applications in economics. One way to compute the number of chambers of any real arrangement is through the coefficients of its characteristic polynomial which are called Betti numbers. We show that the Betti numbers of the resonance arrangement are determined by a fixed combination of Stirling numbers of the second kind. Lastly, we develop exact formulas for the first two non-trivial Betti numbers of the resonance arrangement.

1 Introduction

1.1 The Resonance Arrangement

The main object considered in this article is the resonance arrangement:

Definition 1.1

For a fixed integer $n\ge 1$ we define the hyperplane arrangement $\mathcal {A}_n$ as the resonance arrangement in $\mathbb {R}^n$ by setting $\mathcal {A}_n:=\{H_I\mid \emptyset \ne I\subseteq [n]\},$ where the hyperplanes $H_I$ are defined by $H_I:= \left\{ \sum _{i\in I}x_i = 0 \right\} .$

The term resonance arrangement was coined by Shadrin et al. in their study of double Hurwitz numbers stemming from algebraic geometry [26]. Billera et al. proved that the product of the defining linear equations of $\mathcal {A}_n$ is Schur positive via a so-called Chern phletysm from representation theory [2, 6]. Recently, Gutekunst et al. established a connection between the resonance arrangement and the type A root polytope [15].

The arrangement $\mathcal {A}_n$ is also the adjoint of the braid arrangement [1, Sect. 6.3.12]. It was studied under this name by Liu et al. in its relation to mathematical physics [20]. The relevance of the resonance arrangement in physics was also demonstrated by Early in his work on so-called plates, cf. [12].

In earlier work, the arrangement $\mathcal {A}_n$ was called (restricted) all-subsets arrangement by Kamiya et al. who established its relevance for applications in psychometrics and economics [18, 19].

A first contribution of this article is a universality result of the resonance arrangement for rational hyperplane arrangements:

Theorem 1.2

Let $\mathcal {B}$ be any hyperplane arrangement defined over $\mathbb {Q}$. Then $\mathcal {B}$ is a minor of $\mathcal {A}_n$ for some large enough n, that is $\mathcal {B}$ arises from $\mathcal {A}_n$ after a suitable sequence of restriction and contraction steps. Equivalently, any matroid that is representable over $\mathbb {Q}$ is a minor of the matroid underlying $\mathcal {A}_n$ for some large enough n.

The proof is constructive and the size of the required $\mathcal {A}_n$ depends on the size of the entries in an integral representation of $\mathcal {B}$.

1.2 Chambers of $\mathcal {A}_n$

The chambers of $\mathcal {A}_n$ are the connected components of the complement of the hyperplanes in $\mathcal {A}_n$ within $\mathbb {R}^n$. We denote by $R_n$ the number of chambers of the arrangement $\mathcal {A}_n$. The arrangement $\mathcal {A}_3$ for instance has 32 chambers as shown in Fig. 1.

These chambers appear in various contexts, such as quantum field theory where these regions correspond to generalized retarded functions [13]. Cavalieri et al. proved that the chambers of $\mathcal {A}_n$ are the domains of polynomiality of the double Hurwitz number [8]. Subsequently, Gendron and Tahar demonstrated the significance of the chambers of the resonance arrangement in geometric topology [16].

Billera et al. observed that the chambers of $\mathcal {A}_n$ are also in bijection with maximal unbalanced families of order $n+1$. These are systems of subsets of $[n+1]$ that are maximal under inclusion such that no convex combination of their characteristic functions is constant [5]. Equivalently, the convex hull of their characteristic functions viewed in the $n+1$-dimensional hypercube does not meet the main diagonal. Such families were independently studied by Björner as positive sum systems [4].

Fig. 1

The resonance arrangement $\mathcal {A}_3$ projected onto the hyperplane $H_{\{1,2,3\}}$. There are 16 chambers visible and another 16 antipodal chambers hidden. Thus, $\mathcal {A}_3$ has 32 chambers in total

The values of $R_n$ are only known for $n\le 9$ and are given in Table 1, cf. also [25, A034997]. There is no exact formula known for $R_n$. The work of Odlyzko and Zuev [21, 28] together with the recent one by Gutekunst et al. [15] gives the bounds

$$\begin{aligned} n^2 -10n^2/\ln (n)-n+\log _2(n+1)<\log _2(R_n) < n^2-1, \end{aligned}$$

(1)

which in turn yields the asymptotic behavior $\log _2 (R_n) \sim n^2$. Deza, Pournin, and Rakotonarivo obtained the improved upper bound of $\log _2(R_n) < n^2-3n+2+\log _2(2n+8)$ [11].

Due to a theorem of Zaslavsky the number of chambers of any arrangement over $\mathbb {R}$ equals the sum of all Betti numbers of the arrangement [27]. The Betti numbers can be defined via the characteristic polynomial of an arrangement:

Definition 1.3

For any arrangement of hyperplanes $\mathcal {A}$ in $\mathbb {F}^n$ for any field $\mathbb {F}$ its characteristic polynomial $\chi (\mathcal {A};t)$ is defined to be

$$\begin{aligned} \chi (\mathcal {A};t):= \sum _{S\subseteq \mathcal {A}} (-1)^{|S|}t^{r(\mathcal {A})-r(S)}, \end{aligned}$$

where for any subset $S\subseteq \mathcal {A}$ we set $r(S):={{\,\textrm{codim}\,}}\cap _{H\in S} H$. The absolute value of the coefficient of $t^{n-i}$ in the characteristic polynomial $\chi (\mathcal {A};t)$ is called i-th Betti number. The coefficient of $t^{n-i}$ is sometimes also called Whitney number of the first kind in the literature. One always has $b_0(\mathcal {A})=1$ and $b_1(\mathcal {A})=|\mathcal {A}|$.

In the case of a complex arrangement of hyperplanes, the Betti numbers coincide with the topological Betti numbers of the complement of the arrangement $\mathbb {C}^n \setminus (\cup _{H\in \mathcal {A}}H)$ with coefficients in $\mathbb {Q}$, cf. [22, Chap. 5] for an overview of the topological study of arrangement complements.

A formula for $\chi (\mathcal {A}_n;t)$ would also yield a formula for $R_n$. Unfortunately, there is also no such formula known for $\chi (\mathcal {A}_n;t)$. In fact, the polynomial $\chi (\mathcal {A}_n;t)$ itself is only known for $n\le 9$ as computed in [18] for $n\le 7$ and in [3, 9] for $n=8,9$.

The next result of this article proves that the Betti numbers $b_i(\mathcal {A}_n)$ for any fixed $i>0$ can be computed for all $n>0$ from a fixed finite combination of Stirling numbers of the second kind S(n, k) which count the number of partitions of n labeled objects into k nonempty blocks. The proof is based on Brylawski’s broken circuit complex [7].

Theorem 1.4

There exist some positive integers $c_{i,k}$ for all $i\ge 0$ and $i+1\le k \le 2^i$ such that for all $n\ge 1$,

$$\begin{aligned} b_i(\mathcal {A}_n) = \sum _{k=1}^{2^i} c_{i,k} S(n+1,k). \end{aligned}$$

Moreover, the constants $c_{i,k}$ are bounded by $c_{i,k} \le \left( {\begin{array}{c}2^i-1\\ k-1\end{array}}\right) \frac{(k-1)!}{i!}$.

The first two trivial cases of this theorem are

$$\begin{aligned} b_0(A_n) = S(n+1,1), \quad b_1(\mathcal {A}_n) = S(n+1,2). \end{aligned}$$

Proudfoot and Ramos recently put this theorem in a representation theoretic context and obtained related result for a generalized class of arrangements [24]. Combining the upper bound on the constants $c_{i,k}$ given in Theorem 1.4 with the formula for the Stirling numbers given in (5) yields the upper bound $b_{i}(\mathcal {A}_n)<\frac{2^{in}}{i!}$ for $i,n\ge 1$. Summing up these bounds for $i=0,1,\dots ,n$ we obtain for $n>1$

$$\begin{aligned} \log _2(R_n) < n^2-n+1. \end{aligned}$$

Table 1 The values of $b_i(\mathcal {A}_n)$ for $1\le i \le 4$ and $R_n$ which is the number of chambers of $\mathcal {A}_n$ for $n\le 9$

Analyzing the triangles in the broken circuit in detail we obtain exact formulas for the first two nontrivial coefficients of $\chi (\mathcal {A}_n,t)$, namely $b_2(\mathcal {A}_n)$ and $b_3(\mathcal {A}_n)$, in terms of Stirling numbers of the second kind. That is, we determine the exact constants $c_{2,k}$ and $c_{3,k}$ for all relevant k. The resulting values of $b_2(\mathcal {A}_n)$ and $b_3(\mathcal {A}_n)$ are displayed in Table 1.

Theorem 1.5

For any $n\ge 1$ it holds that

$$\begin{aligned} \mathrm{(i)}\quad b_2(\mathcal {A}_n) =&2S(n+1,3) + 3S(n+1,4), \\ =&\frac{1}{2} (4^n - 3^n - 2^n + 1) \hbox { and} \\ \mathrm{(ii)} \quad b_3(\mathcal {A}_n) =&9S(n+1,4)+80S(n+1,5) + 345 S(n+1,6) \\&+ 840 S(n+1,7) +840S(n+1,8) ,\\ =&\frac{1}{4!} (4\cdot 8^n -15\cdot 6^n +15\cdot 5^n - 14 \cdot 4^n + 18 \cdot 3^n - 7\cdot 2^n-1). \end{aligned}$$

Example 1.6

Using Theorem 1.5 we can compute $\chi (\mathcal {A}_3;t)$ as

$$\begin{aligned} \chi (\mathcal {A}_3;t) = t^3 - 7t^2 + 15t-9. \end{aligned}$$

Thus, the above mentioned result by Zaslavsky again yields $R_3=1+7+15+9=32$.

Remark 1.7

The formula for $b_2(\mathcal {A}_n)$ in Theorem 1.5 (i) was also found earlier by Billera (personal communication). One approach to obtain the exact formulas for the higher Betti numbers $b_i(\mathcal {A}_n)$ from Theorem 1.4 is to interpolate the values of $b_i(\mathcal {A}_n)$ for all $1\le n \le 2^i$ since the matrix of Stirling numbers $(S(n,k))_{n,k=1,\dots , 2^i}$ is invertible. After the first version of this article was posted on the arXiv the method was executed by Chroman and Singhal in [9]. They confirmed the formula for $b_3(\mathcal {A}_n)$ in Theorem 1.5 and obtained a formula for $b_4(\mathcal {A}_n)$ for all n:

$$\begin{aligned}{\scriptstyle b_4(\mathcal {A}_n)=\frac{1}{48} (2\cdot 16^n -18\cdot 12^n +31\cdot 10^n +33\cdot 9^n -119\cdot 8^n +77\cdot 7^n+77\cdot 6^n -173\cdot 5^n +155\cdot 4^n -113\cdot 3^n +64\cdot 2^n -16).} \end{aligned}$$

This article is organized as follows. After reviewing necessary definitions of matroids and their minors in Sect. 2 we will prove Theorem 1.2 in Sect. 3. Subsequently, we state the necessary facts on broken circuit complexes in Sect. 4 and prove Theorem 1.4 in Sect. 5. Lastly, we give the proof of Theorem 1.5 in Sects. 6 and 7.

2 Matroids and Their Minors

In this section we review some basics of matroids and their minors. Details can be found in [23].

Definition 2.1

A matroid M is a pair $(E,\mathcal {I})$ where E is a finite ground set and $\mathcal {I}$ is a nonempty family of subsets of E, called independent sets such that

• (i) for all $A'\subseteq A \subseteq E$ if $A\in \mathcal {I}$ then $A'\in \mathcal {I}$ and

• (ii) if $A,B\in \mathcal {I}$ with $|A|>|B|$ then there exists $a\in A\setminus B$ such that $B\cup \{a\}\in \mathcal {I}$.

Given some finite set E and an $r\times E$-matrix A with entries in some field $\mathbb {F}$ we obtain a matroid M(A) on the ground set E whose independent sets are the columns of A that are linear independent. A matroid M is called representable over a field $\mathbb {F}$ if there exists an $r\times E$-matrix A such that $M=M(A)$.

An arrangement of hyperplanes $\mathcal {A}$ also gives rise to a matroid by writing the coefficients of a linear equation for each $H\in \mathcal {A}$ as columns in a matrix and applying the above construction. Similarly, we also get a matroid $M(\mathcal {A})$ underlying an arrangement $\mathcal {A}$ with ground set $\mathcal {A}$ whose independent set are precisely those whose hyperplanes intersect with codimension equal to the cardinality of the subset.

Definition 2.2

Let $M=(E,\mathcal {I})$ be a matroid and $S\subseteq E$. Then one defines:

• (a) The restriction of M to S, denoted M|S, is the matroid on the ground set S with independent sets $\{ I\in \mathcal {I}\mid I\subseteq S\}$.

• (b) Assume that S is independent in M. Then, the contraction of M by S, denoted M/S, is the matroid on the ground set $E\setminus S$ with independent sets $\{ I \subseteq E{\setminus } S\mid I\cup S\in \mathcal {I}\}$.

A matroid N is called a minor of M if N arises from M after a finite sequence of restrictions and contractions.

Minors play a central role in the theory of matroids. For instance, Geelen et al. announced a proof of Rota’s conjecture which asserts that matroid representability over a finite field can be characterized by a finite list of excluded minors [14].

The restriction of a representable matroid to some subset S is again representable by the same matrix after removing the columns that are not in S. The following lemma establishes a similar connection for contractions of representable matroids. This also motivates the term minor of a matroid as it corresponds to a minor of a matrix in the representable case.

Lemma 2.3

[23, Proposition 3.2.6] Let E be some finite set and A an $r\times E$ matrix over a field $\mathbb {F}$. Suppose $e\in E$ is the label of a nonzero column of A. Let $A'$ be the matrix arising from A through row operations by pivoting on some nonzero element in the column e. Let $A'/e$ be the matrix $A'$ where one removes the row and column containing the unique nonzero entry in the column e. Then,

$$\begin{aligned} M(A)/e =M(A')/e= M(A'/e). \end{aligned}$$

3 Universality of the Resonance Arrangement

Before proving Theorem 1.2 we illustrate the general proof strategy in an example.

Example 3.1

Consider the vectors $a_1{:}{=}(1,-2,-1)^T$ and $a_2{:}{=}(-1,0,-1)^T$ in $\mathbb {Z}^3$. We want to find a big 0/1-matrix which after suitable row operations and removing some rows and columns has exactly the column vectors $a_1,a_2$. This would then show that the matroid defined by $a_1,a_2$ is a minor of some large resonance arrangement as the columns of this 0/1-matrix are a subset of the columns of a resonance arrangement (a restriction of the matroid) and these row operations together with the row and column removal corresponds to restrictions of the matroid as explained in Lemma 2.3. In this example we consider the matrix given below.

Note that the vectors $a_1,a_2$ can be expressed as $a_1 = - \chi _{\{2,3\}} - \chi _{\{2\}}+\chi _{\{1\}}$ and $a_2 = - \chi _{\{ 1,3 \}}$. Also note that the nonzero entries of the above matrix in the first three rows correspond to these characteristic vectors. The next matrix below arises from the one above by pivoting on the first nonzero entry from below in each column except the first and the sixth column.

Restricting to all columns except these two, that is we remove all other columns and all rows except the first three, yields exactly the two column vectors $a_1,a_2$ as desired.

For the general case, let M be a matroid of rank r and size n that is representable over $\mathbb {Q}$. Thus after scaling, we can assume that there is an $r\times n$ matrix A with entries in $\mathbb {Z}$ that represents M. Let $a_1,\dots ,a_n\in \mathbb {Z}^r$ be the column vectors of the matrix A. Expressing each vector $a_i$ for $1\le i \le n$ as a sum of positive and negative characteristic vectors yields

$$\begin{aligned} a_i = \sum _{j=1}^{m_i^+} \chi _{P_j^{i}} - \sum _{k=1}^{m_i^-} \chi _{N_k^{i}}, \end{aligned}$$

(2)

for some $m_i^+,m_i^-\in \mathbb {N}_{\ge 0}$ and $P_j^i,N_k^i\subseteq [r]$ for all $1\le j \le m_i^+$ and $1\le k \le m_i^-$.

We work in the extended vector space

$$\begin{aligned} \mathbb {Q}^N {:}{=}\mathbb {Q}^r \times \mathbb {Q}^{m_1^-}\times \mathbb {Q}^{m_1^+}\times \mathbb {Q}^{m_1^{+}} \times \dots \times \mathbb {Q}^{m_n^-}\times \mathbb {Q}^{m_n^+}\times \mathbb {Q}^{m_n^{+}}, \end{aligned}$$

for some appropriate $N\in \mathbb {N}$. Hence, the vectors $a_1,\dots ,a_n$ naturally live in the first factor $\mathbb {Q}^r$ of $\mathbb {Q}^N$. We fix the standard basis of $\mathbb {Q}^N$ as

$$\begin{aligned} e_1,\dots ,e_r,e_1^{1,-},\dots ,e_{m_1^-}^{1,-},e_1^{1,+}, \dots ,e_{m_1^+}^{1,+},e_1^{1,++},\dots ,e_{m_1^+}^{1,++},\dots . \end{aligned}$$

Now, we describe a construction which will be used in the proof in Theorem 1.2. To this end, we define 0/1-vectors $v_1,\dots ,v_n$ which will eventually represent the matroid M after contracting several other 0/1-vectors. We define for each $1\le i \le n$:

$$\begin{aligned} v_i {:}{=}&\sum _{j=1}^{m_i^+} e_j^{i,++}+ \sum _{k=1}^{m_i^-} e_k^{i,-}, \\ r_k^{i,-} {:}{=}&\chi _{N_k^{i}} + e_k^{i,-} \hbox { for }1\le k \le m_i^-, \\ r_j^{i,+} {:}{=}&\chi _{P_j^{i}} + e_j^{i,+} \hbox { for }1\le j \le m_i^+,\\ r_j^{i,++} {:}{=}&e_j^{i,+} + e_j^{i,++}\hbox { for }1\le j \le m_i^+. \end{aligned}$$

We collect these vectors in the sets $V{:}{=}\{ v_1,\dots ,v_n\}$ and

$$\begin{aligned} R{:}{=}\{ r_k^{i,-}, r_j^{i,+},r_j^{i,++} \mid 1\le i \le n, 1\le k \le m_i^- \hbox { and }1\le j \le m_i^+ \}. \end{aligned}$$

Note that the columns of the matrix given in Example 3.1 are exactly the vectors constructed above for $a_1= (1,-2,-1)^T$ and $a_2= (-1,0,-1)^T$ in the order $v_1, r_1^{1,-}, r_2^{1,-}, r_1^{1,+}, r_1^{1,++}, v_2, r_1^{2,-}$.

(3)

Proof of Theorem 1.2

Assembling the vectors in R and V to a matrix yields the matrix given in Eq. (3). Now, we perform row operations on the matrix in Eq. (3) to ensure that all columns corresponding to vectors in R are standard basis vectors. To this end, we apply the following steps for all $1\le i \le n$:

• 1. We pivot on the entry in row $e_k^{i,-}$ and column $r_k^{i,-}$ for each $1\le k \le m_i^{-}$.

• 2. Next, we pivot on the entry in row $e_j^{i,s}$ and column $r_j^{i,s}$ for each $1\le j \le m_i^{+}$ and each $s\in \{+,++\}$.

By construction and Eq. (2), this procedure yields the matrix given below in Eq. (4). Therefore, we obtain the matrix A from the one given in Eq. (4) by removing all columns corresponding to vectors in R and all rows apart from the first r ones. Hence, Lemma 2.3 implies that the matroid M equals the matroid of the resonance arrangement $\mathcal {A}_N$ after first restricting to $V\cup R$ and then contracting all elements in R. Therefore, M is a minor of the matroid of $\mathcal {A}_N$. $\square$

(4)

4 The Broken Circuit Complex

The Stirling numbers of the second kind are denoted by S(n, k) and count the number of ways to partition n labeled objects into k nonempty unlabeled blocks. We will use the standard formula

$$\begin{aligned} S(n,k) = \frac{1}{k!} \sum _{i=0}^k(-1)^i\left( {\begin{array}{c}k\\ i\end{array}}\right) (k-i)^n. \end{aligned}$$

(5)

A tool to compute the Betti numbers of an arrangement is the broken circuit complex:

Definition 4.1

Let $\mathcal {A}$ be any arrangement and fix any linear order < on its hyperplanes. A circuit of $\mathcal {A}$ is a minimally dependent subset. A broken circuit of $\mathcal {A}$ is a set $C{\setminus } \{H\}$ where C is a circuit and H is its largest element (in the ordering <). The broken circuit complex $BC(\mathcal {A})$ is defined by

$$\begin{aligned} BC(\mathcal {A}){:}{=}\{ T \subset \mathcal {A}\mid T \hbox { contains no broken circuit}\}. \end{aligned}$$

Its significance lies in the following result:

Theorem 4.2

[7] Let $\mathcal {A}$ be any arrangement in a vector space $\mathbb {F}^n$ for some field $\mathbb {F}$ with a fixed linear order < on its hyperplanes. Then for any $1\le i \le n$ it holds that

$$\begin{aligned} b_{i}(\mathcal {A}) = f_{i-1}(BC(\mathcal {A})), \end{aligned}$$

where $f_i$ is the f-vector of the broken circuit complex.

For the rest of the article we will study the broken circuit complex of the resonance arrangement $\mathcal {A}_n$. Each subset of $I \subseteq \left[ n \right]$ can be encoded as a binary number $\sum _{i \in I} 2^i$. This gives rise to a natural ordering of the hyperplanes in $\mathcal {A}_n$ which we will use as to obtain its broken circuit complex. In the subsequent proofs we will identify a hyperplane $H_A$ with its defining subset A or its corresponding characteristic vector $\chi _A$ if no confusion arises.

5 Proof of  Theorem1.4

Throughout this section we use the following notation: Taking all possible intersections of the sets in an i-tuple $(A_1,\dots ,A_i)$ of pairwise different nonempty subsets of [n] yields a partition $\pi =\{P_1,\dots ,P_k\}$ of $[n+1]$ into k blocks with $i+1\le k\le 2^i$ (the block containing $n+1$ exactly contains all elements of [n] which are not contained in any of the sets $A_j$ for $1\le j \le i$). More precisely, the partition $\pi$ is the common refinement of the two-block partitions $(A_1,\left[ n+1 \right] {\setminus } A_1),\dots ,(A_i,\left[ n+1 \right] {\setminus } A_i)$. We order the blocks in the partition $\pi$ by their binary representation as detailed above; in particular we have $n+1\in P_k$.

Moreover, the tuple $(A_1,\dots ,A_i)$ together with the partition $\pi$ determines a map

$$\begin{aligned} f:[k-1]&\rightarrow \mathcal {P}([i])\setminus \{\emptyset \},\\ \ell&\mapsto \{ j\in [i]\mid P_\ell \subseteq A_j \}, \end{aligned}$$

Note that such a map is injective since the sets in the $(A_1,\dots ,A_i)$ are assumed to be pairwise different. Furthermore, there exists for every $j\in \left[ i\right]$ some $\ell \in \left[ k-1 \right]$ such that $j\in f(\ell )$ since $A_j$ is assumed to be nonempty. We call a map satisfying this last property weakly surjective. Moreover, we call a map $f:[k-1]\rightarrow \mathcal {P}([i]){\setminus }\{\emptyset \}$ that is injective and weakly surjective an (i, k)-prototype.

Conversely, given any partition $\pi =\{P_1,\dots ,P_k\}$ of $[n+1]$ and a (i, k)-prototype f we obtain an i-tuple $(A_1,\dots ,A_i)$ which we denote by $A_{f,\pi }$ by setting for $1\le j \le i$

$$\begin{aligned} A_j {:}{=}\bigcup _{\ell \in I^f_j }P_{\ell }, \end{aligned}$$

where we define $I^f_j {:}{=}\{\ell \in [k-1] \mid j\in f(\ell ) \}$ for $1\le j \le i$. Since f is weakly surjective by definition of an (i, k)-prototype these sets $A_j$ are nonempty for all $1\le j \le i$. We call these sets the building blocks of f.

In total, this construction gives a bijection between i-tuples of pairwise different nonempty subsets of [n] and pairs of (i, k)-prototypes together with partitions of $[n+1]$ into k blocks with $i+1\le k \le 2^i$.

Now the main observation is the following. Whether an i-tuple $A_{f,\pi }$ is a broken circuit depends only on the prototype f but not on the partition $\pi$:

Proposition 5.1

In the above notation, let $f:[k-1]\rightarrow \mathcal {P}([i]){\setminus }\{\emptyset \}$ be an (i, k)-prototype. Assume there exists a partition $\pi =\{P_1,\dots ,P_k\}$ of $[n+1]$ such that the i-tuple $A_{f,\pi }=(A_1,\dots ,A_i)$ is a broken circuit of $\mathcal {A}_n$ (in the order induced by the binary representation).

Let ${\widetilde{\pi }}=\{\widetilde{P_1},\dots ,\widetilde{P_k}\}$ be any partition of $[{\widetilde{n}}+1]$ for some ${\widetilde{n}}\ge 1$ into k nonempty parts. Then the i-tuple $A_{f,{\widetilde{\pi }}}=(\widetilde{A_1},\dots ,\widetilde{A_i})$ is also a broken circuit of $\mathcal {A}_{{\widetilde{n}}}$.

Proof

By assumption, the tuple $A_{f,\pi } = (A_1,\dots ,A_i)$ is a broken circuit. Thus, there exists some $C \subseteq [n]$ and $\lambda _1,\dots ,\lambda _i\in \mathbb {R}^*$ such that

$$\begin{aligned} \sum _{j=1}^i \lambda _j\chi _{A_j} = \chi _{C}, \end{aligned}$$

(6)

and $A_j < C$ for all $1\le j \le i$.

This implies that C is also a union of the first $k-1$ parts of the partition $\pi$, that is there exists some $I_C\subseteq [k-1]$ such that $C=\bigcup _{\ell \in I_C}P_\ell$. Hence, we can rewrite Eq. (6) as

$$\begin{aligned} \sum _{j=1}^i \lambda _j\sum _{\ell \in I_j^f} P_\ell = \sum _{\ell \in I_C} P_\ell , \end{aligned}$$

(7)

Subsequently, the fact $A_j < C$ yields $I_j^f < I_C$ for all $1\le j \le i$ where $I_j^f$ are the building blocks of the prototype f and the order is the one induced by the binary representation of subsets of $[k-1]$.

Now consider the partition ${\widetilde{\pi }}$ of $[{\widetilde{n}}+1]$. Using the building block $I_C$ of C we can define a corresponding subset of $[{\widetilde{n}}]$ by setting ${\widetilde{C}}{:}{=}\bigcup _{\ell \in I_C} \widetilde{P_\ell }$. Thus, Eq. (7) implies

$$\begin{aligned} \sum _{j=1}^i \lambda _j\sum _{\ell \in I_j^f} \widetilde{P_\ell } = \sum _{\ell \in I_C} \widetilde{P_\ell }. \end{aligned}$$

Therefore, the tuple $(\widetilde{A_1},\dots ,\widetilde{A_i},{\widetilde{C}})$ is a circuit of $\mathcal {A}_{{\widetilde{n}}}$. Using the fact $I_j^f < I_C$ we obtain again $\widetilde{A_j}<{\widetilde{C}}$ for all $1\le j \le i$ which completes the proof that $A_{f,{\widetilde{\pi }}}$ is a broken circuit in $\mathcal {A}_{{\widetilde{n}}}$. $\square$

In light of Proposition 5.1 we can subdivide prototypes into two sets. We call those which contain a broken circuit for some partition, and thus for all partitions, broken prototypes. Otherwise, we call a prototype functional.

Proof of Theorem 1.4 As explained above, any i-tuple of subsets of [n] can be obtained from an (i, k)-prototype and a partition $\pi$ of $[n+1]$ into k blocks with $i+1\le k \le 2^i$. Theorem 4.2 then implies that we can compute the Betti number $b_i(\mathcal {A}_n)$ for any $i\ge 0$ through functional prototypes and partitions. We correct the fact that latter yields ordered tuples unlike the elements in the broken circuit complex by multiplying the Betti numbers $b_i(\mathcal {A}_n)$ by i! in the following computation:

$$\begin{aligned} b_i(\mathcal {A}_n) i!=&|\{ X=(A_1,\dots ,A_i)\mid A_j\in \mathcal {P}([n])\setminus \{\emptyset \} , A_j\ne A_{j'} \hbox { for all }j\ne j'\hbox { and}\\&\; X \hbox {does not contain a broken circuit} \}|\\ =&\sum _{k=i+1}^{2^i} |\{A_{f,\pi }\mid f \hbox { functional} (i,k)-\hbox {prototype and}\\&\qquad \quad \pi \hbox { partition of }[n+1]\,\,\hbox { into}\,\ k\,\, \hbox {blocks}\}|\\ =&\sum _{k=i+1}^{2^i} |\{\hbox {functional (i,k)-prototypes}\}|S(n+1,k). \end{aligned}$$

This already proves that for each $i\ge 0$ the Betti number $b_i(\mathcal {A}_n)$ can be computed by a combination of Stirling numbers which is independent from n. This settles the first claim of the theorem.

For the second claim, note that the above argument shows

$$\begin{aligned} c_{i,k} = \frac{|\{\hbox {functional (i,k)-prototypes}\}|}{i!}, \end{aligned}$$

for all $i\ge 1$ and $i+1\le k \le 2^i$. Bounding the number of functional (i, k)-prototypes by the number of injective functions $f:[k-1]\rightarrow \mathcal {P}([i])\setminus \{\emptyset \}$ immediately yields for all $i\ge 1$ and $i+1\le k \le 2^i$

$$\begin{aligned} c_{i,k} \le \left( {\begin{array}{c}2^i-1\\ k-1\end{array}}\right) \frac{(k-1)!}{i!}. \end{aligned}$$

$\square$

Remark 5.2

The above upper bound on $c_{2,2^2}$ and $c_{3,2^3}$ actually agrees with the actual value of these constants given in Theorem 1.5 (3 and 840). It can be shown that the given bound on $c_{i,2^i}$ is attained for all $i\ge 1$, that is all (i, k)-prototypes are functional. For $c_{i,k}$ with $i\ge 1$ and $k<2^i$ the upper bound is not tight in general.

6 The Betti Number $b_2(\mathcal {A}_n)$

We compute $b_2(\mathcal {A}_n)$ using Theorem 4.2.

Proposition 6.1

For all $n\ge 1$ it holds that

$$\begin{aligned} f_1(BC(\mathcal {A}_n))= 2S(n+1,3) + 3S(n+1,4). \end{aligned}$$

Proof

The only circuits of $\mathcal {A}_n$ of cardinality three are of the form $\{ H_A,H_B,H_{A\cup B}\}$ where A, B are disjoint subsets of $\left[ n \right]$. Hence, the only broken circuits of cardinality two are of the form $\{ H_A,H_B\}$ where A, B are disjoint subsets of $\left[ n \right]$. Therefore, we are left with counting subsets of the form $\{ H_A,H_B\}$ where both A, B are nonempty subsets of $\left[ n \right]$ and $A\cap B \ne \emptyset$.

Assume $A\not \subseteq B$ and $B\not \subseteq A$. This case corresponds to a partition of $\left[ n+1 \right]$ into four nontrivial blocks $P_1,P_2,P_3,P_4$ where we assume that $n+1\in P_4$. Subsequently, we can choose any $P_i$ with $1\le i \le 3$ to be the intersection and set $A{:}{=}P_j \cup P_i$ and $B{:}{=}P_k\cup P_i$ where $\{j,k \}{:}{=}\{1,2,3\}{\setminus } \{i\}$. Thus, there are $3\,S(n+1,4)$ many possibilities of that type.

Now assume $A\not \subseteq B$. The subsets of the form $\{ H_A,H_B\}$ with $A \subseteq B$ corresponds to a partition of $\left[ n+1 \right]$ into three nontrivial blocks $P_1,P_2,P_3$ where we again assume $n+1 \in P_3$. In this situation we have the two families $\{H_{P_1},H_{P_1\cup P_2}\}$ and $\{H_{P_2},H_{P_1\cup P_2}\}$ which yields $2\,S(n+1,3)$ possibilities in total of that type. $\square$

Remark 6.2

In the language of the previous section, the above proof implies that all three (2, 4)-prototypes are functional whereas only two of the three (2, 3)-prototypes are functional.

Combining this proposition with Theorem 4.2 and Eq. (5) yields a proof of the announced formula for $b_2(\mathcal {A}_n)$:

Proof of Theorem 1.5 (i) We compute:

$$\begin{aligned} b_2(\mathcal {A}_n) =&2S(n+1,3) + 3S(n+1,4) \\ =&\frac{2}{3!}(3^{n+1} -3\cdot 2^{n+1} +3)\frac{3}{4!} + (4^{n+1} -4\cdot 3^{n+1} + 6\cdot 2^{n+1} -4)\\ =&\frac{1}{2} (4^n - 3^n - 2^n + 1). \end{aligned}$$

$\square$

7 The Betti Number $b_3(\mathcal {A}_n)$

To compute $b_3(\mathcal {A}_n)$ we again use the broken circuit complex with the ordering induced by the encoding in binary numbers. Hence, we need to understand which families $\{H_A,H_B,H_C\}$ form a broken circuit of $\mathcal {A}_n$ where A, B, C are subsets of $\left[ n \right]$ that are pairwise not disjoint. We use the following result due to Jovović and Kilibarda:

Theorem 7.1

[17] For any $n\ge 1$, the number of families $\{A,B,C\}$ where A, B, C are subsets of $\left[ n \right]$ that are pairwise not disjoint is

$$\begin{aligned} \frac{1}{3!}(8^n - 3\cdot 6^n + 3\cdot 5^n - 4\cdot 4^n + 3 \cdot 3^n + 2\cdot 2^n - 2). \end{aligned}$$

Expanding this numbers as sum of Stirling number of the second kind we obtain the equivalent formula

$$\begin{aligned} 13 S(n+1,4) + 92S(n+1,5) + 360S(n+1,6) + 840S(n+1,7) + 840 S(n+1,8).\nonumber \\ \end{aligned}$$

(8)

We call such families pairwise intersecting.

As a first step we will classify the circuits of $\mathcal {A}_n$ of cardinality four. To determine the broken circuits it suffices to consider circuits whose first three elements in the ordering < are pairwise intersecting. Otherwise, the edges between these elements are already broken circuits and therefore not part of $BC(\mathcal {A}_n)$.

Definition 7.2

We call a circuit in $\mathcal {A}_n$ relevant if the corresponding subsets of $\left[ n \right]$ which are not maximal in the circuit are pairwise intersecting.

Proposition 7.3

For $n\ge 1$, a four element family in $\mathcal {A}_n$ is a relevant circuit if and only if it is one of the following types for subsets $A_1,A_3,X\subseteq \left[ n\right]$ such that

$$\begin{aligned} A_1\cap A_3\ne \emptyset , A_1\setminus A_3\ne \emptyset ,A_3\setminus A_1\ne \emptyset \hbox { and }A_1\cap A_3 \cap X=\emptyset : \end{aligned}$$

(⋆)

• (i) $\{H_{A_1},H_{A_3},H_{A_1\triangle A_3},H_{A_1\cup A_3}\}$,

• (ii) $\{H_{A_1},H_{A_3},H_{A_1\cap A_3},H_{A_1\triangle A_3}\}$,

• (iii) $\{H_{A_1},H_{A_3},H_{A_1\cap A_3},H_{A_1\cup A_3}\}$ or

• (iv) $\{H_{A_1},H_{A_3},H_{(A_1\cap A_3)\cup X},H_{(A_1\cup A_3)\setminus X}\}$.

In each case, we assume that the last element in each set is the largest with respect to the ordering <.

Before proving this proposition, we give examples for each such type of circuit of cardinality four.

Example 7.4

Consider the following families in the arrangement $\mathcal {A}_4$ corresponding to the cases of Proposition 7.3.

• (i) The family $\{H_{\{1,2\}},H_{\{1,3\}},H_{\{2,3\}},H_{\{1,2,3\}}\}$ is a circuit of $\mathcal {A}_4$ since there is the relation $\chi _{\{1,2\}}+\chi _{\{1,3\}} + \chi _{\{2,3\}} = 2 \chi _{\{1,2,3\}}$.

• (ii) The family $\{H_{\{1,2\}},H_{\{1,3\}},H_{\{1\}},H_{\{2,3\}}\}$ is a circuit of $\mathcal {A}_4$ since there is the relation $\chi _{\{1,2\}}+\chi _{\{1,3\}} = 2\chi _{\{1\}} + \chi _{\{2,3\}}$.

• (iii) The family $\{H_{\{1,2\}},H_{\{1,3\}},H_{\{1\}},H_{\{12,3\}}\}$ is a circuit of $\mathcal {A}_4$ since there is the relation $\chi _{\{1,2\}}+\chi _{\{1,3\}} = \chi _{\{1\}} + \chi _{\{1,2,3\}}$.

• (iv) Setting $A_1{:}{=}\{2,4\},A_3{:}{=}\{1,3,4\}$ and $X{:}{=}\{1\}$ yields the family $\{H_{\{2,4\}},H_{\{1,3,4\}},H_{\{1,4\}},H_{\{2,3,4\}}\}$. This is a circuit of $\mathcal {A}_4$ since there is the relation $\chi _{\{2,4\}}+\chi _{\{1,3,4\}} = \chi _{\{1,4\}} + \chi _{\{2,3,4\}}$.

Proof of Proposition 7.3

Generalizing the relations given in Example 7.4 to arbitrary sets $A_1,A_3,X$ satisfying the conditions in Eq. (⋆) shows that these given families are indeed families of four different subsets of $\left[ n\right]$ which form relevant circuits in $\mathcal {A}_n$.

Conversely, let $\{A_1,\dots ,A_4\}$ be a family of subsets corresponding to a relevant circuit in $\mathcal {A}_n$ with $A_i\ne A_j$ for any $i\ne j$, $A_i\cap A_j\ne \emptyset$ for $1\le i,j\le 3$ and $A_4$ is the maximal element in the ordering <. Since the hyperplanes form a circuit in $\mathcal {A}_n$ there is a relation $\sum _{i=1}^4\lambda _i\chi _{A_i}=0$ for some $\lambda _i\in \mathbb {Z}$ for $1\le i \le 4$. The coefficients $\lambda _i$ need to be nonzero since the circuit would otherwise satisfy a dependency of cardinality less than four.

Using the symmetry of the sets $A_1,\dots ,A_3$ it suffices to consider the two cases $\lambda _1,\lambda _2,\lambda _3>0$ and $\lambda _4<0$ or $\lambda _1,\lambda _3>0$ and $\lambda _2,\lambda _4<0$. Note, that the case $\lambda _1>0$ and $\lambda _2,\lambda _3,\lambda _4<0$ cannot occur since $A_4$ is the maximal element.

Case 1: $\lambda _1,\lambda _2,\lambda _3>0$ and $\lambda _4<0$ In this case, the relation implies $A_1\cup A_2\cup A_3=A_4$. Since the sets $A_1,A_2,A_3$ are by assumption pairwise intersecting every element in $A_4$ is contained in at least two of the sets $A_1,A_2,A_3$. Not all elements of $A_4$ appear in all of the sets $A_1,A_2,A_3$ since otherwise these four sets would all be equal. Hence, the relation then implies that every element in $A_4$ is contained in exactly two of the sets $A_1,A_2,A_3$ which means that we can without loss of generality assume $A_2=A_1\triangle A_3$. Therefore, the family is a circuit of type (i).

Case 2: $\lambda _1,\lambda _3>0$ and $\lambda _2,\lambda _4<0$ Analogously to the first case, the relation now yields $A_1\cup A_3= A_2\cup A_4$. Hence, the maximality of $A_4$ yields $A_1\not \subseteq A_3$ and $A_1\not \supseteq A_3$. Thus, the elements in $A_1\cup A_3$ are partitioned into the three blocks $A_1{\setminus } A_3, A_3{\setminus } A_1$ and $A_1\cap A_3$ appearing with positive coefficients $\lambda _1,\lambda _3$ and $\lambda _1+\lambda _3$ respectively in the relation. Assume there is an element $a\in (A_1\cup A_3){\setminus } A_2$. Then, $a\in A_4$ which implies $\lambda _4=\lambda _1+\lambda _3$ since $a\not \in A_2$. This yields $A_4 \subseteq A_1\cap A_3$ which contradicts the maximality of $A_4$. Therefore, we must have $A_1\cap A_3\subseteq A_2$ and it suffices to consider the following two subcases:

Case 2.1: $A_1 \cap A_3=A_2$ Then we obtain $A_1\triangle A_3 \subseteq A_4$. Since the positive coefficients in the relation are constant on the block $A_1 \cap A_3$ we must have either $A_1\triangle A_3 = A_4$ or $A_1\cup A_3 = A_4$. The former case yields a circuit of type (ii) and the latter one of type (iii) as described in the statement of Proposition 7.3.

Case 2.2: $A_1 \cap A_3\subsetneq A_2$ Assume $(A_1 \cap A_3)\cup X = A_2$ for some nonempty subset $X\subseteq A_1\triangle A_3$. Now, we must have $A_4 \supseteq (A_1\triangle A_3){\setminus } X$ since $A_1\cup A_3= A_2\cup A_4$. Since $X\subseteq A_1\triangle A_3$, the coefficient $\lambda _2$ can be at most $\lambda _1$ or $\lambda _3$. However, the positive coefficient of the elements in $A_1 \cap A_3$ is $\lambda _1 +\lambda _3$. Hence, $A_4 \supseteq (A_1\cap A_3)$. So in total $A_4 \supseteq (A_1\cup A_3)\setminus X$. Since the positive coefficients of the elements in $A_1 \cap A_3$ and $A_1 \triangle A_3$ are different we must have $A_4\cap X = \emptyset$. Therefore, $A_4 = (A_1\cup A_3)\setminus X$ and the circuit is of type (iv). $\square$

Proposition 7.3 implies that all broken circuits of $\mathcal {A}_n$ of cardinality three are of the form $\{H_{A_1},H_{A_3},H_{A_1\triangle A_3}\}$ or $\{H_{A_1},H_{A_3},H_{(A_1\cap A_3)\cup X}\}$ for $A_1,A_3,X\subseteq \left[ n \right]$ with $A_1\cap A_3\ne \emptyset$, $A_1\not \subseteq A_3$, $A_1\not \supseteq A_3$ and $X\subseteq A_1\triangle A_3$. The former ones correspond to circuits of type (i) with the relation $\chi _{\{A_1\}}+\chi _{\{A_2\}} + \chi _{\{A_3\}} = 2 \chi _{\{A_4\}}$. We call them tetrahedron circuits since they exhibit a tetrahedron if we regard the elements as vertices of the n-dimensional hypercube.

The latter broken circuits might not stem from a unique circuit of cardinality four. We can however fix a bijection between these broken circuits and the circuits of type (iii) and (iv) in Proposition 7.3. These all satisfy the relation $\chi _{\{A_1\}} + \chi _{\{A_3\}} = \chi _{\{A_2\}}+ \chi _{\{A_4\}}$. The characteristic functions of these circuits viewed in the n-dimensional hypercube form rectangles which is why we call these circuit rectangle circuits in the following.

Using again Theorem 4.2 to determine $b_3(\mathcal {A}_n)$ we will therefore start from Theorem 7.1 and subtract the number of tetrahedron and rectangle circuits which give broken circuits of cardinality three by removing the largest element in each circuit. Note that a broken circuit can not stem from a tetrahedron and rectangle circuit simultaneously since it can not satisfy a tetrahedron and a rectangle relation at the same time.

Proposition 7.5

For any $n\ge 1$ there are $S(n+1,4)$ tetrahedron circuits in $\mathcal {A}_n$.

Proof

Let $P_1,P_2,P_3,P_4$ be any partition of $\left[ n+1\right]$ where we label the parts so that $n+1\in P_4$. Set $A_4 {:}{=}\left[ n+1\right] {\setminus } P_4$ and $A_i {:}{=}A_4 {\setminus } P_i$ for $1\le i \le 3$.

We claim that the hyperplanes corresponding to $A_1,\dots ,A_4$ form a tetrahedron circuit in $\mathcal {A}_n$. By definition we have $P_k=A_i\cap A_j$ for any possible ordering $\{k,i,j\}=\{1,2,3\}$ and $A_i\subset A_4$ for all $1\le i \le 3$ Hence, the family $A_1,\dots ,A_4$ is pairwise intersecting, i.e. $A_i\cap A_j \ne \emptyset$ for all $i\ne j$. Next, consider $l\in A_4$ such that $l\in P_i$ for some $1\le i \le 3$ and set $\{j,k\}{:}{=}\{1,2,3\}\setminus \{i\}$. Then, we conclude that $l\in A_j, l\in A_k$ and $l\not \in A_i$ which implies that $A_1,\dots ,A_4$ corresponds to a tetrahedron circuit.

Conversely, given the subsets $A_1,\dots , A_4$ of $\left[ n\right]$ corresponding to a tetrahedron circuit with largest subset $A_4$ we can define a partition of $\left[ n+1\right]$ by setting $P_4 {:}{=}\left[ n+1\right] {\setminus } A_4$ and $P_i {:}{=}A_4 {\setminus } A_i$ for $1\le i \le 3$. We claim this defines a partition of $\left[ n+1\right]$. By definition we have $P_i\cap P_4=\emptyset$ for all $1\le i\le 3$. The assumption of $A_1,\dots , A_4$ corresponding to a tetrahedron circuit implies that every $l\in A_4$ is contained in exactly two subsets $A_k,A_j$ for some $1\le k <j\le 3$. This implies that every $l\in A_4$ is contained in exactly one block $P_i$ which proves that $P_1,\dots ,P_4$ is a partition of $\left[ n+1\right]$.

Since these two constructions are inverse to each other the claim follows. $\square$

To count the rectangle circuits we construct corresponding tuples which will be easier to count. Throughout the subsequent discussion we regard the indices cyclically, i.e. given any family of sets $X_1\dots X_n$ we set $X_0{:}{=}X_n$ and $X_{n+1}{:}{=}X_1$.

Proposition 7.6

Let $(A_1,\dots ,A_4)$ be a family of distinct and nonempty subsets of $\left[ n\right]$ forming a relevant rectangle circuit, i.e. $\chi _{A_1}+\chi _{A_3}= \chi _{A_2}+ \chi _{A_4}$ and $A_i\cap A_j \ne \emptyset$ for $1\le i < j \le 3$ with maximal element $A_4$. Then,we define its midpoint as $M{:}{=}\bigcap _{i=1}^4 A_i$ and the sides of the rectangle as $S_i{:}{=}(A_i \cap A_{i+1}) {\setminus } M$ for $1\le i \le 4$.

In this case, the tuple $(S_1,\dots ,S_4,M)$ satisfies

(S1):

$S_i\cap S_j = \emptyset$ for all $i\ne j$ and in particular $S_i\ne S_j$ for all $i\ne j$,

(S2):

$M\cap S_i=\emptyset$ for all $1\le i \le 4$,

(S3):

$M\ne \emptyset$, and

(S4):

at most one of two opposite sides are empty.

We will call a tuple $(S_1,\dots ,S_4,M)$ satisfying (S1) to (S4) a side-midpoint tuple.

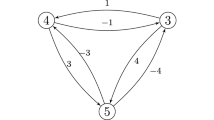
Example 7.7

Figure 2 depicts the general case of a rectangle circuit together with its corresponding side-midpoint tuples as defined in Proposition 7.6 and two examples in $\mathcal {A}_5$.

Fig. 2

Three examples of rectangle circuits together with their side-midpoint tuples

Proof of Proposition 7.6

To prove (S1) assume for a contradiction $a\in S_i\cap S_j$. Without loss of generality we can assume $a\in S_1\cap S_2$. By definition this yields $a\in A_1,A_2,A_3$ but $a\not \in M$. Thus $a\not \in A_4$. This contradicts the relation $\chi _{\{A_1\}} + \chi _{\{A_3\}} = \chi _{\{A_2\}}+ \chi _{\{A_4\}}$ in the element a. Thus, $S_i\cap S_j=\emptyset$ for all $i\ne j$.

The sides $S_i$ are defined as $S_i{:}{=}(A_i \cap A_{i+1}) \setminus M$. This immediately implies property (S2) namely $S_i\cap M=\emptyset$.

By assumption, we have $A_1\cap A_3 \ne \emptyset$. The relation $\chi _{\{A_1\}} + \chi _{\{A_3\}} = \chi _{\{A_2\}}+ \chi _{\{A_4\}}$ then yields $A_1\cap A_3=A_2\cap A_4$. Therefore, $A_1\cap A_3=M\ne \emptyset$ which proves property (S3).

Lastly, assume without loss of generality $S_1=S_3=\emptyset$. This implies $A_1=M\cup S_4 \cup \widetilde{A_1}$ for some $\widetilde{A_1}\subseteq \left[ n \right]$ disjoint from M and $S_4$. This yields $\widetilde{A_1}\cap A_4 = \emptyset$ since any intersection of these sets disjoint from M would be contained in $S_4$. Hence using the fact $A_1\cup A_3= A_2\cup A_4$, we obtain $\widetilde{A_1}\subseteq A_2$. Thus,

$$\begin{aligned} \widetilde{A_1}\subseteq (A_1\cup A_2)\setminus M= S_1=\emptyset . \end{aligned}$$

Hence, $\widetilde{A_1}=\emptyset$ and $A_1=M\cup S_4$. Analogously, we obtain $A_4=M\cup S_4$ which contradicts $A_1\ne A_4$. $\square$

The next proposition shows that we can obtain a rectangle circuit from a side-midpoint tuple:

Proposition 7.8

Let $(S_1,\dots ,S_4,M)$ be a side-midpoint tuple. Set $A_i {:}{=}M \cup S_{i-1} \cup S_{i}$. Then, the family $(A_1,\dots ,A_4)$ corresponds to a relevant rectangular circuit which means it satisfies

(C1):

$A_i\ne A_j$ for all $i\ne j$,

(C2):

$A_i\ne \emptyset$ for all $1\le i \le 4$,

(C3):

$A_i\cap A_j\ne \emptyset$ for all $i\ne j$ and

(C4):

it forms a rectangle circuit, i.e. $\chi _{A_1}+\chi _{A_3}= \chi _{A_2}+ \chi _{A_4}$.

Proof

Assume $A_1=A_2$. This implies $M\cup S_{4}\cup S_1=M\cup S_{1}\cup S_2$. Hence, $S_4=S_2$. By assumption (S1) these sets are disjoint which yields $S_4=S_2=\emptyset$. This contradicts the assumption $(S_4)$ that at most one of two opposite sets is empty. Now assume $A_1=A_3$. This implies $M\cup S_{4}\cup S_1=M\cup S_{2}\cup S_3$. Thus, we have two partitions of the same set by pairwise disjoint sets which can not all be empty which is impossible. Thus we have without loss of generality proven (C1).

By assumption we have $M\ne \emptyset$. Our construction of the sets $A_i$ yields $M\subseteq A_i$ for all $1\le i\le 4$. This immediately implies $A_i\ne \emptyset$ for all $1\le i\le 4$ and $A_i\cap A_j\ne \emptyset$ for all $i\ne j$. Hence, properties (C2) and (C3) hold.

Lastly, we have by construction of the sets $A_i$ and due to the fact that the sets $S_1,\dots ,S_4,M$ are pairwise disjoint

$$\begin{aligned} \chi _{A_1}+\chi _{A_3}=\chi _M+\sum _{i=0}^4\chi _{S_i}=\chi _{A_2}+ \chi _{A_4}. \end{aligned}$$

$\square$

Proposition 7.9

The constructions defined in Propositions 7.6 and 7.8 are inverse to each other.

Proof

Let $(A_1,\dots ,A_4)$ be the vertices of a relevant rectangle circuit satisfying (C1) to (C4). This yields by Proposition 7.6 the side-midpoint tuple with midpoint $M_A {:}{=}\bigcup _{i=1}^4 A_i$ and sides $(A_{i-1}\cap A_i){\setminus } M_A$. Fix some $1\le i \le 4$. The relation in property (C4) then implies $A_i \subseteq A_{i-1}\cup A_{i+1}$. Hence, we obtain $A_i = (A_{i-1}\cup A_i) \cup (A_{i}\cup A_{i+1})$. This yields,

$$\begin{aligned} A_i = M_A \cup ((A_{i-1}\cup A_i)\setminus M_A) \cup ((A_{i}\cup A_{i+1})\setminus M_A). \end{aligned}$$

Thus, the vertices $A_i$ equal the resulting vertices from the construction in Proposition 7.8.

Conversely, let $(S_1,\dots ,S_4,M)$ be a side-midpoint tuple. This yields by Proposition 7.8 the vertices of a rectangle circuit $M\cup S_{i-1}\cup S_i$ for $1\le i \le 4$. Since the sets $S_1,\dots ,S_4,M$ are pairwise disjoint the construction of Proposition 7.6 applied to these vertices yields the side-midpoint tuple $(S_1,\dots ,S_4,M)$. $\square$

In total we have established a bijection between relevant rectangle circuits and side-midpoint tuples. The former correspond to broken circuits of $\mathcal {A}_n$ of the form $\{H_{A_1},H_{A_3},H_{(A_1\cap A_3)\cup X}\}$ for $A_1,A_3,X\subseteq \left[ n \right]$ with $A_1\cap A_3\ne \emptyset$, $A_1\not \subseteq A_3$, $A_1\not \supseteq A_3$ and $X\subseteq A_1\triangle A_3$. We are now able to determine the number of these broken circuits by counting side-midpoint tuples.

Proposition 7.10

For any $n\ge 1$ there are $3S(n+1,4)+12S(n+1,5) + 15 S(n+1,6)$ side-midpoint tuples in $\left[ n\right]$. This number equals the relevant rectangle circuits in $\mathcal {A}_n$.

Proof

We split up the side-midpoint tuples in $\left[ n\right]$ into three cases depending on how many sides are empty. Since at most one of two opposite sides can be empty these cover all side-midpoint tuples.

Case 1: Two adjacent sides are empty. Say $S_1=S_2=\emptyset$. In this case, we need to count partitions of a subset of $\left[ n\right]$ into three blocks, one for each of the sets $S_3,S_4$ and M. The sets $S_3$ and $S_4$ are symmetric and we can choose any of the three blocks for the distinguished set M. Therefore, we obtain $3S(n+1,4)$ side-midpoint tuples in this case.

Case 2: Exactly one side is empty. Say $S_1=\emptyset$. In this case, we need to count partitions of a subset of $\left[ n\right]$ into four blocks, one for each of the sets $S_2,S_3,S_4$ and M. There are $S(n+1,5)$ such partitions. We can choose any of the four blocks as the distinguished midpoint M. The remaining three blocks can be assigned to the sets $S_2,S_3,S_4$ in exactly three nonequivalent ways. These choices correspond to the identity permutations and the two transposition $(1\; 2)$ and $(2\;3)$ in $\mathfrak {S}_3$ Therefore there are in total $12S(n+1,5)$ side-midpoint tuples in this case.

Case 3: All sides are nonempty. This case works almost analogously to Case 2. This time we need to count partitions of a subset of $\left[ n\right]$ into five blocks, one for each of the sets $S_1,S_2,S_3,S_4$ and M. There are $S(n+1,6)$ such partitions. We can choose any of the blocks as the midpoint. Subsequently, we can fix $S_1$ as the first free block without any choices due to the symmetry of the sets $S_1,\dots ,S_4$. As in Case 2 there are now three choices for the assignment of the last three sets. In total we obtain $15S(n+1,6)$ side-midpoint tuples without any empty sides. $\square$

Putting the above statements together we can prove the announced formula for $b_3(\mathcal {A}_n)$:

Proof of Theorem 1.5 (ii) By Theorem 4.2, the Betti number $b_3(\mathcal {A}_n)$ equals the number of intersecting families of cardinality three minus the number of broken circuits of cardinality three. Hence, we can compute $b_3(\mathcal {A}_n)$ using Eq. (8) in Theorem 7.1 subtracted by the number of tetrahedron and rectangle circuits computed in Proposition 7.5 and Proposition 7.10. Thus, we obtain

$$\begin{aligned} b_3(\mathcal {A}_n)= & {} 9S(n+1,4)+80S(n+1,5) + 345 S(n+1,6) + 840 S(n+1,7)\\{} & {} +840S(n+1,8). \end{aligned}$$

Expanding this equation via the formula for the Stirling numbers in Eq. (5) yields

$$\begin{aligned} b_3(\mathcal {A}_n) = \frac{1}{4!} (4\cdot 8^n -15\cdot 6^n +15\cdot 5^n - 14 \cdot 4^n + 18 \cdot 3^n - 7\cdot 2^n-1). \end{aligned}$$

$\square$