Introduction 

Creatine kinase isoenzyme (CK-MB) is one of the main serum indexes for clinical detection of myocardial ischemia injury and myocardial infarction (Xu et al. 2014). It is the most characteristic index among the five indexes of myocardial enzyme spectrum (Wei et al. 2021). CK-MB can also be used as an effective biomarker to predict the occurrence and development of acute pancreatitis (Perry Elliott et al. 2021). Acute coronary syndromes can be diagnosed by its specificity and sensitivity (Baroni 2020). The current coronavirus disease (COVID-19), caused by severe acute Respiratory syndrome coronavirus type 2 infection, has rapidly spread worldwide. Korean scholars compared patients in a hospital in Daegu and found that there were differences in arrhythmia and myocardial enzyme spectrum indexes. When CK-MB > 6.3, it could be used as an independent predictor of severe disease in COVID-19 patients. Appropriate evaluation of prognostic factors and close monitoring, and provision of necessary interventions to high-risk patients at appropriate times, can reduce the fatality rate from COVID-19 (Jang JG et al. 2020).

CK-MB medical health reference value as the most intuitive distinction between myocardial infarction patients and healthy people standard, clinical medicine in the establishment of reference value in the study of innovative practice. At present, researchers in China, by comparing different CK-MB detection methods, the results of reference values are more referential. In order to diagnose early viral myocarditis and ischemic children, Chinese domestic scholars (Chen and Deng 2019), foreign scholars (Soldin et al. 1999). The reference ranges of CK-MB for children of different ages in Hunan, China, and Washington, USA, were established respectively. At present, Habte ML proposed that the change of CK-MB reference value is related to the influence of non-environmental factors, such as gender, age, living habits, human obesity degree, and blood lipid concentration (Habte et al. 2020). Domestic and foreign studies on CK-MB reference value and regional environment are still in a blank state. There are only a few studies on CK-MB pathology, and there is a lack of unified and accurate reference value standards to detect and prevent the incidence of cardiovascular diseases in various countries. China is located in 73°33′E ~ 135°05′E, 3°51′N ~ 53°33′N, spanning many temperature zones and wet and dry zones, with obvious differences between different regions. According to these characteristics, it is very necessary to develop a standard system for the reference range of CK-MB reference value which is accurate and applicable to different regions in China.

In this paper, a set of geographical distribution criteria for predicting the reference values of CK-MB among healthy adults in 2322 cities (counties) in China was established by considering the comprehensive effects of multiple geographical factors, so as to provide scientific basis for clinical diagnosis. Based on hydrology, climate, topography, and soil, spatial autocorrelation test was carried out on the measured values of CK-MB, and the geographical correlation between regions and medical indicators was obtained, which ensured the reasonable feasibility of the prediction model. Through the geographical distribution law of CK-MB reference value of healthy people and the quantitative calculation of the prediction model, a unified model standard was developed nationwide to prevent the incidence of cardiovascular diseases in different regions.

Materials

Reference source of creatine kinase isoenzyme (CK-MB)

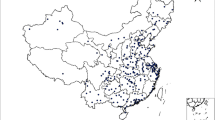
Through searching the Chinese periodical net, China Excellent Master and Doctor Dissertation Full-text Database, China Conference Full-text Database and hospital measurement data. Based on the retrieval of “Reference value of creatine kinase isoenzyme” and “CK-MB,” we collected the CK-MB data of healthy adults for physical examination from 137 cities in China. Most of data are distributed in the second and third steps of China, which coincide with the population distribution density in China with a total of 8697 cases. Distribution of sample points is shown in (Fig. 1). The eastern data were more than the western data, and the data of remote areas such as Lhasa and Xinjiang were relatively scarce, and the data of Hong Kong, Macao, and Taiwan were lacking.

Fig. 1
figure 1

Spatial distribution of CK-MB reference values in healthy adults

Full size image

The geographical factors

China has a varied climate and complex terrain; the geographical differences are wide and obvious; therefore, this article selects three broad types of geographical environment factors named topographic, climate, and soil, including 24 sub-indexes (Table 1).

Table 1 The description of geographical factors
Full size table

Method and analysis

Spatial autocorrelation

In order to further judge whether medical data is geospatial-dependent, global or local indicators are generally used to judge. Among them, global spatial autocorrelation (DeWitt et al. 2021; Wang 2020b) focuses more on the spatial distribution of attribute values of an object in the whole region. We conducted global spatial autocorrelation analysis on CK-MB reference sample data of healthy adults in arc GIS, and obtained Z value and P value by Moran’s I index analysis. Moran’s I value is within the range of [− 1, 1]. The closer the value is to 1, the stronger the positive correlation is; otherwise, the stronger the negative correlation is. Z value represents the spatial distribution state of the whole region, and the significance of P value can prove whether the data is randomly distributed.

Through the calculated data (Table 2 and Fig. 2), we can know that at the confidence level of 0.01, |Z|= 9.6465 ≥ 2.54, the spatial autocorrelation of the reference value of CK-MB is significant. It will be seen from the results that it is affected by the space geographical environment; different environments make the different geographical distributions of CK-MB.

Table 2 Global Moran index report
Full size table
Fig. 2
figure 2

Spatial autocorrelation analysis of CK-MB in healthy adults

Full size image

Correlation analysis

Correlation analysis can further find the geographical factors with significant correlation, which lays a foundation for the establishment of subsequent prediction models. Among them, the common correlation coefficients are Pearson, Spearman, Kendall, etc. The data presented non-normal distribution through K-S test under the non-parametric analysis method. To solve the non-linearity of sample data, Spearman correlation coefficient was selected to judge the monotone form among geographical factors.

Based on SPSS25.0, with 24 geographical indicators as independent variables and CK-MB as dependent variable, the correlation coefficient (r) and significance coefficient (P) between CK-MB of healthy adults in various regions of China and 24 geographical indicators can be obtained (Table 3). Among the 24 geographical factors selected, there are 9 geographical factors that are correlated with the CK-MB reference value of healthy adults, among which the following 5 geographical factors are generally related: latitude (X2), annual sunshine duration (X4), annual mean relative humidity (X6), annual precipitation amount (X7), and annual range of air temperature (X8). The four geographical factors with significant correlation are as follows: annual mean air temperature (X5), topsoil gravel content (X15), topsoil (clay) cation exchange(X18), and topsoil (silt) cation exchange capacity (X19).

Table 3 The r and P values of geographical factors and CK-MB
Full size table

In R language (Muhammad et al. 2021), the correlation coefficients of 9 related geographical factors were taken as independent variables and dependent variables to judge whether there was multicollinearity influence among geographical factors (Fig. 3).

Fig. 3
figure 3

Heat map of correlation coefficient of geographical factors with correlation

Full size image

Latitude has a strong collinearity effect with annual mean temperature, annual precipitation, and annual temperature difference. Therefore, the least square regression analysis is excluded, which leads to the inconsistency between the results and reality. Therefore, appropriate model and method are further selected for optimal prediction.

Ridge regression analysis

For the problem of multicollinearity among factors, A.E. Hoerl first proposed an improved least square estimation method (Hoerl and Kennard 2000), called ridge estimation, in 1962. In 1970, Hall, in collaboration with Kennard, developed a further systematic development of ridge estimation. Ridge estimation is a kind of biased estimation modified to the least square estimation method. There exists a ridge regression estimation with β as k ≥ 0, b(k) = (X ′X + k I) − 1X′ Y. When k = 0, the ridge regression equation is the least square estimation. When there are significant multiple correlations among the independent variables, the regression coefficient can be controlled to reduce the error (Choi et al. 2019).

Based on R language and R Studio programming environment, 9 geographical factors with correlation were loaded and substituted. As shown in Fig. 4(a), the error value became flat when Log (lambda) = 2, and the error of the prediction regression equation was the smallest. The regression equation obtained from Fig. 4(b) and programming code was:

Fig. 4
figure 4

CK-MB reference ridge map for healthy adults Fig. 4（a） CK-MB reference Ridge regression prediction error  Fig. 4（b）CK-MB reference Ridge regression factor contribution

Full size image
$$\widehat{Y}=0.0332{X}_{2}\hspace{0.17em}+\hspace{0.17em}0.0225{X}_{4}\hspace{0.17em}-\hspace{0.17em}0.0271{X}_{5}\hspace{0.17em}-\hspace{0.17em}0.0204{X}_{6}\hspace{0.17em}+\hspace{0.17em}0.0107{X}_{7}\hspace{0.17em}+\hspace{0.17em}0.0447{X}_{8}\hspace{0.17em}-\hspace{0.17em}0.0667{X}_{15}\hspace{0.17em}+\hspace{0.17em}0.0886{X}_{18}\hspace{0.17em}+\hspace{0.17em}0.0762{X}_{19}$$

Lasso regression model

Lasso regression model aims to solve many variables in the prediction process, and the influence of “over fitting” and multicollinearity brought about by OLS linear fitting, so as to improve the explanatory power of the model. Tibshirani proposed Lasso method for the first time. Lasso makes the dimension of independent variable compressed by adjusting lambda. The number of samples was selected based on the punishment method, and the original data was compressed to compress the relative coefficient of non-significant variables to 0. Such methods avoid over-interpretation of the current sample and explore rules that apply to the population (Tibshirani et al. 2005).

Based on R language and R Studio programming environment, when the 9 relevant geographical factor indicators that are useful to the reference value of CK-MB obtained from Fig. 5(a) are reduced to 4, the prediction regression equation has the smallest error, and the corresponding Log (lambda) = 0.1414. The regression equation obtained from the programming code in Fig. 5(b) is as follows:

Fig. 5
figure 5

CK-MB reference ridge map for healthy adults Fig. 5（a）CK-MB reference Lasso regression prediction error Fig. 5（b）CK-MB reference  Lasso regression factor contribution

Full size image
$$\widehat{Y}=0.00224{X}_{8}\hspace{0.17em}-\hspace{0.17em}0.0744{X}_{15}\hspace{0.17em}+\hspace{0.17em}0.188{X}_{18}\hspace{0.17em}+\hspace{0.17em}0.0806{X}_{19}$$

Principal component analysis model

Feasibility of PCA

Prior to PCA, correlation exploration among factors was conducted (Fig. 2). We obtained that the correlation coefficient between latitude and annual mean temperature was 0.95 (> 0.90), the correlation coefficient between latitude and annual precipitation was 0.93 (> 0.90), and the correlation coefficient between latitude and annual temperature was 0.91 (> 0.90). The existence of serious collinearity is suitable for principal component analysis (Beattie and Esmonde-White 2021). 

Principal component extraction and regression equation establishment

First, KMO statistics and Bartlett test of spherical were used for judgment (Table 4). The results showed that the closer KMO was to 1, the stronger the correlation between variables was, and the original variables were suitable for factor analysis. Bartlett’s spherical test value P < 0.001 negates the null hypothesis, indicating that the correlation matrix among variables is not the identity matrix. In other words, it is considered that there is a correlation between variables, and it is necessary to carry out factor analysis. In Table 4, KMO value is 0.779 and Sig. value is 0.000, which is in line with the condition of factor analysis.

Table 4 KMO statistics and Bartlett’s test for sphericity
Full size table

SPSS25.0 was applied to the geographical index—latitude (X2), annual sunshine duration (X4), annual mean air temperature (X5), annual mean relative humidity (X6), annual precipitation amount (X7), and annual range of air temperature (X8), topsoil gravel content (X15), topsoil (clay) cation exchange (X18), and topsoil (silt) cation exchange capacity (X19) were extracted as principal components. The correlation coefficient matrix of geographical indicators (Table 5) and variance decomposition accumulation table (Table 6) were obtained.

Table 5 Correlation coefficient matrix of geographical indicators
Full size table
Table 6 Variance decomposition cumulative table
Full size table

According to the results in Table 6, the cumulative contribution rate of the three factors reached 81.725%, indicating that 81.725% of all geographical variables had been included and the effect was good. When the fourth characteristic root is taken, the characteristic value of the curve has dropped below 1, so three common factors are selected to replace the original nine geographical variables to study the influence on the reference value of adult CK-MB. By extracting the first three principal components, the combined relationship between the first three principal components and geographical factors can be obtained according to the component score coefficient matrix obtained (Table 7):

Table 7 Principal component score coefficient matrix
Full size table

\(\begin{array}{l}{Z}_{1}=-0.966\mathrm{std}{X}_{2}-0.782\mathrm{std}{X}_{4}\hspace{0.17em}+\hspace{0.17em}0.933\mathrm{std}{X}_{5}\hspace{0.17em}+\hspace{0.17em}0.859\mathrm{std}{X}_{6}\hspace{0.17em}+\hspace{0.17em}0.916\mathrm{std}{X}_{7}-0.858\mathrm{std}{X}_{8}-0.1\mathrm{std}{X}_{15}\hspace{0.17em}+\hspace{0.17em}0.129\mathrm{std}{X}_{18}\hspace{0.17em}-\hspace{0.17em}0.028\mathrm{std}{X}_{19}\\ {Z}_{2}=0.069\mathrm{std}{X}_{2}\hspace{0.17em}-\hspace{0.17em}0.116\mathrm{std}{X}_{4}\hspace{0.17em}-\hspace{0.17em}0.052\mathrm{std}{X}_{5}\hspace{0.17em}+\hspace{0.17em}0.106\mathrm{std}{X}_{6}\hspace{0.17em}-\hspace{0.17em}0.064\mathrm{std}{X}_{7}\hspace{0.17em}+\hspace{0.17em}0.096\mathrm{std}{X}_{8}\hspace{0.17em}+\hspace{0.17em}0.15\mathrm{std}{X}_{15}\hspace{0.17em}+\hspace{0.17em}0.879\mathrm{std}{X}_{18}\hspace{0.17em}+\hspace{0.17em}0.867\mathrm{std}{X}_{19}\\ {Z}_{3}=0.049\mathrm{std}{X}_{2}\hspace{0.17em}-\hspace{0.17em}0.177\mathrm{std}{X}_{4}\hspace{0.17em}+\hspace{0.17em}0.043\mathrm{std}{X}_{5}\hspace{0.17em}+\hspace{0.17em}0.087\mathrm{std}{X}_{6}\hspace{0.17em}-\hspace{0.17em}0.026\mathrm{std}{X}_{7}\hspace{0.17em}+\hspace{0.17em}0.092\mathrm{std}{X}_{8}\hspace{0.17em}+\hspace{0.17em}0.966\mathrm{std}{X}_{15}-0.079\mathrm{std}{X}_{18}\hspace{0.17em}-\hspace{0.17em}0.131\mathrm{std}{X}_{19}\end{array}\)  

In the formula, Zi (i = 1,2,3) represents the principal component; StdXi (I = 1,2,3…, 19) represents the standard indicator variable. The standard indicator variables are standardized from the original variables, which can be obtained according to Table 8: stdX2 = (X2 − 31.609)/6.310; stdX4 = (X4 − 2147.831)/436.556; stdX5 = (X5 − 14.896)/4.833; stdX6 = (X6 − 69.850)/9.252; stdX7 (X7 − 989.517)/491.148; stdX8 = (X8 − 24.368)/7.159; stdX15 = (X15 − 1.360)/0.055; stdX18 = (X18 − 6.956)/1.104; stdX19 = (X19 − 45.8)/17.953.

Table 8 Descriptive statistics of geographic indicators
Full size table

Taking Z1, Z2, and Z3 as independent variables and the reference value of CK-MB for healthy middle-aged people as dependent variables, the regression equation was obtained:

Ŷ = 9.04 − 1.047Z1 − 0.292Z2 − 1.448Z3 ± 0.089. Finally, the linear regression equation between CK-MB index and geographical index is obtained by putting the original variable into the multiple regression equation with the original variable:

\(\widehat{Y}\hspace{0.17em}=\hspace{0.17em}19.49\hspace{0.17em}+\hspace{0.17em}0.123{X}_{2}\hspace{0.17em}+\hspace{0.17em}0.00214{X}_{4}\hspace{0.17em}-\hspace{0.17em}0.197{X}_{5}\hspace{0.17em}-\hspace{0.17em}0.081{X}_{6}\hspace{0.17em}-\hspace{0.17em}0.00179{X}_{7}+0.0940{X}_{8}\hspace{0.17em}-\hspace{0.17em}6.929{X}_{15}\hspace{0.17em}-\hspace{0.17em}0.194{X}_{18}\hspace{0.17em}-\hspace{0.17em}0.00190{X}_{19}\)

Model quality assessment

In order to select the appropriate model, the optimal ridge regression method, Lasso method, and principal component analysis method of root mean square error, mean absolute error, and Theil inequality coefficient are compared to eliminate the influence of multicollinearity, and finally get the model with the best prediction accuracy for the optimal prediction model of CK-MB reference value.

Root mean square error (RMSE) is the standard error. Is the square root of the ratio of the square of the deviation between the predicted value Yi and the measured value Yi to the predicted number N. RMSE can better reflect the prediction accuracy of the model, and the smaller RMSE value is, the better the prediction result will be.

$$RMSE=\sqrt{\frac{1}{N}\sum_{t=1}^{N}{\left({Y}_{i}-{y}_{i}\right)}^{2}}$$

Mean absolute error (MAE) excludes the occurrence of maximum or minimum error values and excludes the particularity of predicted values, so as to better reflect the actual situation of predicted values. The smaller the MAE value is, the better the model prediction result is.

$$MAE=\frac{1}{N}\sum_{t=1}^{N}\left|\left({Y}_{i}-{y}_{i}\right)\right|$$

Theil inequality coefficient (TIC), its evaluation standard is more accurate than RMSE, where TIC ∈ [0,1]. The smaller the TIC value is, the better the model prediction result is.

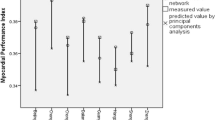
$$TIC=\frac{\sqrt{\frac{1}{N}\sum\limits_{t=1}^{N}{\left({Y}_{i}-{y}_{i}\right)}^{2}}}{\sqrt{\frac{1}{N}\sum\limits_{i=1}^{N}{Yi}^{2}}+\sqrt{\frac{1}{N}\sum\limits_{i=1}^{N}{yi}^{2}}}$$

Furthermore, to establish the forecast model of the TIC data reference value of Chinese healthy adult, using test data, the effect of three kinds of models to forecast assessment (Table 9), according to the results of principal component analysis of RMSE and MAE, TIC value is the smallest, so we choose principal component analysis as Chinese healthy adult CK-MB reference optimal prediction model.

Table 9 Measure of model prediction accuracy
Full size table

Geostatistical analysis

The predicted CK-MB values of 2322 counties and cities in China were imported into the vectorized map of China, and the normal distribution of the data was explored through histogram analysis and normal Q-Q map, and the normal distribution was replaced by the mean value.

The trend distribution chart of predicted CK-MB values in China was further drawn (Fig. 6). The predicted indexes of longitude, latitude, and 2322 observation points were set as X, Y, and Z axes, with the X axis being east and the Y axis being north. The trend distribution of predicted values of CK-MB presents a second-order polynomial on the whole. In the east–west direction of (X-axis), it presents a concave curve, which rapidly drops from west to east and then tends to be flat. In the (Y axis), it presents an upward convex curve from the south to the north, rising first and then falling from the south to the north. The predicted values of healthy adults are basically consistent with the trend analysis results of sample data. In order to further observe the change of reference values in different geographical regions, the geospatial distribution map of the predicted values of CK-MB is also needed.

Fig. 6
figure 6

Trend surface analysis of CK-MB predictive values in Chinese healthy adults

Full size image

Judging from the histogram results, the predicted values of CK-MB in China do not obey normal distribution, and the disjunction Kriging should be used in the interpolation. As can be seen from Fig. 7, the overall geographical distribution characteristics of the predicted values of CK-MB for healthy adults are higher in the north and lower in the south, gradually increasing from the southeast coastal area to the northwest inland area. The general trend is similar to the average temperature in winter and the distribution law of precipitation in north and south of China. The lowest values are located in the tropical and subtropical regions of Guangzhou Guangxi and the south of Yunnan-Guizhou Plateau. The lower values are widely distributed in the south of Qinhuai River and the south of the Tropic of Cancer. The highest values are located in the northwest and northeast plain north of 40°N latitude of China. The predicted distribution law of CK-MB for healthy adults is the most obvious in latitude, which is consistent with the distribution change of annual precipitation and temperature in China.

Fig. 7
figure 7

Geographic distribution of CK-MB predicted values among healthy adults in China

Full size image

Discussion

According to the “Theory of Three Causes” proposed in Neijing and Discourse on Time and Diseases, that is, due to time, person, and place, in different natural geographical environment; warm, hot, and cold climate; and people’s physiological indicators, metabolic function is different, and geographical environment and health are closely related. Based on the comprehensive discussion of spatial autocorrelation, correlation analysis, and geostatistical analysis, this paper concluded that the reference values of CK-MB for healthy adults in China were correlated with 9 geographical factors. After the establishment of principal component analysis model prediction and interpolation mapping, the overall pattern is higher in the north and lower in the south, gradually increasing from the southeast coast to the northwest inland. From the perspective of single-phase correlation coefficient combined with geographical factors, the discussion can be carried out from the following three aspects: terrain index, climate index, and soil index.

In terms of terrain index, latitude is generally positively correlated with the CK-MB reference value of healthy adults in China. China has a large territory and abundant resources, with a wide span of longitude and latitude, and latitude directly affects the distribution of temperature zones and climate types in the north and south (Nguyen et al. 2016). China’s climate types are complex and diverse, with significant characteristics of continental monsoon climate, temperature decreases from south to north, and there is a large temperature difference between north and south. At the same longitude, the reference value of CK-MB in high latitude area is high and decreases to low latitude area in turn (Inclair 1989). Xue Wang proposed that in the northeast of China, winter is cold and long, and summer is warm and short (Wang et al. 2020a). Moreover, in cold areas, human body is often stimulated by low temperature, which is prone to erythrocyte aggregation, increased blood viscosity, capillary constriction, increased blood pressure, increased myocardial oxygen consumption, aggravated myocardial ischemia, and the corresponding CK-MB value is also high. Therefore, in Northwest China with large annual temperature difference, the value of residents in Northeast China is higher than that in Southern China with high annual average temperature, which is consistent with the spatial pattern of high temperature in the north and low temperature in the south of the geographical spatial distribution map.

In terms of climate indicators, the annual sunshine hours, annual average temperature, annual average relative humidity, annual precipitation, and annual temperature are non-negligible factors affecting the CK-MB reference value of healthy people in China. Annual sunshine duration is closely related to latitude and altitude, and geographical factors are interrelated and inseparable. Studies show that the longer the sunshine duration is, the higher the incidence of cardiovascular diseases, and the higher CK-MB value reflects the positive correlation effect of sunshine duration (Scarborough et al. 2012). Relative humidity and annual precipitation are negatively correlated with CK-MB reference value. Studies have shown that low precipitation and relatively low air humidity can increase the incidence of cardiovascular diseases (Afanas’eva et al. 2010). Studies have shown [25–26] that when Humidity is greater than 60%, the human body will feel uncomfortable, blood filling will increase, blood viscosity will decrease, and it will be easier to eliminate the metabolites in the blood vessels (Yin and Wang 2018). Therefore, the CK-MB level in the body will decrease, which reflects the negative correlation effect of humidity. Humidity is lower in northwest area of our country, because this CK-MB reference value is higher than the coastal area value with higher humidity (Goldie et al. 2018).

In terms of soil indexes, most of the CK-MB reference value is indirectly related to soil factors such as topsoil gravel content, topsoil (clay) cation exchange capacity, and topsoil (silt) cation exchange capacity, rather than factors such as longitude, latitude, temperature, and humidity that can directly affect the indexes. The cation exchange capacity of the topsoil (clay) and the cation exchange capacity of the topsoil (silt) are important indexes for evaluating soil fertility. The soil types in China have provincial and regional rules, presenting alternation changes under different land forms of plains, basins, and plateaus in China. Different types of crops are planted in different soil types in different regions (Duan et al. 2016). The soil in southern and northern regions is further differentiated from wheat and rice cultivation, which affects the eating habits of different people in China. For example, according to “Su Wen · On Fever Diseases,” “In the case of Yin deficiency, Yang is bound to co-exist, so when there is less air, it is hot and sweats.” In hot and dry areas, the body reduces blood flow by constricting the arteries, inhibiting the sweating function of the skin, and maintaining water balance in the body. The contraction of arterial vessels is bound to lead to the decrease of cardiovascular systolic function, leading to the decrease of CK-MB index. The reference value of CK-MB is negatively correlated with the topsoil gravel content, because the higher gravel content leads to the decline of soil organic matter and the weakening of soil fertility. Compared with people in fertile soil and water areas, the residents in arid desert areas of China have a single diet and higher lipid and protein, so the higher value of CK-MB will also increase the risk of cardiovascular diseases (Zhang and Yang 2016). 

Conclusion

Spatial analysis shows that there is spatial autocorrelation dependence in CK-MB reference values of healthy Chinese adults. At the same time, combined with the correlation analysis, the latitude, sunshine duration, annual average relative humidity, annual precipitation, annual poor temperature, annual average temperature, topsoil gravel content, topsoil (clay) cation exchange capacity, and topsoil (silt) cation exchange capacity were further determined. Reasonable reference values of CK-MB medical indicators in a certain region can be obtained by integrating the optimal model and local statistical analysis if the above indexes are known. The distribution pattern of CK-MB reference values in China is higher in the north and lower in the south, gradually increasing from southeast coastal areas to northwest inland areas. The reference value of CK-MB of healthy people in the region can be determined through the collected geographical indicators of any region, combined with the principal component analysis prediction model or the obtained geographical distribution map.

As medical index data are derived from online literature, there are problems such as uneven distribution of data points and data deviation. The data of the eastern region is slightly more than that of the western region, which is the result of the differences in population density, economic development level, national policy support, and medical resource level in the eastern and western regions of China. Furthermore, explore models suitable for medical geography, and improve the prediction accuracy of data by combining machine learning, epidemiological learning, public health, and other disciplines. Therefore, with the progress of research, more data should be combined to focus on the selection of human geographical factors, and factors affecting medical indicators at different levels should be considered, so as to improve the practical value and scientific research value brought by research.