Advertisement

International Journal of Biometeorology

, Volume 61, Issue 4, pp 575–588 | Cite as

Implications of atmospheric conditions for analysis of surface temperature variability derived from landscape-scale thermography

  • Albin Hammerle
  • Fred Meier
  • Michael Heinl
  • Angelika Egger
  • Georg Leitinger
Open Access
Original Paper
First Online:

Abstract

Thermal infrared (TIR) cameras perfectly bridge the gap between (i) on-site measurements of land surface temperature (LST) providing high temporal resolution at the cost of low spatial coverage and (ii) remotely sensed data from satellites that provide high spatial coverage at relatively low spatio-temporal resolution. While LST data from satellite (LSTsat) and airborne platforms are routinely corrected for atmospheric effects, such corrections are barely applied for LST from ground-based TIR imagery (using TIR cameras; LSTcam). We show the consequences of neglecting atmospheric effects on LSTcam of different vegetated surfaces at landscape scale. We compare LST measured from different platforms, focusing on the comparison of LST data from on-site radiometry (LSTosr) and LSTcam using a commercially available TIR camera in the region of Bozen/Bolzano (Italy). Given a digital elevation model and measured vertical air temperature profiles, we developed a multiple linear regression model to correct LSTcam data for atmospheric influences. We could show the distinct effect of atmospheric conditions and related radiative processes along the measurement path on LSTcam, proving the necessity to correct LSTcam data on landscape scale, despite their relatively low measurement distances compared to remotely sensed data. Corrected LSTcam data revealed the dampening effect of the atmosphere, especially at high temperature differences between the atmosphere and the vegetated surface. Not correcting for these effects leads to erroneous LST estimates, in particular to an underestimation of the heterogeneity in LST, both in time and space. In the most pronounced case, we found a temperature range extension of almost 10 K.

Keywords

Surface temperature Thermal infrared camera Atmospheric correction Digital elevation model Alpine environment 

Introduction

Land surface temperature (LST) is a key variable for numerous environmental functions. It represents the combined result of all energy exchange processes between the atmosphere and the land surface. Thus, LST has become a basic requirement for model validation or model constraining in surface energy and water budget modelling on various scales (Kalma et al. 2008; Kustas and Anderson 2009; and references therein). It serves as a metric for soil moisture and vegetation condition in eco/hydrological modelling and environmental monitoring (Czajkowski et al. 2000; Kustas and Anderson 2009) and has been used in the area of thermal anomalies and high-temperature events detection (Sobrino et al. 2009; Teuling et al. 2010). Further, LST data is widely used in urban climate studies to quantify the surface urban heat island and to explore its relationship with urban surface properties and air temperature variability as well as for surface-atmosphere exchange processes in urban environments (Voogt and Oke 2003; Weng 2009).

LST can be retrieved from various platforms and instruments, depending on the application requirements regarding spatial and temporal resolution. Remote sensing platforms provide data with global coverage. They can routinely either provide LST at a coarse spatial resolution at relatively high overpass frequencies (e.g., Terra-MODIS, Aqua-MODIS, NOAA-AVHRR) or provide less frequent but moderate resolution LST data (e.g., Terra-ASTER, Landsat). Recent developments in the thermal remote sensing system even show a trend towards coarser spatial resolutions (e.g., Sentinel mission). Airborne systems on the other hand can provide relatively high temporal as well as high spatial resolution LST information on a regional scale, with the drawback of high costs. Infrared radiometers mounted on site provide LST at any temporal resolution integrated over a given field of view on the expense of spatial coverage.

Thermal infrared (TIR) cameras have been continuously refined since their broad commercial launch in the early 1990s and have found wide application since the 2000s due to lower costs for uncooled focal plane sensor arrays and their improved spatial and thermal resolution (Schuster and Kolobrodov 2004). The high spatial and temporal resolution, the operational simplicity, and increasing data storage capabilities led to an increasing popularity of this system in many ecological research areas (e.g., Hristov et al. 2008; Katra et al. 2007; McCafferty 2007).

While thermal remote sensing has already been widely applied in landscape ecology (Quattrochi and Luvall 1999 and references therein), the demand for high-resolution data (both, temporally and spatially) is unabated. Particularly in alpine landscapes that are characterized by high spatial heterogeneity and temporal dynamics (resulting from small-scale variations in slope, aspect, and altitude), highly resolved LST data are needed (Bertoldi et al. 2010; Heinl et al. 2012; Scherrer and Körner 2010; Scherrer et al. 2011).

All thermal remote sensing data, independent of the instrument used, is influenced by atmospheric conditions and radiative processes along the measurement path (Chandrasekhar 1960). Several atmospheric correction approaches have been established depending on sensor characteristics, e.g., the split window technique (SWT) for multi-channel sensors (Becker and Li 1990; Kerr et al. 1992; Price 1984; Sobrino et al. 1991), where “split window” refers to radiance differences observed by each atmospheric window of the respective TIR channel. There are different SWT algorithms depending upon spectral emissivity, water vapor content, view angle, or purely empirical algorithms. Radiative transfer models together with atmospheric profile data of pressure, temperature, and humidity are often used to determine SWT algorithms or to perform atmospheric corrections of TIR data derived from single-channel sensors (Berk et al. 1998; Richter and Schläpfer 2002; Schmugge et al. 1998). While these methods are commonly applied to data derived from satellite (Dash et al. 2002; Prata et al. 1995) or airborne platforms (Jacob et al. 2003; Lagouarde et al. 2000; Lagouarde et al. 2004), such corrections are not routinely applied in ground-based TIR imagery in natural and urban environments at the landscape scale (Heinl et al. 2012; Scherrer and Körner 2010; Scherrer and Körner 2011; Scherrer et al. 2011; Tonolla et al. 2010; Wawrzyniak et al. 2013; Westermann et al. 2011), partially justified by relatively short atmospheric path lengths. Existing methods for ground-based TIR imagery are either simple, i.e., based on the assumption of a homogenous sensor-target distance and constant atmospheric transmission value (Yang and Li 2009), or more complex by using a radiative transfer code, atmospheric data and under consideration of differences in atmospheric path lengths (Meier and Scherer 2012; Meier et al. 2011; Sugawara et al. 2001).

This paper compares LST data measured from different platforms. The main objective is to quantify the differences between LST data from a ground-based TIR imagery (LSTcam) and LST data from on-site radiometry (LSTosr). Subsequently, an empirical model, based on a digital elevation model and measured vertical air temperature profiles, was developed. This model corrects LSTcam for atmospheric influences.

Furthermore, we discuss the consequences of neglecting atmospheric influences on LST data derived from ground-based TIR imagery at the landscape scale.

Methods

The basis of the study was the comparison of surface temperatures measured (i) continuously by infrared radiometers mounted above the canopy (on-site radiometry), (ii) frequently by a TIR camera operated at an elevated position within the study region (ground-based TIR imagery), and (iii) by satellite remote sensing (satellite-based TIR imagery).

Study region and experimental setup

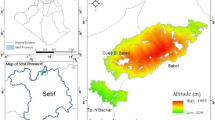
The study was conducted in the region of Bozen/Bolzano in the northernmost part of Italy (Fig. 1). The city of Bozen/Bolzano is located in a basin at the transition of the central Alps to the southern Alps, surrounded by four mountain ranges. Ten microclimate stations were erected in the vicinity of the city which spanned an elevational range from 239 to 857 m a.s.l. and covered three different land-use types (vineyard, orchard, and grassland).
Fig. 1

Study area in the basin of Bozen/Bolzano (I). Numbers denote locations of on-site measurements and corresponding numbers refer to site numbers in Tables 1, 2, and 4. Locations of ground-based TIR imagery and of the microwave radiometer are marked with X and O, respectively. The tetragon within the figure represents the transformed marked section in Fig. 7 and Fig. 8 (black squares). Inset upper left: schematic overview of the experimental setup. Map data: Google, DigitalGlobe

These three land-use types cover 16, 29, and 4 % of the investigated rural area, respectively (woodland 48 %). Three out of ten microclimate stations were located in vineyards, six in orchards, and one in a managed grassland. While vineyards and orchards are by far the dominating land-use types in this region, grasslands only occurred at higher elevations (Table 1). No site was positioned closer than 20 m to any building.
Table 1

Key characteristics of investigated field sites including measures of their positioning relating to the camera position for ground-based TIR imagery (Cam)

Number in Fig. 1

site name

Management

x_GPS

y_GPS

Altitude

(m a. s. l.)

Hillslope

(°)

Aspect

(°)

Situation: cam position-site

Atmospheric path length (APL)

(m)

Horizontal distance

(m)

Altitude difference

(m)

Cutting angle (AC)

(°)

View zenith angle (AVZ)

(°)

1

Schreckbichl

Vineyard

11.295882

46.460708

474

11.0

63

4624

4584

603

18.3

82.5

2

Girlan

Orchard

11.279210

46.470331

400

3.5

340

5759

5719

678

5.7

83.2

3

Unterrain

Orchard

11.279432

46.488236

240

<3

124

6072

6014

837

8.0

82.1

4

Terlan

Orchard

11.252084

46.511405

243

<3

243

9038

8999

834

5.3

84.7

5

Kaiserau

Orchard

11.313778

46.477665

245

<3

323

3260

3152

833

13.7

75.2

6

Jennerhof

Orchard

11.315806

46.486065

245

<3

240

3457

3355

832

13.3

76.1

7

Moritzing

Orchard

11.299137

46.498861

239

<3

20

5275

5208

838

9.1

80.9

8

Alte Mendl Str

Vineyard

11.329031

46.496685

250

<3

192

3523

3424

827

13.8

76.4

9

Glaninger Weg

Vineyard

11.334097

46.509057

430

21.6

164

4535

4488

647

29.7

81.8

10

Wiesmanhof

Grassland

11.339721

46.524530

857

9.3

149

6049

6045

221

10.8

87.9

X

Kohlern

–

11.353672

46.471006

1077

–

–

–

–

–

–

–

Meteorological measurements included air temperature (T air) and relative humidity (RH) at 2 m above ground (Hobo Pro v2-U23-002; onset; Bourne, MA, USA), air temperature 1 m above the canopy (PT 100; EMS; Brno, Czech Republic), incoming solar radiation (SR) (S-LIB-M003; onset; Bourne, MA, USA) above the canopy, soil temperature (T soil) at 0.1 and 0.25 m soil depth (PT 100; EMS; Brno, Czech Republic), and soil water content (SWC) in 0.25 m soil depth (EC-10; Decagon Devices; Pullman, WA, USA). Surface temperatures were derived using an infrared radiometer (SI-111; Apogee Instruments; Logan, UT, USA) mounted 1 m above the canopy. This sensor is sensitive in the electromagnetic spectrum from 8 to 14 μm. Given the half-angle field of view of 22° and the different canopy heights, the visible surface areas ranged from 2 to 8 m2. Data were measured every minute and stored as 10 min average values. Land surface temperatures (LST) derived from on-site radiometry are henceforth referred to as LSTosr.

For ground-based TIR imagery, an elevated site on top of a cliff edge (1077 m a.s.l.) was chosen as camera position (Table 1). Measurements were done using the TIR camera “Jenoptik VarioCAM high resolution” (Infratec; Dresden, Germany), which is sensitive in the electromagnetic spectrum from 7.5 to 14 μm. The camera resolution of 768 × 576 pixels in combination with the standard lens (focal length 25 mm) resulted in pixel sizes ranging from 2.2 to 6.3 m depending on the given atmospheric path length (APL) per site (Table 1).

TIR images were taken on 13 days throughout the summer and autumn season 2012 from an exposed position ca. 840 m above the valley floor. While data were restricted to daytime measurements on some days, we conducted 24-h measurements on others. Measurements were done at least half hourly (higher frequency around sunrise and sunset or at the times of a satellite overpass), resulting in roughly 250 acquisition times where all ten LSTosr sites were covered simultaneously. Image processing was done using IRBIS® software (InfraTec; Dresden, Germany). All TIR images were exported as ASCII files and further analyzed using MATLAB (R2013b, The MathWorks, Inc., USA). Despite the mean absolute differences between LSTosr and LSTcam (0.8 K) being lower than the TIR camera accuracy (±1.5 K), the two systems were intercalibrated in an experimental setup. LST measured by the ground-based TIR imagery are referred to as LSTcam.

Surface emissivity (ε) was considered equal to 1 for both LSTosr and LSTcam unless specified differently, as pixels of interest were completely covered by vegetation having a high emissivity at all wavelengths.

Satellite-based TIR imagery was derived from ASTER Level 2B03 data products with a spatial resolution (pixel size) of 90 m, acquired on demand for seven dates in 2012 (21 and 28 June 2012; 7 July 2012; 8 and 24 August 2012; 11 and 18 October 2012). The images provide kinetic temperatures at about 11:15 CET and represent the single pixel values at the location of each microclimate station. The standard deviation is calculated over this target pixel and the eight neighboring pixels. Data affected by clouds were not considered for the analyses so that the number of remotely sensed data per site ranges between three and seven observations. LST derived from remote sensing are henceforth referred to as LSTsat.

A vertical air temperature profile was measured at the airport in Bozen/Bolzano (BZO) using a microwave radiometer (MTP-5HE; ATTEX Ltd., Moscow, Russia) (Fig. 1). This radiometer measured air temperature profiles up to 1000 m above surface (50 m vertical resolution; 10 min time resolution) with a temperature accuracy from ±0.3 K (0–500 m) up to ±0.4 K (>500 m). Radiometer data were provided by “Autonome Provinz Bozen Südtirol/Provincia autonoma die Bolzano Alto Adige” (Landesagentur für Umwelt/Agenzia provinciale per l’ambiente; Labor für physikalische Chemie/Laboratorio di chimica fisica). Average path temperatures (T path) were calculated for each LSTcam measurement as the arithmetic mean over the corresponding temperature profile segment, defined by the site and camera elevation.

Processing of ground-based TIR imagery

To cover all field sites by ground-based TIR imagery at one time, we had to pan the camera and take five TIR images (scenes). While we always tried to position the camera the same way and choose the same field of view, the different scenes were not perfectly congruent. Thus, we chose one reference thermal image per scene and used the “Computer Vision System Toolbox” of MATLAB (R2013b, The MathWorks, Inc., USA) to align all TIR images of one scene with each other. More precisely, we (i) used the SURF blob detector (detectSURFFeaturs-function; Bay et al. 2008) to identify matching regions in the two TIR images, (ii) estimated the geometric transformation from matching point pairs (estimateGeometricTransform-function; Torr and Zisserman 2000), and (iii) applied the geometric transformation to the TIR image (imwrap-function).

Subsequently transformed TIR images (n = 3169) were filtered based on a three-step quality check. (i) All images obviously not matching the corresponding reference TIR image by visual inspection were selected and removed (remaining n = 2909; 92 %). (ii) Any TIR image not exceeding a certain R 2 value (night 0.6; day 0.8), when compared with the reference scene or with less than five matching points found in the SURF blob detector algorithm described above were removed (remaining n = 2106; 66 %). (iii) For any averaging interval with multiple LSTcam measurements, only the one closest in time to the LSTosr measurement was used, further reducing the number of remaining LSTcam measurements for the ten sites (remaining n = 2011; 63 %). Applying these algorithms and filters resulted in a dataset of TIR image per scene that perfectly matched each other. In order to get the line-of-sight geometry for each TIR image pixel, the procedure described in the following section was applied.

Derivation of line-of-sight geometry parameters for ground-based TIR imagery

The oblique view of the TIR camera and the topography of the observed landscape produce different line-of-sight (LOS) geometry parameters for each TIR image pixel. The LOS is fully described by APL, by the altitude of the observed surface, and by the view zenith angle (A VZ) under which the TIR camera observes the surface. The calculation of spatially distributed LOS values for every TIR image pixel is based on the idea that every TIR image pixel has a corresponding 3D geographic coordinate (x, y, z). In order to find these pixel-specific coordinates, the perspective projection of the three-dimensional (3-D) landscape onto the two-dimensional (2-D) TIR image plane was modelled using a DEM of the study region with a spatial resolution of 20 m (Autonomous Province of Bolzano, South Tyrol, Italy). Further, we had to know the geographic coordinates of the TIR camera location and the geographic coordinates of the center pixel of the TIR image (exterior orientation) as well as the size of the 2-D image plane (768 × 576 pixels) and the horizontal and vertical field of view (FOV) of the camera lens (interior orientation). The horizontal FOV is 30° and the vertical FOV is 23°. A detailed description of the perspective projection of the 3-D DEM and calculation of FOV parameters are given in Meier et al. (2011).

Multiple regression model to correct LSTcam

Establishing the multiple regression model was done using IBM SPSS Statistics for Windows, Version 21.0 (IBM Corp; Armonk, NY). The LST model was built using ordinary least squares (OLS) regression based on 1839 observations with LSTosr as dependent variable and four independent variables (LSTcam; T path; difference of LSTcam and T path; APL). (i) All independent variables were tested regarding multi-collinearity, (ii) scatter plots of the dependent vs. each independent variable were analyzed to check for non-linearity, (iii) the significant independent variables were selected by forced entry OLS using ca. 50 % of available data (897 observations; calibration dataset), (iv) a residual analysis was performed for checking OLS assumptions, and finally (v) the LST model was employed to predict the dependent variable for the remaining validation dataset (942 observations; validation dataset).

Results

Data were collected continuously at the field sites from 1 May 2012 until 31 October 2012. T air ranged from −5.2 °C (30 October 2012) to 37.3 °C (20 August 2012), with a mean T air of 18.8 °C during that period (30-year average for that period, 19.4 °C (Hydrographisches Amt Bozen/Ufficio idrografico Bolzano)). While the coolest site on average was the Wiesmanhof site, representing the highest-located site (Fig. 1, Table 1), the lowest air temperatures were measured at the Terlan site. The highest air temperature was measured at the Alte Mendel Strasse site, a site located in close proximity to Bozen/Bolzano (Fig. 1, Table 2). LSTosr ranged from −5.7 °C (30 October 2012; Terlan) to 49.1 °C (26 July 2012; Wiesmanhof), with an average LSTosr of 18.0 °C during the measurement period (Table 2). Average wind speed ranged from 0.8 m s−1 (Terlan site) up to 1.5 m s−1 (Wiesmanhof), and mean solar radiation (SR) ranged from 196 W m−2 (Girlan) to 226 W m−2 (Glaninger Weg) among the ten field sites (Table 2).
Table 2

Meteorological conditions at the ten field sites throughout the measurement campaign 1 May 2012 until 31 October 2012

Site

T air 200 cm (°C)

LSTosr (°C)

SR (W m−2)

Wind speed (m s−1)

Nr.

Name

Min

Max

Mean

Min

Max

Mean

Mean

Mean

1

Schreckbichl

−1.5

35.9

18.6

−3.1

38.6

17.9

206

1.4

2

Girlan

−2.6

35.9

18.2

−2.6

37.8

17.2

196

1.1

3

Unterrain

−3.8

36.9

19.0

−4.4

33.3

17.6

210

1.1

4

Terlan

−5.2

36.5

18.2

−5.7

33.6

17.4

201

0.8

5

Kaiserau

−2.9

36.7

19.5

−3.3

39.1

18.3

202

1.0

6

Jennerhof

−2.4

36.9

19.8

−3.1

36.1

18.7

205

0.8

7

Moritzing

−3.7

37.0

19.2

−3.7

33.8

18.0

209

1.1

8

Alte Mendl Str

−2.3

37.3

20.2

−3.1

40.2

19.4

196

0.9

9

Glaninger Weg

−1.1

36.8

19.3

−2.9

43.0

18.8

226

1.3

10

Wiesmanhof

−3.5

32.3

16.3

−5.0

49.1

16.8

213

1.5

Numbers (nr.) refer to numbers in Fig. 1

T air air temperature 2 m above ground, LST osr land surface temperature from on-site radiometry, SR shortwave radiation

LSTsat compared to LSTcam and LSTosr

During the measurement campaign, LSTsat could be retrieved from seven satellite overpasses. Excluding data with cloud cover, 58 data points could be used from our ten field sites to compare LSTsat with LSTosr and 32 data points to compare LSTsat and LSTcam. LSTsat data are available as kinetic (kin) LST (routinely corrected for atmospheric effects); thus, LSTosr and LSTcam data had to be recalculated from radiant temperature by applying ε = 0.97 (deciduous vegetation and grass; Jensen 2007) and an environmental temperature (T sky; K) that was modelled as a function of vapor pressure (e a; kPa) and air temperature (T air; K) following Campbell and Norman (1998) (rearranged):
$$ {T}_{\mathrm{sky}}=\sqrt[4]{1.72\cdot {\left(\frac{e_{\mathrm{a}}}{T_{\mathrm{a}\mathrm{ir}}}\right)}^{\frac{1}{7}}\cdot {\left({T}_{\mathrm{a}\mathrm{ir}}\right)}^4} $$

This intercomparison was done using original LSTcam data, not corrected for any atmospheric influences.

Generally, a good correlation of LSTosr (kin) and LSTsat (kin) could be found applying these transformations, whereas there is a distinct outlier datum in the Wiesmanhof dataset (Fig. 2, left panel). In contrast, comparing LSTcam (kin) with LSTsat (kin) did not reveal any outliers for the Wiesmanhof data (Fig. 2, right panel). But, as evident from Fig. 2, LSTcam (kin) and LSTsat (kin) estimates are clearly offset and show a higher mean absolute error (MAE) compared to LSTosr (kin) data.
Fig. 2

Left panel: intercomparison of kinetic land surface temperatures measured on site by radiometry (LSTosr (kin)) and from remote sensing (ASTER Level 2B03) (LSTsat (kin)). Right panel: intercomparison of kinetic land surface temperatures measured by ground-based TIR imagery (LSTcam (kin)) and from remote sensing (ASTER Level 2B03) (LSTsat (kin)). Red line: 1:1 line, black solid line: regression line, black dashed line: 95 % prediction interval of regression line, grey dashed line: 95 % prediction interval of observations, grey shaded area: ±1.5 K on 1:1 line marking camera accuracy. Error bars on LSTsat data refer to the standard deviation within a 3 × 3 pixel area centered around LSTosr locations. Error bars on LSTcam (kin) data refer to the camera accuracy of ±1.5 K

The Wiesmanhof site was excluded in any further analysis because of the following: (i) LSTosr (kin) does not always coincide with LSTsat (kin) at the Wiesmanhof site, while this site does not stand out when comparing LSTsat (kin) with LSTcam (kin) data; (ii) in nine out of ten cases LSTosr (kin) and LSTcam (kin) data are well correlated (except for the Wiesmanhof site at high temperatures) (Fig. 3); and (iii) photographs of the measured plot at Wiesmanhof (taken regularly at times of data collection or maintenance work; not shown) showed withered vegetation right below the sensor during periods with high air temperatures (end of July and around the 20th of August) while no dryness was observed at the rest of the meadow (plot not representative).
Fig. 3

Correlations of land surface temperatures measured by on-site radiometery (LSTosr) and ground-based TIR imagery (LSTcam) per site including correlation statistics. Grey dotted lines: 1:1 line; black bold lines: sls-regression line

LSTcam vs. LSTosr

Radiant LSTcam and LSTosr were well correlated at nine out of our ten sites (Fig. 3). As mentioned in the previous paragraph, the Wiesmanhof field site was excluded from any further analyses. Slope and offset of the regression lines ranged from 0.69 to 0.92 and −0.81 to 5.94 K, respectively (Fig. 3). The coefficient of determination (R 2) and the MAE ranged from 0.82 to 0.95 and 1.51 to 3.63 K, respectively, with an average MAE of 2.61 K (Fig. 3).

As shown in Fig. 3, LSTcam are lower on average in all cases compared to LSTosr, especially at higher temperatures, clearly indicating the necessity to account for atmospheric effects on LST measurements at landscape scales by TIR cameras.

At all sites, uncorrected LSTcam is on average between 1.19 and 3.52 K lower than LSTosr. While these average deviations appear to be rather small, the differences between LSTcam and LSTosr show a pronounced diel cycle. The observed differences between these two methods (ΔLST = LSTosr − LSTcam) ranged from −3.9 up to 11.5 K at the maximum. On average, ΔLST was negative during the night time hours, ranging between −3 and −1 K. At sunrise, mean ΔLST rose, reached its maximum of 3.9 K around noon, and decreased again from then on (Fig. 4).
Fig. 4

Upper panel: mean diel variations of land surface temperatures measured by on-site radiometry (LSTosr) and by ground-based TIR imagery (LSTcam), as well as path temperature (T path). Only data at times with LSTcam data available were used. Lower panel: mean diel variation of the differences between LSTosr and LSTcam as well as the differences between LSTosr and T path. Error bars refer to 1 stdv in any case. For reasons of clarity, error bars are shown for LSTcam data only in the upper panel

Given T path from radiometer measurements, we calculated the difference between LSTosr and T path (ΔT). Given ΔT, the residuals between LSTcam and LSTosr could be explained to a very large extent. Eighty-one percent of the residual variation is explained by ΔT (n = 1839; p < 0.01) (Fig. 5).
Fig. 5

Correlations of the temperature difference between path temperature (T path) and land surface temperatures from on-site radiometry (LSTosr) and the measurement difference between LSTosr and land surface temperatures from ground TIR imagery (LSTcam) (ΔT) (grey dots). Upper panel: absolute difference; grey horizontal bar refers to ±1.5 K (camera accuracy). Lower panel: relative difference. Big black dots refer to bin averaged data including their error bar (1 stdv)

Correcting LSTcam data according to this correlation of the residuals with ΔT does result in slope and offset values ranging from 0.91 to 1.00 and −0.18 to 3.34 K, respectively. R 2 improved noticeably and ranged between 0.98 and 0.99, and the MAE was reduced from 2.61 K on average for uncorrected data to a range of 0.49 to 1.15 K (mean 0.74 K) for the nine sites.

While this finding does show the importance of atmospheric corrections on the data, this correlation is not relevant for any data correction as this method would require information on actual LST on landscape scale.

LST model calibration and validation

In order to correct LST on landscape scale, a multiple linear regression model was set up to model LSTosr by the use of four independent variables (LSTcam, LSTcam − T path, T path, and APL). Given a variance inflation factor (VIF) well above ten indicating multi-collinearity, T path was excluded as an independent variable from further analysis. With VIFs lower than 1.33, none of the remaining three independent variables (LSTcam, LSTcam − T path, and APL) gave evidence for further multi-collinearity (Kutner et al. 2003; Pan and Jackson 2008; Rogerson 2001). Furthermore, no scatterplot of dependent vs. independent variables revealed non-linear dependencies.

The three independent variables generated a highly significant model (p < 0.001) with a determination coefficient of 0.92 (adjusted R 2; root mean squared error (RMSE) = 1.7 K) based on ca. 50 % randomly chosen observations (calibration dataset). Residual analysis revealed no noticeable pattern (heteroscedasticity) and no obvious deviation from normal distribution.

Statistical validation of the model was done applying the model to the remaining 50 % of observation data, which resulted in an adjusted R 2 = 0.93 (LSTosr = 1.00 LSTosr predicted − 0.19; RMSE = 1.68 K).

Based on the available dataset (n = 1839) and the three selected independent variables LSTcam, LSTcam − Tpath, and APL, the LST model was given by:
$$ {LST}_{osr\kern0.5em \mathrm{predicted}}=-3.971+1.086\kern0.5em {LST}_{cam}+0.767\left({LST}_{cam}-{T}_{\mathrm{path}}\right)+0.000469\kern0.5em APL, $$
(1)
representing a highly significant model for LST (p < 0.001; adj. R 2 = 0.93; RMSE = 1.70 K) (Fig. 6).
Fig. 6

a Correlation of measured land surface temperatures from on-site radiometry (LSTosr) with modelled LST including the regression line. b Standardized residuals vs. unstandardized predicted values. c p-p-plot of observed (grey) vs expected (black) cumulative residual distribution

According to the standardized coefficients beta (\( \overset{\sim }{\beta } \)), LSTcam exerted the highest influence on the LST model, followed by the difference of LSTcam and T path (LSTcam − T path) and atmospheric path length (APL) (Table 3).
Table 3

Three variables exhibited significance and were used in our final LST model

LST model

Unstandardized coefficients

Standardized coefficients \( \tilde{\beta} \)

T-value (t)

Significance (p value, two sided)

VIF

β i

S.E.

(Constant)

−3971

0.247

 

−16,060

0.000

 

LSTcam

1.086

0.008

0.909

142.350

0.000

1.086

LSTcam − T path

0.767

0.029

0.194

26.258

0.000

1.256

APL

0.000469

0.000

0.128

16.697

0.000

1.105

S.E. standard error, VIF variance inflation factor, LST cam land surface temperatures measured by ground-based TIR imagery, T path measurement path temperature, APL atmopsheric path length

LST model application

Average differences of LSTosr and T path during all measurement campaigns ranged from −6 to 10 K. To demonstrate consequences of these temperature differences, two different situations for one field of view were selected, including the stations Kaiserau, Jennerhof, Terlan, and Unterrain (scene 2). On 2 August 2012 at 11:30 CET, a mean difference between LSTosr of these sites and T path of 6.7 K was observed (example 1), while on 24 August at 03:00 CET, these two temperatures differed by −2.5 K on average (example 2). These values represent rather high and low measured differences for that scene.

Presented in Table 4 are the meteorological conditions for the times of examples 1 and 2. Data presented in Table 4 represent average conditions for these specific dates of the year and times of the day. 2 August (example 1) was characterized by bright sunshine until the time of presented measurements, while on 24 August (example 2), it was partly cloudy around midday and clear sky conditions for the rest of the day. While LSTosr and Tair were relatively similar at the time of example 1, T path was several degrees cooler on average, with differences ranging from −6 down to −11 K (Table 4). In contrast, at the time of example 2, the average T path was 2.1 K warmer than the average LSTosr, with differences ranging from −0.2 up to 3.5 K.
Table 4

Meteorological conditions on reference days 2 August 2012 11:30 (example 1; E1) and 24 August 2012 03:00 (example 2; E2)

Site

LSTosr (°C)

T air 2 m (°C)

T path (°C)

LSTcam (°C)

SR (W m−2)

Wind speed (m s−1)

RH (%)

Nr.

Name

E1

E2

E1

E2

E1

E2

E1

E2

E1

E2

E1

E2

E1

E2

1

Schreckbichl

31.8

18.5

27.5

20.1

22.9

20.6

26.0

–

728

0

0.28

1.64

61

76

2

Girlan

30.1

17.7

28.4

20.0

23.1

20.7

25.5

20.6

–

0

1.24

0.68

57

77

3

Unterrain

29.3

19.4

32.1

20.7

23.5

20.9

26.5

21.0

728

0

1.00

0.52

60

80

4

Terlan

29.9

18.1

29.7

19.6

23.5

20.9

25.7

20.6

684

0

0.28

0.52

55

84

5

Kaiserau

29.6

17.4

30.7

18.2

23.5

20.9

27.6

20.5

756

0

0.84

0.28

53

95

6

Jennerhof

32.2

18.7

30.7

20.1

23.5

20.9

28.6

20.8

764

0

0.84

0.84

48

82

7

Moritzing

29.6

18.7

29.3

20.0

23.5

20.9

26.8

–

810

0

1.08

0.68

61

86

8

Alte Mendl Str

34.7

21.1

31.2

22.6

23.5

20.9

30.1

–

686

0

1.16

1.00

48

70

9

Glaninger Weg

32.6

18.7

28.3

20.7

23.0

20.6

28.7

–

828

0

1.48

0.76

49

75

 

Mean

31.1

18.7

29.8

20.2

23.4

20.8

27.3

20.7

762

0

0.91

0.77

55

81

Italicized sites are covered by scene 2 shown in Fig. 7 and Fig. 8. Numbers (nr.) refer to numbers in Fig. 1

Consequences of these conditions on LSTcam and according corrections on these data by the LST model at landscape scale are shown in Fig. 7 and Fig. 8. The marked section in panels a–f was used to restrict data to areas covered by vegetation, as the model setup was done using data from such areas only. Results covering settlement or industrial areas (right and lower thermal image area, respectively) could thus not be validated.
Fig. 7

Example 1 (2 August 2012, 11:30 CET)—a elevation model, as seen by ground-based TIR imagery. b Resulting atmospheric path lengths (APL) for each pixel. c Average path temperatures (T path) for the time the infrared images were taken. d Land surface temperatures as measured by ground-based TIR imagery (LSTcam). e Resulting LSTcam from model application (LSTcam corr). f Difference between LSTcam and LSTcam corr. g Temperature ranges of LSTcam and LSTcam corr for the entire scene. h Temperature ranges of LSTcam and LSTcam corr for the marked section in panels a–f. Grey shadings in g and h refer to min–max range, 90 % percentile, 50 % percentile (IQR), and the median (black line), respectively. i Histogram of the differences in panel f for the entire scene

Fig. 8

Example 2 (24 August 2012, 03:00 CET)—a elevation model, as seen by ground-based TIR imagery. b Resulting atmospheric path lengths (APL) for each pixel. c Average path temperatures (T path) for the time the infrared thermograms were taken. d Land surface temperatures as measured by ground-based TIR imagery (LSTcam). e Resulting LSTcam from model application (LSTcam corr). f Difference between LSTcam and LSTcam corr. g Temperature ranges of LSTcam and LSTcam corr for the entire scene. h Temperature ranges of LSTcam and LSTcam corr for the marked section in panels a–f. Grey shadings in g and h refer to min–max range, 90 % percentile, 50 % percentile (IQR), and the median (black line), respectively. i Histogram of the differences in panel f for the entire scene

This application of the LST model on landscape scale clearly shows that correcting for atmospheric influences (i) amplifies the measured LST spectrum (for the pronounced case in Fig. 7, the LST range was extended by as much as 10 K for the marked section) and (ii) shifts median temperatures depending on the difference between T path and surface temperature.

Discussion

Various studies on LST have been conducted using ground-based TIR cameras on landscape scale. These instruments gained popularity in ecosystem research due to their high temporal and spatial resolution as well as their operational simplicity (Corsi 2010; Pron and Bissieux 2004). In this study, we determined the magnitude of atmospheric effects on ground-based radiant surface temperature by comparison of LSTcam with LSTosr. Furthermore, we established a multiple linear regression model to correct LSTcam data and to show the effects of T path and APL on LSTcam data.

While LSTosr and LSTsat data did show a good correlation, LSTcam (kin) data, not corrected for atmospheric effects, were clearly offset compared to LSTsat data (Fig. 2). Once corrected for atmospheric effects, using our multiple linear regression model, LSTsat and LSTcam (kin) agreed reasonably well, reducing the MAE from 3.55 to 2.45 K (data not shown). Beside atmospheric effects, the offset could to some degree also be a result of thermal anisotropy, i.e., the LST depends on the viewing direction of the sensor (Christen et al. 2012; Kimes 1980; Lagouarde et al. 2000; Lagouarde et al. 2004; Voogt and Oke 2003). Under cloudless conditions, the satellite observes predominantly sunlit surfaces because of the nadir view. The oblique view of the TIR camera includes more vertical surfaces which could be cooler due to shading.

Focusing on the LSTosr and LSTcam comparison, we found that LSTcam clearly deviate from LSTosr. ΔLST, the difference between LSTosr and LSTcam, showed a pronounced diel cycle, and ΔLST was negatively correlated (p < 0.001) with the difference between T path and LSTosr, with T path being derived independently from microwave radiometer measurements. These findings show a strong influence of atmospheric properties along the measuring path on the LSTcam measurements. Using a multiple linear regression model, we could show that the measured range of LSTcam data is amplified when accounting for T path and mean LST are shifted either positively or negatively, depending on the temperature difference between LSTosr and T path.

Comparing results of LSTosr with LSTcam of course holds the problem of finding the exact pixel covering the LSTosr site and the fact that these two methods differ in their spatial resolution. To check the validity of our results, we performed a sensitivity analysis on our comparison of methods. To this end, we defined a pixel region for any LSTosr site within a thermal image with the pixel most likely covering the LSTosr site centered within a 5 times 5 pixel domain (center pixel surrounded by 24 pixels). Given these regions, we ran our analysis (i) choosing the pixel within these regions matching the LSTosr readings worst and (ii) choosing the one matching the LSTosr reading closest. Even between these two extreme scenarios, the mean difference in the RMSE comparing LSTosr with LSTcam was as low as 0.16 K (range 0.0–0.63 K) and differences in R 2 were below 0.01 in any case. This low sensitivity on the exact pixel location can be attributed to the land cover in that region, which shows low variability at small scales due to the intensive pomiculture. The site being most sensitive to pixel localization was “Alte Mendel Strasse,” which is located in close proximity to the settlement area of Bozen/Bolzano.

Our findings of a distinct influence of the atmosphere on LST derived from ground-based TIR imagery are in accordance with numerous studies that report on the these influences from satellite-based measurements down to ground-based measurements with APL of some hundred meters (Chandrasekhar 1960; Jacob et al. 2003; Meier et al. 2011; Norman et al. 1995; Voogt and Oke 2003). Meier et al. (2011) and Wawrzyniak et al. (2013), for example, report a magnitude of atmospheric effects during a diel cycle of up to 6.7 K in an urban environment and over natural environments, respectively, at path lengths lower than 800 m. These effects are particularly noticeable under the conditions of a high surface-to-path temperature difference, a pattern described, e.g., by Meier et al. (2011) as well. In the present study, this difference alone explained 81 % of the variation in LSTcam-LSTosr difference (p < 0.01) (Fig. 5).

Huge differences in temperature between a vegetated surface and the air above it may occur at times with (i) a high energy input, especially due to high incoming shortwave radiation (Kahmen et al. 2011; Lambers et al. 1998; Martin et al. 1999; Wilson et al. 1987), (ii) a low transpirational cooling due to water limitation (Camoglu 2013; Fuchs 1990; Gates 1964; Jackson et al. 1981), and (iii) low atmosphere-vegetation coupling (Jones 1992; McNaughton and Jarvis 1983).

Due to the increase in solar radiation and a decrease in air temperature with increasing altitude and the low atmospheric coupling of short alpine vegetation (Goldberg and Bernhofer 2008; Jarvis and Mcnaughton 1986; Tappeiner and Cernusca 1996), mountain landscapes facilitate high surface to air temperature differences. Furthermore, mountain regions feature high spatial variability in slope, aspect, and altitude, which in turn does lead to high spatial differences in the solar energy input (Bertoldi et al. 2010; Garnier and Ohmura 1968; Isard 1983) and thus LST.

Given these conditions, any measurements of LST in mountain landscapes, not accounting for atmospheric effects, do not only result in inaccurate absolute LST data but also underestimate the LST variability, both in space (Fig. 7 and Fig. 8) and time, due to the diel cycle in LST-T path difference. Under these circumstances, the findings of, e.g., Scherrer and Körner (2010) may very likely even have underestimated the described high LST variability within their investigated area.

One could argue that the atmospheric effects on LSTcam data are lower than the camera accuracies. However, in order to stay below a measurement error of 1.5 K (camera accuracy), the absolute differences between LSTosr and T path (ΔT) would have had to be lower than 4.6 and 2.1 K on average for our minimum APL (3260 m; Kaiserau) and our maximum APL (9038 m; Terlan), respectively (data not shown). Given the results shown in Fig. 5, ΔT reaches values as high as 15 K, which is well above the thresholds described above. Put another way, extrapolation of our data implies that an APL of less than 1000 m would be required to stay within the ±1.5 K range given by the accuracy of conventional TIR cameras.

The applied TIR camera is sensitive within a certain range of the electromagnetic spectrum, (7.5–14 μm). Hence, the proposed correction method is comparable with single-channel methods that are applied to satellite sensors with a single TIR band, e.g., LANDSAT (e.g., Sobrino et al. 2004). A standard approach to obtain LST is to solve the radiative transfer equation in the TIR spectrum. The atmospheric parameters, i.e., atmospheric transmissivity, between the surface and the sensor as well as down-welling and up-welling atmospheric radiance can be calculated from vertical profiles of atmospheric temperature and water vapor and using radiative transfer codes like MODTRAN (Berk et al. 2005; Berk et al. 1998). Our method has the advantage that we do not need the radiative transfer simulations, but due to the oblique view of the TIR camera at the landscape scale, we need to consider spatial variability of LOS parameters in contrast to a near nadir view of most satellite-based sensors. All single channel approaches need accurate data on temperature and water vapor distribution in the atmosphere between the surface and the sensor. Therefore, and as our study shows, on-site data about the vertical distribution of at least atmospheric temperature and a DEM of the study region should be available for LST studies on landscape scale by means of ground-based TIR imagery. This should be considered in the conception of experimental setups and field campaigns.

In a further study, we will compare our results with atmospheric correction methods based on simulations with MODTRAN and other models.

Conclusions

While atmospheric corrections on LST measurements are routinely applied on remote sensing or airborne systems, such corrections had been neglected in many landscape-scale studies using TIR cameras, despite atmospheric measurement path lengths of several hundred or thousand meters. Based on our intensive field measurements and on our modelling results, we were able to show that neglecting the atmospheric effect on ground-based TIR imagery does lead to substantial measurement errors. We could demonstrate that, depending on the temperature difference between the land surface and the overlying air masses, these errors are relevant even at relatively short measurement paths and particularly for spatially varying LOS parameters due to an oblique view of the TIR camera. Furthermore, our results suggest that differences in LST on landscape scale are underestimated in both spatial and temporal domains, due to the dampening effect of the atmosphere on the LST measurements.

Notes

Acknowledgments

Open access funding provided by University of Innsbruck and Medical University of Innsbruck. The research was kindly supported by the Province of Bozen-Bolzano (Autonome Provinz Bozen – Suedtirol, Abteilung Bildungsfoerderung, Universitaet und Forschung). We thank the Hydrographic Service of the Province of Bozen-Bolzano for providing radiometer data. We wish to thank all landowners and especially the South Tyrolean Consultancy for Orcharding and Viniculture for their support. UIBK is part of the Interdisciplinary Research Center “Ecology of the Alpine Region” within the major research area “Alpine Space – Man and Environment” at the University of Innsbruck.

References

  1. Bay H, Ess A, Tuytelaars T, Van Gool L (2008) Speeded-Up Robust Features (SURF). Comput Vis Image Und 110:346–359CrossRefGoogle Scholar
  2. Becker F, Li ZL (1990) Towards a local split window method over land surfaces. Int J Remote Sens 11:369–393CrossRefGoogle Scholar
  3. Berk A, Bernstein LS, Anderson GP, Acharya PK, Robertson DC, Chetwynd JH, Adler-Golden SM (1998) MODTRAN cloud and multiple scattering upgrades with application to AVIRIS. Remote Sens Environ 65:367–375CrossRefGoogle Scholar
  4. Berk A, Anderson GP, Acharya PK, Bernstein LS, Muratov L, Lee J, Fox MJ, Adler-Golden SM, Chetwynd JH, Hoke ML, Lockwood RB, Cooley TW, Gardner JA (2005) MODTRAN5: a reformulated atmospheric band model with auxiliary species and practical multiple scattering options. Proceedings of the SPIE, pp 88–95Google Scholar
  5. Bertoldi G, Notarnicola C, Leitinger G, Endrizzi S, Zebisch M, Della Chiesa S, Tappeiner U (2010) Topographical and ecohydrological controls on land surface temperature in an alpine catchment. Ecohydrology 3:189–204. doi: 10.1002/eco.129 Google Scholar
  6. Camoglu G (2013) The effects of water stress on evapotranspiration and leaf temperatures of two olive (Olea europaea L.) cultivars. Zemdirbyste 100:91–98CrossRefGoogle Scholar
  7. Campbell GS, Norman JM (1998) An introduction to environmental biophysics, 2nd edn. Springer, New YorkCrossRefGoogle Scholar
  8. Chandrasekhar S (1960) Radiative transfer. Dover, New YorkGoogle Scholar
  9. Christen A, Meier F, Scherer D (2012) High-frequency fluctuations of surface temperatures in an urban environment. Theor Appl Climatol 108:301–324. doi: 10.1007/s00704-011-0521-x CrossRefGoogle Scholar
  10. Corsi C (2010) History highlights and future trends of infrared sensors. J Mod Opt 57:1663–1686. doi: 10.1080/09500341003693011 CrossRefGoogle Scholar
  11. Czajkowski KP, Goward SN, Mulhern T, Goetz SJ, Walz A, Shirey D, Stadler S, Prince SD, Dubayah RO (2000) Estimating environmental variables using thermal remote sensing. In: Quattrochi DA, Luvall JC (eds) Thermal remote sensing in land surface processes. CRC Press LLC, Boca Ration, Florida, pp. 11–32Google Scholar
  12. Dash P, Göttsche FM, Olesen FS, Fischer H (2002) Land surface temperature and emissivity estimation from passive sensor data: theory and practice-current trends. Int J Remote Sens 23:2563–2594. doi: 10.1080/01431160110115041 CrossRefGoogle Scholar
  13. Fuchs M (1990) Infrared measurement of canopy temperature and detection of plant water stress. Theor Appl Climatol 42:253–261. doi: 10.1007/BF00865986 CrossRefGoogle Scholar
  14. Garnier BJ, Ohmura A (1968) A method of calculating the direct shortwave radiation income of slopes. J Appl Meteorol 7:796–800. doi: 10.1175/1520-0450(1968)007<0796:AMOCTD>2.0.CO;2 CrossRefGoogle Scholar
  15. Gates DM (1964) Leaf temperature and transpiration. Agron J 56:273–277. doi: 10.2134/agronj1964.00021962005600030007x CrossRefGoogle Scholar
  16. Goldberg V, Bernhofer C (2008) Testing different decoupling coefficients with measurements and models of contrasting canopies and soil water conditions. Ann Geophys 26:1977–1992CrossRefGoogle Scholar
  17. Heinl M, Leitinger G, Tappeiner U (2012) Diurnal surface temperature regimes in mountain environments. Phys Geogr 33:344–359CrossRefGoogle Scholar
  18. Hristov NI, Betke M, Kunz TH (2008) Applications of thermal infrared imaging for research in aeroecology. Integr Comp Biol 48:50–59CrossRefGoogle Scholar
  19. Isard SA (1983) Estimating potential direct insolation to alpine terrain. Arctic Alpine Res 15:77–89. doi: 10.2307/1550983 CrossRefGoogle Scholar
  20. Jackson RD, Idso SB, Reginato RJ, Pinter PJ (1981) Canopy temperature as a crop water stress indicator. Water Resour Res 17:1133–1138. doi: 10.1029/WR017i004p01133 CrossRefGoogle Scholar
  21. Jacob F, Gu XF, Hanocq JF, Tallet N, Baret F (2003) Atmospheric corrections of single broadband channel and multidirectional airborne thermal infrared data: application to the ReSeDA experiment. Int J Remote Sens 24:3269–3290. doi: 10.1080/01431160210153958 CrossRefGoogle Scholar
  22. Jarvis PG, Mcnaughton KG (1986) Stomatal vcntrol of transpiration—scaling up from leaf to region. Adv Ecol Res 15:1–49. doi: 10.1016/S0065-2504(08)60119-1 CrossRefGoogle Scholar
  23. Jensen JR (2007) Remote sensing of the environment: an earth resource perspective. Pearson, Prentice HallGoogle Scholar
  24. Jones HG (1992) Plants and microclimate: a quantitative approach to environmental plant physiology, 2nd edn. Cambridge University Press, CambridgeGoogle Scholar
  25. Kahmen A, Sachse D, Arndt SK, Tu KP, Farrington H, Vitousek PM, Dawson TE (2011) Cellulose delta O-18 is an index of leaf-to-air vapor pressure difference (VPD) in tropical plants. P Natl Acad Sci USA 108:1981–1986. doi: 10.1073/pnas.1018906108 CrossRefGoogle Scholar
  26. Kalma J, McVicar T, McCabe M (2008) Estimating land surface evaporation: a review of methods using remotely sensed surface temperature data. Surv Geophys 29:421–469. doi: 10.1007/s10712-008-9037-z CrossRefGoogle Scholar
  27. Katra I, Blumberg DG, Lavee H, Sarah P (2007) Topsoil moisture patterns on arid hillsides—micro-scale mapping by thermal infrared images. J Hydrol 334:359–367. doi: 10.1016/j.jhydrol.2006.10.023 CrossRefGoogle Scholar
  28. Kerr YH, Lagouarde JP, Imbernon J (1992) Accurate land surface-temperature retrieval from Avhrr data with use of an improved split window algorithm. Remote Sens Environ 41:197–209. doi: 10.1016/0034-4257(92)90078-X CrossRefGoogle Scholar
  29. Kimes DS (1980) Effects of vegetation canopy structure on remotely sensed canopy temperatures. Remote Sens Environ 10:165–174. doi: 10.1016/0034-4257(80)90020-6 CrossRefGoogle Scholar
  30. Kustas W, Anderson M (2009) Advances in thermal infrared remote sensing for land surface modeling. Agric For Meteorol 149:2071–2081. doi: 10.1016/j.agrformet.2009.05.016 CrossRefGoogle Scholar
  31. Kutner MH, Nachtsheim CJ, Neter J (2003) Applied linear regression models, 4th edn. McGraw-Hill/Irwin, IllionoisGoogle Scholar
  32. Lagouarde J-P, Ballans H, Moreau P, Guyon D, Coraboeuf D (2000) Experimental study of brightness surface temperature angular variations of maritime pine (Pinus pinaster) stands. Remote Sens Environ 72:17–34. doi: 10.1016/S0034-4257(99)00085-1 CrossRefGoogle Scholar
  33. Lagouarde J-P, Moreau P, Irvine M, Bonnefond J-M, Voogt JA, Solliec F (2004) Airborne experimental measurements of the angular variations in surface temperature over urban areas: case study of Marseille (France). Remote Sens Environ 93:443–462. doi: 10.1016/j.rse.2003.12.011 CrossRefGoogle Scholar
  34. Lambers H, Chapin FS, Pons TL (1998) Leaf energy budgets: effects of radiation and temperature. In: Plant physiological ecology. Springer, New York, p. 540CrossRefGoogle Scholar
  35. Martin TA, Hinckley TM, Meinzer FC, Sprugel DG (1999) Boundary layer conductance, leaf temperature and transpiration of Abies amabilis branches. Tree Physiol 19:435–443CrossRefGoogle Scholar
  36. McCafferty DJ (2007) The value of infrared thermography for research on mammals: previous applications and future directions. Mammal Rev 37:207–223CrossRefGoogle Scholar
  37. McNaughton KG, Jarvis PG (1983) Predicting effects of vegetation changes on transpiration and evaporation. In: Kozlowski TT (ed) Water deficits and plant growth, vol VII. Academc Press, New York, pp. 1–47Google Scholar
  38. Meier F, Scherer D (2012) Spatial and temporal variability of urban tree canopy temperature during summer 2010 in Berlin, Germany. Theor Appl Climatol 110:373–384CrossRefGoogle Scholar
  39. Meier F, Scherer D, Richters J, Christen A (2011) Atmospheric correction of thermal-infrared imagery of the 3-D urban environment acquired in oblique viewing geometry. Atmos Meas Tech 4:909–922CrossRefGoogle Scholar
  40. Norman JM, Divakarla M, Goel NS (1995) Algorithms for extracting information from remote thermal-Ir observations of the earths surface. Remote Sens Environ 51:157–168. doi: 10.1016/0034-4257(94)00072-U CrossRefGoogle Scholar
  41. Pan Y, Jackson RT (2008) Ethnic difference in the relationship between acute inflammation and serum ferritin in US adult males. Epidemiol Infect 136:421–431CrossRefGoogle Scholar
  42. Prata AJ, Caselles V, Coll C, Sobrino JA, Ottlé C (1995) Thermal remote sensing of land surface temperature from satellites: current status and future prospects. Remote Sens Rev 12:175–224. doi: 10.1080/02757259509532285 CrossRefGoogle Scholar
  43. Price JC (1984) Land surface-temperature measurements from the split window channels of the Noaa-7 advanced very high-resolution radiometer. J Geophys Res-Atmos 89:7231–7237. doi: 10.1029/Jd089id05p07231 CrossRefGoogle Scholar
  44. Pron H, Bissieux C (2004) Focal plane array infrared cameras as research tools. Quantitative InfraRed Thermography Journal 1:229–240. doi: 10.3166/qirt.1.229-240 CrossRefGoogle Scholar
  45. Quattrochi DA, Luvall JC (1999) Thermal infrared remote sensing for analysis of landscape ecological processes: methods and applications. Landsc Ecol 14:577–598CrossRefGoogle Scholar
  46. Richter R, Schläpfer D (2002) Geo-atmospheric processing of airborne imaging spectrometry data. Part 2: atmospheric/topographic correction. Int J Remote Sens 23:2631–2649CrossRefGoogle Scholar
  47. Rogerson PA (2001) Statistical methods for geography. Sage Publications Ltd, LondonCrossRefGoogle Scholar
  48. Scherrer D, Körner C (2010) Infra-red thermometry of alpine landscapes challenges climatic warming projections. Glob Change Biol 16:2602–2613. doi: 10.1111/j.1365-2486.2009.02122.x Google Scholar
  49. Scherrer D, Körner C (2011) Topographically controlled thermal-habitat differentiation buffers alpine plant diversity against climate warming. J Biogeogr 38:406–416CrossRefGoogle Scholar
  50. Scherrer D, Schmid S, Körner C (2011) Elevational species shifts in a warmer climate are overestimated when based on weather station data. Int J Biometeorol 55:645–654CrossRefGoogle Scholar
  51. Schmugge T, Hook SJ, Coll C (1998) Recovering surface temperature and emissivity from thermal infrared multispectral data. Remote Sens Environ 65:121–131CrossRefGoogle Scholar
  52. Schuster N, Kolobrodov VG (2004) Infrarotthermografie, 2nd edn. Wiley-VCH Verlag GmbH & Co.KGaA, WeinheimCrossRefGoogle Scholar
  53. Sobrino JA, Coll C, Caselles V (1991) Atmospheric correction for land surface-temperature using Noaa-11 Avhrr channel-4 and channel-5. Remote Sens Environ 38:19–34. doi: 10.1016/0034-4257(91)90069-I CrossRefGoogle Scholar
  54. Sobrino JA, Jiménez-Muñoz JC, Paolini L (2004) Land surface temperature retrieval from LANDSAT TM 5. Remote Sens Environ 90:434–440. doi: 10.1016/j.rse.2004.02.003 CrossRefGoogle Scholar
  55. Sobrino JA, Jimenez-Munoz JC, Zarco-Tejada PJ, Sepulcre-Canto G, de Miguel E, Soria G, Romaguera M, Julien Y, Cuenca J, Hidalgo V, Franch B, Mattar C, Morales L, Gillespie A, Sabol D, Balick L, Su Z, Jia L, Gieske A, Timmermans W, Olioso A, Nerry F, Guanter L, Moreno J, Shen Q (2009) Thermal remote sensing from airborne hyperspectral scanner data in the framework of the SPARC and SEN2FLEX projects: an overview. Hydrol Earth Syst Sc 13:2031–2037CrossRefGoogle Scholar
  56. Sugawara H, Narita K, Mikami T (2001) Estimation of effective thermal property parameter on a heterogeneous urban surface. J Meteorol Soc Jpn 79:1169–1181CrossRefGoogle Scholar
  57. Tappeiner U, Cernusca A (1996) Microclimate and fluxes of water vapour, sensible heat and carbon dioxide in structurally differing subalpine plant communities in the Central Caucasus. Plant Cell Environ 19:403–417. doi: 10.1111/1365-3040.ep8115861 CrossRefGoogle Scholar
  58. Teuling AJ, Seneviratne SI, Stockli R, Reichstein M, Moors E, Ciais P, Luyssaert S, van den Hurk B, Ammann C, Bernhofer C, Dellwik E, Gianelle D, Gielen B, Grunwald T, Klumpp K, Montagnani L, Moureaux C, Sottocornola M, Wohlfahrt G (2010) Contrasting response of European forest and grassland energy exchange to heatwaves. Nat Geosci 3:722–727CrossRefGoogle Scholar
  59. Tonolla D, Acuna V, Uehlinger U, Frank T, Tockner K (2010) Thermal heterogeneity in river floodplains. Ecosystems 13:727–740CrossRefGoogle Scholar
  60. Torr PHS, Zisserman A (2000) MLESAC: a new robust estimator with application to estimating image geometry. Comput Vis Image Und 78:138–156. doi: 10.1006/cviu.1999.0832 CrossRefGoogle Scholar
  61. Voogt JA, Oke TR (2003) Thermal remote sensing of urban climates. Remote Sens Environ 86:370–384. doi: 10.1016/S0034-4257(03)00079-8 CrossRefGoogle Scholar
  62. Wawrzyniak V, Piégay H, Allemand P, Vaudor L, Grandjean P (2013) Prediction of water temperature heterogeneity of braided rivers using very high resolution thermal infrared (TIR) images. Int J Remote Sens 34:4812–4831. doi: 10.1080/01431161.2013.782113 CrossRefGoogle Scholar
  63. Weng QH (2009) Thermal infrared remote sensing for urban climate and environmental studies: methods, applications, and trends. Isprs J Photogramm 64:335–344. doi: 10.1016/j.isprsjprs.2009.03.007 CrossRefGoogle Scholar
  64. Westermann S, Langer M, Boike J (2011) Spatial and temporal variations of summer surface temperatures of high-arctic tundra on Svalbard—implications for MODIS LST based permafrost monitoring. Remote Sens Environ 115:908–922CrossRefGoogle Scholar
  65. Wilson C, Grace J, Allen S, Slack F (1987) Temperature and stature: a study of temperatures in montane vegetation. Funct Ecol 1:405–413. doi: 10.2307/2389798 CrossRefGoogle Scholar
  66. Yang L, Li Y (2009) City ventilation of Hong Kong at no-wind conditions. Atmos Environ 43:3111–3121. doi: 10.1016/j.atmosenv.2009.02.062 CrossRefGoogle Scholar

Copyright information

© The Author(s) 2016

Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Authors and Affiliations

  • Albin Hammerle
    • 1
  • Fred Meier
    • 2
  • Michael Heinl
    • 1
  • Angelika Egger
    • 1
  • Georg Leitinger
    • 1
  1. 1.University of InnsbruckInnsbruckAustria
  2. 2.Departement of EcologyTechnische Universtität BerlinBerlinGermany

Personalised recommendations