Robustness of design flood estimates under nonstationary conditions: parameter sensitivity perspective

Abstract

The changing frequency of flooding in global watersheds, driven by various human and natural factors like land use/cover changes and global warming, necessitates innovative approaches in flood frequency analysis and risk assessment. Nonetheless, the reliability of nonstationary frequency analysis models remains a concern given challenges in accurately measuring the uncertainty introduced by these methods and the impact on design flood values. In this study, deviation-based differential sensitivity indices, including single-parameter (SDDSI) and entire-parameter (EDDSI) measures were developed to assess the influence of parameter uncertainty in nonstationary models using Bayesian statistics and "equivalent reliability" nonstationary design. The Weihe River, the largest tributary of the Yellow River which is experiencing both climate change and heavy impact of human activities, is chosen to be the study area to investigate the impact of precipitation change and land use change on nonstationary flood frequency. Results show that in the One-At-A-Time (OAT) sensitivity analysis under a small uncertainty scenario (SUS) for parameter inputs, the shape parameter stands out as the most influential factor (SDDSI_SUS = 0.347) affecting the 100-year design flood in the Stationary Generalized Extreme Value (SGEV) model. For the Non-Stationary GEV (NGEV) models, the influence of this parameter is less pronounced, with SDDSI_SUS values of 0.095 and 0.093 for the SSP126 and SSP585 scenarios, respectively. Instead, attention turns to the regression coefficient of the grassland area, associated with the GEV scale parameter. In global sensitivity analysis under the posterior uncertainty scenario (PUS) for parameter inputs, the EDDSI_PUS values for SGEV, NGEV_SSP126, and NGEV_SSP585 models were 0.52, 1.41, and 1.30, respectively, inferring heightened sensitivity of NGEV models to perturbations from entire parameters. It is anticipated that incorporating additional evidence, such as historical flood data, is essential for accurate nonstationary hydrological design to mitigating the influence of parameter uncertainty. The sensitivity indices in this study provide significant insights for assessing the robustness of nonstationary hydrological design in flood risk management and applications.

1 Introduction

The robustness of flood design is of utmost importance for infrastructure planning, including the capacities of reservoirs, levees, and spillways (Hu et al. 2018, Xiong et al. 2020). In recent years, hydrological design in nonstationary conditions has gained significant attention, as human activities and climate-induced changes have led to observed and extensively studied non-stationarity of hydrological regimes worldwide (Parey et al. 2010, Rootzen and Katz 2013, Salas and Obeysekera 2014; Read and Vogel 2015, Yan et al. 2017, Hu et al. 2018, Jiang et al. 2019, Li, et al. 2022). However, there are more concerns about the robustness of nonstationary flood design procedures compared to stationary ones (Milly et al. 2015, Montanari and Koutsoyiannis 2014, Serinaldi and Kilsby 2015, Xiong et al. 2020). One of these issues pertains to the sensitivity of models to uncertainties in parameters, particularly in more intricate hydrological design methodologies.

In general, both stationary and nonstationary flood design procedures comprise an at-site flood frequency analysis (FFA) model and design criteria. The FFA model is used to establish statistical distributions for modeling flood variables' magnitudes and their probabilities, while the flood design criteria are primarily derived from risk management requirements. Extensive literature has been dedicated to nonstationary flood frequency analysis (FFA) models (Villarini et al. 2009, Gilroy and McCuen 2012, Toonen 2015, Jiang et al. 2019, Cui et al. 2023), and previous studies have explored two main approaches. The first approach involves the reconstruction method, where non-stationary features are eliminated from hydrological series using hydrological or statistical models. Subsequently, stationary frequency analysis is conducted on the reconstructed past or current series (e.g., Liang et al. 2018, Toonen 2015). The second approach is the time-varying moment or time-varying distribution parameter approach (e.g., Villarini et al. 2009, Li et al. 2022). This method assumes that the probability distribution of flood variables should theoretically depend on temporal or environmental covariates, as a flood-generating system is nonstationary due to environmental changes. Generalized additive models for location, scale, and shape parameters (GAMLSS) (Rigby and Stasinopoulos 2005) are commonly used in this approach to evaluate nonstationary flood series due to their flexibility (Villarini et al. 2009, Xiong et al. 2020, Cui et al. 2023).

Previous studies have examined nonstationary flood design criteria, as traditional average return period calculations become much more complex under nonstationary conditions. Researchers such as Olsen et al. (1998), Salas and Obeysekera (2014), Parey et al. (2007, 2010) initially explored the expected waiting time (EWT) and number of exceedances (ENE) methods, seeking to understand return periods. However, the EWT and ENE approaches neglect to account for the design life of the project, as highlighted by Read and Vogel (2015) and Yan et al. (2017). Rootzen and Katz (2013) introduced the concept of "design life level" to define a new return period. This entails calculating the mean interval between occurrences of flood events exceeding the design life level over the design period. Subsequently, Read and Vogel (2015) proposed the notion of "annual average reliability" to derive the function of "average design life level" relative to the return period over the design life period. Another approach, suggested by Hu et al. (2018), is the adoption of "equivalent reliability" (ER) for nonstationary flood design. In this method, the ER-based return period functions as an equivalent design standard yet remains practical as it permits the use of stationary design reliability based on previous risk decisions, thus avoiding certain application problems (Yan et al. 2017).

In previous studies (e.g., Hu et al. 2020), researchers have explored the effects of various uncertainties on stationary flood estimation, including factors such as data record, statistical models, and parameter estimation methods. However, the sensitivity analysis of nonstationary hydrological design procedures has received limited attention thus far, despite the potential existence of additional uncertainty impacts on nonstationary hydrological design (Milly et al. 2015, Montanari and Koutsoyiannis 2014, Serinaldi and Kilsby 2015).

The primary aim of this research is therefore to create parameter sensitivity indices to evaluate the stability of nonstationary hydrological design procedures. The specific objectives of the study are as follows: (1) to develop single-parameter and entire-parameter sensitivity indices using differential analysis methods; (2) to utilize the single-parameter sensitivity index to rank the significance of parameters in both nonstationary and stationary flood design models; and (3) to evaluate the reliability of nonstationary and stationary flood design models through the application of the entire-parameter sensitivity index.

2 Methods

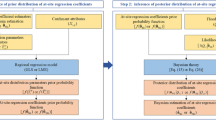
The flowchart (Fig. 1) for parameter sensitivity analysis of design floods under nonstationary conditions is as follows: first, relevant covariates undergo a preliminary filtering process through correlation and collinearity analysis. Second, the optimal nonstationary flood frequency analysis model is obtained using the GAMLSS model with the four 3-parameter probability distribution candidates (GEV, Lognormal3, Pearson-III, and Weibull3), along with model selection criteria (e.g. Akaike Information Criterion (AIC), Schwarz’s Bayesian Information Criterion (SBC)). Third, future predictions of the covariates are input into the nonstationary flood design model to generate the flood design value. Fourth, sensitivity indices are calculated by varying the size of the model parameter distributions considering Bayesian Markov Chain Monte Carlo (MCMC) methods and first-order Taylor approximation. Finally, the One-At-A-Time (OAT) and global parameter sensitivity analysis are conducted to evaluate the robustness of the nonstationary flood design. In the subsequent subsections, the following methods are addressed: introduction of the nonstationary flood design method of equivalent reliability; definition of single-parameter sensitivity index and entire-parameter sensitivity index based on differential sensitivity analysis, along with the application of first-order Taylor approximation to these sensitivity indices; and outline of the nonstationary flood frequency analysis methods. This framework provides a comprehensive approach to analyzing parameter sensitivity and assessing the robustness of nonstationary flood design under changing conditions.

Fig. 1

Flowchart of parameter sensitivity analysis for design floods under nonstationary conditions

2.1 Equivalent reliability (ER) method for nonstationary flood design

Due to the incompatibility of the concepts of 'non-stationarity' and 'return period', Liang et al. (2018) proposed the concept of 'equivalent reliability' (ER) to give the design flood values under non-stationary condition. Within the ER concept, the design criteria given by the return period and its corresponding design value, are replaced by the reliability corresponds to a return period and its corresponding design value. The stationary and nonstationary designs have the same reliability, so the design value for nonstationary conditions can be calculated using classical design criteria, given by the T-year return period, with the following equation:

$$R\left( {z_{{t_{1} - t_{2} }}^{ns} ,\theta ,{\mathbf{x}}_{{\mathbf{t}}} ,t_{2} ,t_{1} ,T} \right) = \prod\limits_{{t = t_{1} }}^{{t_{2} }} {F_{{Y_{t} }} \left( {z_{{t_{1} - t_{2} }}^{ns} \left| {{\mathbf{x}}_{{\mathbf{t}}} ;\theta } \right.} \right)} - \left( {1 - \frac{1}{T}} \right)^{{t_{2} - t_{1} + 1}} = 0$$

(1)

where $R$ is an implicit function for $z_{{t_{1} - t_{2} }}^{ns}$; $z_{{t_{1} - t_{2} }}^{ns}$ is the design flood value under the nonstationary conditions, corresponding to the return period $T$; $F_{{Y_{t} }}$ is the cumulative distribution of the flood variable $Y_{t}$; ${\mathbf{x}}_{{\mathbf{t}}}$ is the vector of the realizations of covariates ${\mathbf{X}}_{{\mathbf{t}}}$ for the variable $Y_{t}$; $\theta = [\theta_{1} ,\theta_{2} ...,\theta_{d} ]$ is the d-dimensional vector of model parameters; $t_{1}$ and $t_{2}$ are the beginning and end of a design life period, respectively. According to Eq. 1, $z_{{t_{1} - t_{2} }}^{ns}$ is determined by the model parameters $\theta = [\theta_{1} ,\theta_{2} ...,\theta_{d} ]$ when the other variables are fixed, such as the design life period $t_{1} \sim t_{2}$, the covariates ${\mathbf{x}}_{{\mathbf{t}}}$, the distribution model structure, and the return period $T$. In this study, we analyze the sensitivity of design values to model parameters using the following explicit function $h$:

$$z_{{t_{1} - t_{2} }}^{ns} = h\left( {\theta_{1} ,\theta_{2} ...,\theta_{d} \left| {T,t_{2} - t_{1} ,{\mathbf{x}}_{{\mathbf{t}}} } \right.} \right)$$

(2)

2.2 Deviation-based differential sensitivity indices (DDSI) for nonstationary flood design model

2.2.1 One-At-A-Time (OAT) sensitivity analysis

Sensitivity analysis deals with the behavior of uncertainty propagation in non-stationary flood design models, resulting from the variability or uncertainty of model parameter. The OAT or single-parameter analysis in this study is to calculate the sensitivity measures considering the variability of one parameter while keeping the others fixed. Its objective is to determine the extent of sensitivity, generating both sensitivity magnitude and a ranking of parameter influence. Based on the differential sensitivity analysis technique, this study developed a single-parameter DDSI (SDDSI) $\phi_{i}$, which is the ratio of the change in modulus deviation of the output to the change in modulus deviation of the input, as follows:

$$\phi_{i} \left( {m_{i}^{{{\text{in}}}} } \right) = \frac{{dm_{z}^{{{\text{out}}}} }}{{dm_{i}^{{{\text{in}}}} }}$$

(3)

$$m_{z}^{{{\text{out}}}} = \frac{{\sigma_{z}^{{{\text{out}}}} }}{{\overline{z}}}$$

(4)

$$m_{i}^{{{\text{in}}}} = \frac{{\sigma_{i}^{{{\text{in}}}} }}{{\hat{\sigma }_{i}^{{{\text{in}}}} }}$$

(5)

where $m_{i}^{{{\text{in}}}}$ and $m_{z}^{{{\text{out}}}}$ are the input and output modulus deviations, respectively; $\sigma_{z}^{{{\text{out}}}}$ is the standard deviation of the output distribution for a flood design estimation under an input parameter uncertainty; $\overline{z}$ is a reference value, provided by the posterior mean for the flood design estimation; $\sigma_{i}^{{{\text{in}}}}$ is the standard deviation of the input distribution for model parameter $\theta_{i}$; $\hat{\sigma }_{i}^{{{\text{in}}}}$ is also a reference value, given by the parameter posterior deviation. A larger value of $\phi_{i}$ indicates that a larger change of the output relative uncertainty for the flood design estimation is caused by the same change of the input relative uncertainty. This study used three classifications based on the value of $\phi_{i}$: low ($\phi_{i} \le 0.5$), moderate ($0.5 < \phi_{i} \le 1$), severe ($\phi_{i} > 1$). Take the ‘severe’ classification as an example: a value greater than 1 indicates that in flood design estimation, due to the influence of model structure or other factors on uncertainty propagation, the proportional change of input parameter uncertainty leads to a large change in output uncertainty, indicating that the model is less robust. For a given model parameter, $\phi_{i}$ allows to compare the sensitivity under the different levels of one factor in the Eq. 2, such as the return period $T$. Obviously, there must be different parameter sensitivity results for the different levels of the return period. Moreover, the integral function of the Eq. 3 is written as:

$$m_{z}^{{{\text{out}}}} = G_{i} \left( {m_{i}^{{{\text{in}}}} } \right)$$

(6)

where $G_{i}$ is a modulus deviation propagation function.

2.2.2 Global sensitivity analysis

In global or entire-parameter sensitivity analysis, the variability of global parameters is considered in calculating the sensitivity measures for a flood design estimation. Similarly, an entire-parameter of DDSI (EDDSI) $\phi_{\Sigma }$ is defined as:

$$\phi_{\Sigma } \left( {m_{\Sigma }^{{{\text{in}}}} } \right) = \frac{{dm_{z}^{{{\text{out}}}} }}{{dm_{\Sigma }^{{{\text{in}}}} }}$$

(7)

$${{\varvec{\Sigma}}} = \left( {m_{\Sigma }^{{{\text{in}}}} } \right)^{2} {\hat{\mathbf{\Sigma }}},m_{\Sigma }^{{{\text{in}}}} > 0$$

(8)

where $m_{\Sigma }^{{{\text{in}}}}$ is the modulus deviation for the entire-parameter case; ${\hat{\mathbf{\Sigma }}}$ is a reference covariance, provided by the parameter posterior covariance; ${{\varvec{\Sigma}}}$ is the input covariance determining the scale of the input multivariate distribution. A larger value of $\phi_{\Sigma }$ also indicates that a larger change of the output relative uncertainty for the flood design estimation is caused by the same change of the input relative uncertainty. The integral function of the Eq. 7 is written as:

$$m_{z}^{{{\text{out}}}} = G_{\Sigma } \left( {m_{\Sigma }^{{{\text{in}}}} } \right)$$

(9)

where $G_{\Sigma }$ is a modulus deviation propagation function for the entire-parameter case.

2.2.3 First-order Taylor approximation

In this section, we give an approximation to the Eqs.3 and 7 using the first-order Taylor expansion. The approximation is based on the following assumptions (Koda et al. 1979): the function $h$ in the Eq. 2 is sufficiently differentiable and the moments of $\theta$ are finite; and either $h$ is weak nonlinear or parameter uncertainties are small. The above modulus deviation propagation is mathematically a nonlinear transformation problem. Consider a first-order Taylor approximation for the Eq. 2,

$$z_{{t_{1} - t_{2} }}^{ns} = h\left( {\theta_{1} ,...,\theta_{d} } \right) \approx h\left( {\hat{\theta }_{1} ,....,\hat{\theta }_{n} } \right) + \nabla h \cdot \left( {\theta - \hat{\theta }} \right)^{{\text{T}}}$$

(10)

where $\hat{\theta } = \left[ {\hat{\theta }_{1} ,....,\hat{\theta }_{n} } \right]$ is the mean of the input distribution; $\nabla h = \left[ {\frac{\partial h}{{\partial \theta_{1} }},...,\frac{\partial h}{{\partial \theta_{d} }}} \right]$ is the gradient of $h$ at $\hat{\theta }$. Taking the derivative of implicit function in the Eq. 1 into consideration, the gradient of $h$ can be calculated as follows:

$$\nabla h = \left[ { - \frac{{R_{{\theta_{1} }} }}{{R_{z} }},..., - \frac{{R_{{\theta_{d} }} }}{{R_{z} }}} \right]$$

(11)

where $R_{{\theta_{i} }}$ and $R_{z}$ are the partial derivatives of $R$ with respect to $\theta_{i}$ and $z_{{t_{1} - t_{2} }}^{ns}$.

The standard deviation of the output distribution for the nonstationary flood design is approximated as:

$$\sigma_{z}^{{{\text{out}}}} \approx \sqrt {\nabla h{{\varvec{\Sigma}}}\nabla h^{{\text{T}}} }$$

(12)

Subsequently, the first-order Taylor approximations of the sensitivity indices for both OAT and global sensitivity analysis considering the aforementioned assumptions, are provided as follows:

$$\phi_{i} \left( 0 \right) = \frac{1}{{\overline{z}}}\left| {\frac{{R_{{\theta_{1} }} }}{{R_{z} }}} \right|$$

(13)

$$\phi_{\Sigma } \left( 0 \right) = \frac{1}{{\overline{z}}}\sqrt {\nabla h{\hat{\mathbf{\Sigma }}}\nabla h^{{\text{T}}} }$$

(14)

2.2.4 SDDSI and EDDSI under the small and posterior uncertainty scenarios

In this section, our in-depth analysis focuses on two specific parameter uncertainty scenarios: the small uncertainty scenario (SUS, characterized by input modulus deviation near 0) and the posterior uncertainty scenario (PUS, marked by input modulus deviation equal to 1). This study carefully observes the effects of parameter uncertainty propagation on the nonstationary design flood model near each of the two specified scenarios. Subsequently, we assign names and mathematical notations to them based on Eqs. 3 and 7, as outlined below: the SUS single-parameter sensitivity index (SDDSI_SUS), denoted as $\phi_{i} \left( 0 \right)$; the SUS entire-parameter sensitivity index (EDDSI_SUS), denoted as $\phi_{\sum } \left( 0 \right)$; the PUS single-parameter sensitivity index (SDDSI_PUS), denoted as $\phi_{i} \left( 1 \right)$; and the PUS entire-parameter sensitivity index (EDDSI_PUS), denoted as $\phi_{\sum } \left( 1 \right)$.

2.3 Nonstationary flood frequency analysis

2.3.1 GAMLSS model

The GAMLSS model is a semi-parametric regression generalized additive model based on generalized linear model (GLM) and generalized additive model (GAM), which is widely used to simulate the variation law of probability distribution parameters with covariates in changing environments (Villarini et al. 2009, Du et al. 2015, Read and Vogel 2015, Yan et al. 2017). In general, probability distributions with equal or less than three distribution parameters are usually considered. It is assumed that the flood variable $Y_{t}$ obeys the distribution of probability density $f_{{Y_{t} }} \left( {\left. {y_{t} } \right|\mu_{t} ,\sigma_{t} ,\xi_{t} } \right)$. Taking the most widely used generalized linear addition formula as an example, the generalized linear addition formula can be expressed as follows:

$$\begin{gathered} g_{1} \left( {\mu_{t} } \right) = \theta_{10} + \theta_{11} X_{11} + ... + \theta_{{1n_{1} }} X_{{1n_{1} }} \hfill \\ g_{2} \left( {\sigma_{t} } \right) = \theta_{20} + \theta_{21} X_{21} + ... + \theta_{{2n_{2} }} X_{{2n_{2} }} \hfill \\ g_{3} \left( {\xi_{t} } \right) = \theta_{30} + \theta_{31} X_{31} + ... + \theta_{{3n_{3} }} X_{{3n_{3} }} \hfill \\ \end{gathered}$$

(15)

where $\mu_{t}$,$\sigma_{t}$ and $\xi_{t}$ are probability distribution parameters,$X_{k} = \left[ {X_{k1} ,X_{k2} ,...,X_{{kn_{k} }} } \right]\left( {k = 1,2,3} \right)$ is explanatory variable, $n_{k}$ is the number of explanatory variables corresponding to each expression. The number of explanatory variables is $n_{1} + n_{2} + n_{3}$. Considering that the same explanatory variable can be used to explain different distribution parameters, the actual number of explanatory variables $n \le n_{1} + n_{2} + n_{3}$; $\theta_{k} = \left[ {\theta_{k0} ,\theta_{k1} ,...,\theta_{{kn_{k} }} } \right]^{{\text{T}}} \left( {k = 1,2,3} \right)$ is the model parameter to be estimated. All model parameters were denoted by $\theta$, and the total number of model parameters is $df = 3 + n_{1} + n_{2} + n_{3}$; if $df$ is equal to 3, no explanatory variable was used to explain the variation of probability distribution parameters, which was a stationary frequency analysis model; if $df$ is larger than 3, the model will be a nonstationary frequency analysis model; $g_{1} \left( \cdot \right)$, $g_{2} \left( \cdot \right)$ and $g_{3} \left( \cdot \right)$ are monotonic link functions, generally logarithmic or identity functions. The logarithmic function is used to require the parameters of the probability distribution to be greater than 0 to ensure that its predicted value is non-negative.

GAMLSS model allows various probability distributions to be used to fit the flood variables, such as GEV, Weibull, Gamma, Gumbel and Lognormal distributions (Rigby and Stasinopoulos 2005). In this study, we selected four 3-parameter probability distributions (i.e., GEV, Lognormal3, Pearson-III, and Weibull3) as the candidates to get the optimal nonstationary frequency analysis model. Table 1 presents the probability density functions, moments, and link functions associated with each distribution parameter of these distributions. Acknowledging the impact of limited extreme flood data on the sensitivity of the shape parameter (Coles 2001, Obeysekera and Salas 2014), this study maintains the shape parameter as a constant and directs its attention towards examining how the location and/or scale parameters vary with covariates.

Table 1 Three-parameter distributions for analyzing flood frequency in this study

2.3.2 Bayesian parameter estimation

Ouarda and El-Adlouni (2011) introduced Bayesian nonstationary frequency analysis. Bayesian estimation of the model parameters with certain restrictions through the prior distribution can lead to more robust estimation results. According to Bayesian theory, the posterior distribution can be written as:

$$p\left( {\theta \left| {AD} \right.} \right) = \frac{{L\left( {AD\left| \theta \right.} \right)\pi \left( \theta \right)}}{{\mathop \smallint \nolimits_{{\Phi }} L\left( {AD\left| \theta \right.} \right)\pi \left( \theta \right)d\theta }} \propto l\left( \theta \right) + \log \pi \left( \theta \right)$$

(16)

where $AD$ represents available observation data; $\pi \left( \theta \right)$ is the prior probability density function; $L\left( {AD\left| \theta \right.} \right)$ is the likelihood function under the data condition; the integral term is a standardized constant, where $\Phi$ is the whole parameter space. In the absence of a priori information, a non-informative (fat) prior distribution can be set. The posterior probability distribution in Eq. 16 is complex, generally without an analytical solution and can usually be obtained by Markov chain Monte Carlo (MCMC) sampling methods (Martins and Stedinger 2000, Adlouni et al. 2007). The Markov chain based on Metropolis–Hastings algorithm (Viglione et al. 2013) was obtained with the help of R package "MHadaptive" (Chivers 2012) in this study.

2.3.3 Model diagnostic evaluation

The Akaike Information Criterion (AIC; Akaike 1974) was applied to select the nonstationary frequency analysis models because AIC deals with both the fitting effect and the complexity of the model. Given the parameter estimation $\hat{\theta }$, the AIC value was calculated as follow:

$$AIC = 2df - 2l\left( {\hat{\theta }} \right)$$

(17)

where $df$ is the degree of freedom of the model, that is, the number of model parameters. Considering a different size of the penalty for model complexity (over-fitting), Schwarz’s Bayesian Information Criterion (BIC or SBC; Schwarz 1978) was also considered:

$$SBC = \ln \left( {n_{d} } \right) \cdot df - 2l\left( {\hat{\theta }} \right)$$

(18)

where $n_{d}$ is the length of data; when $n_{d} \ge 8$, SBC criterion has a greater penalty weight for overfitting than AIC criterion. Furthermore, the reasonableness of the selected model needs to be checked by another step, the goodness-of-fit test (Coles 2001), which is generally based on whether the standardized residuals are normally distributed. In this study, the methods of worm plot (Buuren and Fredriks 2001), the percentile curves plot, and Filliben correlation coefficient (Filliben 1975) were used.

3 Case study design

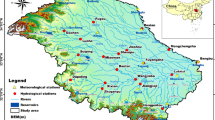
3.1 Weihe river basin

The Weihe River is located between 33°40′ N–37°26′ N latitude and 103°57′ E–110°27′ E longitude (Fig. 2). It is the first major tributary of the Yellow River with a main stream length of 828 km. Its basin area is 134,766 km², accounting for nearly 10% of the entire Yellow River basin area. The basin has a warm temperate semi-humid continental monsoon climate with an annual average precipitation (1954–2009) of 540 mm unevenly distributed temporally and spatially. Precipitation varies from 400 to 1000 mm from north-west to south-east, and is highly seasonal throughout the year, summer and autumn (June to September), account for over 70% of annual precipitation. The annual average runoff of Weihe River basin is approximately 56.2 mm. In recent years, water resources in the Weihe River Basin have a significant decreasing trend due to impacts of climate change and intense human activities (Mcvicar et al. 2007, Zuo et al. 2014, Yan et al. 2017).

Fig. 2

Location and topography of the Weihe River Basin with hydrological and meteorological stations

3.2 Floods and covariates data

The annual maximum daily flows for the period 1956–2015 were obtained at the Huaxian gauging station for at-site flood frequency analysis (FFA). In the nonstationary modeling, changes of three main land use types that are the forestland, farmland, and grassland, and climate variables that are summer and whole-year precipitation were considered as covariates (Table 1). In the nonstationary frequency analysis model, normalized LUCC covariates are denoted as $\left[ {A_{t}^{{{\text{Fo}}}} ,A_{t}^{{{\text{Fa}}}} ,A_{t}^{{{\text{Gr}}}} } \right]$, where $A_{t}^{{{\text{Fo}}}}$ is the normalized annual forest area, $A_{t}^{{{\text{Fa}}}}$ is the normalized annual farmland area, $A_{t}^{{{\text{Gr}}}}$ is the normalized annual grassland area; while normalized precipitation covariates are denoted as $\left[ {d_{t}^{{{\text{SP}}}} ,d_{t}^{{{\text{TP}}}} } \right]$, where $d_{t}^{{{\text{SP}}}}$ is the normalized annual summer precipitation depth, $d_{t}^{{{\text{TP}}}}$ is the normalized annual total precipitation depth. (Table 2).

Table 2 Covariates candidates for the flood frequency fitting

For LUCC covariates, the observations and predictions are from the two datasets. The first one for the observed series is from the 1 km grid dataset of land use/cover (Resource and Environment Science Data Center of Chinese Academy of Sciences, http://www.resdc.cn), in the 1985–2015 period at 5 year intervals. The study used linear interpolation to obtain 1 year intervals. The second one for the predicted series is based on the dataset from Luo et al. (2022) who predicted the future LUCC in China by coupling the global change analysis models and a future land use simulation model. The dataset provides a 1 km gridded land use/cover type predicted data for 2010–2100 under 24 combination scenarios of Shared Socio-economic Pathways (SSPs) and Representative Concentration Pathways (RCPs) at 10 year intervals, and were interpolated into 1 year interval as above. This study, considering the top priority in experimental design (Eyring et al. 2016, O'Neill et al. 2016), selected the five combined scenarios, i.e., the SSP126, SSP245, SSP370, SSP460, and SSP585. The SSP-based scenarios are labelled SSP1 ~ SSP5, representing five climate policy choices, i.e., the sustainability, middle sustainability, regional rivalry, inequality, and fossil-fueled development roads (Riahi et al. 2017). The RCP-based scenarios are labelled 26, 45, 60, 70, and 85 forming the last two digits of above combined scenarios codes, giving different radiative forcing levels over time, e.g., 26 represents a peak in radiative forcing at approximately 3 W/m² mid-century before declining to 2.6 W/m² by 2100.

For precipitation covariates, the observations and predictions were collected. The observed series is from the precipitation gauge data (1951–2017) of the National Climate Center of the China Meteorological Administration (http://cdc.cma.gov.cn/). The predicted precipitation is from the dataset of the Coupled Model Intercomparison Project Sixth Phase (CMIP6, https://esgf-node.llnl.gov/projects/cmip6/). Seven models in the dataset are selected, which are (1) the Canadian Earth System Model version 5 developed by the Canadian Centre for Climate Modelling and Analysis (CanESM5; Swart et al. 2019), (2) Community Earth System Model version 2 with Whole Atmosphere Community Climate Model developed by National Center for Atmospheric Research (CESM2-WACCM, Danabasoglu 2019), (3) the second generation Earth System model developed by the CNRM-CERFACS (CNRM-ESM2-1; Seferian 2018), (4) Flexible Global Ocean–Atmosphere–Land System model version f3 developed by Chinese Academy of Sciences (FGOALS-f3-L, Yu 2019), (5) the climate model developed at Institute Pierre-Simon Laplace (IPSL-CM6A-LR; Boucher et al. 2020), (6) Korea Institute of Atmospheric Prediction Systems Climate Model version 1.0 developed by the National Institute of Meteorological Sciences/Korea Met, and (7) the Administration (KACE-1-0-G, Byun et al. 2019), and Interdisciplinary Research on Climate model version 6 developed by the RIKEN Center for Computational Science (MIROC6, Shiogama et al. 2019). The above data were calculated at the basin scale using the inverse distance weighting (IDW) method and a statistical downscale method, the detrended quantile matching (Cannon et al. 2015) based on rainfall records from 23 stations. Dynamic simulation period for future precipitation in this study is from January 2015 to December 2100. Representative future climate scenarios for the design life spanning from 2000 to 2100 were derived from the CanESM5, CESM2-WACCM, CNRM-ESM2-1, FGOALS-f3-L, IPSL-CM6A-LR, KACE-1-0-G, and MIROC6 models. Figure 3 illustrates the projected whole-year precipitation for the Weihe River Basin during the timeframe of 2015 to 2100 by the seven Global Climate Models (GCMs), alongside historical observations spanning from 1956 to 2014. For each of the SSP126, SSP245, SSP370, SSP460, and SSP585 scenarios, the outcomes of the design flood and sensitivity index, based on the seven GCMs precipitation prediction were combined using the arithmetic mean. In this investigation, the SSP126 and SSP585 scenarios, with the lowest and highest radiative forcing levels respectively, were chosen as representatives to showcase the findings of nonstationary flood design and its accompanying sensitivity analysis.

Fig. 3

Dynamic simulation of future precipitation under five combined shared socio-economic pathway and representative concentration pathway scenarios (SSP126, SSP245, SSP370, SSP460, and SSP585) in the Huaxian Drainage from the 7 Global Climate Models (CanESM5, CESM2-WACCM, CNRM-ESM2-1, FGOALS-f3-L, IPSL-CM6A-LR, KACE-1-0-G, and MIROC6)

3.3 Nonstationary flood design scheme

3.3.1 Covariate selection

To attain an optimal equilibrium between model intricacy and the quality of fit, the process of covariate selection becomes indispensable within a GAMLSS model framework tailored for nonstationary frequency analysis. In the case study, a meticulous preliminary filtering process and enumeration regression process were undertaken, aimed at narrowing the expansive array of potential covariates within the GAMLSS model framework. The preliminary filtering process includes the correlation and collinearity analysis. During the preliminary filtering stage, covariates were omitted from consideration if they displayed weak correlation (with a p value > 0.05) with flood data and concurrently exhibited substantial correlation (a correlation coefficient exceeding 0.8) with other covariates. Based on the aforementioned procedure, the total precipitation depth and grassland area were chosen for progression into the subsequent phase, which involves the enumeration regression process. Conversely, forest area and farmland area were excluded due to their limited correlation (with a p value > 0.05) with flood data, as shown in Fig. 4, while the summer precipitation depth was eliminated owing to its notable correlation with the total precipitation depth. In the realm of enumerative regression, the optimal formulations for location parameters and scale parameters of the GEV, Lognormal3, Pearson-III, and Weibull3 distributions within the GAMLSS models are refined by systematically evaluating every conceivable combination of covariates—specifically, the normalized total precipitation depth $d_{t}^{{{\text{TP}}}}$ and grassland area $A_{t}^{{{\text{Gr}}}}$. The optimal model is then chosen based on the principle of minimizing the AIC value, culminating in the identification of the most advantageous blend of interpretations. The stationary model, devoid of any covariate integration, is further calculated to act as a benchmark for the nonstationary analysis.

Fig. 4

Correlation between floods and covariates

3.3.2 Hydrological design scheme

A specialized flood design scheme is indispensable when evaluating parameter sensitivity in nonstationary design flood models. This study explores a risk management scenario spanning the design life from 2000 to 2100, encompassing return periods of 10, 20, 50, and 100 years. These considerations address the typical design requirements for infrastructure. Note that, for the sake of simplicity, sensitivity indices were exclusively calculated for the 100 year return period within the OAT analysis, aimed to identify the most responsive parameter.

3.3.3 Parameter sampling scheme

In both the OAT and global sensitivity analysis, diverse sets of parameter distribution inputs are necessary to generate the model's output. Subsequently, these outputs are used to calculate the sensitivity indices using Eqs. 3 and 7. During the OAT sensitivity analysis, a univariate normal distribution is employed, encompassing various standard deviations ranging from 0 to 1.5 times the posterior deviation, in increments of 0.1, based on the Eq. 3, while maintaining a constant mean established through the posterior mean. This distribution is used to sample the specific parameter under investigation, while the remaining parameters are held steady at their respective posterior means. Conversely, in the global sensitivity analysis, a multivariate normal distribution is utilized, incorporating diverse covariance matrices, spanning from 0 to 1.5 times the posterior deviation, in intervals of 0.1, based on the Eq. 7. Similar to the univariate case, the mean of this distribution remains constant and is established based on the posterior mean.

4 Results and discussion

4.1 Identification of the flood distribution time-varying types

The study performed the stepwise regression analysis for covariate selection in the order of $d_{t}^{{{\text{TP}}}}$ and $A_{t}^{{{\text{Gr}}}}$ for location and scale parameter formulas of GEV, Lognormal3, Pearson-III, and Weibull3 distributions. Table 3 displays the AIC and SBC values of optimal models associated with these distributions, estimated by maximum likelihood estimation to fit the annual maximum daily flows (AMDF). The nonstationary GEV (NGEV) model has the AIC and SBC minimum values of 993.2 and 1005.8, indicating the NGEV model may be more efficient. The formula for the optimal model, which consists of 6 model parameters, is as follows:

$$\begin{gathered} \mu_{t} = \theta_{10} + \theta_{11} d_{t}^{{{\text{TP}}}} + \theta_{12} A_{t}^{{{\text{Gr}}}} \hfill \\ \sigma_{t} = \exp \left( {\theta_{20} + \theta_{21} A_{t}^{{{\text{Gr}}}} } \right) \hfill \\ \xi_{t} = \theta_{30} \hfill \\ \end{gathered}$$

(19)

where both $\mu_{t}$ and $\sigma_{t}$ are identified as dependent variables, and $\mu_{t}$ varies with both $d_{t}^{{{\text{TP}}}}$ and $A_{t}^{{{\text{Gr}}}}$, while $\sigma_{t}$ only depends on $A_{t}^{{{\text{Gr}}}}$. Table 4 presents the results of Bayesian parameter estimation for the stationary GEV (SGEV) and NGEV, including the posterior means and posterior standard deviations of the model parameters. It was observed that within the SGEV model, the shape distribution parameter $\theta_{30}$ exhibited a relatively wide range, with a mean of 0.11 and a standard deviation of 0.18. In the case of the NGEV model, apart from $\theta_{30}$, which had a mean of 0.03 and a standard deviation of 0.11, $\theta_{21}$ also demonstrated a relatively significant range, with a mean of 0.27 and a standard deviation of 0.12. In addition, the empirical residuals of the SGEV and NGEV models underwent Filliben's probability plot correlation coefficient (PPCC) test. The resulting PPCC values were 0.985 and 0.991 for SGEV and NGEV models, respectively, which are greater than the critical value of 0.980 at the significance level of 0.05 (Filliben 1975). These findings suggest that there is no compelling evidence to reject the null hypothesis, indicating that the empirical residuals conform to the assumed distribution, specifically the normal distribution.

Table 3 Results of covariate selection analysis for the location and scale parameter formulas of GEV, Lognormal3, Pearson-III, and Weibull3 distributions using Akaike Information Criterion (AIC) and Schwarz’s Bayesian Information Criterion (SBC), based on the forward stepwise regression

Table 4 Results of Bayesian parameter estimation and Filliben's PPCC test in the study case

Table 5 displays the correlation between the sample size used in Bayesian Markov chain Monte Carlo sampling for an optimal nonstationary model, utilizing the Metropolis–Hastings algorithm (Xu et al. 2018), and the mean value and standard deviation of the model parameters. The table reveals that once the sample size reaches 100,000 iterations, the values and standard deviations of the parameters tend to stabilize. Additionally, selecting a sampling size greater than 100,000 iterations ensures that the model parameters reach a state of stability for further calculations.

Table 5 Sample size determination for the Bayesian Markov chain Monte Carlo (MCMC) sampling based on the Metropolis–Hastings algorithm for the optimal nonstationary GEV model; "M" and "SD" represent the mean and standard deviation, respectively

Figure 5 provides an assessment of the adequacy of the SGEV and NGEV models in capturing the observed data at the Huaxian station. The intensity of floods has seen a reduction since 1990. Numerous data points recorded from that year onwards lie beneath the 50th percentile curves as outlined by the SGEV model (Fig. 5a). In contrast, all observed data points are evenly spread across the projected percentile range offered by the NGEV model (Fig. 5c). Furthermore, the fluctuation trend of the quantile (represented by the red line) provided by the NGEV model closely aligns with the observed changes in flood samples. This indicates that the NGEV model exhibits a better fit to the data in capturing the nonstationary behavior of floods at the Huaxian station, as compared to the SGEV model. The worm plots (Fig. 5b, d) further support the finding that the NGEV model provides a more reasonable fit, to a certain extent, compared to the SGEV model. The worm points for both SGEV and NGEV fall within the 95% confidence intervals. However, the deviation of the worm plot for the NGEV model is consistently closer to 0 when compared to the SGEV model. This alignment suggests that the NGEV model more reasonably captures the observed data, indicating its superior suitability compared to the SGEV model. Therefore, this further demonstrates the significant relationship between flood distribution characteristics, climate characteristics, and land use and land cover change (LUCC) situations.

Fig. 5

Goodness-of-fit of stationary and nonstationary frequency analysis models for Huaxian station; a and c are the percentile plots; b and d are the worm plots; NGEV, nonstationary GEV; SGEV, stationary GEV

4.2 Parameter sensitivity analysis for ER-based nonstationary flood design using the DDSI

The findings from Table 6 provide valuable insights into the OAT sensitivity analysis of the SGEV and NGEV models, considering the design life of 2000–2100 and two representative future climate scenarios (SSP126 and SSP585). For the SGEV model, the GEV shape parameter ($\theta_{30}$) exhibits both low sensitivity ($\phi_{i} \left( 0 \right) = 0.347$) and moderate sensitivity ($\phi_{i} \left( 1 \right) = 0.698$), indicating that the model is relatively insensitive and robust when there is small uncertainty in the model parameters. Regarding the NGEV model, the analysis shows that the two future climate scenarios have a low effect on sensitivity. And, in both SSP126 and SSP585 scenarios, the model parameter $\theta_{21}$ stands out as the most sensitive, displaying significantly larger values of $\phi_{i} \left( 0 \right)$ and $\phi_{i} \left( 1 \right)$ compared to other parameters. Remarkably, $\theta_{21}$ exhibits low sensitivity ($\phi_{i} \left( 0 \right) = 0.247$ in SSP126, $\phi_{i} \left( 0 \right) = 0.242$ in SSP585) when the standard deviation is close to zero, indicating its insensitivity to variations within a small range. However, its sensitivity becomes significantly higher ($\phi_{i} \left( 1 \right) = 1.289$ in SSP126, $\phi_{i} \left( 1 \right) = 1.470$ in SSP585) near the posterior standard deviation, suggesting a more pronounced impact on the model output as the parameter deviates from its baseline value. Besides, this intriguingly indicates that the shape parameter in the NGEV model exhibits insensitivity ($\phi_{i} \left( 0 \right)$, $\phi_{i} \left( 1 \right)$ < 0.2).

Table 6 Summary of the One-At-A-Time sensitivity analysis based on the single-parameter deviation-based differential sensitivity indices (SDDSI) in small (SUS) and posterior (PUS) for the 100 year design floods, considering the design life of 2000–2100 and two representative future climate scenarios (SSP126 and SSP585);SDDSI_SUS index $\phi_{i} \left( 0 \right)$: 1st-order Taylor (near small parameter uncertainty); SDDSI_SUS index $\phi_{i} \left( 1 \right)$: posterior (near posterior parameter uncertainty); ' ' (low), '*' (moderate), '**' (severe) classify sensitivity indices as < 0.5, 0.5–1, and > 1, respectively

Table 7 presents a comparison of design flood values for the 10, 20, 50, and 100 year return periods obtained from the design flood models, including NGEV and SGEV, with 95% confidence intervals (CI). For the 100 year return period, the NGEV model produces the highest design value (8945 m³/s) under the SSP126 scenario. This surpasses the values from the SGEV model and the NGEV models under the SSP245, SSP370, SSP460, and SSP585 scenarios by 1.72%, 0.45%, 0.90%, 1.95%, and 3.28%, respectively. However, for the 10, 20, 50 year return periods, the SGEV model consistently yields the highest design values (4561, 5652, and 7310 m³/s); and the design values decrease sequentially across the SGEV models and the NGEV models within the SSP126, SSP245, SSP370, SSP460, and SSP585 scenarios. Additionally, under the SSP585 scenario, the NGEV models generate the lowest design values (3755, 5016, 7000, and 8661 m³/s) for the 10, 20, 50, and 100 year return periods. According to the last and second-to-last column of Table 7, in the sequence of the 100, 50, 20, and 10 year return periods, a consistent rise is observed in the percentage changes within the 95% confidence interval length estimations from the NGEV models compared to the SGEV model. Additionally, for each of the 100, 50, 20, and 10 year return periods, the SSP126, SSP245, SSP370, SSP460, and SSP585 scenarios produce similar 95% confidence interval length estimations.

Table 7 Comparison of flood design values for the 10, 20, 50, and 100 year return periods in a 2000–2100 design life scheme. NGEV, nonstationary GEV; SGEV, stationary GEV

Figure 6 displays the outcomes of entire-parameter sensitivity indices under the small and posterior uncertainty scenarios concerning the 10, 20, 50, and 100 year return periods within a design life framework spanning from 2000 to 2100. This analysis takes into account two representative future climate scenarios, namely SSP126 and SSP585. For both the SGEV and NGEV models under SSP126 and SSP585, all the values of EDDSI_SUS index $\phi_{\sum } \left( 0 \right)$—measuring the effects of entire-parameter uncertainty propagation under a small uncertainty scenario—are below 0.3, exhibiting a low sensitivity in the models. However, for the NGEV models with SSP126 and SSP585, the values of EDDSI_PUS index $\phi_{\sum } \left( 1 \right)$—measuring the effects of entire-parameter uncertainty propagation under a posterior uncertainty scenario is larger than 1.2. This suggests that under the posterior parameter uncertainty scenario, the NGEV models become sensitive to the model parameters for the 10, 20, 50, and 100 year return periods design values. Additionally, for the SGEV model, both EDDSI_SUS and EDDSI_PUS indices exhibit an increase with the 10, 20, 50, and 100 year return periods.

Fig. 6

Results of entire-parameter deviation-based differential sensitivity indices (EDDSI) in small (SUS) and posterior (PUS) uncertainty scenarios for the 10, 20, 50, and 100 year return periods in a 2000–2100 design life scheme considering two representative future climate scenarios (SSP126 and SSP585). NGEV, nonstationary GEV; SGEV, stationary GEV (fitted by observed data); CI, confidence intervals; EDDSI_SUS index $\phi_{\sum } \left( 0 \right)$: 1st-order Taylor (near small parameter uncertainty); EDDSI_PUS index $\phi_{\sum } \left( 1 \right)$: posterior (near posterior parameter uncertainty)

Figure 7 illustrates the results of the global sensitivity analysis near various parameter uncertainty scenarios for the 100 year return period in a 2000–2100 design life scheme, presenting output modulus deviation (a) and sensitivity index (b) values. In Fig. 7a, it can be observed that for all three models, the output modulus deviation increases gradually and closely follows the Taylor approximation when relative parameter uncertainties are small ($m_{\sum }^{{{\text{In}}}}$ < 0.6). However, when relative parameter uncertainties are larger ($m_{\sum }^{{{\text{In}}}}$ > 0.6), a more rapid increase in output modulus deviation is observed. This piecewise relationship corresponds to low model sensitivity for smaller uncertainties and increasing model sensitivity for larger uncertainties, as depicted in Fig. 7b. When performing model comparisons, it was observed that the NGEV models exhibit lower sensitivity than the SGEV model when relative parameter uncertainties are small ($m_{\sum }^{{{\text{In}}}}$ < 0.6). However, as the relative parameter uncertainties increase ($m_{\sum }^{{{\text{In}}}}$ > 0.6), the NGEV models demonstrate higher sensitivity than the SGEV model, and this difference becomes more significant with the increase in relative parameter uncertainties.

Fig. 7

Global sensitivity analysis of design flood models for the 100-year return period in a 2000–2100 design life scheme; output modulus deviation (a) and sensitivity index (b) values under input parameter uncertainties; NGEV, nonstationary GEV; SGEV, stationary GEV; note that 'output modulus deviation' involves dividing the output deviation by the posterior design flood mean, and 'input modulus deviation' produces the input parameter covariance by combining its custom value with the posterior parameter covariance (as shown in Eq. 7)

4.3 Discussion

The paramount findings of our study highlight that the NGEV model surpasses not only the SGEV model, but also nonstationary models based on alternative distributions (i.e., GEV distribution, Lognormal3, Pearson-III, and Weibull) in effectively fitting the flood series. In the comparison of design flood values (Table 7), significant differences (greater than 5%) were observed between the SGEV and the NGEV models under the SSP245, SSP370, SSP460, and SSP585 scenarios for the 10 and 20 year return periods. However, for the 50 and 100 year return periods, the differences between the SGEV and NGEV models were within 5%. In the OAT sensitivity analysis (Table 6), the GEV shape parameter in the SGEV model demonstrates the highest sensitivity. However, in the NGEV models, the shape parameter displays low sensitivity, as indicated by the small values of both SDDSI_SUS index $\phi_{i} \left( 0 \right)$ and the SDDSI_PUS index $\phi_{i} \left( 1 \right)$. Instead, the sensitivity shifts to the grassland area's slope, elucidating the fluctuations in the GEV scale parameter. In the global sensitivity analysis (Fig. 7) for the 100 year return period design flood, it was found that the NGEV models exhibit lower sensitivity compared to the SGEV model when the entire parameter uncertainty is relatively small, with an input modulus deviation less than 0.6. However, as the entire parameter uncertainty increases, with an input modulus deviation more than the critical value of 0.6, the NGEV models demonstrate higher sensitivity than the SGEV model, and this difference becomes more significant with the escalation of the entire parameter uncertainty.

The finding of the study that the nonstationary model yields lower design flood estimates and larger parameter uncertainty as compared to the stationary model aligns with the findings reported by Yan et al. (2017). However, it is worth noting that our study indicates a smaller discrepancy between the stationary and nonstationary models, particularly for the 100 year design flood. This reduced difference can be ascribed to variations in probability distribution selection, covariate selection, and nonstationary hydrological design methods. This underscores the presence of significant uncertainty associated with these factors. To address this challenge, previous studies have emphasized the importance of incorporating additional information, such as historical flood data and climate reconstruction information, into both stationary and nonstationary design processes (e.g., Hu et al. 2020, Xiong et al. 2020).

This study addresses existing gaps in our understanding of parameter sensitivity in nonstationary design flood models, contributing to the knowledge in robustness of design flood estimates under nonstationary conditions. The OAT analysis using the SDDSI indices has been instrumental in elucidating the importance of model parameters and sensitivity shifts for the design flood estimates under stationary and nonstationary conditions. The global sensitivity, employing the EDDSI indices, has yielded a critical value associated with the input modulus deviation with substantial significance as it serves as a metric for evaluating the robustness of a nonstationary model. The implication of this finding is significant; theoretically, when the critical value is close to or exceeds 1, it signals that the nonstationary model demonstrates a level of reliability comparable to that of the stationary model, concerning model parameter sensitivity under the posterior uncertainty scenario for inputs.

While our study has made substantial progress in understanding parameter sensitivity in nonstationary design flood models, it is crucial to recognize potential limitations. For simplicity, we have not delved into certain other sources of uncertainty. It is important to exercise caution in calculating design floods in a changing environment, considering these potential uncertainties. Specifically, hydrological designers should pay attention to the influence of probability distribution and covariate selection, as well as nonstationary hydrological design methods. These aspects merit further investigation in future research endeavors.

5 Conclusions

In this study, the deviation-based differential sensitivity indices encompassing both single-parameter and entire-parameter sensitivity indices based on differential analysis methods were defined to investigate the sensitive parameters and robustness of stationary and nonstationary design flood models (SGEV and NGEV models). The proposed methodology was applied in the Weihe basin considering various future climate and LUCC scenarios.

The study concludes that, comparing to stationary flood design model, nonstationary design model exhibits superior fitting performance while displaying heightened sensitivity to the specified uncertainty inputs—namely, the posterior uncertainty of model parameters in our case study. This underscores the need for ample hydrological data evidence to ensure the robustness of nonstationary design. Importantly, this sensitivity does not imply that nonstationary flood design is inherently inferior to stationary design; on the contrary, it allows us to discern potential hydrological risks resulting from changing environmental conditions by providing larger confidence intervals. The sensitivity indices introduced in this study is approved useful to assess the influence of parameter uncertainty on both stationary and nonstationary flood design.