Master equation model for solute transport in river basins: part II basin fluvial scale

Abstract

At basin scale the physical phenomenon of diffusion involves the intricate spreading and dispersion of substances within complex systems as networks of interconnected channels, streams, and land surfaces. Understanding this process is crucial for many purposes as management and conservation of water resources. We extend the model application of our previous work (Part I, Rizzello et al. in Stoch Environ Res Risk Assess 37:3807–3817, 2023) from channel to basin scale. We use conservation of mass and momentum to formulate and apply the Master Equation system at basin scale. The results on simulated events highlight the transition of the model from channel scale to basin scale.

1 Introduction

The assessment and analysis of water pollution from the physical and ecological perspectives has a significant importance.

Complex river systems are dynamic environments susceptible to pollution from various sources. The most common ones are chemical pollutants, which often originate from industrial discharges, agricultural runoff, urban storm-water, and improper waste disposal (Chatwin and Allen 1985; Duarte and Boaventura 2008; Deng and Jung 2009; Alley 2007; Altenburger et al. 2015; Novotny 1994). These pollutants include various chemical substances such as heavy metals (e.g., mercury, lead, cadmium), pesticides, fertilizers (ammonia, nitrogen and phosphorus compounds), industrial chemicals, pharmaceuticals, and petroleum hydrocarbons (Kakade et al. 2021; Boon and Raven 2012). Excessive nutrients like nitrogen and phosphorus, categorized also as nutrient pollutants, can lead to eutrophication, a process where rapid algal growth depletes oxygen levels, harming aquatic life (Strokal et al. 2019; Boon and Raven 2012).

Instead, from a macroscopic perspective, sediments from erosion, construction activities, and agricultural practices can enter rivers and cause turbidity, reducing light penetration and negatively impacting aquatic plants and animals. Suspended solids can also carry attached pollutants, making them potential carriers of chemical contaminants. At the basin scale, fast estimates of the damages on the water quality due to pollution could play essential role in establishing governmental regulations for environmental protection (Kachiashvili et al. 2007; Chatwin and Allen 1985; Duarte and Boaventura 2008).

Estimating pollution using physical models in rivers involves fundamental concepts of fluid mechanics, mass transport, and chemical interactions to simulate and predict the behavior, the dispersion of contaminants within the river system (Alley 2007; Altenburger et al. 2015; Novotny 1994). Capturing all the relevant processes, such as sediment transport, turbulence, and mixing, can be time-consuming and inadequate if an immediate decision is required; further simplifications may be necessary, leading to some level of uncertainty in the model results. Significant amount of data inputs as river geometry, flow characteristics, accurate boundary conditions and pollutant properties, are required. In case of unavailability or inconsistent data quality errors and uncertainty could affect the model (Kachiashvili et al. 2007; Strokal et al. 2019).

To address these limitations, it is essential to complement physical models with other approaches, such as stochastic methods, and field monitoring, to gain a more comprehensive understanding of pollutant behavior (Chatwin and Allen 1985; Duarte and Boaventura 2008). From this point of view, stochastic dispersion models in rivers are a type of mathematical model that incorporates randomness and uncertainty into the simulation of pollutant dispersion in natural water systems. Unlike deterministic models, which provide precise predictions based on known inputs and equations, stochastic models introduce probabilistic elements to account for the inherent variability and unpredictability of certain factors in river environments (King and Turner 2021; Raudkivi 2020).

Stochastic dispersion models are particularly useful when dealing with complex and uncertain systems, as they allow for the consideration of various sources of variability, such as fluctuating river flow rates, changing wind patterns, and varying pollutant release rates (Fernengel and Drossel 2022; Van Kampen 1992; Honerkamp 2012). These models are especially relevant in scenarios where the available data may be limited, or when dealing with long-term pollutant behavior (Wing et al. 2020; Kerachian and Karamouz 2007).

Combining different modeling techniques and data sources can help mitigate uncertainties and improve the accuracy of pollution assessments and management strategies (Wing et al. 2020; Kerachian and Karamouz 2007).

In the previous work (Part I) a numerical technique, computationally less expensive than the existing diffusive methods, was presented (Rizzello et al. 2023). The numerical model was applied at the channel scale with the aim of observing its applicability from a computational point of view, monitoring the first results with the purpose of extending the obtained results to a larger scale (De Bartolo et al. 2006, 2009a, 2022). As described in the previous work, this model is based on two essential physical conservation laws, the principle of mass conservation, represented by the Master Equations (MEs), and the principle of momentum conservation, condensed into the parameter $P_{ij}$ (Botter et al. 2011, 2010; Rodriguez-Iturbe et al. 2009; Rinaldo et al. 2018).

The MEs describe the time and spatial evolution of a complex system, combining the transition probabilities which bind the elements of this system for different states, where the new dynamics can arise (Fernengel and Drossel 2022; Van Kampen 1992; Honerkamp 2012). A particular example of a ME special case is the Fokker-Planck equation, describing the time evolution of continuous probability distribution (Keizer 1972; Van Kampen 1992; Gardiner et al. 1985).

The transition probability, $P_{ij}$, plays a noteworthy role in transport scales, particularly concerning river networks. Specifically, from a physical point of view, $P_{ij}$ represents the conservation of the momentum characterising the process in its evolution, while from a stochastic point of view, it takes into account uncertainties arising e.g. from limited spatial and temporal resolution, accuracy and availability of input data (Rodriguez-Iturbe et al. 2009; Rinaldo et al. 2018; Rizzello et al. 2023).

In relation to the events studied, new considerations have been made for $P_{ij}$ that can lead to possible reformulations to describe, for example, delays or accelerations of the dispersion phenomenon in complex river systems. The aim of this work is to highlight what are the elements of validation, applicability and limits of the basin-scale methodology with respect to the channel-scale. The analysis of the data provided by the USGS was performed and the same Master Equations were applied on a basin reach belonging to the Maumee River basin in Ohio (USA).

The results presented here are a continuation of the research conducted in Part I (Rizzello et al. 2023).

2 Methods

River networks are complex geomorphological systems. Understanding the scaling behavior of network structures is essential in describing numerous hydraulic and hydrological processes (De Bartolo et al. 2006, 2009a, 2022).

Existing dispersion models of river systems integrate hydrodynamic and water quality data to simulate how contaminants interact within the water. In this way, it is possible to estimate pollutant concentrations at different locations and times.

On the basis of a previous work Rizzello et al. (2023), the numerical method for solving the steady one-dimensional advection-dispersion problem for solute transport is extended at basin scale. The boundary conditions consist of multiple point-loading in the outer areas of the basin where pollutant measuring stations record events of interest.

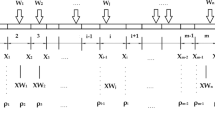
The proposed method starts with the definition of the basin of interest. When that has been identified, the channels of the complex river network are connected through a computational scheme of nodes and lines (arcs). The n channels of the system, with lengths $L_{1}, L_{2} \dots L_{n}$, are partitioned using a base length $\tilde{L}$ and identifying new m partitioned channels of the computational domain. The new pattern obtained has a number of arcs equal to m, where $m=\sum _{k=1}^n L_{k} \tilde{L}^{-1}$ while the number of nodes can be found through the relationships with physical geography by means of an ordering, for example the Horton-Strahler ordering (Strahler and Strahler 2013). The inter-lines defined connect internal nodes where the unknown concentrations are evaluated at subsequent time steps. As a first step, the flow parameters can be assumed to remain constant over time, t, although their spatial variations may be accepted. Therefore, each segment assumes parameters of velocity, dispersion coefficient, or transition probability that are line-constant with respect to time.

While this assumption may impose limitations during the initial stages of pollutant dispersion phenomena in rivers, it represents the minimum first starting condition from the available experimental data to define a global basin probability transition $P^{*}$. Indeed, when information regarding riverbed geometries, sections, and velocity scale measurements is unavailable, these assumptions can still yield initial approximation results. After defining a basin transition probability for the entire catchment area, the channel transition probabilities can be defined to get closer to the solution represented of the experimental data and calibrate the model. These transition probabilities can be constant over time, different from channel to channel or time-functions in order to define local delays or accelerations in the stretches of the complex network (Rizzello et al. 2023; Rodriguez-Iturbe et al. 2009; Rinaldo et al. 2018).

The results are computed starting from a specified time level with a known spatial concentration within the domain. The boundary source nodes, i.e., the terminal upstream nodes of the channels in which the event starts to happen, have specified solute concentration values that are either constant or possibly varying with time, t, and are used to generate the solution through evolution in time. The computed concentration values of the solute along the channel lengths of the basin channels may thus vary with time, although the flow velocities are assumed to be in a steady state in the various channels of the basin.

Specifically, the solute spatial concentration is obtained as a solution of a system of linear equations. These are the principle of mass conservation, expressed through the use of MEs, and the principle of momentum conservation, with the $P_{ij}$ formulation (Rizzello et al. 2023). Hence, the main objective of this work is to characterize the transition probabilities, $P_{ij}$, by a non-direct best fitting procedure. In the next section more details about the transition probabilities, $P_{ij}$ and mathematical formulations are provided.

2.1 Transition probabilities and mathematical formulation at the basin scale

As in the case of channel scale, at basin scale we look for the solution to the mono-dimensional equation system governing the longitudinal spread (dispersion) of the solute concentration in space and time (Benedini and Tsakiris 2013) in the basin. The n basin streams of lengths $L_{1}, L_{2} \dots L_{q} \dots L_{n-1}, L_{n}$ can be discretized, using m nodes and a fixed length $\tilde{L}$, in small stretches of length, $L_{q,ij}$, where i and j are the extreme-boundaries of each stretch and q is the index of the stream considered. The well-know local conservation mass equation as a ME in a discrete form (Rodriguez-Iturbe et al. 2009; Rinaldo et al. 2018; Rizzello et al. 2023) can be written as:

$$\begin{aligned} \rho _{i}(t_{k})=\rho _{i}(t_{k-1})+P_{q,ij}\rho _{j}(t_{k-1}) \end{aligned}$$

(1)

where $\rho _{i}$ and $\rho _{j}$ represent the discrete-time solute concentration in nodes i and j at time $t_{k}$, respectively. The parameter $P_{q,ij}$ denotes the transition probability associated with the reach $L_{q,ij}$. If we assume a steady flow along the channels, the real mass conservation over the time interval ($t_{i}$ to $t_{f}$) during which the phenomenon occurred is described at basin channel by following integral form:

$$\begin{aligned} \int _{t_{i}}^{t_{f}}dt\rho _{i}(t)v_{i}= \sum _{q=1}^{n} \int _{t_{i}+\Delta t_{q}}^{t_{f}+\Delta t_{q}} dt\rho _{q,j}(t)v_{q,j} \end{aligned}$$

(2)

where $t_{i}$, $t_{f}$ are the extremals of the time interval of the event occurring at the basin closure section (node i), $v_{i}$ is the velocity at node i and $\Delta t_{q}$ is the shift-time travel interval along the channel q, with velocity $v_{q,j}$, respect to the event occurred in the closure section.

If the velocity of each channel, $v_{q,j}$, does not deviate much from the mean velocity of the all basin channels, $\bar{v}=\frac{1}{n}\sum _{q=1}^{n} v_{q,j}\approx v_{i}$, it can be simplified in its integral form (2). These deviations from the mean velocity are taken into account by the transition probabilities, $P_{i,j}$, which influence the shape of the pollutant wave. After discretizing the basin domain channels in nodes and lines (arcs), the matrix formulation of equation (1) extended to the entire basin is (Rizzello et al. 2023):

$$\begin{aligned} \tilde{\varvec{\rho }}(t_{k})=\tilde{\varvec{\rho }}(t_{k-1}) +\tilde{\varvec{P_{u}}}\tilde{\varvec{\rho _{u}}}(t_{k-1}) -\tilde{\varvec{P_{d}}}\tilde{\varvec{\rho _{d}}}(t_{k-1}) \end{aligned}$$

(3)

in which $\tilde{\varvec{\rho }}(t_{k})$, $\tilde{\varvec{\rho }}(t_{k-1})$ are the solute concentration vectors at the time $t_{k}$ and $t_{k-1}$, and $\tilde{\varvec{\rho _{u}}}(t_{k-1})$, $\tilde{\varvec{\rho _{d}}}(t_{k-1})$ are the solute concentrations at the upper and lower nodes at the time $t_{k-1}$, respectively.

Therefore, $\tilde{\varvec{P_{u}}}$, $\tilde{\varvec{P_{d}}}$ are the transition probability matrices estimated for each local transition. In the case of the minimal structure and one junction node, a maximum of four nodes and three arcs may be included in each local transition. In other cases, usually three nodes and two arcs are sufficient. The case of local transition with a number of nodes greater than four (Rizzello et al. 2023; Strahler and Strahler 2013) is quite rare.

The procedure is repeated over discrete time steps, until a specified final time is reached. The description of the transition probabilities $P_{i,j}$ between nodes i and j can be made from the definition of the transition probability of the entire basin $P^{*}$ found in the first instance. From a physical point of view $P_{i,j}$ represents the equation of conservation of momentum, while from a stochastic model point of view it can express the probability of the solute passing from one point to another in the complex river system.

We can therefore express the transition probabilities of the river network of n channels (before the discretization on the basis of $\tilde{L}$ occurs) as $P_{ij}=c_{ij}P^{*}$ with $0\le P_{ij}\le 1$, where the coefficients $c_{ij}$ allow to express the behavior of the single channel with respect to the behavior of the entire basin. When defining a localised delay of the phenomenon at a certain instant of time $t'$(this may be the case for source nodes), the transition probability $P_{ij}$ can be expressed as a time-function:

$$\begin{aligned} P_{ij}(t)=c_{ij}P^{*}H(t-t') \end{aligned}$$

(4)

where $H(t-t')$ is the shifted Heaviside step function defined as follows:

$$\begin{aligned} H(t-t')= {\left\{ \begin{array}{ll} 0, &{} \text {if } t < t' \\ 1, &{} \text {if } t \ge t' \end{array}\right. } \end{aligned}$$

(5)

where $t'$ is the time shift. Thus, if the dispersion phenomenon is intermittent, the associated function is a trigonometric function, if it is destined to expire over time with a delay, the time function is decreasing over time, in the general case it is a time-dependent function $P_{ij}(t)$. Some results of this approach involving all the considerations made for the transition probabilities are shown in the next section.

2.2 Study area and sampling dataset localization

The study area that we considered is the Maumee River Basin, also known as the Maumee Watershed, a significant river system located in the northwestern part of Ohio in the United States. The basin is named after the Maumee River, which is the primary watercourse flowing through the region; it is one of the largest watersheds in the Great Lakes region and drains a primarily rural farming region in the watershed of Lake Erie (Martin and Pederson 2022; Stothers and Tucker 2006). The topography of the basin is characterized by flat plains, fertile farmland, and extensive wetlands, therefore it is difficult to find motion traps. The basin includes several tributaries to form the domain area, in particular the upper and lower part of Maumee River, and other tributaries named Tiffin, Auglaize, Blanchlard and Flatrocks. In Fig. 1 it is possible to observe the geographical framework of the basin under consideration, and the representation of the channels included.

Fig. 1

Geographic maps of the Maumee Basin. On the left the geographical framework (41$^\circ$04’58" N 85$^\circ$07’56" W), on the right the complex river network with water quality gauging stations represented as red points and junction points between channels in white

Several pollutant measurement stations are located in the area, which have made it possible to create a database of pollutant concentrations recorded over time. The data on which the model is based were collected by the USGS (see https://www.usgs.gov). Agricultural practices contribute to pollution, especially nitrogen and phosphorus loading in the river and leading to water quality problems. Furthermore soil erosion from agricultural fields and construction sites contributes to sedimentation in the river. Excess sediment can cloud the water, reducing light penetration, and adversely affecting aquatic plants and animals. Indeed, sediment can also transport pollutants, such as pesticides and heavy metals, impacting water quality. Taking into account this environmental condition, the analysis considers various solutes, such as filtered and unfiltered ammonia, phosphorus, nitrate plus nitrite, ammonia plus organic nitrogen, orthophosphates, and suspended sediments. Some of the results obtained from this analysis are presented in the following paragraph.

3 Results and discussion

In order to define the computing domain, the channel map of Maumee Basin in Fig. 1 is represented as a graph with points and arcs in scheme a) of Fig. 2. Considering a first-order scheme in discrete time, two simulation cases are reported below. The first case that we analyzed is concerned with the phosphorus solute P. The second case focuses on the suspended sediments S.

Fig. 2

Domain discretization configurations considered in the computational analysis. Scheme (a) is a graphical representation of the channels included in the basin from which, on the basis of the channel lengths, the domain is discretized by fixing a base length $\tilde{L}$, obtaining the scheme (b)

Considering Fig. 2, starting from scheme (a) we use a length $\tilde{L}$ in order to discretize the basin domain. Dividing the channel lengths that form the hydrographic network by $\tilde{L}$ leads to the second scheme, (b). Furthermore, as in the case of channel scale, a fictitious node is added before each source node also for the basin scale, and similarly a fictitious outlet node is added after the basin closure node (Rizzello et al. 2023). Hence, the scheme used for both simulated cases is the scheme b) shown in Fig. 2 and $\tilde{L}$ was set 5 km. The data, provided by the USGS, for the first case range from mid-November to mid-December 2016, while for the second case they refer to the entire month of February 2017.

Table 1 Summary results for phosphorus solute P

For the phosphorus pollutant P, we analyze the concentration peaks of source nodes (in this case, source nodes are 4, 7, 12, 14, 16, 17) and closure node is 1. Results are shown in Table (1). In particular the trend of nodes 16 and 17 is very low compared to the other source nodes and could also be ignored in the computation.

The MEs system is solved by means of a Computer Algebra System, Reduce (Hearn 2008), which is free software available at Reduce project page (2023). We wrote a program which iteratively updates the values of the solute concentration at each time $t_k$ on each node. The graph is represented by a list which is traversed by a recursive algorithm, which is easy to design using Reduce Lisp system. It is remarkable that the software scales well and delivers results in few minutes even with a very high number of nodes (e.g., several thousands).

After solving the MEs system, the basin transition probability $P^{*}$ was found to be equal to 0.63. In this case, but also in the subsequent case reported, the optimal $P^{*}$ value is obtained in an iterative manner by finding a simulated concentration curve that comes closest to the experimental one and thus minimising the errors between the concentration peaks and the respective time lags, as in Part I (Rizzello et al. 2023).

Fig. 3

Time development of phosporous concentrations $\rho _{P}$ using scheme (b). The peaks and their respective times are highlighted

The relative error defined as $\frac{|\rho _{N}-\rho _{N'} |}{\rho _{N}}$ (where N is the generic node) is evaluated for the considered nodes. Thus, for the outlet node 1 it is 5.7 %, while for the source node 7 is 1.9 %. In addition, there is a time-lag of 0.05 days (about 1 h) for source nodes 7 and 12 and a a time-lag of 0.1 days (about 2 h) for junction node 8. The transition probability $P_{7,5}$ was adjusted to 0.30, instead $P_{12,11}$ was adjusted to 0.35 (result are similar to the cases of Part I at channel scale) (Rizzello et al. 2023).

Similar behaviours can be found in other frameworks and investigations (Rodriguez-Iturbe et al. 2009; Rinaldo et al. 2018). At the basin scale, this makes it possible to estimate the pollutant wave, at intermediate nodes. The trend of the concentrations is shown in Fig. 3.

Table 2 Summary results for suspended sediments S ($\times 10^{3}$)

In the case of suspended sediments S, two peak events occurred leading to increased calculation complexity (see Fig. 4).

Fig. 4

Time development of suspended sediments concentrations $\rho _{S}$ using scheme b). The peaks and their respective times are highlighted

In this case the source nodes are 4, 12, 14, 16 the closure node is the same, 1. The results of our analysis are shown in Table (2). The basin transition probability $P^{*}$ was found equal to 0.65. For the first peak, the percentage error for outlet node 1 is 2.1 %, while on sources node 4 and 16 it is about 3.7 % and 3.5 % respectively. Instead, for the second peak it is 7.3 % for outlet node 1 and for nodes 14 and 16 it is about 2.6 % 9.1 and % respectively. In addition, there is a time-lag of 0.4 days, 0.1 days (about 5 h and 2 h) and 0.3 day (about 4 h) for nodes 1, 8 and 16 respectively. In this case, the transition probability $P_{16,15}$ was adjusted to 0.50, instead $P_{4,3}$ was adjusted to 0.35 respectively. The source node 12 had a delay in its boundary condition, thus it was added was added by the condition $P_{12,11}= 0.81H(t-t_{1})$ where $t_{1}=0.5$ days. Same consideration for node 14 with $P_{14,13}= 0.65H(t-t_{2})$ where $t_{1}=0.7$ days.

At the basin scale, this makes it possible to estimate concentrations of the pollutant wave, at intermediate nodes (Rizzello et al. 2023). On the basis of the results obtained it is important to note that the model exhibits a time-lag in dispersion concerning the peaks, which is approximately 1–5 h within the complete time span of the dispersion phenomenon (about 15–20 days). Furthermore, increasing the complexity and number of internal nodes may introduce errors in peak concentration predictions due to approximation errors that accumulate in each computational operation.

The model provides valuable indications of how variables of interest are spread; it is also important to recognize its limitations. According to (Huang et al. 2022; Ito 1992; Ajami et al. 2007; Van Kampen 1992; Hervouet 2007), dispersion models are based on a set of assumptions and mathematical representations of physical processes, which can introduce uncertainties and errors into the predictions. The accuracy of these models depends on high-quality data inputs, such as river flows and water quality parameters, which may not always be available or accurate (Ito 1992; Hervouet 2007). This type of model often requires a significant amount of data for parameterization and calibration, especially considering complex river systems. To achieve the best calibration of the model at basin scale, all measurement stations available from the USGS were used. Reducing the number of available stations used, obviously errors increase in simulations, often leading to incorrect transport estimates. In particular, the intermediate stations allow to check in their position whether or not any event has modified the transport started upstream. Furthermore, it is important to consider the process type when using these models to make decisions, including field measurements and observational data, to validate the results: the process considered usually is a normal-diffusive type (Rizzello et al. 2023; De Bartolo et al. 2022, 2009a, b).

Despite these limitations, the Master Equation model is a valuable tool for studying pollutant/sediment transport in rivers. When used appropriately and in conjunction with other modeling approaches and field data, it can offer valuable insights into pollutant behavior and aid in developing effective pollution management strategies for reducing the impact on the environment.

Basing on the results obtained, it would be interesting to investigate and compare the hydrodispersive behaviour on complex hydrographic networks characterized by a different geomorphology, more extreme events and a larger number of nodes and channels. That will be the subject of future works.

4 Conclusions

In this work the dispersion analysis of some contaminants within the catchment area of the Maumee River’s Basin in the Ohio State (USA) was addressed at basin scale. Specifically, a set of data concerning phosphorus and suspended sediments were analyzed, on the basis of data provided by the American USGS service. The time period concerned the months November-December 2016 for phosphorus, and February 2017 for suspended sediments. The analysis on the geomorphological basin scale concerned a bain area of approximately 13,000 km$^{2}$.

The hydrodynamic dispersion model used for this purpose has been derived from a particular class of dynamical differential system, derived from the Fokker-Planck equations, called Master Equations, MEs. The MEs model here proposed, according to (Rodriguez-Iturbe et al. 2009; Rinaldo et al. 2018), based on mass and momentum conservation principles, has been implemented on an equivalent graph representing the basin domain. The MEs proposed is able to deal with large amounts of data and intensive computational processing.

The model in its peculiar characteristics has offered interesting results in terms of peak time and maximum solute concentration. It allows a reconnaissance of the dispersion phenomenon at the channel scale to be carried out quickly with an interesting low percentage error (0.1–9 %) and time-lag (1–7 h). Moreover, according to the scientific literature (Rodriguez-Iturbe et al. 2009; Rinaldo et al. 2018; Botter et al. 2010, 2011; Rodriguez-Iturbe and Rinaldo 2001), functional validity was given to the transition probabilities, $P_{ij}$, considering real cases.

The extension of the method to the basin should imply a variation to the definition of the transition probabilities $P_{i,j}$ in order to take into account the possible local delays or accelerations occurring at the channel scale and thus the different velocities. Consequently, the transition probabilities $P_{i,j}$ could be time-dependent. Furthermore, the method makes it possible to carry out estimations of pollutant dispersion in intermediate points of basin-scale.

Based on these encouraging results obtained, in order to make comparisons in results, the model proposed here can be further applied to a different basin which can take into account a greater complexity of the river network, for example large Hortonian structures characterized by a relevant number of internal and external nodes. Indeed, expanding the application to a different basin with diverse characteristics will enhance our understanding of pollutant transport processes in various hydrographic settings. It will also allow for the exploration of potential differences and similarities between river networks, providing valuable information for water quality management and environmental protection strategies on a broader scale. Furthermore, the model can be applied to compare the seasonal events of one or more years with the aim of identifying any dependencies in the transport phenomenon such as those of the seasonal average velocity or the total mass of water flowed.

In any case, calibrating and validating the dispersion model on another basin is a crucial step to ensure the reliability and applicability. High-quality data from field measurements, water quality monitoring, and pollutant concentration measurements are essential for validating the performance of the model. In the case that the model is applied to events that do not satisfy the previously defined hypotheses, it is necessary to modify the equations by introducing appropriate variables that allow to obtain the correct mass balance in the various nodes and momentum conservation along the arches. The most appropriate alternative remains that of combining different modeling techniques and data sources to mitigate uncertainties and improve the accuracy of pollution assessments and management strategies. Additionally, ongoing research and advancements in data collection techniques and computational capabilities may help overcome some of the limitations of physical models.

In conclusions, these processes help build confidence in the model predictions and allow for better decision-making in water resource management and pollution control strategies.