1 Introduction

Large uncertainty is involved in the characterization of different environmental actions, such as snow, wind and temperature and their contributions to the structural response as well. Wind load is one of the most significant actions influencing the integrity of several structural types, especially those at exposed sites such as bridges, wind turbines and telecommunication masts. Compromise has to be found in the structural design process between safety considerations and extra costs of overdesign. Design formulae of structural design codes or standards, such as the Eurocodes, are based on the semi-probabilistic method using partial safety factors on both the resistance and action sides where design values should be conservative estimates. Some studies (Baravalle and Köhler 2018; Vrouwenvelder and Scholten 2010) pointed out that applying one single partial safety factor γQ = 1.50 for all unfavourable environmental variable actions may not be reasonable since these environmental actions, such as wind, snow and temperature, originate from different physical phenomena and are represented by different models. Moreover, it may underestimate the annual exceedance for a desired probability resulting in lower reliability than the Eurocode target. On the other hand, according to the findings of previous research (Georgakis et al. 2009; Nielsen 2019) and our observations, extreme storms caused significantly less structural stress or even damage than expected. Therefore, smaller utilization of telecommunication lattice towers can be verified in several cases with accurate modelling of wind load; thus, more antennae can be installed on the structure. Hence, the following questions are sought to be answered: What causes the discrepancy between the stresses calculated according to the EN 1993-3-1, and the measured values? Which parameter of the model can be adjusted to improve the alignment of the model with the real behaviour?

Advancements in computer technology have paved the way for alternative design procedures that utilize fully probabilistic approaches and simulation techniques. The application of performance-based wind engineering (PBWE) methodology, which considers all available information, has the potential to reduce uncertainties and prevent excessive overdesign in structures. The PBWE effectively addresses various wind engineering problems and has gained widespread acceptance. The general framework of PBWE was published first in 2004 (Paulotto et al. 2004). Since then, several studies (Chuang and Spence 2017; Huang et al. 2012; Kroetz et al. 2017; Paulotto et al. 2004; Petrini and Ciampoli 2012) have illustrated the applicability and improvements of this methodology, while only few studies focused especially on lattice towers (Depina et al. 2021; Tessari et al. 2017). In the present paper, finite element model (FEM) based PBWE assessment of a telecommunication steel lattice tower located in Central Hungary is presented. Reliability analysis and FEM-based investigation can be conducted to assess risk and determine damage grades in situations where the use of partial safety factors from Eurocode standards is not applicable or efficient, such as in the case of corroded members (Kövesdi et al. 2022). Currently under development, the new standard prEN 1993-1-14 (2020) aims to establish design rules for the FEM-based design of steel structures. The integration of site-specific wind loading models into the standardized FEM-based design will prove to be a powerful tool for design engineers.

In the probabilistic modelling of structural performance, the consideration of the parameter estimation uncertainty (PEU) in extreme wind speed models is often overlooked. The PEU stems from the uncertainty associated with model parameters, which cannot be precisely determined using statistical methods. Nevertheless, several studies have demonstrated the substantial impact of PEU on the modelling of extreme environmental actions (Baravalle and Köhler 2018; Bakker et al. 2021; Rózsás and Sýkora 2016). In this study, the assessed parameters of the extreme wind speed model are treated as stochastic variables, allowing for the incorporation of PEU in the modelling of structural performance. Nevertheless, the stochastic modelling of the fundamental basic wind velocity (vb,0) is an open issue, even now. The techniques available for determining the characteristic wind speed for a 50-year return period were reviewed and summarized in the works of Cooley (2016) and Palutikof et al. (1999). The traditional method to derive extreme wind speeds is the annual maximum (AM) approach when yearly maxima are analysed. It has a great advantage that solely few decisions are required during the calculation of the distribution parameters. Nevertheless, the main drawback is the considerable data reduction, i.e., a significant amount of information contained in the weather data is not taken into account in the analysis. Therefore, wind measurement must be long, at least 10–20 extremes should be used to determine reliable results (Cook 1985). One of the main developed techniques to overcome this limitation and enhance efficiency, particularly when dealing with a relatively shorter dataset, is the peaks-over-threshold (POT) method (Baravalle and Köhler 2018; Cook 1982), which is applied in this study.

Furthermore, the paper presents the Bayesian updating of wind velocity model parameters, which combines information from measurements collected at the site of the tower over a relatively short duration with a more extensive dataset from measurement locations across the country provided by the Hungarian Meteorological Service (HMS). In the simulation study conducted by Fawcett and Green (2018), it was found that the posterior predictive return level yields more precise estimates of exceedance probabilities compared to estimative summaries of posteriors, such as the mean, mode, or 95% credible intervals. Moreover, even if an incorrect assumption regarding the temporal or spatial dependence of samples is made while using all excesses as in the study of Fawcett and Walshaw (2016), the posterior predictive return level still provides exceedance probabilities that align more closely with expectations compared to other estimative summaries. In addition, considering practitioners’ preference for a single point summary that adequately accounts for estimation uncertainty, the adoption of the posterior predictive return level within the framework is deemed the optimal summary for practitioners.

Another significant source of uncertainty in the wind-induced response of structures stems from the uncertain interaction phenomenon and its characterization, specifically the drag coefficient. Investigations (Georgakis et al. 2009; Nielsen 2019; Calotescu et al. 2021) including wind-tunnel test on full-scale sections of a lattice mast configurations have shown that the drag coefficients of a mast section under smooth flow condition, or for low velocities, are underestimated, while the drag coefficients corresponding to high wind velocity and turbulent flow conditions are overestimated in EN 1993-3-1 (2006). Hence, drag coefficients derived from scaled tests in the UK in the 70’s, might need to be re-examined and further full-scale wind tunnel tests and computational fluid dynamics simulations are required. On the other hand, Balczó et al. (2006) performed wind tunnel tests and computational fluid dynamics (CFD) simulations on a mast section that is being investigated in the current paper. In comparison to the wind force calculated according to EN 1993-3-1, Balczó et al. observed a lower wind force. This finding also indicates that the formulae in EN 1993-3-1 tend to overestimate the drag coefficient of the mast section at high wind velocities and turbulence intensities.

The manuscript is structured as follows: in Sect. 2, the description of the investigated mast is provided. In Sect. 3, the PBWE methodology, including the wind velocity, aerodynamic, and finite element model, along with the probabilistic analysis, is described. The results obtained from measurements and the probabilistic finite element model, as well as the corresponding discussion, are presented in Sect. 4. Finally, conclusions of the manuscript are drawn in Sect. 5.

2 Case study

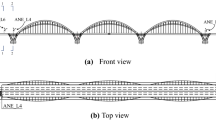
The research paper introduces the PBWE approach in a case study dealing with a freestanding telecommunication lattice tower in the suburban area of Sződliget, Hungary. The lattice mast has a total height of 49.70 m and triangular cross-section. Width of the structures varies along the vertical direction, the maximum width at the bottom is 4.80 m, while it is reduced to 3.00 m at the top. Both the chord members and bracings have circular hollow sections with various diameter (76–159 mm) and wall thickness (2.9–12.5 mm); structural steel grade is S235. Cross-sectional dimensions and section types are presented in detail in Sect. 4. Main dimensions shown in Fig. 1a. The tower is equipped with linear ancillaries, i.e., with ladder and cables, and a total of 23 sector and microwave antennae are installed. Details of the antennae are summarized in Table 7 in the “Appendix”. Antenna numbering, section numbering (divisions shown in Fig. 1a for wind load calculation), notations for face numbering (shown in Fig. 1b), antenna type and total antenna area Aant are listed. For sector antennae, multiplication factors of 1.1 and 1.5 are used for taking the projected area of anchorage ancillaries into account as a conservative assumption. Force coefficient cf,A,0 for the antenna appropriate to the wind direction and wind speed is obtained from wind tunnel tests provided by the manufacturer. Minimum and maximum wind directions αmin and αmax, respectively are listed in the table where each antenna is taken into consideration in the wind load calculation. Vertical position Z of each antenna is summarized as well. Wind and strain measurements are performed on the telecommunication mast; notations for wind direction α and chords with O159 × 13 tubular cross section (S1, S2 and S3) are shown in Fig. 1b.

Fig. 1
figure 1

a Main dimensions of the analysed telecommunication mast in Sződliget, Hungary; b notations of wind direction α and chords (S1, S2 and S3); c detail of a chord with sensors

Full size image

The tower is equipped with cup anemometer wind speed sensors, and strain gauges to measure its response to wind loads. The wind speed was measured for the period between August 2011 and March 2015 with a sampling rate of 0.9 s at the middle and the top of the lattice tower, i.e., 25 and 49.70 m above ground level. The anemometers used for measurement have a measuring range of 1–67 m/s for wind velocity and 0–360° for wind direction. The accuracy of the measurements is within 5% for wind velocity and ± 7° for wind direction. The resolution of anemometers is 0.1 m/s for wind velocity and 1° for wind direction. Since wind speed sensors are installed directly on the chord member of the mast at the height of 25 m (Fig. 1c), the data undergoes filtering to exclude wind directions ranging from 60° to 270° for the calculation of the roughness length. Additionally, filtering is performed to discard invalid data, such as those affected by icing (minimum temperature of 1 °C) or incorrect data recording, such as timeouts, read errors, memory write errors, out-of-memory events resulting in data loss, and warm-up errors. Full-bridge strain gauges, with temperature compensation, are installed on chord members at 4.8 m above ground level.

3 Approach

3.1 PBWE methodology

Advanced investigation on quantitative assessment of structural performance is carried out based on the PBWE framework shown in Fig. 2. In wind engineering, design variables can be derived from the wind by following a chain of cause and effect. This PBWE event chain is similar to Davenport’s chain (Davenport 1983); steps of the approach are the following:

  1. 1.

    Characterizing the wind field and its associated uncertainty is essential in modelling for wind engineering. Key parameters which describe sufficiently and efficiently the climate wind hazard should be chosen as intensity measure parameters (IM), e.g., wind velocity, wind direction, turbulence intensity. In this analysis, the uncertain relation between the mean and short-term fluctuation of wind speed is taken into account through the exposure factor ce which is the product of the gust cg and roughness factor cr. Hence, these two factors are treated as random variables in this study. The roughness factor cr describes the variation of the mean velocity pressure with height above ground and terrain roughness as a function of the reference velocity pressure. The gust factor cg for velocity pressure represents the ratio of the peak velocity pressure to the mean velocity pressure of the wind.

  2. 2.

    Mechanical and material properties of the structure of interest, whose uncertainty may contribute significantly to the structural performance, should be considered as stochastic variable in structural parameters (SP). The IM and SP parameters are assumed to be independent and not correlated.

  3. 3.

    The interaction phenomenon between the environment and the structure is modelled in probabilistic terms. Quasistatic wind loads are applied on the structure accordin to EN 1991-1-4. The force coefficient is chosen as interaction parameters (IP), since it is affected by significant uncertainty.

  4. 4.

    The analysis of structural response is carried out. In order to perform the probabilistic modelling, relevant engineering demand parameter (EDP) should be defined, e.g., deformation, acceleration, load amplification factor, etc. In the current research, an advanced finite element model is developed to assess the Probability Density Function (PDF) of the structural response.

  5. 5.

    Damage measure parameters (DM) should be also defined by one or combination of more EDPs to quantify the structural damage, i.e., unacceptable performance of the structure. Relevant EDP and DM parameters can be identified based on the type of the considered problem. Typical DMs are associated with collapse or with other similar forms of structural failure or correspond to conditions beyond which specified service requirements are no longer fulfilled. Former one is low- and the latter one is highperformance level, respectively.

  6. 6.

    The intended structural performances and consequence of damage are quantified through decision variables (DV). As mentioned above, low- and high- performance level should be distinguished, i.e., the ultimate limit state (ULS) and the serviceability limit state (SLS), respectively. Comprehensive and advanced model shall include loss analysis where decisional strategy is developed in order to minimalize the total risk or maximizing the defined utilization taking the whole lifetime into account. For the reason of ethical and practical difficulties of considering the economic losses or losses of lives, the assessment is simplified to the fulfillment of a limit state; cost analysis is not perfomed in the current study.

Fig. 2
figure 2

Framework of performance-based wind engineering

Full size image

Detailed description of selected stochastic variables can be found in Sect. 4.2. The structural risk is defined as the probability of a relevant decision variable exceeding a threshold level dv, and can be expressed with a complementary cumulative distribution function (CCDF) in Eq. 1:

$$\begin{aligned}&G\text{(dv)}\\&=P\left(DV>dv\right)=\int \int \int \int \int G\left(DV| DM\right)f\left(DM| EDP\right)f\left(EDP| IM,IP,SP\right)\\& \quad \cdot f\left( IP|IM,SP\right)f\left( IM\right)f\left(SP\right) dDM dEDP dIM dIP dSP\end{aligned}$$
(1)

Since loss analysis are not carried out, and the chosen EDP is assumed as the measure of the structural damage (EDP = DM), furthermore, the limit state is quantified in terms of EDP, Eq. 1 is simplified to the following equation:

$$G\text{(EDP)}=\int \int \int G\left(EDP| IM,IP,SP\right)f\left( IP|IM,SP\right)f\left( IM\right)f\left(SP\right) dIM dIP dSP$$
(2)

The probabilistic analysis is performed, and Eq. 2 is assessed using Monte Carlo simulation with random Latin hypercube sampling. Quadratic response surfaces are fitted for output variables, such as the rotation of the top of the mast for SLS, while load amplification factor αULS is used for ULS for response surface fitting. Monte Carlo simulations, with N = 106 simulation loops, are performed on the derived response surfaces to gain the distribution functions of EDPs and the probabilities of exceeding the targeted limit value. The flowchart of the proposed analysing framework is depicted in Fig. 4, where D denotes the data, σi and µi represent the scale and location parameters of the distributions of interest.

3.2 Model of wind velocity

The basis of wind loading is the value of fundamental basic wind velocity vb,0. It is defined as the characteristic value corresponding to the 0.98 quantile, which is equivalent to a mean return period of 50 years of the annual extreme value distribution of 10-min mean wind velocities at 10 m above ground of terrain category II, irrespective of wind direction (EN 1991-1-4 2005). According to the classical extreme value theory (Fisher and Tippett 1928; Gnedenko 1943), the distribution of extreme events has an asymptotic limit, now universally known as the generalized extreme value (GEV) distribution with shape ξ, scale σ and location \(\mu\) parameters (Eq. 3).

$$F_{{\xi ,\sigma ,\mu }} \left( x \right) = \left\{ {\begin{array}{*{20}l} {exp\left( { - \left( {1 + \frac{{\xi \left( {x - \mu } \right)}}{\sigma }} \right)^{{ - \frac{1}{\xi }}} } \right)} & {for\;\xi \ne 0} \\ {exp\left( { - exp\left( { - \frac{{\left( {x - \mu } \right)}}{\sigma }} \right)} \right)} & {for\;\;\xi = 0,} \\ \end{array} } \right.$$
(3)

Three types of the GEV family can be distinguished based on the shape parameter ξ value, i.e., Gumbel (ξ = 0), Fréchet (ξ > 0), and Weibull (ξ < 0), also known as type I, II, and III extreme value distributions, respectively. The Probabilistic Model Code (Joint Committee on Structural Safety 2001) recommends the use of the Weibull distribution to represent vb,0 in Europe. While the Gumbel distribution predicts unlimited wind velocity as the return period increases, the Weibull distribution may be more appropriate for modelling extreme wind speeds based on geophysical reasons (Cook and Harris 2001; Holmes and Moriarty 1999, 2001). However, due to the limited amount of available data, the estimated shape parameter of Weibull distribution may be subject to high statistical uncertainty, potentially leading to unreasonable Weibull parameters and predictions for extreme wind velocities (Baravalle and Köhler 2018). Consequently, in Hungary, the value of the fundamental basic wind velocity has been conservatively determined in the National Annex, employing the Gumbel distribution. For this reason, the Gumbel distribution is adopted in this study to model the extreme wind velocity. In this article, the POT approach with an automatic threshold selection method (Thompson et al. 2009) is implemented to determine parameters of the PDF of the wind speed at Sződliget, due to the relatively short length of available measurement data series. Furthermore, in line with European Union directives, the HMS will make its observation and measurement data (from 2002 onwards) freely available for use through an open data server (https://odp.met.hu/) from 1 to 2021. In this way, the information from Sződliget will be enhanced by incorporating measurement data series from various locations across the country. Alternatively, the possibility of augmenting the information from Sződliget with wind data obtained from the nearest weather station, Penc, is being considered (Fig. 3). For data analysis, including fitting probability distributions to data and conducting hypothesis tests, the MATLAB (R2022a) software is employed, the fitting of parameters for different distributions is performed using maximum likelihood estimation.

Fig. 3
figure 3

The flowchart of the proposed analysing framework

Full size image

The wind velocity data points, averaged over a 10-min interval, are extracted from the wind speed record. The logarithmic wind velocity profile is then employed to estimate the wind velocity at a height of 10 m:

$$v\left(z\right)=\frac{{u}^{*}}{0.4}ln\left(\frac{z}{{z}_{0}}\right){v}_{0}$$
(4)

where u* is the friction velocity, z is the height of interest, z0 is the roughness length, \({v}_{0}\) is the basic wind velocity. Emphasizing the importance, it should be noted that wind information, such as basic wind speed, wind profile, terrain conditions, turbulence intensity, etc., obtained from a standard may frequently deviate from the actual conditions observed at the site. This discrepancy can introduce sources of epistemic or model/load uncertainty when assessing the effects of wind loading on structures. The roughness length is determined based on the measured wind velocities at heights of 25 and 50 m utilizing the logarithmic profile for wind speed averages greater than 10 m/s, where the averaging period is 10 min. The wind speed threshold of 10 m/s corresponds to a height of 25 m. Neutral atmosphere is assumed for simplification, and this model works quite well at higher wind speeds according to experiments (Landberg 2015).

The POT method is based on a conditional distribution. The Generalized Pareto Distribution (GPD) is used to model the behaviour of the wind speed exceedances over the specified threshold (Cook and Harris 2001; Holmes and Moriarty 1999, 2001; Pickands III 1975; Kang and Song 2017). The Cumulative Distribution Function (CDF) of GPD:

$${F}_{{\xi }_{1},{\sigma }_{1},{\mu }_{1}}\left(x\right)=\text{P}\left\{X-{\mu }_{1}\le x|X>{\mu }_{1}\right\}=\left\{\begin{array}{c}1-{\left(1+\frac{{\xi }_{1}\left(x-{\mu }_{1}\right)}{{\sigma }_{1}}\right)}^{-\frac{1}{{\xi }_{1}}}, \text{f}\text{o}\text{r} {\xi }_{1}\ne 0,\\ 1-\text{e}\text{x}\text{p}\left(-\frac{x-{\mu }_{1}}{{\sigma }_{1}}\right), \text{f}\text{o}\text{r} {\xi }_{1}=0,\end{array}\right.$$
(5)

where ξ1, σ1 and \(\mu\)1 are the shape, scale and location parameters, respectively. The location parameter \(\mu\)1 is the selected threshold u (u = \(\mu\)1). The shape parameter ξ1 of the GPD is the same as for the GEV distribution (Pickands III 1975). As discussed previously, the value of the fundamental basic wind velocity has been conservatively determined by setting the parameter ξ1 to 0.

The selection of the threshold and a minimum separation distance between extremes have strong impact on the result, and it is a compromise between bias and variance. While choosing a lower threshold can reduce variance, it may also bias the estimation if it is not a true extreme in an epoch. However, the bias decreases and the variance increase with higher threshold. Procedures of threshold selection on visual basis are widely used, e.g., mean excess plot or mean residual life plot, which require the subjective interpretation of plots. Therefore, a pragmatic automated, simple and computationally inexpensive threshold selection technique proposed by Thompson et al. (2009), described in Eqs. 6–7, is applied to reduce the associated uncertainty of threshold selection. According to the recommendations in Thompson et al. (2009), suitable values of equally spaced candidate thresholds uj should be chosen for the automated threshold selection between the median and the 98% quantile of the dataset, unless fewer than 100 values exceed this value, in which case the upper bound should be set to the 100th data value in descending order. Let define

$${\tau }_{{u}_{j}}={\widehat{\sigma }}_{{u}_{j}}-{\widehat{\xi }}_{{u}_{j}}{u}_{j}, j=1\dots n.$$
(6)

where \({\widehat{\sigma }}_{{u}_{j}}\) and \({\widehat{\xi }}_{{u}_{j}}\) are maximum likelihood estimators of the GPD.

The differences

$${\tau }_{{u}_{j}}-{\tau }_{{u}_{j-1}}, j=2\dots n.$$
(7)

should approximately follow normal distribution with mean value of zero. The Pearson’s Chi-square test is applied as a goodness-of-fit test, and the threshold with the lowest value is selected to satisfy this condition. The parameters of the GPD, along with their standard deviation (STD) are assessed, and the estimation uncertainty of the parameters is taken into consideration in the probabilistic model (Fig. 4).

Fig. 4
figure 4

Flowchart of the POT method with Bayesian inference

Full size image

For the 20-year-long measurement data series from the nearest station, Penc, as well as all the other stations of the HMS, the parameters of the Gumbel distribution (ξ = 0) were calculated using the mean and STD of the wind speed data. This approach assumes that the wind environment will remain constant over a large spatial scale. This assumption is generally valid for flatlands and plateaus, where strong wind events are typically macro-scale or meso-scale occurrences (e.g., Hungary). After that, Bayesian inference is employed to update the bivariate normal distribution of σ and µ, which is associated with the GEV distribution of 20-year-long data series:

$$p\left(\sigma ,\mu |D\right)=\frac{p\left(D|\sigma ,\mu \right)p\left(\sigma ,\mu \right)}{p\left(D\right)}$$
(8)

where D denotes the data from on-site measurement, p(σ,µ|D) is the posterior distribution of GEV parameters, p(σ,µ) is the prior distribution associated with Penc and Hungary. The probability of the observed data, denoted as p(D) and referred to as the marginal likelihood, is determined through numerical integration. The likelihood function p(D|σ,µ) used in this process is derived from the data collected at Sződliget. Finally, the 10-min mean wind velocity having the probability of 0.02 for an annual exceedance is calculated using the inverse cumulative distribution function (ICDF) of the Gumbel distribution with the assessed parameters.

3.3 Wind–structure interaction

Equivalent static wind force acting on the structure is evaluated based on the procedure formulated in EN 1993-3-1 (CEN 2006). It is assumed that the structure is well-designed and sufficiently rigid to avoid unfavourable aeroelastic responses when subjected to real extreme wind loads. While this assumption is reasonably valid for smaller and straightforward cantilevered structures, it often produces results acceptable for the level of precision anticipated in wind loading codes or standards (Holmes 2002). The telecommunication mast is located in a suburban area, and hence the terrain category III is selected for further calculation. The structure is divided into 9 sections (shown in Fig. 1a) with nearly identical panels to enable the wind loading to be adequately modelled for the global analysis. The tower sections are also divided into three faces and all ancillary components are allocated to each face as shown in Fig. 1b. In order to obtain results as accurate as possible, solidity ratios and force coefficients are evaluated corresponding to each angle of attack. The solidity ratio is calculated as:

$$\varphi =\frac{{A}_{s}}{{A}_{c}}$$
(9)

where As is the sum of the projected area of the members of the face projected normal to the face corresponding to each angle of attack, and Ac is the area enclosed by the boundaries of the face projected normal to the face. Figure 5a shows solidity ratios for various angles of attack corresponding to three stages, i.e., the bare structure, structure equipped with linear ancillaries, and structure equipped with discrete ancillaries. The calculated force coefficients are also represented in Fig. 5b; however, the wind load acting on discrete ancillaries are calculated and applied separately in the numerical model.

Fig. 5
figure 5

a Solidity ratio and b force coefficients for various angles of attack of the wind

Full size image

In comparison to the wind force calculated according to EN 1993-3-1, the structural performance is determined by applying the wind force obtained from wind tunnel tests conducted by Balczó et al. (2006), as well. The wind tunnel tests were conducted on a mast section with a diameter of D = 108 mm for the hot dip galvanized legs and D = 75 mm for the bracing members. The drag coefficient of the bare structure fluctuates between 0.87 and 1.03, contingent on the wind direction and computed in accordance with EN 1993-3-1. Conversely, it falls within the range of 0.70 to 0.81 based on wind tunnel measurements. The problem arising from differences between wind load coefficients derived from wind tunnel tests on full-size structures and on reduced-scale models is to be avoided. These differences are reflected not only in the coefficient magnitude but also in the wind velocity range (Reynolds number) at which they occur. Therefore, the measured values from the wind tunnel tests are utilized only for tower Sects. 7–9, because these sections align with the ones utilized in the wind tunnel experiments. Standard wind forces are applied to Sects. 1–6. The performance of the investigated mast is calculated by utilizing the wind load obtained from wind tunnel tests and according to EN 1993-3-1. The results of both calculations are then compared.

3.4 Development of finite element model

Bezas et al. (2022) have demonstrated that the current version of EN 1993-3-1 does not adequately address the buckling instability mode known as segment instability, which involves the buckling of multiple members. However, it is demonstrated in this study that utilizing the innovative standardized FEM-based design approach, structural engineers can effectively account for this phenomenon. Numerical model of the telecommunication mast subjected to wind loading is developed in a general-purpose finite element software (ANSYS v19.0), in order to predict wind load-induced structural response. Main dimensions of the structure and designations of chords and bracings are shown in Fig. 6. Nominal crosssectional properties of the corresponding structural elements are summarised in Table 1. Section type numbering, section name (ODnom×tnom: circular hollow section O, nominal diameter Dnom [mm], nominal wall thickness tnom [mm]), cross-sectional area A, area moment of inertia I, and approximate characteristic length L. Three-dimensional two-node beam elements (BEAM188), with quadratic shape functions an internal node in the interpolation scheme, are used in the finite element model which is suitable for analysing slender to moderately thick beams. The applied element type is based on Timoshenko beam theory including shear-deformation effects using first-order shear-deformation theory, i.e., cross-sections remain plane and undistorted after deformation. Six nodal degrees of freedom (DOF) option is chosen for the analysis with unrestrained warping (optional seventh degrees of freedom) of cross-sections. Finite element mesh of the telecommunication mast is shown in Fig. 6. Mesh sensitivity analysis is carried out using element sizes ranging from 250 to 1000 mm, regarding the rotation of the top of the tower and its load-bearing capacity, in order to verify the applied mesh scheme. This resulted in structural failure probabilities ranging from 4.9·10−5 to 3.1·10−4, with a probability of 3.1·10−4 observed for element sizes of 500 mm. In general, average element size is ~ 500 mm; thus, at least six elements are defined along lines between joints. The number of nodes and elements are 2508 and 1317, respectively. Translational and rotational DOFs of nodes representing the supports are constrained (Fig. 6c). Nodal force loads are defined in accordance with the Eurocodes or wind tunnel tests detailed in Sect. 3.3. Forces are defined in the nodal coordinate system, which is rotated with respect to the actual wind direction for each simulated case (Fig. 6d, e for antennae and structure with linear ancillaries, respectively). Rigid beams are defined for antennae 1, 6 and 10 in order to take into account the eccentric wind loading (Fig. 1; Table 7).

Fig. 6
figure 6

Finite element mesh of the mast: a section types and changes in cross sections, b top view, c boundary conditions, nodal loads for d antennae and e structure with linear ancillaries

Full size image
Table 1 Nominal dimensions of chords and bracings (*approximate length of chord/bracing)
Full size table

Linear material model, with Young’s modulus E and Poisson’s ratio ν = 0.3, is applied in the model for predicting rotations and displacements in serviceability limit state (SLS). Large deflection effects are included in all the simulations. On the other hand, nonlinear material properties, and equivalent geometrical imperfections are included as well in the geometrically and materially nonlinear analysis with imperfections (GMNIA) for assessing load-bearing capacity in ultimate limit state (ULS). Quad-linear isotropic hardening material model is defined for S235 structural steel grade according to Gardner et al. (2019) and prEN 1993-1-14 (CEN 2020) in order to accurately capture yield plateau and strain-hardening behaviour of normal strength steels (Fig. 7). The global (sway imperfection of the entire mast) and local (combined flexural buckling-type imperfection of bracing and chord) imperfections are also taken into consideration. The amplitude of initial sway imperfection (global) is defined as 2/3×H/200, where H is the total height of the structure in accordance with Sect. 5.3.2 in EN 1993-1-1. Local bow imperfections are defined with an amplitude of L/150, where L is the characteristic length, according to Table 5.1 and in Table 6.2 (curve ‘c’ for cold formed hollow sections) in EN 1993-1-1 and EN 1993-1-5. Equivalent geometrical imperfections (Fig. 8), covering the influence of manufacturing-induced geometrical imperfections and residual stresses, are defined in the model based on linear analysis (with prescribed displacement) and first eigenshape calculated by linear buckling analyses for global and local imperfections, respectively. The plane of sway imperfection is identical to the plane defined by the wind direction, while local imperfection is based on the first eigenshape in all the analysed cases for the actual wind loads with variable wind direction and magnitudes.

Fig. 7
figure 7

Quad-linear isotropic hardening material model (Gardner et al. 2019)

Full size image
Fig. 8
figure 8

a Global equivalent geometrical imperfections using linear analysis, b local equivalent geometrical imperfections of chord using eigenshape

Full size image

3.5 Probabilistic analysis

The Probabilistic Design System (PDS) module of the software is used for performing probabilistic calculations for Performance-based Wind Engineering assessment of both SLS criterion and load-bearing capacity for ULS. For high performance level, maximum allowable rotation of the top of the tower is defined as 0.5° as per the telecommunication service provider’s specifications. Probabilistic design variables and the corresponding distribution functions and parameters are summarised in Table 2 for SLS and ULS simulations based on the recommendations of JCSS (Joint Committee on Structural Safety 2001) and measurement results. A range of coefficients of variations (CV) values are defined in the probabilistic model code of JCSS for describing wind effects (cf, cr, cg); the larger values are used in the stochastic analyses for dealing with uncertainties which results in conservative results. The analysis takes into account the uncertainty associated with both the aerodynamic coefficients of the structure and the antennae. Note that the mean density of steel is increased by 5% in order to indirectly consider additional self-weight of welds, bolts, gusset plates, etc. On the other hand, mean yield strength is calculated by fy,nom × a×e− uν-C according to the probabilistic model code of JCSS, where fy,nom is the nominal value, a is spatial position factor (a = 1.00 for cold formed sections), u is assumed to be − 2.0, v is coefficient of variation, while C is a constant for reducing the yield strength with a value of 20 MPa. The probabilistic analysis is performed using Monte Carlo simulation with random Latin hypercube sampling which method ensures to have independent samples without accumulation of clusters of samples by having a memory of previous simulations. On the other hand, extreme ends of distribution functions are also considered in sampling process. A total of n samples is used in the simulation dividing each random input variable into intervals of equal probability (p = 1/n), while random sampling is carried out within each interval. Number of simulation loops, i.e., samples, required in a Monte Carlo simulation to fit a quadratic response surface depends on the number of random input variables. The required sample size for each simulated scenario is determined to be 160, following the guidelines provided in the advanced analysis techniques guide of the software. This sample size is chosen based on the number of probabilistic design variables, which is 9 for SLS and 11 for ULS.

Table 2 Probabilistic design variables for PBWE
Full size table

It should be noted that ANSYS PDS supports multiple distribution functions such as Gaussian, lognormal, uniform, Weibull, etc. However, generalized Pareto and extreme value distribution function, describing the distribution of measurement data, are not among them. Therefore, the corresponding cumulative distribution functions are added manually in the macro file using inverse transform sampling.

Response surfaces are fitted for output variables for SLS for the rotation of the top node θtop, while load amplification factor αULS is used for ULS for response surface fitting. Forward-stepwise-regression model with linear and quadratic terms including cross-terms is used with confidence level of 0.95 for filtering out irrelevant terms of the model. It leads to smaller number of coefficients resulting in increased accuracy of the remaining terms. In addition, Monte Carlo simulations are performed on the derived response surfaces in MATLAB environments. The simulations involve N = 106 simulation loops, which allow for fast calculations and evaluation of the EDPs using approximation functions. As a result, the probability distribution of the selected EDPs, namely θtop and αULS, can be represented by a posterior predictive distribution. This distribution yields more accurate estimates of exceedance probabilities compared to estimative summaries of the posterior distribution of the extreme wind speed model, such as the mean, mode, or 95% credible intervals. The posterior predictive sampling is achieved by the Monte Carlo simulations with N = 106 simulation loops on the derived response surfaces and lognormal distribution is fitted on the outcomes.

$$\text{P}\text{r}\left\{Y\le y|D\right\}={\int }_{\varvec{\theta }}^{}Pr\left\{Y\le y|\varvec{\theta }\right\} p\left(\varvec{\theta }|D\right)d\varvec{\theta }$$
(10)

where θ indicates the parameter set of σ and µ, Y denotes EDPs.

4 Results

4.1 Measurements

Figure 9 shows the wind direction distribution of Sződliget, where the north-western prevailing wind direction can be observed. Gaussian distribution is fitted to the data within the interval [240°, 360°] and distribution parameters µ and σ are assessed as 299.72° and 18.62°, respectively.

Fig. 9
figure 9

Polar histogram and histogram of wind direction distribution

Full size image

The 10-min averaged wind velocity data points are extracted from the wind speed record of Sződliget. The roughness length z0 is estimated as 0.877 based on the measurement. The logarithmic wind velocity profile with the assessed z0 is then employed to estimate the wind velocity at a height of 10 m. Statistically independent events are determined using autocorrelation analysis and maxima for 3 days is assumed as independent events which results 405 samples. For the POT method, wind speed of 6.379 m/s is indicated as a suitable threshold using automatic threshold selection technique, and 129 samples exceed this value. The GPD distribution is fitted to the data, and the estimated parameters can be seen in Table 4.

The mean and STD of the annual maximum peak wind velocity for Hungarian meteorological stations from 2002 to 2022, the current values in the EN 1991-1-4 Hungarian National Annex (2007), and the nearest station of the HMS, Penc (1999–2022), are summarized in Table 3. The wind velocity v0.98, with a probability of 0.02 for an annual exceedance at the Penc station, is 17% lower compared to the averaged Hungarian v0.98 for the period 1999–2022, and it is 22% lower compared to the value v0.98 in the Hungarian National Annex.

Table 3 Means, STDs and wind velocities with p = 0.02 for an annual exceedance [m/s]
Full size table

The bivariate normal distribution of parameters σ and µ of the Gumbel distribution are evaluated from these means and STDs and can be seen in Fig. 10a; Table 4. Thus, the data series from Hungary and Penc serve as the prior distribution of parameters, which is then updated with data from Sződliget using Bayesian inference. The resulting posterior distribution is depicted in Fig. 10b, and its parameters can be found in Table 4 under the labels “Hun—Sződliget” or “Penc—Sződliget”.

Table 4 Evaluated parameters of extreme wind speed models [m/s]
Full size table
Fig. 10
figure 10

The bivariate normal distribution of parameters σ and µ of the Gumbel distribution—Hungary, 10 min-averaged wind speed, a prior distribution b posterior distribution

Full size image

Assuming uniaxial stresses in chord members, internal axial forces are evaluated applying the Hook’s law and using the Young’s modulus E (210,000 MPa) and the cross-sectional area of the measured chords (5963 mm2). Internal axial forces in chords S1, S2 and S3 are sorted corresponding to wind speed of v = 10, 15, 20, 30 m/s, and turbulence intensity of 10, 20, 30%. Then, sinusoidal functions are fitted to these data points and expected values are extracted regarding the interesting directions for the triangular section tower, i.e., 270°, 300° and 330° (Table 8 in the Appendix). Two examples can be seen in Figs. 11 and 12, for the case of wind speed v = 15 m/s.

Fig. 11
figure 11

Internal axial forces S with wind speed v = 15 m/s

Full size image
Fig. 12
figure 12

Internal axial force S1 at v = 15 m/s and turbulence intensities of 10, 20, 30%

Full size image

4.2 Discussion of force coefficients

The results of the deterministic numerical model based on EN 1993-3-1, specifically internal axial forces in chord members, are compared to the extracted values from measurements (Table 9). Due to the north-western prevailing wind direction, the S3 axial force is in the vicinity of the neutral axis; therefore, these values are not presented here. In the case of S1, which is subjected to tension, a noticeable difference of approximately 20–40%, can be observed for high wind velocities (Fig. 13). In the case of S2, the differences for high wind velocities are lower, ~ 10–25% (Fig. 14). By utilizing wind forces measured in the wind tunnel tests, the model was able to reduce these differences by approximately 15–20%. The differences for low wind velocities are less than 14%.

Fig. 13
figure 13

Internal axial force S1 for Iv = 20%, and for various wind velocity, wind direction

Full size image
Fig. 14
figure 14

Internal axial force S2 for Iv = 20%, and for various wind velocity, wind direction

Full size image

4.3 Probabilistic analysis results

The results of Monte Carlo simulation combined with Latin Hypercube (MCS) sampling are presented for high performance level, i.e., SLS, in Fig. 15a. A limit value of 0.5° is used for the rotation of the top of the tower based on the specifications of telecommunication suppliers, and it is represented as a horizontal line in the figure. The probability distribution functions of the chosen EDP are evaluated (Fig. 15c). The results of Monte Carlo simulations with N = 106 simulation loops, performed on the derived response surfaces (RSM), are shown in Fig. 15b, d. Normal, lognormal, and Gumbel distributions were fitted to the samples, and the lognormal gave the best fit using the chi-square goodness-of-fit test. In Tables 10 and 11, the parameters of fitted lognormal distributions are summarized based on MCS and RSM for SLS and ULS.

Fig. 15
figure 15

The rotation of the top in SLS: a and b sample data, c and d PDF, histogram, and CDF with confidence interval of 95% for MCS and RSM simulations, respectively

Full size image

The results of the probabilistic analysis on the load-bearing capacity of the mast, i.e., the load amplification factor, are presented in Fig. 16. The value associated to the ultimate limit state is 1 and represented as a horizontal line in the figure.

Fig. 16
figure 16

The load amplification factor αULS in ULS: a and b sample data c and d PDF, histogram, and CDF with confidence interval of 95% for MCS and RSM simulations, respectively

Full size image

4.4 Discussion of the different scenarios

The probabilities of exceeding the serviceability limit and the structural failure Pf are calculated based on fitted lognormal distributions of RSM simulations (Figs. 17, 18). The level of safety for reliability class RC2, in other words, the target probability of exceeding the limit for reference periods of 50 years is 6.68·10−2 for SLS and 7.23·10−5 for ULS, respectively (EN 1990:2002 2002). By utilizing the force coefficient cf derived from wind tunnel tests, the Pf is reduced by approximately two orders of magnitude. Assuming a roughness length z0 of 0.3, as specified according to the EN 1991-1-4 standard for suburban terrain, instead of using the value of 0.877 based on measurement, leads to an increase in the Pf by approximately half an order of magnitude for the SLS and one order of magnitude for the ULS. Due to the considerably lower observed wind speeds at Sződliget and Penc compared to the Hungarian average, the Pf for Sződliget and “Penc-Sződliget” are significantly lower. The associated Pf are lower by approximately three orders of magnitude for the SLS and around eight orders of magnitude for the ULS. Taking into account raw wind field data from a nearby monitoring station with longer measurements as prior information when estimating the parameters of an on-site extreme wind speed model for a structure may be considered unconservative, as demonstrated in the case of “Penc-Sződliget”.

Fig. 17
figure 17

The probability of exceeding the serviceability limit for different scenarios and the target Pf according to EN 1990 (EC RC2)

Full size image
Fig. 18
figure 18

The probability of structural failure Pf for different scenarios and the target Pf according to EN 1990 (EC RC2)

Full size image

The probability of exceeding the serviceability limit and the structural failure in accordance with the 95% confidence bounds based on MCS and RSM simulations are summarized in Tables 5 and 6. Note, that reliability index β is calculated based on Pf assuming Gaussian distribution according to EN 1990:2002 (2002). However, performance function does not follow the Gaussian distribution, therefore, it is only an informative measure of the reliability in this case. The target reliability index β for reliability class RC2 and reference periods of 50 years is 1.5 for SLS and 3.8 for ULS, respectively. In several instances, it is noticeable that while the probability of failure does not surpass the prescribed limit defined by the EC, the value of β falls below the specified threshold. Consequently, β does not accurately indicate the actual frequency of structural failure. Bayesian updating of the prior information or beliefs associated with the Hungarian average by incorporating the observed data from Sződliget can reduce the probability of failure Pf by approximately one order of magnitude compared to the case of “Hungary”.

Table 5 The probability of exceeding the serviceability limit with the 95% confidence interval (*Gaussian distribution)
Full size table
Table 6 The probability of structural failure Pf with the 95% confidence interval (*Gaussian distribution)
Full size table

The presented estimation process assumes that past recordings of the variable being studied are still representative of its stochastic behaviour in the present and future. This assumption is based on the notion of stationarity, which assumes that the underlying process remains constant over time and assume constant parameter values throughout time. In order to account for potential changes in extreme events, Prosdocimi and Kjeldsen (2021) have formulated a model that assumes a constant coefficient of variation, allowing the location and scale parameters to change simultaneously. This approach, known as non-stationary analysis, allows for the examination of how the behaviour of extremes may have changed over time.

4.5 Sensitivity analysis

The probabilistic sensitivities of Spearman rank-order correlation coefficients are also determined for all probabilistic design variables defined in Table 2 (Figs. 19, 20). It is highlighted that the roughness factor cr, force coefficient cf and gust factor cg have a dominant influence on the EDPs due to their higher COVs, while material parameters have smaller influence on the EPDs. The density of the steel ρ is found to be statistically insignificant at a significance level of 2.5% in all cases. In addition, it is observed that σ has a significant impact on the EDPs for data extracted from Sződliget, where only the POT method was utilized. In the case of the Hungarian 20-year-long measurement data series, the parameters σ and µ have a relatively small impact. However, in the Bayesian updated case, these two parameters are found to be statistically insignificant. Although, the present statements are valid for the dataset under consideration and for similar climatic conditions, methods presented in this paper are applicable for other wind engineering problem.

Fig. 19
figure 19

Probabilistic sensitivities for the SLS for a Hungary, b Hungary–Sződliget, and c Sződliget

Full size image
Fig. 20
figure 20

Probabilistic sensitivities for the ULS for a Hungary, b Hungary–Sződliget, and c Sződliget

Full size image

5 Conclusions

In the present paper, the FEM-based PBWE assessment of a telecommunication steel lattice tower is presented. The telecommunication steel lattice mast is equipped with wind speed and strain sensors and located in Central Hungary. The probabilistic characterization of a meteorological phenomenon, such as wind actions on structures is essential to get correct and accurate answers about the structural performance resulting in economic and optimal design. Furthermore, on-site data acquisition enables the assessment of parameters like stochastic extreme wind velocity, direction and roughness length based on measurements, since these parameters obtained from a standard may frequently deviate from the actual conditions observed at the site. The study shows that Bayesian inference of extreme wind velocity model parameters allows combining short-duration measurements from the tower site with a more extensive dataset from nearby locations or even across the country, improving the design and verification of structures with limited measurement data.

A comprehensive numerical model is developed in a general-purpose finite element software for full probabilistic performance assessment of the lattice structure. It is demonstrated in this study that utilizing the innovative standardized FEM-based design approach, structural engineers can effectively account for the buckling instability mode known as segment instability, which involves the buckling of multiple members. The posterior predictive sampling is achieved by the Monte Carlo simulations on the derived response surfaces.

The analysis reveals that the scale parameter of the extreme wind velocity distribution has a notable influence on the selected EDPs when utilizing a 3.5-year measurement data series extracted from the site, solely applying the POT method. Therefore, it is essential to consider the uncertainty of the scale parameter when performing the calculations in this procedure. On the other hand, for the Hungarian 20-year measurement data series, the parameters σ and µ have a relatively minor impact. However, in the case of Bayesian updating, these two parameters are found to be statistically insignificant; therefore, the uncertainty associated to this parameter can be neglected. The substantially lower wind speeds observed at both the tower site and the nearby station lead to considerably lower probabilities of failure compared to those calculated based on the national standard. The results obtained from the on-site shorter dataset, and the extended dataset that includes nearby lower wind speed measurements, suggest that these estimations may be considered as unconservative. Hence, our findings support the conclusion that the POT procedure without Bayesian updating, when applied with approximately 4 years of wind measurement data, tends to underestimate the basic wind velocity. Consequently, the assessed reliability of the structure may be considered as unconservative. The comparison of internal axial forces in chord members based on measurements and finite element modelling, using wind forces calculated according to EN 1993-3-1 and wind tunnel tests, validates previous findings that the Eurocode tends to overestimate the wind load at higher velocities. Therefore, a higher degree of structural reliability can be attained through the execution of full-scale wind tunnel experiments and/or numerical simulations during the development of the second generation Eurocode.

The objective of this article was to showcase the effectiveness of integrating site-specific wind loading models into the standardized FEM-based design framework as a powerful tool for design engineers.