Spatio-temporal statistical analysis of PM₁ and PM_2.5 concentrations and their key influencing factors at Guayaquil city, Ecuador

Abstract

Guayaquil, Ecuador, is in a tropical area on the equatorial Pacific Ocean coast of South America. Since 2008 the city has been increasing its population, vehicle fleet and manufacturing industries. Within the city there are various industrial and urban land uses sharing the same space. With regard to air quality there is a lack of government information on it. Therefore, the research’s aim was to investigate the spatio-temporal characteristics of PM₁ and PM_2.5 concentrations and their main influencing factors. For this, both PM fractions were sampled and a bivariate analysis (cross-correlation and Pearson's correlation), multivariate linear and logistic regression analysis was applied. Hourly and daily PM₁ and PM2.5 were the dependent variables, and meteorological variables, occurrence of events and characteristics of land use were the independent variables. We found 48% exceedances of the PM_2.5-24 h World Health Organization 2021 threshold’s, which questions the city’s air quality. The cross-correlation function and Pearson’s correlation analysis indicate that hourly and daily temperature, relative humidity, and wind speed have a complex nonlinear relationship with PM concentrations. Multivariate linear and logistic regression models for PM₁-24 h showed that rain and the flat orography of cement plant sector decrease concentrations; while unusual PM emission events (traffic jams and vegetation-fires) increase them. The same models for PM_2.5-24 h show that the dry season and the industrial sector (strong activity) increase the concentration of PM_2.5-24 h, and the cement plant decrease them. Public policies and interventions should aim to regulate land uses while continuously monitoring emission sources, both regular and unusual.

1 Introduction

Particulate matter (PM_i) is a heterogeneous mixture of particle sizes with different chemical and physical characteristics. It is the most common atmospheric contaminant worldwide, generated from natural and/or anthropogenic sources (Ostro et al. 2015). PM is classified according to its equivalent aerodynamic diameter in different fractions (PM_i), mainly PM₁₀, PM_2.5 and PM₁ (particles with an aerodynamic diameter of ≤ 10, 2.5 and 1 μm, respectively) (Seinfeld and Pandis 2016).

Long and short-term exposure to outdoor PM_2.5 has been associated with mortality and morbidity health outcomes. A recent systematic review of chronic or long-term exposures (> 24 h) reported that a 10 µg m⁻³ increase in PM_2.5 concentration is associated with an 8% increase in total mortality (pooled RR 1.08; 95% CI: 1.06–1.09; 25 studies) (Chen and Hoek 2020). There are also consequences for acute or short-term exposure (≤ 24 h); Orellano et al. (2020) reported that a 10 µg m⁻³ increase in PM_2.5 concentration is associated with a 0.65% increase in all-cause mortality (pooled RR 1.0065; 95% CI: 1.0044–1.0086; 29 studies): the WHO (2021) uses the above information to propose PM_i thresholds considered safe for health. This organisation warns that PM_2.5 can penetrate deep into the lungs and even enter the bloodstream, resulting in cardiovascular and respiratory diseases. Furthermore, it reports that there is still not enough quantitative evidence to establish reference threshold concentration for PM₁, but it is expected that PM₁ has a greater lung penetration capacity due to its smaller size (WHO 2021). This has been confirmed by research such as Chen et al. (2017), who warn that most of the adverse health effects of PM_2.5 come from the PM₁ size fraction. Furthermore, Yang et al. (2020) conclude that PM₁ exposure may be more hazardous than PM_2.5 in their study of children’s respiratory health. Likewise, Wang et al. (2021) in a study of childhood pneumonia, found that a 10 ug.m⁻³ increase in PM₁ and PM_2.5 was associated with increased risks of admission to pneumonia by 10.28% (95% CI 5.88−14.87%; Lag 0–2) and 1.21% (95% CI 0.3 − 2.09%; Lag 0–2), respectively.

Spatio temporal analysis refers to the exploration of any information relating to space and time (Gudmundsson et al. 2017). Determining the spatial distribution of an air, soil or waterborne contaminant by its abiotic factors can help to develop an understanding of its background sources and influencing factors and is important for environmental and health risk evaluation (Ambade et al. 2021a,b, 2022a,b; Bisht et al. 2022; Gupta et al. 2022; Ambade and Sethi, 2021; Kurwadkar et al. 2021; Maharjan et al. 2021). This explains the recent expansion of research on the spatio-temporal analysis of PM_i (Deng et al. 2022; Han et al. 2022; Li et al. 2022; Wang et al. 2022a,b; Zhang et al. 2022; Zhao et al. 2022; Owoade et al. 2021; Zhou and Lin 2019). This also applies in Latin America (Carmona, et al. 2020; Encalada-Malca et al. 2021; Chiquetto et al. 2020), but there is a lack of research on Ecuadorian problems. A comprehensive overview of existing work is presented in Table S1, and note that spatio-temporal studies aim to investigate the key factors that influence PM concentrations, considering meteorological and other parameters that vary in time and space. It is also noted that each study relies on different statistical techniques, but most are based on regression analysis. Furthermore, spatio-temporal studies of PM most often focus on a single size fraction (PM_2.5 or PM₁₀) and one temporal scale (hourly, daily or annually). In this study, the spatial dimension is represented by sampling PM_i at different sites of Guayaquil city and the temporal dimension refers to their hourly, daily and seasonal variation (dry and rainy season).

The spatio-temporal analysis of PM_i and their influencing factors can be performed following a myriad of available statistical techniques, varying in their complexity, that are chosen according to the aim of the study (Carmona et al. 2020; Deng et al. 2022; Han et al. 2022; Li et al. 2022; Wang et al. 2022a,b; Zhang et al. 2022; Zhao et al. 2022; Owoade et al. 2021; Zhou and Lin 2019). Multiple linear regression (MLR) is one statistical technique applied in air quality analyses to define linear statistical relationships between PM concentrations and meteorological and anthropogenic variables (Morantes et al. 2019; Kozakova et al. 2017; Nazif et al. 2016). Similarly, logistic regression (RLog) is used in air quality analysis to establish statistical relationships between influencing variables and a predefined contaminant threshold (usually a contaminant concentration) (Ordóñez et al. 2019; Kim et al. 2020; Upadhyay et al. 2017; Vélez-Pereira et al. 2019). Applying RLog needs an established threshold so that the probability of being above or below its value can be determined. The threshold is itself determined from the health impacts of exposure to the contaminant. RLog is also applied to study relationships between health effects and contaminant concentrations (Seifi et al. 2019; Bergstra et al. 2018; Ng et al. 2017; Ware et al. 2016). A main advantage of using logistic regressions is that it can provide a similar level of performance to other more complex techniques, such as neural networks or regression splines, but with lower complexity (Chang et al. 2020, Holdnack et al. 2013).

Guayaquil is one of the two largest cities in Ecuador with an estimated population of 2.7 million inhabitants in 2020 (INEC 2016). It is located on the equatorial Pacific Ocean coast of South America and occupies an area of 355 km². Guayaquil has a highly active maritime-port with several cement production and thermoelectric plants, plus a group of medium and small industries that share the same space with urban land use (IND 2020). Up to the first quarter of 2022, the local government of Guayaquil has not yet included the risks associated with poor air quality in their agenda and so there is no official, systematic, and open information available to the public, nor any public reports on air pollution and its associated risks. The only information found locally is that in scientific literature and in the press. It is important to note that, in Ecuador, it is mandatory for local governments to monitor air quality (Article 191, Environmental Organic Code of Ecuador), and hence official reporting would be expected. This is especially import because there has been an increase in the concentration of the urban population, in vehicular traffic, and in manufacturing industries, in Guayaquil since 2008. This has increased electricity demand and could be detrimental to air quality of the city (Geo Ecuador, 2008). A survey conducted in 2016 shows that Guayaquil’s inhabitants consider the city to be polluted by particulate matter from vehicular traffic and industries. An environmental inventory conducted between 2007 and 2012 reports that PM₁₀ emissions averaged 4.5 kt yr⁻¹ (Efficacitas Consultora 2012). For context, other Latin American cities, such as Santiago de Chile, emitted an average of 14.9, 6.0 and 4.8 kt yr⁻¹ of PM₁₀ from industrial sources in 2015, 2016, and 2017, respectively (Alamos et al. 2022). Moreover, in the city of Bogota, the average industrial emissions of PM₁₀ reached 1 kt yr⁻¹ (Pachon et al. 2018). The Mayor’s Office of Guayaquil (Alcaldía de Guayaquil, 2018) reported that, in 2016, the annual average PM₁₀ concentration was 23 µg m⁻³. This value was higher than the limits suggested by the WHO for 2005 and 2021 of 20 and 15 µg m⁻³, respectively (WHO 2006, 2021). There is little information on air quality in Guayaquil in the scientific literature. Moran-Zuluaga et al. (2021) found that the annual mean concentrations of PM_2.5 and PM₁ were 7 ± 2 and 1 ± 1 µg m⁻³, respectively, at Guayaquil’s airport between 2015 and 2016. Although annual average concentrations of PM_2.5 were below the Ecuadorian standard of < 15 µg m⁻³ (Morantes et al. 2016), they show that daily average concentrations sometimes exceeded the Ecuadorian norm of a PM_2.5-24 h of < 50 µg m⁻³. The authors confirm that the city’s flat orography and the south and south-western trade winds disperse contaminants.

Given the lack of governmental environmental air quality information, the scarcity of research on the topic, and the uncertainty about PM₁ and PM_2.5 pollution in the city of Guayaquil, it is essential to study PM_i contamination at different temporal scales, and their spatial distribution around the city. Therefore, the aim of this study is to investigate the spatiotemporal characteristics of PM₁ and PM_2.5 concentrations for the city of Guayaquil and to identify their key influencing factors using regression and correlation statistical analyses. Any analysis will support the development of adequate policy engagement at the local level by responsible authorities.

2 Study area

The city of Guayaquil is located in a coastal plain below the equator in South America. It is bounded by the Estero Salado and Guayas Rivers, which flow into the Gulf of Guayaquil of the Pacific Ocean. This flat city has some low elevation hills (< 300 m above sea level) (Delgado 2013). Guayaquil is the most important seaport in Ecuador. It has three thermoelectric plants that supply energy to the province and has a group of industries spread throughout the city: cement plants (with open-pit mining), food and beverage industries, chemical industries, and asphalt industries, amongst others. In 2016, the vehicle fleet was 362,857 vehicles with an average age of 12.2 years and a growth of 5.7% over 5 years (INEC 2020). The typical urban landscape is characterised by regular orthogonal streets bordered by low buildings.

The climate of this coastal region is stable, warm, and humid. It is influenced by the cooling effect of the Humboldt Current along the coast and by the warming effect of the El Niño. This generates a rainy and a dry season (Rossel and Cadier 2009) with rainfall between 500 and 2000 mm year⁻¹, and an average relative humidity of above 60%. The wind has a strong maritime influence blowing the Southwest with average speeds of less than 3 m s⁻¹ (Galvez and Regalado 2007). Figure 1 shows meteorology of the city (1992–2017). The rainy season (January-April) and the dry season (May-December) are shown. In the image below the time-varying behaviour of the average temperature and average relative humidity (1992–2017) is shown, evidencing higher temperatures and humidity in the rainy season. The mean temperature remains between 26.3 and 27.4 °C, and the mean relative humidity is 69–80%. Johansson et al. (2018) point out that the hottest thermal conditions are found in the rainy season because the atmospheric temperature and vapour pressure are higher, and the wind speed is slower than at other times of the year.

Fig. 1

Meteorology of the city of Guayaquil, Ecuador (1992–2017)*: Climogram (above); average temperature and average relative humidity (below). * Guayaquil airport weather station—radiosonde (MA2V)

3 Methodology

3.1 Sampling locations and sampling method

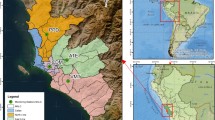
A sampling campaign for PM₁ and PM_2.5 was carried out between October 2016 and March 2017. We sampled in the rainy and dry seasons to perform a temporal analysis of PM behaviour and in four city sectors for the spatial analysis. Figure 2 shows a map of the city of Guayaquil, with close-ups of the four sampling points/sectors:

• The cement plant sector in which two major cement plants operate with capacities of 5.4 and 0.9 Mt year⁻¹, plus others with lower capacity (< 0.4 Mt year⁻¹) (Holcim Ecuador 2015). Raw material for these industries comes from four collocated open-pit quarries. These industries operate continuously 24 h a day, 7 days a week. This sector is crossed by the only road that links the city to the coastline, and has vehicular traffic 24 h a day, 7 days a week. Many middle-class residential areas have been built around the road, which include a set of shopping centres that generally operate from 08:00 to 20:00 h.

• The downtown sector has significant commercial activity and a large number of government and private office buildings, together with lower and lower-middle class residential buildings. Many traffic lights slow traffic, causing frequent traffic jams at rush hour, and much of the public transport is diesel-powered (INEC 2016). There are also recreational activities that are open to the public until late at night. Business hours are from 08h00 to 21h00 and office hours from 08h00 to 17h00.

• The industrial sector is located north of the city and is circumscribed by two highways that surround the city with high vehicular traffic. Industries, wholesale businesses, and residential areas coexist. The industrial activity comprises medium and small industries, such as food and beverages, chemicals, paints, asphalt, carpet factories, and plastics production. Industry hours are generally from 07h00 to 18h30 from Monday through Saturday noon, although some operate 24 h a day, 7 days a week.

• The residential sector is representative of middle-class gated communities that limit vehicular traffic but are generally located near trunk roads with high vehicular traffic and commercial activity. This residential sector is located at the foot of a hill (< 180 m) and has approximately 4 000 residents.

Fig. 2

Location of the four sampling sectors of PM in Guayaquil (Espín 2017)

A real-time environmental particulate air monitor, model EPAM 5000 (Haz-Dust™), with a detection range of 0.001–20.0 and 0.01–200.0 mg m⁻³ and a sampling flow rate of 4.0 L min⁻¹, was used to measure PM concentration. The EPAM 5000 can sample every second; however, data was only recorded every minute as this frequency is sufficient to be translated into hourly averages for the subsequent analysis. An hourly resolution was deemed acceptable because the aim is to describe hourly patterns in the PM_i data per day. The manufacturers calibrated the equipment prior to sampling using the NIOSH gravimetric method. The sampling instrument was positioned at a height of ~ 2.5 m above the floor.

PM₁ and PM_2.5 sampling started in the dry season on October 17 and ended on December 17, 2016. Rainy season measurements were recorded between January 7 and March 5, 2017. Our protocol established that measurements begin in each sector with the PM₁ fraction for 7 consecutive days and then continue with the PM_2.5 fraction for another 7 consecutive days. After sampling in one sector was complete, the sampling station moved to a new sector, and the protocol was repeated until all four sectors were sampled, both in dry and raining seasons. 56 days were sampled for both PM₁ and PM_2.5. Therefore, there were 2 688 hourly data points: 1 344 for PM₁ and 1 344 for PM_2.5. The scheduled measurement protocol makes it possible to know the hourly concentration of each contaminant and calculate the 24-h arithmetic average of particulate matter, as established by environmental regulations. Likewise, concentrations were collected for the seven days of the week in the four sectors and for the two climatic periods.

The surface wind speed, ambient temperature, and relative humidity in each sector were measured at the same time with a Kestrel 4500 pocket weather tracker. The meteorological data was recorded simultaneously with the PM_i concentration and averaged to hourly and daily values. The rainfall was measured using a TFA-47101 rain gauge.

We identified unusual events that occurred during the sampling in the surroundings of the sectors that could influence the PM concentration using social networks. Events were classified as: (i) related to vehicular traffic: traffic blockages, traffic accidents, traffic lights out of service; (ii) related to torrential rain: slow vehicular traffic, avenues cut off by floods or falling trees that interfere with vehicular traffic; and (iii) related to emissions: emissions from fires in green or wooded areas, vehicle fires, building fires, explosions in quarries, street fumigations, exceptional emissions from industries. The collected information was organised by the type of event, its time and date, and sector of the occurrence. As a result, 106 events were identified, of which 80 were related to vehicular traffic, 8 to rainfall, and 18 to exceptional emissions. Industries in social networks did not report operational problems related to emissions. Of these events, 59 occurred during the PM₁ sampling and 47 during the PM₂.₅ sampling. In total, 54 events occurred during the dry season and 52 during the rainy one. A total of 18 events were identified in the cement sector, 6 in the city centre, 81 in the industrial sector and 19 in the residential one.

3.2 Contaminants and temporal scales

3.2.1 PM_i-1 h descriptors

The eight hourly time series (PM₁, T_PM1, RH_PM1, WS_PM1 and PM_2.5, T_PM2.5, RH_PM2.5, WS_PM2.5) for the two climatic seasons were visually analysed separately and descriptive statistics were calculated. The Dickey-Fuller test for stationarity (p < 0.05) was applied to establish stationarity in the time series. Overall, an analysis was made for each fraction (PM_i, i = 1 and 2.5), each season (dry and rainy season), and each sector (cement plant, downtown, industrial, and residential).

Box and whisker plots are used to determine possible patterns in the hourly concentrations of PM_i throughout the day. For the two PM fractions and climatic season, the data are grouped for hours of the day (regardless of the sector). The number of records used for this analysis was: 1 188 from PM₁-1 h, and 1 123 from PM_2.5-1 h, due to failures with the sampling equipment in the industrial sector.

3.2.2 PM_i-24 h descriptors

Hourly data was transformed into 24 h averages. For dry and rainy seasons there were 56 values of PM₁-24 h concentrations and 53 for PM_2.5-24 h, giving 109 sampling days. Daily average values are useful to establish whether a site complies with 24-h reference thresholds. In this research, the reference threshold used for both fractions is the limit value proposed for PM_2.5-24 h by the WHO (2021) (PM_2.5-_WHO-24 h = 15 µg m⁻³). This is because there are no established threshold limit values for human health for PM₁-24 h. Given that in environmental regulations the thresholds set for PM fractions decrease as the particle size decreases, this reference threshold for PM₁ could be underestimating its effects, and so we consider it as a proxy reference value.

3.3 Single influencing factor analysis on PM_i concentrations

3.3.1 Meteorological variables

For the correlation analysis, hourly PM concentration was the dependent variable (PM₁-1 h or PM_2.5-1 h) and hourly meteorological parameters were the independent variables: ambient temperature (T), wind speed (WS), and relative humidity (RH). A cross correlation function (CCF) (r; p-value < 0.01) was applied between these series to determine the correlations simultaneously or with delay. A CCF was applied between PM_i (i = 1 or 2.5) and the meteorological variables. Before applying a CCF, we reviewed the time series to ensure that we had consecutive data over time (hours and days) and each record contained information for all variables (PM_i, T, RH, WS). The time series were examined for each particle fraction, each sector and the two seasons.

Likewise, to determine the influence of meteorological parameters on daily particle concentrations, Pearson’s correlation (r; p-value < 0.05) was applied between PM_i-24 h and the daily average of minimum, mean, and maximum temperatures, relative humidity, and wind speed. The interpretation of the magnitude of the Pearson correlations followed the guidelines proposed by Ratner (2011).

3.3.2 Dichotomous variables

The t-Student test was used to establish the relationship between PM_i-24 h (as continuous variable) and all dichotomous variables of interest: occurrence of rainfall, unusual events, climatic season, and the sector (cement plant, downtown, industrial, residential).

3.4 Multiple linear regression: PM_i-24 h

Multiple linear regression analysis (MLR) is a statistical technique that establishes a relationship between a set of more than two independent variables (IVs) to determine the extent they can explain the dependent variable (DV). For a DV (denoted as $Yi$), its best linear predictor from IVs (${X}_{i}$) can be represented as (Cohen et al. 2014; Weisberg 2014):

$$\begin{gathered} Yi = \beta_{1} X_{1i} + \beta_{2} X_{2i} + \beta_{3} X_{3i} + \beta_{k} X_{ki} + \in i \hfill \\ \left[ {{{Model A}}:{{ standardised model}}} \right] \hfill \\ \end{gathered}$$

(1)

$$\begin{gathered} Yi = Bo + B_{1} X_{1i} + B_{2} X_{2i} + B_{3} X_{3i} + B_{k} X_{ki} \hfill \\ \left[ {{{Model B}}:{{ predictive model}}} \right] \hfill \\ \end{gathered}$$

(2)

where:

$\beta_{0} ;\beta_{1} ; \ldots \beta_{k} {-}B_{0} ; \, B_{1} ; \, B_{2} ; \, \ldots \, B_{k}$, unknown fixed parameters. $X_{1i} , \ldots ,X_{ki}$ independent variables whose values are fixed by the researcher. $\in i$ unobservable random variable. Random error.

Model A allows us to identify the variable that has the most important contribution to the total variance using the standardised regression coefficient (β): a variable has greater importance in the regression equation the higher the absolute value of β (Cohen et al. 2014). Model B is constructed with unstandardized coefficients (B for each variable). The unstandardized B coefficients have the same physical units as the measured variables.

A MLR must meet several assumptions for the model to be generalised. Before performing the regression, the variables were checked for linearity (the relationship must be linear), multicollinearity (most IVs were not highly correlated [r < 0.9]), and normality (normal distributions were checked with Q-Q plot, skewness, kurtosis, and K-S). The final model was checked for multicollinearity (using a variance inflation factor [VIF < 10] and tolerance [> 0.2]), normally distributed errors (checking Q-Q plot and histogram), independence of errors and homoscedasticity (residuals plot has no tendencies) (Cohen et al. 2014). Two models were developed, and the dependent variables used for each MLR were PM₁-24 h and PM_2.5-24 h. In Table 1 we present the type, units and distribution descriptors for the dependent variables of the MLR model.

Table 1 Description of the dependent and independent variables used in PM_i-24 h modelling

To evaluate the goodness of fit for the MLR model, the following performance indicators were used: normalised absolute error (NAE), root mean square error (RMSE), mean absolute error (MAE), index of agreement (IA) and prediction accuracy (PA) (Willmott 1981, 1982). Table 2 shows details of these indicators.

Table 2 Performance indicators

3.5 Exceedance’s analysis

To establish the individual relationship between a dichotomous dependent variable and relevant independent variables, a bivariate analysis is performed using the t-Student test (for variables of different types) and the Pearson correlation “r” (for variables of the same type). The exceedance analysis is performed via logistic regressions (RLog). This type of regressions serve to model the relationship between independent variables (IVs) and a dichotomous response variable (or dependent variable, DV) (Hosmer et al. 2013). The logistic regression models the probability of an outcome based on individual characteristics. Since chance is a ratio, the logarithmic transformation of the chance is modelled by Eq. 3 (LOGIT model):

$${p}_{i}=\frac{1}{1+{e}^{{-(\beta }_{0}{-\beta }_{i}){x}_{i}}}$$

(3)

where:

${p}_{i}$ probability of y = 1 in the presence of covariates x;

${x}_{i}$ set of n covariates;

β_o constant of the model or independent term;

β_i coefficients of the covariates.

Two logistic models were developed. The dependent variable for RLog is defined as the discretization of the exceedance of the concentration for PM_i-24 h (EPM₁-24 h or EPM_2.5-24 h), setting a value equal to “1” when the concentration of PM_i-24 h exceeds or equals 15 µg m⁻³ and a value of “0” if PM_i-24 h is less than 15 µg m⁻³. To discretize the values of PM_i-24 h in binary values, the approach of Rincon et al. (2022) was used. The concentration limit value of PM_2.5-24 h < 15 µg m⁻³ (WHO, 2021) was used as a reference for establishing a threshold for exceedances of PM₁ and PM_2.5. In Table 1 we present the type, units and distribution descriptors for the dependent variables of the RLog model.

3.5.1 Model validation

To understand the effect of adjusting the LOGIT model, chi-squared likelihood statistics were used. It compares the values of the prediction against the observed values when the model does not consider the independent variables and when it does. The model makes an adequate prediction when the chi-squared statistically decreases (p < 0.05), which occurs once the independent variables have been introduced (Hosmer et al. 2013).

The LOGIT model was validated using the summary statistics of a contingency table, which give ways of measuring the goodness of the predictions (Hosmer et al. 2013). The classification table indicates the absolute frequency, the correct classification percentages when exceeding the threshold, and the holistic success rate. It shows the percentage of correctly classified cases when model correctly predicts the threshold is exceeded (sensitivity), as well as the percentage of cases when the model correctly predicts the threshold was not exceeded (specificity). The model was also validated through classification errors (false positives and false negatives). The holistic success rate was calculated based on the values of the main diagonal of the matrix (correct classifications). The R² of Cox and Snell, and the R² of Nagelkerke indicates the part of the variance of the dependent variable explained by the model. The part of the PV explained by the model oscillates between the values of both R², where a good fit is represented by values close to one (Hosmer et al. 2013; Aznarte 2017).

The selection of the independent variables for the MLR and the RLog were made from previous research associating PM_i-24 h concentration with other variables at the same temporality scale. Table 1 lists type, units, and distribution descriptors of the independent variables used in the MLR and RLog models.

4 Results and discussion

4.1 Spatial–temporal analysis of PM_i

4.1.1 PM_i-1 h data and descriptive statistics

Table 3 presents the descriptive statistics for five variables (PM₁-1 h, PM_2.5-1 h, T-1 h, RH-1 h, WS-1 h) for dry and rainy seasons. The average concentration over the 56 days monitored in each season was higher for PM_2.5 than for PM₁. For PM_2.5 in the rainy season the maximum concentration recorded was 955 µg m⁻³ and the median was 12 µg m⁻³. Likewise, the standard deviation indicates the large dispersion of this data set (156 µg m⁻³). During the sampling, the temperature in Guayaquil was stable and warm (T between 20 and 40 °C) with slightly higher temperatures in dry than in the rainy season. The city showed high relative humidity with the greatest values occurring during the rainy season. The predominant wind was calm (WS; < 1 m s⁻¹) and higher speeds in drought (light breezes).

Table 3 Descriptive statistics of hourly series of PM₁ and PM_2.5, temperature, wind speed and relative humidity in dry and rainy seasons

Figure 3 visually shows the tendencies of temperature, relative humidity, and wind speed during the sampling of PM_i. Qualitatively, the meteorological variables do not show variations during the sampling. Instead, changes in the tendencies of these variables are observed during the two seasons. In general, in the rainy season, temperatures were warmer and relative humidity was higher, reaching 22% of the sampling dates at 100% RH. Calm winds predominated (84% of the sampling time) and the velocity rarely exceeded 3 m s⁻¹ (1% of the sampling dates). The highest wind speeds occurred during the dry season. In the rainy season, the wind speed was often 0 m s⁻¹. Finally, the Dickey-Fuller stationarity test showed that all the series were stationary in their original form (p value < 0.01).

Fig. 3

Hourly time series of temperature, wind speed and relative humidity during PM₁ and PM_2.5 sampling in dry and rainy seasons

Figure 4 shows a boxplot of PM_i-1 h for both seasons (88% of PM₁ data; 84% of PM_2.5 data). The highest concentrations of airborne particulate matter are observed between 14h00 and 18h00. The lowest concentrations occur after sunrise (06h00 and 10h00). The city's activities and local meteorology influence the seasonal trend of the hourly PM concentration.

Fig. 4

Boxplot of PM₁-1 h and PM_2.5-1 h for the two seasons. Note: Red dashed line marks the threshold suggested by WHO (2021): PM_2.5-24 h = 15 µg m.⁻³

At night a stable level of pollution is observed as a result of the nocturnal atmospheric stability that prevents the vertical movement of particles in air. During daylight hours, there is a strong diurnal variation, since during the sunny hours, the planetary boundary layer extends to a greater height generating certain atmospheric instability that helps the dispersion of contaminants (Azad 2012; Vilà-Guerau de Arellano et al. 2015). This behaviour of the boundary layer and the timetable of anthropogenic activities helps to explain the hourly seasonal PM pattern during a day.

4.1.2 PM_i-24 h data and descriptive statistics

Figure 5 shows the concentration of PM_i-24 h in the four sampling sectors in dry and rainy seasons; the reference threshold (PM_i-24 h = 15 µg m⁻³) is marked with a dashed line. Three days for PM_2.5-24 h-dry in the industrial sector are not shown because less than two-thirds of the hourly concentrations were recorded on each of those days. This figure shows that the concentration is lower in the rainy season due to the wet deposition generated by the high precipitation that is common in Guayaquil. For both fractions and seasons, the reference threshold was exceeded a total of 45% of the time, which serves to question the acceptability in the air quality in these sectors.

Fig. 5

PM₁-24 h and PM_2.5-24 h concentrations by sector and season. Note: Red dashed line marks the threshold suggested by WHO (2021): PM_2.5-24 h = 15 µg m.⁻³

In the Cement plant sector, three days were recorded with very high concentrations of PM_2.5-24 h-rain (see Fig. 5). It should be noted that no event was identified on the social networks on those dates to justify it; this could be atypical and the result of some fortuitous situation. Under this premise, it can be suggested that this sector has good air quality. It is necessary to make continuous measurements in this sector to verify whether the recorded concentrations are unusual.

In the Industrial sector, the PM_i-24 h concentrations were exceeded on all sampling days, with higher concentrations observed in the dry season. High PM_2.5 concentrations could be a consequence of the strong industrial activity and the continuous occurrence of traffic-related events on the two expressways that circumscribe the sector. The downtown sector has a high influx of diesel-powered public transport and has elevated PM₁ concentrations during the dry season (slightly exceeding the threshold in this season). Meanwhile, the threshold is not exceeded during the rainy season, possibly because of precipitation that occurred on the sampling days.

In the Industrial sector for PM_2.5-24 h, during the rainy season, insufficient hourly data were collected on three dates to estimate the 24-h concentration.

In the Cement plant sector for PM_2.5-24 h, during the rainy season, the outstanding concentrations were: 643, 181 and 113 µg m⁻³.

The Residential sector exceeded the PM_2.5-24 h threshold on most days. In this sector, unusual events were published in social networks on every sampling day. These events were vehicle blockages and fires (one of the fires coincided with the day of highest concentration: 20.6 µg m⁻³). During the dry season, ten vegetation/forest fires were published on social networks during the 28 days of monitoring. Therefore, it would be advisable to carry out continuous maintenance of green areas to reduce the probability of vegetation fires.

Overall, in the dry season, PM₁-24 h exceeds the threshold in the industrial and downtown sectors. Meanwhile, in the rainy season the threshold is exceeded in the Industrial and Residential sectors. For PM_2.5-24 h all sectors continuously surpass the threshold in the dry season, while in the rainy season the threshold is exceeded for the cement plant, and the industrial and residential sectors.

Chen et al. (2017) mention that the health effects of PM₁ are potentially more harmful than those of PM_2.5. This becomes relevant when noticing that PM₁-24 h exceeded the proposed threshold 50% of the monitored days. Moreover, Hu et al. (2022) conducted a systematic review finding that, for a 10 µg m⁻³ increase in PM₁, there is a pooled odds ratio of 1.05 (95% CI 0.98–1.12) for total respiratory diseases, 1.25 (95% CI 1.00–1.56) for asthma, and 1.07 (95% CI 1.04–1.10) for pneumonia. This establishes that there is a positive association between this contaminant and these health outcomes. Similarly, an increase of 10 µg m⁻³ of PM_2.5 was associated with a 0.65% increase in mortality by Orellano et al. (2020).

4.2 Single influencing factor analysis on PM_i concentrations

4.2.1 Meteorological variables

The continuous variables are the meteorological parameters measured during the sampling campaign (Table 1). The influence of ambient temperature and relative humidity, wind speed and direction, and the planetary boundary layer height on PM_i remains a topic of interest in air quality research (Chen et al. 2020). To measure the hourly temporal influence of meteorological parameters (T-1 h; WS-1 h; RH-1 h) on PM_i, cross-correlation functions (CCFs) were estimated for the dry and rainy seasons, enabling the determination of time lags at which a statistical relationship arises (Table 4 for PM₁ and Table 5 for PM_2.5).

Table 4 Cross correlation function results for PM₁

Table 5 Cross correlation function results for PM_2.5

The sign of the relationship between ambient temperature and PM₁-1 h was positive in both seasons and for all sectors. The correlations for PM_2.5-1 h and ambient temperature were positive during the dry season. Relative humidity was negatively correlated with PM₁-1 h in both seasons and for PM_2.5-1 h in the dry season, and for one sector in the rainy season. However, two sectors showed positive correlations in the rainy season. The relationships between PM and WS were highly variable for all sectors and seasons, having both positive and negative directions. All correlations between the meteorological variables and the PM_i are observed between 0 and 12 h.

To measure the daily temporal influence of meteorological parameters (T-24 h; WS-24 h; RH-24 h) on PM_i-24 h, the Pearson correlation was applied (see Tables 6 and 7). PM₁-24 h has a moderate negative correlation with minimum temperature and relative humidity and a positive moderate linear correlation with wind speed. PM_2.5-24 h also has a moderate negative correlation with minimum temperature and relative humidity.

Table 6 Pearson correlations between PM₁-24 h and meteorological parameters

Table 7 Pearson correlations between PM_2.5-24 h and meteorological parameters

The negative bivariate relationship between PMi-24 h and T-24 h is opposite to that found in the hourly analysis, but this is not uncommon in air quality analysis. Perez-Martinez and Miranda (2015) [PM10-1 h] found positive and statistically significant relationships between PM and temperature using CCF. Wang and Ogawa (2015) [PM2.5-monthly] [PM10-PM2.5-1 h] and Morantes et al. (2019) [PM1-24 h] also reported positive relationships between temperature and PM for different fractions applying correlation techniques. The simplest and best model recommended by Rybarczyk and Zalakeviciute (2018) [PM2.5-imin] has a positive relationship between PM and Temperature. Studies that apply MLR, such as Ul-Saufie et al. (2012) [PM10-24 h], Rybarczyk and Zalakeviciute (2018) [PM2.5-imin], Chelani (2019) [PM2.5-24 h] and Zhao et al. (2018) [PM2.5-4 h], report both negative and positive relationships between PM and T. They also report that the change in the direction of the relationship may be due to the type of variables included in the model, such as changes in meteorological parameter conditions, modification of the time scale, seasonality, and may also be due the statistical technique applied and small sample sizes.

Zhao et al. (2022) [PM2.5-annual] and Alvarez et al. (2022) [PM2.5-24 h] found positive correlations for temperature and PM2.5, applying complex statistical techniques. Reasons for the positive correlation are: more energy consumption in cold temperatures (hence more combustion emissions) and atmospheric stability on days of lower surface temperature leading to higher PM2.5 concentrations. However, Zhang et al. (2022) [PM2.5-1 h], Deng et al. (2022) [[[PM2.5-24 h], Wang et al. (2022b) [PM2.5-24 h], Yu et al. (2022) [PM2.5-1 h], Li et al. (2022) [PM2.5-24 h], Han et al. (2022) [PM2.5-1 h], Ambade et al. (2021b) [BC—PM2.5 Month], Deng et al. (2022) [PM2.5-24 h], Owoade et al. (2021) [PM2.5-24 h] all found negative correlations for temperature and PM_2.5 when applying complex statistical techniques. The main explanation for these correlations is attributed to temperature-related atmospheric convections: an increase in the air temperature increases the atmospheric turbulence (vertical diffusion depends on an increase in ambient temperatures at the urban boundary layer), which accelerates the dispersion, diffusion, and dilution of pollutants.

Both negative and positive relationships between PM and temperature are found for different sectors, particle fraction sizes, and sampling periods (1 h, 4 h, 24 h), which might indicate that the relationship between PM and T is polynomial. This is was also identified by a review of the effects of meteorological conditions on PM_2.5 concentrations, and showing that temperature had both positive and negative influences of the contaminant (Chen et al. 2020).

The negative coefficient between RH and PM_i-1 h-24 h suggests that there is a process of particle scavenging from the atmosphere. However, one positive correlation was found for PM_2.5-1 h-rainy with a lag of 12 h, suggesting that the correlation between PM and RH could have both positive and negative directions. Ul-Saufie et al. (2011, 2012) [PM₁₀-24 h], Deng et al. (2022) [PM_2.5-24 h], Owoade et al. (2021) [PM_2.5-24 h], Li et al. (2022) [PM_2.5-24 h], Alvarez et al. (2022) [PM_2.5-24 h] reported positive relationships between PM and RH performing MLR and other more complex statistical approaches. The reason is that PM_2.5 attaches to water vapour when the relative humidity is high (hygroscopic growth of the particles) and so particulate pollutants tend to cluster, and environmental quality worsens. However, Wang et al. (2022a) [PM_2.5-annual], Wang et al. 2022b [PM_2.5-24 h], Ambade et al. (2021b) [BC—PM_2.5 Month] reported negative correlations between PM and RH. The direction of the relationship is attributed to the diffusion and deposition of particulate matter occurring at higher RH when particulate pollutants tend to gather mass and fall to the ground on days with a high relative humidity. Both positive and negative relationships between PM and RH were found by Wang and Ogawa (2015) [PM_2.5-monthly] [PM₁₀-PM_2.5-1 h] and Zhao et al. (2018) [PM_2.5-4 h], Zhang et al. (2022) [PM_2.5-1 h], Yu et al. (2022) [PM_2.5-1 h], Han et al. (2022) [PM_2.5-1 h]. The main reason for a change in the direction of the relationship between these variables is that, with increasing relative humidity, the bulk PM_2.5 concentration rises at first and later declines. Overall, it appears that the correlation between PM_2.5 and RH would represent a complex nonlinear relationship (Chen et al. 2020). This is consistent with the findings of this study.

When investigating the relationships between PM_i-1 h-24 h and wind speed, Zhao et al. (2022) [PM_2.5-annual], Zhang et al. (2022) [PM_2.5-1 h], Wang et al. (2022a) [PM_2.5-annual], Wang et al. (2022b) [PM_2.5-24 h], Li et al. (2022) [PM_2.5-24 h], Ambade et al. (2021b) [BC—PM_2.5 Month], Alvarez et al. (2022) [PM2.5-24 h] reported a negative correlation between these parameters, explained by the diffusion of PM_2.5 due to higher wind, or inversely, slower winds would be related to the increase in particulate matter (PM₁₀ and PM_2.5) in the atmosphere (He et al. 2013; González and Torres, 2015; and Taheri and Sodoudi, 2016). Positive correlations between PM and WS have been found by Ul-Saufie et al. (2011) [PM₁₀-24 h]; Munir et al. (2017) [PM₁₀-PM_2.5-1 h] and Rybarczyk & Zalakeviciute (2018) [PM_2.5-_imin]. Wang and Ogawa (2015) and Munir et al. (2017) concluded that if the wind speed is high enough, it can transport large quantities of contaminants from neighbouring regions, at the local, regional, and global scales. Ul-Saufie et al. (2012) [PM₁₀-24 h], Wang and Ogawa (2015) [PM_2.5-monthly], Nazif et al. (2016) [PM₁₀-24 h], Giri et al. (2008) [PM₁₀-24 h]; Chelani (2019) [PM_2.5-24 h] found circumstances when the sign of the relationship changed for the same sample. Deng et al. (2022) [PM_2.5-24 h] and Han et al. (2022) [PM_2.5-1 h] reported that the impacts of the wind speed on PM_2.5 are nonlinear over time: when wind speeds are low, air pollutants cannot be transmitted or diffused, a moderate increase in wind speed is conducive to the dispersion and dilution of pollutants, while high wind speeds with a dry surface environment lead to the dust events. You et al. (2017) caution that the sign of the PM-WS relationship can change for the same location due to seasonal effects, and this correlates with the outcomes of this study. In addition, the authors point out that the sign change is also due to the temporal scale or the geographic location. This suggests that the PM-WS relationship is polynomial (Chen et al. 2020).

All the above would serve to explain that, although there are expected relationships between PM and meteorology (local meteorology is an important driver for local air quality), different relationships between meteorological variables (T, RH and WS) and several fractions of PM (PM_2.5; PM₁₀; TSP) measured for various averages (hourly, daily, weekly and annual) are reported in the bibliography, reflecting complex linear and nonlinear relationships between all these parameters. Moreover, the temporal scale of the measurement (i.e. hourly, daily—with and without delays) also influences the relationships that could be found. Furthermore, every study would have variables outside its scope, resulting in relationships that are not always fully explained.

4.2.2 Dichotomous variables

The dichotomous variables measured during the sampling campaign are meteorological, geographic and event-related parameters (Table 1). The specific location, emissions resulting from habitual industrial activities, common public transport, unusual events (vegetation fires, significant variations in vehicular traffic) and the seasons are among variables of interest when assessing the spatio-temporal variations of PM_i concentrations (Taheri and Sodoudi 2016).

Tables 8 and 9 show a comparison between the dichotomous variables and PM_i-24 h concentrations using the Student’s t-test for independent samples with α ≤ 0.05. Means that are statistically different from each other are highlighted in bold.

Table 8 Student’s t-test for the influence of dichotomous variables on PM₁-24 h

Table 9 Student’s t-test for the influence of dichotomous variables on PM_2.5-24 h

Occurrences of unusual events that promote emissions of PM_i are related to higher PMi-24 h concentrations. The season is also relevant, showing that in the dry season there is an increase in PM_i concentrations. Alvarez et al. (2022) and Morantes et al. (2019) report similar trends by region (Colombia and Venezuela, respectively), and by countries with rainy and dry seasons as well. For PM₁-24 h, this is also related to the inverse relationship with daily precipitation events. Results indicate that the increase in rainfall can effectively reduce PM_i pollution (Alvarez et al. 2022; Carmona et al. 2020; Morantes et al. 2019; Deng et al. 2022; Li et al. 2022; Han et al. 2022; Ambade et al. 2021b; Chen et al. 2020). The characteristic emissions of each sector also influence the PM concentration; for example, the industrial sector showed the highest PM_i concentrations where there are a large number of emission sources from the chimneys of medium and small industries, and vehicular traffic on fast roads that circumscribe it. It should be noted that during the sampling approximately 87% of the unusual events occurred there. On the other hand, the Student t-test showed that the cement plant sector is associated with lower PM_i concentrations. This result seems to be independent of the fact that high pollution events (atypical) were recorded. However, in the rest of the sampling, comparatively low concentrations were generally recorded, regardless of the fraction size. Downtown is associated with higher PM concentrations; however, the result is only significant for PM_2.5-24 h. The results above confirm that land-use plays a significant role in pollutant concentrations (Owoade et al. 2021; Encalada-Malca et al. 2021; Chiquetto et al. 2020; Zhou and Lin, 2019).

4.3 Multiple linear regression: PM_i-24 h

A linear regression was performed with the variables that were found to be significantly related to PM_i-24 h in the bi-variate analysis; the MLRs are reported in Tables 10 and 11. The model for PM₁-24 h is able to explain 57% of the variance (adjusted R² = 0.537; p < 0.000) from three IVs: Rain, Unusual Events, and the Cement Plant. Model A (Eq. 4) and model B (Eq. 5) are constructed from the information in Table 9:

$$\begin{array}{*{20}l} {\left[ {{\text{Model A}} - {\text{PM}}_{1} {\text{:standardised model}}} \right]:} \hfill \\ {\left[ {{\text{PM}}_{1} - 24{\text{h}}} \right] = - 0.552\left[ {{\text{Rain}}} \right] + 0.438\left[ {{\text{Unusual Event}}} \right] - 0.528\left[ {{\text{Cement Plant}}} \right] + \EUR } \hfill \\ \end{array}$$

(4)

$$\begin{gathered} \left[ {{\text{Model B}} - {\text{PM}}_{1} :{\text{predictive model}}} \right]: \hfill \\ \left[ {{\text{PM}}_{1} - 24{\text{h}}} \right] = 15.193 - 4.558\left[ {{\text{Rain}}} \right] + 3.177\left[ {{\text{Unusual Event}}} \right] - 4.635\left[ {{\text{Cement Plant}}} \right] \hfill \\ \end{gathered}$$

(5)

Table 10 Summary of the multivariate model for PM₁

Table 11 Summary of the multivariate model for PM_2.5

The model shows that the independent variable with the highest weight when predicting PM₁ concentrations is the occurrence of a rain event on the sampling day (see β in Table 10). It also indicates that, when anthropogenic events occur, PM₁ concentration increases, which agrees the results of the bi-variate analysis. The cement plant sector produces a reduction of 0.528 units, possibly due to comparatively low PM concentrations measured in this sector. Overall, it was found that the sectors (sector-specific emission sources) together with emissions from unusual events combined with local meteorological parameters influenced the PM₁-24 h concentrations.

Model B indicates that if all independent variables are held constant, except for a single selected variable, a one-unit increase in the selected variable gives an increase in PM₁-24 h equivalent to the variable’s attached B coefficient. For Unusual Events, an increase in its value by one unit implies an increase of 3.177 units of PM₁-24 h (in µg m⁻³). A similar analysis is applied for the other variables.

The model for PM_2.5-24 h can explain 73% of the variance (adjusted R² = 0.691; p < 0.000) from three IVs: Dry season, and the Industrial and Cement Plant sectors. Model A (Eq. 6) and model B (Eq. 7) are constructed from the information in Table 9:

$$\begin{aligned}& \left[ {{{Model A}} - {{PM}}_{{{2}.{5}}} :{{ standardised model}}} \right]: \hfill \\ &\left[ {{{PM}}_{{{2}.{5}}} - {{24h}}} \right] \, = \, 0.559 \left[ {{Dry season}} \right] \, + \, 0.557 \left[ {{{Industrial}}} \right] \, - \, 0.247 \left[ {{Cement Plant}} \right] \, + \, \EUR \hfill \\ \end{aligned}$$

(6)

$$\begin{gathered} \left[ {{{Model B}} - {{PM}}_{{{2}.{5}}} :{{ predictive model}}} \right]: \hfill \\ \left[ {{{PM}}_{{{2}.{5}}} - {{24h}}} \right] \, = { 11}.{158 } + { 5}.{328 }\left[ {{Dry season}} \right] \, + { 5}.{851 }\left[ {{{Industrial}}} \right] \, - { 2}.{892 }\left[ {{Cement Plant}} \right] \hfill \\ \end{gathered}$$

(7)

The most influential variable when predicting PM_2.5 concentration is the dry season, since in Guayaquil it rarely rains during this climatic season. The association between the industrial sector and PM_2.5-24 h indicates that emissions in this sector add a value of 0.557 units to the value of PM, possibly due to the concentration of medium and small industries, and most traffic events occurred in the surrounding area. The Cement Plant sector is associated with lower PM concentrations. Overall, the sectors (sector-specific emission sources) and long-term local meteorological parameters influenced the PM_2.5-24 h concentrations. The relationships described herein for the Model B PM_2.5 also explain those for Model B PM₁.

Performance indicators (Tables 10 and 11) were used to measure accuracy and errors in the MLR models. Accuracies were measured by PA, R² and IA indicators, and errors by RMSE, MAE and NAE. Although there is no consensus on the acceptability of the magnitude of the PIs, but accuracies tending to 1 and errors tending to 0 are desirable. The values for PA, R² and IA were higher than 0.5, which indicates good accuracy of the MLR models, the PM_2.5 model having a slightly higher accuracy. The values of RMSE, MAE and NAE were low and close to zero, indicating that the models had low errors, with the PM₁ model reporting lower errors. Our values are within those presented by UI-Saufie et al. (2012) for other MLR studies.

4.4 Exceedance’s analysis

4.4.1 Bivariate analysis

Tables 12 and 13 show the results of applying the Student’s t-test between EPM_i-24 h and continuous IVs. The results indicate that the maximum and minimum temperatures influence the exceedances of the PM₁ threshold (Table 12). The minimum and average temperatures, and the lower wind speeds influence PM_2.5 exceedances (Table 13).

Table 12 Comparison of means of the Student’s t-test between dichotomous predicted variable (PM₁) and continuous independent variables

Table 13 Comparison of means of the Student’s t-test between dichotomous predicted variable (PM_2.5) and continuous independent variables

Tables 14 and 15 show the results of applying the Pearson correlation between EPM_i-24 h and dichotomous IVs. The Industrial sector is associated with exceeding the PM₁ threshold. For PM_2.5, the Industrial sector and the dry season are associated with exceeding the threshold. For both size fractions, the Cement Plant sector is linked to not exceeding the threshold. The reasoning for this relationship is explained by the single influencing factor analysis on PM_i concentrations (see Sect. 4.2).

Table 14 Pearson correlations for EPM₁-24 h – Rlog

Table 15 Pearson correlations for EPM_2.5-24 h – Rlog

4.4.2 Logistic regressions (RLog)

Table 16 shows the classification table for the dependent variable without the IVs for PM₁-24 h. There is a 50% probability of success when it is assumed that the PM₁-24 h threshold is always exceeded.

Table 16 Classification table for predicted variable without independent variables for PM₁-24 h

The LOGIT model (Table 17) was developed with the IVs that were shown to be significantly related to the PV by the bivariate analysis. The positive sign of the coefficient B attached to the unusual event variable indicates that the occurrence of anthropogenic events increases the probability of exceeding the PM₁-24 h threshold. This most likely to be because of the emissions of fine PM associated with them. Registering an episode of rain on the sampling day, and sampling in the Cement plant sector, are associated with maintaining PM₁ concentrations below the threshold. The results of the RLog were aligned with the relationships obtained by the MLR: local short-term meteorology and the sampling sector influenced PM₁ concentrations. The mathematical expression of the LOGIT model is defined by Eq. (6) with the values given by Table 17.

Table 17 LOGIT model for PM₁-24 h

The mathematical expression of the LOGIT model is as follows:

$$pi=\frac{1}{\left(1+{e}^{-0.540-2.932\times Rainfall+2.438\times Unusual.event-23.427\times Cement.Plant}\right)}$$

(8)

pi: Probability that PM₁-24 h exceeds the threshold when the values of each of the independent variables are equal to their average value.

Table 18 presents the classification table of the LOGIT model. It shows the observed group (rows) and the dependent group (columns) with a sensitivity of 96% and a specificity of 61%. These values show the model adequately classifies positive responses slightly better than negative responses. Validation using the indicators of false positives and false negatives, shows 29% of false positives and 7% of false negatives, which indicates a tendency to overestimate results. Overall, the model presents a holistic success rate of 78%.

Table 18 LOGIT model Validation for EPM₁-24 h

For PM_2.5-24 h, Table 19 shows there is a 69% probability of always exceeding the threshold. The LOGIT model for exceeding the PM_2.5 (Table 20) threshold indicates that the dry season and the Industrial sector are associated with exceeding the PM_2.5 threshold and the Cement Plant sector is associated with concentrations below the threshold. Overall, it can be said that long-term meteorological variables and the sampling sector influenced PM_2.5 concentrations during the sampling campaign. This model has an 82% holistic success rate and ~ 1/5^th of false predictions (Table 21). The mathematical expression of the EPM_2.5-24 h-LOGIT model is defined as follows:

Table 19 Classification table for predicted variable without independent variables for PM_2.5-24 h

Table 20 LOGIT model for EPM_2.5-24 h

Table 21 LOGIT model Validation for EPM_2.5-24 h

$$pi=\frac{1}{\left(1+{e}^{-\left(-1.207\right)+2.915\times dry.season+1.993\times industrial-3.143\times Cement.Plant}\right)}$$

(9)

pi: Probability that PM_2.5-24 h exceeds the threshold when the values of each of the independent variables are equal to their average value.

4.5 Air quality assessment, main findings and envision for future work.

To argue what constitutes good or bad air quality is a complex task because many indicators can be used when trying to define it. Some common indicators include or rely on peoples’ perception of air quality, physiological-acute responses (i.e. sensory irritation or odour) and visual/tangible aspects of the air (i.e. SMOG). However, the most common approach is one that is based on thresholds where a contaminant’s concentrations are compared to corresponding guidelines or referenced standards. The major weaknesses of a threshold-based approaches when defining air quality are, (i) that they provide insufficient information to infer population health because being above or below a threshold is the only criteria and, (ii) there is a lack of consensus on the magnitude of the threshold values among recognized health agencies and governments. On the other hand, the biggest strength of threshold-based approaches is their usefulness for identifying the tendencies of contaminant concentrations, which is the reason why it is the most commonly used approach by stakeholders in the decision making process for assessing air quality. Moreover, efforts have been made into defining the constituents of acceptability of air quality (Persily, 2015) and, although this is proposed in an indoor environment context, the overall message is easily applicable to other air quality contexts, as acceptable air quality is air in which there are not likely to be contaminants at concentrations that are known to pose a health risk.

Given these arguments, and considering the PM_2.5-24 h concentrations exceeded the WHO thresholds (WHO 2021) on 48% of days, we argue that the air quality in Guayaquil should be classified as unacceptable because there are likely to be contaminants at concentrations that are known to pose a health risk. Currently, the national air quality standard of Ecuador for ambient PM_2.5-24 h is 50 ug.m⁻³ and so the PM_2.5-24 h concentrations found her are below this magnitude. However, this threshold could be unacceptable using Persily’s definition of acceptable air quality. Guayaquil is not currently described as one of the most polluted cities in Latin America and this study aims to provide cautionary tale that may help the city to avoid its PM pollution levels reaching those of cities in neighbouring countries.

The results of the single factor analysis showed that ambient air temperature, relative humidity, and wind speed influence the PM_i-1 h-24 h concentration at both temporal scales. Overall, the influence of meteorological parameters on PM_i includes a positive correlation with hourly temperature (atmospheric stability at hours of lower surface temperature lead to higher PM_i concentrations, throughout the day), a negative correlation with 24 h average temperature (daily temperature increase atmospheric turbulence accelerating the dispersion of pollutants) and relative humidity (high RH promotes the process of particle scavenging from the atmosphere) and both positive and negative correlations with hourly and 24 h wind speed (when wind speeds are low, PM_i is not dispersed, moderate increase in wind speed is conducive to the dispersion and dilution of the contaminants, and high wind speeds could leading to the transport of PM from areas surrounding the city). The spatiotemporal variations and connections of single meteorological factors on PM_i concentrations agreed with the work of others that applied more complex statistical techniques. Nevertheless, a limitation is that the techniques used in this study could only identify one directional relationships showing only one part of the picture, because in cases of polynomial relationships only the strongest relation was identified.

The linear regression model and the exceedance model for PM₁ show the variables that are most influential on this contaminant are anthropogenic events (emissions from traffic jams and vegetation/forest fires), and rainfall events (due to their cleaning effect). For PM_2.5, the most influential variables are emissions from the industrial sector (land use related factor) and the dry season (associated with the lack of rain). All the models identified the Cement Plant sector with a negative sign (land use related factor), possibly associated with the sector’s flat orography and the winds that disperse contaminants. The models indicate that precipitation has a cleaning effect on both size fractions; however, we found that the precipitation effect is significant for PM₁ on a daily scale, whereas it is influential at the seasonal scale for PM_2.5. The exceedance models were designed in agreement with the WHO (2021) monitoring air quality guidelines and to be used for making policy decisions. The models show that adequate air quality (below WHO thresholds) is highly dependent on sector emissions (land use) and precipitation patterns.

The models presented here provide information on air quality that is not given by local government monitoring, and also plays a fundamental role in defining the potential factors that contribute to PM pollution, and the current air quality acceptability. It presents a much needed update to information on Guayaquil's air quality.

One limitation in our study is that the sampling of PM_2.5 and PM₁ was not simultaneous, because of equipment availability. This limits our understanding of the behaviour of each fraction related to the other. Another limitation is the relatively short sampling periods that resulted in a low number of samples taken in each of the four locations. However, the sampling times and periods include different seasonal variations and show weekday to weekend variations. Moreover, the results indicate that, even for this relatively low number of samples, different emission sources of PM were accounted for. Nevertheless, it is recommended to monitor PM throughout the year, at least in these four sectors of the city.

The current work results could be used for: (i) designing an adequate and complete monitoring system; (ii) improving local regulations with more appropriate thresholds for acceptable PMi concentrations that meet a definition of acceptability; (iii) focus on mitigation by sector (location) by setting targets for decreasing emissions; (iv) developing adequate adaptation policies; and (v) designing an effective early warning system (EWS) to cope with this environmental hazard.

5 Conclusions

We applied bi-variate correlation techniques and performed multiple linear and logistic regression models to extend the study on the spatio-temporal evolution of PM1 and PM2.5 concentrations in Guayaquil city, Ecuador. The results are equivalent to similar studies made in other regions that using more complex statistical techniques.

The results of the spatio-temporal study question the air quality in the city because the exceedances of the PM_2.5-24 h of World Health Organisation thresholds occurred on 48% of measured days. The industrial sector is the most compromised, by its own industrial activity, and because it is surrounded by fast roads where unusual anthropogenic events tend to happen.

The multiple linear regression model for PM₁-24 h showed that rain (due to its cleaning effects) and the being located in the cement plant sector (due to its flat orography) are factors that improve air quality (β_PM1-rainfall = −0.552, p < 0.00; β_{PM1-cement_plant} = −0.528, p < 0.00, respectively) while unusual events (emissions from traffic jams and vegetation/forest fires) deteriorate air quality (β_{PM1-unusual_events} = 0.438, p < 0.00). Conversely, a multiple linear regression model for PM_2.5-24 h shows that the dry season (because of the lack of rain) and the industrial sector (due to its strong industrial activities) deteriorate air quality (β_{PM2.5-dry_season} = 0.559, p < 0.00; β_{PM2.5-industial} = −0.557, p < 0.00, respectively) while the cement plant sector promotes lower PM concentrations (β_{PM2.5-cement_plant} = −0.247, p < 0.00). The logistic regression models reflect the same results as the linear regression models, indicating that those are the same variables that help to maintain concentrations below the WHO’s daily thresholds or to promote its exceedance (PM_i-24 h > 15 µg m⁻³).

The influence of meteorological variables on hourly concentrations was evidenced through a bivariate cross-correlation function analysis. This analysis showed that in general, a higher hourly temperature (Lag = 4 h, CC_[T~PM1]-1 h Max = 0.680, p < 0.00) and lower relative humidity (Lag = 5 h, CC_{[RH~PM1]-1 h} Max = −0.693, p < 0.00) were associated with higher PM₁-1 h concentrations, while the effect of hourly wind speed is variable, both promoting higher PM (Lag = 6 h, CC_{[WS~PM1]-1 h} Max = 0.254 p < 0.00) and lower PM (Lag = 10 h, CC_{[WS~PM1]-1 h} Max = −0.269, p < 0.00). Similarly, higher hourly temperature (Lag = 6 h, CC_{[T~PM2.5]-1 h} Max = 0.673, p < 0.00) and lower relative humidity (Lag = 6 h, CC_{[RH~PM2.5]-1 h} Max = −0.687, p < 0.00) were associated with higher PM_2.5-1 h concentrations, while the effect of hourly wind speed is variable, both promoting higher PM (Lag = 0 h, CC_{[WS~PM2.5]-1 h} Max = 0.495 p < 0.00) and lower PM (Lag = 10 h, CC_{[WS~PM2.5]-1 h} Max = −0.360, p < 0.00). The influence of meteorological variables on daily concentrations was evidenced through a bivariate Pearson correlation analysis. It was observed that higher PM₁-24 h and PM_2.5-24 h are associated with lower temperature (r_T~PM1 = −0.393, p = 0.01; r_T~PM2.5 = −0.534, p = 0.01, respectively) and lower relative humidity (r_RH~PM1 = −0.344, p = 0.05; r_RH~PM2.5 = −0.321, p = 0.05, respectively), while higher wind speeds appear to increase PM_2.5-24 h (r_WS~PM2.5 = −0.362, p = 0.05). Overall, the bi-variate analysis showed that temperature, relative humidity, and wind speed are significantly linked to PM₁ and PM_2.5 concentrations. Our results show that hourly and daily air temperatures, relative humidity, and wind speed have a complex nonlinear relationship with PM concentrations in the city of Guayaquil.

The results shows the need to improve the air quality monitoring system in Guayaquil because there is currently a scarcity of updated information and no particulate matter monitoring. Public policies and interventions should be aimed at regulating land use together with the constant monitoring of emission sources, both those that are regular and unusual.