1 Introduction

The number of hydro-meteorological extreme events such as floods and droughts are increasing in frequency and intensity globally (Thomas and López 2015; Grillakis 2019; Marsooli et al. 2019). The spatial distribution of these hazards is expected to increase throughout the South Pacific region (Shen et al. 2018). These hydrological hazards can be impacted by a range of climatic phenomena. For instance, the South Pacific Convergence Zone (SPCZ), a mass of convective cloud bands, is one of the leading climate drivers in the oceanic nations, in the South Pacific (SP) region (Vincent 1994). Minute changes in the sea surface temperature can displace the SPCZ, triggering anomalies in annual precipitation (Strauch et al. 2015). Fiji, one of the oceanic islands in the South-Western Pacific, is prone to hydro-meteorological hazards (Anshuka et al. 2020; Moishin et al. 2020; Varo et al. 2020). The movement of SPCZ northward or southward in Fiji results in extreme wet and dry conditions, respectively.

Risk management entails reducing harm to life, livelihoods, property and the surrounding environment (Zschau and Küppers 2013). A pivotal step to risk management necessitates establishing efficient early warning systems. Empirical studies in the Pacific have shown that informational and behavioural adaptive strategies such as responding to warnings are more practical in mitigating hydro-meteorological risks (Handmer and Iveson 2017; Anshuka et al. 2021; Pauli et al. 2021). Therefore, an early warning system providing climate outlooks on extremes is of utmost importance (Iese et al. 2021). An ideal hydrological early warning system would consist of a dense observation network that monitors key precipitation, temperature, and discharge parameters. However, insufficient gauge stations are often a deterrent to efficient hazard monitoring in Pacific nations. Despite the challenges, there are opportunities to devise an early warning system in these countries. Instead of investing in expensive observation networks, a cost-beneficial strategy would be to use data-driven methods such as machine learning models.

Among the many machine learning methods (Elman 1990), deep learning methods have shown innovation in the area of forecasting across a range of fields (Chandra et al. 2016; Lin et al. 2018; Shi et al. 2019). The method considers different neural network architectures and learning algorithms that are particularly suited for big data and multimedia  problems (Xu and Mo 2020). Deep learning models can be loosely characterised into feedforward and recurrent neural network (RNN). Simple neural networks, also known as multilayer perceptron (Gardner and Dorling 1998) and convolutional neural networks (CNN) (Albawi et al. 2017), are distinguished examples of feedforward neural networks. RNN feature feedback (recurrent) connections for modelling temporal sequences and dynamical systems (Elman 1990; Medsker and Jain 1999). The long short term memory (LSTM) network model (Hochreiter and Schmidhuber 1997); is a prominent RNN used for temporal sequences (Shi and Kim 2017) and language modelling (Wilcox et al. 2018).

Deep learning methods have seen an application for hydrological extreme modelling (Anshuka et al. 2019; Poornima and Pushpalatha 2019; Kaur and Sood 2020). However, several studies have handled the problem from a point forecast perspective using a univariate approach (Poornima and Pushpalatha 2019; Liu et al. 2020; Moishin et al. 2021). Specifically for Fiji, previous studies established point-based hydrological index forecasting with time series models (Anshuka et al. 2018) and simple neural network (Anshuka et al. 2020). Point forecasts only consist of memory in a single variable and disregard the interactive effects of other variables or features (Reichstein et al. 2019). On the other hand, a spatio temporal forecast can look at the relationships across the entire spatial extent and make a more accurate forecast based on the information learnt from multiple features for a response variable. Spatio temporal predictions are useful in accounting for the local climate, topography, and orographic effects (Verma et al. 2021). The deep learning model architectures have been shown to understand complex spatial and temporal characteristics of hydrological data (Ren et al. 2019). As the climate becomes more erratic, there is a need to employ models that can better understand more extreme and complex relationships (Agana and Homaifar 2017). In Fiji, the effective drought index (EDI) is considered a good indicator of hydrological extremes (Anshuka et al. 2020); based on sensitivity to precipitation and vegetation. Therefore, the index can be used to investigate extreme wet events (Deo et al. 2019; Moishin et al. 2020) and extreme dry events (Malik et al. 2021).

Relatedly, ocean-atmospheric circulation, such as large-scale sea surface temperature (SST) gradients, can also contain meaningful information which affects precipitation patterns (Griffiths et al. 2003; McGree et al. 2014). Multivariate analysis, such as principal component analysis (PCA), can be used to yield information on multi-dimensional climate features (Barnett and Preisendorfer 1987; Salinger et al. 2001). Other advantages of PCA include the use of smaller memory, reduction in execution time and bandwidth requirement due to dimensionality reduction (Kaur and Sood 2020). While PCA is a powerful tool in extracting useful information from multi-dimensional datasets, it does not fully account for non-linear relationships in the data (Lever et al. 2017). However, PCA can be used in conjunction with deep learning models to better understand non-linear behaviour (Oja 1989; Mohsen et al. 2018; Sammen et al. 2021). Given their success in other domains, there is a potential in adapting these hybrid methods to aid in understanding and predicting of spatio temporal hydro-meteorological extremes.

This study presents a spatial–temporal hydro-meteorological extreme forecasting framework in the South Pacific region, using Fiji as a case study. The framework forecasts EDI with the LSTM model using three different approaches: (i) univariate (ii) multivariate with neighbouring spatial points (iii) multivariate with neighbouring spatial points together and the principal components of SST. The novelty of this study exists in demonstrating the effectiveness of advanced deep learning methods for spatio temporal hydrological extreme events. Notably, the result from the framework could be used to help in long term decision making and policy design.

2 Related works deep learning for hydrological extremes

Deep learning methods have shown innovation in hydrological extreme forecasting (Hu et al. 2018; Ham et al. 2019; Anshuka et al. 2019; Dikshit et al. 2021). The advanced learning algorithm and model architectures of deep learning models can provide automatic feature extraction (such as CNNs) and enhanced memory (such as LSTM) which facilities learning of complex relationships within large datasets (LeCun et al. 2015; Janiesch et al. 2021). Recently, Dikshit et al. (2021), used the LSTM model to forecast drought index and concluded that LSTM models show superiority compared to conventional machine learning models. Similarly, deep belief networks for streamflow prediction, showed high accuracy over the simple neural network; however, its performance compared to support vector machine was low (Agana and Homaifar 2017). Wu et al. (2021), coupled wavelet analysis with an autoregressive integrated moving average (ARIMA) based LSTM model, and reported better drought forecasts. In another study, low-flow hydrological time-series predictions were generated, and conclusions suggested better performance of the RNN-LSTM model rather than the RNN model on its own (Sahoo et al. 2019). Shen et al. (2019), used multi-source remote sensing data for drought monitoring using a combination of LSTM, support vector regression, and PCA to classify extreme events with high accuracy. Furthermore, the performance of deep learning models has also been compared to climate models. Climate models are sensitive and generally accurate to model primary phenomena or variables such as temperature and rainfall; however, climate models tend to be less sensitive for secondary and tertiary phenomena such as droughts and floods (Maity et al. 2021). This notion was used to develop a drought assessment model based on multiple hydro-meteorological precursors such as wind speed, air temperature, rainfall and geo-potential height using deep learning algorithms, which showed higher skills compared to climate models on its own for drought monitoring (Maity et al. 2021).

Fang et al. (2021), considered a local sequential LSTM model to predict flood susceptibility using a feature engineering method. This technique showed improved skill in capturing information on flood conditioning factors and increased ability to deal with sequential modelling capabilities within different spatial relationships. Hu et al. (2019), created a spatio temporal flood prediction model using LSTM and a reduced-order framework. The hybrid framework reduced the dimensionality of large spatial datasets and retained the important orthogonal features and singular value decomposition. Due to the reduced features, the model showed high computational efficiency while maintaining the accuracy for real-time flood forecasting (Hu et al. 2019). Gude et al. (2020) used deep learning models, which showed better performance for flood peak predictions than other statistical models (such as ARIMA) as well as physical models (hydrological and hydraulic), despite the latter’s ability in establishing understanding based on equations between the provided datasets. Therefore, in this paper, we exploit spatio temporal forecasting with a combination of linear and non-linear approaches, given the ability of deep learning models to understand complex relationships in data.

3 Materials and methods

3.1 Study region

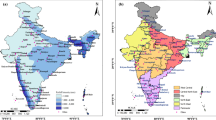
The boundaries of Fiji’s islands span between 16°–9.5° S and 177–180.25° E, occupying an area of 18,270 square kilometres (Neall and Trewick 2008) in the South-West Pacific (SWP) region. Fiji has a tropical climate with a mean annual precipitation of 1676–3544 mm. The average annual precipitation is unequally distributed as most of it is concentrated in the summer season (wet season). Fiji is a low-lying island with mainly low elevation (Fig. 1); however, a mountain range on the main island results in orographic effect induced rainfall (Terry 2005). Consequently, the rainfall distribution among the island differs; as such, the windward of the island receives 13% more rainfall (Terry 2005). The most recent station-based temperature trend analysis indicated increases in mean and extreme temperature together with warming for countries located in the Western Pacific Ocean, including Fiji (McGree et al. 2019). The effects of global warming on SST influences the SPCZ, and induces El-Niño Southern Oscillation (ENSO) conditions (Lorrey et al. 2012), which is the leading climate driver affecting precipitation patterns in the SWP (McGree et al. 2014). The La Niña phase in Fiji is correlated with many flooding events (McAneney et al. 2017), while the El Niño is associated with dry spells.

Fig. 1
figure 1

Map of Fiji showing the two major islands (Viti Levu and Vanua Levu), and the associated elevation resulting in orographic effects

Full size image

3.2 Data

3.2.1 Precipitation data

Data-driven model development is contingent on reliable data records; however, lack of dense gauge networks and uneven distribution often makes the data records sparse, presenting challenges for modellers (Sun et al. 2018). In such circumstances, satellite data tends to be a better choice due to its equidistant spatial scale, reliability, and longer temporal scale. In this study, we use the NOAA Climate Prediction Centre Global Unified Gauge-Based Analysis of Daily Precipitation data (hereon referred to as CPC data). The dataset has a daily temporal resolution from January 1979 to the present, and the spatial resolution is 0.5°. The product has been validated using 30,000 rain gauge stations globally (Sun et al. 2018). The suitability of satellite rainfall estimates was previously undertaken for the Fiji region (Anshuka 2019; Anshuka et al. 2022) where the CPC satellite data showed the highest correlation (~ 0.8) with the on-the-ground data. Therefore, the CPC  satellite data is one of the best available options as it also  has the longest record (time frame). The data was extracted for the entire spatial region of Fiji from 1980 to 2020, resulting in 22 individual grid cells for analysis.

3.2.2 Sea surface temperature data

We retrieve the global analyses of monthly Kaplan Sea Surface temperature anomalies data (Kaplan et al. 1998), with a spatial resolution of 5.0° latitude by 5.0° longitude. The data comprises a large area, spanning from 100° E to 200° and 50° S to 10° N (Fig. 2), covering the Southwest Pacific region using the Arc GIS software. We use the monthly data from 1980 to 2020 to match the temporal scale and resolution of the satellite rainfall data.

Fig. 2
figure 2

Plot of spatial area extent for the average sea surface temperature anomalies (1980–2020)

Full size image

3.3 Index calculation

In previous work, Anshuka et al. (2020), evaluated the suitability of different hydrological indices for Fiji. The study  revealed EDI to be sensitive in the early detection of precipitation anomalies and is considered a suitable index for extreme hydrological events monitoring. The EDI, developed by Byun and Wilhite (1999), is calculated using daily precipitation which is based on the principle of harmonic sum, in such a way  that water resources decline as time progresses from Day 1 to Day 365. While most of the hydrological indices operate on a monthly timescale, the EDI can operate on a daily scale, making it suitable also to investigate short-duration events such as floods. However, for this study, the daily EDI was aggregated to a monthly timescale for the entire area of Fiji. The monthly EDI values can be categorised based on a classification scale to give insight into the different intensities of hydrological extremes. In the results analysis and visualisation each EDI category has been assigned a ‘number’ value as a numerical category (Table 1). A Mann Kendall trend analysis was taken for the entire Fiji region on monthly EDI using the Python Mann–Kendall module (Hussain and Mahmud 2019). The Mann Kendall analysis is a rank-based non-parametric test applied to hydrological time series data to understand underlying trends (Wang et al. 2020). The trend analysis shows increasing EDI values for most months (April, May, June, July, August, September) indicating an increase in precipitation trend (Fig. 3); while for other months, an increase in EDI is noted initially which then reaches a plateau (January, February, March, October, November, December).

Table 1 Effective drought index classes from normal to extremely dry and wet conditions
Full size table
Fig. 3
figure 3

Monthly EDI with trendline (1980 to 2020) showing an overall increase in EDI values for the specific months

Full size image

3.4 Framework for spatio temporal prediction

3.4.1 LSTM model

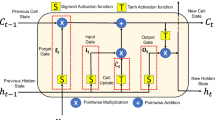
RNNs can be seen as  deep feedforward neural networks with one-way flow of information during training. RNNs had major challenges for training sequences with long-term dependencies, in which the temporal information between the input and the output sequences extends for a long time span (Bengio et al. 1994). Consequently, this results in problems associated with the backpropagation of errors as the time span  of the long-term dependencies increases. This leads to the problem of vanishing gradient in RNN training resulting in weight updates to become insignificant as the error  is back-propagated (Hochreiter 1998). The LSTM model, in contrast to the canonical RNN, does not have such problems due to augmented memory components such as memory cells and gates, which retain lengthy sequences of information for longer durations (Mikolov et al. 2014; Bai et al. 2019). Hence, the LSTM serves to be more valuable than its other counterparts due to its ability to retain information over long time series and multiple-time steps. LSTM networks have recently been further improved with the emergence of bidirectional LSTM (Huang et al. 2015), encoder-decoder LSTM (Cho et al. 2014), attention LSTM (Wang et al. 2016) and transformer LSTM models (Sun et al. 2021). Although these derivatives are mainly suited for language modelling tasks, they can be used for time series prediction (Chandra et al. 2021). Hence, LSTM  is the designated model for our forecasting framework, although other machine learning models or LSTM derivatives  can also be implemented.

3.4.2 Data pre-processing

In this study, we use the 80:20 partition (train/test) for model development. While there is no fixed rule for the amount of data needed for model training and validation (Shirzadi et al. 2018; Umar Ibrahim et al. 2021); we use larger training set in order to ensure that we have specific extreme wet events and ENSO induced extreme dry events covered. The split also ensured that both the train and test sets reflected occurrence of significant extreme wet and dry events.

We process the data in a 3D tensor, the specific structure required for the LSTM model. This was based on Taken’s theorem, where the data is transformed by embedding or reconstruction  (Noakes 1991). Therefore, in our case, we create the 3D tensor structure using a sliding window based on [input samples, window timesteps, features]. Hence, we implement this windowing technique in a way such that the prediction y*(t) is made using regressed Y1, i.e., y(t−1), y(t−2), y(t−d) for a window size (WS), given by d which is user-defined (Fig. 4). Based on the WS = 3, the data series was split at every third step for each consecutive value in the entire train and test set, for which a y value was predicted.

Fig. 4
figure 4

Spatio temporal forecasting framework with data reconstruction  for three different approaches of model development: 1. univariate, 2. multivariate, and 3. multivariate with SST-PCA

Full size image

3.4.3 Spatio temporal framework

In this study, the spatio temporal framework provides a multi-step ahead forecast, whereby the forecast is made for three-time steps (horizons). Forecasting refers to time-series prediction mapped from past data into future data at a longer time scale (Gaitán 2020). In our forecasting method, we consider the immediate history of the time series (window) to make a future prediction. For instance, monthly EDI data for the previous three months (January, February, and March), are used to predict an EDI value for the subsequent three months (April, May, and June). This also corresponds to the earlier selected WS = 3. Since the forecast is done iteratively using the windowing technique, the model is continually being updated as new data becomes available. The training was done to simulate this process, and this means that the model can learn and cope with any irregularities arising in the test data.

Below, the three different approaches to model development are described.

3.4.3.1 Univariate approach

For the univariate approach, the immediate history of the time series y*(t) is considered for three steps using y(t−1), y(t−2), y(t−d). We note that our framework considers multi-step ahead prediction i.e., y*(t + 2), y*(t + 1), y*(t). We represent y in the data with the EDI time series of a particular spatial location in (given by a grid) the region selected. Hence, using the univariate approach, our framework will provide three-step ahead predictions for the 7 × 8 grid (22 spatial locations) shown in Fig. 1. Note that each grid cell in Fig. 1 represents a different time-series data which  is processed by our framework independently.

3.4.3.2 Multivariate approach

In the multivariate approach, we examine relationships between the different features given by the adjacent grid locations. Hence, this is the spatio temporal approach, where we take the spatial data into account. We implement a Pearson correlation feature selection approach (Pearson and Filon 1898) on the entire study region, using monthly EDI to obtain a correlation matrix. Based on this information, we select four features with the highest correlation for a given grid location. This ensures that the spatial patterns observed in the data are considered for model development.

Thereafter, the framework is similar to the univariate approach that concerns taking immediate past information (given by a window) and making a three-step ahead prediction. In the multivariate approach, the spatial data from the neighbouring grid cells are augmented to the univariate approach (except that the number of features used in this approach increases to four).

3.4.3.3 Multivariate approach with sea-surface temperature (SST-PCA)

For the multivariate approach with SST-PCA, our goal is to augment the previous multivariate approach with sea surface temperature data using PCA (SST-PCA). The first step entails PCA, which identifies new orthogonal feature vectors that extract the main information on the entire multi-dimensional dataset, giving us the principal component series. The PCA is implemented using R studio software (Wilks 2011). The first step requires SST data processing, by standardising and centring the data. Thereafter, we calculate the covariance matrix and perform eigenvalue decomposition. The loading patterns derived from the PCA indicate the extent to which the features correlate with each other, mainly in linear combinations. These can be used to spatially visualise the influence of large-scale processes such as ENSO. The eigenvalues and eigenvectors, which comprise the PCA series, represents the sea surface temperature anomalies.

In the second step, we undertake a correlation analysis to understand the relationship between the top ten selected principal components of SST and the entire gridded EDI data, similar to the plain multivariate approach. We select the PCA-SST series, which had the highest correlation with the gridded EDI. In this case, we augment the data in the earlier multivariate approach using the SST derived from the principal components.

3.4.4 Technical setup

The framework for LSTM model is implemented in Python using the Keras application from the TensorFlow module (Abadi et al. 2016) (Ketkar 2017). We fine-tuned the model's training parameters in trial experiments, such as identifying the optimal number of hidden layers, the number of hidden neurons in the respective layers, and the number of epochs (training iterations). The model architecture comprises one LSTM layer and 10 neurons in the hidden layer, and an output layer with three neurons representing the three predicting horizons.

We use the adaptive moment (Adam) optimiser (Kingma and Ba 2014), with a ‘relu’ activation function for dense LSTM layers. We utilise the root mean square error (RMSE) as the loss function to measure the model’s performance by quantifying the difference between the predicted and observed values. Overfitting the data causes errors in the testing stage due to the large starting weights of the network. To avoid this issue, we use a dropout regularisation of 0.2 in the model training phase. Additionally, we set the training to only 30 epochs to prevent overfitting. Each independent experiment ensures that the LSTM model begins with a different initial set of weights and biases (LSTM model parameters), allowing the model to deal with non-stationarity in the data. We summarise the model hyperparameters in Table 2.

Table 2 Summary of hyperparameters used for LSTM model training.
Full size table

3.5 Performance metrics

Both the training and the independent test sets are evaluated as follows:

Quantitative metrics We calculate the RMSE, MSE and R2 for the three timesteps and compute the average for the 30 independent experimental runs. In addition, the overall RMSE in the train and test stages is also calculated for each grid cell.

Uncertainty quantification We calculate the higher and lower percentile on the mean predicted value (for 30 experimental runs) using the standard deviation for uncertainty quantification in the forecast.

Categorical forecast We evaluate the categorical forecast by obtaining a classification report using the sk learn package for the following scores: precision, recall, F-1 score and accuracy. The categorical forecast categories are cross tabulated in a confusion matrix for the approach with the best prediction. A confusion matrix table indicates the number of hits and misses for the predicted and the observed categories.

Spatio temporal maps We visualise spatio temporal maps for two time periods that correspond to the two seasons in Fiji. This shows the spatio temporal pattern comparison of the predicted and actual forecasts in the different seasons.

4 Results

4.1 PCA results

We applied PCA on the SST data and retained the top 10 principal components (PC) for further analysis. The percent of variation explained by the first 10 PCs is 99%. The loadings of PC 3 and PC 7 are shown in Fig. 5, highlights the dominance of SST anomalies in a given spatial location. We observe the strongest correlations for the third principal component loadings present North of Australia near the equator. The third PC loadings are also more apparent in the South Pacific region (~ 0.4), indicating short-term climate phenomena such as ENSO. The loadings of PC7 are more evident in the South-West Pacific region, just South-East of Fiji.

Fig. 5
figure 5

Visualization of the PC loadings for PC3 and PC7 shows its spatial location in equatorial and South Pacific regions. Note: Scale shows the correlation coefficient

Full size image

4.2 Feature correlations

In this section, we look at data visualisation and analysis using Pearson’s correlation feature matrix (Pearson and Filon 1898), as shown in Fig. 6 with reference to the ‘grid’ in Fig. 1, which denotes the features for the spatio temporal problem. We observe that the individual grid cell points are highly correlated with other spatial points. We select four other spatial points with high correlations with a corresponding grid cell for model development in the entire study area. For instance, Grid 1 is highly correlated with Grid 2, Grid 4, Grid 5, and Grid 9 with Pearson’s correlation value of ~ 0.97. The ten principal components also correlates with the spatial EDI grids. We observe that the principal components 3 and 7 have a reasonable correlation ~ 0.45 with the spatial EDI. Hence, PC 3 and PC 7 are used for model development in the multivariate approach using SST. The high correlation of PC3 and PC7 also corresponds with the PC loadings plot in Fig. 5 as these are spatially located and apparent in the South Pacific region close to Fiji.

Fig. 6
figure 6

Pearson’s correlation feature matrix of EDI for the entire spatial area with 2 principal components   of the SST. Note: Spatial locations are labelled as ‘Grid’. The scale represents the measure of the correlation between the different features

Full size image

4.3 LSTM model performance

For ease of understanding, the multivariate approach with neighbouring spatial points will be referred to as multivariate-standard. The multivariate approach with SST, will be referred to as multivariate-SST, hereafter.

In Table 3, the average RMSE, MSE, and R2 values have been reported and summarised for the 30 independent experiments across 22 grid locations. The metrics are provided for the overall train and test sets where the LSTM model is used in all the approaches for three prediction horizons (three step-ahead predictions). The results show that the mean RMSE for the train set averaged across all the grid locations; i.e.  0.49 for multivariate SST, 0.54 for multivariate-standard, and 0.56 for univariate approach. Furthermore, the results also show the mean RMSE for the test set, averaged across the grid locations; i.e. 0.584 for the standard multivariate approach, 0.60 for the multivariate-SST, and 0.588 for the univariate approach. It can be noted that although the error value is low for multivariate-SST in the training stage, the error increases in the testing stage. This is also applicable to the mean square error values, which were 0.25 for the multivariate-SST approach during the training stage and then increased to 0.37 during the testing stage. The highest R2 value recorded in the test set for the first-time horizon is 0.66 for the multivariate-standard. It is also evident that the R2 value is the highest for the first-time horizon prediction and then decreases for the third time horizon for all three approaches. Overall, the multivariate-standard has the lowest error and highest R2 values in the test stage.

Table 3 Performance metrics: RMSE, MSE and R2 values, together with the standard deviation (STD) reported for the training set and testing set for the three different approaches (UV, MV, MV-SST) used for model development
Full size table

4.4 Prediction visualisation

We next visualise the forecast from trained LSTM models for the period covered by the test dataset. The predictions are only shown for the multivariate-standard and the first-time horizon as it rendered the best results (Fig. 7). The plot is shown only for 6 spatial locations in Fiji. We plot the observed and the predicted (mean). In addition, the lower and the upper percentile has been plotted using standard deviation within 95% confidence interval to show uncertainty quantification. From the plots, we observe that the predictions closely follow the observed patterns in the actual test set. There are instances of slight under-prediction and over-prediction for some of the grid-cell. The model performs well to predict the extremes, with the exception of a few where the forecast is within the 0 range. It is also worth pointing out that the uncertainty fluctuation between the lower and the upper percentile is low.

Fig. 7
figure 7

Predicted (mean) values plotted against the observed values (Actual) with uncertainty (Std) for the multivariate approach in the testing stage. Note the plots are only shown for six grid locations

Full size image

4.5 Verification of categorical forecast

For an operational early warning system, the EDI time series needs to be converted to a form that the public can interpret and use. Therefore, we convert the EDI series into the respective categories and quantify the scores for the predicted and the observed EDI categories (Table 4). The classification report is only shown for the multivariate-standard as it renders the best results. The average precision, recall, F1-score, and accuracy scores are 0.73, 0.75, 0.73, and 0.75, respectively. The report also shows that selected grid locations have an accuracy of approximately 85%, while the lowest accuracy is around 65%.

Table 4 Classification report for predicted and observed EDI categories for the multivariate-standard approach
Full size table

The confusion matrix plot has only been shown for the multivariate-standard which rendered better results (Fig. 8). In the confusion matrix, we observe that the most prevalent categories are Normal, Moderately Wet, Very Wet, Extremely Wet. An extremely wet event may coincide with a flooding episode in many cases. There are a few instances of under-prediction, Grid 16 and Grid 17, respectively, whereby category 6 (Extremely Wet) has been predicted as Very Wet. The misclassification of category 5 (Moderately Wet) is higher, with a few grid locations indicated as ‘Very Wet’. However, it is essential to note that all the events have been correctly predicted on a diverging range, where the midpoint is classified as the ‘normal’ category which then branches out to wet and dry events.

Fig. 8
figure 8

Confusion matrix for multivariate approach note: the EDI Categories are represented by numbers

Full size image

4.6 Spatial plots

The spatial plots have been generated for two time periods reflecting the wet and the dry season in Fiji to evaluate model performance in each season. The spatial plot contains the observed, predicted, and the residuals for the three different model development approaches (Fig. 9). The colour ramp is indicative of the EDI values. The spatial plot corresponds to Fiji’s peak dry season months. We observe that the multivariate-standard has a better prediction than the multivariate-SST and the univariate approach. The other observation is that even though it is peak dry season, most EDI values range between -0.5 and 0.75, which is still considered to be the ‘normal’ category.

Fig. 9
figure 9

Spatial plot of Predicted and Observed values for a selected month in the peak dry season

Full size image

Figure 10 shows a spatial plot for the second time period, which corresponds to the peak wet season in Fiji. Most of the actual EDI values for the peak wet season range between 0 and 2.5. These values are depictive of extreme wet conditions. Ideally, we aim to predict extreme events; therefore, we chose a window slice for visualisation which shows the extreme events. From the spatial plot, it appears that the multivariate-SST is better able to predict extreme wet events. The univariate approach does not show good performance in predicting extreme wet events. The residual plot shows the difference between the actual and the predicted values, where the lightest residual colour indicates low error values. All three approaches give predictions with high accuracy for the ‘normal’ category.

Fig. 10
figure 10

Spatial plot of predicted and observed values for a selected month in the peak dry season

Full size image

5 Discussion

According to our study, the performance metrics showed that the lowest MSE (~ 0.2) is achieved for the plain multivariate approach. While the RMSE and MSE values may vary for different studies due to the usage of different datasets; however, it can provide a baseline threshold for result comparison. The error values achieved in our study is consistent with other studies; for instance, a study used multi-source remote sensing data to develop a deep learning-based drought model and reported RMSE values from 0.295 to 0.357, coefficient of correlation values between 0.772 and 0.910, and an accuracy of 80% (Shen et al. 2019). Similarly, another study explored the internet of things (IoT) and PCA in real-time to classify extreme dry events, achieving an accuracy of 95% (Kaur and Sood 2020). This agrees with our study, whereby the accuracy ranged from 69 to 90%.

Furthermore, the results can be influenced in the data processing and reconstruction phase. For instance, we used a fixed sliding window of size three where the respective LSTM model used information from three data points in the past to generate forecasts for three-prediction horizons in future as the model iterated through the entire training and test set. Zan et al. (2020) and Baig et al. (2020) tested two approaches for identifying the optimum sliding window, that is using a fixed or an adaptive window size, and concluded that the latter produces better forecast. Similarly, Chandra et al. (2018), presented a neural network method based on multi-task learning that dynamically selected the window size and applied it for cyclone wind-intensity forecasting with the motivation to make a prediction given limited information. The window size determines the amount of data available from which the model learns and uses  for forecasting. Although not within the scope of our study, this warrants further investigation to understand the effect of the sliding window size on model performance. This can also provide critical information on climate features influencing the precipitation patterns; for instance, a 20-month window will show effects of features such as ENSO, while a 10-year window will show effects of elements that occur at decadal scales.

The results show that a better prediction of extreme wet events is obtained when using the principal components of SST data. Using linear combinations of patterns in the data can be successfully paired with deep learning models to generate better forecasts. The principal components may also indicate certain climate phenomena like ENSO or Madden Julian oscillation. However, it is essential to consider that these climatic phenomena have a certain irregularity attached and are not prevalent every year or every season. In such cases, other phenomena may influence or trigger the precipitation activity in the Pacific (Landman and Mason 1999). For instance, precipitation can also be affected by other topographical features such as orography (Ntale et al. 2003; Lal et al. 2008). Our study showed that the multivariate-SST model performed better during the summer months. This is because sea surface temperature induced SPCZ movement is the dominant climate feature during the summer season. In contrast, the multivariate-standard approach showed better performance in the drier months. This may be because the orographic effects are more predominant in drier months than summer, and can generate localised weather events instead of ocean-atmospheric influenced weather events prevalent in winter. A plausible reason for this is that in the dry season the SST fluctuations results in reduced SPCZ activity, which results in the Westward movement of SPCZ near the equatorial region (Griffiths et al. 2003; McGree et al. 2014).

Additionally, we note from this study that the extreme dry events were not well captured based on the effective drought index classification scale. It is essential to note the importance of class classification, which forms an integral component in long term early warning systems. Empirical studies on Fiji and the Pacific have shown more severe dry periods in Fiji (McGree et al. 2019; Anshuka et al. 2021); however, this is not captured well by the EDI, where the lower range which falls within 0 to − 1 still indicates a ‘normal’ category. With the current classification, some crucial aspects of drought, such as duration, intensity, and initiation, may be overlooked. To ensure that the drought conditions are correct, we recommend adjusting the scale by a value of 0.5. At the same time, it is essential to note that values larger than 2 will correspond to flooding events.

A number of studies have shown that as the forecast horizon increases, so does the corresponding error (Aghelpour et al. 2019; Ashrafzadeh et al. 2020). The extreme events are rare occurrences, which can also results in a class imbalance problem in the case of classification problem using deep learning methods (Johnson and Khoshgoftaar 2019). This becomes challenging for the model to learn and predict extreme events. The challenge is even more significant with the unpredictable climate, which introduces more noise in the data making it harder for the model to learn patterns of these low-frequency extreme events. It has been noted that “the only practical indication of the likely margin of future error is provided by the past forecast errors” (Knüppel 2018). Although not within the scope of this study, future studies can compute uncertainty analysis with more advanced methods such as Monte Carlo simulation and Bayesian inference (Chandra et al. 2019), particularly for longer-term time horizons. Additionally, uncertainty quantification for a predicted outcome can allow authorities to make more informed decision (Wang et al. 2019).

6 Conclusion

In this study, we presented a spatiotemporal deep learning-based framework for hydrological extreme forecasting. We found that the  hybrid approach in the framework that employs a multivariate approach with neighbouring spatial points and principal components of the SST, generates better forecasts when compared to their counterparts. Notably, the framework incorporates deep learning-based approach to understand meaningful information in different spatial and temporal domains. By establishing the framework for the multivariate approach in two forms, it is evident that the model accuracy is contingent on understanding the dominant feature which influences precipitation regimes. In extreme dry events, the plain multivariate approach has good performance that features neighbouring spatial points. However, the multivariate approach with SST is a better predictor for extreme wet events. As part of future studies, other variables such as sea level pressure, relative humidity and geopotential height can be used as predictors for hydrological extremes. The current system can be coupled with the local forecasting system and be fully automated to provide climate outlooks. Finally,  the framework can be used with other LSTM network and machine learning based models and applied to other regions.