Abstract
In the literature, the theory of complex-valued random fields is usually recalled to describe the evolution of vector data in space, without including the temporal dimension. However, as in the real case, the development of the complex formalism in a spatio-temporal context and the construction of some new classes of spatio-temporal complex covariance models are of sure interest for the scientific community partly due to the ongoing explosion in the availability of vector observations in space–time. In this paper, after presenting the fundamental aspects of the complex formalism of a spatio-temporal random field in a complex domain and the extension of some classes of complex-valued covariance models from a spatial domain to a spatio-temporal one, a new family of spatio-temporal complex-valued models obtained through a positive mixture of an infinite number of terms is proposed and various examples are discussed. A case study on modeling the spatio-temporal complex correlation structure of vectorial data is also provided.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Recalling the theory of complex-valued random fields is justifiable for describing phenomena, which can be naturally decomposed in modulus and direction, as a wind speed, sea current or electric field. One of the first contributions on the complex formalism and on the methodology to model these phenomena in one-dimension can be found in Yaglom (1987); subsequently, for a spatial domain in two or more dimensions the pioneer works of Lajaunie and Béjaoui (1991), Grzebyk (1993), Wackernagel (2003) and De Iaco et al. (2003) can be cited. Moreover, together with some advances focused on some parametric classes of covariance models defined on complex domains (Posa 2020, 2021), in the last decade practical aspects regarding the fitting procedure and the related computational difficulties were also discussed, as shown in De Iaco and Posa (2016). In addition, De Iaco (2017) presented the cgeostat software in the R environment, which can support the users in all the steps of the spatial analysis of vectorial data with two components.
Thanks to the potentiality of this area of research in the applications, it is also in great demand the development of tools for space–time complex analysis. Indeed, in the literature there are a lot of studies, focused essentially, on spatio-temporal modeling and prediction of scalar variables, (Stein 1986; Posa 1993; Rouhani and Hall 1989; Cressie and Wikle 2011; Christakos 2017; Wikle et al. 2019). However, in the framework of complex analysis, recently Cappello et al. (2020a, 2020b) tried to include the temporal dimension by presenting a class of time-varying complex covariance functions and its application. It is clear that this class cannot be used to describe the joint spatial and temporal correlation structure of a complex-valued second-order stationary random field, defined on space–time, since it is not a function of both the spatial and temporal lags, but it is a function of the spatial lags, whose parameters depend on time. Apart from this attempt, there exists only the contribution of Cappello et al. (2022), where the spatio-temporal complex-valued random fields and their correlation modeling, based on Bochner’s characterization, were introduced.
The novelty of this paper concerns the construction of wide families of spatio-temporal complex covariance models, for second order stationary spatio-temporal complex-valued random fields, based on different techniques. The first approach proposes an extension, to the space–time domain, of existing complex covariance models given by Lajaunie and Béjaoui (1991), who built the imaginary component of a continuous complex covariance model on the basis of the real component through Radon–Nikodym’s theorem, and by De Iaco et al. (2003), which started from the spectral representation of positive definite functions. Note that the latter presents by definition a periodic factor, whose effect can be damped through the product with a real monotonically decaying covariance model, while for the former the periodic component can be optionally included in the model. The other approach allows for building a new family of complex covariance models, which can cover a wide range of correlation structures. In particular, this family can be used to describe nonnegative real part or real and imaginary parts with or without a periodic component. Moreover, they can be used to generalize the convolution based class. It is also clarified that the potentiality of these techniques is comes from the possibility of building wide families of spatio-temporal complex-valued covariance functions, by easily defining the real and imaginary parts exploiting what is already known on real-valued spatio-temporal covariance functions.
In this paper, an introduction of the complex-valued random fields in space–time has been provided in Sect. 2, together with the second-order stationarity hypothesis and the space–time complex covariance characterization. After presenting the extension of some families of complex covariance models, from space to space–time in Sect. 3, the construction of a new class of spatio-temporal complex covariance models by using positive mixtures has been given in Sect. 4, together with some examples of complex models in space–time, obtained from the provided classes. Then, in Sect. 5 some interesting details on parameters estimation and modeling have been offered. At the end, an application on data related to sea currents in the US East has been proposed and the spatio-temporal complex correlation structure has been modeled through the use of the new classes (Sect. 6) and their performance has been compared with respect to the classical models only extended to space–time (Sect. 7).
2 Theory of spatio-temporal complex random fields
A complex-valued random field in space–time is defined as follows
where U and V are two real-valued spatio-temporal random fields, defined on \({\mathbb {R}}^N\times {\mathbb {R}}\), and \(i=\sqrt{-1}\) is the imaginary number.
Assuming that Z has finite variance, the first-order moment \({{\mathbb {E}}}[Z({\mathbf {w}})]\) of Z is finite and is defined through the following complex-valued deterministic function
where \(m_U\) and \(m_V\) are the expected values of U and V, respectively, whereas the covariance function \(R({\mathbf {w,w}}^{\prime })\) is finite and defined as
where \(R_U\) and \(R_V\) denote, respectively, the spatio-temporal covariance functions associated of U and V whereas \(R_{VU}\) and \(R_{UV}\) represent the related cross-covariances. As usually done, the complex conjugation is denoted with an overline in Eq. (2).
Note that the difference between the complex formalism and the well known multivariate geostatistical approach is not only formal, but conceptual, when data, with a reasonable complex representation, have to be analyzed over a spatial or spatio-temporal domain. For example, wind fields data or oceanographic vectorial data, composed of speed and direction can find their appropriate description in the framework of complex-valued random fields. From a modeling point of view, the main difference between a complex formalism and a multivariate approach is based on the consideration that the complex covariance completely characterizes the correlation structure of vectorial data in two dimensions; this enables the computation of correlations functions in an easier and more flexible way compared to bivariate techniques. Indeed, the complex covariance depends on the direct covariances (in the real part) and on the cross covariances (in the imaginary part); however, it is not necessary to model separately the two direct covariances and the two cross covariances, but just the sum of the former and the difference of the latter. Further details on this aspect can be found in Wackernagel (2003) and De Iaco and Posa (2016). It is worth highlighting that these perks are even more appreciable when these data have a spatio-temporal structure.
2.1 Second-order stationarity hypothesis
Given a random field as in (1), it is second-order stationary in space–time, if its complex-valued expected value is constant, that is \({{\mathbb {E}}}[Z({\mathbf {w}})]= m = m_{_U}+i \, m_{_V},\) where the expected values of U and V are constant for any point of the domain and the space–time covariance function R depends, for any pair of points \({\mathbf {w}}=({\mathbf {w}}_s,w_t)\) and \({\mathbf {w}}^{\prime }=({\mathbf {w}}_s^{\prime },w_t^{\prime })\), on the separation lags vector \({\mathbf {h}}_s={{\mathbf {w}}_s^{\prime }-{\mathbf {w}}_s} \in {\mathbb {R}}^N\), \(h_t=w_t-w_t^{\prime } \in {\mathbb {R}}\), that is
where the corresponding real part, indicated with \(R^{{ re}}\), is given as follows
and the imaginary part, denoted with \(R^{{ im}}\), is defined as
Note that, by definition, the even function in Eq. (4) is also a space–time covariance function on the basis of the convexity property (Chilès and Delfiner 2012), on the other hand the odd function in Eq. (5) is not a space–time covariance function.
For a second-order stationary complex-valued random field Z, the space–time covariance function R satisfies the following properties, i.e.
-
it is nonnegative at zero, \(R(\mathbf{0},0)\ge 0,\)
-
it is symmetric, \(R(-{\mathbf {h}}_s,-h_t)=\overline{R({\mathbf {h}}_s,h_t)},\) that is the covariance matrix is Hermitian,
-
it is bounded, \(|R({\mathbf {h}}_s,h_t)|\le R(\mathbf{0},0).\)
Moreover, any complex covariance function must be nonnegative definite, i.e.,
\(\forall \; {\mathbf {w}}_1, {\mathbf {w}}_2,\ldots ,{\mathbf {w}}_k \in {\mathbb {R}}^N\times {\mathbb {R}}, \quad \forall \; a_1,\ldots , a_k \in {{\mathbb {C}}}.\)
2.2 Bochner’s theorem and space–time complex covariance
On the basis of the full characterization given for any continuous complex covariance function by Bochner’s theorem (Bochner 1933), the definition of a space–time complex continuous covariance function is provided as follows:
where \({\mathbf {h}}_s\cdot {\mathbf {q}}_s\) denotes the inner product \(\sum _{i=1}^N h_i q_i\) and F, called the space–time spectral distribution function of R, is a bounded, real-valued function, such that
The Bochner’s characterization of a space–time covariance function is often worthwhile for analyzing its properties. Hence, from (7)
then, the space–time covariance function of Z is conveniently expressed as the sum of an even part and an odd one.
If the spectral distribution function F is absolutely continuous, the space–time spectral density f exists and is a bounded and continuous nonnegative function. Thus, the Fourier integral representation for the complex covariance function R can be written as:
Note that the covariance function in (7) and (9) is, in general, complex-valued. However, it is real-valued, if the spectral distribution F is symmetric about the origin of \({\mathbb {R}}^N\times {\mathbb {R}}\) or if a spectral density function f is an even function, then the covariance function is real-valued.
Moreover, If the spectral density is assumed to be separable, i.e. \(f({\mathbf {q}}_s,q_t)=f_1({\mathbf {q}}_s)f_2(q_t)\), then this implies the separability of \(R\)
where \(R_1\) and \(R_2\) are spatial and temporal complex covariance functions, respectively.
Thus, two different subclasses can be derived by assuming that only one of the spectral density, \(f_1\) or \(f_2\), is symmetric. If the spectral density function \(f_1\) is symmetric, then \(R_1\) is a real spatial covariance function and \(R_2\) is a complex temporal covariance function; on the other hand, if the spectral density function \(f_2\) is symmetric, then \(R_1\) is a complex spatial covariance function and \(R_2\) is a real temporal covariance function.
Note that, only for the real case, the covariance function R is an even function, since the imaginary part of (3) is zero.
3 Some complex families from space to space–time
In a spatio-temporal context, various families of complex-valued covariance models can be obtained by extending the spatial complex covariance model, defined on \({\mathbb {R}}^N\), to a space–time domain \({\mathbb {R}}^N\times {\mathbb {R}}\). This generalization is proposed hereafter for the spatial complex covariance model built by Lajaunie and Béjaoui (1991), through Radon–Nikodym’s theorem, and for the spatial complex covariance model based on the translation of the spectral density (De Iaco et al. 2003).
3.1 Convolution of the real part
One of the first contributions on complex covariance models, defined on a spatial domain, was presented by Lajaunie and Béjaoui (1991), who built the imaginary component of a continuous complex covariance model on the basis of the real component. By using this result, given the spatio-temporal real part \(R^{ re}({\mathbf {h}}_s,h_t)\), the imaginary part can be defined in consequence of Radon–Nikodym’s theorem, as specified below:
where \(*\) represents the convolution operation and F is a complex distribution whose Fourier transform is a real odd function f with values in the interval \([-1,1]\). Thus, the following class of complex spatio-temporal covariance model can be obtained
The imaginary components \(R^{ im}({\mathbf {h}}_s,h_t)\), associated with a real continuous covariance function \(R^{ re}({\mathbf {h}}_s,h_t)\) through Eq. (12), are usually known as compatible imaginary parts.
In particular, a class of compatible imaginary components can be given by:
where \(\mu \) is a real bounded measure such that \(|f ({{\varvec{\omega }}}_s,\omega _t) |<1\) with \(f({{\varvec{\omega }}}_s,\omega _t)=-\int \sin ({{\varvec{\omega }}}_s\cdot {{\varvec{\tau }}}_s,\omega _t\tau _t)\mu (d{{\varvec{\tau }}}_s,d\tau _t)\). In other terms, the imaginary parts of this class can be got through the expected value of the difference \([R^{ re}({\mathbf {h}}_s-{{\varvec{\tau }}}_s,h_t-\tau _t)-R^{ re}({\mathbf {h}}_s+{{\varvec{\tau }}}_s,h_t+\tau _t) ]\) with respect to \({{\varvec{\tau }}}_s\) and \(\tau _t\), i.e.,
As a special case of (14), it is worth introducing the following simple complex covariance model in space–time:
where the imaginary component is determined through the difference of the real-valued covariance function \(R^{ re}\) translated backward and forward of the vector \(({{\varvec{\tau }}}_s,\tau _t)\). An example of a class of compatible imaginary parts associated with the Gneiting class of real-valued covariance functions has been proposed below.
Example 3.1
Suppose that the real component of Eq. (15) is described by the following class of Gneiting covariance models:
with \(a,b\in ]0,+\infty ]\), \(\alpha ,\gamma ,\beta \in ]0,1]\), then the corresponding compatible imaginary part can be obtained on the basis of the above mentioned difference, that is
Figure 1 provides a graphical representation of the spatial and temporal marginals of the complex model obtained from the class (15), that is the real marginals in space and time
and the imaginary marginals in space and time
where \(a'={(a|\tau _t|^{2\alpha }+1)}\), \(b'={b\Vert {\varvec{\tau }}}_s\Vert ^{2\gamma }\).
Real and imaginary marginals of the complex model, based on the construction given in (15) with \(\alpha =\gamma =1, a=2.5, b=1, \beta =1, {{\varvec{\tau }}}_s=(0.2,0.2), \tau _t=0.5\)
It is clear that any periodic component can be included, for example through the sum or the product of the class in (15) with the basic complex covariance function, that is \(R({\mathbf {h}}_s,h_t)=\cos ({\mathbf {h}}_s \cdot {\mathbf {c}}_s+h_tc_t)+i\,\sin ({\mathbf {h}}_s \cdot \mathbf {c}_s+h_tc_t),\) or just with the real part of the same basic complex covariance function.
3.2 Construction based on translated spectral density
A class of complex covariance models for the spatial case was proposed by De Iaco et al. (2003) starting from Bochner’s characterization of a real-valued covariance function and translating the even spectral density function. In Cappello et al. (2022), the above approach has been suitably generalized to build a class of complex-valued spatio-temporal covariance models. Indeed, given a spectral representation of a real-valued covariance function \({{\tilde{R}}}({\mathbf {h}}_s,h_t)\) and its spectral representation with the corresponding even spectral density function \(f({\mathbf {q}}_s,q_t)\), then the translated function \(f({\mathbf {q}}_s - {\mathbf {c}}_s, q_t-c_t)\), which is a not-even spectral density function \(\forall \,{\mathbf {c}}=({\mathbf {c}}_s,c_t) \in {\mathbb {R}}^N\times {\mathbb {R}} , {\mathbf {c}}=({\mathbf {c}}_s,c_t) \ne \mathbf{0}\), generates the following class of space–time complex covariance models
This can be also expressed as follows
where \({{\tilde{R}}}({\mathbf {h}}_s,h_t)\) is a real space–time covariance function and \( {\mathbf {c}}=({\mathbf {c}}_s,c_t) \in {\mathbb {R}}^N\times {\mathbb {R}}\) represents the shifting factor.
On the basis of Eqs. (3) and (22), it is clear that the real part \(\cos ({\mathbf {h}}_s \cdot {\mathbf {c}}_s+h_tc_t) {{\tilde{R}}}({\mathbf {h}}_s,h_t)\) describes the behavior of the sum of the covariances \(R_U({\mathbf {h}}_s,h_t)\) and \(R_V({\mathbf {h}}_s,h_t)\), while the imaginary part \(\sin ({\mathbf {h}}_s \cdot {\mathbf {c}}_s+h_tc_t){{\tilde{R}}}({\mathbf {h}}_s,h_t)\) represents the model for the difference of the two cross-covariances \(R_{VU}\) and \(R_{UV}\).
From (22), the spatial and temporal complex marginal covariance models are, respectively:
Under a computational point of view, it can be convenient to estimate the real and imaginary parts of the marginals, they can be employed to separately estimate the spatial shifting factor and the temporal one, by following the same idea given in De Iaco and Posa (2016) and De Iaco (2017). A discussion on the effect of the shifting factor can be found in De Iaco et al. (2013b).
Moreover, given that the isotropy assumption does not make any sense in space–time, it is common to adopt spatio-temporal covariance models which are isotropic only in space, thus it is worth introducing the corresponding space–time complex covariance, as a special case of (22):
In the following examples, some spatio-temporal models on \({\mathbb {R}}^N\times {\mathbb {R}}\), with \(N=2\) and the vector coordinate \(({\mathbf {h}}_s,h_t)=(h_x,h_y,h_t)^T\), are presented. In particular, they are obtained starting from some specific classes of spatio-temporal covariance models used for defining \(\tilde{R}({\mathbf {h}}_s,h_t)\).
Although in various applications these models depend on the modulus \(\Vert {\mathbf {h}}_s\Vert \) of the spatial lag and on the modulus \(|h_t|\) of the temporal lag, the presence of a spatial anisotropy can be also included.
Example 3.2
Let R be a space–time continuous complex-valued product model, defined as follows:
where \(R_1: {\mathbb {R}}^N \rightarrow {\mathbb {C}}\) and \(R_2: {\mathbb {R}}\rightarrow {\mathbb {C}}\) are spatial and temporal complex covariance models, respectively and \(N=2\). By using the construction in (21), the product model in (26) can be further written as
where \(\tilde{R}_1\) and \(\tilde{R}_2\) are spatial and temporal real-valued covariance models, respectively. In particular, let \(\tilde{R}_1\) be described by a Gaussian spatial model and \(\tilde{R}_2\) be an exponential temporal model, that is
where a geometric spatial anisotropy is assumed, with \(h'_s=\sqrt{h_{\psi }^2+(\kappa h_{\tau })^2}\), \(h_{\psi }=(h_x \cos \tau - h_y \sin \tau )\) and \(h_{\tau }=(h_x \sin \tau + h_y \cos \tau )\).
Note that a spatial geometric anisotropy is introduced in a two-dimensional spatial domain by adopting the isotropic Gaussian model \(\tilde{R}_1(h'_s)\), \(h'_s=\Vert {\mathbf {h}}'_s\Vert \), in a new system of coordinates obtained by applying a rotation matrix \(\mathbf{A}\) and rescaling matrix \(\mathbf{B}\) to the original vector coordinates, so that:
then
where \(h_{\psi }\) and \(h_{\tau }\) are the new coordinates, \(\kappa \) is the anisotropy factor defined by the ratio of the minor range to the major range and \(\tau \) is the angle that the coordinate axis y forms with the axis corresponding to the direction of maximum continuity (clockwise).
The complex separable covariance function in space–time can be obtained as follows:
where the real part and the imaginary part are, respectively:
In particular, the spatial and temporal marginals of both the real and imaginary parts of the complex product model in (29), obtained for \(h_t=0\) and \({\mathbf {h}}_s=(h_x,h_y)=(0,0)\), are given below:
Example 3.3
Let \({{\tilde{R}}}\) be the class of Gneiting covariance models in Eq. (16), then given the complex class in (25), the following space–time complex covariance model can be built:
Note that the real-valued covariance component \({\tilde{R}}({\mathbf {h}}_s,h_t)\) is assumed to be isotropic in space. Moreover, the spatial and temporal complex marginal covariance models are defined as follows:
Figure 2 provides a graphical representation of the real and imaginary parts of the spatial and temporal marginals of the complex model in (32), together with the marginals of the model in example 3.1 for comparison purposes. Indeed, both models are based on the Gneiting class defined in Eq. (16), with the same values for the parameters. It is clear the effect of the factors containing the shifting vector \({\mathbf {c}}\), however the \({{\tilde{R}}}\) produces a damping effect for both the real and imaginary components of the spatial and temporal marginals. The damped periodicity might be further mitigated by using lower values for the shifting factor, as shown in Fig. 2b.
Real and imaginary marginals of the complex models based on: the construction given in (15), written in terms of the Gneiting class in Eq. (16), with \(\alpha =\gamma =1, a=2.5, b=1, \beta =1\) and \({{\varvec{\tau }}}_s=(0.2,0.2), \tau _t=0.5\) (continuous line) and the construction in (32), with \({{\tilde{R}}}\) defined as in Eq. (16) with the same parameter values values \(\alpha =\gamma =1, a=2.5, b=1, \beta =1\) (dashed line) and a \({\mathbf {c}}_s=(1.5,1.5), c_t=1.8\), b \({\mathbf {c}}_s=(0.5,0.5), c_t=1\)
4 Construction through positive mixtures
In this section, a new class of complex-valued spatio-temporal covariance models is proposed and its peculiarities are discussed. This new class has been obtained by applying the limit of a positive mixture of the class in (22) and have the advantage to describe in a very flexible way a wide range of correlation structures.
4.1 Infinite positive power mixture
As will be clarified, this family of complex-valued spatio-temporal covariance models has been generated through a combination of an infinite number of terms, as in (22), weighted with a power of a constant in the interval ]0, 1[.
Theorem 4.1
Let \({{\tilde{R}}}({\mathbf {h}}_s,h_t)\) be a real-valued covariance function and \( a\in ]0,1[,\) then
is a class of complex-valued covariance models.
Proof
Given the complex covariance function (22) and a positive discrete function \(p(x)=a^x\), \(x=0,1,\ldots \), with \(a\in ]0,1[\), then the following finite combination
is a complex-valued covariance function by recalling the properties according which: (1) the product of the positive term \(a^x\) with the positive definite covariance function \(\cos [x({\mathbf {h}}_s \cdot {\mathbf {c}}_s+h_tc_t)]{{\tilde{R}}}({\mathbf {h}}_s,h_t) + i \; \sin [x({\mathbf {h}}_s \cdot {\mathbf {c}}_s+h_tc_t)]{{\tilde{R}}}({\mathbf {h}},h_t)\) for \(x=0,1, \ldots , n\), is a complex-valued covariance function, and (2) the class of the complex-valued covariance functions is closed with respect to the sum. Then, the limit to infinity of \(R_n\) is applied, that is
It is known that if \(R_n({\mathbf {u}}_1,{\mathbf {u}}_2)\) is a complex-valued covariance function, for \(n =0,1, 2, \ldots \), and if the following limit exists for all pairs \(({\mathbf {u}}_1,{\mathbf {u}}_2)\in {\mathbb {R}}^M\times {\mathbb {R}}^M, M\in {\mathbb {N}}_+\)
then \(R({\mathbf {u}}_1,{\mathbf {u}}_2)\) is a complex-valued covariance function (Matern 1980, p. 10). As already underlined \({R}_n({\mathbf {h}}_s,h_t; a,{\mathbf {c}})\) is a complex-valued covariance function, for \(n =0,1, 2, \ldots \), thus in order to prove that the function in (36) is a class of complex-valued covariance models, it is necessary to verify that the limit exists. In this case, the limit of the partial sums \({R}_n ({\mathbf {h}}_s,h_t; a,{\mathbf {c}})\) in (36) can be equivalently written as follows:
and then
where, apart from \({{\tilde{R}}}({\mathbf {h}}_s,h_t)\) which does not depend on x, each term converges as reported below
Since each terms converges, the proof is complete. \(\square \)
One of the advantages of this class is related to the minimum and the maximum of the factors (38) and (39), which are different for the real and the imaginary parts, that is \([1/(1+a), 1/(1-a)]\) for (38) and \([-a/(1-a^2), a/(1-a^2)]\) for (39), as proved hereafter.
Given the factor (38), the stationary points have to satisfy the following equation:
where \(k= {\mathbf {h}}_s \cdot {\mathbf {c}}_s+h_tc_t\), thus the minimum and the maximum are respectively
Given the factor (39), the stationary points have to satisfy the following equation:
By considering the Pythagorean identity and then by solving the equation with respect to \(\cos (k)\), it results
thus \(\sin (k)=\pm\sqrt{1-cos^2(k)}\). Then, the minimum and the maximum of the function (39) are obtained as follows:
The behavior of the factors (38) and (39) for different values of the parameter a is illustrated in Fig. 3.
Real and imaginary parts of the spatial and temporal marginals of the complex models, based on the construction given in a (22) with \(({\mathbf {c}}_s,c_t)=(1.5,1.5,3)\); b (41), with \(({\mathbf {c}}_s,c_t)=(1.5,1.5,3)\) and \(a=0.4\), where \({{\tilde{R}}}\) is defined in Eq. (40), with \((b_s,b_t,\alpha ,\gamma )=(1,0.5,0.5,0.5)\)
Moreover, apart from the amplitude of the periodic component of this class, which can be smoothed by fixing low values of the parameter a, it is worth pointing out the flexibility of the class (35), with respect to (22), in describing real and imaginary parts which are not affected by the presence of periodic components, as shown in the following example.
Example 4.1
Let \({{\tilde{R}}}\) be described by the integrated class, obtained by integrating the stable model with the gamma function, that is
with \(b_s,b_t\in ]0,+\infty ]\) and \(\alpha, \gamma \in ]0,1]\), then from (35), the obtained complex spatio-temporal covariance function is given below
where the real and imaginary parts are respectively:
with \({{\varvec{\theta }}}= (a,b_s,b_t, {\mathbf {c}},\alpha ,\gamma ) \).
Figure 4 provides a graphical comparison between the spatial and temporal marginals of the classes (22) and (41), where the parameters related to the shifting factors in space and time are assumed to be the same for the two classes. It is worth highlighting that the amplitude of the periodic component of the class (41) is smoothed by fixing a value of the parameter a less than 0.5.
Figure 5 illustrates the flexibility of the class (41), with respect to (22), in describing real and imaginary parts which are not characterized by periodic components. In particular, the continuous lines in Fig. 5a, b are used to represent the real and imaginary marginals of (22) and (41), by considering the same values for both the shifting factors and the \(\tilde{R}\) parameters, in order to make consistent the comparison. It is clear that the class (41) is able to describe random fields whose correlation decays monotonously, while for the class (22) the effect of the periodic component can be completely left out by keeping low the \(\tilde{R}\) parameters associated with the ranges, as shown by the dashed lines in Fig. 5a.
Real and imaginary parts of the spatial and temporal marginals of the complex models, based on the construction given in a (22), with \(({\mathbf {c}}_s,c_t)=(0.3,0.3,0.3)\) and \({{\tilde{R}}}\) as in Eq. (40) with \((b_s,b_t,\alpha ,\gamma )=(1,2.5,0.5,0.5)\) (continuous line) or \({{\tilde{R}}}\) as in Eq. (40) with \((b_s,b_t,\alpha ,\gamma )=(12,12,0.5,0.5)\) (dashed line); b (41), with \(({\mathbf {c}}_s,c_t)=(0.3,0.3,0.3)\), \(a=0.4\) and \((b_s,b_t,\alpha ,\gamma )=(1,2.5,0.5,0.5)\)
4.2 Another equivalent formulation
The class of complex-valued spatio-temporal covariance models in (35) can be equivalently derived through a combination of an infinite number of terms, as in (22), weighted with the positive discrete function \(p(x)=\exp(-ax)\), \(x=0,1,\ldots,\) with \(a>0,\) which leads to the following formulation
Indeed, given the complex covariance function (22) and a positive discrete function \(p(x)=\exp (-ax)\), \(x=0,1,\ldots \), with \(a>0\), then
is a class of complex-valued covariance models by recalling that the same properties recalled before on the sum, the product and the limit of a complex-valued covariance function, where the hyperbolic functions can be defined in terms of the exponential function, that is
Then, Eq. (45) can be written as
where, apart from \({{\tilde{R}}}({\mathbf {h}}_s,h_t)\) which does not depend on x, each term converges as reported below
Note that, although the class in (44) is characterized by an apparently different functional form with respect to the one in (35), it is easy to prove that they are equivalent.
The minimum and the maximum of the factors (46) and (47) are different for the real and the imaginary parts, that is \([0.5[\sinh (a)/(\cosh (a)+1)+1], 0.5[\sinh (a)/(\cosh (a)-1)+1]]\) for (46) and \([-0.5/\sinh (a), 0.5/\sinh (a)]\) for (47), as proved hereafter.
Given the factor (46), the stationary points have to satisfy the following equation:
where \(k= {\mathbf {h}}_s \cdot {\mathbf {c}}_s+h_tc_t\), thus the minimum and the maximum are respectively
Given the factor (47), the stationary points have to satisfy the following equation:
By considering the Pythagorean identity and then by solving the equation with respect to \(\cos (k)\), it results
thus \(\sin (k)= \pm \sqrt{1-{\textit{cos}}^2(k)}\). Then, the minimum and the maximum of the function (47) are obtained as follows:
A special case of the model (44) can be obtained by fixing
then
is a class of complex-valued covariance models.
Note that the above-mentioned hyperbolic functions can be expressed in terms of the exponential function
Remark
Given the basic complex covariance function, that is
then its generalization can be derived through the positive mixture, as follows:
where \( a\in ]0,1[\), \(({\mathbf {c}}_s,c_t) \in {\mathbb {R}}^N\times {\mathbb {R}} , {\mathbf {c}}=({\mathbf {c}}_s,c_t) \ne \mathbf{0},\) or by using the alternative formulation
where \( a>0\), \(({\mathbf {c}}_s,c_t) \in {\mathbb {R}}^N\times {\mathbb {R}} , {\mathbf {c}}=({\mathbf {c}}_s,c_t) \ne \mathbf{0}\).
4.3 Advantages and further generalizations
The potentiality of the proposed approach is related to the flexibility of building wide families of spatio-temporal complex-valued covariance functions, where the real and imaginary parts exploiting what is already known on real-valued positive definite functions in space–time. Indeed, the real component used in the convolution-based class, given in (15), or the real-valued covariance factor in the construction based on translated spectral density, as in (22), as well the real-valued covariance factor in the construction through a positive mixture, as in (35) and (44), can be explicated by selecting a model within numerous separable and nonseparable spatio-temporal classes of covariance models available in the literature (Rouhani and Hall 1989; Dimitrakopoulos and Luo 1994; De Iaco et al. 2001; Cressie and Huang 1999; Gneiting 2002; De Iaco et al. 2002; Kolovos et al. 2004; Stein 2005; Ma 2002, 2003, 2005; Porcu et al. 2006, 2008; Rodrigues and Diggle 2010).
Moreover, the classes proposed in this section can be further used to generalize the convolution based class in (15), as specified below.
Let \({R}^{re}({\mathbf {h}}_s,h_t)\) be a real-valued covariance function and \( a\in ]0,1[\), then
is a class of complex-valued covariance models.
This model is obtained by recalling the property according to which the product of a complex covariance function and a real covariance function is still a complex covariance function. Indeed, given the complex covariance function (15) and the real component of the class in (50), which is itself a real-valued covariance function, then the function, generated by multiplying these two factors, represents a valid class of complex-valued covariance models.
Similarly, by using the real part of the class in (51), the following equivalent formulation of the generalized convolution based class can be obtained:
where \( a>0\), \(({\mathbf {c}}_s,c_t) \in {\mathbb {R}}^N\times {\mathbb {R}} , {\mathbf {c}}=({\mathbf {c}}_s,c_t) \ne \mathbf{0}\).
It is also worth highlighting that the convolution-based class and its generalization, the class based on translated spectral density and the class obtained through a positive mixture cover an extensive range of complex correlation structures, whose real part (not necessarily nonnegative) and imaginary part do/do not exhibit a periodic component. In particular, the convolution-based class can be easily applied to describe complex covariance surfaces with a nonnegative real part, the class based on translated spectral density is marked by a periodic factor for both the real and imaginary components, whose effect is often damped through the product with a real monotonically decaying covariance model. Thus, it can be typically used for complex covariance surfaces, whose real part can assume negative values.
The family of mixture models are flexible enough to encompass all the above mentioned features, since the real part is nonnegative unless the model used for the real-valued covariance factor assumes negative values; moreover, the amplitude and the frequency of the periodic factor can be conveniently fixed according to the empirical behavior of the real and imaginary components or if necessary the effect of the periodic factor can be left out, without producing a contextual flattening of the imaginary part as happens for the class based on translation of a symmetric spectral density.
5 Estimation and modeling
Given the classes of parametric spatio-temporal complex-valued covariance functions introduced in the previous section, it is interesting to offer some details on parameters estimation and modeling.
The first step in structural analysis is to compute the sample real and imaginary components of the spatio-temporal complex covariance function for different spatio-temporal lags. In particular, the sample real part, \({\hat{R}}^{re}\), is obtained through the sum of the sample covariance functions for U and V, that is (\({\widehat{R}}_U ({\mathbf {h}}_s,h_t)+{\widehat{R}}_V ({\mathbf {h}}_s,h_t)\)), while the imaginary part, \({\widehat{R}}^{im}\), is determined through the difference between the sample cross-covariances (\({\widehat{R}}_{VU} ({\mathbf {h}}_s,h_t)-{\widehat{R}}_{UV} ({\mathbf {h}}_s,h_t)\)).
For the proposed classes of complex covariance models, the real and imaginary parts are defined as a product of two factors, i.e. a periodic function and a real-valued covariance function (\({{\tilde{R}}}\)). Thus, the estimation process regards on one hand the parameter a and the shifting vector which characterize the periodic function and on the other hand the covariance function \(\tilde{R}\) with its parameters (such as range, nugget and sill value).
For the class (35), the parameter a and the shifting factor can be easily estimated by using the sample components \({{\widehat{R}}}^{ re}({\mathbf {h}}_{s_i},h_{t_i})\) and \({{\widehat{R}}}^{ im}({\mathbf {h}}_{s_i},h_{t_i})\) of the complex covariance function determined for \(n_l\) lag vectors \(({\mathbf {h}}_{s_i},h_{t_i})\in {\mathbb {R}}^N\times {\mathbb {R}}\), \(i=1,2,\ldots ,n_l\). In particular, by using the definition of a complex covariance function, given in (3), and the family of complex covariance models, as in (35), it is easy to obtain the equalities:
where the periodic factors in (54) and (55) will be denoted in what follows with \(k^{{\textit{re}}}\) and \(k^{{\textit{im}}}\), respectively. Then the ratio between the imaginary part and the real part depends on the parameter a and the shifting vector, thus it is independent from the real-valued covariance function \({\tilde{R}}\), that is
Consequently, the least squares estimates of the parameter a and the vector \({\mathbf {c}}=({\mathbf {c}}_s,c_t)\) correspond to the minimum of the following function:
for all \({{\widehat{R}}}^{ re}({\mathbf {h}}_{s_i},h_{t_i})\ne 0\) and \(({\mathbf {h}}_{s_i},h_{t_i})\).
Alternatively, for the class (44),
and the ratio between the imaginary part and the real part is
Thus, given the sample components \({{\widehat{R}}}^{ re}({\mathbf {h}}_{s_i},h_{t_i})\) and \({{\widehat{R}}}^{ im}({\mathbf {h}}_{s_i},h_{t_i})\) of the complex covariance function R in (3), determined for \(n_l\) lag vectors \(({\mathbf {h}}_{s_i},h_{t_i})\in {\mathbb {R}}^N\times {\mathbb {R}}\), \(i=1,2,\ldots ,n_l\), the least squares estimates of the parameters can be computed by minimizing the following function:
for all \({{\widehat{R}}}^{ re}({\mathbf {h}}_{s_i},h_{t_i})\ne 0\) and spatio-temporal lags \(({\mathbf {h}}_{s_i},h_{t_i}) \).
Consequently, after modeling the parameter a and the shifting vector \({\mathbf {c}}\), the estimation of the parameter vector \(\varvec{\theta }\) of the spatio-temporal covariance model \(\tilde{R}(\cdot ;\varvec{\theta })\) can be executed a) by using the spatial and temporal marginals and then by fixing ranges (in space and time) and the sill value through a graphical inspection, or b) by recalling the method of nonlinear weighted least squares proposed by (Cressie 1993). According to this method, given the selected class of covariance models \(\tilde{R}(\cdot ;\varvec{\theta })\), the empirical direct and cross covariances, \({{\widehat{R}}}_{U}({\mathbf {h}}_{s_i},h_{t_i}), \widehat{R}_{V}({\mathbf {h}}_{s_i},h_{t_i}),\) \( {{\widehat{R}}}_{VU}({\mathbf {h}}_{s_i},h_{t_i})\) and \({{\widehat{R}}}_{UV}({\mathbf {h}}_{s_i},h_{t_i})\), determined for fixed spatio-temporal lags \(({\mathbf {h}}_{s_i},h_{t_i})\), \(i=1,2,\ldots ,n_l\) and the estimates, \({{{\hat{a}}}}\) and \(\hat{\mathbf {c}}=(\hat{\mathbf {c}}_s,{{\hat{c}}}_t)\) of the parameters a and \({\mathbf {c}}=( {\mathbf {c}}_s, c_t)\), then the function to be optimized is built on the discrepancies between the empirical real and imaginary parts and the theoretical ones:
where \(k^{re}\) and \(k^{im}\) represent the periodic factors for the real and imaginary parts, estimated in the first step and the weight \(w_i\) for the i-th lag are often fixed equal to the number of pairs of points in the same lag. Thus, the best estimate of \(\varvec{\theta }\) corresponds to the values that minimizes the above function.
For the classes (52) or (53), the above mentioned nonlinear weighted least squares method can be applied to the real part in order to estimate the parameter a, the shifting factor \(({\mathbf {c}}_s, c_t)\), together with range and sill value included in \(\varvec{\theta }\), then it is applied to the imaginary part to estimate the backward and forward vector \(({{\varvec{\tau }}}_s, \tau _t)\).
6 An application on oceanographic data
The main focus of the following application regards the estimation of the spatio-temporal complex covariance function of the Mexican sea currents and its modeling. This kind of oceanographic data are naturally decomposed in modulus and direction and can be reasonably considered as a finite realization of a complex-valued random field Z, defined in (1) for \(N=2\), for which the components U and V represent the Cartesian coordinates of the ocean current vector. In other terms, this is consistent under a physical perspective, since the currents measurements are vectorial data with a sensible complex representation.
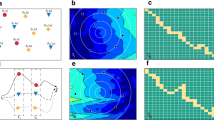
In particular, the data are provided by the National Centers for Environmental Information and are referred to hourly measurements of the ocean currents, obtained from high frequency radar systems, during the 26th to the 30th of April 2016 from 182 stations in the Eastern part of the Gulf of Mexico (https://www.nodc.noaa.gov/gocd/hfportal.html). Figure 6 shows the location maps of the data, available over a grid with cell size (2 km \( \times \) 2 km), registered at 12 am of the five days 26–30 April 2016.
It is worth pointing out that the presence of a periodicity at 12 hours for both components of Z has been treated by using the moving average estimation technique; thus, after detecting the seasonal effect for each location, the residuals for both components have been retained for the subsequent structural analysis.
In the following, the new class of complex-valued covariance model based on an infinite positive mixture and its generalization have been used for fitting the sample covariance function, thus their performance has been compared with the one obtained from fitting the classical complex covariance model derived from the convolution of the real or from translated spectral density.
6.1 Estimation of the complex covariance
As already underlined, structural analysis starts with the computation of the sample real and imaginary components of the spatio-temporal complex covariance function for different spatio-temporal lags. In particular, after estimating the sample covariance functions for U and V, that is \({\widehat{R}}_U ({\mathbf {h}}_s,h_t), {\widehat{R}}_V ({\mathbf {h}}_s,h_t)\), and the sample cross-covariances \({\widehat{R}}_{VU} ({\mathbf {h}}_s,h_t), {\widehat{R}}_{UV} ({\mathbf {h}}_s,h_t)\), then the sample real part, \({\widehat{R}}^{re}\), is obtained through the sum of the sample covariance functions (\({\widehat{R}}_U ({\mathbf {h}}_s,h_t)+{\widehat{R}}_V ({\mathbf {h}}_s,h_t)\)), while the imaginary part, \({\widehat{R}}^{im}\), is determined through the difference between the sample cross-covariances (\({\widehat{R}}_{VU} ({\mathbf {h}}_s,h_t)-{\widehat{R}}_{UV} ({\mathbf {h}}_s,h_t)\)):
The estimation of the direct covariance functions of the variables U and V has been performed for 260 spatio-temporal distances (13 spatial lags \(\times \) 20 temporal lags) and for 4 main directions, i.e., North, North-East, East, South-East, associated with the angles \(0^{\circ }\), \(45^{\circ }\), \(90^{\circ }\), \(135^{\circ }\) applied clockwise from the North; these directions are abbreviated with the letters N, NE, E, SE, respectively. At the same time, the spatio-temporal cross-covariance functions have been estimated. Figure 7 illustrates the 3D diagram of the empirical components of the complex covariance functions (the real and imaginary parts) for the indicated directions and distances together with their spatial and temporal marginals.
6.2 Modeling the empirical complex covariance function
In the following the new classes of models in (35) and (52), built through a positive mixture and through a generalization of the convolution model, respectively, have been fitted to the empirical complex covariance function.
6.2.1 Modeling through the positive mixture class
Given the class of spatio-temporal complex covariance model in (35), the parameter a and the shifting vector \({\mathbf {c}}=({\mathbf {c}}_s,c_t)\) have been estimated by minimizing the function in (57). By using the sample components \({{\widehat{R}}}^{ re}({\mathbf {h}}_{s_i},h_{t_i})\) and \({{\widehat{R}}}^{ im}({\mathbf {h}}_{s_i},h_{t_i})\) of the complex covariance function R in (3), determined for \(n_l\) lag vectors \(({\mathbf {h}}_{s_i},h_{t_i})\in {\mathbb {R}}^N\times {\mathbb {R}}\), \(i=1,2,\ldots ,n_l\), the nonlinear least-squares estimates of the parameters a and \(({\mathbf {c}}_s,c_t)\) have been obtained through the Gauss–Newton algorithm (Bates and Watts 1988), as reported in Table 1.
As a further step, the selection of the spatio-temporal model for \(\tilde{R}\) with its parameter vector \(\varvec{\theta }\) has been addressed.
For this aim, starting from the following equality:
the contribution of the factor \(\tilde{R}\) to the real and imaginary parts of the complex covariance function has been empirically determined through the ratios given below
where the estimates \({\hat{a}}, \hat{\mathbf {c}}_s,{\hat{c}}_t\) are reported in Table 1. In the consideration that the above ratios were very similar, with differences, on average, equal to 0.0009, only the first one has been retained for the subsequent analysis.
Regarding the class of spatio-temporal covariance models to be used for describing \(\tilde{R}\), the study of the sample nonseparability index has supported the selection of the product model, defined as follows
where \(\tilde{R}_S\) and \(\tilde{R}_T\) are real-valued positive definite functions in \({\mathbb {R}}^N\) and \({\mathbb {R}}\), respectively (De Iaco and Posa 2013). Indeed, the empirical index of nonseparability, obtained by dividing the sample \(\hat{\tilde{\small {R}}}\) by the product of the marginals for different lags \(({\mathbf {h}}_{s_i},h_{t_i})\), i.e.,
has assumed values approximately equal to 1 for all lags (1.067), leading not to reject the product model hypothesis (Cappello et al. 2018; Cappello et al. 2020c). Looking at the sample marginals \( \hat{\tilde{{R}}}({\mathbf {h}}_{s_i},0)\) and \(\hat{\tilde{{R}}}(\mathbf{0},h_{t_i})\), the exponential model has been adopted for both the spatial and temporal marginals; then, as usually done in spatio-temporal analysis, the corresponding parameters have been determined by graphical inspection (De Iaco et al. 2013a). For the spatial marginal, the exponential model is characterized by geometric anisotropy, with direction of maximum (minimum) continuity \(\tau \) (\(\psi \)) equal to \(90^{\circ }\) (\(0^{\circ }\)) and maximum (minimum) effective range \(r_{\tau }\) (\(r_{\psi }\)) equal to 0.750 (0.450), while for the temporal marginal, the exponential model presents an effective range equal to 12. Note that the value at zero is common for both and is equal to 0.0201. Thus, the covariance function \(\tilde{R}\) of the complex covariance model in (35) has been modeled as specified below:
where \(h'_s=\sqrt{h_{\psi }^2+(\kappa h_{\tau })^2}\), with \(\kappa =r_{\psi }/r_{\tau }=0.450/0.750\). In particular, \(h'_s\) represents the Euclidean distance, where an anisotropy correction is applied to the vector \({\mathbf {h}}_{s}=(h_x,h_y)\), in terms of rotation (clockwise) of the coordinate axes, i.e:
and in terms of scale, since the coordinate axes are rescaled to a circle whose radius is coincident with the minor range \(r_\psi \).
Then, the fitted space–time complex covariance model (35), as shown in Fig. 8, is such that
where \({{\tilde{R}}}({\mathbf {h}}_s,h_t)\) is specified in (65).
Spatio-temporal complex covariance model (67): a real and b imaginary parts
6.2.2 Modeling through the generalized convolution class
In addition, the generalized class presented in (52) has been also fitted by recalling the nonlinear weighted least squares method, which has been applied to the real part in order to estimate the parameter a, the shifting factor \(({\mathbf {c}}_s, c_t)\), together with range and sill value included in \(\varvec{\theta }\), and then to the imaginary part to estimate the backward and forward parameter vector \(({{\varvec{\tau }}}_s, \tau _t)\).
The covariance function \(R^{re}\), which appears in the real part of the class (52) and in its convolution, has been modeled by using the separable model, that is the same functional form assumed for \(\tilde{R}\) in (35). Through the optimization procedure of the real part, the estimates for a and the vector \({\mathbf {c}}\) are \({\hat{a}}=0.491\) and \(\hat{\mathbf {c}}=(\hat{\mathbf {c}}_s,{\hat{c}}_t)=({\hat{c}}_x,{\hat{c}}_y,{\hat{c}}_t)=(-4.203, -1.260, 0.195)\), while the parameters estimates of \(R^{re}\) (defined as the product of two exponential models, one for the spatial marginal and the other for the temporal one) are such that the maximum (minimum) spatial range \(r_{\tau }\) (\(r_{\psi }\)), along the direction of maximum (minimum) continuity \(\tau =90^{\circ }\) (\(\psi =0^{\circ }\)), is equal to 0.820 (0.390), and the temporal range is equal to 12. Moreover, the value at zero is equal to 0.0175. Thus, the covariance function \({R}^{re}\) of the complex covariance model in (52) has been modeled as specified below:
where \(h'_s=\sqrt{h_{\psi }^2+(\kappa h_{\tau })^2}\), with \(\kappa =r_{\psi }/r_{\tau }=0.390/0.820\), is the Euclidean distance, where rotation and scale anisotropic correction is applied to the vector \({\mathbf {h}}_{s}=(h_x,h_y)\).
For the imaginary part, the estimate of the backward and forward parameter vector \(({{\varvec{\tau }}}_s,\tau _t)\) has been computed by minimizing the following function:
where \(n_l\) is the number of spatio-temporal lags. By applying the Gauss–Newton algorithm, the estimate of the backward and forward parameter vector \(({{\varvec{\tau }}}_s,\tau _t)\) is \(( \hat{{\varvec{\tau }}}_s,{\hat{\tau }}_t)=({\hat{\tau }}_x,{\hat{\tau }}_y,{\hat{\tau }}_t)=(-0.122, -0.022, 5.440)\). The estimates are all statistically significant with a p-value not greater than 0.03. Thus, the fitted model of the class (52) is given below:
where \(R^{re}\) is specified in (68).
Both models fits well the real and the imaginary parts of the sample complex-valued covariance function, as can be highlighted through the computation of the relative mean square error for the real part (\(\Delta ^{re}\)) and the analogous for the imaginary part (\(\Delta ^{im}\)), i.e.,
where \({{\widehat{R}}}^{ re}({\mathbf {h}}_{s_i},h_{t_i})\) and \({\widehat{R}}^{ im}({\mathbf {h}}_{s_i},h_{t_i})\) are the sample components of the complex covariance function R in (3), determined for \(n_l\) lag vectors \(({\mathbf {h}}_{s_i},h_{t_i})\in {\mathbb {R}}^N\times {\mathbb {R}}\), \(i=1,2,\ldots ,n_l\), while \(R^{ re}({\mathbf {h}}_{s_i},h_{t_i}; {{\varvec{\theta }}})\) and \( R^{ im}({\mathbf {h}}_{s_i},h_{t_i}; {{\varvec{\theta }}})\) are the fitted real and imaginary theoretical components. Note that the above indexes are well defined since the denominator is assumed different from zero.
As an index of the overall discrepancy between the empirical and the theoretical surfaces of the complex model, the following ratio is proposed:
Indeed, the values for both indexes, \(\Delta ^{re}\) and \(\Delta ^{im}\) have highlighted a slight better performance of model (70) with respect to (67), which is also consistent with the higher number of parameters characterizing the former model (3 more) compared to the latter one. In particular, the above indexes, computed over 49 spatio-temporal lags (where the correlation is higher), are on average 0.0733 for the first model and 0.0637 for the second one, with a reduction in terms of the \(\Delta ^{cx}\) of 13.05%.
7 Some comparative results
The aim of this section is to assess and analyze the performance of the proposed classes of spatio-temporal complex covariance models in describing the empirical behavior of the complex covariance function for the spatio-temporal current dataset.
First of all the comparative analysis has regarded the class of models in (22), built on the basis of translated spectral density, and the class in (35), obtained from the former through an infinite positive mixture. Subsequently, the comparison has focused on the class of models, based on the convolution of the real part, given in (15), and its generalized class presented in (52).
Thus as a first step of this comparison, the complex model in (22) has been fitted to the spatio-temporal sample complex covariance function. The shifting vector \({\mathbf {c}}=({\mathbf {c}}_s,c_t)\) has been estimated by minimizing the following function:
for all \({{\widehat{R}}}^{ re}({\mathbf {h}}_{s_i},h_{t_i})\ne 0\) and \(({\mathbf {h}}_{s_i},h_{t_i})\). The nonlinear least-squares estimates of the parameters \(({\mathbf {c}}_s,c_t)\) are \((\hat{\mathbf {c}}_s,{\hat{c}}_t)=({{\hat{c}}}_1,{{\hat{c}}}_2,{{\hat{c}}}_t)=(-2.130, -0.879, 0.099)\), which are statistically different from zero with p-value not greater than 0.02.
The \(\tilde{R}\) of model (22) has been modeled through the product class consistently with the previous choice, where the spatial marginal has been modeled through the exponential model with geometric anisotropy, characterized by a direction of maximum (minimum) continuity \(\tau \) (\(\psi \)) equal to \(90^{\circ }\) (\(0^{\circ }\)) and maximum (minimum) effective range \(r_{\tau }\) (\(r_{\psi }\)) equal to 0.570 (0.480), while the temporal marginal has been described by the exponential model which presents an effective range equal to 12. The value at zero is common for both and is equal to 0.035.
The fitted space–time complex covariance model (22) is specified below:
where \({{\tilde{R}}}({\mathbf {h}}_s,h_t)=0.035\exp (-3h'_s/0.480) \exp (-3|h_t|/12),\) with \(h'_s=\sqrt{h_{\psi }^2+(\kappa h_{\tau })^2}\), \(\kappa =r_{\psi }/r_{\tau }=0.480/0.570\). Note that \(h'_s\) represents the Euclidean distance, taking into account that an anisotropy correction is applied to the vector \({\mathbf {h}}_{s}=(h_x,h_y)\), in terms of rotation (clockwise) of the coordinate axes, as clarified in (66), and in terms of scale.
The errors between the sample complex covariance function and the theoretical one have been computed in terms of the index \(\Delta \) determined separately for the real and the imaginary parts, as given in (71) and (72), respectively. Table 2 shows that both indexes, \(\Delta ^{re}\) and \(\Delta ^{im}\), have highlighted a better performances of model (67) with respect to (75) , with a reduction of the \(\Delta ^{cx}\) of 19.67%.
In the second part of this section, the comparison between the class of complex-valued covariance functions, obtained through the convolution of the real part in (15), and the corresponding generalized class given in (52) is presented.
The real part \(R^{re}\) of (15) has been modeled by using the separable model, as done for \(R^{re}\) of (52), while the imaginary part is obtained through the convolution of the real covariance model. In particular, the covariance function \({R}^{re}\) is defined as the product of two exponential models, one for the spatial profile and the other for the temporal profile, where the spatial marginal presents the same geometric anisotropy detected previously, characterized by a direction of maximum (minimum) continuity \(\tau \) (\(\psi \)) equal to \(90^{\circ }\) (\(0^{\circ }\)) and maximum (minimum) effective range \(r_{\tau }\) (\(r_{\psi }\)) equal to 0.570 (0.340), while the temporal marginal has been described by the exponential model with a range equal to 12. The value in zero is common for both and is equal to 0.033. For the imaginary part, the estimate of the backward and forward parameter vector \(({{\varvec{\tau }}}_s,\tau _t)\), computed by minimizing the following function:
are \(( \hat{{\varvec{\tau }}}_s,{\hat{\tau }}_t)=({\hat{\tau }}_x,{\hat{\tau }}_y,{\hat{\tau }}_t)=(-0.1221, -0.0316, 3.8402)\). Thus, the fitted space–time complex covariance model (15) is given below:
where \({ R}^{re}({\mathbf {h}}_s,h_t)=0.033\exp (-3h'_s/0.340) \exp (-3|h_t|/12),\) with \(h'_s=\sqrt{h_{\psi }^2+(\kappa h_{\tau })^2}\), \(\kappa =r_{\psi }/r_{\tau }=0.340/0.570\).
From Table 2, it is evident that the two indexes \(\Delta ^{re}\) and \(\Delta ^{im}\) are lower for the generalized convolution model (70) with respect to the classical convolution (77), with a decrease of the \(\Delta ^{cx}\) of 30,34%. Moreover, the model (70) has highlighted a better performance also with respect to (75), indeed the \(\Delta ^{re}\) and \(\Delta ^{im}\) are respectively equal to 0.0578 and 0.2044 for the first model, and 0.0860 and 0.2151 for the second one, with a reduction of the \(\Delta ^{cx}\) of 30.15%. The same conclusion can be reached if the new model (67), obtained through an infinite positive mixture, is also compared with the model (77). The comparison in terms of \(\Delta ^{cx}\) confirms that model (67) performs 19.88% better than model (77), with values of the index equal to 0.0733 and 0.0915, respectively.
8 Conclusions
In this paper, the formalism of complex-valued random fields was extended to a space–time domain and new classes of spatio-temporal complex covariance models were presented. It was underlined that the theory of complex-valued random fields in space–time is particularly useful to provide a suitable representation of vectorial data in two dimensions, where the decomposition in modulus and angle is natural and has a physical interpretation.
Different approaches for generating covariance functions for second order stationary spatio-temporal complex-valued random fields were proposed, various examples obtained on the basis of well-known classes of real-valued space–time covariance functions were given and some comparisons among the classes of complex covariance models were also offered.
Note also that all the proposed families of complex-valued covariance models provide a variety of modeling options. However, these advances of the complex-valued random fields in space–time can be considered a good starting point for future works, focused on practical aspects concerning the classes of spatio-temporal complex covariance models and their applications.
Availability of data and material
Data can be found at the link https://www.ncei.noaa.gov/access/data/global-ocean-currents-database/hfportal.html and the name of the used repository is GOCD 0151726 (which contains the data for the year/month 2016/04 and the area US East & Gulf Coast).
References
Bates DM, Watts DG (1988) Nonlinear regression analysis and its applications. Wiley, New York, p 365
Bochner S (1933) Monotone funktionen, Stieltjessche integrale und harmonische analyse. Math Ann 108(1):378–410
Cappello C, De Iaco S, Maggio S, Posa D (2020) Time varying complex covariance functions for oceanographic data. Spat Stat 42(4):100426
Cappello C, De Iaco S, Maggio S, Posa D (2020) Modeling ocean currents through complex random fields indexed in time. Math Geosci 53:999–1025
Cappello C, De Iaco S, Maggio S, Posa D (2020) Modeling spatio-temporal complex covariance functions for vectorial data. Spat Stat. https://doi.org/10.1016/j.spasta.2021.100562
Cappello C, De Iaco S, Posa D (2018) Testing the type of non-separability and some classes of space-time covariance function models. Stoch Environ Res Risk Assess 32:17–35
Cappello C, De Iaco S, Posa D (2020) covatest: An R package for selecting a class of space-time covariance functions. J Stat Softw 94(1):1–42
Chilès JP, Delfiner P (2012) Geostatistics: modeling spatial uncertainty, 2nd edn. Wiley, New York, p 722
Christakos G (2017) Spatio-temporal random fields: theory and applications. Elsevier Science Publishing Co Inc., 696 p
Cressie N (1993) Statistics for spatial data. Wiley, New York, p 900
Cressie N, Huang H (1999) Classes of nonseparable, spatio-temporal stationary covariance functions. J Am Stat Assoc 94(448):1330–1340
Cressie N, Wikle CK (2011) Statistics for spatio-temporal data. Wiley & Sons Inc., Hoboken, p 624
De Iaco S (2017) The cgeostat software for analyzing complex-valued random fields. J Stat Softw 79(5):1–32
De Iaco S, Posa D (2013) Positive and negative non-separability for space-time covariance models. J Stat Plan Inference 143(2):378–391
De Iaco S, Posa D (2016) Wind velocity prediction through complex kriging: formalism and computational aspects. Environ Ecol Stat 23(1):115–139
De Iaco S, Myers DE, Posa D (2001) Space-time analysis using a general product-sum model. Stat Probab Lett 52(1):21–28
De Iaco S, Myers DE, Posa D (2002) Nonseparable space–time covariance models: some parametric families. Math Geol 34(1):23–42
De Iaco S, Palma M, Posa D (2003) Covariance functions and models for complex-valued random fields. Stoch Environ Res Risk A 17(3):145–156
De Iaco S, Posa D, Myers DE (2013) Characteristics of some classes of space–time covariance functions. J Stat Plan Inference 143(11):2002–2015
De Iaco S, Posa D, Palma M (2013) Complex-valued random fields for vectorial data: estimating and modeling aspects. Math Geosci 45(5):557–573
Dimitrakopoulos R, Luo X (1994) Spatiotemporal modeling: covariances and ordinary kriging systems, Geostatistics for the next century. Kluwer Academic Publishers, pp 88–93
Gneiting T (2002) Nonseparable, stationary covariance functions for space-time data. J Am Stat Assoc 97(458):590–600
Grzebyk M (1993) Ajustement d’une Coregionalisation Stationnaire. Ph.D. thesis, Ecoles des Mines, Paris, 154 p
Kolovos A, Christakos G, Hristopulos DT, Serre ML (2004) Methods for generating non-separable spatiotemporal covariance models with potential environmental applications. Adv Water Resour 27(8):815–830
Lajaunie C, Béjaoui R (1991) Sur Le Krigeage des Fonctions Complexes. Note N-23/91/G, Centre de Geostatistique, Ecole des Mines de Paris, Fontainebleau, 25 p
Ma C (2002) Spatio-temporal covariance functions generated by mixtures. Math Geol 34:965–975
Ma C (2003) Families of spatio-temporal stationary covariance models. J Stat Plan Inference 116:489–501
Ma C (2005) Linear combinations of space–time covariance functions and variograms. IEEE Trans Signal Process 53(3):857–864
Matern B (1980) Spatial variation, lecture notes in statistics, 2nd edn, vol 36. Springer, New York, 151 p. First edition published in Meddelanden fran Statens Skogsforskningsinstitute Swed., Band 49, no. 5, 1960
Porcu E, Gregori P, Mateu J (2006) Nonseparable stationary anisotropic spacetime covariance functions. Stoch Environ Res Risk Assess 21:113–122
Porcu E, Mateu J, Saura F (2008) New classes of covariance and spectral density functions for spatio-temporal modelling. Stoch Environ Res Risk A 22:65–79
Posa D (1993) A simple description of spatio-temporal processes. Comput Stat Data Anal 15(4):425–437
Posa D (2020) Parametric families for complex valued covariance functions: some results, an overview and critical aspects. Spat Stat. https://doi.org/10.1016/j.spasta.2020.100473
Posa D (2021) Models for the difference of continuous covariance functions. Stoch Environ Res Risk Assess 35:1369–1386
Rodrigues A, Diggle PJ (2010) A class of convolution-based models for spatio-temporal processes with non-separable covariance structure. Scand J Stat 37(4):553–567
Rouhani S, Hall TJ (1989) Space-time kriging of groundwater data. In: Armstrong M (ed) Quantitative geology and geostatistics, vol 4. Springer, Dordrecht, pp 639–651
Stein ML (1986) A simple model for spatial-temporal processes. Water Resour Res 22(13):2107–2110
Stein ML (2005) Space–time covariance functions. J Am Stat Assoc 100(469):310–321
Wackernagel H (2003) Multivariate geostatistics: an introduction with applications. Springer series in statistics. Springer, Berlin, p 388
Wikle CK, Zammit-Mangion A, Cressie N (2019) Spatio-temporal statistics with R. Chapman & Hall/CRC, Boca Raton, p 380
Yaglom AM (1987) Correlation theory of stationary and related random functions. Springer series in statistics, vol. I, II. Springer, Berlin
Acknowledgments
The author is grateful to the Editor and the anonymous referees for their precious suggestions which contribute to improve the paper.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author declares that she has no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
De Iaco, S. New spatio-temporal complex covariance functions for vectorial data through positive mixtures. Stoch Environ Res Risk Assess 36, 2769–2787 (2022). https://doi.org/10.1007/s00477-022-02171-9
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00477-022-02171-9