1 Introduction

In ecology, a eutrophic crisis of an aquatic ecosystem can be described as accelerated aging as a consequence of water nutrient enrichment caused by anthropogenic activities. The most widespread use refers to the contribution of inorganic nutrients containing Nitrogen and Phosphorus in an aquatic ecosystem, such as a reservoir or lake (Arauzo and Álvarez Cobelas 1994; Ansari et al. 2010). Eutrophication is a kind of water contamination, giving place to modifications such as the presence of colored waters, absence of see-through quality and poisoning by specific algae releases (Reynolds 2006; Van der Valk 2006; Howell 2017). At present, agriculture is taken into account to be a principal underlying and lasting cause of eutrophication in many basins around the world.

Water pollution, such as the eutrophication of lakes, has gradually become an urgent environmental issue worldwide (Liu et al. 2011; Lin et al. 2021). According to statistics from the Water Research Commission, South Africa, 53%, 54%, 46%, and 28% of lakes in Europe, Asia, North America, and Africa face eutrophication problems, respectively (Lin et al. 2021). The eutrophication of lakes occurs under the combined effect of natural factors and human activities, and leads to the growth of great amount of algae. The causes of eutrophication are complex, as eutrophication involves various ecological, social, economic, and other factors (Álvarez et al. 2017). The natural evolution of reservoirs and lakes from oligotrophic to eutrophic is slow, but has been accelerated under human intervention. Therefore, adopting a scientific method for assessing water quality and identifying potential risk sources is urgent, which will help to strengthen ecological and environmental management (Reynolds 2006; García-Nieto et al. 2019; Lin et al. 2021).

The development of biomass in an ecosystem is limited by the scarcity of nitrogen or phosphorus, which primary producers need to develop. Urban effluents, or diffuse pollution from agrarian or atmospheric sources, can contribute increasing the concentration of these limiting substances. The results are important consequences on the composition, structure and dynamics of the ecosystem.

With eutrophication diversity decreases and biomass increases (Harper 1991; Reynolds 2006; Howell 2017). When cyanobacteria begin to be dominant, the potable and recreational use of lake and reservoir waters may be threatened.

The quality of the water decreases with the proliferation of algae and when it becomes explosive, it can cause the appearance of toxins, particularly when cyanobacteria are predominant; large chlorophyll-a contents, usually mean harmful algal blooms (HAB) including toxins—(Pip and Bowman 2014; Yuan et al. 2014). The cyanotoxins liberated by some cyanobacteria in water pose a menace to recreational and drinking (Watzin et al. 2006; Kalaji et al. 2016). In this sense, the knowledge of the concentration of Chl-a can be seen as an optional indicator to evaluate the possibility of blooms of harmful cyanobacteria (HABs) (Huisman et al. 2010; McQuaid et al. 2011; Shumway et al. 2018) in water bodies. Thus, it is important to predict the amount of chlorophyll-a when assessing the water quality so the pollution due to this problem and its health dangers are avoided (Wheeler et al. 2012; Kinkaid 2014; Shumway et al. 2018). Nevertheless, chlorophyll-a is still far from being adequately predicted in lakes and reservoirs (Di Toro et al. 1971; Brown et al. 2000; Tufford and McKeller 1999).

The overabundance of algae that characterizes eutrophication causes the water to become cloudy, preventing sunlight from penetrating the bottom of the ecological community. As a consequence, photosynthesis becomes impossible, while the oxygen-consuming metabolic activity of decomposers increases. In this sense, at the bottom of the ecosystem oxygen is exhausted quickly and becomes anoxic. The alteration caused by these variations makes unviable the life of most of the species of the ecological community.

The eutrophication process can end up turning a reservoir or lake into dry land. This occurs because the nutrients generate large biomass of organisms that are not totally consumed by degrading organisms. Natural eutrophication processes can be in ancient channels of the rivers that are transformed into swamps and later are covered with vegetation.

Modelling is regarded as an interesting tool (Barnes and Chu, 2010; Vinçon-Leite and Casenave 2019) since predictions and understanding of the different process stages can be made. Chl-a and phosphorus are the main indicators to assess continental water trophic state (Beiras 2018).

Chl-a is the principal compound involved in photosynthesis, and it is commonly employed as an indicator for algae growth (Reynolds 2006; Van der Valk 2006). Checking the amount of chlorophyll, using its optical characteristics, helps to control the eutrophication processes that can arise in reservoirs.

Laplacian mathematical models of water quality relied on inner physico-chemical actions in reservoirs and lakes demand a very big quantity of information that is not reachable from the practical point of view, either because it cannot be acquired in its completeness, or because it is complicated to implement or take up too much time to evaluate (Gul et al. 2020). For this reason, there are more and more research works that make use of machine learning techniques to model water quality. For example, Shamshirband et al. (2019) have developed ensemble models using the Bates–Granger approach and least square method to combine forecasts of multi-wavelet artificial neural network (ANN) models for multi-day ahead forecasting of chlorophyll a concentration in coastal waters; Tiyasha and Yaseen (2020) reports the state of the art of various artificial intelligent models implemented for river water quality simulation over the past two decades (2000–2020); Hadjisolomou et al. (2021) have used artificial neural networks (ANNs) to model freshwater eutrophication with limited limnological data; Deng et al. (2021) have implemented two different machine learning methods (artificial neural networks (ANN) and support vector machines (SVM)) to accurately forecast algal growth and eutrophication in Tolo Harbour in Hong Kong carrying out a comparative analysis with 30-year measured data.

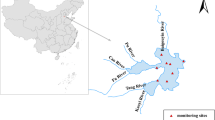
In this investigation, a novel approximation obtained performing a regression that relies on support vector regression (SVR) in combination with whale optimization algorithm (WOA) (Mirjalili and Lewis 2016) has been used to successfully predict the phosphorus and chlorophyll concentration in a reservoir located in Principality of Asturias (an autonomous community placed in Northern Spain) known as Tanes reservoir (see Figs. 1a, b). Algal atypical rapid reproduction is a grave health matter in lakes and reservoirs like the Tanes one that provides water to the main city of the region, Oviedo, that is, it is the supply to one million inhabitants. To prevent toxic algae blooms Chl-a and TP concentrations are used as an early alarm.

Fig. 1
figure 1

Images from Tanes reservoir: a overview of the study area showing its location; and b a close-up image of this water body

Full size image

This new methodology, which mixes the SVM approach (Cristianini and Shawe-Taylor 2000; Hansen and Wang 2005; Steinwart and Christmann 2008) with the whale optimization algorithm (WOA) (Mirjalili and Lewis 2016; Gharehchopogh and Gholizadeh 2019; Ebrahimgol et al. 2020), to foretell the Chl-a and TP concentrations could be an interesting procedure that has not been used so far. Moreover, the SVM method is a mathematical technique relied on the statistical machine learning which has the capacity to tackle nonlinearities as well as interactions among variables (Schölkopf et al. 2000; Steinwart and Christmann 2008; Bishop 2011). The SVM technique provides some advantages with respect to the classical regression methods (Li et al. 2008; Barnes and Chu 2010; Kuhn and Johnson 2013): (1) The SVM eludes mathematical hydraulic models of the reservoir; (2) In SVMs, the knowledge of the physico-chemical involved in the pollutants transport in the reservoir is not required; (3) SVMs allow to deal with the nonlinear relationships among the input variables of the water body; and (4) by training and testing SVR (support vector regression) enables to find nonlinear relationships between data showing an obvious significance. Certainly, the WOA optimizer has been employed well enough to determine the optimal SVM hyperparameters in this investigation. Moreover, earlier researches point out that SVM is a suitable instrument in a big number of existing applications as the foretold modelling for solar thermal energy systems (Waseem Ahmad et al. 2018), air and water quality estimation (García-Nieto et al. 2013; Xu et al. 2019), weighted multiscale SVR combined with ultraviolet–visible spectra for quantitative analysis of edible blend oil (Wu et al. 2021), prediction of the short-term electricity load employing SVR in conjunction with grey catastrophe and random forest techniques (Fan et al. 2021), analysis of SVR kernels for energy storage efficiency prediction (Ighravwe and Mashao 2020), SVR for prediction the number of Dengue infections in the capital of Indonesia (Tanawi et al. 2021), etc. Nevertheless, SVR remains a new method for assessing Chlorophyll-a and TP concentrations using biological and physico-chemical variables and thus to evaluate the quality of the water in lakes and reservoirs.

The foremost aim of the present investigation was to prognosticate the dependent Chl-a and TP concentrations using the input physico-chemical and biological variables in Tanes reservoir-obtained sampling the reservoir periodically (Directive 2000/60/EC; Spatharis and Tsirtsis 2021)—employing SVR in conjunction with WOA. This methodology describes a novel technique to study closely Chl-a and TP in water bodies (i.e., lakes and reservoirs), obtaining measurements of the Chl-a and TP concentrations in them (Smith 2006; Riegl et al. 2014). Certainly, the Chl-a concentration can be taken into account as an essential indicator of surplus nutrients such as TP concentration in a lake or reservoir, and basically, of the presence of eutrophication in these water bodies.

This research work is organized as follows: To start with, the variables and data for the investigation along with mathematical principles are detailed. Next we present the results and discoveries acquired with this new approximation by comparing the observed values with SVR results and next determining the relevance order for the parameters of the model including the discussion. Finally, conclusions derived from this work are explained in detail.

2 Materials and methods

2.1 Study area

The Tanes reservoir is located in the south of the Principality of Asturias (an autonomous community located in the north of Spain), specifically within the Redes Natural Park (this park is considered a biosphere reserve) and in the Nalón river valley. Furthermore, Tanes reservoir supplies drinking water to almost the entire urban nucleus of the Principality of Asturias, including its capital, the city of Oviedo. Therefore, its importance is paramount from several points of view (Kerich 2020; Çadraku 2021). The Tanes reservoir has the following hydrological characteristics: (a) volume: 33.27 hm3; (b) area: 159 ha; and (c) 95 m of depth in the deepest point. Three kilometers downstream from the Tanes reservoir is the Rioseco reservoir. The Rioseco reservoir has the following hydrological characteristics: (a) capacity of 4.3 hm3; (b) surface area of 63 ha; and (c) maximum depth of 28.5 m. Rioseco and Tanes reservoirs provide water supply to approximately one million inhabitants. In addition, the Tanes reservoir has hydroelectric and recreational uses as well as ornithological interest.

The geological area of the Tanes reservoir is the Central Carboniferous Basin, whose lithologies are mainly quartzites and limestones. Therefore, the nature of the most common materials is basic.

2.2 Experimental dataset

The data collection in the WOA/SVR-based study were picked up during ten years. The 268 samples were obtained monthly, starting in January 2006 and ending in December 2015 (Smith et al. 2008; World Health Organization 1998). The data was obtained employing a Niskin bottle at the point in the reservoir where the depth is maximum (see Fig. 2a). The samples were taken at equally spaced depth intervals determined in relation to Secchi depth (the design is not observable on a Secchi disk as a result of the water turbidity) (see Fig. 2b). In this way, five subsamples were picked up (Brönmark and Hansson 2005; Quesada et al. 2006) and next homogenized to acquire a unique sample.

Fig. 2
figure 2

a Niskin device; b Secchi disks

Full size image

The physical–chemical parameters were analyzed by an ISO17025 accredited laboratory, following the corresponding methods in the Standard Methods for the Examination of Water and Wastewater (American Public Health Association 2005; Negro et al. 2000; Van der Valk 2006). A quality assessment program including internal laboratory control (use of standards, blanks and replicates during analysis) as well as analysis of blanks, replicates and blind samples collected in the Tanes reservoir was applied. During the sampling procedure, field blanks were also collected. A total of 10% of samples were replicated to assess variability. Some of these variables were obtained directly, like the temperature or the pH of the water, while obtaining others required a certified laboratory.

2.3 Variables of the model

The ultimate purpose of this investigation was to predict the Chl-a and TP concentrations (µg/L). Chlorophyll-a is broadly used as an indicator of the biomass of algae and therefore, as an index of eutrophication (Latif et al. 2003; Karydis 2009). Very high concentrations of chlorophyll generally point out the presence of algal blooms (United States Environmental Protection Agency 2014) and hence a diminishing in the water quality. Chlorophyll is the substance directly related with the photosynthesis. Thus, phytoplankton and Chlorophyll are mutually linked (American Public Health Association 2005). Besides, as cyanobacteria are predominant in phytoplankton for eutrophic ecosystems, Chlorophyll concentration is considered as a subrogate indicator of them and a measure of the potential risk to public health since cyanobacteria can generate cyanotoxins (Wheeler et al. 2012). The constructed model (SVR) employs the data from different kinds of phytoplankton (biological variables) together with physico-chemical variables as independent parameters, supplied by the Cantabrian Basin Authority, agency primarily responsible for the management of the hydrographic basins in the Cantabrian Sea.

Independent variables:

  • Biological parameters:

  • Cyanobacteria concentration (mm3/L): they have photosynthetic capacity (see Fig. 3a), advertised in environments. They should not be present is freshwater (Quesada et al. 2006; Texeira and Rosa 2006; Willame et al. 2005).

  • Diatoms concentration (mm3/L): another common organism in phytoplankton community and the major group of algae concentration (Fig. 3b).

  • Euglenophytes concentration (mm3/L): phytoplankton with photosynthetic capacity contains it (Fig. 3c).

  • Dinophlagellata concentration (mm3/L): it is also a type of phytoplankton (Fig. 3d).

  • Chrysophytes concentration (mm3/L): they are fundamentally photosynthetic (Fig. 3e).

  • Chlorophytes concentration (mm3/L): they are one of the most numerous groups of algae (Fig. 3f).

  • Chryptophytes concentration (mm3/L): diminutive type of phytoplankton (Fig. 3g).

Fig. 3
figure 3

Microscopic organisms used in this study: a Cyanobacteria; b Diatoms; c Euglenophytes; d Dinophlagella; e Chrysophytes; f Clorophytes; and g Chryptophytes

Full size image

Physico-chemical variables (all of them referred to water column):

  • Water temperature (ºC): this parameter refers to the average value of measures at different depths on water column. Many chemical and biological processes that influence, among others, plant development, are sensitive to temperature.

  • Orthophosphates concentration (mg \({\text{PO}}_{4}^{3 - }\)/L): this represents the phosphorus fraction assimilated by plants and, consequently, it is also related to plant development and eutrophication (it is an essential nutrient for autotrophic organisms such as phytoplankton and other chlorophyll organisms).

  • Total phosphorus concentration (mg P/L): it includes all phosphorus compounds so it comprises forms not assimilated by plants but that can be converted into them when environmental conditions turn into the appropriate. Phosphorus is known as a limiting macronutrient for plant development.

  • Nitrite concentration (mg \({\text{NO}}^{2 - }\)/L): it is one of the nitrogen compounds, an intermediate in the oxidizing process from ammonia to nitrate. It causes several effects such as, for example, methemoglobinemia in many species.

  • Nitrate concentration (mg NO3−/L): nitrate is the most frequent nitrogen ion in water-and this is the nitrogen form usually taken up by plants. Nitrate is also one of the nutrients responsible for waters eutrophication.

  • Ammonium concentration (mg \({\text{NH}}_{4}^{ + }\)/L): ammonium is the reduced form of nitrogen. It is a toxic excreted by aquatic organisms. In water, a high amount of this substance blocks that excretion causing damages even the death of the organism.

  • Dissolved oxygen concentration (mg O2/L): it refers to the density of oxygen dissolved in water, a key factor for many chemical and biological processes and tightly related to algae whose blooms release a lot of oxygen at daytime and gives place to its depletion at night or when bacteria decompose the dead algae.

  • Iron concentration (mg Fe/L): it is a micronutrient for phytoplankton growth. Despite being a life essential element in high concentrations can be toxic. Its precipitates can cause unbalance in waterbodies.

  • Manganese concentration (mg Mn/L): like iron, manganese is an essential trace element for phytoplankton. However, ferromanganese depositions constrain algal colonization and growth (Sheldon and Skelly 1990).

  • Conductivity (μS/cm): it is an indirect measure of salts content in watertight related to phytoplankton composition and abundance (Redden and Rukminasari 2008).

  • Volume of water (hm3): it is an important parameter since nutrients availability for phytoplankton depends on it. High values imply the dilution of toxic substances but also the dilution of nutrients diminishing toxicity and trophic degree, respectively, and therefore, improving waterbody state.

  • pH: it is an expression of acid substance concentration in water. High values indicate low acid concentration (high basic substance concentration), typically of eutrophic waterbodies.

  • Secchi depth (m) or depth at which a Secchi disk immersed in water is no longer visible, measures turbidity that is mainly generated by phytoplankton so it is an indicator of its abundance.

2.4 Feature selection using multivariate adaptive regression splines (MARS)

The feature or variable selection process involves the picking of only some of the most important characteristics (known as variables or predictors) for their employ in modeling construction. Feature selection techniques are employed for five compelling reasons:

  • This permits the simplification of the models for the purpose of making them easier to understand for users and researchers;

  • It reduces training time: less data indicates that algorithms can be trained quicker;

  • The precision is improved: less erroneous data indicates that modeling precision ameliorates.

  • The curse of dimensionality can be eluded; and

  • It reduces overfitting (formally, variance reduction): less duplicate data means less chance to come to decisions relied on noise.

One of the most efficient and robust techniques in the selection of variables is multivariate adaptive regression splines (MARS). The MARS tool is used here to handle complex data and to select the important features from the entire experimental dataset. Some advantages of applying the MARS method over other existing techniques in-clude (Friedman and Roosen 1995; Hastie et al. 2003): (1) it provides more flexible models than linear regression models; (2) it is easy to interpret and understand; (3) it can manage continuous and categorical data; (4) the hinge functions automatically partition the input data, so the effect of outliers is contained; (5) it does automatic var-iable selection (meaning that it includes important variables in the model and excludes unimportant ones); (6) it tends to have a good bias-variance trade-off; and (7) it of-fers an explicit mathematical expression of the dependent variable as a function of independent variables through an expansion of the base functions (hinge functions and products of several hinge functions or interactions).

Next, we will briefly describe the mathematical basics and benefits of the MARS technique. Multivariate adaptive regression splines (MARS) is a statistical approach (Friedman 1991; Sekulic and Kowalski 1992) and it is a generalization of recursive partitioning regression (RPR) that can consider complex relationships between a set of k predictor independent variables, which are denoted by \(X_{1} ,X_{2} ,...,X_{k}\) and a dependent variable designated by Y, and does not make starting assumptions about any type of relationship between input and output parameters. The MARS model is defined as (Friedman and Roosen 1995; Hastie et al. 2003; García-Nieto et al. 2019):

$$ \hat{y} = f\left( X \right) = \beta_{0} + \sum\limits_{m = 1}^{M} {\beta_{m} h_{m} \left( X \right)} + \varepsilon $$
(1)

where X is a function of the independent variables and their interactions, \(\beta_{0}\) is the intercept parameter, \(\beta\) is a vector of coefficients of the basis function, M is the total number of these basis functions, \(h\left( X \right)\) the spline basis function in the model and \(\varepsilon\) is the fitting error.

To approximate the nonlinear relationships between the input variables X and the response parameter Y, basis functions (BF) are used. They consist of a unique spline function or the product of two or more spline functions for distinct predictors. Spline functions are piecewise linear functions, that is, truncated left-hand and right-hand functions, and take the form of hinge functions that are joined at the knots (Chou et al. 2004; Zhang et al. 2015; García-Nieto et al. 2019):

$$ \left( {x - t} \right)_{ + } = \left\{ {\begin{array}{*{20}c} {x - t} & {{\text{if}}} & {x > t} \\ 0 & {{\text{if}}} & {x \le t} \\ \end{array} } \right\} $$
(2)
$$ \left( {t - x} \right)_{ + } = \left\{ {\begin{array}{*{20}c} {x - t} & {{\text{if}}} & {x > t} \\ 0 & {{\text{if}}} & {x \le t} \\ \end{array} } \right\} $$
(3)

where t is a constant called a node that specifies the boundary between the regions that have continuity from the base functions of the regions from left to right and that are smoothly joined at the given node and adaptively selected from the data. The “+” sign refers to the positive part and sets a value equal to zero for negative values of the argument. For example, Fig. 4 indicates a pair of splines for q = 1 at the node t = 3.5.

Fig. 4
figure 4

A graphical representation of a spline basis function. The left spline (\(x < t\),\(- \left( {x - t} \right)\)) is shown as a dashed line and the right spline (\(x > t\),\(+ \left( {x - t} \right)\)) as a solid line

Full size image

As stated in some references (Xu et al. 2004; Cheng and Cao 2014; Zhang et al. 2015), MARS forms reflected pairs for each predictor variable with knots of each value \(x_{j} ,\,\,j \in \left\{ {1,...,k} \right\}\) with knots at each observed value \(x_{ij} ,\,\,i \in \left\{ {1,...,n} \right\}\) of that variable, where n is the sample size. The set of all possible pairs with the corresponding knots and the truncated linear basis functions can be expressed by the set \(D = \left\{ {\left( {x_{j} - t} \right)_{ + } ,\left( {t - x_{j} } \right)_{ + } \left| {t \in \left\{ {x_{1j} ,x_{2j} ,...,x_{nj} } \right\},j \in \left\{ {1,...,k} \right\}} \right.} \right\}.\)

An adaptive regression algorithm is taken during a recursive partition strategy to automatically select the locations of the node or breakpoints, including the two-stage process: forward-stepwise regression selection and backward-stepwise elimination procedure (Cheng and Cao 2014; Zhang et al. 2015).

The first step, also called the construction phase, begins with the intersection and then, in order, adds to the approximation the predictor that further improves the fit; that is, when the maximum diminishing in the sum-of-squares residual error happens. The search for the best combination of variable and node is done iteratively. Keeping in mind a model that contains M hinge functions, the following couple will be added to the approximation in the form of \(\beta_{M + 1} h_{m} \left( X \right)\mathop {\max }\limits_{{}} \left( {0,X_{j} - t} \right) + \beta_{M + 2} h_{m} \left( X \right)\mathop {\max }\limits_{{}} \left( {0,t - X_{j} } \right).\) Given a choice for the \(h_{m}\), the coefficients \(\beta_{m}\) that make up the vector \(\beta\) are estimated by minimizing the residual sum-of-squares, that is, by standard linear regression (Friedman and Roosen 1995; Hastie et al. 2003; Chou et al. 2004).

This procedure persists until a predetermined number of base functions \(\left( {M_{\max } } \right)\) is accomplished or the R2 alters less than a limit (Friedman and Roosen 1995; Chou et al. 2004). A big number of BFs are summed one after another so that an overfitting model is built. Generally, the maximum number of BF is 2–4 times the number of predictor variables (Cheng and Cao 2014; Zhang et al. 2015).

The second step, also called the pruning phase, begins with the full model and simplifies it by eliminating terms by applying a backward procedure to avoid oversizing. MARS identifies the hinge functions that are less relevant for the model and removes the least significant terms sequentially. The final model is chosen employing the generalized cross-validation method (GCV), an adjustment of the sum-of-squares of the residuals that penalizes the complexity of the models by the number of hinge functions and the number of knots (Hastie et al. 2003; Cheng and Cao 2014; Zhang et al. 2015) and it is given by:

$$ GCV\left( M \right) = \frac{{\frac{1}{n}\sum\nolimits_{i = 1}^{n} {\left( {y_{i} - \hat{f}_{M} \left( {x_{i} } \right)} \right)^{2} } }}{{\left( {1 - C\left( M \right)/n} \right)^{2} }} $$
(4)

where M is the number of terms in Eq. (1) (equal to the number of BFs), n is the number of data sets, \(y_{i}\) are the observed values and \(\hat{f}_{M} \left( {x_{i} } \right)\) denotes the predicted values from MARS and, finally the value \(C\left( M \right)\) increases with the number of basis functions used in the model. The formula for this value is (Sekulic and Kowalski 1992; Friedman and Roosen 1995; Hastie et al. 2003):

$$ C\left( M \right) = \left( {M + 1} \right) + d\,M $$
(5)

so that d is a coefficient that establishes the relevance of this parameter.

The relevance of the variables used as predictors can be assessed in different ways (Xu et al. 2004; Cheng and Cao 2014; Zhang et al. 2015): (a) using the GCV related to the variables: when we drop a variable from the model the GVC index increases. This increment is the associated value; (b) similarly, using the residual sums of squares (RSS); and (c) we can count the number of subsets (Nsubsets) that contains a specific variable. The more subsets, the greater its relevance.

2.5 Support vector regression (SVR)

Support vector machines (SVM) have originally emerged to address binary classification problems. In view of the situation, it was rapidly noted that the fundamental guidelines that endorse them could be employed to confront another type of issues such as the regression problems (Vapnik 1998; Pal and Goel 2007; Chen et al. 2013). In this sense, let's consider a dataset, the training set comprises the values of the output dependent variable \(y_{i} \in \Re ,\,\,\forall i = 1,2,...,m\) and the covariates \({\mathbf{x}}_{i} \in \Re^{p} ,\,\,i = 1,2,...,m\). Thus, the method termed support vector regression (SVR) builds a function \(f\left( {\mathbf{x}} \right) = {\mathbf{w}}^{T} {\mathbf{x}} + b\), so that w represents the perpendicular vector to the hyperplane, called director vector of the hyperplane, and \({b \mathord{\left/ {\vphantom {b {\left\| {\mathbf{w}} \right\|}}} \right. \kern-\nulldelimiterspace} {\left\| {\mathbf{w}} \right\|}}\) is the perpendicular distance from the coordinate’s origin to the hyperplane. Furthermore, this approximation gives places to not more than a deviation equal to \(\varepsilon\) from \(y_{i}\) for all training cases \({\mathbf{x}}_{i}\), and simultaneously, it must be as flat as possible. Flatness is achieved by minimizing the Euclidean norm \(\left\| {\mathbf{w}} \right\|_{2}\), while the model is fitted by penalizing the sum of deviations greater than \(\varepsilon\). Indeed, the SVR method intends to solve the next optimization problem (Steinwart and Christmann 2008; Cristianini and Shawe–Taylor 2000; Gu et al. 2006):

$$ \mathop {\min }\limits_{{{\mathbf{w}},b,{{\varvec{\upxi}}}^{ + } ,{{\varvec{\upxi}}}^{ - } }} \frac{1}{2}\left\| {\mathbf{w}} \right\|^{2} + C\sum\limits_{i = 1}^{m} {\left( {\xi_{i}^{ + } + \xi_{i}^{ - } } \right)} $$
(6)

subject to

$$ \left\{ {\begin{array}{*{20}c} {y_{i} - \left( {{\mathbf{w}}^{T} {\mathbf{x}}_{i} + b} \right) \ge \varepsilon + \xi_{i}^{ + } } & {} & {i = 1,...,m} \\ {\left( {{\mathbf{w}}^{T} {\mathbf{x}}_{i} + b} \right) - y_{i} \ge \varepsilon + \xi_{i}^{ - } } & {} & {i = 1,...,m} \\ {\xi_{i}^{ + } ,\xi_{i}^{ - } \ge 0} & {} & {i = 1,...,m} \\ \end{array} } \right\} $$
(7)

so that C is termed the regularization constant and \({{\varvec{\upxi}}}^{ + } ,{{\varvec{\upxi}}}^{ - } \in \Re^{m}\) are called slack variables. The constant C in Eq. (6) takes a positive numeric value that restrains the penalty enforced on observations that are outside the interval \(\varepsilon\) and facilitates avoiding the overfitting. This value ascertains the trade-off between the horizontality of the objective function and the complexity reduction of the model. The slack variables are presented for each training vector for the purpose of permitting deviations greater than \(\varepsilon\), but penalizing these digressions in the objective function. The zone enclosed by \(y_{i} \pm \varepsilon ,\,\,\,\forall i\) is termed an \(\varepsilon\)-insensitive tube (see Fig. 5).

Fig. 5
figure 5

Representation of the \(\varepsilon\)-insensitive tube in case of regression

Full size image

To tackle highly nonlinear problems like this one, we will use the kernelization method. This method relies on mapping the original dataset to a larger dimensional space H termed the feature space. The application is carried out via a kernel function \(K\left( {{\mathbf{x}}_{i} ,{\mathbf{x}}_{j} } \right)\), which determines a scalar product in H. In order to solve the primal optimization problem given by Eqs. (6) and (7), we are going to express this problem in its dual form. The dual formulation of the optimization problem is obtained applying the Karush–Kuhn–Tucker (KKT) conditions (Li et al. 2008; Gu et al. 2006; Shawe-Taylor and Cristianini 2004):

$$ \mathop {\max }\limits_{{{{\varvec{\upalpha}}}^{ + } ,{{\varvec{\upalpha}}}^{ - } }} \,\,\sum\limits_{i = 1}^{m} {y_{i} \left( {\alpha_{i}^{ + } - \alpha_{i}^{ - } } \right)} - \varepsilon \sum\limits_{i = 1}^{m} {\left( {\alpha_{i}^{ + } + \alpha_{i}^{ - } } \right)} - \frac{1}{2}\sum\limits_{i,j = 1}^{m} {\left( {\alpha_{i}^{ + } - \alpha_{i}^{ - } } \right)\left( {\alpha_{j}^{ + } - \alpha_{j}^{ - } } \right)K\left( {{\mathbf{x}}_{i} ,{\mathbf{x}}_{j} } \right)} $$
(8)

subject to

$$ \left\{ {\begin{array}{*{20}c} {\sum\limits_{i = 1}^{m} {\left( {\alpha_{i}^{ + } - \alpha_{i}^{ - } } \right)} = 0,} & {} & {} \\ {0 \le \alpha_{i}^{ + } \le C,} & {} & {i = 1,...,m} \\ {0 \le \alpha_{i}^{ - } \le C,} & {} & {i = 1,...,m} \\ \end{array} } \right\} $$
(9)

The regression estimation for a new sample x can be obtained with the function \(f\left( {\mathbf{x}} \right)\) given by (Steinwart and Christmann 2008; García-Nieto et al. 2013; Gu et al. 2006):

$$ f\left( {\mathbf{x}} \right) = \sum\limits_{i = 1}^{m} {\left( {\alpha_{i}^{ + } - \alpha_{i}^{ - } } \right)K\left( {{\mathbf{x}},{\mathbf{x}}_{i} } \right)} + b $$
(10)

Various common functions utilized as kernels in the technical bibliography are expressed as (Shawe-Taylor and Cristianini 2004; Hansen and Wang 2005; Abbaszadeh et al. 2016):

  • Radial basis function termed RBF kernel:

    $$ k\left( {{\mathbf{x}}_{i} ,{\mathbf{x}}_{j} } \right) = e^{{ - \sigma \left\| {{\mathbf{x}}_{i} - {\mathbf{x}}_{j} } \right\|^{2} }} $$
    (11)

  • Polynomial kernel:

    $$ k\left( {{\mathbf{x}}_{i} ,{\mathbf{x}}_{j} } \right) = \left( {\sigma {\mathbf{x}}_{i} \cdot {\mathbf{x}}_{j} + a} \right)^{b} $$
    (12)

  • Sigmoid kernel:

    $$ k\left( {{\mathbf{x}}_{i} ,{\mathbf{x}}_{j} } \right) = \tanh \left( {\sigma {\mathbf{x}}_{i} \cdot {\mathbf{x}}_{j} + a} \right) $$
    (13)

where a, b and \(\sigma\) are parameters that demonstrate the operation of the kernel.

Furthermore, typical parameters of the SVR approach can be synthesized as (Shawe–Taylor and Cristianini 2004; Steinwart and Christmann 2008; García-Nieto et al. 2013):

  • Regularization constant (C): it is also called cost function. This constant represents the balance (or trade-off) between the margin and the slack variables. It is one of the hyperparameters of the SVR technique that must be previously determined by tuning.

  • \(\varepsilon\) parameter: This value restrains the width of the allowable margin of error. The second term of the objective function (see Eq. 8) that relied on \(\varepsilon\) factor is called the empirical error and is determined by means of the insensitive loss function, which points out that it does not ignore errors less than \(\varepsilon\) (that is, at a distance \(\varepsilon\) of the real value).

  • a, b and \(\sigma\): these parameters define the mathematical expression of the distinct kernels in the final model.

Hence, it is convenient to employ some mathematical technique that determines the above hyperparameters with sufficient precision. Moreover, the whale optimizer algorithm (WOA) explained in more detail below was employed (Mirjalili and Lewis 2016; Gharehchopogh and Gholizadeh 2019) with triumph in this research work. To fix ideas, the whale optimizer algorithm (WOA) expounded in the following subsection was used (Mirjalili and Lewis 2016; Gharehchopogh and Gholizadeh 2019; Ebrahimgol et al. 2020) in this investigation with success.

2.6 Whale optimization algorithm (WOA)

The Whale Optimization Algorithm (WOA) is an optimization algorithtm first suggested by Mirjalili and Lewis (Mirjalili and Lewis 2016). It emulates the clever hunt process performed by humpback whales. The gathering performance is termed the bubble-net feeding methodology, that originate bubbles to surround their victim as they hunt. They plunge into the water at a depth of about 12 m and next originate the spiral of bubbles surrounding their victim. Then they go up pursuing the bubbles. The model that inspires the spiral bubble-net feeding performance is described below (Mirjalili and Lewis 2016; Gharehchopogh and Gholizadeh 2019; Ebrahimgol et al. 2020):

  • Surrounding prey

The whales identify the position of the victim surround it. Assuming that the optimum point is not known, WOA supposes that the present best point is the prey and that this is close to the optimum. When the best scout is established, the other scouts will bring up to date their locations to the best scout. This fact is given by the following mathematical expressions:

$$ \begin{gathered} \vec{D} = \left| {\vec{C} \cdot \vec{X}_{p} \left( t \right) - \vec{X}\left( t \right)} \right| \hfill \\ \vec{X}\left( {t + 1} \right) = \vec{X}_{p} \left( t \right) - \vec{A} \cdot \vec{D} \hfill \\ \end{gathered} $$
(14)

so that:

  • t: This points out the present iteration;

  • \(\vec{A}\) and \(\vec{C}\): they are called coefficient vectors;

  • \(\vec{X}_{p}\): represents the position of the prey; and

  • \(\vec{X}\): This represents the whale’s location.

Moreover, the coefficient vectors \(\vec{A}\) and \(\vec{C}\) are constructed according to equations:

$$ \begin{gathered} \vec{A} = 2\vec{a} \cdot \vec{r}_{1} - \vec{a} \hfill \\ \vec{C} = 2\vec{r}_{2} \hfill \\ \end{gathered} $$
(15)

so that components of \(\vec{a}\) diminish in a linear form from 2 to 0 with advancing iterations, while \(\vec{r}_{1}\), \(\vec{r}_{2}\) are random vectors whose components lie in the interval [0,1].

  • Exploitation phase: bubble-net attack procedure

The bubble-net technique is a procedure that mixes two mathematical approximations given by Mirjalili and Lewis (2016), Gharehchopogh and Gholizadeh (2019), and Ebrahimgol et al. (2020):

  1. 1.

    Shrinking surrounding mechanism: This procedure is accomplished by diminishing \(\vec{a}\). As \(\vec{A}\) takes a random value in the interval \(\left[ { - a,a} \right]\) so a diminishes from 2 to 0 with advancing iterations. Choosing values for \(\vec{A}\) in \(\left[ { - 1,1} \right]\) randomly, the fresh location of a scout can be set in any point between the novel location and the position of the best point found so far.

  2. 2.

    Spiral upgrading location: First, the distance between the whale \(\left( {\vec{X},\vec{Y}} \right)\) and the prey \(\left( {\vec{X}^{ * } ,\vec{Y}^{ * } } \right)\) is calculated. Next, an equation called spiral is produced joining the whale and prey position with an helix:

    $$ \vec{X}\left( {t + 1} \right) = \vec{D}^{\prime}e^{bt} \cos \left( {2\pi t} \right) + \vec{X}^{ * } $$
    (16)

    being:

  • \(\vec{D}^{\prime} = \left| {\vec{X}^{ * } \left( t \right) - \vec{X}\left( t \right)} \right|\) is the distance between the prey and (present best solution until now) and i-th whale;

  • b is a constant that determines the form of the logarithmic spiral; and

  • t takes random values that are in the interval \(\left[ { - 1,1} \right]\).

The spiraling path of the whales around their prey shrinks more and more. To implement this concurrent performance, we suppose that we choose with a 50% probability and the spiral path to update the position of the whales. This is given by the expression (Mirjalili and Lewis 2016; Gharehchopogh and Gholizadeh 2019; Ebrahimgol et al. 2020):

$$ \vec{X}\left( {t + 1} \right) = \left\{ {\begin{array}{*{20}c} {\vec{X}^{*} \left( t \right) - \vec{A} \cdot \vec{D}} & {{\text{if}}} & {p < 0.5} \\ {\vec{D}^{\prime}e^{bt} \cos \left( {2\pi t} \right) + \vec{X}^{ * } } & {{\text{if}}} & {p \ge 0.5} \\ \end{array} } \right\} $$
(17)

so that p is a number chosen randomly that takes values in the interval \(\left[ {0,1} \right]\). Besides the bubble-net approach, the whales look for a victim at random. The model is described below:

  • Exploration phase: search for prey

The approximation that relied on the fluctuation of \(\vec{A}\) can be employed to look for victims (this stage is termed exploration). Indeed, humpback whales look for at random as stated by their comparative location to each other. As a consequence, we employ \(\vec{A}\) random values within the range \(\left( { - \infty , - 1} \right) \cup \left( {1,\infty } \right)\) to compel the scout to distance itself from a given whale. Unlike the exploitation phase, the location of a scout at this stage is upgraded by means of a chosen search scout at random. This and \(\left| {\vec{A}} \right| > 1\) highlight exploration and allows WOA algorithm to perform an overall exploration. This is expressed (Mirjalili and Lewis 2016; Gharehchopogh and Gholizadeh 2019; Ebrahimgol et al. 2020):

$$ \begin{gathered} \vec{D} = \left| {\vec{C} \cdot \vec{X}_{rand} - \vec{X}} \right| \hfill \\ \vec{X}\left( {t + 1} \right) = \vec{X}_{rand} - \vec{A} \cdot \vec{D} \hfill \\ \end{gathered} $$
(18)

so that \(\vec{X}_{rand}\) gives the random position of the whale (it is called a random whale).

WOA begins with a collection of random possible solutions. Hence, according to this methodology, search agents upgrade their locations taking into account a selected search agent at random or the best solution acquired up until now at each iteration. The parameter a diminishes from 2 to 0 for the purpose of supplying both exploration and exploitation. A search scout at random is selected when \(\left| {\vec{A}} \right| > 1\), but if \(\left| {\vec{A}} \right| < 1\), the best solution is found upgrading the location of the search agents. Finally, WOA ends when a certain stopping criterion is fulfilled.

2.7 Approach accuracy

Twenty independent variables already specified earlier in subsection 2.3 were used in this investigation to create this innovative WOA/SVR-relied method. As is well known, the concentration of Chlorophyll-a is the predicted parameter. For the purpose of foretelling Chl-a from the twenty independent variables with enough assurance, we must choose a good approach to the experimental data. There are some indexes frequently employed to determine the goodness-of-fit in a regression problem, but the norm used in this investigation was the coefficient of determination R2 (Freedman et al. 2007; Knafl and Ding 2016; McClave and Sincich 2016). To fix ideas, we will term the experimental values \(t_{i}\) and the predicted values \(y_{i}\). Hence, it is feasible to specify the following additions as follows (Freedman et al. 2007; Knafl and Ding 2016; McClave and Sincich 2016):

  • \(SS_{tot} = \sum\limits_{i = 1}^{n} {\left( {t_{i} - \overline{t}} \right)^{2} }\): is called the total sum of squares, and it is directly related to the sample variance.

  • \(SS_{reg} = \sum\limits_{i = 1}^{n} {\left( {y_{i} - \overline{t}} \right)^{2} }\): it is called the regression sum of squares, or the explained sum of squares.

  • \(SS_{err} = \sum\limits_{i = 1}^{n} {\left( {t_{i} - y_{i} } \right)^{2} }\): it is called the residual sum of squares.

so that \(\overline{t}\) is the average of the n experimental data:

$$ \overline{t} = \frac{1}{n}\sum\limits_{i = 1}^{n} {t_{i} } $$
(19)

Thus, the coefficient of determination is defined by the mathematical expression:

$$ R^{2} \equiv 1 - \frac{{SS_{err} }}{{SS_{tot} }} $$
(20)

The closer the R2 statistic is to the value 1.0, the smaller the disagreement between the experimental and foretold data. Similarly, the mathematical expressions for the other two statistics used in this study (RMSE and MAE) are as follows (Freedman et al. 2007; Knafl and Ding 2016):

$$ RMSE \equiv \sqrt {\frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {t_{i} - y_{i} } \right)^{2} } } $$
(21)
$$ MAE = \frac{1}{n}\sum\limits_{i = 1}^{n} {\left| {t_{i} - y_{i} } \right|} $$
(22)

Higher values of R2 are preferred, i.e. closer to 1 means better model performance and regression line fits the data well. Conversely, the lower the RMSE and MAE values are, the better the model performs.

3 Results and discussion

Tables 1 and 2 show the input variables in this study. Seven variables are biological (see Table 1) and the remaining thirteen are physic-chemical (see Table 2). The dataset consists of 268 samples from Tanes reservoir (Directive 2000/60/EC).

Table 1 Ensemble of biological independent parameters employed in this work
Full size table
Table 2 Ensemble of physico-chemical independent parameters employed in this work
Full size table

In this study, firstly we have performed a choice of the principal characteristics or feature selection (input variables or biological and physicochemical predictors) for the two eutrophication indicators (Chl-a and TP) in bodies of water (reservoirs, lakes, etc.) using the MARS technique (ARESLab package) (Jekabsons 2016; Ciaburro 2017). This allowed us to build two simplified models (one model for Chl-a and another model for TP) in order to facilitate their interpretation for researchers and reduce overfitting. The feature selection for Chl-a and TP eutrophication indicators according to the MARS technique are shown in Tables 3 and 4, respectively. Specifically, the reduced model for Chl-a consists of thirteen input variables or predictors while the reduced model for TP consists of eleven input variables or predictors.

Table 3 Feature selection for the eutrophication indicator Chl-a according to MARS technique
Full size table
Table 4 Feature selection for the eutrophication indicator TP according to MARS technique
Full size table

The dataset was split into a training set (80% of the data) and a testing set (20%). The model is built with the training data using the SVR model. Previously, the metaheuristic WOA has been used to optimize the hyperparameters using a five-fold cross-validation scheme with the training dataset. The flowchart in Fig. 6 illustrates this stage. Once the parameters have been chosen, and the model obtained, this is tested with the testing dataset and predictions for these values are obtained.

Fig. 6
figure 6

Flowchart of the construction of the WOA/SVR model

Full size image

As we have previously indicated, the two output variables (dependent variables) in this study are the Chl-a concentration and TP concentration both treated with the WOA/SVR-relied method. A most important issue in the efficiency of this technique is the selection of the optimal hyperparameters noted above: (1) the constant C of regularization; (2) \(\varepsilon\) the insensitive tube width; and (3) parameter \(\sigma\), which condition the shape of the RBF (radial basis function) kernel in the ultimate model. The grid search method used by most computational codes is a brute force method, and as such, almost any optimization method improves its efficiency. The grid search is a very simple method that promotes an extensive searching within a predetermined grid. It can be easily improved with smarter searching methods such as the one we have chosen for this paper, WOA optimization, which is more efficient while maintaining the simplicity. Indeed, it has been applied to tune the SVR parameters with success in this study. Table 5 shows the intervals where the three parameters of SVR are searched by WOA for optimal performance of the model.

Table 5 Search intervals for the RBF–SVR hyperparameters fitted by using the WOA optimizer during the tuning process
Full size table

Following this process, we get the optimal parameters for the RBF-SVR model with the WOA optimizer, which are shown in Table 6.

Table 6 Optimal parameters for the RBF–SVR–relied models for the training set encountered with the WOA optimizer for the Chl-a and TP eutrophication indicators
Full size table

The value of R2 was obtained with this model and the testing dataset. The library for support vector machines, termed LIBSVM, was used here to implement the MARS technique (Chang and Lin 2011), in combination with the WOA optimizer (Mirjalili and Lewis 2016).

Taking into account these calculations, the WOA/RBF-SVR-relied method has permitted to build of a novel hybrid model that is able to predict the Chl-a and TP concentrations using the test dataset. Moreover, in Table 7 we can see the different metrics for the evaluation of the performance of this WOA/SVR model with different types of kernels and three additional models adjusted for the Chl-a and TP concentrations.

Table 7 Coefficient of determination (R2), correlation coefficient (r), root-mean-square error (RMSE) and mean absolute error (MAE) for the novel WOA/SVR-relied model with different types of kernels and linear regression (LR), multilayer perceptron (MLP) and random forest (RF) models for the Chl-a and TP concentrations for the test dataset
Full size table

The R2 value for the optimal SVR model was 0.8582 for the variable Chl-a predicted with RBF kernel and 0.9750 for the variable TP also predicted with RBF kernel. Similar works obtain worse results (Jimeno-Sáez et al. 2020; Liao et al. 2021).

3.1 Importance of the variables

A significant outcome of the actual research is the relative importance of the parameters used as predictors in the models that predict Chl-a and TP concentrations. Table 8 shows the weights of the thirteen variables in the WOA/SVR-RBF model for the Chl-a forecast. Similarly, Table 9 shows the weights for the eleven variables WOA/SVR-RBF model for the TP prediction. Taken in absolute value, these weights illustrate the relative relevance of the variables in this methodology. The greater the absolute value of the weight, the greater the relative relevance of the variable within the model.

Table 8 Relevance of the variables used as predictors in the WOA/SVR-RBF model for the Chl-a forecast
Full size table
Table 9 Relevance of the variables used as predictors in the WOA/SVR–RBF model for the TP forecast
Full size table

In this sense, Chlorophytes concentration is the weightiest variable in WOA/SVR approach for Chl-a prediction followed, far away, by Cyanobacteria concentration, volume of water, Euglenophytes, Chryptophytes, Dinophlagellata, Manganese, Water temperature, Diatoms, Total phosphorus, Secchi depth, Phosphates and Conductivity (Table 8 and Fig. 7).

Fig. 7
figure 7

Relevance ranking of the variables used as predictors for the WOA/SVR-relied approach to forecast the Chl-a concentration

Full size image

However, in the TP forecasting using WOA/SVR approach Iron concentration is the weightiest variable. The second one, Chryptophytes concentration, has similar significance. The remaining input variables have much less weight (see Table 9 and Fig. 8): Chlorophytes (0.8964), Chl-a (0.85939), Dinophlagellata (0.7661), Volume of water (0.7285), Diatoms (0.6987), Euglenophytes (0.6869), Cyanobacteria (0.4799), Nitrate (0.3303) and Phosphates with only a thirtieth of the Iron weight (0.0581 versus 1.4933 for Iron).

Fig. 8
figure 8

Relevance ranking of the variables used as predictors for the WOA/SVR-relied approach to forecast the TP concentration

Full size image

As Fig. 7 shows, Chlorophytes influence in Chl-a is nearly three times all the others. Consequently, in Tanes reservoir Chl-a concentration can be predicted from Chlorophytes concentration with remarkably precision since this water body is mesotrophic. One of the reasons why chlorophytes outcompete cyanobacteria at high nutrient levels may be the balance between the rates of cellular growth and losses (Reynolds 2006; Ansari et al. 2010). Chlorophytes have a high demand for nutrients as reflected in their high growth rates.

Cyanobacteria is the second most important input variable in the prediction of Chl-a. Indeed, cyanobacteria include bacteria capable of oxygenic photosynthesis. They are the only prokaryotes that carry out this type of photosynthesis, which is why they are also called oxyphotobacteria. Cyanobacteria have also been known by the names of blue-green or chloroxybacteria algae, due both to the presence of chlorophyll pigments that give it that characteristic tone, and to its similarity with the morphology and functioning of algae.

Among the non-biological variables, Water Volume is the most important one in Chl-a forecast and the third in the general ranking. The relationship between Water Volume and phytoplankton growth, or Chl-a concentration, was pointed out by other authors (Brasil et al. 2016; Costa et al. 2016) who conclude that in a deep reservoir the reduction in its Water Volume favours phytoplankton growth and consequently, Chl-a concentration.

Euglenophytes, Chryptophytes and Dinophlagellata concentrations are less relevant than other kinds of phytoplankton in Chl-a concentration forecasting according to their fourth, fifth and sixth position, respectively, in the ranking and their weight, nearly four times lower than Chlorophytes concentration weight and also lower than Cyanobacteria concentration weight. The concentration of Euglenophytes is the fourth most significant variable in the prediction of Chl-a (output variable) because dammed waters are usually rich in Euglenophytes. The concentration of Chryptophytes is the fifth most important variable in Chl-a concentration foretelling. They are important members of phytoplankton and can be found in stagnant waters, withstanding moderate levels of contamination. They are especially abundant in cold waters such as high mountain reservoirs and lakes. In general, cryptophytes are mixotrophic, that is, capable of both photosynthesis and phagotrophy. The concentration of Dinophlagellata is the sixth most important variable due to the photosynthetic nature of these organisms.

The less important phytoplanktonic predictor of Chl-a is Diatoms concentration, the ninth input variable in relevance, despite dominating the phytoplankton groups in Tanes reservoir. They are important producers within the food chain (Reynolds 2006; Van der Valk 2006).

Manganese concentration is an essential micronutrient in phytoplankton growth and appears in position seven in the ranking of the Chl-a ranking. It is well known for quite some time that manganese concentration concerns phytoplankton structure (Patrick et al. 1969).

Water temperature is the most relevant physico chemical variable and it is the eighth one in importance for Chl-a concentration prediction. Increasing temperature favor phytoplankton growth. In fact, Climate Change is a matter of concern in water eutrophication (Moss et al. 2011; Havens 2019).

Much less important is Total phosphorus, the tenth input variable in significance to predict Chl-a density. Total phosphorus is correlated to Chl-a because it is a nutrient for phytoplankton. The other essential nutrient to grow phytoplankton and, as a consequence, to increase Chl-a, is Nitrogen. However, this element is not relevant in Chl-a forecast perhaps because it is not a limiting factor for phytoplankton since it can take the Nitrogen up from the atmosphere (Fields 2004; Moura Ado et al. 2012).

The other input variables (Secchi depth, Phosphates concentration and Conductivity) hardly are influential on Chl-a prediction.

The higher the Secchi depth value the lower the turbidity value and therefore more light availability and more phytoplankton biomass (Costa et al. 2016) or, in other words, more Chl-a.

Phosphates are the highly biological available form of phosphorus. They are the soluble fraction of total phosphorus, the part easily used by phytoplankton to grow. They foster the biomass increase of phytoplankton reducing water quality and unbalancing the ecosystem leading to some species disappearance. However, they barely have influence as predictor of Chl-a (weight 0.0231 and twelfth position in the ranking).

Conductivity seems to have an irrelevant contribution predicting Chl-a density in the studied reservoir (the thirteenth input variable in importance and it has even less weight than phosphates).

In the case of TP content forecasting, as Fig. 8 shows, Iron and Chryptophytes concentrations are the most important input variables. An expected result considering the strong affinity Iron has for phosphorus (Koopmans et al. 2020) and the significance of Chryptophytes in phytoplankton. They can be found in stagnant waters, supporting moderate levels of contamination, which correspond to contributions of nutrients rich in phosphorus, which can be the reason for the importance of this input variable in the TP foretelling (Abirhire et al. 2015).

The rest of the input variables are much less relevant in PT prediction-about 50% of the iron or Chryptophytes weights, or less, depending on the variable considered. Most of them, except Volumen (the sixth relevant variable in the foretelling), are phytoplankton species or related to them as Chl-a concentration.

An explanation of the phytoplankton relevance in total phosphorus forecast could be that this latter is a nutrient that stimulates the growth for all these species since the phosphorus is the limiting nutrient in plant growth, particularly in lakes and reservoirs as is the case at hand. In fact, most Chlorophytes, one of the most numerous groups of algae and the most relevant phytoplanktonic predictor excluding Chryptophytes, have a wide distribution and many are cosmopolitan, hence their presence in waters contaminated with organic material, linked to contributions rich in phosphorus (Arauzo and Álvarez Cobelas 1994; Reynolds 2006). Furthermore, Dinophlagellata, the fifth significant variable—third of phytoplankton species—to predict PT density, proliferates as the amount of phosphorus increases in the water body causing the decrease in phytoplankton diversity and productivity.

Among all the phytoplankton species, cyanobacteria are the less relevant predictor of PT content according to the fact that this kind of organism only dominates environments with high trophic degree (Quesada et al. 2004), but Tanes reservoir has a fair trophic state. Cyanobacteria are a group of photosynthetic bacteria, some of which fix nitrogen, living in a wide variety of moist soils and water freely or in a symbiotic relationship with lichen-forming plants or fungi.

Chl-a concentration is related to the sum of all kinds of phytoplankton species measured since all of them are photosynthetic. Chl-a concentration is the fourth important variable for TP content.

Volume of water is another relevant variable (the sixth one according to the proposed model) to predict TP concentration; an expected result since concentration depends on the water volume.

After phytoplankton species, nitrate concentration is the next input variable ¬the tenth one in the rank for predicting TP content, with an influence nearly 70% of cyanobacteria influence in the prediction—it is another nutrient and it is usually together with phosphorus in waste water inputs. This predictor is also connected with the Chl-a concentration since it is a necessary nutrient for the growth of the phytoplankton, which contains chlorophyll. Excessive nitrate concentrations in reservoirs and lakes can cause accelerated eutrophication and loss of dissolved oxygen.

The last input variable in importance to forecast TP content in Tanes reservoir, and with much less influence, is Phosphates concentration. Obviously, there is a relationship between the amount of phosphates and the total phosphorus given that phosphates are a fraction of total phosphorus. However, the relationship is not so tight as with other variables as iron or the measured phytoplankton species.

On the whole, the SVR–RBF method is an accurate tool to predict the concentration of Chl-a and TP (output variables or eutrophication indicators), taking as input parameters that can be measured easily and frequently. Certainly, Figs. 9 and 10 compares the observed and predicted concentrations of Chl-a and TP using the SVR-RBF technique over the test dataset, respectively. In this method, it is important to optimize the hyperparameters of the SVR effectively and robustly. This function is performed by the metaheuristic optimizer WOA. Conclusively, the observed and predicted Chl-a and TP concentrations obtained with these models were correlated to a high degree.

Fig. 9
figure 9

Observed versus predicted Chl-a concentrations employing the WOA/SVR-RBF for model the testing dataset (\(R^{2} = 0.8582\))

Full size image
Fig. 10
figure 10

Observed versus predicted TP concentrations employing the WOA/SVR-RBF model for the testing dataset (\(R^{2} = 0.9750\))

Full size image

4 Conclusions

According to the earlier results, several key findings from this study can be deduced and reported as follows: (1) analytical (or Laplacian) models for predicting Chl-a and TP concentrations from experimental parameters do not give good enough results due to the nonlinear character of the problem and the required simplifications. Hence, the necessity of a machine learning method such as the WOA/SVR is the verification that Chl-a and TP concentrations can be calculated precisely using this hybrid approximation based on WOA/SVR. Indeed, coefficients of determination of values 0.8582 and 0.9750 were obtained for the concentrations of Chl-a and TP, respectively; (2) Moreover, the relative importance of the predictors in the models was established. This finding can be considered one of the main ones of this investigation. In particular, Chlorophytes concentration must be kept in mind as the most noteworthy input variable in the foretelling of Chl-a concentration. Similarly, Iron appears as the most important variable in the prediction of TP; (3) conclusively, the importance of the hyperparameters precise tuning in the SVR-based approximation concerning the regression performance accomplished for Chl-a and TP concentrations was determined. The calculation of the optimal hyperparameters requires solving an optimization problem with inequality constraints. Here we have used the WOA optimizer with success.

Moreover, further application to other aquatic environments with similar characteristics such as ponds in gardens or rivers in zones with low speed where the assessment of the eutrophic state is of first importance would be desirable. Also, more experimentation is needed to take advantage of this study, modifying the relevant parameters obtained in this study to improve the prediction of the eutrophic state. For instance, an additional future line of research will be to build other novel hybrid mathematical models to address new challenges.